Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2011 Jan 31;108(7):2825–2830. doi: 10.1073/pnas.1008895108

Role of social networks in shaping disease transmission during a community outbreak of 2009 H1N1 pandemic influenza

Simon Cauchemez a,1, Achuyt Bhattarai b, Tiffany L Marchbanks c, Ryan P Fagan b, Stephen Ostroff c, Neil M Ferguson a, David Swerdlow b; the Pennsylvania H1N1 working groupb,c, Samir V Sodha d,e, Mària E Moll f,g, Frederick J Angulo h,i, Rakhee Palekar j,k, W Roodly Archer l,m, Lyn Finelli n,o
PMCID: PMC3041067  PMID: 21282645

Abstract

Evaluating the impact of different social networks on the spread of respiratory diseases has been limited by a lack of detailed data on transmission outside the household setting as well as appropriate statistical methods. Here, from data collected during a H1N1 pandemic (pdm) influenza outbreak that started in an elementary school and spread in a semirural community in Pennsylvania, we quantify how transmission of influenza is affected by social networks. We set up a transmission model for which parameters are estimated from the data via Markov chain Monte Carlo sampling. Sitting next to a case or being the playmate of a case did not significantly increase the risk of infection; but the structuring of the school into classes and grades strongly affected spread. There was evidence that boys were more likely to transmit influenza to other boys than to girls (and vice versa), which mimicked the observed assortative mixing among playmates. We also investigated the presence of abnormally high transmission occurring on specific days of the outbreak. Late closure of the school (i.e., when 27% of students already had symptoms) had no significant impact on spread. School-aged individuals (6–18 y) facilitated the introduction and spread of influenza in households, but only about one in five cases aged >18 y was infected by a school-aged household member. This analysis shows the extent to which clearly defined social networks affect influenza transmission, revealing strong between-place interactions with back-and-forth waves of transmission between the school, the community, and the household.

Keywords: epidemiology, infectious diseases, Bayesian statistics, data augmentation, mathematical modelling

There is a large body of theoretical literature on how social networks and population structures may affect the spread of communicable diseases and hence influence the design of optimal control strategies (1–8). Such work often makes use of detailed data on populations (e.g., demographics in households, schools, and workplaces; mobility and land-use data; contact surveys; or time-use data) but then makes assumptions about how transmission rates change with the type of interaction (e.g., as a function of the setting and the spatial or social distance between individuals, etc.). Validating these assumptions can be challenging due to the scarcity of appropriate epidemiological data. Consider influenza, for example: Good data on household transmission (9–14) and to a certain extent on transmission at the population level are available, but only very limited data exist to characterize transmission in other places (such as schools) (15, 16). Meanwhile, the impact of social networks and risk factors on transmission has never been properly quantified. These uncertainties obviously affect our ability to assess the efficacy of interventions such as closure of school classes, grades, or entire schools.

Here, we analyze data from an H1N1 pandemic (H1N1pdm) influenza outbreak that started in an elementary school in April and May 2009 and spread in a semirural community in Pennsylvania to investigate how social networks and population structures affect influenza transmission.

Results and Discussion

Outbreak Investigation.

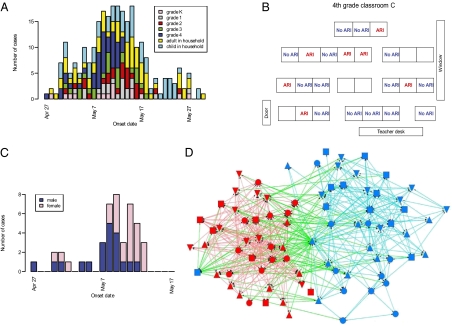
Fig. 1 presents the data that were collected during the outbreak investigation. Demographic and clinical information on 370 (81%) students from 295 (81%) households and their 899 household contacts was collected during two rounds of phone interviews (May 16–21 and May 26–June 2). One hundred twenty-nine (35%) students and 141 (16%) household contacts were reported to have had acute respiratory illness (ARI, defined as at least two symptoms among fever, cough, sore throat, and runny nose) from late April to their last interview (Fig. 1A). Because fourth graders appeared to be the most affected group at the time the school was investigated (54% reported ARI over the study period), a survey was dedicated to this subset of individuals: Information on seating charts (Fig. 1B), activities (Tables S1 and S2), and social networking (“Who are your playmates?”; Fig. 1D) was collected. Here, we set up a transmission model for which parameters are estimated from the data via Markov chain Monte Carlo sampling and data augmentation techniques (Materials and Methods and SI Materials and Methods).

Fig. 1.

Fig. 1.

Open in a new tab

Epidemiological data collected in the school. (A) Number of acute respiratory illness (ARI) cases by date of symptom onset for different types of individuals. (B–D) Survey of fourth graders with (B) seating charts and diagnosis for ARI in classroom C, (C) number of ARI cases by date of symptom onset and sex among fourth graders, and (D) social networking among fourth graders based on the question “Who are your playmates?” [color of the nodes, red, female; blue, male; color of the lines, red, girl–girl interaction; cyan, boy–boy interaction; green, boy–girl interaction (one symbol shape per class)]. The algorithm used to draw the network aims at (i) distributing nodes evenly, (ii) making edge length uniform, (iii) minimizing edge crossings, and (iv) keeping nodes from coming too close to edges (32, 33) (software: Netdraw). It does not use data on sex to position the nodes.

Transmission Characteristics in Different Settings.

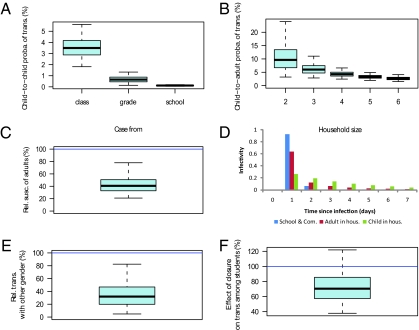
Fig. 2A shows that the structuring of the school in classes and grades had a strong impact on transmission rates. Child-to-child transmission probabilities were estimated to be 3.5% [95% credibility interval (CI): 1.8%, 5.6%] within a class. Transmission probabilities between students of the same grade but different class were about five times smaller than between classmates (Fig. 2A). Similarly, transmission probabilities between students from different grades were about five times smaller than those between students from the same grade. Fig. 2B shows that, in the household setting, the child-to-adult transmission probability decreased with household size, from 9.6% (95% CI: 3.2%, 24.0%) in households of size 2 to 2.6% (95% CI: 1.5%, 4.2%) in households of size 6 (9, 10; see also Fig. S1). Relative susceptibility of adults to infection was estimated to be about half that of children (41%; 95% CI, 21%, 78%; Fig. 2C) but adults were as infectious as children when infected (infectiousness of adults relative to children: 92%; 95% CI, 38%, 204%), in agreement with another study on H1N1pdm (10). The mean household generation time of 2.3 d (95% CI: 1.4, 3.6) for individuals >10 y old was also consistent with that of other studies (Fig. 2D) (10, 15, 17). With a mean of 3.7 d (95% CI: 2.3, 5.0), there was substantial evidence that children aged ≤10 had a longer household generation time than older individuals [Bayes factor (BF): 10.8; see SI Materials and Methods for information on Bayes factors]. Our analysis also suggests that the generation time in the school and the community, with an estimated mean of 1.1 d (95% CI: 1.0, 1.7), was substantially shorter than the household generation time (Fig. 2D; BF = 64 for the comparison with adult household generation time). This can be explained, for example, if sick (and infectious) children are likely to stay home shortly after symptom onset, meaning that exposure to sick individuals in the school context is likely to be truncated at an earlier time than would occur in the household.

Fig. 2.

Fig. 2.

Open in a new tab

Estimated transmission risk factors and generation times in places. (A) Transmission probability from an infected student to a classmate, to a student from the same grade but a different class, and to a student from a different grade during his/her infectious period. (B) Transmission probability in the household from an infected child to an adult of the household during his/her infectious period, as a function of household size. (C) Susceptibility of adults relative to children (≤10 y old), ρadult. (D) Generation time in the school/community, in the household for adults and children. (E) Transmission to children from the other sex relative to that to children from the same sex, ρsex. (F) Transmission between students during school closure relative to that during the rest of the outbreak, ρSC. Boxplots give percentiles 2.5%, 25%, 50%, 75%, and 97.5% of the posterior distribution. The mathematical definition of parameters is given in SI Materials and Methods.

Detecting Events of Abnormally High Transmission.

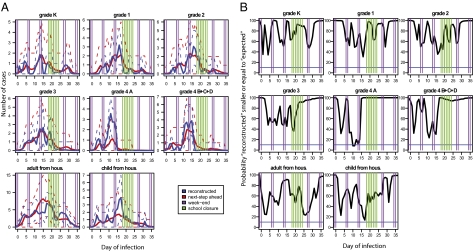
In an attempt to detect abnormal transmission events, we consider the model in which transmission rates do not change with time. For this model, we plot in Fig. 3A the predictive distribution of the number of infections (subsequently referred to as the “reconstructed” number of infections) per day for different groups of individuals along with the “next-step ahead” predictions giving for each day d the number of infections predicted by the model given what has happened up to day d − 1. In general, there is good agreement between the two distributions. However, the next-step ahead predictions tend to largely underestimate the reconstructed number of cases among students from fourth grade class A in the time period May 6 and 7 (respectively, day 10 and day 11 of the outbreak). This is the only group of individuals and the only 2 d for which transmission is found to be abnormally high; i.e., there is <10% posterior probability P that the next-step ahead prediction is strictly larger than the reconstructed number of infections (Fig. 3B). In an exploratory analysis described in SI Materials and Methods, different mechanisms that could have been responsible of this phenomenon are explored. This model comparison also suggests that abnormally high transmission took place on those days (BF: 28) (Table S3), although it is not conclusive concerning the mechanisms that may have been involved. Overall, this analysis suggests that abnormally high transmission may have taken place on May 6 and 7 although we cannot rule out the possibility that discrepancies between reconstructed numbers of infections and next-step ahead predictions were due to chance.

Fig. 3.

Fig. 3.

Open in a new tab

Detection of abnormal transmission events in the different groups of individuals. (A) “Reconstructed” numbers of infections per day for different groups of individuals (blue line) along with the “next-step ahead” predictions giving for each day t the number of infections predicted by the model given what has happened up to day t − 1 (red line). Dashed lines give the 95% CI. The different groups of individuals are students from grades K, 1, 2, and 3 and fourth graders from classroom A and from other classrooms (classrooms B, C, and D) and adult and child household contacts. (B) For each day and each group, the posterior probability that the reconstructed number of infections is smaller or equal to the “next-step ahead” predictions. The blue line gives the 10% limit below which adequacy is rejected. See Materials and Methods and SI Materials and Methods for details.

Sex-Related Mixing Patterns.

Fig. 1D shows that sex is an important determinant of social mixing between children of the same grade: Children were four times more likely to play with children of the same sex than with children of the opposite sex. We investigated whether this aspect of social networking affected transmission dynamics in the school. We considered the model where the transmission rate with the opposite sex was ρsex multiplied by the rate with children of the same sex. There was substantial evidence that the model ρsex < 1 accounting for the effect of sex-related mixing patterns on spread had a better fit than the model ρsex = 1 that did not account for such an effect (BF: 9.7). We estimated ρsex = 32% (95% CI: 5%, 82%) (Fig. 2E). This effect of sex on spread can be noted in the epidemic curve of fourth graders (Fig. 1C) where spread among boys (average time of onset: May 6, 8 PM) significantly preceded spread among girls (average time of onset: May 9, 12 AM) (P = 0.023).

Late Closure of the School.

The school closed May 14–20 (days 18 and 24 of the outbreak, respectively) because of the outbreak. Fig. 3 and Fig. S2 show no signal of reduced transmission among students during the closure. When we formally estimated the change in transmission rates between students during the closure relative to the rest of the outbreak, we did not detect a significant difference, although the point estimate suggested a 30% reduction (transmission rate after closure relative to that before: ρclosure = 70%; 95% CI, 38%, 122%) (Fig. 2F). This result was confirmed by the analysis of the school reproduction number, which was found to be similar on the week when the school closed (0.3; 95% CI, 0.1, 0.7) and on the following week (0.3; 95% CI, 0.0, 0.7) (Fig. 4C).

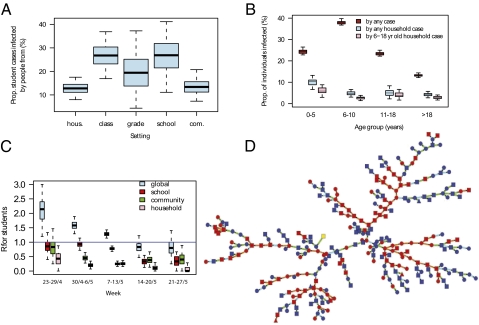
Fig. 4.

Fig. 4.

Open in a new tab

Reconstruction of the transmission tree. (A) Proportion of student cases infected by people from their household, class, grade, school, or from the community. (B) Proportion of individuals infected by any other case (red), by any household case (blue), or by a household case aged 6–18 y (pink), as a function of the age of the individual. (C) Weekly estimates of the effective reproduction number in the outbreak (“global” R) and in places (school, household, and community). (D) Reconstructed transmission tree drawn from its predictive distribution (color of the nodes, yellow, first case; red, student of the school; blue, household member of a student; color of the lines for the type of transmission, orange, among students of the school; light blue, among household members; green, in the community; shape of the nodes, circle, female; square, male; triangle, sex is missing). Boxplots give percentiles 2.5%, 25%, 50%, 75%, and 97.5% of the predictive distribution.

The lack of a statistically significant effect of school closure may be because the closure was implemented relatively late in the outbreak (27% of students already had had symptoms at the time the closure started). This result meant that few cases would have been expected to have occurred from the date of closure, limiting the maximum possible effect of closure on overall case numbers and reducing the statistical power to detect a difference. Our findings are consistent with modeling and epidemiological studies that show that for reactive closure to have a significant impact on spread, it is important that closure takes place early in the school outbreak (2, 3, 18, 19).

Transmission Trees and Place of Transmission.

To assess the contribution of the students to the general outbreak, we probabilistically reconstructed the full transmission tree (Fig. 4), drawing from the predictive distribution of 2,500 trees consistent with the data. Fig. 4A shows the proportion of students who got infected by people from different places. In this large school outbreak, we estimate that 74% (95% CI: 65%, 82%) of sick students were infected by other students (Fig. 4A). The fivefold reductions in person-to-person transmission rates between class/grade and grade/school (Fig. 2A) are balanced by similar increases in population size so that proportions of students infected in each of those settings are approximately equal (Fig. 4A).

Households that were interviewed do not constitute a representative sample of households in the community, because those that did not have a school-aged child in the school were not represented. Nonetheless, those households constitute an informative “sentinel group,” as they are arguably among households that were the most affected by the school outbreak. Impact of the school outbreak on this subset may therefore be expected to give an upper bound of impact on the general outbreak.

The relative risk that a case aged 0–5, 6–10, or 11–18 y old was the introducer of influenza in the household (i.e., the first case of the household) was 1.02 (95% CI: 0.85, 1.24), 1.84 (95% CI: 1.60, 2.12), and 1.20 (95% CI: 1.01,1.43), respectively (reference group: >18-y-old cases), indicating that school-aged individuals (6–18 y old) facilitated the introduction of influenza in households.

Children aged 6–10 y old had the highest infection rate (38%; 95% CI, 37%, 40%), followed by individuals 0–5 y old (24%; 95% CI, 23%, 26%), 11–18 y old (23%; 95% CI, 22%, 25%), and >18 y old (13%; 95% CI, 12%, 14%) (Fig. 4B). Conditional on infection, the probability of getting infected in the household was 41% (95% CI: 26%, 54%), 13% (95% CI: 8%, 17%), 21% (95% CI: 10%, 35%), and 32% (95% CI: 53%, 84%) for individuals 0–5, 6–10, 11–18, and >18 y old, respectively (Fig. 4B and Fig. S3). In the household context, school-aged individuals (6–18 y old) were the main source of transmission as they were responsible for 65% (95% CI: 55%, 75%) of household transmissions (Fig. 4B and Fig. S3). Overall, school-aged individuals were therefore important introducers and spreaders of influenza in the household; but transmission from outside the household was the predominant source of infection for all age groups and only about one in five cases aged >18 y old was infected by a school-aged household member. A substantial proportion of transmissions from outside the household may come from school-aged individuals that lived in other households; but it is not possible to reliably quantify it due to the way households were sampled.

Seating Charts and Playmate Networks.

Focusing on fourth graders for whom data on seating charts and playmate networks are available, the transmission trees are used to compare the proportion of between-classmate transmission that occurred between classroom neighbors (pY = 8%; 95% CI, 0%, 19%) with the proportion that would have been expected if sitting next to a case was not a risk factor of transmission (pX = 7%; 95% CI, 0%, 19%). The procedure, which is presented in SI Materials and Methods, controls for the effects of classroom, sex, and the depletion of susceptible individuals (Table S4). Sitting next to a case is therefore not found to significantly increase the risk of transmission.

Similarly, we find no significant difference between the proportion of between- fourth grader transmission that occurred between playmates (pY′ = 17%; 95% CI, 6%, 29%) and the proportion that would have been expected if being a playmate with a case was not a risk factor of transmission (pX′ = 19%; 95% CI, 6%, 34%). The mean number of playmates for cases (13.8) was not significantly different from the one for noncases (12.1) (P = 0.37).

Reproduction Number in Places.

Under the assumption that the outbreak in the school was a closed outbreak (i.e., students can be infected only by other students), transmission in the school would appear to be sustained, with a reproduction number among students on the first 2 wk of the outbreak that was significantly larger than (although close to) 1 (1.4, 95% CI, 1.2, 1.5 for an estimated school generation time of 1.5; 95% CI, 1.1, 2.1 d). However, analysis of the more detailed data accounting for household and community transmission reveals a more complex picture. The global reproduction number of students was 1.7 (95% CI: 1.4, 2.0) on the first 2 wk but decomposed as follows in the different places: 0.9 (95% CI: 0.7, 1.1) in schools, 0.5 (95% CI: 0.3, 0.7) in the community, and 0.2 (95% CI: 0.1, 0.4) in the household. With a reproduction number in the school ∼1 early on, the school outbreak needed repeated introductions from outside and/or abnormally high transmission events to be sustained. This result is confirmed in Fig. 4D, which shows a transmission tree drawn from the predictive distribution and where back-and-forth waves of transmission between the school, the community, and the households are visible. The global reproduction number for a “typical” case (i.e., averaged over cases of the dataset) was 1.3 (95% CI: 1.2, 1.4) in the first 2 wk and moved below 1 on the fourth week of the outbreak.

Sensitivity Analysis.

In a sensitivity analysis (SI Materials and Methods, and Tables S5–S9), we explored the robustness of our results to a set of modeling assumptions and prior specifications. Estimates appeared to be robust to most of them. The household generation time was sensitive to prior specification with a mean in the range 2.3–2.8 d for adults and 3.7–4.6 d for children; however, the difference between child and adult generation times (1.4–1.8 d) was relatively robust to the prior specification.

Limitations and Conclusion.

The study was subject to the following limitations. We used a syndromic definition to identify possible influenza cases and most cases were not laboratory confirmed. It is therefore likely that some cases were not infected by H1N1pdm (see sensitivity analysis in SI Materials and Methods, Fig. S4, and Table S9.). However, among the 36 cases with influenza-like illness (fever and cough or sore throat or both) that were tested, the proportion who were infected by H1N1pdm was high (72%) (20). Conversely, some individuals that did not meet the clinical definition were likely to have been infected (21). The survey data were self-reported and the main caregiver provided information for all of the household members. Interview with the school nurse, reviews of nurse logs, and absentee records indicated that the first clinical cases among students occurred around late April/early May. The surveys therefore focused on symptoms occurring from that period onward. Students with symptoms before this period would have been detected from the data gathered in the school; but it is possible that some very early cases among household contacts were missed. The sample of interviewed households was not a representative sample of the community (see above).

It is likely that a substantial proportion of transmission among students of the school took place in the school. However, in the eventuality where students also met and transmitted the virus to each other outside the school, we would not be able to estimate the proportion of student-to-student transmission taking place outside the school. We are indeed able to estimate only the global probability of transmission between students (i.e., either in or out of the school) (SI Materials and Methods). To estimate the proportion of student-to-student transmission taking place inside the school, one would, for example, need to have a good proxy for the proportion of effective contacts occurring between students in and out of the school.

Nonetheless, the data analyzed here provide relatively unique insights into how influenza is transmitted among students in a school, into the complex nature of influenza spread in structured populations (household/school/community), and, to a lesser extent, into the role of informal networks (e.g., boys mixing more with other boys than with girls). The relatively low estimates of the reproduction number (with estimates within each population structure that are smaller than or ∼1) mean that for an outbreak to be sustained in a place, multiple introductions and/or abnormally high-transmission events are to be expected. This outcome gives the picture of strong between-place interactions with back-and-forth waves of transmission between the school, the community, and the households. Structuring of the school into classes and grades had a strong impact on spread. School-aged individuals facilitated the introduction and spread of influenza in households, but most cases were not infected by school-aged household members. Such detailed outbreak investigations are critically needed to improve our understanding of disease spread in human populations. It is also important that the agent-based simulation models that are now commonly used to inform policy (1, 3) are properly calibrated on the basis of the type of analysis presented here.

Materials and Methods

Data Collection.

The outbreak investigation was performed by the teams from the Centers for Disease Control and Prevention (CDC) and the Pennsylvania Department of Health. During May 16–21, the team attempted to conduct a telephone interview with a parent or guardian in each student household. During May 26–June 2, all student households were contacted by phone except those that refused further participation in the investigation when they were contacted for the rapid questionnaire. For fourth graders, documents such as seating charts, school activity schedules, school calendars, bus schedules, nurse logs, and absentee records were collected and reviewed. During June 2 and 3, investigation team members administered questionnaires to fourth graders who had obtained permission to participate in the study.

The school has a population of 456 students from 364 households. Three hundred thirteen households (86.0%) completed at least one of the two surveys. Of those, 18 (5.8%) were excluded from the analysis because the age of at least 1 household contact was unknown. The analysis was therefore performed on data collected from 295 (81%) households with 370 students (81% of the students of the school) and 899 household contacts (i.e., any person residing in the respondent's household since May 1). A more detailed summary of the data that were collected and the way they were processed can be found in SI Materials and Methods. Children were defined as individuals aged ≤10 y.

Statistical Inference.

Assuming that individuals with ARI were infected with the influenza virus, we built a statistical model to estimate from the data how social networks (i.e., structuring of the school in classes and grades, structuring of the population in households, and sex-related mixing patterns) affected transmission dynamics.

Transmission model.

We build a transmission model for the force of infection exerted on individual i at time t,

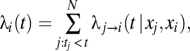graphic file with name pnas.1008895108uneq1.jpg

where 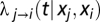Inline graphic is the instantaneous hazard of transmission from individual j to individual i at time t:

graphic file with name pnas.1008895108eq1.jpg

The first term of Eq. 1 characterizes the transmission rate between individuals j and i. The transmission rate is estimated for five types of pairs of individuals,

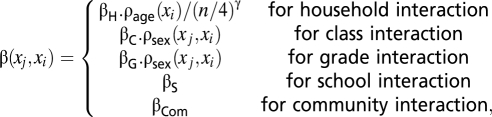graphic file with name pnas.1008895108uneq2.jpg

where n is the size of the household, ρage(xi) characterizes age-related susceptibility (children are the reference group), and ρsex(xj, xi) characterizes sex-related mixing patterns (reference group: transmission with children of the same sex).

The second term of Eq. 1 characterizes infectivity of the case over time. The model allows for different infectivity profiles in households (for adults and for children) and in the school/community and Weibull distributions are used to model infectivity profiles. The last term of Eq. 1 is used to investigate potential changes in transmission on specific days, such as days with abnormally high transmission and the impact of school closure. Details about the transmission model are given in SI Materials and Methods.

Estimation.

If the diagnosis, date of infection, and date of symptom onset were fully observed for each individual of the dataset, it would be relatively straightforward to perform likelihood-based inference (SI Materials and Methods). However, missing data make estimation of transmission parameters challenging: (i) Individuals who were not interviewed at the end of the outbreak (40%) may have been sick between their last interview and the end of the outbreak without being reported (truncated data); (ii) dates of infection were unobserved; and (iii) the clinical diagnosis was missing for 18 individuals (1.4%) and 7 cases had no documented date of symptom onset.

Here, we use a Bayesian data augmentation framework to tackle the missing data problem (9, 22–24). In the past, this approach has been successfully used to deal with similar problems (9, 25–29). The dataset is “augmented” with missing dates of infection, the few missing diagnoses, and the few missing/censored dates of symptom onset (i.e., the statistical model allows for the possibility that individuals may have been infected after their last interview and that those with missing diagnoses may have been infected too). If we schematically denote y the observed data, z the augmented data, and θ the parameter vector, the joint posterior distribution of augmented data and model parameters is proportional to

graphic file with name pnas.1008895108eq2.jpg

Eq. 2 shows the hierarchical structure of our Bayesian model. On the right-hand side of the equation, the first term, which is referred to as the “observation model,” ensures that the augmented data are consistent with observed data. In agreement with a range of studies on seasonal and H1N1pdm influenza (1, 15, 17, 30, 31), the observation model relies on the assumption that the incubation period of influenza has a mean of 1.5 d and a variance of 0.3 d2. The second term of Eq. 2 corresponds to the “transmission model,” which describes the latent transmission process and is characterized by Eq. 1. The last term of Eq. 2 gives the prior distribution of the parameters, which are detailed in SI Materials and Methods.

The joint posterior distribution of augmented data and parameters is explored via a reversible-jump (RJ) Markov chain Monte Carlo sampling (9, 22–24). We report the posterior median and equal-tailed 95% CI of the parameters. The statistical framework is detailed in SI Materials and Methods.

Acknowledgments

We thank Drs. Bob Kirkcaldy, Deborah Dowell, Alexandra Oster, and Christina Dorell at the Centers for Disease Control and Prevention for their inputs on data collection for social network analysis during field investigation. S.C. and N.M.F. thank the Medical Research Council, the Bill and Melinda Gates Foundation, the National Institute of General Medical Sciences Models of Infectious Disease Agent Study initiative, the European Union FP7 FluModCont project, and Research Councils United Kingdom for research funding. This study/report was supported in part by an appointment to the Applied Epidemiology Fellowship Program administered by the Council of State and Territorial Epidemiologists and funded by the Centers for Disease Control and Prevention Cooperative Agreement U60/CCU007277.

Footnotes

Conflict of interest statement: S.C. received consulting fees from Sanofi Pasteur MSD on a project on the modeling of the transmission of varicella zoster virus.

This article is a PNAS Direct Submission.

2Members of the Pennsylvania H1N1 working group are as follows: Samir V. Sodha, Mària E. Moll, Frederick J. Angulo, Rakhee Palekar, W. Roodly Archer, and Lyn Finelli.

This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1008895108/-/DCSupplemental.

Contributor Information

Samir V. Sodha, Centers for Disease Control and Prevention, Atlanta, GA 30333; and Pennsylvania Department of Health, Harrisburg, PA 17120-0701.

Mària E. Moll, Centers for Disease Control and Prevention, Atlanta, GA 30333; and Pennsylvania Department of Health, Harrisburg, PA 17120-0701.

Frederick J. Angulo, Centers for Disease Control and Prevention, Atlanta, GA 30333; and Pennsylvania Department of Health, Harrisburg, PA 17120-0701.

Rakhee Palekar, Centers for Disease Control and Prevention, Atlanta, GA 30333; and; Pennsylvania Department of Health, Harrisburg, PA 17120-0701.

W. Roodly Archer, Centers for Disease Control and Prevention, Atlanta, GA 30333; and; Pennsylvania Department of Health, Harrisburg, PA 17120-0701.

Lyn Finelli, Centers for Disease Control and Prevention, Atlanta, GA 30333; and; Pennsylvania Department of Health, Harrisburg, PA 17120-0701.

References

  • 1.Ferguson NM, et al. Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature. 2005;437:209–214. doi: 10.1038/nature04017. [DOI] [PubMed] [Google Scholar]
  • 2.Ferguson NM, et al. Strategies for mitigating an influenza pandemic. Nature. 2006;442:448–452. doi: 10.1038/nature04795. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Germann TC, Kadau K, Longini IM, Jr., Macken CA. Mitigation strategies for pandemic influenza in the United States. Proc Natl Acad Sci USA. 2006;103:5935–5940. doi: 10.1073/pnas.0601266103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Longini IM, Jr, et al. Containing pandemic influenza at the source. Science. 2005;309:1083–1087. doi: 10.1126/science.1115717. [DOI] [PubMed] [Google Scholar]
  • 5.Eubank S, et al. Modelling disease outbreaks in realistic urban social networks. Nature. 2004;429:180–184. doi: 10.1038/nature02541. [DOI] [PubMed] [Google Scholar]
  • 6.Riley S, Ferguson NM. Smallpox transmission and control: Spatial dynamics in Great Britain. Proc Natl Acad Sci USA. 2006;103:12637–12642. doi: 10.1073/pnas.0510873103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Meyers LA, Pourbohloul B, Newman MEJ, Skowronski DM, Brunham RC. Network theory and SARS: Predicting outbreak diversity. J Theor Biol. 2005;232:71–81. doi: 10.1016/j.jtbi.2004.07.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Newman MEJ. Spread of epidemic disease on networks. Phys Rev E Stat Nonlin Soft Matter Phys. 2002;66:016128. doi: 10.1103/PhysRevE.66.016128. [DOI] [PubMed] [Google Scholar]
  • 9.Cauchemez S, Carrat F, Viboud C, Valleron AJ, Boëlle PY. A Bayesian MCMC approach to study transmission of influenza: Application to household longitudinal data. Stat Med. 2004;23:3469–3487. doi: 10.1002/sim.1912. [DOI] [PubMed] [Google Scholar]
  • 10.Cauchemez S, et al. Household transmission of 2009 pandemic influenza A (H1N1) virus in the United States. N Engl J Med. 2009;361:2619–2627. doi: 10.1056/NEJMoa0905498. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Longini IM, Jr, Koopman JS. Household and community transmission parameters from final distributions of infections in households. Biometrics. 1982;38:115–126. [PubMed] [Google Scholar]
  • 12.Longini IM, Jr, Koopman JS, Haber M, Cotsonis GA. Statistical inference for infectious diseases. Risk-specific household and community transmission parameters. Am J Epidemiol. 1988;128:845–859. doi: 10.1093/oxfordjournals.aje.a115038. [DOI] [PubMed] [Google Scholar]
  • 13.Longini IM, Jr, Koopman JS, Monto AS, Fox JP. Estimating household and community transmission parameters for influenza. Am J Epidemiol. 1982;115:736–751. doi: 10.1093/oxfordjournals.aje.a113356. [DOI] [PubMed] [Google Scholar]
  • 14.Yang Y, Halloran ME, Longini IM., Jr A Bayesian model for evaluating influenza antiviral efficacy in household studies with asymptomatic infections. Biostatistics. 2009;10:390–403. doi: 10.1093/biostatistics/kxn045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Lessler J, et al. New York City Department of Health and Mental Hygiene Swine Influenza Investigation Team (2009) Outbreak of 2009 pandemic influenza A (H1N1) at a New York City school. N Engl J Med. 361:2628–2636. doi: 10.1056/NEJMoa0906089. [DOI] [PubMed] [Google Scholar]
  • 16.Calatayud L, et al. Pandemic (H1N1) 2009 virus outbreak in a school in London, April-May 2009: An observational study. Epidemiol Infect. 2010;138:183–191. doi: 10.1017/S0950268809991191. [DOI] [PubMed] [Google Scholar]
  • 17.Ghani AC, et al. The early transmission dynamics of H1N1pdm influenza in the United Kingdom. PLoS Curr. 2009;1:RRN1130. doi: 10.1371/currents.RRN1130. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Cauchemez S, et al. Closure of schools during an influenza pandemic. Lancet Infect Dis. 2009;9:473–481. doi: 10.1016/S1473-3099(09)70176-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Cowling BJ, et al. Effects of school closures, 2008 winter influenza season, Hong Kong. Emerg Infect Dis. 2008;14:1660–1662. doi: 10.3201/eid1410.080646. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Bhattarai A, et al. Viral shedding duration of pandemic influenza A H1N1 virus during an elementary school outbreak - Pennsylvania, May–June 2009. CID 52. 2011;(S1):S102–S108. doi: 10.1093/cid/ciq026. [DOI] [PubMed] [Google Scholar]
  • 21.Miller E, et al. Incidence of 2009 pandemic influenza A H1N1 infection in England: A cross-sectional serological study. Lancet. 2010;375:1100–1108. doi: 10.1016/S0140-6736(09)62126-7. [DOI] [PubMed] [Google Scholar]
  • 22.Cauchemez S, et al. Investigating heterogeneity in pneumococcal transmission: A Bayesian-MCMC approach applied to a follow-up of schools. J Am Stat Assoc. 2006;101:946–958. [Google Scholar]
  • 23.Gilks WR, Richardson S, Spiegelhalter DJ. Markov Chain Monte Carlo in Practice. London: Chapman & Hall; 1996. [Google Scholar]
  • 24.Green PJ. Reversible jump Markov chain Monte Carlo computation and Bayesian model determination. Biometrika. 1995;82:711–732. [Google Scholar]
  • 25.Cori A, Boëlle PY, Thomas G, Leung GM, Valleron AJ. Temporal variability and social heterogeneity in disease transmission: The case of SARS in Hong Kong. PLoS Comput Biol. 2009;5:e1000471. doi: 10.1371/journal.pcbi.1000471. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.O'Neill PD. A tutorial introduction to Bayesian inference for stochastic epidemic models using Markov chain Monte Carlo methods. Math Biosci. 2002;180:103–114. doi: 10.1016/s0025-5564(02)00109-8. [DOI] [PubMed] [Google Scholar]
  • 27.O'Neill PD, Balding DJ, Becker NG, Eerola M, Mollison D. Analyses of infectious disease data from household outbreaks by Markov chain Monte Carlo methods. J R Stat Soc C. 2000;49:517–542. [Google Scholar]
  • 28.O'Neill PD, Roberts GO. Bayesian inference for partially observed stochastic epidemics. J R Stat Soc Ser A Stat Soc. 1999;162:121–129. [Google Scholar]
  • 29.Walker PG, et al. A Bayesian approach to quantifying the effects of mass poultry vaccination upon the spatial and temporal dynamics of H5N1 in Northern Vietnam. PLoS Comput Biol. 2010;6:e1000683. doi: 10.1371/journal.pcbi.1000683. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Lessler J, et al. Incubation periods of acute respiratory viral infections: A systematic review. Lancet Infect Dis. 2009;9:291–300. doi: 10.1016/S1473-3099(09)70069-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Moser MR, et al. An outbreak of influenza aboard a commercial airliner. Am J Epidemiol. 1979;110:1–6. doi: 10.1093/oxfordjournals.aje.a112781. [DOI] [PubMed] [Google Scholar]
  • 32.Davidson R, Harel D. Drawing graphs nicely using simulated annealing. ACM Trans Graph. 1996;15:301–331. [Google Scholar]
  • 33.Kamada T, Kawai S. A general framework for visualizing abstract objects and relations. ACM Trans Graph. 1991;10:1–39. [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES