An Efficient Bayesian Method for Predicting Clinical Outcomes from Genome-Wide Data

Abstract

This paper compares the predictive performance and efficiency of several machine-learning methods when applied to a genome-wide dataset on Alzheimer’s disease that contains 312,318 SNP measurements on 1411 cases. In particular, a Bayesian algorithm is introduced and compared to several standard machine-learning methods. The results show that the Bayesian algorithm predicts outcomes comparably to the standard methods, and it requires less total training time. These results support the further development and evaluation of the Bayesian algorithm.

Introduction

Classification and prediction are key components of clinical care, including individual risk assessment, diagnosis, and prognosis. Improvements in classification and predictive performance have the potential to significantly improve patient outcomes and reduce healthcare costs.

Genome-wide patient-specific data are likely to become available to inform clinical care in the foreseeable future. In combination with traditional clinical data, genome-wide data have the potential to improve clinical classification and prediction over what is currently possible. However, the sheer magnitude of the number of variables in these data (in the hundreds of thousands to millions) presents formidable computational and modeling challenges. Beyond sheer numbers of variables, there is the possibility that some of the best predictive models may need to include numerous variables that interact in non-linear ways to influence the outcome being predicted. It is therefore important to explore efficient ways to learn highly predictive and potentially complex models from genome-wide data. This paper introduces and evaluates the predictive performance and computational efficiency of a new Bayesian method for predicting clinical outcomes

Background

This section provides background information about Bayesian networks, Alzheimer’s disease, and SNP gene chips, because this paper introduces a new Bayesian network learning algorithm that is applied to predict Alzheimer’s disease using genome-wide data that was obtained from SNP gene chips.

Measuring Single Nucleotide Polymorphisms

A single base mutation is the commonest genetic variation in the human genome. A single base mutation is called a single nucleotide polymorphism (SNP) when different sequence alternatives (alleles) exist in individuals in the population. The human genome is estimated to have about 10 million SNPs that constitute approximately 0.1% of the genome. With the development of gene chips that can measure half a million SNPs or more (e.g., the Affymetrix 500K GeneChip), it is now possible to obtain a snapshot of some of the most important information in the human genome.

The availability of gene-chip technology has led to a flurry of genome-wide association studies (GWAS). The most common goal of GWASs is to identify SNPs (and corresponding genes) that are associated with diseases. Fewer studies have investigated how well the genotype measurements of an individual predict outcomes of clinical interest about that individual, such as his or her risk of acquiring a disease. It is this latter application that is the focus of this paper.

Bayesian Networks

The Bayesian classification method that we introduce in this paper is based on learning a special class of Bayesian network (BN) models. A BN consists of a directed, acyclic graph and a probability distribution for each node in that graph given its immediate predecessors (parents) [1]. The density of the arcs in a BN is one measure of its complexity. Sparse BNs can represent simple probabilistic models (e.g., naive Bayes models and hidden Markov models), whereas dense BNs can capture highly complex models. Thus, BNs provide a flexible method for probabilistic modeling.

Researchers have developed numerous methods for learning BNs from data and prior knowledge [2]. Several research efforts have involved learning BNs from SNP data, as for example the research reported in [3] and in the references cited there. To our knowledge, however, BNs have not been learned from genome-wide data containing more than 300K SNPs in constructing a classifier to predict a clinical outcome, as we report in this paper. Indeed, such a task is challenging for any statistical or machine-learning method, and most approaches depend on first performing feature selection [4] before learning a model from among those features that are selected.

Alzheimer’s Disease

Late onset Alzheimer’s disease (LOAD) is the commonest form of dementia in the above 65-year-old age group and affects 50% of those over 85 years old [5]. It is a progressive neurodegenerative disease that affects memory, thinking, and behavior. The cause and progression of LOAD are not well understood, and the genetic mechanisms of the disease remain largely unexplained, although it appears to have high heritability. The only genetic risk factor for LOAD that has been consistently replicated involves the apolipoprotein E (APOE) gene. The ɛ4 APOE genotype increases the risk of development of LOAD, while the ɛ2 genotype is believed to have a protective effect. Several GWASs for LOAD have been conducted and in this paper we utilize the data from one such study [6].

Methods

This section describes the machine-learning algorithms that we evaluated, the Alzheimer’s disease SNP dataset that we used to evaluate them, and the methods we used to perform the evaluation.

Dataset

We obtained LOAD genome-wide data from a publically available download website at the Translational Genomics Research Institute (http://www.tgen.org/). These data were originally studied by [6]. The dataset consists of three cohorts containing a total of 1411 participants. Of the 1411 participants, 861 had LOAD and 550 did not, and 644 were APOE ɛ4 carriers (one or more copies of the ɛ4 genotype) and 767 were noncarriers. We used the binary LOAD variable as the target outcome to be predicted. The original study investigators used an Affymetrix chip to type 502,627 SNPs for each participant, from which 312,316 SNPs were analyzed after applying quality controls. The average rate of missing SNPs per individual in the LOAD dataset is about 1.5%. In the present paper, we used those 312,316 SNPs, plus two additional SNPs whose genotypes indicate the ɛ4 status of the APOE gene [6], namely, SNPs rs429358 and rs7412. Our goal was to accurately predict LOAD using these 312,318 SNPs as predictors.

Control Algorithms

As control algorithms, we included naive Bayes, logistic regression, and linear and non-linear support vector machines [7]. Naive Bayes (NB) is a probabilistic classifier that assumes the features (predictors) are independent given the target variable (e.g., LOAD status). The distribution of the features for each target value is learned from training data. Although features are often not independent, NB has been frequently shown to classify well. We implemented the NB algorithm in MATLAB (version R2009a) using Laplace smoothing. Every SNP feature can have one of 4 possible nominal states (genotypes), including a possible missing-value state; the specific genotype values can vary from SNP to SNP.

Logistic regression (LR) learns a posterior probability distribution for the outcome by fitting a logit function to the data. We applied the implementation of LR that is in the MATLAB statistics toolbox.

Support vector machines (SVMs) are binary classifiers that classify on the basis of a boundary in some feature space. The boundary is a function of a few samples (support vectors) of the training data. If the boundary is linear, the classifier is a linear SVM; otherwise, it is named according to the form of the function (kernel) used to map the original feature space to the training space. In this paper, we use a radial basis function (i.e., an RBF SVM). We applied an implementation of SVMs from the SVM-light repository [8]. The linear SVM requires only one penalty parameter to be specified. In addition, RBF SVM requires a parameter that specifies the spread of the kernel. These SVM parameters were set using standard heuristics.

For each of the above control algorithms, the process of predicting an outcome involved the following steps: data pre-processing, feature selection, model learning, and classification. Feature selection was necessary before training with the control algorithms, which computationally cannot handle the 312K+ variables in the LOAD dataset. We used the ReliefF algorithm to perform feature selection, because the algorithm has worked well when applied previously to genomic data [9]. ReliefF ranks a set of predictor variables in terms of how well they predict the target variable. By using a stratified nearest-neighbor-based search, it avoids assuming that the predictors are conditionally independent of each other.

The EBMC Algorithm

We have developed and implemented an efficient Bayesian multivariate classification algorithm, which is called EBMC. The algorithm searches over a particular class of Bayesian network (BN) models [1] to find a model that is highly probable given the training data and prior probabilities. EBMC emphasizes efficiency, while maintaining generality. Due to space limitations, we will describe EBMC using an illustrative example, which will convey the basic ideas of the general algorithm.

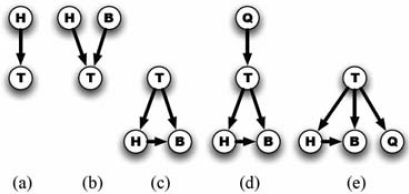
Figure 1 shows a simple example of EBMC searching over BN models. T denotes the target variable (e.g., LOAD) and the other nodes denote predictor variables (e.g., SNPs). All variables are assumed to be discrete or to have been discretized. Starting from an empty model, EBMC performs a greedy forward-stepping search to find the variable (node) that best predicts T, using a scoring measure that is described below. Figure 1a shows that H is found to be the single best predictor of T. Therefore, H is fixed henceforth as a predictor of T. EBMC next searches for an additional predictor that in conjunction with H best predicts T. Figure 1b shows it to be B.

Figure 1.

An example of EBMC models and EBMC search.

Suppose there is no additional predictor that in conjunction with H and B predicts T better than does H and B. EBMC then converts the BN in Figure 1b to the statistically equivalent BN in Figure 1c. These BNs are equivalent in the sense that they can represent the same distributions, and therefore, they receive the same scores. EBMC checks if removing one or more of the arcs in Figure 1c would improve the prediction of T; suppose it would not, and thus, all the arcs are retained.

The search now continues as before in seeking additional predictors (parents) of T, in light of H and B being children of T. Figure 1d shows that Q is the single predictor that best improves the prediction of T. Suppose there is no additional predictor that in conjunction with H, B, and Q predicts T better. Then the BN in Figure 1d is converted to the statistically equivalent BN in Figure 1e. Finally, suppose there is no additional predictor that when added as a parent of T improves on the score of the BN in Figure 1e. In that case, the search stops and the BN in Figure 1e is returned and used to predict the test cases. This BN allows both of the included rules to collaboratively influence T.

EBMC uses two types of BN models that have been previously investigated. The models in Figures 1a and 1b are effectively Bayesian rules [10] that predict a target. The BNs in Figures 1c and 1e are called augmented naive Bayes (ANB) networks [11], because they each augment a naive Bayes model with arcs among the child nodes; if enough arcs are included among the children, any distribution of the form P(T | children) can be represented. EBMC searches over hybrids of these two types of BN structures (rules and ANBs), one hybrid of which is shown in Figure 1d. It is always looking for an additional rule that can improve the prediction of the target in light of the predictor variables that are the children of the target. We note that EBMC can be viewed as a search strategy for locating a high-scoring Markov blanket BN of the target T. Markov blankets have been shown to yield highly effective probabilistic classifiers; Aliferis et al. [12] provide an excellent review and investigation of this topic.

A key advantage of EBMC’s hybrid search method is its efficiency. In particular, the time complexity of search is O(r·s²·m·n), where r is the total number of rules incorporated into the model (e.g., two in the example above), s is the maximum number of parents of target T in any model (e.g., two in the example), n is the total number of potential predictors, and m is the number of cases (records) in the training database. Often r and s will be quite small compared to m and n, and thus, the run time will be dominated by the size of the training dataset, which is m·n. Any algorithm that considers all the data will require time that is proportional to m·n or greater.

EBMC uses the supervised (prequential) scoring method described in [13] in conjunction with the BDeu scoring measure described in [14]. This scoring approach evaluates how well the predictor variables (both parents and children) predict the target, which is an appropriate focus when constructing a predictive model. The BDeu scoring measure has a prior equivalent sample size (pess) parameter that in essence controls how much smoothing occurs in estimating probability parameters; the higher is pess, the greater the smoothing that occurs. EBMC also has a parameter enp that controls the probability that any given variable should be included as a predictor of T. Briefly, we use a binomial distribution to represent this structure prior, and enp denotes the expected number of predictors of T. The larger we make enp, the more predictors that are likely to be included in the model M that is output by EBMC.

If a predictor variable had a missing value, we assigned it a special value (the value MISSING in EBMC and −1 in the control algorithms) and treated it as being a known value. Thus, we did not assume that data were necessarily missing at random.

Experimental Methods

We randomly partitioned the 1411 cases in the LOAD dataset into five approximately equal parts such that each part had a similar proportion of LOAD cases. We used these partitions to perform five-fold cross validation. For each machine-learning method, we trained a model on four partitions and tested on the remaining partition. We repeated this process for each possible test partition. In this way, we obtained a LOAD prediction for each of the 1411 cases. The results below are based on these 1411 predictions. This five-fold cross-validation process generated five models for each of the machine-learning methods. The results reported below about modeling characteristics of a method are based on the average over the five models produced by the method.

We provided each of the control algorithms with the n top-ranked SNP features that were produced by ReliefF, where n varied over selected values from 1 to 500; it seemed to us that these values would provide a plausible range over which a best model would be induced. The control algorithms and ReliefF were run on a MacPro (dual quad-core Intel Xeon 2.93 GHz processor) with 16 GB of RAM.

We ran EBMC with parameter settings in which pess = 1, 10, and 20, and enp = 1, 10, and 20, which seemed to be reasonable ranges for these parameters. EBMC was run on a PC with a 2.33 GHz Intel processor and 2 GB of RAM.

We evaluated predictive performance using the area under ROC curve (AUROC). For methods that output probabilities, we evaluated calibration using calibration plots. For each method, we recorded the time required for model construction on the training cases and for model inference on the test cases.

Results

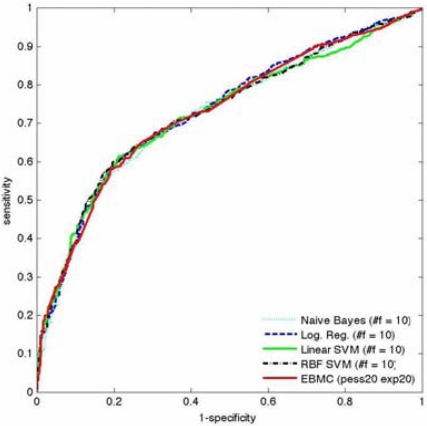
Table 1 shows that all the control algorithms and EBMC had a maximum AUROC of 0.72 or 0.73. A pairwise comparison of the difference in AUROCs between EBMC and each of the control algorithms was not statistically significant (p > 0.7; minimum 95% CI of −0.017 to 0.023). The control algorithms each had a maximum AUROC when using the top 10 variables output by ReliefF. EBMC had a maximum AUROC with pess = 20 and enp = 20, shown as “p20 e20” in Table 1. Figure 2 shows for each method the ROC curve with the highest AUROC. It is visually apparent that the methods perform quite similarly. The inflection point near 1-specificity = 0.2 is due to an APOE SNP that is a strong predictor of LOAD; the best EBMC and control models all contained this SNP as a predictor. The last row in Table 1 shows that the AUROC of EBMC was the most stable over the range of models constructed for each method.

Table 1.

Area under the ROC curve (AUROC) for models induced by the control and EBMC methods.

#features (#f)	Naive Bayes	Log. Reg.	Linear SVM	RBF SVM	EBMC Params.	EBMC
1	0.699	0.70	0.714	0.705	p10 e1	0.699
2	0.71	0.707	0.707	0.714	p10 e10	0.714
5	0.720	0.718	0.72	0.71	p10 e20	0.721
10	0.724	0.732	0.725	0.729	p1 e1	0.703
20	0.704	0.723	0.722	0.714	p1 e10	0.709
50	0.688	0.717	0.696	0.693	p1 e20	0.711
100	0.675	0.710	0.685	0.684	p20 e1	0.706
200	0.644	0.676	0.66	0.657	p20 e10	0.717
500	0.628	0.613	0.640	0.641	p20 e20	0.728
range:	0.096	0.119	0.065	0.088		0.029

Figure 2.

Shown here for each method is the ROC curve with the highest AUROC.

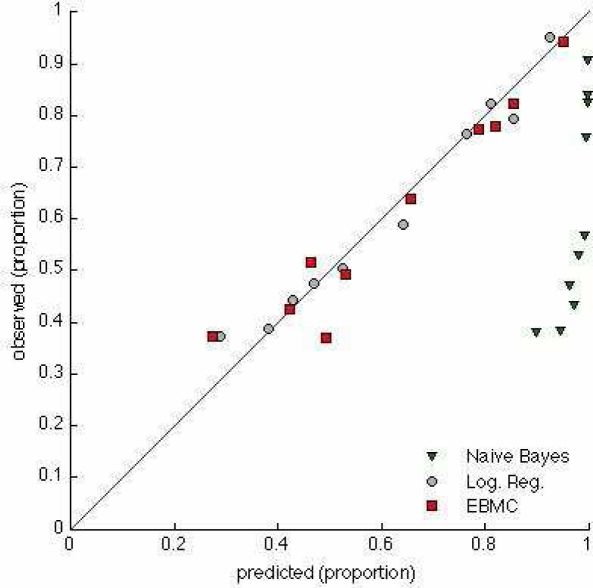
Figure 3 shows a calibration plot for the three models from Figure 2 that output posterior probabilities, namely, NB, LR, and EBMC. The calibration of LR and EBMC appear good, although LR has better calibration according to the Hosmer-Lemeshow (HL) statistic (0.25 for LR vs 0.04 for EMBC). For the other EBMC models listed in Table 1, the HL statistic ranged from 0.16 to 0.92. NB had poor calibration with a HL statistic below 0.00001, which is consistent with NB often being poorly calibrated.

Figure 3.

Calibration plots for NB, LR, and EBMC.

In terms of computation time, ReliefF required approximately 4400 seconds of CPU time. The best control models from Figure 2 were trained in less than one second on average, except RBF SVM, which required about 8 seconds. Thus, the total time to train the control models (feature selection plus model induction) was about 4400 seconds. EBMC required on average about 1700 seconds to find the best model, and it searched approximately 2.7M models to find it. EBMC’s best model on average contained about 5 predictors.

The time required to predict all 1411 tests cases was less than one second for all methods and models.

Discussion

The results show that EBMC performed statistically indistinguishably from the control algorithms in terms of AUROC and almost as well in terms of calibration. The predictive performance of all the models was strongly influenced by a single APOE SNP that is highly predictive of LOAD. EBMC was able to use high dimensional genome-wide data without needing a feature-selection preprocessing step. On average, EBMC was more than twice as fast in learning its best model as were the control algorithms, when feature-selection time is considered.

Limitations of this study include that only one genome-wide dataset was used, albeit an interesting one on an important disease. Also, although the control algorithms in the study were standard methods of comparison in performing machine learning evaluations, additional control methods can be applied in future evaluations. Similarly, it will be useful to apply additional feature-selection methods.

Now that EBMC has been shown to run in an acceptable amount of time and perform competitively with several standard machine-learning methods, directions for future research include (1) providing EBMC with informative priors based on knowledge from the literature and (2) performing inference using model averaging, both of which are natural extensions to make within a Bayesian framework. Also, we plan to investigate additional genome-wide datasets, as well as the prediction of clinical outcomes when using as predictors both traditional clinical variables and genome-wide variables.