Identifying Deviations from Usual Medical Care using a Statistical Approach

Abstract

Developing methods to detect deviations from usual medical care may be useful in the development of automated clinical alerting systems to alert clinicians to treatment choices that warrant additional consideration. We developed a method for identifying deviations in medication administration in the intensive care unit that is based on learning logistic regression models from past patient data that when applied to current patient data identifies statistically unusual treatment decisions. The models predicted a total of 53 deviations for 6 medications on a set of 3000 patient cases. A set of 12 predicted deviations and 12 non-deviations was evaluated by a group of intensive care physicians. Overall, the predicted deviations were assessed to often warrant an alert and to be clinically useful, and furthermore, the frequency with which such alerts would be raised is not likely to be disruptive in a clinical setting.

Introduction

The rising deployment of electronic medical records makes it feasible to construct statistical models of usual patient care in a given clinical setting. Such models of care can be used to determine if the management of a current patient case is unusual in some way. If so, an alert can be raised. While unusual management may be intended and justified, it sometimes may indicate suboptimal care that can be modified in time to help the patient. We are investigating the extent to which alerts of unusual patient management can be clinically helpful. This paper describes a laboratory-type (offline) study of alerting. In particular, it describes a study of alerts that were raised for ICU patients who were expected to receive particular medications but did not, according to statistical models that were constructed from past ICU patients.

Background

Characterization of deviations and their identification have been studied in several domains, such as identification of fraudulent credit card transactions, identification of network intrusions, and characterization of aberrations in medical data (1). In healthcare, rule-based expert systems are a commonly used computerized method for identifying deviations and errors. We propose that statistical methods can be a complementary approach to rule-based expert systems for identifying deviations (2). Rule-based methods excel when expected patterns of care are well established, considered important, and can be feasibly codified. Statistical methods have the potential to “fill in” many additional expected patterns of care that are not as well established, are complex to codify, or both.

Rule-based expert systems apply a knowledge base of rules to patient data. The advantage of rule-based systems is that they are based on established clinical knowledge, and thus, are likely to be clinically useful. In addition, such rules are relatively easy to automate and can be readily applied to patient data that are available in electronic form. Rule-based systems have been developed and deployed for medication decision support (e.g., automated dosing guidelines and identifying adverse drug interactions), monitoring of treatment protocols for infectious diseases, identification of clinically important events in the management of chronic conditions such as diabetes (3), as well as other tasks. However, hand-crafted rule-based systems have several disadvantages. The creation of rules requires input from human experts, which can be tedious and time consuming. In addition, rules typically have limited coverage of the large space of possible adverse events, particularly more complex adverse events.

We can apply statistical methods to identify anomalous patterns in patient data, such as laboratory tests or treatments that are statistically highly unusual with respect to past patients with the same or similar conditions. A deviation is also known as an outlier, an anomaly, an exception, or an aberration. The basis of such an approach is that (1) past patient records stored in electronic medical records reflect the local standard of clinical care, (2) events (e.g., a treatment decisions) that deviate from such standards can often be identified, and (3) such outliers represent events that are unusual or surprising as compared to previous comparable cases, and may indicate patient-management errors. This approach has several advantages. It does not require expert input to build a detection system, clinically valid and relevant deviations are derived empirically using a large set of prior patient cases, the system can be periodically and automatically re-trained, and alert coverage can be broad and deep.

In this study, we develop and evaluate a statistical method for identifying deviations from expected medications for patients in the intensive care unit. In particular, we (1) developed logistic regression models for usual medication administration patterns during the first day of stay in a medical intensive care unit (ICU), (2) applied these models to identify medication omissions that were deemed by the models to be statistical deviations, and (3) estimated the clinical validity and utility of these deviations based on the judgments of a panel of critical care physicians.

Methods

Data

The data we used comes from the HIgh-DENsity Intensive Care (HIDENIC) dataset that contains clinical data on patients admitted to the ICUs at the University of Pittsburgh Medical Center. For our study, we used the HIDENIC data from 12,000 sequential patient admissions that occurred between July 2000 and December 2001. We developed probabilistic models that predict which medications will be administered to an ICU patient within the first 24 hours of stay in the ICU, and used those models to identify deviations from expected medication administration.

For predictors, we selected five variables whose values were available for all patients in the data at the time of admission to the ICU. These included the admitting diagnosis of the patient, the age of the patient at admission, the gender of the patient, the particular ICU where the patient is staying, and the Acute Physiological and Chronic Health Evaluation (APACHE III) score of the patient at admission. The admitting diagnosis for a patient was coded by the ICU physician or nurse as one of the diagnoses listed in the Joint Commission on Accreditation of Healthcare Organization’s (JCAHO’s) Specifications Manual for National Hospital Quality Measures-ICU (4). The APACHE III score was generated by an outcome prediction model and has been widely used for assessing the severity of illness in acutely ill patients in ICUs; it is based on measurements of 17 physiological variables, age, and chronic health status. The APACHE III score has a range from 0 to 299 and correlates with the patient’s risk of mortality. Three of the variables we used are categorical variables, namely, admitting diagnosis, gender of the patient, and the particular ICU, and the remaining two, namely, age and APACHE III, are continuous variables.

While the data for the five predictor variables were originally captured in coded form in the hospital’s ICU medical record system, the administered medications were entered into the medical record as free text that resulted in variations in the medication names. We pre-processed the medication entries to correct misspellings and to expand abbreviated names. We then mapped each medication name to the standard generic medication name obtained from the Federal Food and Drug Administration (FDA) Approved Drug Products with Therapeutic Equivalence Evaluations 26th Edition Electronic Orange Book. This process resulted in a total of 307 unique medications. For each patient admission, a medication indicator vector was created that contained the value 1 if the medication was administered during the first 24 hours of stay and the value 0 if not.

Statistical Models

The dataset of 12,000 patient admissions was temporally split into three sets of 6,000 training cases (cases 1 to 6,000 in chronological order), 3,000 validation cases (cases 6,001 to 9,000), and 3,000 test cases (cases 9001 to 12,000). Medications that were administered fewer than 20 times in the training and validation cases were excluded from the study, due to a sample size too small to support reliable model construction. After filtering such rarely used medications that constituted approximately 2.5% of all medication entries, 152 medications were included in the study. We applied logistic regression to the 6,000 training cases to model the relationship between the five predictor variables and the medications administered within the first 24 hours of stay. For each of the 152 medications, we constructed a distinct logistic regression model using the implementation in the machine-learning software suite Weka version 3.5.6 (University of Waikato, New Zealand) (5).

We then used a set of validation cases to identify models that were deemed to be reliable. Each of the 152 logistic regression models was applied to the 3,000 validation cases to derive the probability that the medication defined by the model was administered, and these probabilities were used to measure discrimination and calibration of the model. Discrimination measures how well a model differentiates between patients who had the outcome of interest from those who did not. Calibration assesses how close a model’s estimated probabilities are to the actual frequencies of the outcome. We used the area under the Receiver Operating Characteristic (ROC) curve (AUROC) to measure discrimination, and the Hosmer-Lemeshow Statistic (HLS) to measure calibration (6). A high AUROC indicates good discrimination. For HLS, a low p-value implies that the model is poorly calibrated, and a large p-value suggests that either the model is well-calibrated or that data is insufficient to tell if it is poorly calibrated.

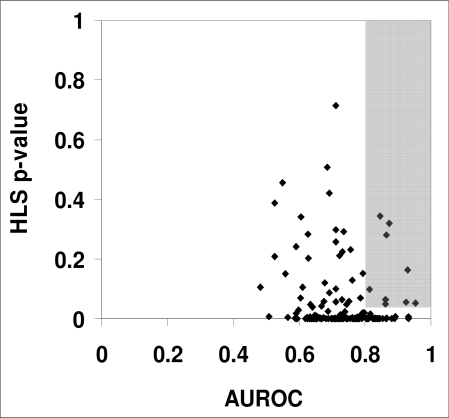
The AUROC and the HLS p-values were computed using the procedures “roctab” and “hl”, respectively, in the statistical program Intercooled Stata version 8.0 (Stata Corporation, College Station, TX). We identified those medication models as reliable that had AUROC ≥ 0.80 and HLS p-value ≥ 0.05 on the validation cases. There were nine such models (Figure 1).

Figure 1.

Plot of the HLS p-value and the AUROCs for the 152 medication-administration models, where each point represents a model predicting a specific medication. The shaded box shows the nine models with AUROC ≥ 0.80 and HLS p-value ≥ 0.05 that were selected for further evaluation.

Identification of Deviations

Each of the nine medication models was applied to an independent set of 3,000 test cases to predict the probability of the patient receiving that medication. A prediction was designated as a deviation if the predicted probability of the patient receiving the medication (in the first 24 hours of stay in the ICU) was at least 0.80, and the patient in reality did not receive the medication. We evaluated only deviations of medication omissions in the current study. For the identified deviations, other medications given to the patient were examined, and if the patient received a clinically equivalent medication then a deviation was not counted. For example, a purported deviation that oxycodone should be given was not considered to be a deviation if the patient was given hydrocodone, a clinically similar analgesic medication.

Results for Predicted Deviations

The nine logistic regression models that were identified as reliable predicted the administration of the following medications: bacitracin, phenytoin, lactulose, octreotide, nitroprusside, acetoaminophenoxycodone, dobutamine, nystatin, and free water. Free water is given enterally in situations of free water depletion that results, for example, from nasogastric suctioning and the use of osmotic diuretics.

The application of the nine medication models to the 3,000 test cases yielded 53 deviations (53/3,000 = 1.7%). Of the nine models, only six models identified one or more deviations in the 3,000 test cases and these are shown in Table 1. Let M denote these six models.

Table 1.

Number of deviations identified by each of the medication models. Of the nine models selected for study, six models identified deviations that were defined as a predicted probability of at least 0.80 that a patient should have received the medication and the patient did not.

Medication model	# deviations
acetaminophen-oxycodone	22
nitroprusside	13
lactulose	8
phenytoin	4
octreotide	4
nystatin	2
bacitracin	0
dobutamine	0
free water	0
total	53

Evaluation of Deviations

An anonymous paper-based questionnaire was administered to critical care physicians to assess the appropriateness and the clinical utility of the deviations identified by the models. Each case included a summary that contained a brief history of the patient, vital signs, a list of the current medications, and a list of relevant laboratory values. The evaluators were requested to respond to two questions on a five-point Likert scale. The first question assessed whether giving the missing medication was judged appropriate and the second question assessed what would be the clinical utility of receiving an alert that the medication has not been given.

The questionnaire included 24 cases that consisted of four cases for each of the six medication models M. For each set of four cases, two cases were selected such that the probability predicted by the relevant medication model was high (≥ 0.8); a third case had intermediate predicted probability (0.4 – 0.6); the fourth case had low predicted probability (≤ 0.2). Thus, for each medication, two of the cases for which the predicted probability was ≥ 0.8 were considered deviations from usual care (and were drawn from the 53 identified deviations) and the remaining two were not. The predicted probabilities and the deviation status were not revealed to the clinician evaluators. However, the evaluators were informed that some of the cases were identified as deviations by computer-based models and others were not.

Twenty-three physicians completed the questionnaires. For each of the six medication models, we computed the Spearman’s rank correlation coefficient between the model’s predicted probabilities and a given physician’s assessments for the four cases related to the relevant medication. We applied the t-test to the resulting 23 correlation coefficients (one for each physician) to test the null hypothesis that there is no correlation, that is a correlation of 0, between the predicted probabilities and a physician’s assessment. The mean correlation coefficients with the 95% confidence intervals and the two-tailed p-values are given in Table 2. For both appropriateness and utility, the mean correlation coefficients have a similar range, from the low 0.30s to the mid 0.80s, and for each medication model the two correlation coefficients agree closely with each other. All 12 mean correlation coefficients are statistically significantly different from 0 (no correlation) at the 0.05 significance level. Three models (octreotide, phenytoin, and nystatin) show moderate to high correlation for both appropriateness and utility, while the remaining three (lactulose, nitroprusside, and acetoaminophen-oxycodone) show less strong correlation.

Table 2.

Mean Spearman’s rank correlation coefficient for each of the six medication models that were evaluated. Each correlation coefficient was obtained from 23 evaluators who evaluated four cases for the indicated medication model. The 95% confidence intervals for the correlation coefficients are given in square brackets. The p-values shown in curved brackets were obtained from a two-tailed t-test of the null hypothesis that the correlation is 0.

Medication model	Mean correlation of appropriateness vs. predicted probability	Mean correlation of clinical utility vs. predicted probability
octreotide	0.81 [0.72 – 0.91] (<0.001)	0.84 [0.75 – 0.93] (<0.001)
phenytoin	0.63 [0.51 – 0.76] (<0.001)	0.61 [0.50 – 0.74] (<0.001)
nystatin	0.54 [0.43 – 0.66] (0.002)	0.63 [0.51 – 0.77] (<0.001)
lactulose	0.41 [0.19 – 0.68] (0.001)	0.43 [0.26 – 0.67] (0.002)
nitroprusside	0.33 [0.12 – 0.55] (0.005)	0.31 [0.10 – 0.54] (0.004)
acetoaminophen-oxycodone	0.31 [0.11 – 0.50] (0.003)	0.30 [0.10 – 0.49] (0.002)

We also derived several additional statistics from the study results. The mean number of deviations per patient per day provides an indication for how often the above alerting models would raise alerts. We estimated it to be about one alert per 57 patients (1.8%) per day. Based on the results from the questionnaire, we estimated that those alerts would be clinically heeded as much as 38% of the time. Thus, we estimated that as many as one out of every 150 ICU patients (1/57 × 0.38) may have clinical care that would change on the basis of the alerts that would be sent by the models we developed in this study.

Discussion

We propose that statistical methods can provide a complementary approach to knowledge-based rules in alerting clinicians about deviations from usual medical care. We developed a statistical method for identifying deviations in medication administration in the first 24 hours of ICU stay that was based on learning logistic regression models from past data for each medication of interest. We applied the medication models to an independent set of data to identify high probability deviations where a model predicted that the corresponding medication would be administered but in reality it was not. A set of high, moderate, and low probability deviations was assessed by a group of intensive care physicians for appropriateness and the clinical utility of the deviations. These results provide support that we can learn medication models from data that can be applied to generate high probability deviations that appear to be both appropriate and clinically useful. Furthermore, the frequency with which the deviations were generated by the models (one every 57 patients) is not likely to be disruptive in a clinical setting.

Such statistical methods in conjunction with rule-based methods can form the basis of computerized clinical decision support systems that automatically identify deviations in patient data and report them in real time. The method described here attempts to identify deviations with respect to a population of past patient cases, in contrast to the approach described in (7, 8) where deviations are identified with respect to patients who suffer from the same or similar conditions.

There are several limitations to our study. We chose to limit the number of variables to five and use a simple modeling method like logistic regression in this early study in order to make its execution and data analysis relatively clear-cut. It seems plausible that the inclusion of more variables combined with advanced modeling approaches such as Support Vector Machines and Bayesian networks in future studies will yield better performing models.

We used medication data that had a coarse time resolution of only 24 hours; this may partly explain why we did not find good models for predicting medications such as epinephrine, which are typically given in acute care life support settings. We also did not aggregate medications into classes which would have reduced the number of LR models to be considered. Another limitation is that the complete patient charts were not reviewed by the evaluators, but only abstracted case summaries.

Our study examined and evaluated deviations in which the models predicted a medication that should be administered, yet in reality it was not; these are thus deviations of omission. We did not evaluate the complementary type of deviation in which the models predicted a medication that should not be given, yet in reality it was; these are deviations of commission. Thus, if a model predicted a probability of a medication being given lower than a threshold for a particular patient case, then deviations would be flagged if the medication was actually given. We plan to evaluate these types of deviations as well in a future study.

Conclusions

This study provides support that identifying deviations from usual medical care using statistical models constructed from data of past care is a promising approach. Despite a limited set of predictor variables used to construct the medication models, the models that were selected identified deviations that were judged to be clinically appropriate and useful. In future clinical decision support systems, we believe it is likely that statistical detection of deviations will complement rule-based methods for identifying deviations and potential errors.