Parametric Survival Models for Predicting the Benefit of Adjuvant Chemoradiotherapy in Gallbladder Cancer

Abstract

The Cox proportional hazards model is the most commonly used survival model in oncology; however, this semi-parametric model may not be the most appropriate survival model when the proportionality assumption does not hold. In this study, we consider the use of several types of accelerated failure time parametric survival techniques for modeling the benefit of adjuvant chemoradiotherapy for gallbladder cancer. In comparing the Weibull, exponential, log-logistic, and log-normal models, we found that the log-normal had the most favorable Akaike Information Criterion, and additional analyses of this model indicated that our gallbladder cancer dataset exhibited a good fit with the log-normal cumulative hazard function. This log-normal survival model can be used to help predict which patients will benefit from adjuvant chemoradiotherapy.

Introduction

Oncologists must consider a large number of prognostic factors when making a recommendation on whether an individual cancer patient should receive adjuvant therapy. When possible, decisions for an individual patient are based on the results of randomized clinical trials, but for some rare cancers such as gallbladder cancer, large clinical trials have not been conducted, which leaves treatment recommendations unclear and sometimes controversial.¹ In these settings, the use of multivariate survival models built from large observational databases may be helpful in providing guidance when more rigorous data are not available. Furthermore, multivariate models may yield insight into how specific patient demographic, clinical, and pathological characteristics may influence outcomes.

The most commonly used multivariate survival model in oncology is the Cox proportional hazards (CPH) model.² Its popularity stems from its mathematical elegance, semi-parametric nature, and simple intuitive interpretation. In many clinical settings, however, its underlying premise of proportionality of hazards does not hold. There are a number of alternative parametric survival modeling methods that have been shown in some settings to be more appropriate than the CPH model.^3–8 For example, Chapman et al⁷ compared the performance of CPH and log-normal models for a series of node-negative breast cancer patients and found that estimates of disease-specific survival varied by almost 6%. Royston⁶ compared CPH and log-normal models and found that the estimates of prognosis of breast cancer patients could vary up to 1 year. Also, Tai et al⁸ compared the performance of 4 different types of survival models on a cohort of 244 limited stage small cell lung cancer patients and found that 3-year disease-specific survival estimates varied up to 12% depending upon whether a Cox model or a log-normal model was used.

The specific aim of this study was to evaluate the performance of several types of parametric accelerated failure time survival models for their fit for our gallbladder cancer dataset. The long-term goal is to select the best performing survival model for future implementation as an interactive online tool to provide individualized outcome estimates for different therapy options to assist clinicians with adjuvant treatment decisions.

Methods

The study cohort for this project was taken from the SEER-Medicare database, 2007 release.⁹ We used the most recent 10 years of Medicare data available (1995–2005) linked to patients diagnosed between 1995–2002. The analysis was limited to patients who had equal and continuous Medicare Part A & B coverage during the first four months after diagnosis. Initial cases were selected using Site Recode = 31 for gallbladder cancer. Patients were included if they at least underwent a surgical resection with curative intent. Patients with in situ or metastatic disease and those diagnosed with more than one primary cancer were not included. To account for post-operative mortality, patients who survived less than two months from surgery were also excluded. In addition, patients were excluded if the exact dates of diagnosis or death were not known.

Using the SEER Extent of Disease 10 fields (EOD 10) for Extent (e10ex1) and Nodes (e10nd1), we grouped patients according to AJCC 7th edition TNM staging.

Patients who received adjuvant external beam radiotherapy within the first 4 months of diagnosis (PEDSF rad1 codes 1, 4, 5, or 6) were coded has having received adjuvant RT. To determine which patients received chemotherapy, the linked Medicare Carrier Claims (NCH) and Outpatient (OUTSAF) files were used. Patients who who had a claims code for 5-FU (HCPCS J9190) within 4 months of diagnosis were coded as having received adjuvant chemotherapy. Patients who had >3 lymph nodes resected were coded as having had an extended lymphadenectomy.

All statistical analyses were performed using the “R” software package (http://www.r-project.org).

Covariates to be included in the models were selected based on known clinically prognostic factors and availability in the SEER database. Included covariates were age, sex, race (White, Black, Asian/Pacific Islander, Alaskan/American Indian), AJCC 7th edition TNM stage, extended lymphadenectomy (>3 nodes resected), and receipt of adjuvant chemoradiotherapy (CRT) (yes/no). All covariates were treated as discrete and converted to binary variables, except for age, which was modeled as a continuous variable and fitted to a smoothed restricted cubic spline function.¹⁰ Stage groupings with less than 11 cases for analysis were grouped with the closest neighboring group. Interaction terms were also included between CRT and certain other variables (stage and lymphadenectomy) to reflect their influence on the benefit of adjuvant CRT. All covariates were included in the final model with no variable selection performed, since it has been shown that inclusion of non-statistically significant variables can still improve the accuracy of a predictive model.¹⁰

The primary endpoint in this study was overall survival. Multivariate regression survival analysis was performed using several survival modeling methods and results were compared. We first built a CPH model and evaluated the proportional hazards assumption. We then built several accelerated failure time parametric models: Weibull, exponential, log-logistic, and log-normal. All survival models were constructed using the “rms” R library by Harrell (http://cran.r-project.org/web/packages/rms/). Performance between models was compared using the Akaike information criterion (AIC), a measure of the goodness of fit for statistical models.¹¹ The AIC is a measure of the goodness of fit of regression models that is based on the concept of entropy. It can be viewed as the amount of information lost when a model is used to describe a set of observations. The AIC includes a penalty for number of model parameters and thus represents the tradeoff between bias and variance. Lower AIC values indicate a better model fit. The formula for AIC is:

$$\text{AIC}\hspace{0.17em}=\hspace{0.17em}-2\hspace{0.17em}\text{log}\hspace{0.17em}L+2\text{k}$$

where log L is the log likelihood of the proposed model, and k is the number of model parameters.

Unlike the CPH model, parametric survival models assume a specific functional form for the hazard function of the underlying data. We evaluated the fit of these models by plotting the appropriate transformed cumulative hazard vs time.

Results

A total of 870 patients met the inclusion criteria and were included in the study. The baseline patient and tumor characteristics are shown in Table 1. Overall, 74% of the study population was female and 80% were white. Twenty-six percent of patients had T2 disease, and 39% had T3 disease. Eighteen percent had node-positive disease. A total of 52 patients (6%) in this series received adjuvant CRT after surgical resection.

Table 1.

Patient & Tumor Characteristics (N=870)

Median Age (range)	76	(46–98)
Female Sex (%)	646	(74%)
Race
White	697	(80%)
African-American	69	(8%)
Asian/Pacific Islander	90	(10%)
American Indian/Alaskan	11	(1%)
Other/Unknown	3	(0%)
TNM Stage
T1	253	(29%)
T2	227	(26%)
T3	335	(39%)
T4	55	(6%)
N0	516	(59%)
N1	136	(16%)
N2	16	(2%)
Lymphadenectomy (>3 nodes)	43	(5%)
Chemoradiotherapy	52	(6%)

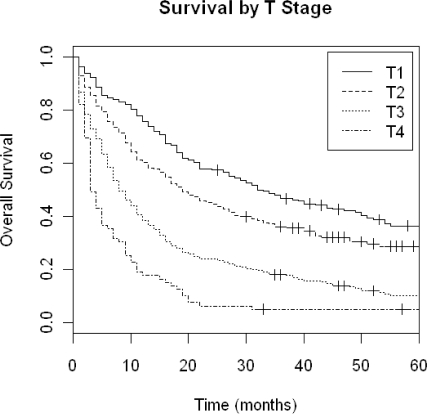
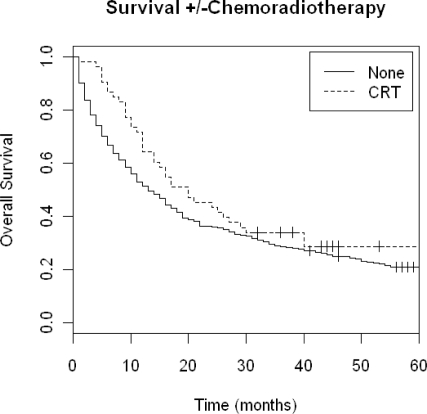
A Kaplan-Meier (KM) overall survival plot for all patients by T-stage is shown in Figure 1. The unadjusted median overall survival for all patients was 18 months. Figure 2 shows a KM plot of survival grouped by receipt of adjuvant CRT.

Figure 1.

Kaplan-Meier Overall Survival by T stage.

Figure 2.

Kaplan-Meier Overall Survival by receipt of adjuvant chemoradiotherapy.

For the first analysis, a CPH model was constructed, and a test of proportionality of hazards using Schoenfeld residuals showed that the proportionality assumption was not satisfied for several covariates, including sex and T stage. When this occurs, it means that the hazard ratios are not constant over time, which is an underlying premise for use of the CPH model.

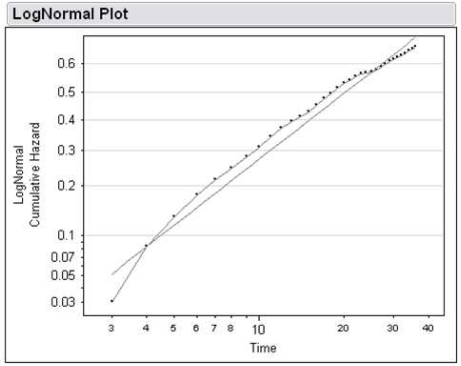
We then constructed 4 types of parametric survival models---Weibull, exponential, log-logistic, and log-normal---and compared their AIC (Table 2). The log-normal model had the lowest AIC, indicating a better overall fit than the other models. To determine if the functional form of the log-normal model fit the observed distribution of our dataset, we plotted Φ⁻¹ [1-S(t)] vs ln(t), where Φ⁻¹ is the inverse of the standard normal cumulative distribution function, S(t) is the Kaplan-Meier estimate of the survival, ln(t) is the natural logarithm of time. As can be seen in Figure 3, a straight line fit of the data on this plot indicates that a log-normal distribution function can appropriately model this data.

Table 2.

Comparison of survival models. The Akaike Information Criterion (AIC) is a measure of goodness of fit of the model. Lower AIC values indicate a better fit.

Model	AIC
Cox proportional hazards	5,037
Weibull	3,683
Exponential	3,700
Log-logistic	3,628
Log-normal	3,611

Figure 3.

Plot of the log-normal transformed cumulative hazard function vs log time.

Because the log-normal model had the lowest AIC score and demonstrated a good fit of the hazard distribution, this parametric model was selected as the best model.

Table 3 shows the beta coefficients for the log-normal survival model. The CRT interaction terms indicate how the influence of adjuvant CRT varies by stage and whether lymphadenectomy was performed.

Table 3.

Gamel Boag log-normal multivariate regression model parameters.

Covariate	Beta Coefficient	p-value
Intercept	5.7053	<0.001
age	−0.0276	0.018
age′	−0.0347	0.286
age″	0.2145	0.123
sex=male	0.0445	0.525
race=African-American	−0.3267	0.003
race=Asian/Pacific Islander	−0.0502	0.611
race=American Indian/Alaskan	−0.3163	0.305
T stage=T2	−0.4292	<0.001
T stage=T3	−0.8574	<0.001
T stage=T4	−1.4002	<0.001
N stage=N1	−0.2779	0.002
N stage=N2	−0.1842	0.469
lymphadenectomy	0.6584	<0.001
CRT	−1.0881	<0.001
T2 * CRT	1.8257	<0.001
T3 * CRT	1.2955	<0.001
T4 * CRT	1.1025	<0.001
N1 * CRT	0.6856	<0.001
N2 * CRT	−0.2175	0.633
lymphadenectomy * CRT	−1.7721	<0.001
Log(sigma)	−0.1581	<0.001

Abbreviations: CRT=chemoradiotherapy

Age was modeled using a restricted cubic spline function with 4 knots, requiring 3 independent coefficients: age, age′, age″.

Discussion

In this study, we found that a log-normal parametric survival model demonstrated the best performance in fitting our gallbladder dataset as evidenced by the lowest AIC score compared to other parametric models tested and also compared to the traditional CPH survival model.

The lognormal survival model is an accelerated failure time parametric survival model that has a long history of usage in cancer survival³ although it is not as popularly used as the semi-parametric CPH model.

Royston⁶ theorizes 2 reasons why the CPH model has become widespread in use despite the availability of other survival models. One reason is the convenience and robustness of not needing to specify an underlying baseline survival distribution. The second reason may be simply due to the timing of the publication of the seminal Cox paper² in 1972 around the same time that computing software became widely available to easily implement this semi-parametric model.

In many settings where the proportionality assumption does not hold, however, the lognormal model has been shown to be a more appropriate survival model, such as for breast cancer^4,5,7 and for lung cancer.⁸ Gamel and McLean¹² developed an extension to the original Boag model that allows prognostic covariates to be incorporated into the lognormal model. In this lognormal survival model, the log of the survival time has a normal distribution and is a linear function of covariates. In this setting, the hazard function is not constant over time, but rather rises quickly to a peak and then declines over time. We have previously demonstrated that this lognormal model performs well in modeling extrahepatic cholangiocarcinoma,¹³ thus it appears consistent that in the current study we found that a lognormal model also showed the best fit for this closely related hepatobiliary cancer.

In the log-normal model, unlike the CPH, positive values for a beta coefficient depict better survival, and negative values depict worse survival. This can be seen by examining the functional form of the Gamel-Boag¹² log-normal survival model with covariates:

$$S_f(t_j|x_j)=1-{\int }_0^{t_j}\frac{1}{s\sigma \sqrt{(2\pi )}}{e}^{-\frac{1}{2{\sigma }^2}{(\mathit{\text{lns}}-{x^{\prime }}_j\beta )}^2}\mathit{\text{ds}}$$

Several insights can be gained from inspection of the log-normal beta coefficients in Table 3. For example, the negative beta coefficient (−0.3267) for African-American race indicates that these patients are observed to have a worse prognosis compared to Whites. As one would expect, increasing T stage shows increasingly negative beta coefficients, which indicates worse survival compared to T1 patients. Having an extended lymphadenectomy is associated with markedly improved survival (beta = +0.6584). While the negative beta for CRT may seem to imply a worse prognosis for patients who receive adjuvant CRT, it is important to note that the CRT interaction terms must also be added in to yield the overall influence of CRT. Specifically, CRT is associated with a worse prognosis for T1 or N0-1 patients, but is associated with an improved prognosis for patients with T2 or greater stage disease. Interestingly, while patients who have undergone an extended lymphadenectomy have better survival than those who do not, our model predicts that these patients do not appear to obtain further benefit from adjuvant CRT.

There are several limitations to this study. This study was performed using SEER-Medicare data, and was therefore limited to predictive factors available in this database. SEER does not have information on margin status or performance status so these potentially important prognostic factors could not be included in this model.

We used the AIC to evaluate model performance, as this is one of the most widely used metrics. However, other criteria can be used, such as the Bayesian Information Criterion,¹⁴ which imposes a steeper penalty for model complexity. There is ongoing debate as to the merits and tradeoffs between these metrics.¹⁵ Future work will entail the use of alternate metrics to determine if they yield similar results.

While prediction models can never substitute for evidence from large prospective randomized clinical trials, these models can lend insight into potentially important prognostic factors, particularly in settings of rare tumors where no clinical trial data are available and where the optimal adjuvant therapeutic management is controversial. The use of multivariate survival models are becoming increasingly important, enabling a “personalized medicine” approach to allow for individualized recommendations for a particular patient. The long-term goal of this project is to create interactive online tools from these types of survival models in order to assist clinicians in making treatment decisions for patients by comparing outcomes between different therapeutic options for an individual patient. The next step in this project will be to incorporate this log-normal survival model into a browser-based online calculator that can be used by clinicians and patients to make individualized estimates of prognosis.

Conclusion

In conclusion, we have demonstrated that parametric survival models can be used to model outcomes for resected gallbladder cancer, and for our dataset the log-normal model demonstrated the best performance compared to other parametric models.