Mining Clinical Data using Minimal Predictive Rules

Abstract

Modern hospitals and health-care institutes collect huge amounts of clinical data. Those who deal with such data know that there is a widening gap between data collection and data comprehension. Thus, it is very important to develop data mining techniques capable of automatically extracting useful knowledge to support clinical decision-making in various diagnostic and patient-management tasks. In this paper, we develop a new framework for rule mining based on minimal predictive rules (MPR). Our goal is to minimize the number of rules in order to reduce the information overhead, while preserving and concisely describing the important underlying patterns. We develop an algorithm to efficiently mine these MPRs and apply it to predict Heparin Platelet Factor 4 antibody (HPF4) test orders from electronic health records.

Introduction

The increasing availability of medical data in modern hospitals and health-care institutions prompts the development of appropriate data mining techniques to extract relevant information and patterns from this wealth of data. An important aspect of a successful medical data mining method is its ability to interact with medical experts in a human-friendly way by presenting the discovered knowledge in a concise and easy to understand form.

Rule induction methods represent a very important class of knowledge discovery tools. The advantage of these methods is that they represent the knowledge in terms of if-then rules that are easy to interpret by humans. This facilitates the process of discovery and utilization of new practical findings. As an example, assume a rule mining algorithm identifies a subpopulation of patients that respond better to a certain treatment than the rest of the patients. If the rule clearly and concisely defines this subpopulation, it can speed up the validation process of this finding (through subsequent clinical trials) and its future utilization in patient-management.

Association rule mining¹ is a popular data mining technique to extract rules from the data. Association rules gained a lot of popularity in the medical data mining research^2,3,4,5. The key strength of association rule mining is that it searches the space of rules completely by examining all patterns that occur frequently in the data. Its disadvantage is that the number of association rules it finds is often very large. Moreover, many rules are redundant because they can be explained by other rules. This may hinder the discovery process and the interpretability of the results. The objective of this work is to filter out these redundant rules and provide the user with a small set of rules that are sufficient to capture the essential underlying patterns in the data.

To achieve our goal, we first introduce the concept of the minimal predictive rules (MPR) set that assures a good coverage of all important patterns with a small number of rules. After that, we describe an algorithm for mining such rules. Briefly, the algorithm builds the MPR set by examining more general rules first and gradually testing and adding more specific rules to the set. The algorithm relies on a statistical significance test to ensure that every rule in the result is significantly better predictor than any of its generalizations. Finally, we present a more efficient version of the algorithm that mines a subset of the MPR set and can scale much better to larger datasets.

We test our methods by analyzing data patterns for predicting orders of the Heparin Platelet Factor 4 antibody (HPF4) test from electronic health records. This test is prescribed when the patient is at risk of Heparin induced thrombocytopenia (HIT)⁶. We show the advantage of our framework by returning a smaller and more concise rule set than the other existing methods.

Methodology

In this section, we first define basic terminology used throughout the paper. Then we present an example illustrating the challenges of rule mining. Next, we propose the minimal predictive rules (MPR) concept. Finally, we present an algorithm for mining the MPR set and a very efficient algorithm for mining a more restricted version of MPR.

I. Definitions

Rule induction methods assume that the attributes take a discrete set of values. Hence, when the data contain numeric attributes, these attributes should first be discretized⁷. We call an attribute value pair an item and a conjunction of items a pattern. A rule is defined as R: A ⇒c, where A is a pattern and c is the class label that R predicts. We say that pattern P′ is a subpattern of pattern P if P′ ⊂ P (P is a superpattern of P′). We say that rule R′: A′⇒c′ is a subrule of rule R: A⇒c if c′=c and A′⊂ A.

A pattern P can be viewed as defining a subpopulation of the instances (e.g. patients) that satisfy P. Hence, we sometimes refer to pattern P as group P. If P′ is a subpattern of P, then P′ is a supergroup of P (group P′ contains group P).

The support of pattern P, denoted as sup(P), is the ratio of the number of records that contain P to the total number of records: sup(P) ≈ Pr(P). The confidence of rule R: A ⇒ c is the posterior probability of class c in group A: conf(R) ≈ Pr(c|A). Note that confidence of the empty rule is the prior probability: conf (φ ⇒ c) ≈ Pr(c).

II. Example

Assume our objective is to identify subpopulations of patients that are at high risk of developing coronary heart disease (CHD). Assume our dataset contains 200 instances and that CHD prior is Pr(CHD)=30%. We want to evaluate the following 3 rules:

• R1: Family history=yes ⇒ CHD

  [sup=50%, conf=60%]

• R2: Family history=yes ∧ Race=Caucasian ⇒ CHD

  [sup=20%, conf=55%]

• R3: Family history=yes ∧ Race=Black ⇒ CHD

  [sup=20%, conf=65%]

We can see that a positive family history is probably an important risk factor for CHD because the confidence of R1 (60%) is two times higher than CHD prior (30%). However, we expect many rules that contain a positive family history in their antecedents to have a high confidence as well. So how can we know which of these rules are truly important for describing the CHD condition?

The original association rules framework¹ outputs all frequent rules that have a higher confidence than a minimum confidence threshold (min_conf). For instance, if we set min_conf=50%, all three rules will be returned to the user.

In order to filter out some of the uninteresting associations, the original support-confidence framework is sometimes augmented with a correlation measure. Commonly, a χ² test is used to assure that there is a significant positive correlation between the condition of the rule and its consequent⁹. However, because the posteriors of all three rules are much higher than the prior, we expect all of them to be statistically significant! Moreover, these rules will be considered interesting using most existing interestingness measures⁸.

The main problem with this approach is that it evaluates each rule individually without considering the relations between the rules. For example, if we are given rule R2 by itself, we may think it is an important rule. However, by looking at all three rules, we see that R2 should not be reported because it is more specific than R1 (applies to a smaller population) and has a lower confidence. Even rule R3 may not be important and its observed improvement in the confidence over R1 can be due to chance rather than actual causality. So should we report rule R3? To answer this question, we define the minimal predictive rules concept.

III. Minimal Predictive Rules (MPR)

Definition: A rule R: A ⇒ c is a minimal predictive rule (MPR) if and only if R predicts class c significantly better than all its subrules.

This definition implies that every item in the condition (A) is an important contributor to the predictive ability of the rule. We call these rules minimal because removing any non-empty combination of items from the condition would cause a significant drop in the predictability of the rule.

The MPR significance test:

In order to check if a rule is significant with respect to its subrules, we use the binomial distribution as follows: Assume we are interested in testing the significance of rule R: A ⇒ c. Assume that group A contains N instances, out of which N_c instances belong to class c. Assume P_c represents the highest confidence achieved by any subrule of R: P_c = max_{A′ ⊂ A} Pr(c|A^′). The null hypothesis presumes that N_c is generated from N according to the binomial distribution with probability P_c. The alternative hypothesis presumes that the true underlying probability that generated N_c is significantly higher than P_c. Hence, we perform a one sided significance test and calculate a p-value:

$$p={\mathit{\text{Pr}}}_{\mathit{\text{binomial}}}\hspace{0.17em}(x\ge N_c|N,P_c)$$

If this p-value is significant (smaller than a significance level α), we conclude that R significantly improves the predictability of c over all its simplifications, and hence R is an MPR.

Example: Going back to our CHD example, rule R3 covers 40 instances, out of which 26 have CHD. For R3 to be an MPR, it should be significantly more predictive than all its simplifications, including rule R1. By applying the MPR significance test we get: Pr_binomial (x ≥ 26|40, 0.6) = 0.317. This rule is not an MPR at significance level α = 0.05. On the other hand, if we evaluate each rule individually against the CHD prior (by always setting P_c = Pr(CHD)), the p-values we get for R1, R2 and R3 are respectively: 5.13e-10, 8.54e-4 and 5.10e-6, meaning that all three rules are (very) significant!.

IV. The Mining Algorithm

The algorithm takes as input a dataset (D) and a minimum support threshold (min_sup). It outputs all MPRs in D that have a support higher than min_sup.

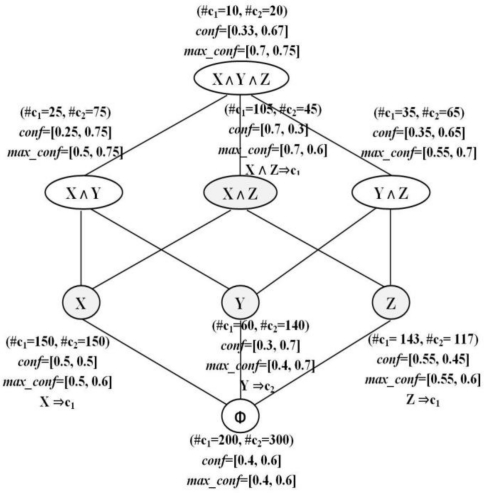
Our algorithm is gracefully incorporated in the Apriori algorithm¹ and explores the space by performing a level-wise search. The progress of the algorithm can be seen as building a lattice structure level by level starting with the empty pattern φ (see Figure 1 for an example). For each generated pattern P (a node in the lattice), the algorithm checks if P forms an MPR. However, the MPR definition requires examining all of P’s subpatterns, which is very inefficient (a pattern with l items contains 2^l subpatterns). We avoid this inefficiency by cashing at each pattern P the maximum confidence score for every class that can be obtained in the sublattice with top P (including P itself):

$$\text{max}\_{\mathit{\text{conf}}}_P[\text{c}]\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}{\text{max}}_{{\text{P}}^{\prime }\hspace{0.17em}\subseteq \hspace{0.17em}\text{P}}\{\text{Pr}(\text{c}|P^{\prime })\}.$$

Figure 1:

An illustrative example showing the lattice associated with pattern X∧Y∧Z.

These max_conf values are computed from the bottom up as algorithm progresses. Now, in order to perform the MPR test for pattern P, we need only to access the max_conf values of P’s direct children, as opposed to accessing all of P’s descendents.

Figure 1 illustrates the algorithm using a small lattice on a dataset that contains 200 instances from class c₁ and 300 instances from class c₂. For example, c₁ can represent the cases (patients with a specific condition) and c₂ can represent the controls. X, Y and Z represent different items (attribute-value pairs). For each pattern P (node), we show the number of instances in group P in each class, the distribution of the classes (conf) and the maximum confidence achieved by any node of P’s sublattice (max_conf). Let us look for example at pattern X ∧ Z. This pattern is predictive of class c₁ because Pr(c₁| X ∧ Z)=0.7 > Pr(c₁)=0.4. The best predictive subrule of rule X ∧ Z⇒c₁ is Z⇒c₁ with confidence 0.55. By applying the MPR test: Pr_binomial (x ≥ 105|150, 0.55) = 0.00012, we conclude that X ∧ Z ⇒ c₁ is an MPR. The MPRs from this example are: X⇒c₁, Y⇒c₂, Z ⇒c₁ and X ∧ Z ⇒ c_1.

V. Efficient Mining using RMPR

The mining algorithm presented above relies on the Apriori algorithm to mine the MPR set. It is known that the efficiency of Apriori heavily depends on the min_sup parameter: The higher the min_sup, the faster the algorithm runs. However, most datasets we encounter in the medical domain are highly unbalanced with a very small number of cases compared to the number of controls. Therefore, in order to capture the important patterns in the cases, we have to set a low value to min_sup, which makes the mining algorithm very slow. In order to scale up our algorithm, we propose a stricter definition of MPR, which we call recursive minimal predictive rules (RMPR).

Definition: A rule R is a recursive minimal predictive rule (RMPR) if R is MPR and all its subrules, excluding the empty rule, are MPRs.

For example, rule X ∧ Z ⇒ c₁ in Figure 1 is RMPR because it is an MPR and both of its subrules X⇒c₁ and Z⇒c₁ are MPRs. Note that the RMPR set is always contained in the MPR set.

The RMPR definition allows us to perform a very aggressive pruning on the search space as follows: if pattern P does not produce an MPR, it can be pruned since all of its superpatterns are guaranteed not to produce RMPRs. For example, since patterns X ∧ Y in Figure 1 is not an MPR, it is pruned and we do not have to generate and test pattern X ∧ Y ∧ Z.

Experimental Evaluation

In this section, we test and present results of our approach on clinical data by predicting the orders of the Heparin Platelet Factor 4 antibody (HPF4) test. This test is important for detecting and confirming Heparin-induced thrombocytopenia (HIT)⁶. HIT is a pro-thrombotic disorder induced by Heparin exposure with subsequent thrombocytopenia and associated thrombosis. HIT is a life-threatening condition if it is not detected and managed properly.

Our objective is to automatically learn from the data when an HPF4 test should be ordered for a patient on Heparin. In other words, given a specific point in time (we call the anchor point) for a specific patient, we want to detect whether this patient starts to exhibit the HIT symptoms, which requires an order of HPF4.

Dataset:

We use a database of 4,281 records of post cardiac surgical patients treated at one of the University of Pittsburgh Medical Center (UPMC) hospitals. In this database, we have 220 patients for which the HPF4 test was ordered. We set the anchor point for these patients to the time HPF4 was ordered. The other 4,061 patients are also treated by Heparin, but did not have an HPF4 test. We set their anchor points randomly by the arrival of a new platelet result, a key feature used in HIT detection⁶.

Features:

For each patient, we consider the following 6 lab tests: platelet counts (PLT), activated partial thromboplastin time (APTT), prothrombin time (PT), hemoglobin (Hgb), red blood cell count (RBC), and white blood cell count (WBC).

For a specific patient, each of these labs is a represented by time series starting from the patient hospitalization up to the anchor point. We preprocess the data using temporal abstractions¹⁰ to obtain a qualitative description of these series. We use two types of abstractions:

• Trend abstractions: represent the lab series in terms of its local trends and can take one of the values: {decreasing (D), steady (S), increasing (I)}.

• Value abstractions: can take one of the values: {low (L), normal (N), high (H)}, depending on whether the result is below, within, or above the normal range.

The most recent lab values are usually the most important for predicting the patient’s state at a specific time¹¹. Therefore, we use the most recent trend and the most recent abstract value of each of the 6 labs to be our data features. In addition to these 12 features, we use an indicator feature that is set to one if Heparin was administered to the patient in the last 24 hours. Hence, the number of different items (attribute-value) to consider is 12*3+2=38 items.

Experiment settings:

In our experiments, we compare the performance of MPR and RMPR with the following rule induction methods:

• complete: The set of all association rules (all frequent patterns).

• corr_chi: A subset of complete that contains rules with significant positive correlations between the condition and conclusion according to the χ² test⁹.

• corr_chi_FDR: A subset of corr_chi that is post-processed using the false discovery rate (FDR)¹² technique, which is used to reduce the number of false positives in multiple hypothesis testing.

For the methods that use a statistical test: corr_chi, corr_chi_FDR, MPR and RMPR, we set the significance level to the conventional α= 0.05. For all methods, we set the min_sup threshold to 5% the number of instances in the dataset.

In order to objectively evaluate the usefulness of the rules in the different methods, we use the classification accuracy of the corresponding rule-based classifier. We define the classifier as follows: To classify instance x, we weight each rule that satisfy x in the result by its confidence and calculate the following odds ratio:

$$R\hspace{0.17em}=\hspace{0.17em}\frac{{\sum }_{x\subseteq A}\mathit{\text{conf}}\hspace{0.17em}(A\hspace{0.17em}\Rightarrow \hspace{0.17em}\mathit{\text{HPF}}4)}{{\sum }_{x\subseteq A}\mathit{\text{conf}}\hspace{0.17em}(A\hspace{0.17em}\Rightarrow \hspace{0.17em}\mathit{\text{NOT}}\hspace{0.17em}\mathit{\text{HPF}}4)}$$

Results:

Table 1 shows the number of rules and the area under the ROC curve (AUC) for the different methods. These results are averaged using the 5-folds cross validation scheme.

Table 1:

The number of rules and the classification performance (AUC) for the different rule induction methods on the HIT dataset.

Method	Number of rules	AUC
Complete	10,680	0.819
corr_chi	7,530	0.820
corr_chi_FDR	2,502	0.774
MPR	71	0.812
RMPR	63	0.818

First notice that evaluating the rules individually based on their statistical significance (corr_chi and corr_chi_FDR) does not help much in reducing the number of rules (even by using the FDR correction). It is clear from the table that the number of MPRs and RMPRs is much smaller than the number of rules in the other approaches (MPRs are about two orders of magnitude smaller than all associations).

We can see that MPR does not sacrifice the classification accuracy. An important benefit of using the compact set of MPRs for classification is that the classification time is very fast. So instead of consulting 10,680 rules to classify each instance, MPR summarizes the classifier in only 71 rules.

Table 2 shows the top 5 rules found by both MPR and RMPR according to the J-measure⁸. The first four rules predict HPF4 orders, while the fifth rule predicts that no HPF4 order should be made. Rules 1 and 4 describe conditions used in detecting HIT⁶. Rule 2 (that refines Rule 1) found that the chance of ordering HPF4 increases if the APTT value is high. The relation between the HIT and APTT is discussed in¹³. Finally Rule 3 suggests the HPF4 order (hence the risk of HIT) is more likely if WBC values are high, which is an interesting finding and would require further validation.

Table 2:

The top 5 MPRs according to the J-measure⁸. {L, N, H} denote {low, normal, high}and {D, S, I} denote {decrease, steady, increase}. On_Hep is true if the patient took Heparin within the last 24 hours. The HPF4 prior is Pr(HPF4)=0.05.

Rule	Sup	conf
1. D[PLT] ∧ L[PLT] ⇒ HPF4	20%	18%
2. D[PLT] ∧ L[PLT] ∧ H[APTT] ⇒HPF4	8.5%	25%
3. D[PLT] ∧ L[PLT] ∧ H[WBC] ⇒ HPF4	8%	26%
4. D[PLT] ∧ L[PLT] ∧ On_Hep ⇒ HPF4	9.8%	22%
5. N[PLT] ⇒ NOT HPF4	55%	99%

MPR vs. RMPR:

Notice that the RMPR method is able to recover most of the MPRs (63 out of 71) and produce a good classifier. In order to show the efficiency of RMPR mining, we compare the number of patterns (nodes in the lattice) that each method has to generate and test in order to find the results. Methods that rely only on Apriori pruning (complete, corr_chi, corr_chi_FDR and MPR) had to examine 22,661 different candidate patterns, while RMPR had to examine only 387 candidate patterns. Hence, RMPR was able to prune almost 98% of the search space, offering a great savings in the execution time.

To further test the scalability of RMPR, we repeated the experiments by adding 9 more labs to the original 6 labs. This creates 92 distinct items to consider. We kept the min_sup level at 5%. We tried to run Apriori on this expanded dataset, but the algorithm ran for several days without finishing. The inefficiency in Apriori is due to the exponential growth in the number of generated candidate patterns when the support is low. On the other hand, the RMPR set was mined in less than 2 minutes, producing a good classifier with AUC=0.834.

Conclusion

Rule mining methods are very important in the medical domain because they represent the knowledge in terms of if-then rules that are easy to interpret by clinicians. This paper proposes a novel rule mining technique based on the concept of minimal predictive rules. Our experiments show that the small set of MPRs can concisely represent the important patterns in the data by producing classification models comparable with the models obtained using the complete set of association rules. We also propose a very efficient algorithm to approximately mine the MPR set, making the approach more suitable to large scale medical data.