Private Medical Record Linkage with Approximate Matching

Abstract

Federal regulations require patient data to be shared for reuse in a de-identified manner. However, disparate providers often share data on overlapping populations, such that a patient’s record may be duplicated or fragmented in the de-identified repository. To perform unbiased statistical analysis in a de-identified setting, it is crucial to integrate records that correspond to the same patient. Private record linkage techniques have been developed, but most methods are based on encryption and preclude the ability to determine similarity, decreasing the accuracy of record linkage. The goal of this research is to integrate a private string comparison method that uses Bloom filters to provide an approximate match, with a medical record linkage algorithm. We evaluate the approach with 100,000 patients’ identifiers and demographics from the Vanderbilt University Medical Center. We demonstrate that the private approximation method achieves sensitivity that is, on average, 3% higher than previous methods.

INTRODUCTION

The decentralized nature of healthcare systems creates fragmentation of a patient’s medical data across various institutions. Without the existence of a universal patient identifier, record linkage, the automated process of resolving which records refer to the same patient, has become a critical process in the biomedical domain¹. In operations, record linkage can provide a more complete view of a patient’s medical information to increase patient safety and determine if certain examinations have already been rendered, thus minimizing replication of services.

Beyond primary care, patient information collected or studied with federal research funds needs to be de-identified and shared for reuse². In this setting, resolving which records refer to the same patient is essential to mitigate bias in statistical analyses. For instance, when patient data is submitted from multiple institutions to a centralized repository, such as the database of Genotypes and Phenotypes (dbGaP), users would like to submit queries of the form “How many patients in the repository have DNA sequence X and disease Y?” However, an additional federal regulation requires that data be de-identified before it is shared to such a repository². This is often achieved by stripping records of identifiers in accordance with the Safe Harbor policy of the HIPAA Privacy Rule³. Removal of such data, however, prevents the resolution of a patient’s record within a centralized repository. Private record linkage (PRL) is not intended to be a de-identification technique, but rather a pre-processing step before de-identification and data sharing occurs.

It is critical to integrate records in such a setting in a manner that obscures patient identity. Notably, several PRL techniques have been proposed^4–6 and are based upon the comparison of encoded features. Many of these approaches obscure identifiers and work in environments where identifying values are recorded consistently across disparate databases. Yet, variation and error can corrupt patient identifiers⁷. In such cases, the application of traditional encode-and-compare models of PRL, which require that features match exactly across records, thwarts the ability to determine similarity between patient features and can results in less accurate record linkage. For example, the hashed value of Jon is equally distant from the hashed values of John and Alice.

Recent advances have yielded private string comparators that allow for approximate matching^4,8–9 and could be incorporated into PRL. However, these approaches need to be integrated into a record linkage scheme and evaluated in the medical domain on a real world dataset in order to determine their usefulness and feasibility. This paper performs such an evaluation. Specifically, we modify a private approximate string comparator to compare eleven fields representing demographics from a medical record set. We then adapt a widely used record linkage algorithm¹⁰, to work with the approximate similarity measure. We compare the approximate approach to several existing approaches with identifiers and demographics from over 100,000 real patient records. The results indicate a statistically significant increase in the performance of record linkage, which demonstrates that approximate PRL approaches are feasible for real world medical data integration.

BACKGROUND

Notation and Problem Statement

For this work, we assume each patient’s record is comprised of k fields that are useful for record linkage purposes. For example, first name, last name, and date of birth (DOB) are fields included in each record. We let A denote a set of records, a indicates a record within set A, and a[i] refers to the value of the i^th field in record a, where i ∈ {1,…,k}. We use B, b, and b[i], to represent a second set of records. The goal of record linkage is to correctly classify all record pairs 〈a,b〉, into the class match or the class non-match.

Record Linkage Background

Binary Field Comparison and Deterministic Linkage (BIN-DET):

A deterministic record linkage method uses a rule-based approach. Specifically, a deterministic method was evaluated with patient identifiers from the Regenstrief Institute¹¹, which identified Social Security Number (SSN), phonetically filtered first name, birth month, and gender as the best combination of fields for record linkage. This method used binary field comparison (i.e. fields agree or disagree), such that when each of the four fields was equivalent between a pair of records, the pair was classified as a match. Otherwise, it was classified as a non-match.

Binary field comparison and probabilistic linkage (BIN-PROB)

Further research showed that a probabilistic approach to record linkage can produce better results and did not require human review¹². However, this method also relied on a binary perspective of field comparison and the notion of similar values in a field was not addressed.

Approximate field comparison and probabilistic linkage (APPROX-PROB)

Recently, the probabilistic approach was extended to approximate discrete field comparators¹³. Our approach builds on this technique and we defer further details of this approach to the Methods section.

METHODS

Materials

To conduct this study, we selected identifiers and demographics from patient records in StarChart, the electronic medical record system of the Vanderbilt University Medical Center. There were eleven fields used in our evaluation, which are depicted at the top of Figure 1. To develop a clean, controlled dataset for evaluation and comparison purposes, we chose a subset of the records that agreed with expected format, contained only alphanumeric characters, and were devoid of missing data. This provided 756,629 clean records. From these records, we randomly selected (without replacement) 100 datasets of 1000 records each, which we refer to as A₁, …, A₁₀₀.

Figure 1.

Example of a record and its corrupted counterpart. Values that changed during corruption are indicated in bold.

In order to generate datasets B₁, …, B₁₀₀ to which we link the aforementioned sets, we implemented a “data corrupter” based on the research of Pudjijono¹⁴. The corrupter introduced optical character recognition errors (e.g., S and 8), phonetic errors (e.g., ph and f), and typographic errors, such as insertions, deletions, transpositions, and substitutions. The probability with which the errors are introduced is consistent with the error rates seen in real datasets¹⁴. Figure 1 provides an example of a record a, and its corrupted counterpart b. Following generation of the corrupt dataset, all letters were converted to the same case.

We performed record linkage for each A_i and B_i pair. The goal for each linkage experiment was to identify the 1,000 out of the 1,000,000 record pairs that are true matches, which corresponds to 0.01% of the record pairs. We assumed a centralized framework with a semi-trusted third party performing.

Record Linkage Approaches

In this study, we compare three record linkage approaches. Each methods was implemented in the Perl programming language. The approaches differ in the way they compute the similarity between records’ fields and the algorithm used to predict the linkage class. The following provides details regarding how each method was implemented and adapted.

BIN-DET Method:

The deterministic method proposed in Grannis et al.¹¹ and described in the background section was evaluated.

BIN-PROB Method:

Fellegi and Sunter (FS)¹⁰ introduced a formal mathematical model for record linkage that is widely used today. In this model, each record pair 〈a,b〉 is modeled as a vector γ_〈a,b〉 of length k, where k is the number of fields contained in each record. The field comparison vector, γ is filled in as follows:

$${\gamma }_{\langle a,b\rangle }[i]=\hspace{0.17em}\{\begin{array}{l}0,\hspace{0.17em}\mathit{\text{if}}\hspace{0.17em}\mathit{\text{record}}\hspace{0.17em}a[i]\hspace{0.17em}\ne \hspace{0.17em}\mathit{\text{record}}\hspace{0.17em}b[i]\hfill \\ 1,\hspace{0.17em}\mathit{\text{if}}\hspace{0.17em}\mathit{\text{record}}\hspace{0.17em}a[i]\hspace{0.17em}=\hspace{0.17em}\mathit{\text{record}}\hspace{0.17em}b[i]\hfill \end{array},i=1,\dots ,k$$

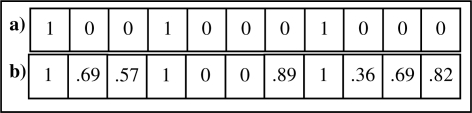
The field comparison vector for the sample record pair is shown in Figure 2. The linkage score for each record pair γ 〈a,b〉 is calculated according to:

$$\begin{array}{l}\mathit{\text{linkage}}\hspace{0.17em}\mathit{\text{score}}\left({\gamma }_{\langle a,b\rangle }\right)\hspace{0.17em}=\hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\sum _{i=1}^k\text{log}\hspace{0.17em}{\left(\frac{m_i}{u_i}\right)}^{{\gamma }_{\langle a,b\rangle }[i]}\text{log}{\left(\frac{1-m_i}{1-u_i}\right)}^{1-{\gamma }_{\langle a,b\rangle }[i]}\hspace{0.17em}\end{array}$$

where m_i is the probability that field i matches given the record pair is a match, and u_i is the probability that field i matches given the pair is a nonmatch.

Figure 2.

Comparison vector of record pair (a,b) shown in Figure 1 from a) binary matching of fields and b) approximate field comparison filter.

The FS algorithm requires knowledge of the conditional probabilities that a feature agrees given the match status of the record pair. A test set for which the true match status has been manually determined can be used to estimate these conditional probabilities for each field. Alternatively, the Expectation Maximization algorithm, a probabilistic method that determines maximum likelihood estimates for unknown parameters can be used to estimate these conditional probabilities¹⁶. As the true match status is known, we are able to calculate the conditional probabilities of the FS algorithm exactly.

APPROX-PROB Method:

Recent work¹³ incorporates field similarity (rather than just their binary agreement or disagreement) into the FS algorithm using the following field comparison and linkage score equations:

$$\begin{array}{l}{\gamma }_{\langle a,b\rangle }[i]=\hspace{0.17em}\mathit{\text{similarity}}\hspace{0.17em}(a[i],\hspace{0.17em}b[i])\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em},i=1,\dots ,k\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathit{\text{linkage}}\hspace{0.17em}\mathit{\text{score}}\hspace{0.17em}\left({\gamma }_{\langle a,b\rangle }\right)\hspace{0.17em}=\hspace{0.17em}\sum _{\text{i}=1}^{\text{k}}\text{log}\left(\frac{m{(\delta )}_i}{u{(\delta )}_{\text{i}}}\right)\end{array}$$

where m_i is the probability of similarity score δ amongst values in field i, given the record pair is a match, and u_i is the probability of similarity score δ amongst values in field i, given the record pair is a non-match. Any metric that determines the similarity of two strings can be used. See Figure 2 for an example comparison vector.

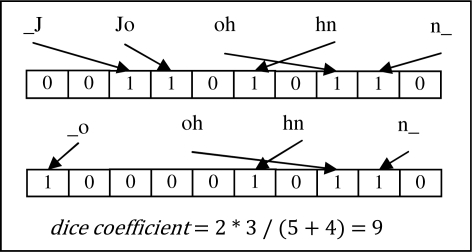
For feature comparison, we selected a Bloom filter method, recently proposed by Schnell et al⁴, due to its simplicity and its ability to determine the similarity between strings in a manner that preserves privacy. This method hashes all bigrams of a string, padded with spaces on both ends, into a bit vector, initialized with all zeroes, using i hash functions. The similarity between the set of bigrams in filters X and Y is assessed via the Dice coefficient:

$$\mathit{\text{Dice}}\hspace{0.17em}\mathit{\text{coefficient}}\hspace{0.17em}(X,Y)\hspace{0.17em}=\hspace{0.17em}2\hspace{0.17em}*\hspace{0.17em}\left(|X\hspace{0.17em}\cap \hspace{0.17em}Y|\right)/\left(\left|X\right|\hspace{0.17em}+\left|\hspace{0.17em}Y\right|\right)$$

where |•| is the number of bits in the filter set to 1. Figure 3 provides an example.

Figure 3.

The first names from records a and b shown in Figure 1 hashed into 10-bit Bloom filters with one hash function.

Since the Dice coefficient corresponds to a similarity score in the range [0,1], we discretized the scores into 10 bins based on the 10^th percentiles of the similarity scores over all record pairs.

For the Bloom filter, we used a 1000-bit vector with 30 hash functions for each field, except gender and race. The latter are a single character each and were hashed and compared for binary agreement. All hash functions were variations of SHA-1.

Evaluation Metrics

We evaluated the performance methods from several perspectives. First, we evaluated the ability of the methods to separate the record pairs into the match and non-match classes. We adopted several information retrieval metrics¹⁵ for this analysis. In particular, we use sensitivity, specificity, precision, and recall, which are defined as:

$$\begin{array}{l}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathit{\text{sensitivity}}\hspace{0.17em}=\hspace{0.17em}\mathit{\text{recall}}\hspace{0.17em}=\hspace{0.17em}\frac{\mathit{\text{TP}}}{\mathit{\text{TP}}\hspace{0.17em}+\hspace{0.17em}\mathit{\text{FN}}}\\ \mathit{\text{specificity}}\hspace{0.17em}=\hspace{0.17em}\frac{\mathit{\text{TP}}}{\mathit{\text{TP}}\hspace{0.17em}+\hspace{0.17em}\mathit{\text{FP}}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathit{\text{precision}}\hspace{0.17em}=\frac{\mathit{\text{TP}}}{\mathit{\text{TP}}\hspace{0.17em}+\hspace{0.17em}\mathit{\text{FP}}}\hspace{0.17em}\end{array}$$

where TP is the number of true matches, TN is the number of true non-matches, FP is the number of false matches, and FN is the number of false non-matches. Sensitivity and specificity provide a general overview of the effectiveness of the classification, while precision and recall allow us to “zoom in” on the relatively small class of matches.

Second, we investigated the runtime of the methods, considering the field comparison and linkage times individually, in order to evaluate the tradeoff between classification exactness and speed.

RESULTS

Table 1 summarizes the comparison of the classification capability by classifying the record pairs with the top 1,000 highest linkage scores as matches (as it is known that 1,000 true matches exist in each dataset). While BIN-DET correctly classified all non-matches (specificity = 1), it rarely correctly identified the majority of true matches (sensitivity = 0.14). This supports our intuition as this approach only considers four fields and classifies a record pair as a match when all four fields agree. BIN-PROB still correctly identified most of the non-matches, but, by contrast, was much more effective at identifying matches (sensitivity = 0.97). Due to the large number of fields within each record, many features are still likely to match exactly, even if several features disagree. This is in contrast to the number of fields that one would expect to match by coincidence among record pairs that are non-matches which enabled BIN-PROB to achieve strong separation in the linkage scores of matches and non-matches.

Table 1.

Average performance of the methods (± 1 standard deviation).

Measure	BIN-DET	BIN-PROB	APPROX-PROB
Sensitivity	.14 ±.01	.97 ± .007	1.0 ± .001
Specificity	1 ± 0	1 ± 6−6	1 ± 1−6

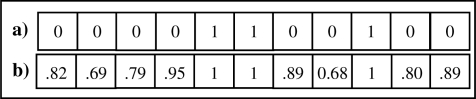
APPROX-PROB was able to correctly classify (on average) 30 out of the 37 record pairs that BIN-PROB misclassified as false negatives (non-matches). As an example, consider the γ comparison vectors shown in Figure 4 for a record pair that BIN-PROB misclassified as a false negative that APPROX-PROB correctly classified as a true positive. In this case, many of the fields disagreed slightly. BIN-PROB was not able to use this information in classifying the record pair whereas APPROX-PROB was.

Figure 4.

The comparison vectors for a record pair that was a match. a) BIN-PROB incorrectly classified the pair, whereas b) APPROX-PROB correctly classified it.

We expect that APPROX-PROB would perform more effectively if the Bloom filter parameters (length of Bloom filter and number of hash functions used) are tuned to each field based on expected size of the field. For example, fewer bits are set when comparing 2-digit state abbreviations than lengthier street addresses.

Table 2 summarizes the runtime analysis. The comparison of fields with APPROX-PROB requires slightly longer runtime due to the additional hash and Bloom filter calculations. However, handling data in a private manner always requires additional computation, and the comparison times are on the same order as the other approaches. The matching also takes longer for APPROX-PROB due to the fact that 10^th percentiles must be calculated, and that 10 (rather than 2) parameters must be estimated for all features compared with approximate comparison. We believe that the computational times are reasonable for the private nature of the process and the increase in performance.

Table 2.

Average runtime in seconds (±1 standard deviation).

Computation	BIN-DET	BIN-PROB	APPROX-PROB
Field Comparison	216 ± 3	644 ± 9	808 ±141
Linkage	28 ± 3.1	132 ± 3	874 ± 51
Total	244 ± 4.5	775 ± 10	1682 ± 152

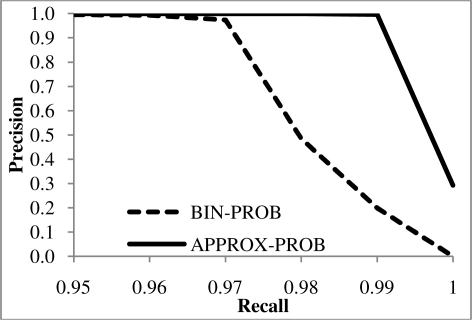
Table 1 is based on knowledge that 1,000 matches exist, which provided insight on where to draw the classifying line between matches and non-matches. However, in practice a user may want to draw the classification line elsewhere based on their requirements. Figure 5 addresses this by considering the precisions of BIN-PROB and APPROX-PROB with recall held constant. Note the x-axis begins at 0.95 as precision values for both methods prior to this point are ∼1.0, indicating the ease with which both methods are correctly to able to classify the majority of non-matches. These results show that for a given recall value, APPROX-PROB has greater precision than BIN-PROB.

Figure 5.

Precision for the BIN-PROB and APPROX-PROB methods with recall held constant.

DISCUSSION AND CONCLUSION

This work adapted and compared several privacy preserving record linkage methodologies with data from a real world medical record system. Our findings indicate a method that incorporates an approximate field comparison with a probabilistic linkage algorithm outperforms existing approaches that rely on deterministic and binary comparisons. Our evaluation demonstrates that approximate match PRL techniques can be applied to medical datasets and the runtimes are practical for real world use.

Despite the merits of this research, there are several limitations and opportunities for extensions that we wish to point out. First, from a technical perspective, this work is limited in that it examined controlled datasets, such that we could control the parameterization of the probabilistic record linkage algorithms. In particular, we were able to calculate the conditional probabilities required for the FS algorithm because we knew the true match status for each record pair. This provides a best case scenario for tuning the parameters of the algorithm and before we implement such a solution in a live setting, we will need to investigate the accuracy of such parameters in an environment when such knowledge is not available. In addition, we acknowledge that the corruption incorporated into the patient identifiers and demographics were systematically generated in accordance with known typographical errors. Yet, there are many more types of errors that can arise in electronic medical record systems and are likely to be found in real datasets submitted to privacy-enhanced repositories. For example, our approach does not consider how nicknames and changes to last name (e.g., due to marriage) would be addressed.

Second, we recognize that, in practice, datasets generated in the medical domain are often much larger. As a result, in practice, record linkage is almost always complemented by blocking, a technique to reduce the number of comparisons that need to be made together and compared only to records within this block¹⁰. We assume that larger datasets could, in practice, be blocked to record sets of size 1000×1000. The datasets we used are intended to be representative of a single block. The integration of blocking into a PRL method is an open research question.