Abstract
Surgical reconstruction of natural-appearing breasts is a challenging task. Currently, surgical planning is limited to the surgeon’s subjective assessment of breast morphology. Therefore, it is useful to develop objective measurements of breast contour. In this paper, a novel quantitative measure of the breast contour based on catenary theory is introduced. A catenary curve is fitted on the breast contour (lateral and inferior) and the key parameter determining the shape of the curve is extracted. The new catenary analysis was applied to pre- and post-operative clinical photographs of women who underwent tissue expander/implant (TE/Implant) reconstruction. A logistic regression model was developed to predict the probability that the observed contour is that of a TE/Implant reconstruction from the catenary parameter, patient age, and patient body mass index. It was demonstrated that the parameters contain useful information for distinguishing TE/Implant reconstructed breasts from pre-operative breasts.
Introduction
Breast cancer is the most common type of cancer for women in U.S, with approximately 200,000 new cases of invasive breast cancer diagnosed each year. [1] Fortunately, due to early detection techniques and improved cancer treatments, the death rate caused by breast cancer has decreased since 1990. [1–3] Current breast cancer treatment encompasses not only surgical removal of the tumor and medical adjuvant and neo-adjuvant therapies to control the cancer, but also an increasing emphasis on restoration of the quality of life. The goal of breast reconstruction is to recreate a breast form that is satisfying to the patient, facilitating her psychosocial adjustment to living as a breast cancer survivor. We propose that the outcomes of breast reconstruction be quantified in terms of the changes to the physical characteristics of the breasts such as shape, symmetry, and ptosis. [4]
Background
In breast reconstruction surgery, recreating natural-appearing lateral and inferior breast contours is important to the replication of a natural appearing breast mound. This is particularly challenging and currently depends largely on the individual surgeon’s subjective assessments of breast morphology. Therefore, it is useful to quantify the form of the breast contours and increase the reliability of the assessment.
Only a few previous studies have investigated methods for quantifying characteristics related to breast contour. However, all measures developed from previous studies are based on simple asymmetry measures and they cannot account for the actual shape of the lateral and inferior breast contours. Cardoso and Cardoso [5] developed a breast conservation therapy outcome estimate system by using features extracted from clinical photographs of the patient taken in four different postures. The extracted features of their study include well-known asymmetry measures as well as some new ones. They used the difference between the levels of the inferior left and right breast contours, the difference between the lengths of the left and right breast contours, and the non-overlapping area of the two breasts to capture the asymmetry of the breast contours. Van Limbergen et al. [6] used nipple displacement and breast contour retraction as quantitative measurements and correlated those to the subjective, qualitative scoring. The breast contour retraction measure was based on the vertical and horizontal length differences between the breasts.
We introduce a novel quantitative measure of the breast contour based on catenary theory. [7] Catenary is the theoretical shape of a flexible chain suspended by two fixed points and it can be used to approximate any string-like objects. A catenary curve is fitted on a breast on the clinical photograph, and the curve parameter, which is the degree of breast contour convexity, is extracted. Catenary theory has been adapted to approximate interesting curves in other medical applications, especially in orthodontics. [8, 9] However, our study is the first to apply catenary theory to fit the contour of breasts and quantify breast contours by using a key parameter of the catenary curve.
The study dataset consists of clinical photographs of patients who underwent or were scheduled for breast reconstruction surgery. We compared the contour measurements of subjects who underwent tissue expander/implant (TE/Implant) reconstruction to those of other pre-operative (untreated) women as previous studies indicate possible shape difference between these two groups. [10–13] The expected shape difference between two groups is that the contour of TE/Implant reconstructed breast will be less convex than the pre-operative (untreated) breasts. To show that the catenary parameter is able to meaningfully quantify the shape of the breast contour (lateral and inferior), we developed a logistic regression model to distinguish between the pre-operative and TE/Implant subjects based on the extracted curve parameter, patient age, and patient body mass index.
By establishing a reference database of the catenary parameter for different surgeries and patient history variables, the proposed parameter could be used to help both plastic surgeons and breast cancer survivors in decision making for breast reconstruction.
Materials and Methods
Datasets
The study population for this paper consists of women aged 21 or older who underwent or were scheduled for breast reconstruction surgery from January 1, 2004 to October 31, 2009. Anterior-posterior (AP) photographs were taken with a Nikon Coolpix 8400 (Nikon, USA). AP images of 26 patients (43 breasts) were included. Among the 43 breasts, 32 were either healthy or pre-operative (untreated) breasts and 11 were either completed or in process of TE/Implant reconstruction surgery. 3 subjects who had a TE/Implant reconstructed breast on one side and untreated breast on the other were included in this study.
Rotated Catenary
To quantify lateral and inferior breast contours, catenary theory was adopted from the differential geometry field. Catenary is a perfectly flexible and inextensible string of uniform density supported by two vertically distinct points. [7] Catenary curve has been used for approximating most hanging string-like shapes of objects such as arches, anchor rods, and suspension bridges. [14]
The equation of a catenary curve in Cartesian coordinates has the form
| (1) |
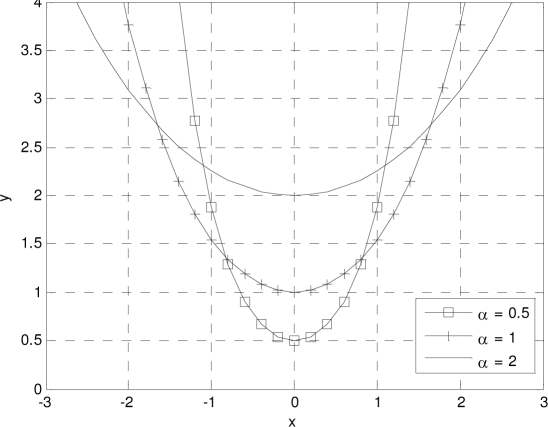
where b and c are the offset of x-axis and y-axis respectively, and α is the ratio of the tension to the weight applied to each point on the curve. The variable α is the key factor to determine the shape of a catenary curve. A smaller α makes the curve less convex whereas a larger α makes the curve more convex. Figure 1 summarizes how α determines the shape of a catenary.
Figure 1.
Graph of catenaries for different α values. A smaller α makes the curve looser whereas a larger α makes the curve more convex.
As previously stated, catenary theory can be easily extended to approximate the lateral and inferior contours of a patient’s breasts. Small α will represent a less convex breast contour and large α will denote a more convex breast contour. However, due to the weight of breasts and the shape of a person’s chest wall, breast contours are at an angle to the imaginary horizontal line. In order to capture this angle, a rotation parameter θ is introduced. Thus, the final equation for the proposed rotated catenary curve is
| (2) |
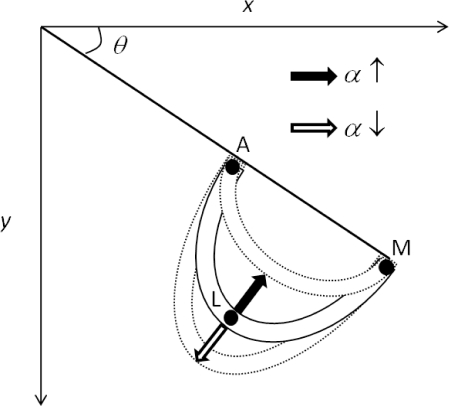
and Figure 2 shows how α and θ affect the appearance of the proposed catenary curve when it approximates a right breast contour.
Figure 2.
Catenary with α and θ to approximate a right breast contour. α approximates the breast contour convexity and θ captures the orientation of the breast contour from the x-axis.
Fitting a Rotated Catenary on a Breast Contour
In order to obtain the catenary curve parameter α and the rotation parameter θ from a given photograph, we need to solve the following equation
| (3) |
where F denotes the catenary curve on a breast contour and x and y represent the x- and y-coordinates of the breast contour itself. However, it should be noted that it is hard to find an analytic solution for Equation (1). Therefore, for a given breast contour (x- and y-coordinates), we decided to find the numerical solution P that satisfies the above equation.
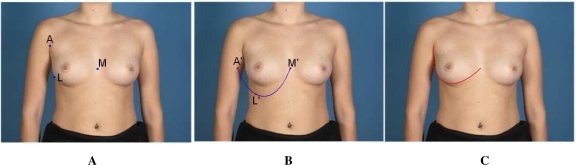
Three manually localized points were used to solve Equation (3). These points are the midline point (M), the anterior axillary point (A), and the lateral most point (L) on the breast mound which are illustrated in Figure 3.A. Once the above reference points are located, the numerical solution P is obtained by:
θ is the angle between the line from point M to point A and the x-axis in Figure 2.
Rotate the three reference points (M, A, L) by −θ and let (M′, A′, L′) be the rotated reference points. This process is equivalent to apply inverse rotation matrix to Equation (2), which changes it to Equation (1). (Figure 3.B.)
Compute [α, b, c] from the given x- and y-coordinates of the (M′, A′, L′). (Figure 3.B.)
Figure 3.
A. The blue dots indicate the right anterior axillary point (A), the lateral most point on the right breast mound (L), and the midline point (M). B. Rotated three reference points (red dots M′,A′,L′) with a catenary curve are passing through those points. Catenary feature α is computed at this stage. C. The final rotated catenary curve is fitted on the subject’s right breast.
For the above procedures, we used the non-linear curve-fitting algorithm ‘lsqcurvefit’ in MATLAB® (The Mathworks, Natick, MA). Once the numerical solution P is found, the catenary curve passing through points (M′, A′, L′) can be easily drawn and we can obtain the final curve by rotating the former curve by θ as shown Figure 3.C.
In order to compare the parameter α values of different individuals, they must be unitless quantities. Therefore, we normalized α by the length of the curve. The normalized version of parameter α is
| (4) |
where l denotes the length of the catenary curve.
Statistical Analysis
Our hypothesis is that there is a difference in the shape of the contour between TE/Implant reconstructed breasts and pre-operative (untreated) breasts, and the proposed normalized catenary parameter α′ can capture the difference. However, the shape of breast contour also depends on patient history variables such as age and Body Mass Index (BMI). Therefore, we developed three logistic regression (LR) models to check whether α′ and other patient history variables (age and BMI) can be used for predicting the breast reconstruction outcome, and therefore to show that α′ has useful information about the breast contour. The LR models predict the breast reconstruction outcome O from the feature vector V
| (5) |
| (6) |
| (7) |
| (8) |
where subscript i denotes the parameters associated with ith breast in the datasets. If we denote the resulting LR model from the feature vector Vi,j as jth model, we have three models as follows
| (9) |
where β0,j = [β0, β1, … ,βj] and pi represents the probability of patients having a TE/Implant reconstructed breast based on the given feature vector Vi,j.
Leave-one-out cross-validation was utilized to evaluate the efficacy of the LR models. We used the area under the Receiver Operating Characteristic curve (AUC) of as the efficacy metric of the LR model. The AUC values of three LR models were compared to show the effectiveness of the full model (α′, age, and BMI) over the partial models (α′ only and patient history variables only).
Results
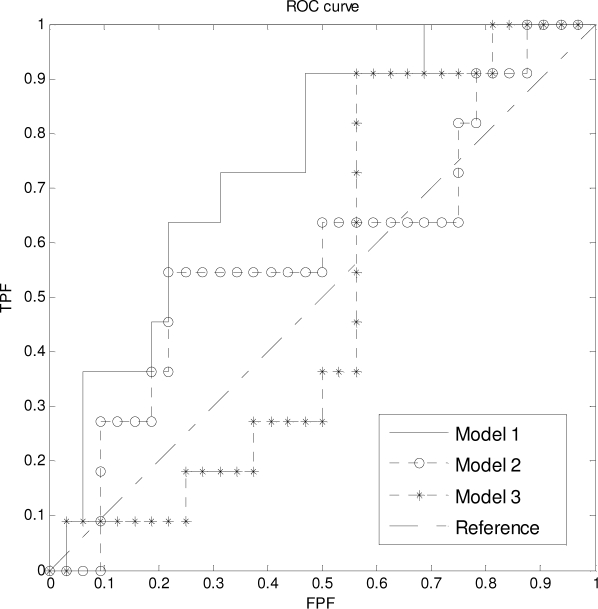
The median and the range of parameters extracted from 43 breasts are summarized in Table 1. Three LR models were trained and tested on the feature vector V (Table 1) and the reconstruction outcome O by the leave-one-out cross-validation analysis. Figure 4 shows the resulting Receiver Operating Characteristic (ROC) curves of the LR models and the chance reference line of the random predictive model. The area under curve (AUC) of the 1st LR model is 0.75, while the AUC of 2nd and 3rd LR models are 0.59 and 0.51 respectively. This result demonstrates that the feature vector Vi,1 contains useful information for distinguishing TE/Implant reconstructed breasts from the pre-operative (untreated) breasts. Moreover, the 2nd and 3rd LR models showed only slightly better performance than the random predictive model. As expected, it demonstrates that the patient history variables alone have little predictive value. Moreover, it is apparent that the curve parameter α′ alone is insufficient. By combining both α′ and patient history variables, the LR model can capture the differences between the TE/Implant reconstructed breasts and the pre-operative (untreated) breasts. The interaction between the patient history variables and α′ is obvious as shown in the ROC analysis.
Table 1.
Statistics of the feature vector V extracted from 26 patients (43 breasts) in the dataset.
| Median | Min | Max | |
|---|---|---|---|
| 0.1525 | 0.0800 | 0.2361 | |
| 0.1794 | 0.1283 | 0.2263 | |
| BMIUntreated | 23.97 | 19.68 | 34.70 |
| BMITE/Implant | 26.10 | 20.35 | 32.47 |
| AgeUntreated | 51 | 37 | 63 |
| AgeTE/Implant | 41 | 36 | 56 |
Figure 4.
ROC curve of the resulting logistic regression models. AUC of 1st, 2nd, and 3rd models are 0.75, 0.59, and 0.51 respectively. Only the 1st model distinguishes the TE/Implant reconstructed breasts from the pre-operative breasts effectively.
In the 1st LR model developed from the leave-one-out cross-validation, coefficients associated with parameter α′ ranged from 30.82 to 52.97. The values of those coefficients demonstrate that increasing α′ is associated with increasing probability that the contour is from a TE/Implant reconstructed breast. In other words, a TE/Implant reconstructed breast will result in relatively high α′, which means a more convex breast contour. Moreover, as seen in Table 1, the median of α′ values from TE/Implant reconstructed breasts is higher than that of the pre-operative breasts. These findings are encouraging since it confirms qualitative remarks of previous studies. Specially, TE reconstruction surgery typically results in unwanted lift of the breast mound and, therefore, additional follow up surgeries or anatomical implants are required to recreate a natural appearing breast with appropriate ptosis. [11, 13] As expected from these qualitative observations, our quantitative analysis demonstrates that TE/Implant reconstructed breasts have a lifted and more convex contour compared to pre-operative (untreated) breasts.
Discussion
The objective of this study is to introduce a novel quantitative measure of the lateral and the inferior breast contours. We propose a normalized version (α′) of the catenary curve parameter α to quantify the shape of the breast contour. In order to show that the proposed parameter α′ captures relevant information about the breast contour, we analyzed α′ and some patient history variables (age and BMI) for patients who underwent or were scheduled for breast reconstruction surgeries. We focused on women with TE/Implant reconstructed breasts and pre-operative (untreated) breasts since the surgical literature provides clear qualitative descriptions of the typical differences in the shape of the breast contour between these two groups. A logistic regression model was applied to the catenary parameter α′ and patient history variables (age and BMI). The logistic model showed the expected association between the parameter α′ and TE/Implant reconstructed breast contour. We found that the TE/Implant breast contour results in higher values of the parameter α′, which corresponds to a more convex breast contour (or lift of breast mound) relative to the pre-operative/untreated breast contour.
This study is the first to capture breast contour using a sophisticated model. Prior work employed simple asymmetry measures. [5, 6] Our new contour measure lays the groundwork for developing systems to support both plastic surgeons and breast cancer survivors in decision making for breast reconstruction. By establishing a reference database of the contour parameter α′ for different surgeries and patient history variables, a case-based reasoning system could be developed to predict the likely changes to a woman’s breast shape if she were to undergo a given reconstructive procedure.
Conclusion
We proposed a new quantitative measure of the lateral and inferior breast contour. We demonstrated that the proposed measure based on the catenary curve contains useful information about breast contour by using a mathematical predictive model. In the future, the proposed catenary parameter could be used to help patients in deciding among their reconstructive options and to facilitate surgeons with surgical planning.
Acknowledgments
This study was supported in part by grant RSGPB-09-157-01-CPPB from the American Cancer Society.
References
- 1.Cancer facts and figures 2009 . American Cancer Society; 2009. [Google Scholar]
- 2.Khoo A, Kroll SS, Reece GP, et al. A comparison of resource costs of immediate and delayed breast reconstruction. Plast Reconstr Surg. 1998;101(4):964–8. doi: 10.1097/00006534-199804040-00011. [DOI] [PubMed] [Google Scholar]
- 3.Kroll SS, Evans GR, Reece GP, et al. Comparison of resource costs of free and conventional tram flap breast reconstruction. Plast Reconstr Surg. 1996;98(1):74–7. doi: 10.1097/00006534-199607000-00011. [DOI] [PubMed] [Google Scholar]
- 4.Kim MS, Reece GP, Beahm EK, Miller MJ, Atkinson EN, Markey MK. Objective assessment of aesthetic outcomes of breast cancer treatment: Measuring ptosis from clinical photographs. Comput Biol Med. 2007;37(1):49–59. doi: 10.1016/j.compbiomed.2005.10.007. [DOI] [PubMed] [Google Scholar]
- 5.Cardoso JS, Cardoso MJ. Towards an intelligent medical system for the aesthetic evaluation of breast cancer conservative treatment. Artif Intell Med. 2007;40(2):115–26. doi: 10.1016/j.artmed.2007.02.007. [DOI] [PubMed] [Google Scholar]
- 6.Van Limbergen E, van der Schueren E, Van Tongelen K. Cosmetic evaluation of breast conserving treatment for mammary cancer. 1. Proposal of a quantitative scoring system. Radiother Oncol. 1989;16(3):159–67. doi: 10.1016/0167-8140(89)90016-9. [DOI] [PubMed] [Google Scholar]
- 7.Yates RC. Curves and their properties. Washington: National Council of Teachers of Mathematics; 1974. [Google Scholar]
- 8.Mutinelli S, Manfredi M, Cozzani M. A mathematic-geometric model to calculate variation in mandibular arch form. Eur J Orthod. 2000;22(2):113–25. doi: 10.1093/ejo/22.2.113. [DOI] [PubMed] [Google Scholar]
- 9.Pepe SH. Polynomial and catenary curve fits to human dental arches. J Dent Res. 1975;54(6):1124–32. doi: 10.1177/00220345750540060501. [DOI] [PubMed] [Google Scholar]
- 10.Clough KB, O’Donoghue JM, Fitoussi AD, Nos C, Falcou M-C. Prospective evaluation of late cosmetic results following breast reconstruction: I. Implant reconstruction. Plast Reconstr Surg. 2001;107(7):1702–9. doi: 10.1097/00006534-200106000-00010. [DOI] [PubMed] [Google Scholar]
- 11.Hugo DL, Horacio FM, Manuel S. Pocket work for optimising outcomes in prosthetic breast reconstruction. J Plast Reconstr Aesthet Surg. 2009;62(5):626–32. doi: 10.1016/j.bjps.2007.08.037. [DOI] [PubMed] [Google Scholar]
- 12.McGeorge DD, Mahdi S, Tsekouras A. Breast reconstruction with anatomical expanders and implants: Our early experience. Br J Plast Surg. 1996;49(6):352–7. doi: 10.1016/s0007-1226(96)90002-8. [DOI] [PubMed] [Google Scholar]
- 13.Topol BM, Dalton EF, Ponn T, Campbell CJ. Immediate single-stage breast reconstruction using implants and human acellular dermal tissue matrix with adjustment of the lower pole of the breast to reduce unwanted lift. Ann Plast Surg. 2008;61(5):494–9. doi: 10.1097/SAP.0b013e31816d82d9. [DOI] [PubMed] [Google Scholar]
- 14.Oprea J. Differential geometry and its applications. Washington, D.C.: Mathematical Association of America; 2007. [Google Scholar]