Pattern Discovery in Breast Cancer Specific Protein Interaction Network

Abstract

The interest in indentifying novel biomarkers for early stage breast cancer (BRCA) detection has become grown significantly in recent years. From a view of network biology, one of the emerging themes today is to re-characterize a protein’s biological functions in its molecular network. Although many methods have been presented, including network-based gene ranking for molecular biomarker discovery, and graph clustering for functional module discovery, it is still hard to find systems-level properties hidden in disease specific molecular networks. We reconstructed BRCA-related protein interaction network by using BRCA-associated genes/proteins as seeds, and expanding them in an integrated protein interaction database. We further developed a computational framework based on Ant Colony Optimization to rank network nodes. The task of ranking nodes is represented as the problem of finding optimal density distributions of “ant colonies” on all nodes of the network. Our results revealed some interesting systems-level pattern in BRCA-related protein interaction network.

Introduction

The interest in indentifying novel biomarkers for early stage breast cancer (BRCA) detection has become grown significantly in recent years1–3. Known BRCA susceptibility genes, e.g. P53, BRCA1, BRCA2, ERBB2 and PTEN, only account for 15–20% of the familial risk4. Identification of these genes5, while extremely precious, is only a first step to understand BRCA progression. From a view of network biology6, these genes never function in isolation7, one study re-characterized them in a molecular interaction network for BRCA, and identified HMMR as a new susceptibility locus3. Another study integrated protein interaction network and gene expression data to improve the prediction of BRCA metastasis8. These works suggest that protein interaction networks, although noisy and incomplete, can serve as a molecule-level conceptual roadmap to guide future network biomarkers studies9.

On the other hand, it is found that both biological shape10, 11 and physiological signals12, 13 have chaotic and/or fractal characteristics14, which indicate that many biological systems and networks could be analyzed effectively by applying nonlinear dynamical approaches involving chaos, fractal, bifurcation, pattern formation and complex systems15. For these studies, the concept of dynamical biomarkers was firstly introduced on a speech by A.L. Goldberger in 200616, which can be seen as an initiation of using nonlinear dynamical properties as biomarkers, although this concept has not extended to the area of molecular networks.

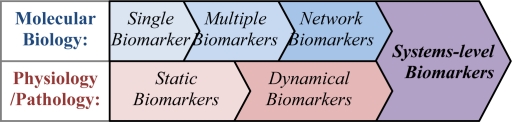
Based on the relationship between features of complex networks (e.g. scale-free) and nonlinear dynamical properties (e.g. fractals)17, systems-level biomarkers (sys-biomarkers), as an innovative concept shown in Figure 1, derive from the marriage of network biomarkers and dynamical biomarkers. Although many methods have been presented in network biology, including network-based gene ranking for molecular biomarker discovery18, and graph clustering for functional module discovery19, it is still hard to find sys-biomarkers hidden in disease specific molecular networks.

Figure 1.

Evolvement of concepts on diagnostic biomarkers.

Starting with the initial motivation of systems biology20, we reconstructed BRCA-related protein interaction network by taking BRCA-associated genes/proteins as seeds, using the nearest-neighbor expansion method21, and expanding them in an integrated protein interaction database.

Our method allows BRCA experts to merge their prior knowledge on the BRCA-associated genes/proteins into a manually curated list (protein seeds), which could be obtained from the OMIM™ database (Online Mendelian Inheritance in Man™).

Here, we use the latest high-quality subsets of protein interaction data integrated into the Human Annotated and Predicted Protein Interaction (HAPPI, http://bio.informatics.iupui.edu/HAPPI) database. In this database, all protein interactions are weighted, with a confidence score (SC) encoding prior knowledge of experimental and literature evidence supporting each protein interaction.

We further developed a computational framework based on Ant Colony Optimization (ACO) 22 to rank network nodes. The task of ranking nodes is represented as the problem of finding optimal density distributions of “ant colonies” on all nodes of the network. Our results revealed some interesting systems-level pattern in BRCA-related protein interaction network.

Results

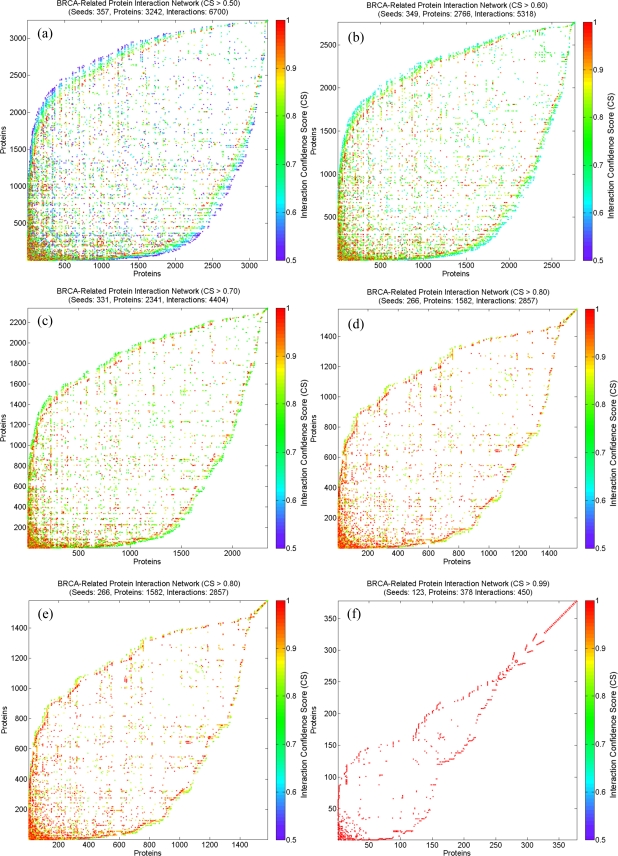
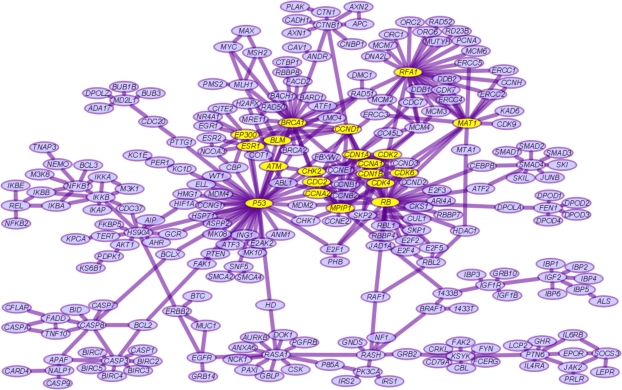
In our experiments, we firstly constructed an BRCA-related protein interaction network as described above. Using the ACO ranking algorithm, the ranking results of the weighted BRCA-related protein interaction network are shown in Figure 2, which show the ranked adjacency matrix according to the final density distribution. The top 20 proteins from the ranking result shown in Figure 2(f) are highlighted in Figure 3, which shows a high-quality BRCA-related protein interaction network when taking interaction confidence scores CS > 0.99. Node degree distributions plotted in Figure 4 for each BRCA-related protein interaction network taking different CS thresholds, are all very close to power-law distribution, which implies scale-free features.

Figure 2.

Node ranking of the weighted BRCA-related protein interaction network. (a) CS > 0.50; (b) CS > 0.60; (c) CS > 0.70; (d) CS > 0.80; (d) CS > 0.90; (d) CS > 0.99.

Figure 3.

A visual layout of the BRCA protein interaction network (CS > 0.99). Top 20 proteins from the ranking result shown in Figure 2(f) are highlighted.

Discussion

ACO is a dynamic process effective in solving optimization problems such as those of phylogenetic analyses in biology15. Here, we represent the task of finding network relevant nodes as an ant colony optimization problem, in which simulated ants (s-ant) roam all possible network paths iteratively. By designing various strategies of s-ants for each step taken to walk in a network, the iteration process can be manipulated to get the density distribution of s-ants crowding on each node. According to this density distribution, the adjacency matrix of the network with ranked nodes is shown as a map in order to reveal the system-level features of the network. Experiments on an BRCA-relevant protein interaction network demonstrated that this method finds the key nodes in the network, and also reveals a fractal feature of the scale-free network through a quick-populating strategy of colonization. Analyses for both unweighted and weighted protein interaction networks based on this framework are given to exhibit the feasibility and flexibility of our method. Comparisons with previous works on BRCA-related protein interaction networks show the reliability of ACO.

Conclusion

Proteins ranked from an BRCA network using our method not only show system-level fractal characteristics but are also useful for subsequent translational biomedical discoveries of gene/protein-disease associations. The highly-ranked proteins from the case study for BRCA could be prioritized for “drug target candidates” and, with additional validation, for “disease biomarker candidates”, where proteins may be differentially and specifically expressed in tissues/biofluids based on an associated condition of health or disease. We found that ACO-adapted framework to be robust in identifying fractal-like organization with or without confidence weightings of network connections. Our results revealed fractal features not previously reported in disease-specific molecular interaction networks. Our results are comparable but seem more sensitive than a previous study11, suggesting convergence of different algorithmic approaches in revealing the same network characteristics of BRCA-related proteins. Proteins in this disease-specific network could have dramatically different characteristics than in the global network. For example, as labeled in Figure 2, CDK5 is a major BRCA-related protein and a “mini-hub” in the BRCA protein interaction network, but it is not a major hub in the global networks based on having a node degree of only 22 in the HAPPI database12. If we accept that fractal features reflect a high level of “orderness” eventually interpretable in biology, the results of our study and methodology could point to a brand-new direction of finding and ranking proteins and genes systematically for all human diseases with public data available to bioinformatics researchers today.

Methods

In this framework, node ranking is seen as an optimization problem, which is why the concept of an “ant colony” can be utilized. ACO is mostly like a multi-agent system, but each s-ant (also can be seen as an agent in the system) will mark its path in ACO in a manner comparable to the natural situation where a real ant will leave a pheromone on its track. The pheromone on the ground will stimulate other ants to work together and the whole ant colony will become more cooperative, in a phenomenon of self-organizing communication called stigmergy13. This characteristic of self-organization leads to an emergence of a complex system, and we propose to leverage this characteristic into solving the problem of complex biological networks by using it as a basis for complex systems modeling. In our developed methodology, s-ants roam all possible network paths iteratively, and marks signed by the s-ants act to accelerate the optimization process. By designing various strategies F_i of s-ants for each step taken to walk in a network, the iteration process can be manipulated to get the density distribution s_i of s-ants crowding on each node, as shown in Eq. (1). According to this density distribution, the ranked adjacency matrix of the network will be shown as a map to reveal the system-level feature of the network.

$$\begin{array}{l}{s}_{i+1}={\mathbf{\text{F}}}_i({\mathbf{\text{M}}}_i)\times s_i,s_i\in R^n,{\mathbf{\text{M}}}_i\in R^{n\times n},\\ {\mathbf{\text{F}}}_i\in R^{n\times n}\to R^{n\times n},i=0,1,\dots ,N-1\\ \end{array}$$ (1)

Here M_i is determined by both the network features under analysis (including topology and weighted information) and the marks signed by s-ants. The initial column vector can be evaluated as s₀ = (1/n, 1/n,…, 1/n)^T to describe the equivalence of each node in the network. The final density distribution s_N will determine the rank of each node. Moreover, marks signed from outside will easily switch this scheme from an unsupervised mode into a supervised one.

In a simple case of the proposed scheme, s-ants never sign a mark on the network, and M_i is only determined by the network, which means it is invariable. Eq. (1) can be reduced as:

$$\begin{array}{l}{s}_{i+1}={\mathbf{\text{F}}}_i({\mathbf{\text{M}}}_i)\times s_i={\mathbf{\text{F}}}_i(\mathbf{\text{M}})\times s_i\\ ={\mathbf{\text{F}}}_i\cdot \cdot \cdot {\mathbf{\text{F}}}_1\cdot {\mathbf{\text{F}}}_0(\mathbf{\text{M}})\times s_0\end{array}$$ (2)

For further simplification, s-ants can be modeled by the constraint of maintaining a constant walking strategy, and Eq. (2) can be reduced as:

$$s_{i+1}={\mathbf{\text{F}}}_i(\mathbf{\text{M}})\times s_i={\mathbf{\text{F}}}^{(i)}(\mathbf{\text{M}})\times s_0={\mathbf{\text{M}}}^i\times s_0$$ (3)

Here M becomes the state transition probability matrix about the network. From Eq. (3), we observe there to be a typical Markov Chain. Let P denote the adjacency matrix of the network (in spite of directed versus undirected or unweighted versus weighted). In the event where s-ants fail to populate, M can be obtained by Eq. (4).

$$\begin{array}{l}\mathbf{\text{P}}=\{p_{i,j}\},\hspace{0.17em}\mathbf{\text{M}}=\{m_{i,j}\},\\ m_{i,j}=\frac{p_{i,j}}{1+\sum _j{p}_{i,j}},i,j=1,2,\dots ,n\end{array}$$ (4)

We established by proof that the final density distribution s_N has a convergent limit as described by Eq. (5).

$$\begin{array}{l}\underset{N\to \infty }{\text{lim}}{s}_N\hspace{0.17em}=\hspace{0.17em}S\hspace{0.17em}=\hspace{0.17em}\{S^{(i)}\},\\ s^{(i)}\hspace{0.17em}=\hspace{0.17em}\frac{1+\sum _j{p}_{i,j}}{n+\sum _i\sum _j{p}_{i,j}},i,\hspace{0.17em}j\hspace{0.17em}=\hspace{0.17em}1,2,\dots ,n\end{array}$$ (5)

If s-ants populate quickly, M can be simply evaluated as M = P. In this situation however, a convergent property of this algorithm cannot be assured for all kinds of networks. In our experiments, it seems to be related with a scale-free feature.