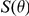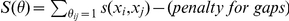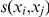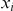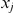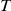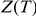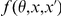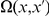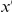Abstract
In a number of estimation problems in bioinformatics, accuracy measures of the target problem are usually given, and it is important to design estimators that are suitable to those accuracy measures. However, there is often a discrepancy between an employed estimator and a given accuracy measure of the problem. In this study, we introduce a general class of efficient estimators for estimation problems on high-dimensional binary spaces, which represent many fundamental problems in bioinformatics. Theoretical analysis reveals that the proposed estimators generally fit with commonly-used accuracy measures (e.g. sensitivity, PPV, MCC and F-score) as well as it can be computed efficiently in many cases, and cover a wide range of problems in bioinformatics from the viewpoint of the principle of maximum expected accuracy (MEA). It is also shown that some important algorithms in bioinformatics can be interpreted in a unified manner. Not only the concept presented in this paper gives a useful framework to design MEA-based estimators but also it is highly extendable and sheds new light on many problems in bioinformatics.
Introduction
In estimation problems in bioinformatics, the space of solutions is generally large and often high-dimensional. Among them, a number of fundamental problems in bioinformatics, such as alignment of biological sequences, prediction of secondary structures of RNA sequences, prediction of biological networks, and estimation of phylogenetic trees, are classified into estimation problems whose solutions are in a high-dimensional binary space. Such problems are generally difficult to solve, and the estimates are often unreliable.
The popular solutions for these problems, such as for the secondary structure of RNA with minimum free energy, are the maximum likelihood (ML) estimators. The ML estimator maximizes the probability that the estimator is exactly correct, but that probability is generally very small. Noticing the drawbacks of the ML estimators, Carvalho and Lawrence have proposed the centroid estimator, which represents an ensemble of all the possible solutions and minimizes the expected Hamming loss of the prediction [1].
In this paper, we conduct a theoretical analysis of estimation problems in high-dimensional binary space, and present examples and solutions in bioinformatics. The theories in this paper provide a unified framework for designing superior estimators for estimation problems in bioinformatics. The estimators discussed in this paper, including the ML estimator and the centroid estimator, are formalized as maximum expected gain (MEG) estimators, which maximize the estimator-specific gain functions with respect to the given probability distribution. The objective of the estimation is not always to find the exact solution with an extremely small probability or to find the solution with the minimum Hamming loss, but rather to find the most accurate estimator. Therefore, we adopt the principle of maximum expected accuracy (MEA), which has been successfully applied to various problems in bioinformatics, such as the alignment of biological sequences [2]–[4], the secondary structure prediction of RNA [5]–[8] and other applications [9]–[11].
Theoretical analysis, however, shows that those MEA estimators are not always robust with respect to accuracy measures. To address this, we previously proposed the  -centroid estimator in a few specific problems [4], [12]. In this paper, in order to make the
-centroid estimator in a few specific problems [4], [12]. In this paper, in order to make the  -centroid estimator easily applicable to other estimation problems, we introduce an abstract form of the
-centroid estimator easily applicable to other estimation problems, we introduce an abstract form of the  -centroid estimator, which is defined on general binary spaces and designed to fit to the commonly used accuracy measures. The
-centroid estimator, which is defined on general binary spaces and designed to fit to the commonly used accuracy measures. The  -centroid estimator is a generalization of the centroid estimator, and offers a more robust framework for estimators than the previous estimators. We extend the theory of maximum expected gain (MEG) estimators and
-centroid estimator is a generalization of the centroid estimator, and offers a more robust framework for estimators than the previous estimators. We extend the theory of maximum expected gain (MEG) estimators and  -centroid estimators for two advanced problems: the estimators that represent the common solutions for multiple entries, and the estimators for marginalized probability distributions.
-centroid estimators for two advanced problems: the estimators that represent the common solutions for multiple entries, and the estimators for marginalized probability distributions.
Materials and Methods
Problem 1 (Pairwise alignment of two biological sequences)
Given a pair of biological (DNA, RNA, protein) sequences
 and
and
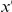 , predict their alignment as a point in
, predict their alignment as a point in
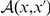 , the space of all the possible alignments of
, the space of all the possible alignments of
 and
and
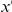 .
.
Problem 2 (Prediction of secondary structures of RNA sequences)
Given an RNA sequence
 , predict its secondary structure as a point in
, predict its secondary structure as a point in
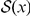 , the space of all the possible secondary structures of
, the space of all the possible secondary structures of
 .
.
A point in 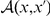 , can be represented as a binary vector of
, can be represented as a binary vector of 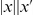 dimensions by denoting the aligned bases across the two sequences as “1” and the remaining pairs of bases as “0”. A point in
dimensions by denoting the aligned bases across the two sequences as “1” and the remaining pairs of bases as “0”. A point in 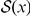 can also be represented as a binary vector of
can also be represented as a binary vector of 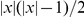 dimensions, which represent all the pairs of the base positions in
dimensions, which represent all the pairs of the base positions in  , by denoting the base pairs in the secondary structures as “1”. In each problem, the predictive space (
, by denoting the base pairs in the secondary structures as “1”. In each problem, the predictive space (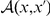 or
or 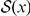 ) is a subset of a binary space (
) is a subset of a binary space (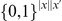 or
or 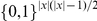 ) because the combinations of aligned bases or base pairs are restricted (see “Discrete (binary) spaces in bioinformatics” in Appendices for more formal definitions). Therefore, Problem 1 and Problem 2 are special cases of the following more general problem:
) because the combinations of aligned bases or base pairs are restricted (see “Discrete (binary) spaces in bioinformatics” in Appendices for more formal definitions). Therefore, Problem 1 and Problem 2 are special cases of the following more general problem:
Problem 3 (Estimation problem on a binary space)
Given a data set
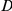 and a predictive space
and a predictive space
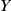 (a set of all candidates of a prediction), which is a subset of
(a set of all candidates of a prediction), which is a subset of
 -dimensional binary vectors
-dimensional binary vectors
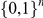 , that is,
, that is,
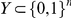 , predict a point
, predict a point
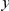 in the predictive space
in the predictive space
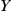 .
.
Not only Problem 1 and Problem 2 but also a number of other problems in bioinformatics are formulated as Problem 3, including the prediction of biological networks and the estimation of phylogenetic trees (Problem 4).
To discuss the stochastic character of the estimators, the following assumption is introduced.
Assumption 1 (Existence of probability distribution)
In Problem 3, there exists a probability distribution
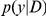 on the predictive space
on the predictive space
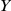 .
.
For Problem 3 with Assumption 1, we have the following Bayesian maximum likelihood (ML) estimator.
Definition 1 (Bayesian ML estimator [1] ) For Problem 3 with Assumption 1, the estimator
which maximizes the Bayesian posterior probability
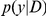 , is referred to as a Bayesian maximum likelihood (ML) estimator.
, is referred to as a Bayesian maximum likelihood (ML) estimator.
For problems classified as Problem 3, Bayesian ML estimators have dominated the field of estimators in bioinformatics for years. The classical solutions of Problem 1 and Problem 2 are regarded as Bayesian ML estimators with specific probability distributions, as seen in the following examples.
Example 1 (Pairwise alignment with maximum score)
In Problem 1 with a scoring model (e.g., gap costs and a substitution matrix), the distribution
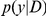 in Assumption 1 is derived from the Miyazawa model
[13]
(See “Probability distributions
in Assumption 1 is derived from the Miyazawa model
[13]
(See “Probability distributions
 on
on  ” in
Appendices
), and the Bayesian ML estimator is equivalent to the alignment that has the highest similarity score.
” in
Appendices
), and the Bayesian ML estimator is equivalent to the alignment that has the highest similarity score.
Example 2 (RNA structure with minimum free energy)
In Problem 2 with a McCaskill energy model
[14]
, the distribution
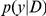 in Assumption 1 can be obtained with the aid of thermodynamics (See “Probability distributions
in Assumption 1 can be obtained with the aid of thermodynamics (See “Probability distributions
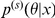 on
on
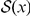 ” in
Appendices
for details), and the Bayesian ML estimator is equivalent to the secondary structure that has the minimum free energy (MFE).
” in
Appendices
for details), and the Bayesian ML estimator is equivalent to the secondary structure that has the minimum free energy (MFE).
When a stochastic model such as a pair hidden Markov model (pair HMM) in Problem 1 or a stochastic context-free grammar (SCFG) in Problem 2 is assumed in such problems, the distribution and the ML estimator are derived in a more direct manner.
The Bayesian ML estimator regards the solution which has the highest probability as the most likely one. To provide more general criteria for good estimators, here we define the gain function that gives the gain for the prediction, and the maximum expected gain (MEG) estimator that maximizes the expected gain.
Definition 2 (Gain function)
In Problem 3, for a point
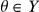 and its prediction
and its prediction
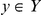 , a gain function is defined as
, a gain function is defined as
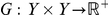 ,
,
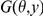 .
.
Definition 3 (MEG estimator) In Problem 3 with Assumption 1, the maximum expected gain (MEG) estimator is defined as
If the gain function is designed according to the accuracy measures of the target problem, the MEG estimator is considered as the maximum expected accuracy (MEA) estimator, which has been successfully applied in bioinformatics (e.g., [9]).Although in estimation theory a loss function that should be minimized is often used, in order to facilitate the understanding of the relationship with the MEA, in this paper, we use a gain function that should be maximized.
The MEG estimator for the gain function 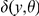 is the ML estimator. Although this means that the ML estimator maximizes the probability that the estimator is identical to the true value, there is an extensive collection of suboptimal solutions and the probability of the ML estimator is extremely small in cases where
is the ML estimator. Although this means that the ML estimator maximizes the probability that the estimator is identical to the true value, there is an extensive collection of suboptimal solutions and the probability of the ML estimator is extremely small in cases where  in Problem 3 is large. Against this background, Carvalho and Lawrence proposed the centroid estimator, which takes into account the overall ensemble of solutions [1]. The centroid estimator can be defined as an MEG estimator for a pointwise gain function as follows:
in Problem 3 is large. Against this background, Carvalho and Lawrence proposed the centroid estimator, which takes into account the overall ensemble of solutions [1]. The centroid estimator can be defined as an MEG estimator for a pointwise gain function as follows:
Definition 4 (Pointwise gain function)
In Problem 3, for a point
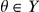 and its prediction
and its prediction
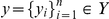 , a gain function
, a gain function
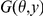 written as
written as
| (1) |
where
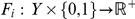 (
(
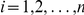 ), is referred to as a pointwise gain function.
), is referred to as a pointwise gain function.
Definition 5 (Centroid estimator
[1]
)
In Problem 3 with Assumption 1, a centroid estimator is defined as an MEG estimator for the pointwise gain function given in Eq.
(1)
by defining
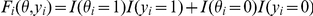 .
.
Throughout this paper, 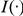 is the indicator function that takes a value of 1 or 0 depending on whether the condition constituting its argument is true or false. The centroid estimator is equivalent to the expected Hamming loss minimizer [1]. If we can maximize the pointwise gain function independently in each dimension, we can obtain the following consensus estimator, which can be easily computed.
is the indicator function that takes a value of 1 or 0 depending on whether the condition constituting its argument is true or false. The centroid estimator is equivalent to the expected Hamming loss minimizer [1]. If we can maximize the pointwise gain function independently in each dimension, we can obtain the following consensus estimator, which can be easily computed.
Definition 6 (Consensus estimator
[1]
)
In Problem 3 with Assumption 1, the consensus estimator 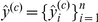 for a pointwise gain function is defined as
for a pointwise gain function is defined as
The consensus estimator is generally not contained within the predictive space  since the predictive space
since the predictive space  usually has complex constraints for each dimension (see “Discrete (binary) spaces in bioinformatics” in Appendices). Carvalho and Lawrence proved a sufficient condition for the centroid estimator to contain the consensus estimator (Theorem 2 in [1]). Here, we present a more general result, namely, a sufficient condition for the MEG estimator for a pointwise function to contain the consensus estimator.
usually has complex constraints for each dimension (see “Discrete (binary) spaces in bioinformatics” in Appendices). Carvalho and Lawrence proved a sufficient condition for the centroid estimator to contain the consensus estimator (Theorem 2 in [1]). Here, we present a more general result, namely, a sufficient condition for the MEG estimator for a pointwise function to contain the consensus estimator.
Theorem 1
In Problem 3 with Assumption 1 and a pointwise gain function, let us suppose that a predictive space
 can be written as
can be written as
| (2) |
where 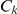 is defined as
is defined as
for an index-set
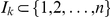 . If the pointwise gain function in Eq.
(1)
satisfies the condition
. If the pointwise gain function in Eq.
(1)
satisfies the condition
| (3) |
for every
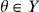 and every
and every
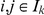 (
(
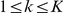 ), then the consensus estimator is in the predictive space
), then the consensus estimator is in the predictive space
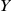 , and hence the MEG estimator contains the consensus estimator.
, and hence the MEG estimator contains the consensus estimator.
The above conditions are frequently satisfied in bioinformatics problems (see Appendices for examples).
Results
 -centroid estimator: generalized centroid estimator
-centroid estimator: generalized centroid estimator
In Problem 3, the “1”s and the “0”s in the binary vector of a prediction 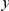 can be interpreted as positive and negative predictions, respectively. The respective numbers of true positives (TP), true negatives (TN), false positives (FP) and false negatives (FN) for a point
can be interpreted as positive and negative predictions, respectively. The respective numbers of true positives (TP), true negatives (TN), false positives (FP) and false negatives (FN) for a point 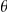 and its prediction
and its prediction 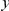 are denoted by
are denoted by 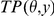 ,
, 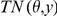 ,
, 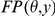 and
and 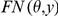 , respectively (See also Eqs (15)–(18)).
, respectively (See also Eqs (15)–(18)).
To design a superior MEG estimator, it is natural to use a gain function of the following form, which yields positive scores for the number of true predictions (TP and TN) and negative scores for those of false predictions (FP and FN):
| (4) |
where 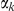 is a positive constant (
is a positive constant (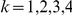 ). Note that this gain function is a pointwise gain function.
). Note that this gain function is a pointwise gain function.
This gain function is naturally compatible with commonly used accuracy measures such as sensitivity, PPV, MCC and F-score (a function of TP, TN, FP and FN; see “Evaluation measures defined using TP, TN, FP and FN” in Appendices for definitions). The following Definition 7 and Theorem 2 characterize the MEG estimator for this gain function.
Definition 7 (
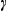 -centroid estimator)
In Problem 3 with Assumption 1 and a fixed
-centroid estimator)
In Problem 3 with Assumption 1 and a fixed
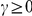 , the
, the
 -centroid estimator is defined as the MEG estimator for the pointwise gain function given in
Eq. (1)
by
-centroid estimator is defined as the MEG estimator for the pointwise gain function given in
Eq. (1)
by
| (5) |
Theorem 2
The MEG estimator for the gain function in
Eq. (4)
is equivalent to a
 -centroid estimator with
-centroid estimator with
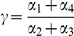 .
.
Theorem 2 (see Appendices for a formal proof) is derived from the following relations:
The  -centroid estimator maximizes the expected value of
-centroid estimator maximizes the expected value of 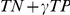 , and includes the centroid estimator as a special case where
, and includes the centroid estimator as a special case where 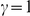 . The parameter
. The parameter  adjusts the balance between the gain from true negatives and that from true positives.
adjusts the balance between the gain from true negatives and that from true positives.
The expected value of the gain function of the  -centroid estimator is computed as follows (see Appendices for the derivation):
-centroid estimator is computed as follows (see Appendices for the derivation):
| (6) |
where
| (7) |
Since the second term in Eq. (6) does not depend on 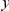 , the
, the  -centroid estimator maximizes the first term. The following theorem is obtained by assuming the additional condition described below.
-centroid estimator maximizes the first term. The following theorem is obtained by assuming the additional condition described below.
Theorem 3
In Problem 3 with Assumption 1, the predictive space
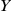 satisfies the following condition: if
satisfies the following condition: if
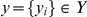 , then
, then
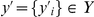 where
where
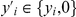 for all
for all
 . Then, the
. Then, the
 -centroid estimator is equivalent to the estimator that maximizes the sum of marginalized probabilities
-centroid estimator is equivalent to the estimator that maximizes the sum of marginalized probabilities
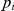 that are greater than
that are greater than
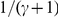 in the prediction.
in the prediction.
The condition is necessary to obtain 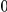 for the
for the  that produces negative values in the first term in Eq. (6). Problem 2, Problem 1, and many other typical problems in bioinformatics satisfy this condition. Because the pointwise gain function of the
that produces negative values in the first term in Eq. (6). Problem 2, Problem 1, and many other typical problems in bioinformatics satisfy this condition. Because the pointwise gain function of the  -centroid estimator satisfies Eq. (3) in Theorem 1, we can prove the following Corollary 1.
-centroid estimator satisfies Eq. (3) in Theorem 1, we can prove the following Corollary 1.
Corollary 1 (
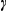 -centroid estimator for
-centroid estimator for
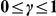 )
In Problem 3 with Assumption 1, the predictive space
)
In Problem 3 with Assumption 1, the predictive space
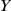 is given in the same form in
Eq. (2)
of Theorem 1. Then, the
is given in the same form in
Eq. (2)
of Theorem 1. Then, the
 -centroid estimator for
-centroid estimator for
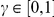 contains its consensus estimator. Moreover, the consensus estimator is identical to the following estimator
contains its consensus estimator. Moreover, the consensus estimator is identical to the following estimator
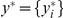 :
:
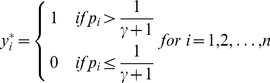 |
(8) |
where
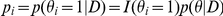 .
.
Here, 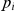 is the marginalized probability of the distribution for the
is the marginalized probability of the distribution for the  -th dimension of the predictive space. In Problem 1, it is known as the alignment probability, which is defined as the probability of each pair of positions across the two sequences being aligned. In Problem 2, it is known as the base pairing probability, which is defined as the probability of each pair of positions forming a base pair in the secondary structure. These marginalized probabilities can be calculated by using dynamic programming algorithms, such as the forward-backward algorithm and the McCaskill algorithm, depending on the model of the distributions. (see “Probability distributions on discrete spaces” in Appendices for those distributions).
-th dimension of the predictive space. In Problem 1, it is known as the alignment probability, which is defined as the probability of each pair of positions across the two sequences being aligned. In Problem 2, it is known as the base pairing probability, which is defined as the probability of each pair of positions forming a base pair in the secondary structure. These marginalized probabilities can be calculated by using dynamic programming algorithms, such as the forward-backward algorithm and the McCaskill algorithm, depending on the model of the distributions. (see “Probability distributions on discrete spaces” in Appendices for those distributions).
Corollary 1 does not hold for 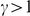 , but in typical problems in bioinformatics the
, but in typical problems in bioinformatics the  -centroid estimator for
-centroid estimator for 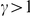 can be calculated efficiently by using dynamic programming, as shown in the following examples.
can be calculated efficiently by using dynamic programming, as shown in the following examples.
Example 3 (
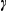 -centroid estimator of pairwise alignment)
In Problem 1 with Assumption 1, the
-centroid estimator of pairwise alignment)
In Problem 1 with Assumption 1, the
 -centroid estimator maximizes the sum of the alignment probabilities which are greater than
-centroid estimator maximizes the sum of the alignment probabilities which are greater than
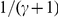 (Theorem 3), and for
(Theorem 3), and for
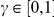 it can be given as the consensus estimator calculated from
Eq. (8)
(Corollary 1). For
it can be given as the consensus estimator calculated from
Eq. (8)
(Corollary 1). For
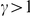 , the
, the
 -centroid estimator is obtained by using a dynamic programming algorithm with the same type of iterations as in the Needleman-Wunsch algorithm:
-centroid estimator is obtained by using a dynamic programming algorithm with the same type of iterations as in the Needleman-Wunsch algorithm:
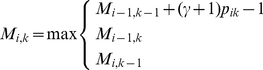 |
(9) |
where
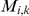 stores the optimal value of the alignment between two sub-sequences,
stores the optimal value of the alignment between two sub-sequences,
 and
and
 (see “Secondary structure prediction of an RNA sequence (Problem 2)” in
Appendices
for detailed descriptions).
(see “Secondary structure prediction of an RNA sequence (Problem 2)” in
Appendices
for detailed descriptions).
Example 4 (
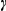 -centroid estimator for prediction of secondary structures)
In Problem 2 with Assumption 1, the
-centroid estimator for prediction of secondary structures)
In Problem 2 with Assumption 1, the
 -centroid estimator maximizes the sum of the base pairing probabilities that are greater than
-centroid estimator maximizes the sum of the base pairing probabilities that are greater than
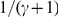 (Theorem 3), and for
(Theorem 3), and for
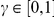 it can be given as the consensus estimator calculated from
Eq. (8)
(Corollary 1). For
it can be given as the consensus estimator calculated from
Eq. (8)
(Corollary 1). For
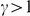 , the
, the
 -centroid estimator is obtained with the aid of a dynamic programming algorithm with the same type of iterations as in the Nussinov algorithm:
-centroid estimator is obtained with the aid of a dynamic programming algorithm with the same type of iterations as in the Nussinov algorithm:
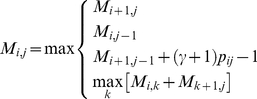 |
(10) |
where
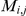 stores the best score of the sub-sequence
stores the best score of the sub-sequence
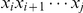 (see “Pairwise alignment of biological sequences (Problem 1)” in
Appendices
for the detail descriptions).
(see “Pairwise alignment of biological sequences (Problem 1)” in
Appendices
for the detail descriptions).
The  -centroid estimators are implemented in LAST [4] for Problem 1 and in CentroidFold [12], [15] for Problem 2.
-centroid estimators are implemented in LAST [4] for Problem 1 and in CentroidFold [12], [15] for Problem 2.
Problem 4 (Estimation of phylogenetic trees)
Given a set of operational taxonomic units
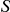 , predict their phylogenetic trees (unrooted and multi-branched trees) as a point in
, predict their phylogenetic trees (unrooted and multi-branched trees) as a point in
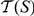 , the space of all the possible phylogenetic trees of
, the space of all the possible phylogenetic trees of
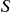 .
.
The phylogenetic tree in 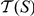 is represented as a binary vector with
is represented as a binary vector with 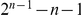 dimension where
dimension where  is the number of units in
is the number of units in 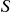 , based on partition of
, based on partition of  by cutting every edge in the tree (see “The space of phylogenetic trees:
by cutting every edge in the tree (see “The space of phylogenetic trees: 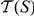 ” in Appendices for details). A sampling algorithm can be used to estimate the partitioning probabilities approximately [16].
” in Appendices for details). A sampling algorithm can be used to estimate the partitioning probabilities approximately [16].
Example 5 (
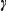 -centroid estimator of phylogenetic estimation)
In Problem 4 with Assumption 1, the
-centroid estimator of phylogenetic estimation)
In Problem 4 with Assumption 1, the
 -centroid estimator maximizes the number of the partitioning probabilities which are greater than
-centroid estimator maximizes the number of the partitioning probabilities which are greater than
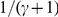 (Theorem 3), and for
(Theorem 3), and for
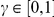 it can be give as the consensus estimator calculated from
Eq. (8)
(Corollary 1) (see “Estimation of phylogenetic trees (Problem 4)” in
Appendices
for details).
it can be give as the consensus estimator calculated from
Eq. (8)
(Corollary 1) (see “Estimation of phylogenetic trees (Problem 4)” in
Appendices
for details).
Because the Hamming distance between two trees in 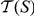 is known as topological distance [17], the 1-centroid estimator minimizes the expected topological distance. In contrast to Example 3 and Example 4, it appears that no method can efficiently compute the
is known as topological distance [17], the 1-centroid estimator minimizes the expected topological distance. In contrast to Example 3 and Example 4, it appears that no method can efficiently compute the  -centroid estimator with
-centroid estimator with 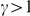 in Example 5. Despite the difficulties of the application to phylogenetic trees, recently, a method applying the concept of generalized centroid estimators was developed [18].
in Example 5. Despite the difficulties of the application to phylogenetic trees, recently, a method applying the concept of generalized centroid estimators was developed [18].
Generalized centroid estimators for representative prediction
Predictions based on probability distributions on the predictive space were discussed in the previous sections. However, there are certain even more complex problems in bioinformatics, as illustrated by the following example.
Problem 5 (Prediction of common secondary structures of RNA sequences)
Given a set of RNA sequences
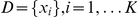 and their multiple alignment of length
and their multiple alignment of length
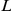 and the same energy model for each RNA sequence, predict their common secondary structure as a point in
and the same energy model for each RNA sequence, predict their common secondary structure as a point in
 , which is the space of all possible secondary structures of length
, which is the space of all possible secondary structures of length
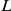 .
.
In the case of Problem 5, although the probability distribution is not implemented in the predictive space, each RNA sequence 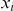 has a probability distribution on its secondary structure derived from the energy model. Therefore, the theories presented in the previous section cannot be applied directly to this problem. However, if we devise a new type of gain function that connects the predictive space with the parameter space of the secondary structure of each RNA sequence, we can calculate the expected gain over the distribution on the parameter spaces of RNA sequences. In order to account for this type of problem in general, we introduce Assumption 2 and Definition 8 as follows.
has a probability distribution on its secondary structure derived from the energy model. Therefore, the theories presented in the previous section cannot be applied directly to this problem. However, if we devise a new type of gain function that connects the predictive space with the parameter space of the secondary structure of each RNA sequence, we can calculate the expected gain over the distribution on the parameter spaces of RNA sequences. In order to account for this type of problem in general, we introduce Assumption 2 and Definition 8 as follows.
Assumption 2
In Problem 3 there exists a probability distribution
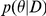 on the parameter space
on the parameter space
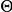 which might be different from the predictive space
which might be different from the predictive space
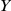 .
.
Definition 8 (Generalized gain function)
In Problem 3 with Assumption 2, for a point
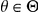 and a prediction
and a prediction
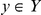 , a generalized gain function is defined as
, a generalized gain function is defined as
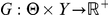 ,
,
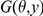 .
.
It should be emphasized that the MEG estimator (Definition 3), pointwise gain function (Definition 4) and Theorem 1 can be extended to the generalized gain function.
In the case of Problem 5, for example, the parameter space is the product of the spaces of the secondary structures of each RNA sequence, and the probability distribution is the product of the distributions of secondary structures of each RNA sequence. Here, the general form of the problem of representative prediction is introduced.
Problem 6 (Representative prediction)
In Problem 3 with Assumption 2, if the parameter space is represented as a product space (
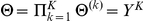 ) and the distribution of
) and the distribution of
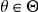 has the form
has the form
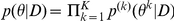 , predict a point
, predict a point
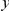 in the predictive space
in the predictive space
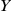 .
.
The generalized gain function for the representative prediction should be chosen such that the prediction reflects as much as each data entry. Therefore, it is natural to use the following generalized gain function that integrates the gain for each parameter.
Definition 9 (Homogeneous generalized gain function) In Problem 6, a homogeneous generalized gain function is defined as
where
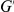 is the gain function in Definition 2.
is the gain function in Definition 2.
Definition 10 (Representative estimator)
In Problem 6, given a homogeneous generalized gain function
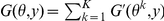 , the MEG estimator defined as
, the MEG estimator defined as
is referred to as the representative estimator.
Proposition 1
The representative estimator is equivalent to an MEG estimator with averaged probability distribution on the predictive space
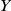 :
:
and a gain function
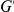 .
.
This proposition shows that a representative prediction problem with any homogeneous generalized gain function can be solved in a manner similar to Problem 3 (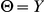 ) with averaged probability distribution. Therefore, the
) with averaged probability distribution. Therefore, the  -centroid estimator for a representative prediction satisfies Corollary 2.
-centroid estimator for a representative prediction satisfies Corollary 2.
Corollary 2
In Problem 6, the representative estimator where
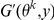 is the gain function of the
is the gain function of the
 -centroid estimator on
-centroid estimator on
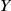 , is the
, is the
 -centroid estimator for the averaged probability distribution and satisfies the same properties in Theorem 2, Theorem 3, and Corollary 1.
-centroid estimator for the averaged probability distribution and satisfies the same properties in Theorem 2, Theorem 3, and Corollary 1.
Estimators based on marginal probabilities
In the previous section, we introduced Assumption 2, where there is a parameter space 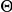 that can be different from the predictive space
that can be different from the predictive space 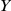 , and we discussed the problem of representative prediction. In this section, we discuss another type of problems where
, and we discussed the problem of representative prediction. In this section, we discuss another type of problems where 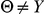 . An example is presented below.
. An example is presented below.
Problem 7 (Pairwise alignment using homologous sequences)
Given a data set
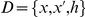 , where
, where
 and
and
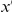 are two biological sequences to be aligned and
are two biological sequences to be aligned and
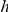 is a sequence that is homologous to both
is a sequence that is homologous to both
 and
and
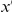 , predict a point
, predict a point
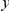 in the predictive space
in the predictive space
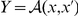 (the space of all possible alignments of
(the space of all possible alignments of
 and
and
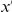 ).
).
The precise probabilistic model of this problem might include the phylogenetic tree, ancestor sequences and their alignments. Here, we assume a simpler situation where the probability distribution of all possible multiple alignments of 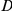 is given. We predict the pairwise alignment of two specific sequences according to the probability distribution of multiple alignments. Although the parameter space
is given. We predict the pairwise alignment of two specific sequences according to the probability distribution of multiple alignments. Although the parameter space 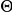 , which is the space of all the possible multiple alignments, can be parametrized using the parameters of the spaces of the alignments of all pairs that can be formed from the sequences in
, which is the space of all the possible multiple alignments, can be parametrized using the parameters of the spaces of the alignments of all pairs that can be formed from the sequences in 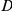 ,
, 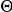 itself is not the product space of these spaces because these pairwise alignments are not independent: for
itself is not the product space of these spaces because these pairwise alignments are not independent: for 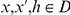 ,
, 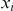 must be aligned to
must be aligned to 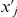 if both
if both 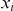 and
and 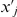 are aligned to
are aligned to 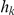 . This type of problems can be generalized as follows.
. This type of problems can be generalized as follows.
Problem 8 (Prediction in a subspace of the parameter space)
In Problem 3 with Assumption 2, if the parameter space
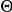 is represented as
is represented as
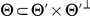 , predict a point
, predict a point
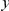 in the predictive space
in the predictive space
 .
.
For the problem of representative prediction (Problem 6), generalized gain functions on 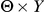 were introduced (Definition 8 and Definition 9). In contrast, in Problem 8, the values of the parameters in
were introduced (Definition 8 and Definition 9). In contrast, in Problem 8, the values of the parameters in 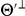 are not important, and a point in
are not important, and a point in  is predicted. In Problem 7, for example, the optimal multiple alignment of
is predicted. In Problem 7, for example, the optimal multiple alignment of 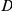 , the pairwise alignment of
, the pairwise alignment of 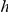 and
and  , and the pairwise alignment of
, and the pairwise alignment of 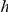 and
and 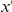 are irrelevant, but instead we predict the pairwise alignment of
are irrelevant, but instead we predict the pairwise alignment of  and
and 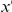 . The MEG estimator for the gain function defined on
. The MEG estimator for the gain function defined on 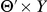 can be written as
can be written as
where 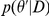 on
on  is the marginalized distribution
is the marginalized distribution
| (11) |
From the above MEG estimator, it might appear that Problem 8 is trivial. However, it is not a simple task to calculate the marginalized distribution in Eq. (11) in actual problems.
To reduce the computational cost, we change Problem 8 by introducing an approximated probability distribution on the product space  a follows.
a follows.
Problem 9 (Prediction in product space)
In Problem 3 with Assumption 2, if the parameter space
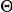 is represented as
is represented as
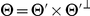 and the probability distribution on
and the probability distribution on
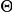 is defined as
is defined as
| (12) |
predict a point
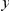 in the predictive space
in the predictive space
 .
.
This factorization of spaces and probability distributions creates a number of inconsistencies in the parameter space with respect to the original Problem 8. In other words, the approximated distribution yields non-zero values for a point that is not included in the original 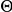 (in Problem 8) but in
(in Problem 8) but in 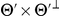 . To reduce these inconsistencies, a new type of gain function and a new estimator are introduced as follows.
. To reduce these inconsistencies, a new type of gain function and a new estimator are introduced as follows.
Definition 11 (
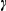 -type pointwise gain function)
In Problem 8, a
-type pointwise gain function)
In Problem 8, a
 -type pointwise gain function is defined as
-type pointwise gain function is defined as
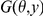 in
Eq. (1)
in Definition 4 having
in
Eq. (1)
in Definition 4 having
| (13) |
where the value
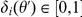 in the gain function should be designed to reduce the inconsistencies resulting from the factorization.
in the gain function should be designed to reduce the inconsistencies resulting from the factorization.
Definition 12 (Approximated
 -type estimator)
In Problem 9, with a
-type estimator)
In Problem 9, with a
 -type pointwise gain function with
-type pointwise gain function with
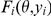 in
Eq. (13)
on
in
Eq. (13)
on
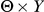 , an approximated
, an approximated
 -type estimator is defined as an MEG estimator:
-type estimator is defined as an MEG estimator:
Example 6 (PCT in pairwise alignment)
We obtain the approximate estimator for Problem 7 with the following settings. The parameter space is given as
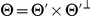 , where
, where
and the probability distribution on the parameter space
 is given as
is given as
for
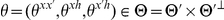 . The
. The
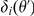 in
Eq. (13)
of the
in
Eq. (13)
of the
 -type pointwise gain function is defined as
-type pointwise gain function is defined as
The approximated
 -type estimator for this
-type estimator for this
 -type pointwise gain function is employed in a part of probabilistic consistency transformation (PCT)
[19]
, which is an important step toward accurate multiple alignments. See “Pairwise alignment using homologous sequences” in
Appendices
for precise descriptions.
-type pointwise gain function is employed in a part of probabilistic consistency transformation (PCT)
[19]
, which is an important step toward accurate multiple alignments. See “Pairwise alignment using homologous sequences” in
Appendices
for precise descriptions.
It is easily seen that Theorem 3 applies to the approximated  -type estimator if
-type estimator if 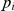 in Theorem 3 is changed as follows:
in Theorem 3 is changed as follows:
Moreover, to confirm whether approximated  -type estimator contains the consensus estimator for the same gain function, it is only necessary to check if
-type estimator contains the consensus estimator for the same gain function, it is only necessary to check if
| (14) |
instead of Eq. (3) in Theorem 1. (Note that Theorem 1 can be extended to the generalized (pointwise) gain function: see Theorem 4.)
Discussion
Properties of the  -centroid estimator
-centroid estimator
In this paper, general criteria for designing estimators are given by the maximum expected gain (MEG) estimator (Definition 3). The Bayesian ML estimator is an MEG estimator with the delta function 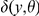 as the gain function, which means that only the probability for the “perfect match” is counted. To overcome the drawbacks of the Bayesian ML estimator, the centroid estimator [1] takes into account the overall ensemble of solutions and minimizes the expected Hamming loss. Because the Hamming loss is not the standard evaluation measures for actual problems, we have proposed an estimator of a more general type, the
as the gain function, which means that only the probability for the “perfect match” is counted. To overcome the drawbacks of the Bayesian ML estimator, the centroid estimator [1] takes into account the overall ensemble of solutions and minimizes the expected Hamming loss. Because the Hamming loss is not the standard evaluation measures for actual problems, we have proposed an estimator of a more general type, the  -centroid estimator (Definition 7), which includes the centroid estimator as a special case,
-centroid estimator (Definition 7), which includes the centroid estimator as a special case, 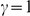 . The
. The  -centroid estimator is an MEG estimator that maximizes the expected value of
-centroid estimator is an MEG estimator that maximizes the expected value of 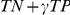 , which generally covers all possible linear combination of the numbers of true positives (TP), true negatives (TN), false positives (FP) and false negatives (FN) (Theorem 2). Since most of the evaluation measures of the prediction accuracy are functions of these numbers [20], the
, which generally covers all possible linear combination of the numbers of true positives (TP), true negatives (TN), false positives (FP) and false negatives (FN) (Theorem 2). Since most of the evaluation measures of the prediction accuracy are functions of these numbers [20], the  -centroid estimator is related to the principle of maximum expected accuracy (MEA). It should be noted that MEG estimators have been proposed that are similar to the
-centroid estimator is related to the principle of maximum expected accuracy (MEA). It should be noted that MEG estimators have been proposed that are similar to the  -centroid estimator for some specific problems, for example, the alignment metric accuracy (AMA) estimator [21] (see Appendices for the formal definition) for pairwise alignment (Problem 1) and the MEA-based estimator [5] (see Appendices for the formal definition) for prediction of secondary structure of RNA (Problem 2). However, these estimators display a bias with respect to the accuracy measures for the problem (see Eqs. (20) and (22)), and are therefore inappropriate from the viewpoint of the principles of MEA. Moreover, these estimators cannot be introduced in a general setting, that is, Problem 3. It has been also shown that the
-centroid estimator for some specific problems, for example, the alignment metric accuracy (AMA) estimator [21] (see Appendices for the formal definition) for pairwise alignment (Problem 1) and the MEA-based estimator [5] (see Appendices for the formal definition) for prediction of secondary structure of RNA (Problem 2). However, these estimators display a bias with respect to the accuracy measures for the problem (see Eqs. (20) and (22)), and are therefore inappropriate from the viewpoint of the principles of MEA. Moreover, these estimators cannot be introduced in a general setting, that is, Problem 3. It has been also shown that the  -centroid estimator outperforms the MEA-based estimator [5] for various probability distributions in computational experiments [12]. (See “Pairwise alignment of biological sequences (Problem 1)” and “Secondary structure prediction of an RNA sequence (Problem 2)” in Appendices for relations between the
-centroid estimator outperforms the MEA-based estimator [5] for various probability distributions in computational experiments [12]. (See “Pairwise alignment of biological sequences (Problem 1)” and “Secondary structure prediction of an RNA sequence (Problem 2)” in Appendices for relations between the  -centroid estimator and other estimators in Problems 1 and 2, respectively.)
-centroid estimator and other estimators in Problems 1 and 2, respectively.)
How to determine the parameter in  -centroid estimator
-centroid estimator
The parameter  in
in  -centroid estimators adjusts sensitivity and PPV (whose relation is tradeoff). MCC or F-score is often used to obtain a balanced measure between sensitivity and PPV. In RNA secondary structure predictions, it has been confirmed that the best
-centroid estimators adjusts sensitivity and PPV (whose relation is tradeoff). MCC or F-score is often used to obtain a balanced measure between sensitivity and PPV. In RNA secondary structure predictions, it has been confirmed that the best  (with respect to MCC) of the
(with respect to MCC) of the  -centroid estimator with CONTRAfold model was larger than that with McCaskill model [12]. It shows that the best
-centroid estimator with CONTRAfold model was larger than that with McCaskill model [12]. It shows that the best  (with respect to a given accuracy measure) depends on not only estimation problems but also probabilistic models for predictive space. The parameter
(with respect to a given accuracy measure) depends on not only estimation problems but also probabilistic models for predictive space. The parameter  trained by using reference structures was therefore employed as the default parameter in CentroidFold [12]. In order to select the parameter automatically (with respect to a given accuracy measure such as MCC and F-score), an approximation of maximizing expected MCC (or F-score) with the
trained by using reference structures was therefore employed as the default parameter in CentroidFold [12]. In order to select the parameter automatically (with respect to a given accuracy measure such as MCC and F-score), an approximation of maximizing expected MCC (or F-score) with the  -centroid estimator can be utilized [22].
-centroid estimator can be utilized [22].
Accuracy measures and computational efficiency
The reader might consider that it is possible to design estimators that maximize the expected MCC or F-score which balances sensitivity (SEN) and positive predictive value (PPV). However, it is much more difficult to compute such estimators in comparison with the  -centroid estimator, as described below.
-centroid estimator, as described below.
The expected value of the gain function of the  -centroid estimator can be written with marginalized probabilities as in Eq. (7), which can be efficiently computed by dynamic programming in many problems in bioinformatics, for example, the forward-backward algorithm for alignment probabilities and the McCaskill algorithm for base pairing probabilities. Under a certain condition of the predictive space, which many problems in bioinformatics satisfy, the
-centroid estimator can be written with marginalized probabilities as in Eq. (7), which can be efficiently computed by dynamic programming in many problems in bioinformatics, for example, the forward-backward algorithm for alignment probabilities and the McCaskill algorithm for base pairing probabilities. Under a certain condition of the predictive space, which many problems in bioinformatics satisfy, the  -centroid estimator maximizes the sum of marginalized probabilities greater than
-centroid estimator maximizes the sum of marginalized probabilities greater than 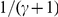 (Theorem 3). Moreover, under an additional condition of the predictive space and the pointwise gain function, which again many problems in bioinformatics satisfy, the
(Theorem 3). Moreover, under an additional condition of the predictive space and the pointwise gain function, which again many problems in bioinformatics satisfy, the  -centroid estimators for
-centroid estimators for 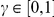 can be easily calculated as the consensus estimators, which collect in the binary predictive space the components that have marginalized probabilities greater than
can be easily calculated as the consensus estimators, which collect in the binary predictive space the components that have marginalized probabilities greater than 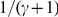 (Corollary 1). For
(Corollary 1). For 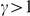 , there often exist dynamic programming algorithms that can efficiently compute the
, there often exist dynamic programming algorithms that can efficiently compute the  -centroid estimators (Examples 4 & 3), but there are certain problems, such as Problem 4, which seem to have no efficient dynamic programming algorithms.
-centroid estimators (Examples 4 & 3), but there are certain problems, such as Problem 4, which seem to have no efficient dynamic programming algorithms.
The gain function of the estimators that maximize MCC or F-score, and also SEN or PPV contain multiplication and/or division of TP, TN, FP and FN, while the gain function of the  -centroid estimator contains only the weighted sums of these values (i.e.,
-centroid estimator contains only the weighted sums of these values (i.e., 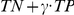 ). Therefore, the expected gain is not written with marginalized probabilities as in Eq. (7), and it is difficult to design efficient computational algorithms for those estimators. In predicting secondary structures of RNA sequences (Problem 2), for example, it is necessary to enumerate all candidate secondary structures or sample secondary structures for an approximation in order to compute the expected MCC/F-score of a predicted secondary structure.
). Therefore, the expected gain is not written with marginalized probabilities as in Eq. (7), and it is difficult to design efficient computational algorithms for those estimators. In predicting secondary structures of RNA sequences (Problem 2), for example, it is necessary to enumerate all candidate secondary structures or sample secondary structures for an approximation in order to compute the expected MCC/F-score of a predicted secondary structure.
Probability distributions are not always defined on predictive space
After discussing the standard estimation problems on a binary space where the probability distribution is defined on the predictive space, we have proposed a new category of estimation problems where the probability distribution is defined on a parameter space that differs from the predictive space (see Assumption 2). Two types of estimators for such problems, for example, estimators for representative prediction and estimators based on marginalized distribution, have been discussed.
Prediction of the common secondary structure from an alignment of RNA sequences (Problem 5) is an example of representative prediction. The probability distribution is not implemented in the predictive space, the space of common secondary structure, but each RNA sequence has a probability distribution for its secondary structure. Because the “correct” reference for the common secondary structure is not known in general, direct evaluation of the estimated common secondary structure is difficult. In the popular evaluation process for this problem, the predicted common secondary structure is mapped to each RNA sequence and compared to its reference structure. Using the homogeneous generalized gain function exactly implements this evaluation process and the MEG estimator for the averaged probability distribution is equivalent to the MEG estimator for homogeneous generalized gain function. Therefore, we can use the averaged base pairing probabilities according to the alignment as the distribution for the common secondary structure (see “Common secondary structure prediction from a multiple alignment of RNA sequences” in Appendices for detailed discussion). The representative estimator for Problem 5 is implemented in software CentroidAlifold. Another example of representative prediction is the “alignment of alignments” problem, which is the fundamental element of progressive multiple alignment of biological sequences. The evaluation process using the sum of pairs score corresponds to using the homogeneous generalized gain function. (see “Alignment between two alignments of biological sequences” in Appendices for detailed discussion).
Estimation problems of marginalized distributions can be formalized as prediction in a subspace of the parameter space (Problem 8). If we can calculate the marginalized distribution on the predictive space from the distribution on the parameter space, all general theories apply to the predictive space and the marginalized distribution. In actual problems, such as pairwise alignment using homologous sequences (Problem 7), however, computational cost for calculation of the marginalized probability is quite high. We introduced the factorized probability distribution (Eq. (12)) for approximation, the  -type pointwise gain function (Definition 11) to reduce the inconsistency caused by the factorization, and the approximated
-type pointwise gain function (Definition 11) to reduce the inconsistency caused by the factorization, and the approximated  -type estimator (Definition 12). In Problem 7, the probability consistency transformation (PCT), which is widely used for multiple sequence alignment, is interpreted as an approximated
-type estimator (Definition 12). In Problem 7, the probability consistency transformation (PCT), which is widely used for multiple sequence alignment, is interpreted as an approximated  -type estimator. Prediction of secondary structures of RNA sequences on the basis of homologous sequences [23] (see Problem 13 in Appendices) and pairwise alignment for structured RNA sequences are further examples of this type of problems.
-type estimator. Prediction of secondary structures of RNA sequences on the basis of homologous sequences [23] (see Problem 13 in Appendices) and pairwise alignment for structured RNA sequences are further examples of this type of problems.
Application of  -centroid estimator to cluster centroid
-centroid estimator to cluster centroid
In case probability distribution on the predictive space is multi-modal,  -centroid estimators can provide unreliable solutions. For example, when there are two clusters of secondary structures in predictive spaces and those structures are exclusive, the
-centroid estimators can provide unreliable solutions. For example, when there are two clusters of secondary structures in predictive spaces and those structures are exclusive, the  -centroid estimator might give a “chimeric” secondary structure whose free energy is quite high. To avoid this situation, Ding et al.
[24] proposed a notion of the cluster centroid, which is computed by the centroid estimator with a given cluster in a predictive space. We emphasize that the extension of cluster centroid by using
-centroid estimator might give a “chimeric” secondary structure whose free energy is quite high. To avoid this situation, Ding et al.
[24] proposed a notion of the cluster centroid, which is computed by the centroid estimator with a given cluster in a predictive space. We emphasize that the extension of cluster centroid by using  -centroid estimator is straightforward and would be useful.
-centroid estimator is straightforward and would be useful.
Conclusion
In this work, we constructed a general framework for designing estimators for estimation problems in high-dimensional discrete (binary) spaces. The theory is regarded as a generalization of the pioneering work conducted by Carvalho and Lawrence, and is closely related to the concept of MEA. Furthermore, we presented several applications of the proposed estimators (see Table 1 for summary) and the underlying theory. The concept presented in this paper is highly extendable and sheds new light on many problems in bioinformatics. In future research, we plan to investigate further applications of the  -centroid and related estimators presented in this paper.
-centroid and related estimators presented in this paper.
Table 1. Summary of applications in bioinformatics.
| Alignment | (1) Pairwise alignment of biological sequences | (4) Pairwise alignment of two multiple alignments | (6) Pairwise alignment using homologous sequences | |
| Section | Section | Section | Section | |
Data 
|
|
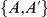
|
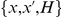
|
|
Predictive space 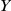
|
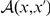
|
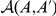
|
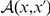
|
|
Parameter space 
|
|

|
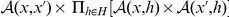
|
|
Probability 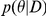
|
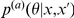
|
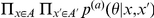
|

|
|
| Type of estimator |
 -centroid -centroid |
representative | approximate | |
| Software | LAST |

|

|
|
| Reference | [4] | [19], This work | [19], This work | |
| RNA | (2) Secondary structure prediction of RNA | (5) Common secondary structure prediction | (7) Secondary structure prediction using homologous sequences | (8) Pairwise alignment of structured RNAs |
| Section | Section | Section | Section | Section |
Data 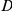
|
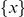
|
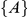
|
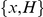
|
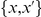
|
Predictive space 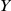
|
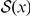
|
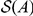
|
|
|
Parameter space 
|
|
|
|
|
Probability 
|
|
|
|
|
| Type of estimator |
 -centroid -centroid |
representative | approximate | approximate |
| Software | CentroidFold | CentroidAlifold | CentroidHomfold | CentroidAlign |
| Reference | [12] | [12], [49] | [23] | [52] |
| Phylogenetic tree | (3) Estimation of phylogenetic tree | |||
| Section | Section | |||
Data 
|
|
|||
Parameter space 
|
|
|||
Predictive space 
|
|
|||
Probability 
|
|
|||
| Type of estimator |
 -centroid -centroid |
|||
| Reference | This work |
The top row includes problems about RNA secondary structure predictions and the middle row includes problems about alignment of biological sequences. Note that the estimators in the same column corresponds to each other.
Appendices
Discrete (binary) spaces in bioinformatics
In this section, we summarize three discrete spaces that appear in this paper. These discrete spaces are often used in the definition of the predictive spaces and the parameter spaces. It should be noted that every discrete space described below is identical in form to Eq. (2).
The space of alignments of two biological sequences: 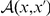
We define a space of the alignments of two biological (DNA, RNA and protein) sequences  and
and 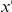 , denoted by
, denoted by 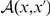 , as follows. We set
, as follows. We set 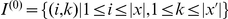 as a base index set, and a binary variable
as a base index set, and a binary variable 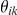 for
for 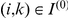 is defined by
is defined by
Then 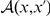 is a subset of
is a subset of 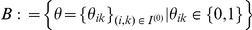 and is defined by
and is defined by
Here 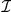 is a set of index-sets:
is a set of index-sets:
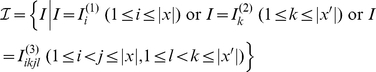 |
where
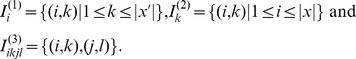 |
The inclusion 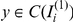 means that position
means that position  in the sequence
in the sequence  aligns with at most one position in the sequence
aligns with at most one position in the sequence 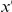 in the alignment
in the alignment 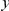 ,
, 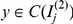 means that position
means that position 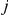 in the sequence
in the sequence 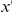 aligns with at most one position in the sequence
aligns with at most one position in the sequence  and
and 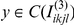 means the alignment
means the alignment 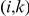 and
and 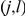 is not crossing. Note that
is not crossing. Note that 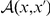 depends on only the length of two sequences, namely,
depends on only the length of two sequences, namely, 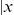 and
and 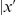 .
.
The space of secondary structures of RNA: 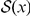
We define a space of the secondary structures of an RNA sequence  , denoted by
, denoted by 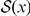 , as follows. We set
, as follows. We set 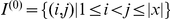 as a base index set, and a binary variable
as a base index set, and a binary variable 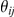 for
for 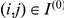 is defined by
is defined by
Then 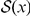 is a subset of
is a subset of 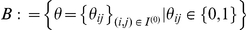 and is defined by
and is defined by
Here 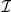 is a set of index-sets
is a set of index-sets
where
The inclusion 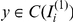 means that position
means that position  in the sequence
in the sequence  belongs to at most one base-pair in a secondary structure
belongs to at most one base-pair in a secondary structure 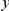 , and
, and 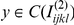 means two base-pairs whose relation is pseudo-knot are not allowed in
means two base-pairs whose relation is pseudo-knot are not allowed in 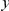 . Note that
. Note that 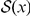 depends on only the length of the RNA sequence
depends on only the length of the RNA sequence  , that is,
, that is, 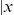 .
.
The space of phylogenetic trees: 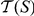
We define a space of phylogenetic trees (unrooted and multi-branch trees) of a set of 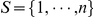 , denoted by
, denoted by 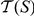 , as follows. We set
, as follows. We set 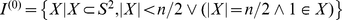 , where
, where 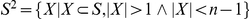 , as a base index set and we define binary variables
, as a base index set and we define binary variables 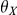 for
for 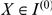 by
by
 |
Then 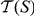 is a subset of
is a subset of 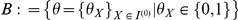 and is defined by
and is defined by
where 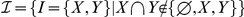 . Note that
. Note that 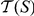 depends on only the number of elements in
depends on only the number of elements in 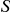 . We now give several properties of
. We now give several properties of 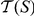 that follow directly from the definition.
that follow directly from the definition.
Lemma 1
The number of elements in
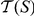 (i.e.
(i.e.
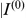 ) is equal to
) is equal to
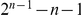 where
where
 .
.
Lemma 2
The topological distance [17]
between two phylogenetic trees
 and
and
 in
in
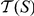 is
is
where
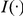 is the indicator function.
is the indicator function.
Remark 1
If we assume the additional condition
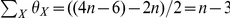 , then
, then
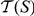 is a set of binary trees.
is a set of binary trees.
Probability distributions on discrete spaces
We use three probability distributions in this paper.
Probability distributions 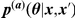 on
on 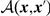
For two protein sequences  and
and 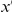 , a probability distribution
, a probability distribution 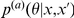 over the space
over the space 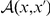 , which is the space of pairwise alignments of
, which is the space of pairwise alignments of  and
and 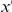 defined in the previous section, is given by the following models.
defined in the previous section, is given by the following models.
- Pair Hidden Markov Model (pair HMM) [19]:
where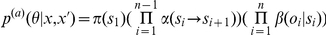
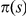 is the initial probability of starting in state
is the initial probability of starting in state  ,
, 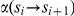 is the transition probability from
is the transition probability from 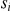 to
to 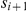 and
and 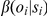 is the omission probability for either a single letter or aligner residue pair
is the omission probability for either a single letter or aligner residue pair 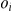 in the state
in the state 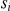 .
.
Remark 2
Strictly speaking, the alignment space in the pair hidden Markov model and the CONTRAlign model consider the patterns of gaps. In these cases, we obtain the probability space on
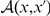 by a marginalization.
by a marginalization.
Probability distributions 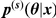 on
on 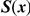
For an RNA sequence  , a probability distribution
, a probability distribution 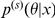 over
over 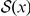 , which is the space of secondary structures of
, which is the space of secondary structures of  defined in the previous section is given by the following models.
defined in the previous section is given by the following models.
- McCaskill model [14]: This model is based on the energy models for secondary structures of RNA sequences and is defined by
where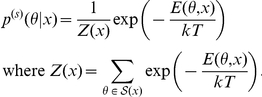
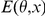 denotes the energy of the secondary structure that is computed using the energy parameters of Turner Lab [27],
denotes the energy of the secondary structure that is computed using the energy parameters of Turner Lab [27], 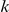 and
and 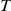 are constants and
are constants and 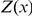 is the normalization term known as the partition function.
is the normalization term known as the partition function. - Stochastic Context free grammars (SCFGs) model [28]:
where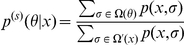
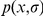 is the joint probability of generating the parse
is the joint probability of generating the parse  and is given by the product of the transition and emission probabilities of the SCFG model and
and is given by the product of the transition and emission probabilities of the SCFG model and 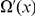 is all parses of
is all parses of  ,
, 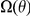 is all parses for a given
is all parses for a given 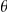 .
. - CONTRAfold (CRFs; conditional random fields) model [5]: This model gives us the best performance on secondary structure prediction although it is not based on the energy model.
where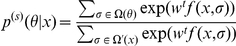
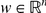 ,
, 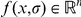 is the feature vector for
is the feature vector for  in parse
in parse  ,
, 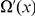 is all parses of
is all parses of  ,
, 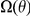 is all parses for a given
is all parses for a given 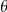 .
.
Probability distributions 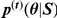 on
on 
A probability distribution 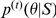 on
on  is given by probabilistic models of phylogenetic trees, for example, [29], [ 30]. Those models give a probability distribution on binary trees and we should marginalize these distributions for multi-branch trees.
is given by probabilistic models of phylogenetic trees, for example, [29], [ 30]. Those models give a probability distribution on binary trees and we should marginalize these distributions for multi-branch trees.
Evaluation measures defined using TP, TN, FP and FN
There are several evaluation measures of a prediction in estimation problems for which we have a reference (correct) prediction in Problem 3. The Sensitivity (SEN), Positive Predictive Value (PPV), Matthew's correlation coefficient (MCC) and F-score for a prediction are defined as follows.
where TP (the number of true positive), TN (the number of true negative), FP (the number of false positive) and FN (the number of false negative) are defined by
| (15) |
| (16) |
| (17) |
| (18) |
It should be noted that these measures can be written as a function of TP, TN, FP and FN. See [20] for other evaluation measures.
Schematic diagrams of representative and approximated  -type estimators
-type estimators
The schematic diagrams of the MEG estimator (Definition 3), the representative estimator (Definition 10) and the approximated  -type estimator (Definition 12) are shown in Figure 1, Figure 2 and Figure 3, respectively.
-type estimator (Definition 12) are shown in Figure 1, Figure 2 and Figure 3, respectively.
Figure 1. Schematic diagram of the MEG estimator (Definition 3).
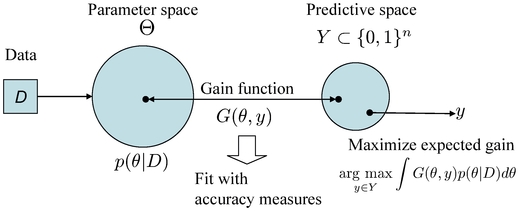
Figure 2. Schematic diagram of the representative estimator (Definition 10).
The parameter space  is a product space and is different from the predictive space
is a product space and is different from the predictive space  .
.
Figure 3. Schematic diagram of the approximated 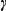 -type estimator (Definition 12).
-type estimator (Definition 12).
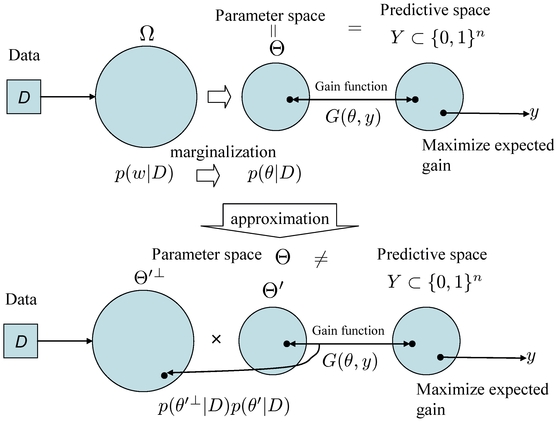
The estimator in the top figure shows the  -centroid estimator with the marginalized probability distribution, and the one in the bottom figure shows its approximation.
-centroid estimator with the marginalized probability distribution, and the one in the bottom figure shows its approximation.
Applications in bioinformatics
In this section we describe several applications to bioinformatics of the general theories. Some of these applications have already been published. In those cases, we briefly explain the applications and the readers should see the original paper for further descriptions as well as the computational experiments. All of the applications in this section are summarized in Table 1.
Pairwise alignment of biological sequences (Problem 1)
The pairwise alignment of biological (DNA, RNA, protein) sequences (Problem 1) is another fundamental and important problem of sequence analysis in bioinformatics (cf. [31]).
The  -centroid estimator for Problem 1 can be introduced as follows:
-centroid estimator for Problem 1 can be introduced as follows:
Estimator 1 (
 -centroid estimator for Problem∼:align)
For Problem 1, we obtain the
-centroid estimator for Problem∼:align)
For Problem 1, we obtain the
 -centroid estimator where the predictive space
-centroid estimator where the predictive space
 is equal to
is equal to
 and the probability distribution on
and the probability distribution on
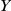 is taken by
is taken by
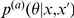 .
.
First, Theorem 2 and the definition of 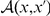 lead to the following property.
lead to the following property.
Property 1 (A relation of Estimator 1 with accuracy measures)
The
 -centroid estimator for Problem 1 is suitable for the accuracy measures: SEN, PPV, MCC and F-score with respect to the aligned-bases in the predicted alignment.
-centroid estimator for Problem 1 is suitable for the accuracy measures: SEN, PPV, MCC and F-score with respect to the aligned-bases in the predicted alignment.
Note that accurate prediction of aligned-bases is important for the analysis of alignments, for example, in phylogenetic analysis. Therefore, the measures in above are often used in evaluations of alignments e.g. [4].
The marginalized probability 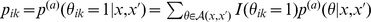 is called the aligned-base (matching) probability in this paper. The aligned-base probability matrix
is called the aligned-base (matching) probability in this paper. The aligned-base probability matrix 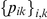 can be computed by the forward-backward algorithm whose time complexity is equal to
can be computed by the forward-backward algorithm whose time complexity is equal to 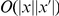 [31]. Now, Theorem 3 leads to the following property.
[31]. Now, Theorem 3 leads to the following property.
Property 2 (Computation of Estimator 1)
The pairwise alignment of Estimator 1 is found by maximizing the sum of aligned-base probabilities
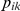 (of the aligned-bases in the predicted alignment) that are larger than
(of the aligned-bases in the predicted alignment) that are larger than
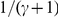 . Therefore, it can be computed by a Needleman-Wunsch-style dynamic programming (DP) algorithm
[32]
after calculating the aligned-base matrix
. Therefore, it can be computed by a Needleman-Wunsch-style dynamic programming (DP) algorithm
[32]
after calculating the aligned-base matrix
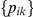 :
:
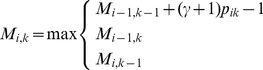 |
(19) |
where
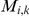 stores the optimal value of the alignment between two sub-sequences,
stores the optimal value of the alignment between two sub-sequences,
 and
and
 .
.
The time complexity of the recursion of the DP algorithm in Eq. (19) is equal to 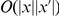 , so the total computational cost for predicting the secondary structure of the
, so the total computational cost for predicting the secondary structure of the  -centroid estimator remains
-centroid estimator remains 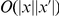 .
.
By using Corollary 1, we can predict the pairwise alignment of Estimator 1 with 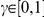 without using the DP algorithm in Eq. (19).
without using the DP algorithm in Eq. (19).
Property 3 (Computation of Estimator 1 with
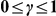 )
The pairwise alignment of the
)
The pairwise alignment of the
 -centroid estimator can be predicted by collecting the aligned-bases whose probabilities are larger than
-centroid estimator can be predicted by collecting the aligned-bases whose probabilities are larger than
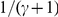 .
.
The genome alignment software called LAST (http://last.cbrc.jp/) [4], [ 33] employs the  -centroid estimator accelerated by an X-drop algorithm, and the authors indicated that Estimator 1 reduced the false-positive aligned-bases, compared to the conventional alignment (maximum score estimator).
-centroid estimator accelerated by an X-drop algorithm, and the authors indicated that Estimator 1 reduced the false-positive aligned-bases, compared to the conventional alignment (maximum score estimator).
Relations of Estimator 1 with existing estimators are summarized as follows:
A relation with the estimator by Miyazawa [13] (i.e. the centroid estimator): Estimator 1 where
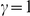 and the Miyazawa model is equivalent to the centroid estimator proposed by Miyazawa [13].
and the Miyazawa model is equivalent to the centroid estimator proposed by Miyazawa [13].A relation with the estimator by Holmes et al. [34]: Estimator 1 with sufficiently large
 is equivalent to the estimator proposed by Holmes et al., which maximizes the sum of matching probabilities in the predicted alignment.
is equivalent to the estimator proposed by Holmes et al., which maximizes the sum of matching probabilities in the predicted alignment.A relation with the estimator in ProbCons: In the program, ProbCons, Estimator 1 with pair HMM model and the sufficient large
 was used. This means that ProbCons only take care the sensitivity (or SPS) for the predicted alignment.
was used. This means that ProbCons only take care the sensitivity (or SPS) for the predicted alignment.- A relation with the estimator by Schwartz et al.: For Problem 1, Schwartz et al. [21] proposed an Alignment Metric Accuracy (AMA) estimator, which is similar to the
 -centroid estimator (see also [3]). The AMA estimator is a maximum gain estimator (Definition 3) with the following gain function.
-centroid estimator (see also [3]). The AMA estimator is a maximum gain estimator (Definition 3) with the following gain function.
for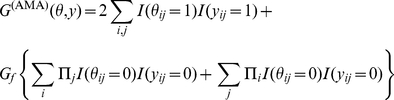
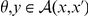 . In the above equation,
. In the above equation, 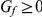 is a gap factor, which is a weight for the prediction of gaps. We refer to the function
is a gap factor, which is a weight for the prediction of gaps. We refer to the function 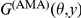 as the gain function of the AMA estimator. In a similar way to that described in the previous section, we obtain a relation between
as the gain function of the AMA estimator. In a similar way to that described in the previous section, we obtain a relation between 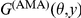 and
and 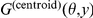 (the gain function of the
(the gain function of the  -centroid estimator). If we set
-centroid estimator). If we set 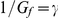 , then we obtain
, then we obtain
where
(20)
and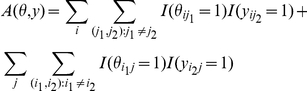
 is a value which does not depend on
is a value which does not depend on  . If
. If 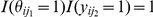 for
for 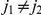 , then we obtain
, then we obtain 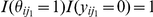 and
and 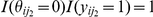 , and this means that
, and this means that 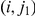 is an aligned pair that is a false negative and
is an aligned pair that is a false negative and 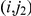 is an aligned pair that is a false positive when
is an aligned pair that is a false positive when 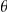 is a reference alignment and
is a reference alignment and 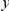 is a predicted alignment. Therefore, the terms
is a predicted alignment. Therefore, the terms 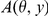 (in Eq. (20)) in the gain function of AMA are not appropriate for the evaluation measures SEN, PPV, MCC and F-score for aligned bases. In summary, the
(in Eq. (20)) in the gain function of AMA are not appropriate for the evaluation measures SEN, PPV, MCC and F-score for aligned bases. In summary, the  -centroid estimator is suitable for the evaluation measures: SEN, PPV and F-score with respect to the aligned-bases while the AMA estimator is suitable for the AMA.
-centroid estimator is suitable for the evaluation measures: SEN, PPV and F-score with respect to the aligned-bases while the AMA estimator is suitable for the AMA.
Secondary structure prediction of an RNA sequence (Problem 2)
Secondary structure prediction of an RNA sequence (Problem 2) is one of the most important problems of sequence analysis in bioinformatics. Its importance has increased due to the recent discovery of functional non-coding RNAs (ncRNAs) because the functions of ncRNAs are closely related to their secondary structures [35].
 -centroid estimator for Problem 2 can be introduced as follows:
-centroid estimator for Problem 2 can be introduced as follows:
Estimator 2 (
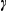 -centroid estimator for Problem 2)
For Problem 2, we obtain the
-centroid estimator for Problem 2)
For Problem 2, we obtain the
 -centroid estimator (Definition 7) where the predictive space
-centroid estimator (Definition 7) where the predictive space
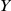 is equal to
is equal to
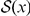 and the probability distribution on
and the probability distribution on
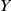 is taken by
is taken by
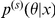 .
.
The general theory of the  -centroid estimator leads to several properties. First, the following property is derived from Theorem 2 and the definition of
-centroid estimator leads to several properties. First, the following property is derived from Theorem 2 and the definition of  .
.
Property 4 (A relation of Estimator 2 with accuracy measures)
The
 -centroid estimator for Problem 2 is suitable for the widely-used accuracy measures of the RNA secondary structure prediction: SEN, PPV and MCC with respect to base-pairs in the predicted secondary structure.
-centroid estimator for Problem 2 is suitable for the widely-used accuracy measures of the RNA secondary structure prediction: SEN, PPV and MCC with respect to base-pairs in the predicted secondary structure.
Because the base-pairs in a secondary structure are biologically important, SEN, PPV and MCC with respect to base-pairs are widely used in evaluations of RNA secondary structure prediction, for example, [5], [ 12], [ 36].
The marginalized probability 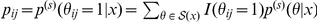 is called a base-pairing probability. The base-paring probability matrix
is called a base-pairing probability. The base-paring probability matrix 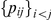 can be computed by the Inside-Outside algorithm whose time complexity is equal to
can be computed by the Inside-Outside algorithm whose time complexity is equal to 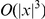 where
where 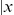 is the length of RNA sequence
is the length of RNA sequence  [14], [ 31]. Then, Theorem 3 leads to the following property.
[14], [ 31]. Then, Theorem 3 leads to the following property.
Property 5 (Computation of Estimator 2)
The secondary structure of Estimator 2 is found by maximizing the sum of the base-pairing probabilities
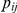 (of the base-pairs in the predicted structure) that are larger than
(of the base-pairs in the predicted structure) that are larger than
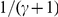 . Therefore, it can be computed by a Nussinov-style dynamic programming (DP) algorithm
[37]
after calculating the base-pairing probability matrix
. Therefore, it can be computed by a Nussinov-style dynamic programming (DP) algorithm
[37]
after calculating the base-pairing probability matrix
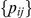 :
:
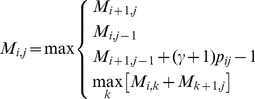 |
(21) |
where
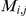 stores the best score of the sub-sequence
stores the best score of the sub-sequence
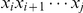 .
.
If we replace “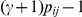 ” with “
” with “ ” in Eq. (21), the DP algorithm is equivalent to the Nussinov algorithm [37] that maximizes the number of base-pairs in a predicted secondary structure. The time complexity of the recursion of the DP algorithm in Eq. (21) is equal to
” in Eq. (21), the DP algorithm is equivalent to the Nussinov algorithm [37] that maximizes the number of base-pairs in a predicted secondary structure. The time complexity of the recursion of the DP algorithm in Eq. (21) is equal to 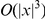 . Hence, the total computational cost for predicting the secondary structure of the
. Hence, the total computational cost for predicting the secondary structure of the  -centroid estimator remains
-centroid estimator remains 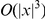 , which is the same time complexity as for standard software: Mfold [38], RNAfold
[39] and RNAstructure
[40].
, which is the same time complexity as for standard software: Mfold [38], RNAfold
[39] and RNAstructure
[40].
By using Corollary 1, we can predict the secondary structure of Estimator 2 with  without using the DP algorithm in Eq. (21).
without using the DP algorithm in Eq. (21).
Property 6 (Computation of Estimator 2 with
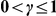 )
The secondary structure of the
)
The secondary structure of the
 -centroid estimator with
-centroid estimator with
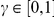 can be predicted by collecting the base-pairs whose probabilities are larger than
can be predicted by collecting the base-pairs whose probabilities are larger than
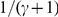 .
.
The software CentroidFold [12], [ 15] implements Estimator 2 with various probability distributions for the secondary structures, such as the CONTRAfold and McCaskill models.
Relations of Estimator 2 with other estimators are summarized as follows:
A relation with the estimator used in Sfold [41], [ 42]: Estimator 2 with
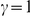 and the McCaskill model (i.e. the centroid estimator with the McCaskill model) is equivalent to the estimator used in the Sfold program.
and the McCaskill model (i.e. the centroid estimator with the McCaskill model) is equivalent to the estimator used in the Sfold program.- A relation with the estimator used in CONTRAfold: For Problem 2, Do et al. [5] proposed an MEA-based estimator, which is similar to the
 -centroid estimator. (The MEA-based estimator was also used in a recent paper [6].) The MEA-based estimator is defined by the maximum expected gain estimator (Definition 3) with the following gain function for
-centroid estimator. (The MEA-based estimator was also used in a recent paper [6].) The MEA-based estimator is defined by the maximum expected gain estimator (Definition 3) with the following gain function for 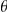 and
and 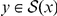 .
.
where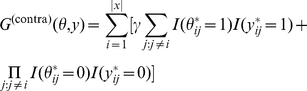
(22) 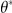 and
and 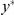 are symmetric extensions of (upper triangular matrices)
are symmetric extensions of (upper triangular matrices) 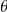 and
and  , respectively (i.e.
, respectively (i.e. 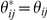 for
for 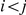 and
and 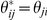 for
for 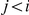 ; the definition of
; the definition of 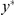 is similar.). It should be noted that, under the general estimation problem of Problem 3, the gain function of Eq. (22) cannot be introduced, and the gain function is specialized for the problem of RNA secondary structure prediction. The relation between the gain function of the
is similar.). It should be noted that, under the general estimation problem of Problem 3, the gain function of Eq. (22) cannot be introduced, and the gain function is specialized for the problem of RNA secondary structure prediction. The relation between the gain function of the  -centroid estimator (denoted by
-centroid estimator (denoted by 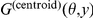 and defined in Definition 7) and the one of the MEA-based estimator is
and defined in Definition 7) and the one of the MEA-based estimator is
where the additional term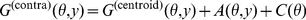
(23) 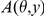 is positive for false predictions of base-pairs (i.e.,
is positive for false predictions of base-pairs (i.e.,  and
and 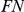 ) and
) and 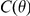 does not depend on the prediction
does not depend on the prediction 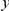 (see [12] for the proof). This means the MEA-based estimator by Do et al. possess a bias against the widely-used accuracy measures for Problem 2 (SEN, PPV and MCC of base-pairs) compared with the
(see [12] for the proof). This means the MEA-based estimator by Do et al. possess a bias against the widely-used accuracy measures for Problem 2 (SEN, PPV and MCC of base-pairs) compared with the  -centroid estimator. Thus, the
-centroid estimator. Thus, the  -centroid estimator is theoretically superior to the MEA-based estimator by Do et al. with respect to those accuracy measures. In computational experiments, the authors confirmed that the
-centroid estimator is theoretically superior to the MEA-based estimator by Do et al. with respect to those accuracy measures. In computational experiments, the authors confirmed that the  -centroid estimator is always better than the MEA-based estimator when we used the same probability distribution of secondary structures. See [12] for details of the computational experiments.
-centroid estimator is always better than the MEA-based estimator when we used the same probability distribution of secondary structures. See [12] for details of the computational experiments.
Estimation of phylogenetic trees (Problem 4)
The  -centroid estimator for Problem 4 can be introduced as follows:
-centroid estimator for Problem 4 can be introduced as follows:
Estimator 3 (
 -centroid estimator for Problem 4)
For Problem 4, we obtain the
-centroid estimator for Problem 4)
For Problem 4, we obtain the
 -centroid estimator (Definition 7) where the predictive space
-centroid estimator (Definition 7) where the predictive space
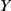 is equal to
is equal to
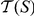 and the probability distribution on
and the probability distribution on
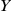 is taken by
is taken by
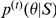 .
.
The following property is easily obtained by Theorem 2 and [17].
Property 7 (Relation of 1-centroid estimator and topological distance)
The
 -centroid estimator with
-centroid estimator with
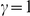 (i.e. centroid estimator) for Problem 4 minimizes expected topological distances.
(i.e. centroid estimator) for Problem 4 minimizes expected topological distances.
For 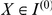 (
( is a set of partitions of
is a set of partitions of  and is formally defined in the previous section), we call the marginalized probability
and is formally defined in the previous section), we call the marginalized probability 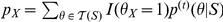 partitioning probability. However, it is difficult to compute
partitioning probability. However, it is difficult to compute 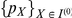 as efficiently as in the prediction of secondary structures of RNA sequences, where it seems possible to compute the base-pairing probability matrix in polynomial time by using dynamic programming). Instead, a sampling algorithm can be used for estimating
as efficiently as in the prediction of secondary structures of RNA sequences, where it seems possible to compute the base-pairing probability matrix in polynomial time by using dynamic programming). Instead, a sampling algorithm can be used for estimating 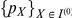 approximately [16] for this problem. Once
approximately [16] for this problem. Once 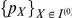 is estimated, Theorem 3 leads to the following:
is estimated, Theorem 3 leads to the following:
Property 8 (Computaion of Estimator 3)
The phylogenetic tree of Estimator 3 is found by maximizing the sum of the partitioning probabilities
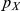 (of the partitions given by the predicted tree) that are larger than
(of the partitions given by the predicted tree) that are larger than
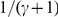 .
.
In contrast to Estimator 1 (the  -centroid estimator for secondary structure prediction of RNA sequence) and Estimator 2 (the
-centroid estimator for secondary structure prediction of RNA sequence) and Estimator 2 (the  -centroid estimator for pairwise alignment), it appears that there is no efficient method (such as dynamic programming algorithms) to computed Estimator 3 with
-centroid estimator for pairwise alignment), it appears that there is no efficient method (such as dynamic programming algorithms) to computed Estimator 3 with 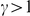 . Estimator 1 with
. Estimator 1 with 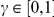 , however, can be computed by using the following property, which is directly proven by Corollary 1 and the definition of the space
, however, can be computed by using the following property, which is directly proven by Corollary 1 and the definition of the space  .
.
Property 9 (Estimator 3 with
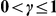 )
The
)
The
 -centroid estimator with
-centroid estimator with
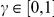 for Problem 4 contains its consensus estimator.
for Problem 4 contains its consensus estimator.
Alignment between two alignments of biological sequences
In this section we consider the problem of the alignment between two multiple alignments of biological sequences (Figure 4), which is often important in the multiple alignment of RNA sequences [19]. This problem is formulated as follows.
Figure 4. Alignment between two multiple alignments  and
and  (Problem 10).
(Problem 10).
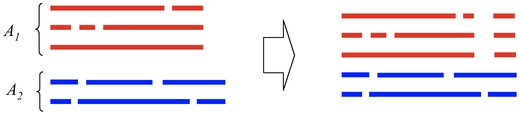
Problem 10 (Alignment between two alignments of biological sequences)
The data is represented as
 where
where
 and
and
 are alignments of biological sequences and the predictive space
are alignments of biological sequences and the predictive space
 is equal to
is equal to
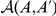 , that is, the space of the alignments of
, that is, the space of the alignments of
 and
and
 .
.
In the following,  and
and 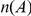 denote the length of the alignment and the number of sequences in the alignment
denote the length of the alignment and the number of sequences in the alignment  , respectively. If both
, respectively. If both  and
and 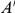 contain a single biological sequence (with no gap), Problem 10 is equivalent to conventional pairwise alignment of biological sequences (Problem 1). As in common secondary structure prediction, the representative estimator plays an important role in this application.
contain a single biological sequence (with no gap), Problem 10 is equivalent to conventional pairwise alignment of biological sequences (Problem 1). As in common secondary structure prediction, the representative estimator plays an important role in this application.
Estimator 4 (Representative estimator for Problem 10)
For Problem 10, we obtain the representative estimator (Definition 10). The gain function
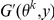 is the gain function of the
is the gain function of the
 -centroid estimator. The parameter space
-centroid estimator. The parameter space
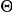 is represented as a product space
is represented as a product space
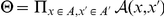 where
where
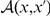 is defined in the previous section. The probability distribution on the parameter space
is defined in the previous section. The probability distribution on the parameter space
 is given by
is given by
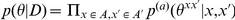 for
for
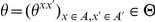 where
where
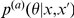 is given in the previous section (when
is given in the previous section (when
 or
or
 contains some gaps,
contains some gaps,
 is defined by the sequences with the gaps removed).
is defined by the sequences with the gaps removed).
Corollary 2 proves the following properties of Estimator 5.
Property 10 (A Relation of Estimator 4 with accuracy measures)
Estimator 4 is consistent with the accuracy process for Problem 10 that is shown in
Figure 5
. We compare every pairwise alignment of
 and
and
 with the reference alignment. These comparisons are made using TP, TN, FP and FN with respect to the aligned-bases (e.g., using SEN, PPV and F-score).
with the reference alignment. These comparisons are made using TP, TN, FP and FN with respect to the aligned-bases (e.g., using SEN, PPV and F-score).
Figure 5. An evaluation process for Problem 10.
The comparison between every pairwise alignment and the reference alignment is conducted using TP, TN, FP and FN with respect to the aligned-bases.
Property 11 (Computation of Estimator 4)
Estimator 4 can be given by maximizing the sum of probabilities
 that are larger than
that are larger than
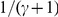 where
where
| (24) |
Therefore, the pairwise alignment of Estimator 4 can be computed by the Needleman-Wunsch-type DP algorithm of
Eq. (19)
in which we replace
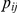 with
Eq. (24)
.
with
Eq. (24)
.
Property 12 (Computation of Estimator 4 with
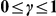 )
The Estimator 4 with
)
The Estimator 4 with
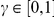 contains the consensus estimator. Moreover, the consensus estimator is identical to the estimator
contains the consensus estimator. Moreover, the consensus estimator is identical to the estimator
 :
:
 |
where
 is defined in
Eq. (24)
.
is defined in
Eq. (24)
.
The probability matrix 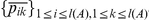 is often called an averaged aligned-base (matching) probability matrix of
is often called an averaged aligned-base (matching) probability matrix of  and
and  . In the iterative refinement of the ProbCons [19] algorithm, the existing multiple alignments are randomly partitioned into two groups and those two multiple alignments are re-aligned. This procedure is equivalent to Problem 10.
. In the iterative refinement of the ProbCons [19] algorithm, the existing multiple alignments are randomly partitioned into two groups and those two multiple alignments are re-aligned. This procedure is equivalent to Problem 10.
The estimator used in ProbCons is identical to Estimator 4 in the limit  . Therefore, the estimator used in ProbCons is a special case of Estimator 4 and it only takes into account the SEN or SPS (sum-of-pairs score) of a predicted alignment.
. Therefore, the estimator used in ProbCons is a special case of Estimator 4 and it only takes into account the SEN or SPS (sum-of-pairs score) of a predicted alignment.
Common secondary structure prediction from a multiple alignment of RNA sequences
Common secondary structure prediction from a given multiple alignment of RNA sequences plays important role in RNA research including non-coding RNA (ncRNA) [43] and viral RNAs [44], because it is useful for phylogenetic analysis of RNAs [45] and gene finding [43], [ 46]–[48]. In contrast to conventional secondary structure prediction of RNA sequences (Problem 2), the input of common secondary structure prediction is a multiple alignment of RNA sequences and the output is a secondary structure whose length is equal to the length of the input alignment (see Figure 6).
Figure 6. Common secondary structure prediction (Problem 11).
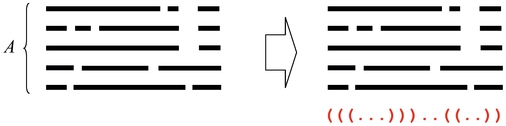
Problem 11 (Common secondary structure prediction)
The data is represented as
 where
where
 is a multiple alignment of RNA sequences and the predictive space
is a multiple alignment of RNA sequences and the predictive space
 is identical to
is identical to
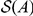 (the space of secondary structures whose length is equal to the alignment).
(the space of secondary structures whose length is equal to the alignment).
The representative estimator (Definition 10) directly gives an estimator for Problem 11.
Estimator 5 (The representative estimator for Problem 11)
For Problem 11, we obtain the representative estimator (Definition 10) as follows. The gain function
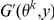 is the gain function of the
is the gain function of the
 -centroid estimator. The parameter space is equal to
-centroid estimator. The parameter space is equal to
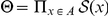 where
where
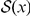 is the space of secondary structures. The probability distribution on
is the space of secondary structures. The probability distribution on
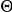 is given by
is given by
 where
where
 is the probability distribution of the secondary structures of
is the probability distribution of the secondary structures of
 after observing the alignment
after observing the alignment
 .
.
For example,  can be given by extending the
can be given by extending the  , although we have also proposed more appropriate probability distribution (see [49] for the details).
, although we have also proposed more appropriate probability distribution (see [49] for the details).
Corollary 2 proves the following properties of Estimator 5.
Property 13 (A relation of Estimator 5 with accuracy measures) Estimator 5 is consistent with an evaluation process for common secondary structure prediction: First, we map the predicted common secondary structure into secondary structures in the multiple alignment, and then the mapped structures are compared with the reference secondary structures based on TP, TN, FP and FN of the base-pairs using, for example, SEN, PPV and MCC ( Figure 7 ).
Figure 7. An evaluation process for common secondary structure prediction (Problem 11).
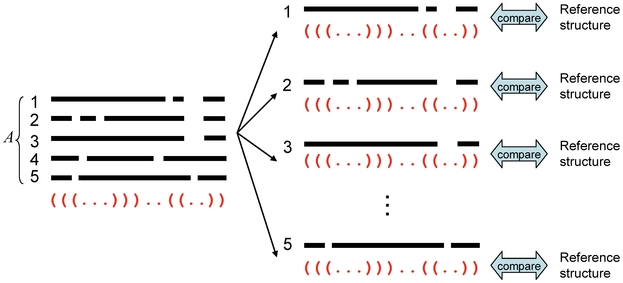
The comparison between each secondary structure and the reference secondary structure is done using TP, TN, FP and FN with respect to the base-pairs.
Much research into common secondary structure prediction employs the evaluation process in Figure 7 (e.g., [50]).
Property 14 (Computation of Estimator 5)
The common secondary structure of Estimator 5 is given by maximizing the sum of the averaged base-pairing probabilities
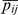 where
where
| (25) |
Therefore, the common secondary structure of the estimator can be computed using the dynamic programming algorithm in
Eq. (10)
if we replace
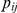 with
with
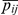 .
.
Also, we can predict the secondary structure of Estimator 5 without conducting Nussinov-style DP:
Property 15 (Computation of Estimator 5 with
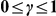 )
The secondary structure of Estimator 5 with
)
The secondary structure of Estimator 5 with
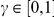 can be predicted by collecting the base-pairs whose averaged base-paring probabilities are larger than
can be predicted by collecting the base-pairs whose averaged base-paring probabilities are larger than
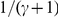 .
.
It should be noted that the tools of common secondary structure prediction, RNAalifold [50], PETfold [8] and McCaskill-MEA [7] are also considered as a representative estimators (Definition 10). In [49], the authors systematically discuss those points. See [49] for details.
Pairwise alignment using homologous sequences
As in the previous application to RNA secondary structure prediction using homologous sequences, if we obtain a set of homologous sequences  for the target sequences
for the target sequences  and
and  (see Figure 8), we would have more accurate estimator for the pairwise alignment of
(see Figure 8), we would have more accurate estimator for the pairwise alignment of  and
and 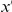 than Estimator 1. The problem is formulated as follows.
than Estimator 1. The problem is formulated as follows.
Figure 8. Pairwise alignment using homologous sequences (Problem 12).

Problem 12 (Pairwise alignment using homologous sequences)
The data is represented as
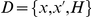 where
where
 and
and
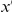 are two biological sequences that we would like to align, and
are two biological sequences that we would like to align, and
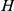 is a set of homologous sequences for
is a set of homologous sequences for
 and
and
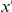 . The predictive space
. The predictive space
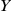 is given by
is given by
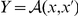 which is the space of the pairwise alignments of two sequences
which is the space of the pairwise alignments of two sequences
 and
and
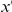 .
.
The difference between Problem 1 and this problem is that we can use other biological sequences (that seem to be homologous to  and
and 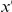 ) besides the two sequences
) besides the two sequences  and
and 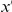 which are being aligned.
which are being aligned.
We can introduce the probability distribution (denoted by 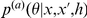 ) on the space of multiple alignments of three sequences
) on the space of multiple alignments of three sequences  ,
, 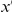 and
and 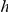 (denoted by
(denoted by 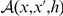 and whose definition is similar to that of
and whose definition is similar to that of 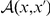 ) by a model such as the triplet HMM (which is similar to the pair HMM). Then, we obtain a probability distribution on the space of pairwise alignments of
) by a model such as the triplet HMM (which is similar to the pair HMM). Then, we obtain a probability distribution on the space of pairwise alignments of  and
and 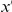 (i.e.,
(i.e., 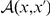 ) by marginalizing
) by marginalizing 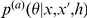 into the space
into the space 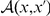 :
:
| (26) |
where 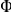 is the projection from
is the projection from 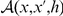 into
into 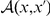 . Moreover, by averaging these probability distributions over
. Moreover, by averaging these probability distributions over 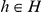 , we obtain the following probability distribution on
, we obtain the following probability distribution on  :
:
| (27) |
where 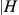 is the number of sequences in
is the number of sequences in 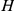 .
.
The  -centroid estimator with the distribution in Eq. (27) directly gives an estimator for Problem 12. However, to compute the aligned-base-pairs (matching) probabilities
-centroid estimator with the distribution in Eq. (27) directly gives an estimator for Problem 12. However, to compute the aligned-base-pairs (matching) probabilities 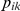 with respect to this distribution demands a lot of computational time, so we employ the approximated
with respect to this distribution demands a lot of computational time, so we employ the approximated  -type estimator (Definition 12) of this
-type estimator (Definition 12) of this  -centroid estimator as follows.
-centroid estimator as follows.
Estimator 6 (Approximated
 -type estimator for Problem 12)
We obtain the approximated
-type estimator for Problem 12)
We obtain the approximated
 -type estimator (Definition 12) for Problem 12 with the following settings. The parameter space is given by
-type estimator (Definition 12) for Problem 12 with the following settings. The parameter space is given by
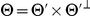 where
where
and the probability distribution on the parameter space
 is defined by
is defined by
| (28) |
for
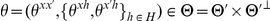 . The pointwise gain function (see Definition 4) in Eq. (11) is defined by
. The pointwise gain function (see Definition 4) in Eq. (11) is defined by
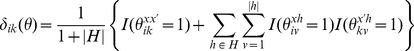 |
(29) |
where
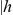 is the length of the sequence
is the length of the sequence
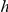 .
.
Property 16 (Computation of Estimator 6)
The alignment of Estimator 6 is equal to the alignment that maximizes the sum of
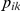 larger than
larger than
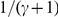 where
where
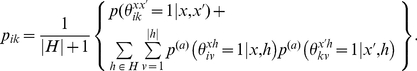 |
(30) |
Therefore, the recursive equation of the dynamic program to calculate the alignment of Estimator 6 is given by replacing
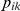 in
Eq. (19)
with
Eq. (30)
.
in
Eq. (19)
with
Eq. (30)
.
Moreover, by using Theorem 1, we have the following proposition, which enables us to compute the proposed estimator for 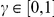 without using (Needleman-Wunsch-type) dynamic programming.
without using (Needleman-Wunsch-type) dynamic programming.
Property 17 (Computation of Estimator 6 for
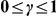 )
The pairwise alignment of Estimator 6 with
)
The pairwise alignment of Estimator 6 with
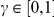 can be predicted by collecting the aligned-bases whose probability
can be predicted by collecting the aligned-bases whose probability
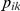 in (30) is larger than
in (30) is larger than
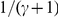 .
.
It should be noted that 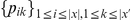 is identical to the probability consistency transformation (PCT) of
is identical to the probability consistency transformation (PCT) of  and
and 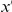 [19]. In ProbCons [19], the pairwise alignment is predicted by the Estimator 6 with sufficiently large
[19]. In ProbCons [19], the pairwise alignment is predicted by the Estimator 6 with sufficiently large  . Therefore, the estimator for Problem 12 used in the ProbCons algorithm is a special case of Estimator 6.
. Therefore, the estimator for Problem 12 used in the ProbCons algorithm is a special case of Estimator 6.
RNA secondary structure prediction using homologous sequences
If we obtain a set of homologous RNA sequences for the target RNA sequence, we might have a more accurate estimator [23] for secondary structure prediction than the  -centroid estimator (Estimator 2). This problem is formulated as follows and was considered in [23] for the first time (See Figure 9).
-centroid estimator (Estimator 2). This problem is formulated as follows and was considered in [23] for the first time (See Figure 9).
Figure 9. RNA secondary structure prediction using homologous sequences (Problem 13).

Problem 13 (RNA secondary structure prediction using homologous sequences)
The data
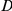 is represented as
is represented as
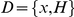 where
where
 is the target RNA sequence for which we would like to make secondary structure predictions and
is the target RNA sequence for which we would like to make secondary structure predictions and
 is the set of its homologous sequences. The predictive space
is the set of its homologous sequences. The predictive space
 is identical to
is identical to
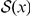 , the space of the secondary structures of an RNA sequence
, the space of the secondary structures of an RNA sequence
 .
.
The difference between this problem and Problem 2 is that we are able to employ homologous sequence information for predicting the secondary structure of the target RNA sequence. In this problem, it is natural that we assume the target sequence  and each homologous sequence
and each homologous sequence  share common secondary structures. The common secondary structure is naturally modeled by a structural alignment (that considers not only the alignment between bases but also the alignment between base-pairs), and the probability distribution (denoted by
share common secondary structures. The common secondary structure is naturally modeled by a structural alignment (that considers not only the alignment between bases but also the alignment between base-pairs), and the probability distribution (denoted by 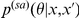 ) on the space of the structural alignments of two RNA sequences
) on the space of the structural alignments of two RNA sequences  and
and  (denoted by
(denoted by 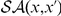 ) is given by the Sankoff model [51]. By marginalizing the distribution
) is given by the Sankoff model [51]. By marginalizing the distribution 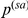 into the space of secondary structures
into the space of secondary structures 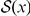 of the target sequence
of the target sequence  , we obtain more reliable distribution
, we obtain more reliable distribution 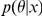 on
on 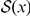 :
:
| (31) |
where 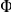 is the projection from
is the projection from 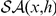 into
into  . Moreover, by averaging these probability distributions on
. Moreover, by averaging these probability distributions on 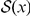 , we obtain the following probability distribution of secondary structures of the target sequence.
, we obtain the following probability distribution of secondary structures of the target sequence.
| (32) |
where  is the number of sequences in
is the number of sequences in  . The
. The  -centroid estimator with the probability distribution in Eq. (32) gives a reasonable estimator for Problem 13, because Eq. (32) considers consensus secondary structures between
-centroid estimator with the probability distribution in Eq. (32) gives a reasonable estimator for Problem 13, because Eq. (32) considers consensus secondary structures between  and
and  . However, the calculation of the
. However, the calculation of the  -estimator requires huge computational cost because it requires
-estimator requires huge computational cost because it requires 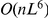 for computing the base-paring probability matrix
for computing the base-paring probability matrix 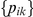 where
where 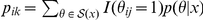 with the distribution of Eq. (32). Therefore, we employ the approximated
with the distribution of Eq. (32). Therefore, we employ the approximated  -type estimator (Definition 12) of the
-type estimator (Definition 12) of the  -centroid estimator, which is equivalent to the estimator proposed in [23].
-centroid estimator, which is equivalent to the estimator proposed in [23].
Estimator 7 (Approximated
 -type estimator for Problem 13)
We obtain the approximated
-type estimator for Problem 13)
We obtain the approximated
 -type estimator (Definition 12) for Problem 13 with the following settings. The parameter space is given by
-type estimator (Definition 12) for Problem 13 with the following settings. The parameter space is given by
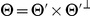 where
where
and the probability distribution on
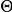 is defined by
is defined by
for
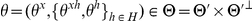 . Moreover,
Eq. (11)
in the pointwise gain function is defined by
. Moreover,
Eq. (11)
in the pointwise gain function is defined by
for
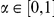 .
.
It should be noted that Estimator 13 is equivalent to the estimator proposed in [23]. The secondary structure of the estimator can be computed by the following method.
Property 18 (Computation of Estimator 7)
The secondary structure of Estimator 7 is computed by maximizing the sum of
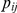 larger than
larger than
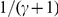 where
where
| (33) |
Here,
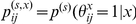 and
and
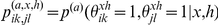 . Therefore, the secondary structure of Estimator 7 can be computed by the Nussinov-type DP of
Eq. (10)
in which we replace
. Therefore, the secondary structure of Estimator 7 can be computed by the Nussinov-type DP of
Eq. (10)
in which we replace
 by
Eq. (33)
.
by
Eq. (33)
.
The computational cost with respect to time for computing the secondary structure of Estimator 7 is 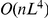 where
where  is the number of RNA sequences and
is the number of RNA sequences and 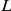 is the length of RNA sequences. In [23], we employed a further approximation of the estimator, and reduced the computational cost to
is the length of RNA sequences. In [23], we employed a further approximation of the estimator, and reduced the computational cost to 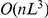 . We implemented this estimator in software called CentroidHomfold. See [23] for details of the theory and results of computational experiments. Although the authors did not mention it in their paper [23], the following property holds.
. We implemented this estimator in software called CentroidHomfold. See [23] for details of the theory and results of computational experiments. Although the authors did not mention it in their paper [23], the following property holds.
Property 19 (Computation of Estimator 7 with
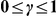 )
Estimator 7 with
)
Estimator 7 with
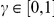 can be predicted by collecting the aligned-bases where the (pseudo-)base-paring probability of
Eq. (33)
is larger than
can be predicted by collecting the aligned-bases where the (pseudo-)base-paring probability of
Eq. (33)
is larger than
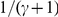 .
.
Pairwise alignment of structured RNAs
In this section, we focus on the pairwise alignment of structured RNAs. This problem is formulated as Problem 1, so the output of the problem is a usual alignment (contained in 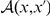 ). In contrast to the usual alignment problem, we can consider not only nucleotide sequences but also secondary structures in each sequence for the problem. Note that this does not mean the structural alignment [51] of RNA sequences, because the structural alignment produces both alignment and the common secondary structure simultaneously.
). In contrast to the usual alignment problem, we can consider not only nucleotide sequences but also secondary structures in each sequence for the problem. Note that this does not mean the structural alignment [51] of RNA sequences, because the structural alignment produces both alignment and the common secondary structure simultaneously.
The probability distributions 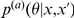 on
on 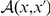 described in the previous section are not able to handle secondary structures of each RNA sequence. In order to obtain a probability distribution on
described in the previous section are not able to handle secondary structures of each RNA sequence. In order to obtain a probability distribution on 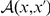 that considers secondary structure, we employ the marginalization of the Sankoff model [51] that gives a probability distribution (denoted by
that considers secondary structure, we employ the marginalization of the Sankoff model [51] that gives a probability distribution (denoted by 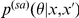 ) on the space of possible structural alignments between two RNA sequences (denoted by
) on the space of possible structural alignments between two RNA sequences (denoted by 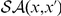 ). In other words, we obtain a probability distribution on the space
). In other words, we obtain a probability distribution on the space 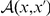 by marginalizing the probability distribution of structural alignments of two RNA sequences (given by the Sankoff model) into the space
by marginalizing the probability distribution of structural alignments of two RNA sequences (given by the Sankoff model) into the space 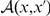 as follows.
as follows.
| (34) |
where  is the projection from
is the projection from 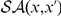 into
into 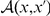 ,
, 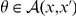 and
and 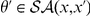 . The difference between this marginalized probability distribution and the distributions such as Miyazawa model is that the former considers secondary structures of each sequence (more precisely, the former considers the common secondary structure).
. The difference between this marginalized probability distribution and the distributions such as Miyazawa model is that the former considers secondary structures of each sequence (more precisely, the former considers the common secondary structure).
Then, the  -centroid estimator with this distribution Eq. (34) will give a reasonable estimator for the pairwise alignment of two RNA sequences. However, the computation of this estimator demands huge computational cost because it uses the Sankoff model (cf. it requires
-centroid estimator with this distribution Eq. (34) will give a reasonable estimator for the pairwise alignment of two RNA sequences. However, the computation of this estimator demands huge computational cost because it uses the Sankoff model (cf. it requires 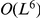 time for computing the matching probability matrix of structural alignments). Therefore, we employed the approximated
time for computing the matching probability matrix of structural alignments). Therefore, we employed the approximated  -type estimator (Definition 12) of the
-type estimator (Definition 12) of the  -centroid estimator with the marginalized distribution as follows.
-centroid estimator with the marginalized distribution as follows.
Estimator 8 (Approximated
 -type estimator for Problem 1 with two RNA sequences)
In Problem 1 where
-type estimator for Problem 1 with two RNA sequences)
In Problem 1 where
 and
and
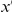 are RNA sequences, we obtain the approximated
are RNA sequences, we obtain the approximated
 -type estimator (Estimator 2) with the following settings. The parameter space is given by
-type estimator (Estimator 2) with the following settings. The parameter space is given by
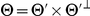 where
where
and the probability distribution on the parameter space
 is defined by
is defined by
for
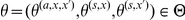 . The pointwise gain function of
Eq. (11)
is defined by
. The pointwise gain function of
Eq. (11)
is defined by
where
and
 ,
,
 and
and
 are positive weights that satisfy
are positive weights that satisfy
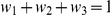 .
.
This approximated  -type estimator is equivalent to the estimator proposed in [52] and the alignment of the estimator can be computed by the following property.
-type estimator is equivalent to the estimator proposed in [52] and the alignment of the estimator can be computed by the following property.
Property 20 (Computation of Estimator 8)
The alignment of Estimator 8 can be computed by maximizing the sum of probabilities
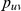 that are larger than
that are larger than
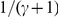 where
where
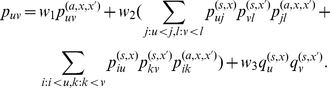 |
(35) |
Here, we define
Therefore, the pairwise alignment of Estimator 8 can be computed by a Needleman-Wunsch-type dynamic program of
Eq. (19)
in which we replace
 with
Eq. (35).
with
Eq. (35).
Note that 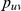 in Eq. (35) is considered as a pseudo-aligned base probability where
in Eq. (35) is considered as a pseudo-aligned base probability where 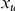 aligns with
aligns with 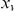 .
.
By checking Eq. (14), we obtain the following property:
Property 21 (Computation of Estimator 8 with
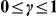 )
The pairwise alignment of Estimator 8 can be predicted by collecting aligned-bases where the probability in
Eq. (35)
is larger than
)
The pairwise alignment of Estimator 8 can be predicted by collecting aligned-bases where the probability in
Eq. (35)
is larger than
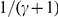 .
.
Proofs
In this section, we give the proofs of the theorems, propositions and corollary.
Proof of Theorem 1
We will prove a more general case of Theorem 1 where the parameter space  is different from the predictive space
is different from the predictive space  and a probability distribution on
and a probability distribution on  is assumed (cf. Assumption 2).
is assumed (cf. Assumption 2).
Theorem 4
In Problem 3 with Assumption 1 and a pointwise gain function, suppose that a predictive space
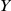 can be written as
can be written as
| (36) |
where
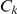 is defined as
is defined as
for an index-set
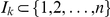 . If the pointwise gain function in
Eq. (1)
(we here think
. If the pointwise gain function in
Eq. (1)
(we here think
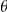 is in a parameter space
is in a parameter space
 which might be different from
which might be different from
 ) satisfies the condition
) satisfies the condition
| (37) |
for every
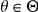 and every
and every
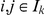 (
(
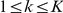 ), then the consensus estimator is in the predictive space
), then the consensus estimator is in the predictive space
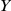 , and hence the MEG estimator contains the consensus estimator.
, and hence the MEG estimator contains the consensus estimator.
(proof)
It is sufficient to show that the consensus estimator
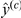 is contained in the predictive space
is contained in the predictive space
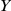 because
because
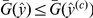 for all
for all
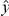 in the MEG estimators, where
in the MEG estimators, where
If we assume that
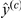 is not contained in the predictive space,
is not contained in the predictive space,
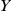 that is,
that is, 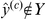 , then there exists a
, then there exists a
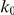 such that
such that 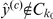 . Because
. Because
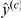 is a binary vector, there exist indexes
is a binary vector, there exist indexes
 such that
such that
 ,
,
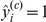 and
and
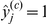 . By the definition of
. By the definition of
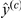 , we obtain
, we obtain
Therefore, we obtain
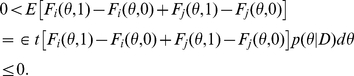 |
In order to prove the last inequality, we use Eq. (??). This leads to a contradiction and the theorem is proved.
Remark 3 It should be noted that the above theorem holds for an arbitrary parameter space including continuous-valued spaces.
Proof of Theorem 2. (proof)
Because
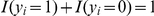 for arbitrary
for arbitrary
 , we obtain, using the definitions given in
equations (15
),(16),(17) and (18),
, we obtain, using the definitions given in
equations (15
),(16),(17) and (18),
Therefore, we have
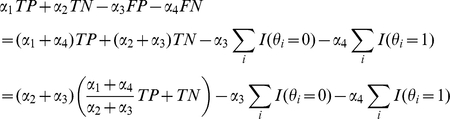 |
and this leads to the proof of the theorem.
Proof of Theorem 3. (proof)
The expectation of the gain function of the
 -centroid estimator is computed as
-centroid estimator is computed as
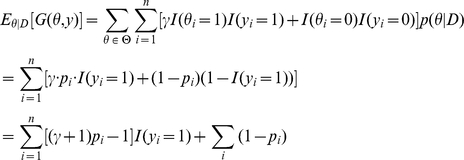 |
where
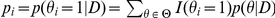 is the marginalized probability. Therefore, we should always predict
is the marginalized probability. Therefore, we should always predict
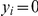 whenever
whenever
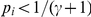 , because the assumption of Theorem 3 ensures that the prediction
, because the assumption of Theorem 3 ensures that the prediction
 never violate the condition of the predictive space
never violate the condition of the predictive space
 . Theorem 3 follows by using those facts.
. Theorem 3 follows by using those facts.
Proof of Corollary 1. (proof)
For every
 ,
,
 ,
,
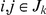 ,
,
 , we have
, we have
 |
and the condition of
Eq. (3)
in Theorem 1 is satisfied (in order to prove the last inequality, we use
 because
because
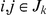 ). Therefore, by Theorem 1, the
). Therefore, by Theorem 1, the
 -centroid estimator contains its consensus estimator.
-centroid estimator contains its consensus estimator.
The last half of the corollary is easily proved using the equation
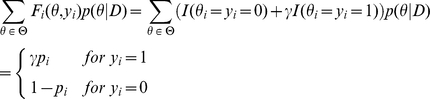 |
where
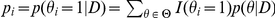 .
.
Proof of Proposition 1. (proof) 5 The representative estimator in Definition 10 can be written as
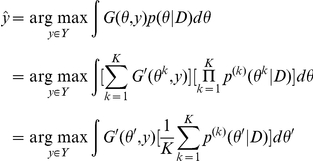 |
Then, we finish the proof of Proposition 1.
Derivation of Eq. (14)
The equation is easily derived from the equality 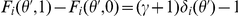 .
.
Acknowledgments
The authors are grateful to Drs. Luis E. Carvalho, Charles E. Lawrence, Kengo Sato, Toutai Mituyama and Martin C. Frith for fruitful discussions. The authors also thank the members of the bioinformatics group for RNA at the National Institute of Advanced Industrial Science and Technology (AIST) for useful discussions.
Footnotes
Competing Interests: The authors have declared that no competing interests exist. MH is an employee of Mizuho Information & Research Institute but there is no competing interest that can bias this work. This affiliation does not alter the authors' adherence to all the PLoS ONE policies on sharing data and materials.
Funding: This work was supported in part by the "Functional RNA Project" of the New Energy Technology Development Organization (NEDO), and in part by a Grant-in-Aid for Scientific Research on Innovative Areas. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Carvalho L, Lawrence C. Centroid estimation in discrete high-dimensional spaces with applications in biology. Proc Natl Acad Sci USA. 2008;105:3209–3214. doi: 10.1073/pnas.0712329105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bradley RK, Roberts A, Smoot M, Juvekar S, Do J, et al. Fast statistical alignment. PLoS Comput Biol. 2009;5:e1000392. doi: 10.1371/journal.pcbi.1000392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bradley RK, Pachter L, Holmes I. Specific alignment of structured RNA: stochastic grammars and sequence annealing. Bioinformatics. 2008;24:2677–2683. doi: 10.1093/bioinformatics/btn495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Frith MC, Hamada M, Horton P. Parameters for accurate genome alignment. BMC Bioinformatics. 2010;11:80. doi: 10.1186/1471-2105-11-80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Do C, Woods D, Batzoglou S. CONTRAfold: RNA secondary structure prediction without physics-based models. Bioinformatics. 2006;22:e90–98. doi: 10.1093/bioinformatics/btl246. [DOI] [PubMed] [Google Scholar]
- 6.Lu ZJ, Gloor JW, Mathews DH. Improved RNA secondary structure prediction by maximizing expected pair accuracy. RNA. 2009;15:1805–1813. doi: 10.1261/rna.1643609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kiryu H, Kin T, Asai K. Robust prediction of consensus secondary structures using averaged base pairing probability matrices. Bioinformatics. 2007;23:434–441. doi: 10.1093/bioinformatics/btl636. [DOI] [PubMed] [Google Scholar]
- 8.Seemann S, Gorodkin J, Backofen R. Unifying evolutionary and thermodynamic information for RNA folding of multiple alignments. Nucleic Acids Res. 2008;36:6355–6362. doi: 10.1093/nar/gkn544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kall L, Krogh A, Sonnhammer EL. An HMM posterior decoder for sequence feature prediction that includes homology information. Bioinformatics. 2005;21(Suppl 1):i251–257. doi: 10.1093/bioinformatics/bti1014. [DOI] [PubMed] [Google Scholar]
- 10.Kato Y, Sato K, Hamada M, Watanabe Y, Asai K, et al. RactIP: fast and accurate prediction of RNA-RNA interaction using integer programming. Bioinformatics. 2010;26:i460–466. doi: 10.1093/bioinformatics/btq372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gross S, Do C, Sirota M, Batzoglou S. CONTRAST: a discriminative, phylogeny-free approach to multiple informant de novo gene prediction. Genome Biol. 2007;8:R269. doi: 10.1186/gb-2007-8-12-r269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hamada M, Kiryu H, Sato K, Mituyama T, Asai K. Prediction of RNA secondary structure using generalized centroid estimators. Bioinformatics. 2009;25:465–473. doi: 10.1093/bioinformatics/btn601. [DOI] [PubMed] [Google Scholar]
- 13.Miyazawa S. A reliable sequence alignment method based on probabilities of residue correspondences. Protein Eng. 1995;8:999–1009. doi: 10.1093/protein/8.10.999. [DOI] [PubMed] [Google Scholar]
- 14.McCaskill JS. The equilibrium partition function and base pair binding probabilities for RNA secondary structure. Biopolymers. 1990;29:1105–1119. doi: 10.1002/bip.360290621. [DOI] [PubMed] [Google Scholar]
- 15.Sato K, Hamada M, Asai K, Mituyama T. CENTROIDFOLD: a web server for RNA secondary structure prediction. Nucleic Acids Res. 2009;37:W277–280. doi: 10.1093/nar/gkp367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Metropolis N, Rosenbluth A, Teller M, Teller E. Equations of state calculations by fast computing machine. J Chem Phys. 1953;21:1087–1091. [Google Scholar]
- 17.Robinson DF, Foulds LR. Comparison of phylogenetic trees. Mathematical Biosciences. 1981;53:131–147. [Google Scholar]
- 18.Iwasaki W, Takagi T. An intuitive, informative, and most balanced representation of phylogenetic topologies. Syst Biol. 2010;59:584–593. doi: 10.1093/sysbio/syq044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Do C, Mahabhashyam M, Brudno M, Batzoglou S. ProbCons: Probabilistic consistency-based multiple sequence alignment. Genome Res. 2005;15:330–340. doi: 10.1101/gr.2821705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Baldi P, Brunak S, Chauvin Y, Andersen CA, Nielsen H. Assessing the accuracy of prediction algorithms for classification: an overview. Bioinformatics. 2000;16:412–424. doi: 10.1093/bioinformatics/16.5.412. [DOI] [PubMed] [Google Scholar]
- 21.Schwartz AS, Myers EW, Pachter L. Alignment metric accuracy 2005.
- 22.Hamada M, Sato K, Asai K. Prediction of RNA secondary structure by maximizing pseudo-expected accuracy. BMC Bioinformatics. 2010;11:586. doi: 10.1186/1471-2105-11-586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hamada M, Sato K, Kiryu H, Mituyama T, Asai K. Predictions of RNA secondary structure by combining homologous sequence information. Bioinformatics. 2009;25:i330–338. doi: 10.1093/bioinformatics/btp228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ding Y, Chan C, Lawrence C. RNA secondary structure prediction by centroids in a Boltzmann weighted ensemble. RNA. 2005;11:1157–1166. doi: 10.1261/rna.2500605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Roshan U, Livesay D. Probalign: multiple sequence alignment using partition function posterior probabilities. Bioinformatics. 2006;22:2715–2721. doi: 10.1093/bioinformatics/btl472. [DOI] [PubMed] [Google Scholar]
- 26.Do CB, Gross SS, Batzoglou S. Apostolico A, Guerra C, Istrail S, Pevzner PA, Waterman MS, editors. Contralign: Discriminative training for protein sequence alignment. 2006. pp. 160–174. RECOMB. Springer, volume 3909 of Lecture Notes in Computer Science.
- 27.Mathews DH, Sabina J, Zuker M, Turner DH. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J Mol Biol. 1999;288:911–940. doi: 10.1006/jmbi.1999.2700. [DOI] [PubMed] [Google Scholar]
- 28.Dowell R, Eddy S. Evaluation of several lightweight stochastic context-free grammars for RNA secondary structure prediction. BMC Bioinformatics. 2004;5:71. doi: 10.1186/1471-2105-5-71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ronquist F, Huelsenbeck JP. MrBayes 3: Bayesian phylogenetic inference under mixed models. Bioinformatics. 2003;19:1572–1574. doi: 10.1093/bioinformatics/btg180. [DOI] [PubMed] [Google Scholar]
- 30.Huelsenbeck JP, Ronquist F. MRBAYES: Bayesian inference of phylogenetic trees. Bioinformatics. 2001;17:754–755. doi: 10.1093/bioinformatics/17.8.754. [DOI] [PubMed] [Google Scholar]
- 31.Durbin R, Eddy S, Krogh A, Mitchison G. Cambridge, UK: Cambridge University press; 1998. Biological sequence analysis. [Google Scholar]
- 32.Needleman S, Wunsch C. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J Mol Biol. 1970;48:443–453. doi: 10.1016/0022-2836(70)90057-4. [DOI] [PubMed] [Google Scholar]
- 33.Frith MC, Wan R, Horton P. Incorporating sequence quality data into alignment improves DNA read mapping. Nucleic Acids Res. 2010;38:e100. doi: 10.1093/nar/gkq010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Holmes I, Durbin R. Dynamic programming alignment accuracy. J Comput Biol. 1998;5:493–504. doi: 10.1089/cmb.1998.5.493. [DOI] [PubMed] [Google Scholar]
- 35.Griffiths-Jones S, Moxon S, Marshall M, Khanna A, Eddy SR, et al. Rfam: annotating non-coding RNAs in complete genomes. Nucleic Acids Res. 2005;33:121–124. doi: 10.1093/nar/gki081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Andronescu M, Condon A, Hoos H, Mathews D, Murphy K. Efficient parameter estimation for RNA secondary structure prediction. Bioinformatics. 2007;23:19–28. doi: 10.1093/bioinformatics/btm223. [DOI] [PubMed] [Google Scholar]
- 37.Nussinov R, Pieczenk G, Griggs J, Kleitman D. Algorithms for loop matchings. SIAM Journal of Applied Mathematics. 1978;35:68–82. [Google Scholar]
- 38.Zuker M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003;31:3406–3415. doi: 10.1093/nar/gkg595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hofacker I, Fontana W, Stadler P, Bonhoeffer S, Tacker M, et al. Fast folding and comparison of RNA secondary structures. Monatsh Chem. 1994;125:167–188. [Google Scholar]
- 40.Mathews D, Disney M, Childs J, Schroeder S, Zuker M, et al. Incorporating chemical modification constraints into a dynamic programming algorithm for prediction of RNA secondary structure. Proc Natl Acad Sci USA. 2004;101:7287–7292. doi: 10.1073/pnas.0401799101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Chan CY, Lawrence CE, Ding Y. Structure clustering features on the Sfold Web server. Bioinformatics. 2005;21:3926–3928. doi: 10.1093/bioinformatics/bti632. [DOI] [PubMed] [Google Scholar]
- 42.Ding Y, Chan CY, Lawrence CE. Sfold web server for statistical folding and rational design of nucleic acids. Nucleic Acids Res. 2004;32:135–141. doi: 10.1093/nar/gkh449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bernhart SH, Hofacker IL. From consensus structure prediction to RNA gene finding. Brief Funct Genomic Proteomic. 2009;8:461–471. doi: 10.1093/bfgp/elp043. [DOI] [PubMed] [Google Scholar]
- 44.Schroeder SJ. Advances in RNA structure prediction from sequence: new tools for generating hypotheses about viral RNA structure-function relationships. J Virol. 2009;83:6326–6334. doi: 10.1128/JVI.00251-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Stocsits RR, Letsch H, Hertel J, Misof B, Stadler PF. Accurate and efficient reconstruction of deep phylogenies from structured RNAs. Nucleic Acids Res. 2009;37:6184–6193. doi: 10.1093/nar/gkp600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Washietl S, Hofacker IL, Stadler PF. Fast and reliable prediction of noncoding RNAs. Proc Natl Acad Sci U S A. 2005;102:2454–2459. doi: 10.1073/pnas.0409169102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Washietl S, Hofacker IL, Lukasser M, Huttenhofer A, Stadler PF. Mapping of conserved RNA secondary structures predicts thousands of functional noncoding RNAs in the human genome. Nat Biotechnol. 2005;23:1383–1390. doi: 10.1038/nbt1144. [DOI] [PubMed] [Google Scholar]
- 48.Okada Y, Sato K, Sakakibara Y. Improvement of structure conservation index with centroid estimators. Pac Symp Biocomput. 2010:88–97. doi: 10.1142/9789814295291_0011. [DOI] [PubMed] [Google Scholar]
- 49.Hamada M, Sato K, Asai K. Improving the accuracy of predicting secondary structure for aligned RNA sequences. Nucleic Acids Res. 2010 doi: 10.1093/nar/gkq792. doi: 10.1093/nar/gkq792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Bernhart S, Hofacker I, Will S, Gruber A, Stadler P. RNAalifold: improved consensus structure prediction for RNA alignments. BMC Bioinformatics. 2008;9:474. doi: 10.1186/1471-2105-9-474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sankoff D. Simultaneous solution of the RNA folding alignment and protosequence problems. SIAM J Appl Math. 1985:810–825. [Google Scholar]
- 52.Hamada M, Sato K, Kiryu H, Mituyama T, Asai K. CentroidAlign: fast and accurate aligner for structured RNAs by maximizing expected sum-of-pairs score. Bioinformatics. 2009;25:3236–3243. doi: 10.1093/bioinformatics/btp580. [DOI] [PubMed] [Google Scholar]