LAPLACE-BELTRAMI NODAL COUNTS: A NEW SIGNATURE FOR 3D SHAPE ANALYSIS

Abstract

In this paper we develop a new approach of analyzing 3D shapes based on the eigen-system of the Laplace-Beltrami operator. While the eigenvalues of the Laplace-Beltrami operator have been used previously in shape analysis, they are unable to differentiate isospectral shapes. To overcome this limitation, we propose here a new signature based on nodal counts of the eigenfunctions. This signature provides a compact representation of the geometric information that is missing in the eigenvalues. In our experiments, we demonstrate that the proposed signature can successfully classify anatomical shapes with similar eigenvalues.

1. INTRODUCTION

The analysis of 3D shapes is an important problem in medical imaging. By studying shapes, we can obtain detailed information about morphometry changes of anatomical structures. Recently there has been increasing interests in using the eigenvalues of the Laplace-Beltrami operators to study shapes [1, 2]. Features based on eigenvalues, however, have limitations in resolving isospectral shapes. To overcome this difficulty, we propose in this work a new signature derived from the nodal counts of eigenfunctions and demonstrate its advantage in classifying medical shapes.

Using the eigenvalues of the Laplace-Beltrami operator, the shape DNA feature was proposed in [1] as a vector of eigenvalues ordered according to their magnitude. The shape DNA feature has been successfully applied to the classification of anatomical structures [2]. One limitation of the shape DNA feature, however, is that it cannot resolve so called isospectral shapes with the same eigenvalues. There were various examples of isospectral surfaces created by mathematician [3–8]. In practice, we have also observed shapes with quite different geometry but very similar distribution of eigenvalues. To address this ambiguity in the shape DNA feature, we propose here a new signature derived from the eigenfunctions of the Laplace-Beltrami operator. This new feature is intrinsically defined over the surfaces and is pose and scale invariant. Using the nodal counts of the eigenfunctions, this feature provides a compact representation of the new geometric information that is not described by the eigenvalues. In our experiments, we show that it has the ability of resolving the ambiguity in the shape DNA feature.

2. LAPLACE-BELTRAMI SPECTRUM

Let (M, g) denote a Riemannian surface. For any point p ∈ M, we assume a local coordinate chart {U, (x¹, x²)} and represent the metric as g(p) = (g_ij(x))_i,j=1,2 in this chart. For a smooth function ϕ ∈ C^∞(M), the Laplace-Beltrami operator is defined as:

$${\mathrm{\Delta }}_M\varphi =\frac{1}{\sqrt{G}}\sum _{i=1}^2\frac{\partial }{\partial x_i}(\sqrt{G}\sum _{j=1}^2{g}^{ij}\frac{\partial \varphi }{\partial x_j})$$ (1)

where (g^ij) is the inverse matrix of (g_ij) and G = det(g_ij).

The Laplace-Beltrami operator is self adjoint and elliptic, so its spectrum is discrete. We denote the eigenvalues of Δ_M as 0 = λ₀ < λ₁ < λ₂ < · · · and the corresponding eigenfunctions as ϕ₀, ϕ₁, ϕ₂, · · · such that

$${\mathrm{\Delta }}_M{\varphi }_n={\lambda }_n{\varphi }_n,n=0,1,2,\cdots .$$ (2)

The eigen-system $({\lambda }_n,{\varphi }_n){\mid }_{n=0}^{\infty }$ of Δ_M is intrinsic to the manifold M and has the nice property of being isometric invariant. Thus properties derived from the eigen-system of Δ_M are robust to natural pose variations such as rotation and translation.

From a signal processing point of view, the eigenfunctions of the Laplace-Beltrami operator is an extension of the Fourier basis on Euclidean domains to general manifolds [9]. One famous example is the spherical harmonics, which are the eigenfunctions of the Laplace-Beltrami operator on the unit sphere, and they have been used in various shape analysis tasks. On the other hand, our focus is quite different from Fourier analysis. We believe the eigenfunctions by themselves contain rich information about surface geometry. In fact, the heat kernel embedding theorem in [10] shows eigenfunctions of the Laplace-Beltrami operator should determine the surface itself. So we are interested in using them to analyze the underlying domain, i.e., the surface. We refer [11] to more detailed properties about the eigen-system of the Laplace-Beltrami operator. In our previous work [12, 13], we showed that the Reeb graph of the eigenfunctions are useful tools for the analysis of anatomical shapes such as hippocampus and demonstrated its value in establishing point-wise mapping of sub-cortical surfaces. In the next section, we develop a new approach of utilizing the eigenfunctions for shape analysis.

3. THE NODAL COUNT SEQUENCES

In this section, we will introduce the mathematical concept of nodal counts and propose its use for shape analysis.

Let (M, g) be a given two dimensional compact Riemannian manifold and ϕ be an eigenfunction of its Laplace-Beltrami operator. The set ϕ⁻¹(0) is then called nodal lines of ϕ on (M, g). Every connected component of M\ϕ⁻¹(0) is called a nodal domain of ϕ and the number of nodal domains is called the nodal number of ϕ. Theoretically one can have the following properties about the nodal lines and nodal domains of eigenfunctions [14].

Theorem 3.1

1. (Courant’s nodal domain theorem) The number of nodal domains of the n-th eigenfunction ≤ n+1;

2. The nodal lines are C²-immersed one dimensional closed submanifolds. Therefore, nodal lines are closed C²-immersed contours on M.

As a demonstration, we plot out the nodal domains of three different shapes in Fig. 1. From these examples, we can clearly see the above properties are observed.

Fig. 1.

(a): Nodal lines and nodal domains of the 2-nd eigenfunction of a putamen and the nodal number is 3. (b) Nodal lines and nodal domains of the 4-th eigenfunction of an armadillo, the nodal number is 5. (c) Nodal lines and nodal domains of the 4-th eigenfunction of a cow and the nodal number is 3.

Given the eigenfunction sequence {ϕ₁, ϕ₂, · · ·} of (M, g), we can define the Laplace-Beltrami nodal count sequence of M as the sequence {l₁, l₂, · · ·}, where l_n is the number of nodal domains of the n-th eigenfunction. Similar to the eigenvalues of Δ_M, the nodal count sequence is rotation and translation invariant. In addition, it has the nice property of being scale invariant. The notion of nodal count sequence has previously been explored in the physics literature [15–19]. In particular, it poses the question: “can one count the shape of a drum?” This is an analog of Kac’s famous question: “Can one hear the shape of a drum?” Intuitively, if two isospectral surfaces share the same shape DNA and have different geometry, they should have different eigenfunctions, which implies the possibility of the nodal count sequence containing more information than the shape DNA about the surface geometry. In our work, we extend this idea to the analysis of anatomical shapes. More specifically, we will study whether the nodal count sequences can provide extra information than the feature of shape DNA.

Numerically, we use the finite element method (FEM) to compute the eigen-system of the Laplace-Beltrami operator. For any given surface M in ℝ³, we represent M as a triangular mesh { $V={\{v_i\}}_{i=1}^N,T={\{T_l\}}_{l=1}^L$}, where v_i is the i-th vertex and T_l is the l-th triangle. We denote h_l as the diameter of the triangle T_l and h = max {h_l}. One can choose linear elements ${\{{\psi }_i^h\}}_{i=1}^N$, such that ${\psi }_i^h(v_j)={\delta }_{i,j}$ and write $S^h={\mathit{Span}}_{\mathbb{R}}{\{{\psi }_i^h\}}_{i=1}^N$. Then the discrete version of the continuous variational problem is to find a ϕ^h ∈ S^h, such that

$$\sum _l{\int }_{T_l}{\nabla }_M{\varphi }^h{\nabla }_M{\psi }_n^h={\lambda }^h\sum _l{\int }_{T_l}{\varphi }^h{\psi }_n^h,\forall {\psi }_n^h\in S^h.$$ (3)

If we write

$$\{\begin{array}{l}{\varphi }^h={\sum }_i^N{x}_i{\psi }_i^h\hfill \\ A^h={(a_{ij})}_{N\times N},a_{ij}={\sum }_l{\int }_{T_l}{\nabla }_M{\psi }_i^h{\nabla }_M{\psi }_j\hfill \\ B^h={(b_{ij})}_{N\times N},b_{ij}={\sum }_l{\int }_{T_l}{\psi }_i^h{\psi }_j^h\hfill \end{array}$$ (4)

Then the discrete variational problem is equivalent to the generalized matrix eigen-problem that can be easily solved with MATLAB:

$$\{\begin{array}{l}{A}^{h}x={\lambda }^h{B}^{h}x,\text{where}x={(x_1,\cdots ,x_N)}^T\hfill \\ {\varphi }^h={\sum }_i^N{x}_i{\psi }_i^h\hfill \end{array}$$ (5)

To compute the nodal number of a given eigenfunction ϕ_n of surface (M, g), we count the number of connected components of the triangular mesh with the same sign of ϕ.

Following [20], we have the upper bounds for the numerical accuracy in computing the eigenfunction and eigenvalues.

Theorem 3.2

Let ( ${\varphi }_n^h,{\lambda }_n^h$) be the eigen-system computed with FEM, then we have:

$$\left|\right|{\varphi }_n-{\varphi }_n^h\left|\right|\le {Ch}^2{\lambda }_n$$ (6)

$${\lambda }_n\le {\lambda }_n^h\le {\lambda }_n+2\delta h^2{\lambda }_n^2$$ (7)

where (ϕ_n, λ_n) are the true eigen-system, and C and δ are constants.

From the above theorem, we can see the accuracy of the eigenfunction decreases as the order n increases for a given h. As a result, the nodal counts for high order eigenfunctions are noisier than that of the low order eigenfunctions. However, the more eigenfunctions we can use, the more geometric information can be obtained. We need to find a balance between using the nodal number of high frequency eigenfunction and overcoming the numerical issue. Based on this consideration, we propose the following weighted l² distance between two nodal count sequences ${\{l_n\}}_{n=1}^{\infty }$ and ${\{{\stackrel{\sim }{l}}_n\}}_{n=1}^{\infty }$:

$$\mathit{Dist}({\{l_n\}}_{n=1}^{\infty },{\{{\stackrel{\sim }{l}}_n\}}_{n=1}^{\infty })=\sqrt{\sum _{n=1}^{\infty }{(\frac{1}{n^{\alpha }})}^2{(l_n-{\stackrel{\sim }{l}}_n)}^2}$$ (8)

where α > 0. In our experiments, we demonstrate that the nodal count sequences under this weighted l² distance provide robust performance for shape classification.

4. EXPERIMENTAL RESULTS

In this section, we present experimental results to demonstrate the application of the nodal count sequence in shape analysis. In particular, we show that the nodal counts of the Laplace-Beltrami operator is able to resolve isospectral shapes.

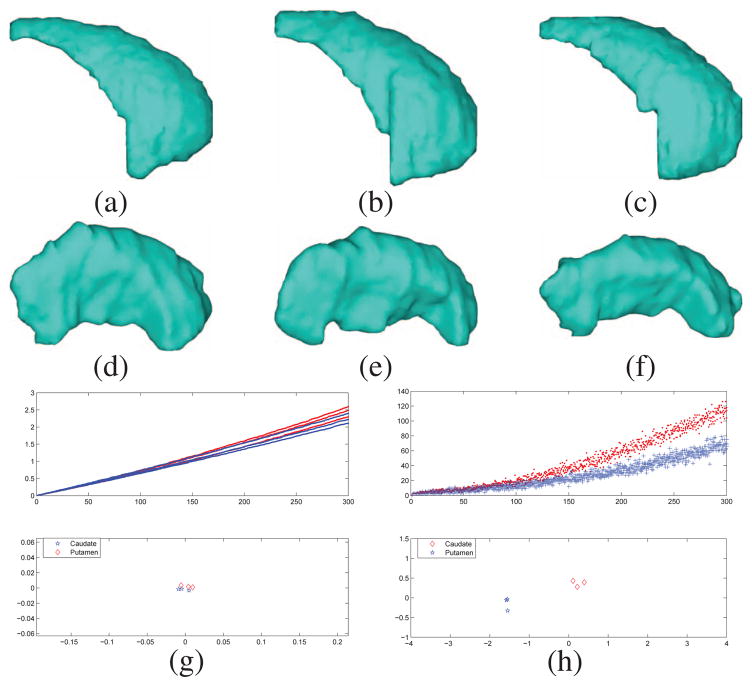
The 3D shapes used in the first experiment are three putamen and three caudate surfaces shown in Fig. 2. While the putamen and caudate are visually quite different, they share very similar distribution of eigenvalues, i.e., the shape DNA, as shown in Fig. 2(g). For each group of surfaces, we use their nodal count sequences and the shape DNA to embed them into a 2D space with multi-dimensional scaling(MDS) technique. The details of this embedding process is summarized as follows.

Fig. 2.

(a)(b)(c) Caudate surfaces. (d)(e)(f) Putamen. (g) Top: the first 300 eigenvalues of the 6 shapes. Bottom: MDS embedding results with the shape DNA. (h) Top: The first 300 nodal counts of the 6 shapes. Bottom: MDS embedding results with the nodal count sequences. (red: caudate; blue: putamen.)

1. For a given surface (M, g) represented by a triangle mesh, we compute the first N eigenvalues and eigenfunctions of the Laplace-Beltrami operator by the finite element method to obtain the signature.

2. For a group of surfaces, we compute the pairwise weighted l² distance of their corresponding signatures. The pairwise distances are stored in a distance matrix.

3. Using the distance matrix, the MDS technique is applied to embed the surfaces into the Euclidean space.

In our experiment, we choose N = 300, α = 1, and the embedding results with the shape DNA and the nodal count sequences are shown in Fig. 2(g) and (h). From the results, we can see clearly that the nodal counts provide better separation of these two groups. This demonstrates the ability of the nodal count sequences in resolving isospectral surfaces.

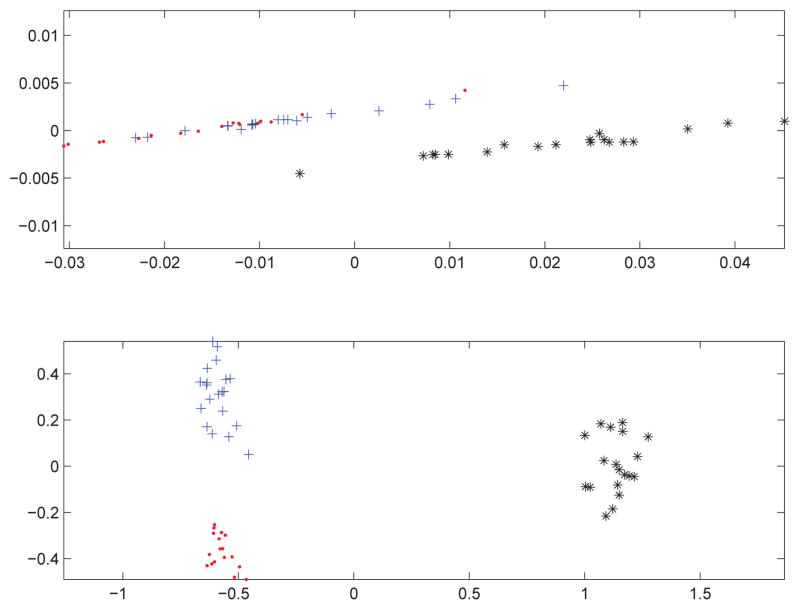
In the second experiment, we demonstrate the above shape classification procedures to a larger data set. This data set includes three groups of surfaces: 20 hippocampus, 20 putamen, and 20 caudate. For the three groups, the eigenvalue sequences and nodal count sequences were computed. By applying the same MDS technique as in the first experiment to these signatures, we can embed the 60 surfaces into a 2D space and the results are shown in Fig. 3. Clearly this results show that the nodal count sequence provides better classification.

Fig. 3.

Top: the MDS embedding of the surfaces with the shape DNA signature. Bottom: the MDS embedding of the surfaces with the nodal count sequences. The first 300 eigenvalues and eigenfunctions were used in both embeddings. (red ’ ·’: caudate; blue ’+’: putamen; black ’*’: hippocampus.)

5. CONCLUSIONS AND FUTURE WORK

In this paper we proposed to use the nodal count sequences of the Laplace-Beltrami eigenfunctions as a novel signature of 3D shapes. We demonstrated its ability of resolving isospectral shapes by classifying anatomical structures with very similar distribution of eigenvalues. In our future work, we will apply it to the task of shape retrieval from databases. We are also investigating its application in classifying hippocampal surfaces from normal controls and Alzheimer’s disease.