The Aggregation of Capped Hexaglycine Strands into Hydrogen-Bonding Motifs Representative of Pleated and Rippled β-Sheets, Collagen, and Polyglycine I and II Crystal Structures. A Density Functional Theory (DFT) Study

Abstract

We compare the energies and enthalpies of interaction of three and seven stranded capped polyglycine aggregates in both the pleated and rippled antiparallel and parallel β-sheet structures as well as the collagenic (3-strand) or polyglycine II-like (7-strand) forms using DFT theory at the B3LYP/D95(d,p) level. We present the overall interaction energies as broken down into pure H-bonding between the strands at the geometries they assume in the aggregates and the distortion energies required to achieve those geometries starting from the fully relaxed single strands. While the antiparallel sheets represent the most stable structures for both the three and seven strand structures, the pure H-bonding interactions are the smallest for these structures. The overall interaction energies are dominated by the energy required to distort the relaxed polyglycine strands rather than the H-bonding energies. The antiparallel β-sheet constrained to C_s symmetry has a lower enthalpy, but higher energy, of interaction than the fully optimized structure.

Polyglycine crystalizes in three forms, polyglycine I (actually a dimorph) and II. Polyglycine I includes two different crystal structures each containing a different type of β-sheet. ^1–5 The structure of polyglycine II (PII) consists of parallel β-sheets oriented 120 degrees to each other.^6,7 Three of these sheets intersect at each polyglycine strand. Each triad of nearest neighbor strands bears a striking resemblance to collagen, the most abundant protein in the human body. In collagen, the three strands of polyglycine taken from the crystal structure are replaced with strands comprised of triads of XYG (where X and Y can be any amino acid, most often proline and 4-hydroxyproline) and G is glycine. These are connected by H-bonds from the glycines (donors) on one strand to C=O’s (acceptors) of the amide couplings on another peptide strand. The 'sheets' each contain only two strands in collagen-like structures. The principal differences between collagen-like structures and PII lie in the inability of collagen to form the infinite pattern of H-bonds normal to the peptide backbone (found in PII) beyond the three strands of the collagenic triple helix, due to a) the lack of N-H donors on the proline and hydroxyproline residues and b) the steric impediments caused by the side chains of all the amino acids except for glycine. Comparison of the PII and collagen structures begs the questions: a) Does the triple helical (XYG)_N structure of collagen result from an evolutionary selection against structures that could form additional H-bonds such as those present in polyglycine? b) How competitive are the PII structures with β-sheets of the same size? While β-sheets are generally thought to form a pleated sheet structure, the anti-parallel polyglycine β-sheets that comprise the polyglycine I form are known to also assume a rippled sheet structure.⁸ Rippled structures require alternating strands of L and D amino acids. Of the natural amino acids, only glycine (which is enantiomorphic) can assume such a structure. Recent Hartree-Fock and DFT calculations have found small models of infinite strands of polyglycine⁹ and antiparallel β-sheets to be essentially planar.^10,11 Earlier MO calculations were based upon pleated sheet structures without geometry optimization.^12–15

Polyglycine is the only short peptide that can form H-bonding motifs that resemble all the H-bonding motifs studied here. As such, it is the only short peptide that can be used to compare the 'natural' relative energies of all these motifs without the influence of the side chains that differentiate between the amino acids. In this paper, we compare the several possible ways in which polyglycine strands can aggregate. We base our calculations upon the capped peptide, formyl(gly₆)NH₂. Use of the formyl (rather than acetyl) capping group prevents the methyl of the acetyl from becoming an obstacle to achieving planarity. We consider trimers and heptamers of the peptides in PII-like and antiparallel and parallel β-sheet-like (both pleated and rippled) conformations which we shall designate as PII_N, β– (PL or R)AP_N, or β–(Pl or R)P_N, respectively, where N=3 or 7.

Methods

Density functional theory (DFT) calculations were performed using the GAUSSIAN 09¹⁶ suites of computer programs. All calculations used the D95(d,p) basis set and the B3LYP functional. We have used this combination in several previous studies involving H-bonds in peptides and similar systems.^17–23 This combination performs well for the water dimer,²⁴ while several other combinations of functionals and medium sized basis sets have significant problems.²⁵ This method combines Becke’s 3-parameter functional,²⁶ with the non-local correlation provided by the correlation functional of Lee, Yang and Parr.²⁷ The geometries of all the β-sheet species were completely optimized and the AP_N structures were also optimized in C_s symmetry. As the PII_N species could not be completely optimized without constraints for reasons discussed below, we kept each strand of formylGly₆NH₂ equivalent for the PII₃ and PII₇ structures. The β-sheets were also optimized with the same constraints for comparison. The vibrational frequencies were calculated for all unconstrained and C_s structures, using the normal harmonic approximations employed in the GAUSSIAN 09 program, to verify the stationary points and calculate the enthalpies, and free energies of the completely optimized species using the harmonic approximation. All frequencies were real for the completely optimized β-sheet structures. Those structures where the strands were kept equivalent are not proper minima, so no enthalpies were calculated for these. The single-point a postieri counterpoise corrections (CP) were calculated using the procedure incorporated in GAUSSIAN 09. Optimization on the CP-corrected potential energy surfaces (CP-OPT)²⁸ were not completed due to the excessive CPU time required.

While there have been several reports of problems with the B3LYP functional in other applications,²⁹ this functional has been tested with the D95(d,p) and D95++(d,p) basis sets and shown to give reasonable results for polyglycine⁹ dihedrals and for H-bonding interactions.^17,24 One would expect that other problems that this functional might have would cancel in calculating the interaction energies between the strands.

Since these studies involve short peptides, which differ considerably from globular proteins in that their crystals have not been reported to contain water, we did no consider any solvation interactions.

Results and Discussion

Table 1 presents the calculated interaction energies (simple DFT energies), ΔE's, and enthalpies (at 298 K), ΔH's, for the PII_N, β-P_N and β-AP_N (both Pl and R) species relative to the equivalent number of optimized extended strands of formyl(gly)₆NH₂. The figures presented below show the structures of the seven-stranded optimized species. Figures illustrating the geometries of the three-stranded species and the complete geometries (Cartesian coordinates) can be found in the supplementary information. The comparisons made all refer to the CP corrected results, unless otherwise indicated.

Table 1.

Relative energies of the species considered in kcal/mol. The relative energies of the SE structures on a different scale from the others.

Speciesa	H- bonds	ΔE/H- bond	ΔE/H- bond (CP)b	Distortion/re sidue	ΔE/H-bond (CP) from optimized strandb	ΔH/H-bond (CP) from optimized strandc	Relative total energies( CP)	Relative total ΔHs (CP)
Fully optimized (except Cs symmetric structure)
3 strands
β-R-P3	14	−7.2	−5.6	1.8	−3.3	−2.7	13.3	19.1
β-Pl-P3	14	−8.1	−6.4	2.2	−3.5	−2.8	10.6	18.0
β-Pl-AP3	14	−6.6	−5.0	0.5	−4.3	−3.8	0	3.6
β-Cs-AP	14	−6.4	−4.8	0.4	−4.2	−4.1	0.4	0
7 strands
β-R-P7	42	−8.2	−6.5	2.6	−3.9	−3.2	26.1	42.5
β-Pl-P7	42	−8.3	−6.5	2.6	−3.9	−3.2	24.9	42.4
β-R-AP7	42	−7.7	−6	1.5	−4.5	−3.9	0.3	11.2
β-Pl-AP7	42	−7.8	−6.2	1.7	−4.5	−3.9	0	11.7
β-C s-AP7	42	−6.7	−5.0	0.7	−4.4	−4.2	4.4	0
Structures with strands equivalent
3 strands
SE-PII3	7	−8.6	−6.0	3.0	1.8		60.5
β-SE-P3	14	−7.6	−5.9	2.5	−2.7		9.8
β-SE-AP3	14	−5.8	−4.0	0.4	−3.4		0
7 strands
SE-PII7	28	−9.5	−6.8	3.4	−1.7		130.7
β-SE-P7	42	−8.2	−6.4	2.8	−3.5		29.8
β-SE-AP7	42	−6.5	−4.9	0.6	−4.2		0

^aSE, strands are equivalent; Pl, pleated sheet; R, rippled sheet; C_s, C_s symmetric (planar).

^bSee text for complete definition of the difference between these entries.

^cThe enthalpies were calculated from the completely optimized β-sheets. This was not possible for the PII structures which were constrained.

Extended formyl(gly)₆NH₂

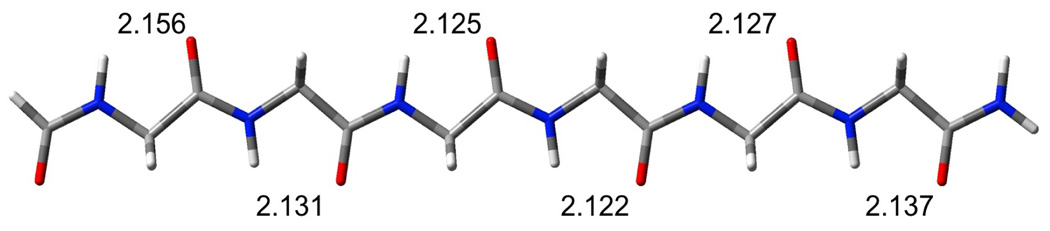
Extended formyl(gly)₆NH₂ exhibits many of the characteristics of the extended acetyl(ala)_NNH₂ strands that have been reported in previous studies.^20,30 In particular, slightly cooperative C₅ H-bonding interactions stabilize these strands. The cooperativity can be deduced from the shorter C₅ O…H distances found near the center of the strand (see figure 1). The necessary sacrifice of this stabilizing factor upon formation of β-sheets contributes to the overall low cooperativity of simple β-sheets.^10,11

Figure 1.

Optimized single strand with C₅ O—H distances (Angstroms) noted.

We have calculated the energies of the extended strands in two different ways: a) completely optimized, and b) fixed in the geometries of the appropriate cluster of strands (sheets collagenic helix or PII model). The energy differences between the latter and the optimized strands measures the distortion energies required for the optimized strands to achieve the requisite geometries of the aggregates. The fixed geometries of each strand in the fully optimized clusters differ from each other as do their energies. The sum of the distortion energies of the individual strands constitutes the total distortion energy for the aggregate. The fixed geometries for those calculations where the strands are kept equivalent are necessarily identical, as are their distortion energies.

The interaction energies of the strands to form the trimeric and heptameric structures can be broken down into two parts: a) the energy required to distort the relaxed strand into the geometry it assumes as part of the larger aggregate, and b) the interaction energy between the (already distorted) fragments. The interaction energy defined by part (b) above will not depend upon the reference geometry of the strand, but the distortion energy will. Thus, the total energies of interaction for the aggregates considered will depend upon the (arbitrary) choice of the relaxed extended single strand. In reality, the unassociated strands can almost certainly exist in many different conformations which will differ in different environments. Many such conformations may have one or more intramolecular H-bonds. These may be higher or lower in energy than the fully extended strand. The distortion energy from any optimized structure of the single strand to that taken in the optimized aggregate must always be > 0 unless the relaxed geometry is exactly the same as that of the strand in the optimized structure (in which case it will be zero). Thus, the distortion energy for each strand makes a positive contribution to the interaction energy. The difference in the distortion energy for a strand with a known structure different from the fully extended structure used here as a standard can easily be calculated. This calculated difference will give the energy of forming the aggregate from any other conformation of the strand that may be relevant including multiple conformations that might exist in solution.

β-sheets

Both the parallel and antiparallel β-sheets form seven H-bonds between each pair of adjacent strands (six between the glys and another involving the capping formyl group), totaling 14 for the(β-AP₃) and parallel (β-P₃) sheet; 42 for the seven stranded β-antiparallel (β-AP₇) and parallel (β-P₇) sheets. In addition, the completely optimized parallel (but not antiparallel) β-sheet structures also contain C₇ intramolecular H-bonds in one of the terminal strands. β-P₃ contains two such interactions and β-P₇ only one. We have not been able to find optimized parallel β-sheet structures without C₇ H-bonds using basis sets that have polarization functions on hydrogen. Such structures can be found with basis sets that do not have hydrogen polarization functions. However, we do not consider basis sets without polarization functions on the H's adequate for H-bonding studies. Antiparallel β-sheets can form quasi planar structures as expected from previous theoretical studies,^10,11 as well as pleated and rippled structures. Parallel polyglycine β-sheets form only pleated and rippled structures.

Antiparallel (AP) β-Sheets

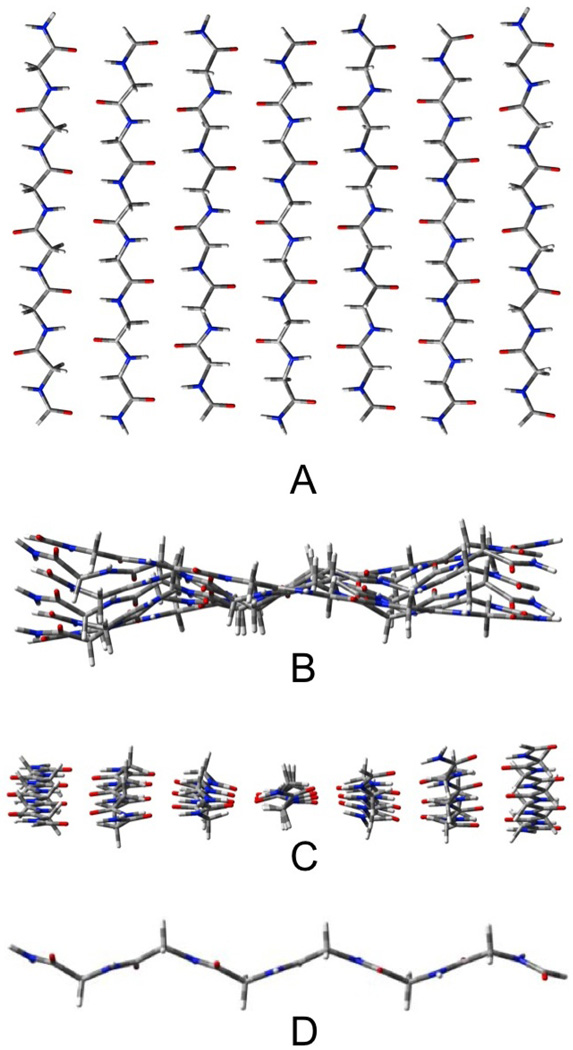
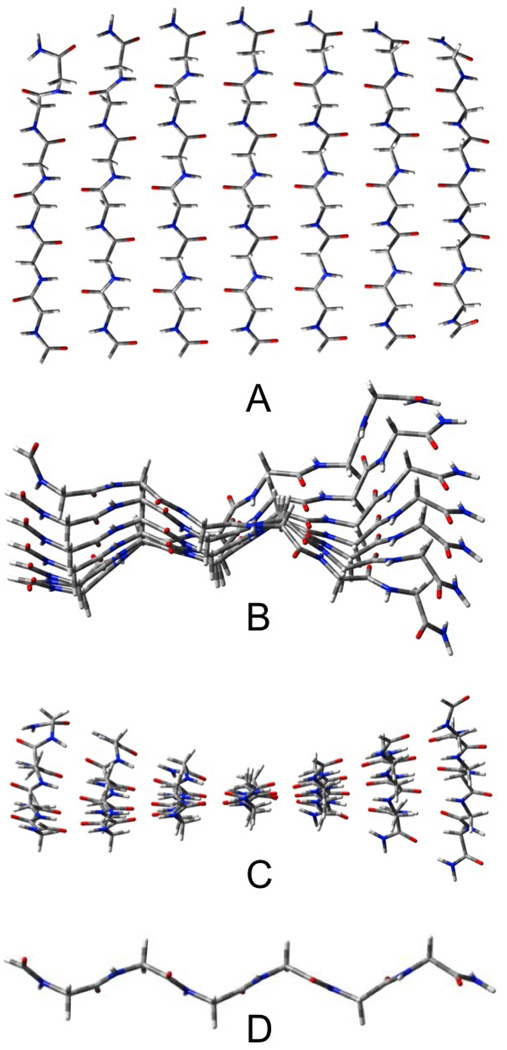
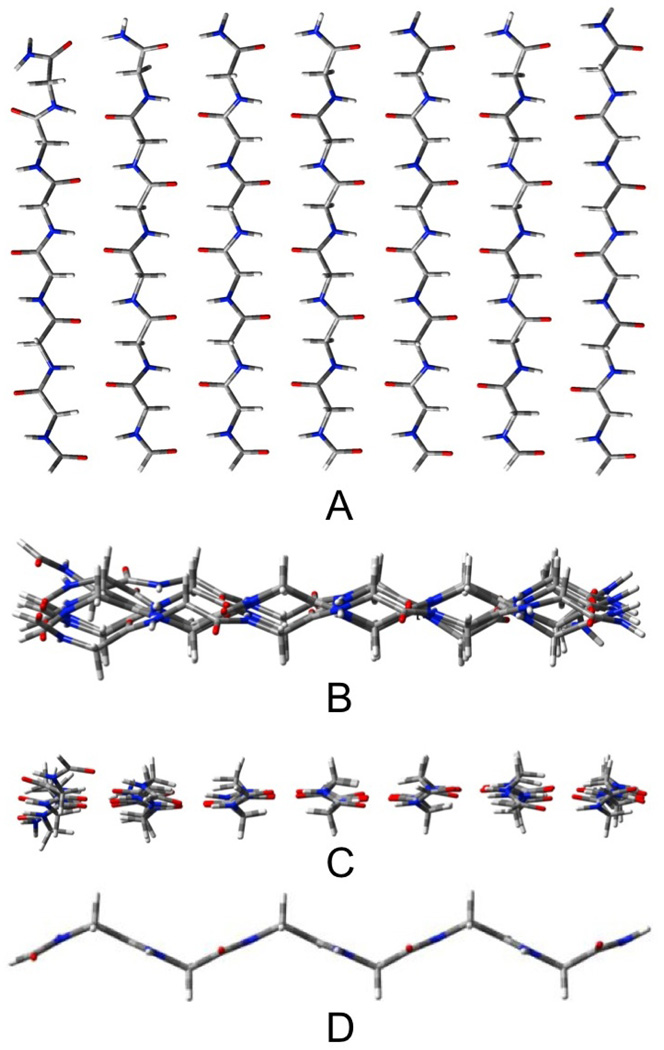
The AP β-sheets have been geometrically optimized in three forms: pleated (Pl), rippled (R) shown in figures 2 and 3, respectively, and planar (C_S). These figures (as well as those depicting the other β-sheet structures that will follow) contain four views: A) a top view, B) a side view, C) an end view and D) a view of the most central single strand (to illustrate the distortion). The outermost strands of these structures remain almost planar (see figures 2B and 3B), while the inner strands take on the pleated or rippled structure (figures 2D and 3D). As a result, the three-stranded AP sheets, which have only one inner strand, and contain 14 H-bonds and 18 residues, remain essentially planar. The three-stranded Pl and R structures cannot be distinguished as their geometries converge to the same structure upon optimization. The seven stranded sheets contain both 42 H-bonds and 42 residues. The Pl structure (figure 2) has the most negative ΔE/H-bond, but it also has the most distortion per residue. As a result of this energy compensation between interaction and distortion energies, the total energies and enthalpies of the Pl and R structures do not differ substantially. The Pl structure has the lower energy by only 0.3 kcal/mol, but the R structure (figure 3) the lower enthalpy (298 K) by 0.5 kcal/mol. The variation of the relative enthalpies and free energies with T will be discussed below. The ΔE/H-bond for the C_S structure is about 1 kcal/mol less negative than for the Pl and R, but the lower distortion energy per residue roughly cancels this, so that the total energy exceeds that of the Pl structure by only 4.4 kcal/mol, or about 0.1 kcal/mol per H-bond. However, upon calculation of the enthalpy, the C_S structure becomes more stable than the R-structure by 11.2 kcal/mol or about 0.3 kcal/mol/H-bond. This result must be tempered by the fact that the optimized C_S structure has 17 low frequency imaginary vibrational modes, consistent with our earlier report.¹¹ For the calculated enthalpy to be meaningful, the zero point vibration would have to be higher than the barriers that separate the local minima, which cannot be accurately determined with the harmonic approximation to the vibrations. Nevertheless, several examples of this phenomenon have been reported. The spectroscopic equivalence of the H's in water trimer³¹ provides one of the more dramatic cases. We have discussed this problem elsewhere.³² We note that the three stranded AP structure does not deviate significantly from planarity, while corresponding C_S structure has six imaginary frequencies, suggesting that the saddle points on the PES that are associated with the imaginary vibrations of the C_S structure do not significantly differ in energy or geometry from nearby minima. We could not find separate optimized structures for the Pl and R structures for the three stranded AP sheets as either a pleated or rippled starting geometry converged to the same structure. The total interaction energy for the C_S constrained structure exceeds that of the optimized by only 0.4 kcal/mol, while the total enthalpy favors the C_S structure by 3.6 kcal/mol for AP₃.

Figure 2.

Seven stranded antiparallel pleated sheet β-Pl-AP₇. A) top view, B) end view, C) edgeview, D) most central strand.

Figure 3.

Seven stranded antiparallel rippled sheet β-R-AP₇ A) top view, B) end view, C) edge view, D) most central strand.

Parallel (P) β-Sheets

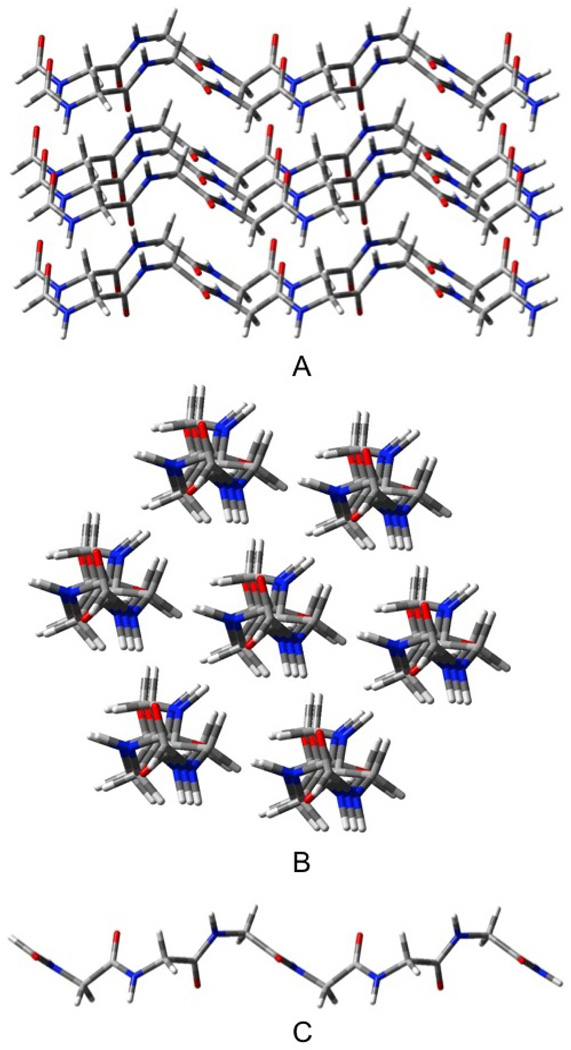
We have found optimized structures of parallel β-sheets in both the pleated and rippled forms. The P₃ (unlike the AP₃) sheets, converge to two distinct forms when optimized, with the pleated slightly more stable than the rippled structure. However, both are less stable than the AP₃ sheet. The rippled and pleated P₇ sheets have much more similar energies and enthalpies, but are again less stable than their AP counterparts. As seen from table 1, the distortion energy increases more while the ΔE/H-bond becomes more negative for the rippled than pleated structure upon going from three to seven strands. As a result the relative overall interaction energies and enthalpies for these two structures remain essentially equivalent, but higher than for their AP counterparts. However, the ΔH/H-bond relative to the optimized strand becomes more negative by 0.4–0.5 kcal/mol upon increasing the number of strands from three to seven, while the corresponding changes for the AP sheets are only 0.1 (see table 1). This suggests that larger sheets might eventually favor the parallel forms, consistent with the report that one of the polymorphs of polyglycine has a parallel structure.⁵

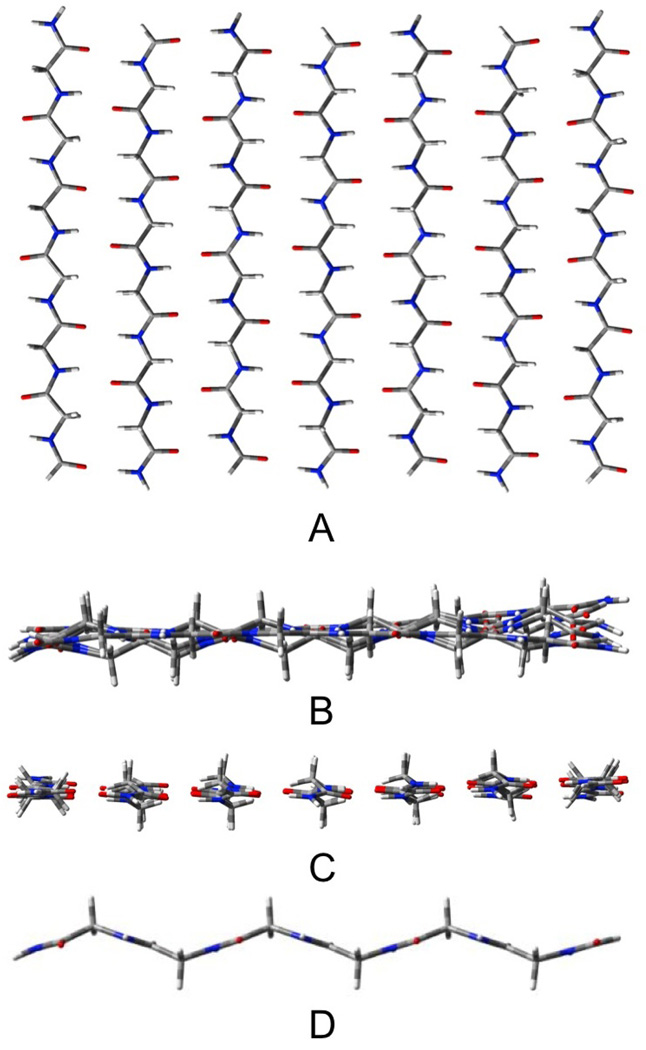
Despite their similar energies, the structures of the pleated and rippled P₇ sheets are quite different (see figures 4 and 5). The pleated sheet twists considerably, while the rippled sheet remains closer to planarity. For the pleated sheets, the inner strands are, again, more distorted than those at the ends of the sheet.

Figure 4.

Seven stranded parallel pleated sheet β-Pl-AP₇ A) top view, B) end view, C) edge view, D) most central strand.

Figure 5.

Seven stranded parallel rippled sheet β-R-AP₇. A) top view, B) end view, C) edge view, D) most central strand.

PII_N

In order to keep the geometry as close to what one would expect from a seven strand fragment of an infinite crystal, we constrained the structure so that each strand has the same structure and the six outer strands of PII₇ are symmetrically disposed around the central strand (see figure 6). All attempts to achieve a completely optimized PII₃ structure failed as the strands moved apart. We recalculated the AP_N and P_N using the same constraint for comparison. The sheets structures discussed in this section refer to those optimized with this constraint. The positive ΔE/H-bond of PII₃ (see table 1) indicates that this structure is repulsive compared to three separate strands.

Figure 6.

Seven stranded PII-like structure, PII₇. A) top or edge, B) end, C) individual strand (all strands equivalent).

The PII₃ structure (roughly equivalent to a collagen triple helix), cannot H-bond cooperatively as no H-bonding chains (longer than one H-bond) exist. However the PII₇ structure can be viewed as three β-P₃ sheets passing through the same central strand at 120 degree angles to each other. If one were to expand the PII₇ structure to a polyglycine crystal, the three β-sheets that pass through the central strand would become quasi-infinite in size and exhibit cooperativity equal or greater to that found in PII₇. The average H-bond energy (after CP) for PII₇ is lower than that for β-P₇ by 0.3 kcal/mol despite the fact that each sheet within the PII₇ structure contains only three strands. The distortion energies favor the β-P₇ structure by 0.6 kcal/mol/residue, however, the PII₇ structure has 14 fewer H-bonds but the same number of residues as β-P₇. The higher relative total energy of PII₇ compared to β-P₇ (130.7 vs. 29.8, for a difference of 100.9 kcal/mol) should be corrected by the added stabilization of the additional H-bonds that would be formed in a crystal of PII. If one adds a stabilization of 14 H-bonds at −6.8 kcal/mol each to compare with the β-SE-P₇ structure, the difference in the relative energies would decrease by 95.2 to 5.7 kcal/mol. However, the 'sheets' in the PII₇ structure contain only three strands, rather than the seven in β-P₇. We see from table 1 that the ΔE/H-bond becomes more negative by 0.5 kcal/mol upon going β-SE-P₃ to β-SE-P₇, presumably due to increased cooperativity. If one adds this cooperative stabilization for each of the 42 H-bonds (28 +14), the PII₇ structure would become relatively more stable by about another 21 kcal/mol, making the PII₇ structure more stable than either the β-SE-P₇ or even the β-SE-AP₇ structure by about 15 kcal/mol or roughly 0.4 kcal/mol/residue. While the above demonstrates the plausibility that the PII structure could be the most stable if an infinite crystal be considered, one must remember that all interactions between strands are considered in the PII structures, while the structures considered for the sheets do not take the stabilizing interaction between the sheets into account. Also, the calculations using the PII structures use equivalent strands and do not include vibrational corrections.

Trimeric structures

For the structures containing three peptide units, the antiparallel sheets (β-AP₃) are the most stable based both upon relative energies and enthalpies. However, this structure contains the weakest H-bonds based upon the energies of the optimized trimeric structures and the single strands frozen in the geometries they assume in the trimer. PII₃ contains the strongest H-bonds despite being the least stable of the three structures. In fact, PII₃ is the only structure that is unstable relative to three unassociated extended strands, when completely optimized. Palfi and Perczel have reported similar behavior for strands containing the AAG triad.³³ The low stability of the SE-PII₃ structure must largely be due to the fewer H-bonds (seven) than in the sheets (14). As seen from table 1, the distortion energy/residue of SE-PII₃ is 3.0 kcal per residue (or about 63 kcal/mol for 18 residues), while the H-bonding energy is −6.0 kcal/mol per H-bond (or about −42 kcal/mol for seven H-bonds). Among the fully optimized sheet structures, β-AP₃ (rippled and pleated optimized to the same structure) has the lowest energy primarily because the lower distortion energies more than compensate for the weaker H-bonds. The low distortion energy (0.5 kcal/mol per residue) for β-AP₃ arises from the quasi-planarity of this structure, which keeps the individual strands close to the geometries they assume in the optimized extended strand. The β-P₃, and especially the PII₃ structures require much greater distortions from the optimized extended strand.

Heptameric structures

The relative energies and enthalpies of the heptameric peptides, as well as the individual contributions to these, follow the same qualitative order as those of the trimers. Nevertheless, several important differences become apparent. The CP-corrected energies per H-bond all become more negative compared to those of the trimers. At the same time, the distortion energies per residue all increase. The ΔE/H-bond compared to optimized strands for the PII_N structures goes from being repulsive (1.8 kcal/mol in PII₃) to attractive (−1.7 kcal/mol in PII₇) which corresponds to a relative increase in H-bond stability of 3.5 kcal/mol. The relative instability of PII₇ compared to its isomers appears to be due to the reduced number of H-bonds in this structure (28) as compared to the two sheets (42). The data suggest that larger isomeric structures will eventually favor the PII_N over the β-P_N form, which would be consistent with the fact that all three crystalline forms of polyglycine have the same number of H-bonds (see above)

Distortion Energies

As seen from table 1, the distortion energies per residue contribute most to the difference in ΔE's/H-bond for the different structures (compare figure 1 with figures 2–6D). One must bear in mind that the number of residues is coincidentally the same as the number of H-bonds (including those involving the formyl and NH₂ caps) for the sheet structures, but exceeds the number of H-bonds for the PII structures. The distortion energies per residue increase upon increasing the aggregate from three to seven strands for all structures. As noted above, the seven stranded structures all have stronger H-bonds than their three stranded analogs. The stronger H-bonds allow the individual strands to accept more strain. In fact, the β-AP₃ and β-AP₇ (both pleated and rippled) structures, each of which is the lowest energy structure among the isomers, each have the smallest ΔE's/H-bond. These are more than compensated for by the lowest distortion energies.. The small distortion energy for the C_S-structure derives from the weakening of the C₅ intra-strand H-bonds in the optimized structure. They open in the β-sheet to allow for better inter-strand H-bonds. The geometries of the frozen strands taken from the β-P₇ and PII₇ structures exhibit considerable changes in the backbone dihedral angles compared to the optimized strand in addition to the breaking of the C₅ H-bonding interactions. The distorted strand taken from PII₇ assumes the polyproline II-like backbone structure, as expected from the crystal structures.^6,34 For the PII₇ structure, the relative values of distortion energy/residue and ΔE/H-bond can be somewhat misleading, as in the polyglycine crystal each strand would have seven H-bonds (rather than the four in the model) while the distortion energy per strand should not change appreciably. Assuming that the PII₇ structure had 49 H-bonds (instead of 28) would lower the distortion energy/H-bond (not per residue) from 5.1 to about 2.9 kcal/mol. Of course, the β-AP₇ and β-P₇ structures should also form 49 H-bonds if inserted in infinite sheets. However, the resulting reduction in the distortion energies/H-bond would be much smaller.

H-Bond distances

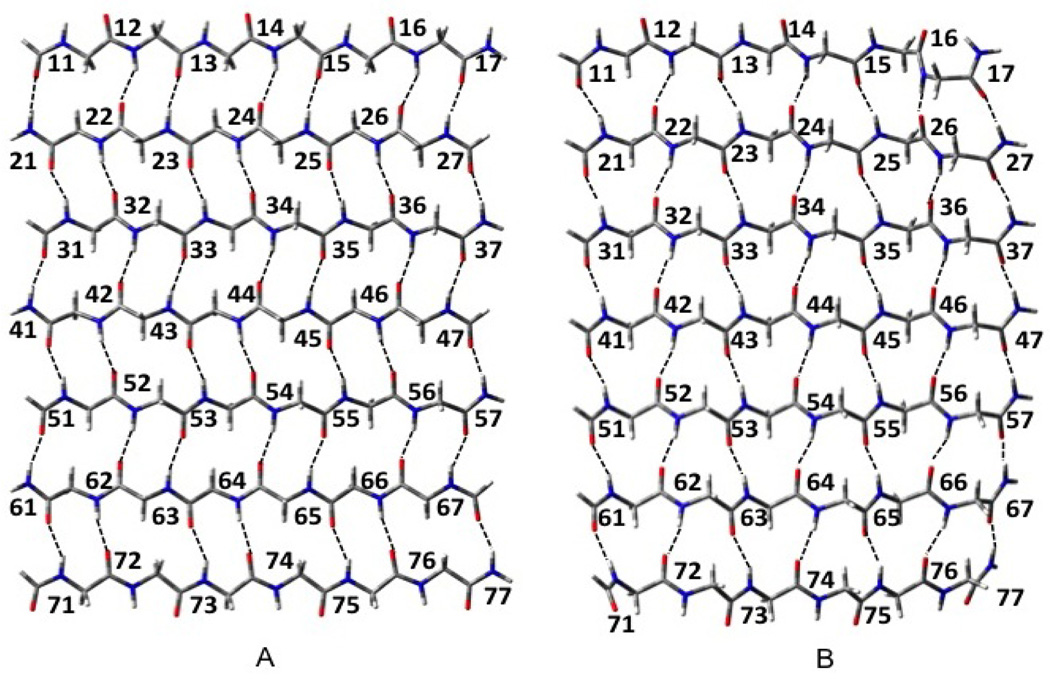
Table 2 compares the H-bond distances for the fully optimized and C_s β-AP₃ and β-AP₇ structures. The H-bond lengths for the fully optimized structures follow the descriptions in figure 7) In the fully optimized structures, the H-bonds nearer the ends of each strand tend to be somewhat shorter than those nearer the center, particularly in the β-AP₇ structure. We suggest that this indicates the occurrence of attractive strain³⁵ in that the H-bonds near the ends of the strands have more configurational freedom to form the shorter H-bonds expected from the increasing cooperativity expected from growing H-bond chains.²² Those H-bonds near the center of the strands remain more constrained by the other interstrand interactions such as repulsions between the -CH₂- fragments. When constrained to C_s symmetry, the lengths of the H-bonds near the ends of the strands remain much more similar to those near the middle, while the differences between the H-bond lengths become significantly smaller. Due to H-bond cooperativity, the H-bonds between the strands near the center of the sheets tend to be shorter than those between the strands at the edges of the sheets. The shortest H-bonds occur at the ends of the fully optimized AP sheets between the strands near the middle of the sheets. The H-bonds lengths for the fully optimized structure vary from 1.841 to 2.051 while those for the C_s structure vary from 1.883 to 2.024 Angstroms. Thus, the constraint to C_s increases the attractive strain beyond that encountered in the fully optimized structure.

Table 2.

Interstrand H-bonds between Nn and Nn for the species considered.^a Correspondence to each H-bond type is shown in Figure 7. N and n refer to the strand and residue number, respectively.

		n=1	n=2	n=3	n=4	n=5	n=6	n=7	AVG
3 strands
SE-PII3 b		1.987	1.953	1.973	1.971	1.942	1.962	1.964	1.965
β-SE-P3 b		1.951	1.950	1.931	1.949	1.930	1.947	1.928	1.941
β-SE-AP3
Nn,Nn = 1n,2n		1.883	1.886	1.884	1.878	1.876	1.871	1.868	1.878
	2n,3n	1.868	1.871	1.876	1.878	1.884	1.886	1.883	1.878
β-R-P3
	1n,2n	1.914	1.988	2.012	2.088	1.956	2.216	1.851	2.004
	2n,3n	1.981	1.891	2.056	1.970	2.160	1.890	1.996	1.992
β-Pl-P3
	1n,2n	1.923	2.022	2.012	1.922	1.943	1.734	1.885	1.920
	2n,3n	1.846	1.847	1.906	1.881	2.057	1.849	1.971	1.908
β-Pl-AP3
	1n,2n	1.885	2.017	1.983	2.037	2.019	1.974	1.999	1.988
	2n,3n	1.988	1.925	2.058	2.019	2.028	1.977	1.918	1.988
β-Cs-AP
	1n,2n	1.908	2.012	2.008	2.028	2.010	1.968	2.003	1.991
	2n,3n	2.012	1.969	2.034	2.020	2.029	1.980	1.915	1.994
7 strands
SE-PII7 b		1.889	1.885	1.894	1.887	1.887	1.897	1.890	1.890
β-SE-P7 b		1.888	1.882	1.869	1.882	1.869	1.882	1.869	1.877
β-SE-AP7
	1n,2n	1.938	1.945	1.948	1.954	1.957	1.963	1.966	1.953
	2n,3n	1.966	1.963	1.957	1.954	1.948	1.945	1.938	1.953
	3n,4n	1.938	1.945	1.948	1.954	1.957	1.963	1.966	1.953
	4n,5n	1.966	1.963	1.957	1.954	1.948	1.945	1.938	1.953
	5n,6n	1.938	1.945	1.948	1.954	1.957	1.963	1.966	1.953
	6n,7n	1.966	1.963	1.957	1.954	1.948	1.945	1.938	1.953
β-R-P7
	1n,2n	1.918	2.004	1.995	1.893	1.967	1.734	1.854	1.909
	2n,3n	1.880	1.826	1.895	1.855	1.900	1.846	1.826	1.861
	3n,4n	1.868	1.831	1.868	1.871	1.886	1.838	1.818	1.854
	4n,5n	1.873	1.826	1.875	1.883	1.867	1.873	1.823	1.860
	5n,6n	1.870	1.841	1.893	1.893	1.886	1.879	1.803	1.866
	6n,7n	1.880	1.868	1.999	1.986	2.045	1.948	1.990	1.960
β-Pl-P7
	1n,2n	1.920	2.034	1.968	1.944	1.986	1.730	1.880	1.923
	2n,3n	1.845	1.856	1.864	1.841	1.868	1.821	1.849	1.849
	3n,4n	1.854	1.844	1.848	1.833	1.842	1.822	1.838	1.840
	4n,5n	1.861	1.833	1.848	1.836	1.821	1.840	1.827	1.838
	5n,6n	1.869	1.826	1.862	1.846	1.827	1.861	1.815	1.844
	6n,7n	1.871	1.848	1.992	1.947	2.018	1.930	1.955	1.937
β-R-AP7
	1n,2n	1.850	2.004	1.932	2.036	1.966	1.981	1.967	1.962
	2n,3n	1.892	1.878	1.922	1.946	1.902	1.942	1.837	1.903
	3n,4n	1.833	1.893	1.899	1.909	1.917	1.856	1.885	1.885
	4n,5n	1.893	1.864	1.910	1.911	1.894	1.891	1.832	1.885
	5n,6n	1.856	1.894	1.950	1.916	1.954	1.865	1.914	1.907
	6n,7n	1.979	1.897	2.036	1.976	2.042	1.926	1.911	1.967
β-Pl-AP7
	1n,2n	1.848	2.009	1.920	2.036	1.946	1.983	1.954	1.957
	2n,3n	1.871	1.898	1.896	1.936	1.902	1.930	1.841	1.896
	3n,4n	1.840	1.874	1.887	1.894	1.889	1.875	1.861	1.874
	4n,5n	1.870	1.867	1.889	1.884	1.892	1.872	1.840	1.873
	5n,6n	1.871	1.868	1.932	1.893	1.935	1.871	1.897	1.895
	6n,7n	1.992	1.873	2.047	1.939	2.048	1.911	1.917	1.961
β-C s -AP7
	1n,2n	1.900	2.027	2.007	2.024	1.998	1.963	2.004	1.989
	2n,3n	1.975	1.944	1.969	1.978	1.977	1.979	1.889	1.959
	3n,4n	1.883	1.966	1.971	1.970	1.973	1.946	1.980	1.956
	4n,5n	1.985	1.953	1.969	1.972	1.965	1.964	1.881	1.955
	5n,6n	1.889	1.955	1.971	1.975	1.984	1.954	1.981	1.958
	6n,7n	2.021	1.978	2.038	2.015	2.019	1.965	1.899	1.991

^aSE, strands are equivalent; Pl, pleated sheet; R, rippled sheet; Cs, Cs symmetric.

^b1n,2n = 2n,3n = 3n,4n= 4n,5n= 5n,6n = 6n,7n for n = 1 to 7.

Figure 7.

H-bond numbering scheme. (A) anti parallel sheet (B) parallel sheet.

Polymorphism

Polyglycine exists in at least three different polymorphs. Crick established the structure of polyglycine II in 1955.⁶ Several suggestions for the structure of polyglycine I have appeared.^1–4,36 Kajava reported two polymorphs of polyglycine I.⁵ One which forms from low molecular weight polyglycine (about ten residues) strands consists of parallel β-sheets, the other formed from high molecular weight (>90 residues) strands, consists of antiparallel rippled β-sheets.

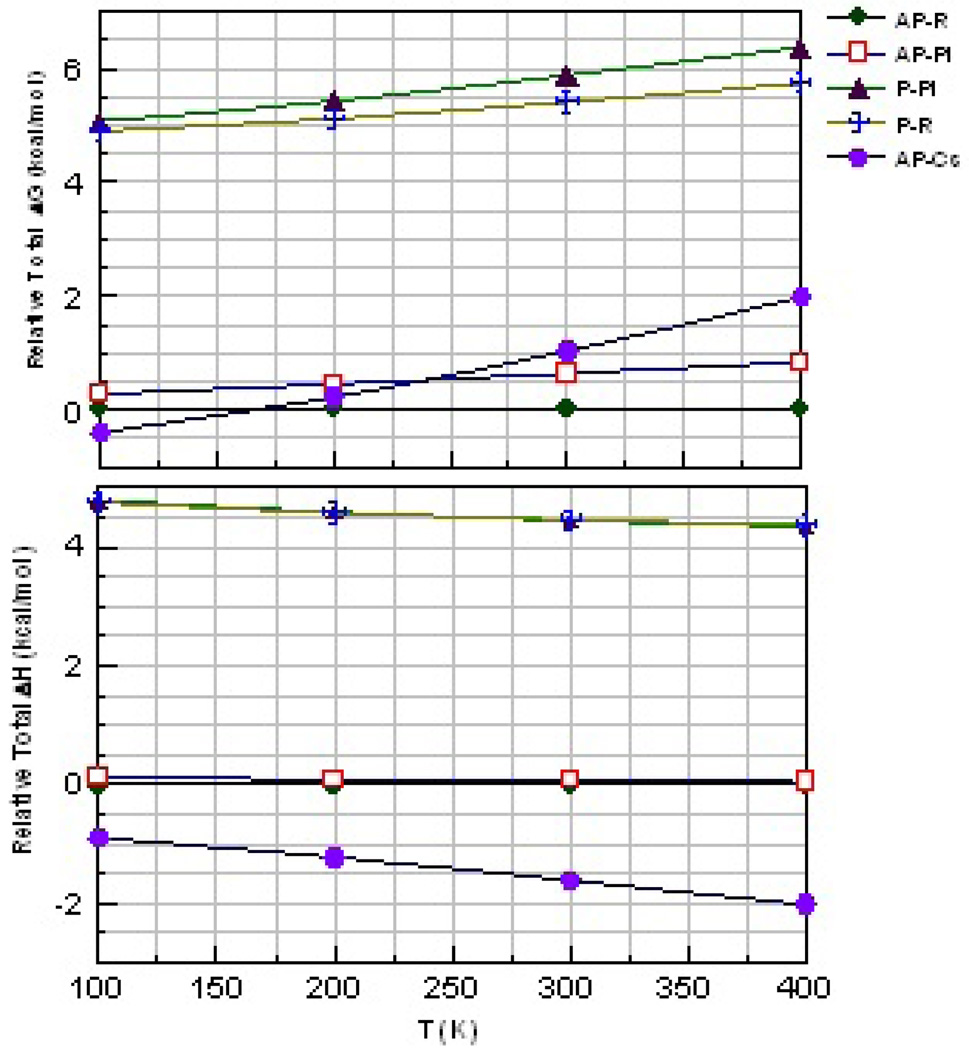
We make a limited attempt to address the temperature dependence of the relative stabilities of the optimized seven membered β-stranded aggregates by comparing the relative ΔG's and ΔH's as a function of T (figure 8). We note that the entropic component of ΔG's may not be completely reliable when the frequencies are calculated using the harmonic vibrational frequencies. The problem is especially large for the torsional modes, many of which almost freely rotate. However, while a simple strand of polyglycine contains several of such modes, they stiffen considerably upon forming the hexameric structures. Thus, comparison of the relative ΔG's may have significance. Figure 8 shows AP-R to be the preferred form for T>150K. The enthalpically favored AP-C_S form becomes the least stable of the AP forms for T>250K, while the P forms are both 4 to 5 kcal/mol/strand higher in energy for all T<400 K.

Figure 8.

Variation of relative free energy (top) and enthalpy (bottom) per capped hexaglycine strand with T for the hexameric β-strand

The results presented here do not contain all the information needed to compare the three dimensional crystal structures. However, they do suggest the energetic differences between the H-bonding motifs that contribute to the structures to be small and to depend upon the size of the aggregate. Thus, the β-P_N structures (both Pl and R), while higher in enthalpy than their AP counterparts, appear to increase in stability more as the sheets acquire additional strands, as discussed above and indicated in table 1. Some polymorphs may be kinetically stable and only form under specific conditions, while others may be thermodynamically stable. Many interesting example have been reported.³⁷ One cannot be sure that all the polymorphs of polyglycine have been characterized.

Implications for collagen

Our results show the collagen-like triple helix to be unstable relative to separate strands of polyglycine largely due to the distortion energy required for each strand to assume the geometry of the collagen-like structure. As collagen contains substantial amounts of proline and hydroxyproline, the individual isolated strands should have a structure more similar to that of polyproline II, which is close to the geometries of the strands in the collagen triple helix. Comparing the distortion energies per residue for the glycine strands (3.0 kcal/mol) of the current study with those that can be derived from capped strands of PPG (about 1.7 kcal/mol based upon 31.4 kcal/mol for three six stranded strands, or 18 residues) calculated using similar methods, confirms this hypothesis.²¹ One sees that a major reason for the energetic preference of proline and hydroxyproline in the X and Y positions of the proline XYG triad must be that the strands containing the amino acids have small distortion energies for forming the triple helix. Furthermore, in a collagen triple helix, the X and Y residues (when proline or hydroxyproline) cannot form the additional H-bonds required for a structure like PII₇. Palfi and Perczel's comparison of strands containing AAG with those containing PPG gives results in agreement with those presented here.³³ We suggest that these two effects combine to cause a preference for the sheets in G₆ and a preference for collagen in (PPG)₂.

Conclusions

Strands of polyglycines can interact via hydrogen-bonding in several different motifs. Of those studied here, the antiparallel β-sheets are most stable for aggregates containing both three and seven individual strands. The relative stability of these antiparallel β-sheets derives principally from the lower strain in the individual strands rather than from strong H-bonding interactions, as indicated in table 1. In fact, these sheets have the smallest H-bonding interactions. The polyglycine II-like heptamer has the strongest H-bonds, but is the least stable of the heptameric structures as it has fewer H-bonds than its isomeric structures and a relatively large amount of distortion energy/residue. When we make approximate corrections to make the number of H-bonds equivalent in number and cooperative enhancement to the isomeric structures, the relative energy of the PII₇ implies a stable PII crystal. The parallel β-sheets are intermediate between the other two forms, both in H-bonding energies and strain within the individual strands.