Abstract
Motivation: Bead arrays are becoming a popular platform for high-throughput expression arrays. However, the number of the beads targeting a transcript and the variation of their intensities differ from sample to sample in these arrays. This property results in different accuracy of expression intensities of a transcript across arrays.
Results: We provide evidence, with publicly available spike-in data, that the false discovery rate of differential expression is reduced by modeling bead-level variability with a multi-level mixed effects model. We compare the performance of our proposed model to existing analysis methods for bead arrays: the unweighted t-test and other weighted methods. Additionally, we provide theoretical insights into when the multi-level mixed effects model outperforms other methods. Finally, we provide a software program for differential expression analysis using the multi-level mixed effects model that analyzes tens of thousands of genes efficiently.
Availability: The software program is freely available on web at http://ephpublic.aecom.yu.edu/sites/rkim/Supplementary.
Contact: ryung.kim@einstein.yu.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Bead arrays are becoming a popular platform to generate high-throughput expression data (Becanovic et al., 2010; Fernando et al., 2009; Young et al., 2009). One of the advantages of the technology is that all beads targeting a transcript have exactly the same sequence and length (Kuhn et al., 2004): this property rids the concerns for averaging intensities from probes with different affinities and a common target transcript. However, in bead arrays, the number of beads targeting a transcript differs from sample to sample, usually between 5 and 80 beads. Moreover, variation of the bead-level intensities targeting a common transcript differs across samples. Given these differences in the number of beads and the variation of their intensities, the average expression intensity for a given transcript will have varying precision across samples. Although measures of precision are typically generated along with the computed average gene expression intensities, it is commonplace to simply compare the intensity levels across experimental groups using Analysis of Variance (ANOVA; more than two groups) or t-test (two groups), ignoring the bead-level variability. This approach is problematic. For example, the standard error of the average is inversely proportional to square root of the number of beads, and intensities for a transcript averaged over 5 beads will be four times more variable than that over 80 beads.
Recently, there are increasing efforts to incorporate bead-level technical variability as weights in linear methods (Dunning et al., 2008a; Fernando et al., 2009; Wong et al., 2008). For example, Dunning et al. and Fernando et al. used variance of bead-level intensities as the inverse weight in comparing two sample groups. Wong et al. (2008), proposed a test statistic based on unweighted average of bead-level intensities but used bead-level variability to compute standard errors. Any reasonable use of bead variability will likely improve the accuracy of differential expression analysis. However, to our knowledge, formal consideration of under which model the weighting scheme is optimal, or comparisons between different weighting schemes, have not been reported. Noticeably, in all these weighting methods, weights are completely determined by bead-level technical variation and are independent of the magnitude of array-level biological variation. Our work adds to the body of research by modeling bead-level variation by a multi-level mixed effects model (MLM). Under this model, the weights for the bead averages are determined by the relative magnitudes of both bead-level technical variation and array-level biological variation. In addition, using publicly available spike-in data, we compare the false discovery rate (FDR), sensitivity, specificity, empirical Type I error and empirical power of our proposed model to six other methods.
2 METHODOLOGY
2.1 Modeling bead-level intensity with MLM
For simplicity, we consider an experimental design to detect differential expression in K independent sample groups. We propose to model bead-level intensity using the following multi-level mixed effects model.
| (Model 1-MLM) |
for i = 1,…, nk, j = 1,…, mki, k = 1,…, K. Here xkij is the bead-level expression intensity of j-th bead in i-th sample in k-th group. The fixed effect θk is the population average intensity of k-th sample group and represents the parameter of interest in our comparison. The random effect bik represents array-level variation within each sample group and εkij represents bead-level variation: they are assumed to be mutually independent. There are measures for two levels of variation: τk2 is the array-level biological variance and σki2 is the bead-level technical variance. To detect differential expression using this model, we can perform a statistical test of the null hypothesis that all θk's are equal. The model is also known as the random effect one-way ANOVA when τk2 are assumed to be constant across sample groups.
The parameters can be estimated by maximum likelihood (ML) or restricted ML (REML; Patterson and Thompson, 1971). See Appendix for an iterative Fisher's scoring algorithm for ML and REML estimation of all parameters: the biological variance (τk2), the technical variance (σki2) and the average group intensities (θk). The resulting ML (and REML) estimator of θk is the weighted average of average bead-level intensities (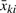 ) using the variance of
) using the variance of  , i.e. σki2/mki + τk2, as the inverse weights. That is,
, i.e. σki2/mki + τk2, as the inverse weights. That is,
The standard error of the estimator is
Since the bead-level sample mean 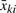 and variance ski2 are sufficient statistics (Appendix A), one can fit MLM using only the typical ‘bead summary data’ (the average, the s.d. and the number of beads for each array). These can be produced by Illumina's BeadScan software.
and variance ski2 are sufficient statistics (Appendix A), one can fit MLM using only the typical ‘bead summary data’ (the average, the s.d. and the number of beads for each array). These can be produced by Illumina's BeadScan software.
Once the parameters are estimated, a Wald-type test can be used to compare K groups using the following test statistics:
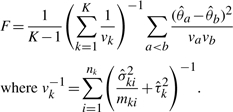 |
See Appendix A for derivation of the test statistics. Although asymptotically, the test for fixed effects in MLM can be performed using χ2 distribution, it has been reported that, even with a moderately large sample size, it tends to be anticonservative (Pinheiro and Bates, 2000) and it is instead desired to use F-test. Still an active research area, there are a few established approaches in choosing what denominator degrees of freedom to use for F statistics when sample size is small (Kenward and Roger, 1997; Pinheiro and Bates, 2000; Schaalje et al., 2002). Under a balanced design with common random effects variance, these approaches result in the denominator degrees of freedom of n1 + n2 − K or a value close to it. Note that, in two-group comparison studies, the test statistics is the square of the following:
By accounting for the number of beads and the variation of their intensities using the proposed multi-level model, we see in the following sections an immediate improvement in the accuracy of detection of differential expressions. The variance structure of the technology is more complicated than having multiple beads on an array and the current model can be extended to address different levels of biological and technical variability. For example, it can incorporate longitudinal or correlated design, or multiple batch design, or it can be extended to address correlation between bead intensities that are located closely on the chip. This is the first work using multi-level modeling framework in addressing the variance structure. More in-depth discussions on multi-level modeling can be found in Pinheiro and Bates (2000).
2.2 An efficient program for multi-level modeling of bead-level intensity
MLM has been rarely used to model bead-level intensities mainly because there are restrictions on the size of data that can feasibly be analyzed. We provide a software program for differential expression analysis using multi-level model comparing K independent groups, in R statistical environment. One can choose biological variation τk2 to be constant, or to vary, in K groups. Because the software reads the bead-summary data as input, the computational burden is reduced dramatically. To efficiently compute and simultaneously fit multi-level models for thousands of genes, it was important for us to develop the algorithm that avoids inversion of Fisher's information matrix at each gene level. In the Appendix A, we provide technical details of Fisher's scoring algorithm for ML and REML estimation. For example, performing two-group comparisons of 34 699 genes, 12 samples in each group, the parameter estimation and hypothesis testing were completed within 5 min on a Dell Precision T3400 computer (Intel Quad 2.83 GHz processor with 3.25 GB of RAM).
The software can read in ‘bead summary data’ generated by Illumina's proprietary software, if researcher decides to analyze bead array data in raw scale. However, it is often desirable to analyze data in log scale (Section 5).
2.3 Theoretical comparison with other approaches
2.3.1 Unweighted analysis
A typical differential expression analysis (t-test when K = 2, ANOVA when K > 2) without consideration of bead-level variability is optimal under the following model:
| (Model 2-Unweighted Method) |
One may either assume variances τk2 to be identical across K groups or modify Student's t-test or ANOVA to allow different variances. In both cases, the model is inappropriate because it assumes bead averages to have same accuracy across arrays in each sample group when in reality they must depend on the the numbers of beads and the variation of their intensities. Under this naïve model, the mean intensity of each group θk can be estimated by the unweighted average of 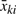 's across the samples. It is straightforward to compute the relative efficiency, which is the asymptotic ratio of variances of the unweighted average and MLM estimate:
's across the samples. It is straightforward to compute the relative efficiency, which is the asymptotic ratio of variances of the unweighted average and MLM estimate:
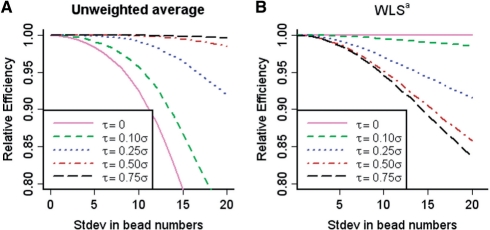
Figure 1A shows the relative efficiency after fixing the bead-level technical variation σ to be constant across samples and the array-level biological variation τ to be 0, 10, 25, 50 or 75% of σ. We generated bead numbers across 100 000 samples from a normal distribution with mean 40. We repeated the process of computing the relative efficiency by gradually increasing the variation of the bead numbers. When biological variation is substantially less than technical variation, the estimate under MLM is more accurate than the unweighted estimate, especially as the variation in the number of beads increases. As we increased the biological variation to be close to the technical variation, the difference between two methods decreased. We confirmed this theoretical property to be true in the spike-in data in the later sections.
Fig. 1.
(A) Relative efficiency of unweighted average compared with the estimate from MLM. If it is close to 1, standard errors of unweighted average and MLM estimate are similar. The less it is, the less standard error MLM has compared with the unweighted average. The technical variation is fixed constant across hundred thousand samples at σ and the biological variation τ are set to be 0, 10, 25, 50 or 75 of σ. The bead numbers were first generated from normal distribution with mean 40, and then rounded and replaced with five if the number is less than five. We repeated the process of computing the relative efficiency by gradually increasing the variation of the bead numbers. (B) Relative efficiency of the WLSa estimate under our proposed model MLM.
2.3.2 Weighted analysis using only bead-level variation
There are recent efforts to incorporate bead-level technical variation in linear analysis using the weighted least square estimation (WLS). First, consider using bead-level variance divided by the number of beads as inverse weights in a linear model. This weighting scheme is optimal under the following model:
| (Model 3-WLSa) |
Although an iterative algorithm is needed to estimate the parameters, it is a common practice to assume σki2 = ski2 and use the weighted least squares estimator of θk. That is,
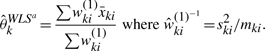 |
Both estimates based on MLM and WLSa can be viewed as weighted average of average bead intensities. The weights are different, however, as they are inverse of σki2/mki in WLSa and σki2/mki + τk2 in MLM. Drawbacks of WLSa are that the biological variance c2 has no influence on estimator of the θk and that it must be constant across K groups.Figure 1B shows the relative efficiency of the WLSa estimate under our proposed model MLM. When biological variation is substantially greater than technical variation, the MLM estimate outperforms WLSa estimate, especially as the variation in bead numbers increases. This is opposite to what we observed with Student's t-test, which performs as well as MLM with large biological variation. We confirmed this theoretical property to be also true in the spike-in data in the later sections.
The weights used in recent reports are in fact different from WLSa. Dunning et al. (2008a) used variance of bead-level intensities (ski2) as inverse weights and demonstrated that it improves power to detect differential expression. That is, their test is based on
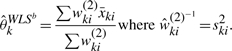 |
Since WLS estimation is most efficient when the weights are inverse of the variances of measurements (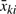 ), this weighting scheme is optimal under the following model:
), this weighting scheme is optimal under the following model:
| (Model 4-WLSb) |
However, we find that the assumption that variance of 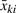 does not depend on bead numbers is unrealistic. As a result, WLSb does not take the numbers of beads into account, and will perform poorly when variation in the number of beads is large.
does not depend on bead numbers is unrealistic. As a result, WLSb does not take the numbers of beads into account, and will perform poorly when variation in the number of beads is large.
3 MATERIALS AND METHODS
3.1 Microarray data
We examined the difference between the analysis methods of differential expression by performing two group comparison of a publicly available spike-in dataset (Dunning et al., 2008a). In their study, Dunning et al. hybridized 48 arrays on Illumina Mouse-6 chips with a complex mouse background. In addition to the standard ∼48 000 bead types, the chips were modified to include 33 bead types (spikes) targeting bacterial and viral genes absent from the Mouse genome. The spikes were added at 12 concentration levels, each on four arrays: 1000, 300, 100, 30, 10, 3, 1, 0.3, 0.1, 0.03, 0.01 and 0 pM. The spikes on a given array were all added at the same concentration.
3.2 Preprocessing
Bead-level data for the spike-in experiment has gone through image sharpening and background subtraction and was summarized in the log2 scale (Dunning et al., 2008b). We further normalized all 48 arrays using the robust spline normalization (Du et al., 2008). We included in our analysis the 33 spikes and all 34 666 non-spike bead-types targeting genes annotated with Genbank IDs.
3.3 Differential expression analysis
We performed seven different differential expression analyses comparing two sample groups: (i) Student's t-test, (ii) Welch's t-test, (iii) WLSa, (iv) WLSb, (v) MLM, (vi) MLM assuming common biological variance and (vii) Student's t-test after the variance stabilization transformation (VST; Lin et al., 2008). First six tests were applied to log2 scale data. For the last test, VST was performed on unlogged raw data: VST becomes similar to log2 transformation for high intensities. We ranked genes from the most differentially expressed to the least differentially expressed based on the corresponding P-values from each test. For WLSa, we performed the weighted linear regression analysis with an intercept and a group indicator variable and used bead-level variance divided by number of beads as the inverse weights. Then, we used the standard P-value for testing non-zero coefficient of the indicator variable to rank the transcripts. For WLSb, we used the bead-level variance as the inverse weights. For both MLM methods, we used the software we developed. For the analyses in this article, the degrees of freedom for MLM-based tests were set to be n1 + n2 − 2 because we have balanced design and we assumed common biological variance (τ2).
3.4 Measuring the performance of differential expression analysis
For each analysis result of differential expression, we counted the number of spikes and non-spikes (i.e. annotated transcripts in the Mouse genome) among up to top 100 detected transcripts. For a given gene list, the number of false discovery is defined as the number of non-spikes in the list and false discovery rate is defined as the number of false discovery divided by the size of the list. For a given gene list, sensitivity is defined as the number of spikes in the list divided by the total number of spikes, 33, and specificity is defined as the number of non-spikes not included in the list divided by the total number of non-spikes, 34 666. In differential expression analysis of microarrays, specificity is often >0.99 in even poor analyses because the number of differentially expressed transcripts is typically much smaller than total number of transcripts in the array. For this reason, we only considered up to top 100 transcripts, and receiver operating characteristic (ROC) curves are only defined above the specificity at 0.998.
In addition, for each of seven methods, we computed empirical Type 1 error and power as nominal Type I error changes. For a given nominal Type I error, the corresponding empirical Type I error is defined as the number of non-spikes with P-values less than the nominal value divided by the number of all non-spikes. The corresponding empirical power is defined as the number of spikes with P-values less than the nominal value divided by 33, the number of spikes.
4 RESULTS
In the dataset, the number of beads ranged from 3 to 86. For all 33 spikes (bead types), the largest bead-level standard error among 48 arrays was at least 324 times larger than the smallest standard error. These observations confirmed that the accuracy of mean intensity differs greatly across samples, justifying the need to incorporate bead-level technical variability in the analysis.
4.1 When biological variation is less than technical variation
For each gene, we performed seven tests to detect differentially expressed transcripts between four arrays with 0.01 pM spikes and four arrays with no spikes (i.e. 0 pM): (i) Student's t-test, (ii) Welch's t-test, (iii) WLSa, (iv) WLSb, (v) MLM, (vi) MLM assuming common biological variance and (vii) Student's t-test after the VST. We counted the number of spikes and non-spikes among up to top 100 detected transcripts to compute sensitivity, specificity and false discovery rates. We then repeated the whole process with other 10 non-zero concentration levels. Although we do not view our model as a scaling method, we included the last method in our comparison because VST is often regarded as the current best practice; if VST can be expanded to bead-level data, then the transformation can be used in conjunction with our method.
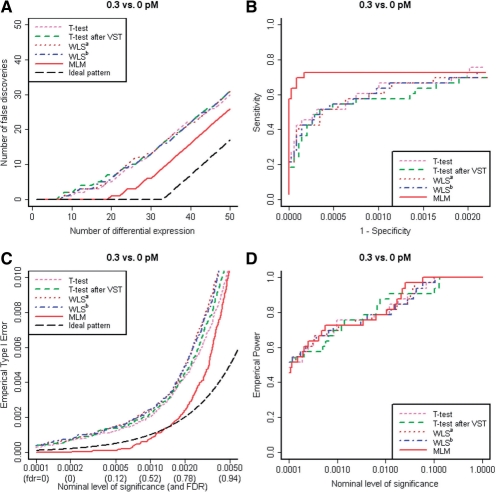
When the difference in true concentration is too small (e.g. 0.01 versus 0 pM), all methods failed to detect differential expression. On the other hand, when the difference is too large (e.g. 1 versus 0 pM), all methods successfully detected differential expression. When comparison is made between moderately different concentration levels (0.3 versus 0 pM; Fig. 2A and Table 1), MLM resulted in the least false discoveries. For example, the numbers of false discoveries in the top 20 transcripts are 5 (t-test), 6 (WLSa) and 1 (MLM). In the top 33 transcripts, they are 16 (t-test), 16 (WLSa) and 9 (MLM). Table 1 shows the results for all seven tests. Figure 2B shows that the ROC curve for MLM is consistently higher than that of t-test and WLS. The sensitivity among top 33 transcripts by MLM (73%) is statistically significantly higher than that of t-test (52%) and WLS (52%): MLM detected seven spikes that were not detected by t-test (or WLS) and missed none that was detected by t-test (or WLS; P-value <0.016; Exact McNemar's Test). Supplementary Figure S1 shows the number of false discoveries and ROC curves when comparing each of 11 non-zero concentration levels to the four samples with no spikes.
Fig. 2.
(A) Number of false discoveries in comparison between 0.3 versus 0 pM: only results assuming constant biological variance (τ2) are shown. (B) An ROC curve for up to top 100 transcripts. (C) Empirical Type 1 error estimated by non-spikes. (D) Empirical power estimated by 33 spikes.
Table 1.
False discovery rates among top 20 and 33 genes and sensitivities among the top 33 transcripts (0.3 versus 0 pM)
| FDR of top 20 (and 33) transcripts | Sensitivity of top 33 transcripts | ||
|---|---|---|---|
| Student's t-test | τ1 = τ2 | 5/20 (16/33) | 17/33 |
| t-test after VST | τ1 = τ2 | 7/20 (16/33) | 17/33 |
| WLSa | τ1 = τ2 | 6/20 (16/33) | 17/33 |
| WLSb | τ1 = τ2 | 6/20 (16/33) | 17/33 |
| MLM | τ1 = τ2 | 1/20 (9/33) | 24/33 |
| Welch's t-test | τ1 ≠ τ2 | 7/20 (17/33) | 16/33 |
| MLM | τ1 ≠ τ2 | 0/20 (9/33) | 24/33 |
In addition, we compared empirical Type I error and power of the seven methods as nominal Type I error changes. Figure 2C shows the empirical Type I error in the range of nominal values that results in FDR < 0.9. For practically meaningful results (FDR < 0.3), MLM was conservative but all other methods were anticonservative. Nonetheless, the power (Fig. 2D) of MLM was comparable with that of other six tests. With small degrees of freedom, we expect empirical Type I errors to be different from the nominal values (ideal pattern) since all seven tests are based on model assumptions: it is advisable to use the tests to order genes and determine the number of differential expressions, e.g. by permuting the sample labels to estimate false discovery rate.
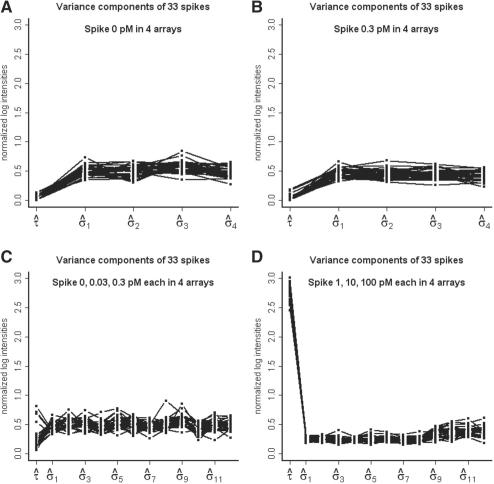
Figure 3A and B show the relative size of estimated variance components of 33 spikes in the multi-level model for samples with 0 and 0.3 pM spike concentration. The result for non-spikes is in Supplementary Figure S2. By averaging over replicates, τ/σ for spikes at 0.3 and 0 pM are estimated at 0.06 and 0.07, respectively. For non-spikes, they are 0.08 and 0.09. Therefore, technical variation is much larger than biological variation and it is clear that one needs to avoid using unweighted methods, which uses only the biological variation in estimating sampling variation for their test statistics. The assumption of common biological variation seems to be appropriate for both spikes and non-spikes.
Fig. 3.
Estimate of variance components of 33 spikes under multi-level model across (A) four samples with true mean spike-in concentration at 0 pM and SD 0 pM, (B) four samples with mean 0.3 pM and SD 0 pM, (C) 12 samples with mean 0.11 pM and SD 0.14 pM and (D) 12 samples with mean 37.0 pM and SD 46.7 pM.
Supplementary Figure S3 shows the variance components, weights under different models and standard errors of the genes in three groups: (i) spike-ins detected by both MLM and t-test, (ii) spike-ins detected by MLM but not by t-test and (iii) non-spikes detected by t-test but not by MLM.
Notice that, even with small biological variation, WLS methods perform as poorly as unweighted method, while Figure 1 seems to suggest that WLS can perform as well as MLM. When τ is small, the WLS and MLM estimates of θk essentially become the same because the weights become similar. Nevertheless, the standard error, or the denominator of the test statistics, differs in two tests due the difference in model assumptions. Specifically, the statistic based on WLS is further scaled by the residual standard error ĉ:
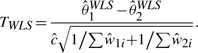 |
This difference in standard error is causing the relatively poor performance of WLS tests although the estimates for the mean intensities are similar in WLS and MLM.
While the results so far show that MLM outperforms other methods, the true variation among spike-ins in each group is close to zero, so the array-level biological variation is much smaller than the bead-level technical variation. This may not represent the settings in many transcriptional experiments. In fact, for in vivo data, it is quite common to compare heterogeneous populations with multiple unknown subgroups or outliers in each group (Tibshirani, 2007; Wu, 2007). To compare methods across a wide range of possible study settings, we performed the similar comparison using an altered spike-in dataset in the following section.
4.2 When biological variation among differentially expressed genes is greater than technical variation
As shown in Figure 1, when biological variation is greater than the technical variation, it is possible for unweighted t-test to perform similarly to MLM. On the other hand, the relative performance of WLS will likely be poor because it does not use biological variation in the weights. To test this hypothesis, we increased the heterogeneity and sample sizes within each sample group: three groups of arrays with relatively high concentration (100, 10 and 1 pM) were pooled and another three groups of arrays with low concentration (0.3, 0.03 and 0 pM) were pooled. Overall, there were 12 samples with high-concentration level (mean = 37.0 pM; SD = 46.7 pM) and 12 samples with low-concentration level (mean = 0.11 pM; SD = 0.14 pM). That is, the means and SD of spikes are both 1000/3 times larger in high-concentration group. For each gene, we again performed the seven tests to detect differentially expressed transcripts.
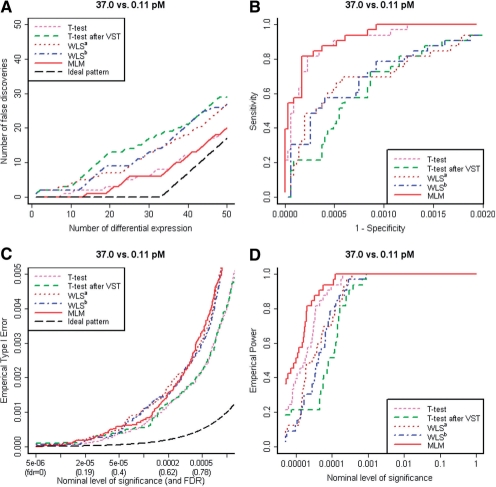
Figure 4 demonstrates that MLM again detects differential expression with the least false discoveries. For example, the numbers of false discoveries in the top 20 transcripts are 3 (t-test), 7 (WLSa) and 2 (MLM). In the top 33 transcripts, they are 8 (t-test), 14 (WLSa) and 6 (MLM). Table 2 shows the results for all seven tests. The ROC curve (Fig. 4B) shows that the sensitivities of MLM and t-test are similar and they are consistently higher than that of WLS. The sensitivity among top 33 transcripts by MLM (82%) is significantly higher than that of WLS (58%; P-value <0.008; exact McNemar's test; MLM detected eight spikes that were not detected by t-test and missed none that was detected by t-test). In this comparison, biological variation between samples is much bigger than the bead-level technical variations, and Student's t-test performs as well as MLM as we expected. However, the performance of tests based on WLS is poor because the weighting depends only on technical variation.
Fig. 4.
(A) Number of false discoveries in comparison between 37.0 versus 0.11 pM; only results assuming constant biological variance (τ2) are shown. (B) An ROC curve for up to top 100 transcripts. (C) Empirical Type 1 error estimated by non-spikes. (D) Empirical power estimated by 33 spikes.
Table 2.
False discovery rates among the top 20 and 33 transcripts and sensitivities among top 30 transcripts (37.0 versus 0.11 pM)
| FDR of top 20 (and 33) transcripts | Sensitivity of top 33 transcripts | ||
|---|---|---|---|
| Student's t-test | τ1 = τ2 | 3/20 (8/33) | 25/33 |
| t-test after VST | τ1 = τ2 | 13/20 (18/33) | 15/33 |
| WLSa | τ1 = τ2 | 7/20 (14/33) | 19/33 |
| WLSb | τ1 = τ2 | 9/20 (14/33) | 19/33 |
| MLM | τ1 = τ2 | 2/20 (6/33) | 27/33 |
| Welch's t-test | τ1 ≠ τ2 | 13/20 (21/33) | 12/33 |
| MLM | τ1 ≠ τ2 | 1/20 (8/33) | 25/33 |
Figure 4C shows the empirical Type I error in the range of nominal values that results in FDR < 0.9. For practically meaningful results (FDR < 0.3), all seven tests were mildly anticonservative. The power (Fig. 4D) of MLM was higher than other tests.
Figure 3C and D show the relative size of estimated variance components in the multi-level model of 33 spikes for samples with mean spike concentration at 0.11 and 37.0 pM. The result for non-spikes is in Supplementary Figure 2. By averaging replicates, for spikes, τ/σ for 37.0 and 0.11 pM are estimated at 9.74 and 0.64, respectively. For non-spikes, they are 0.09 and 0.11. The assumption of common biological variation seems to be appropriate for non-spikes but not for spikes. Since biological variation in spikes is much larger than technical variation, it is clear that one needs to avoid using WLS methods, which does not account for biological variation in weights. We also notice that the log2 transformation stabilized the variance, as the bead-level variation does not increase as intensity level increases.
Supplementary Figure 4 shows the variance components, weights under different models and standard errors of the genes in three groups: (i) spike-ins detected by both MLM and WLSa, (ii) spike-ins detected by MLM but not by WLSa and (iii) non-spikes detected by WLSa but not by MLM.
It is not surprising that Student's test outperforms Welch's test (Table 2) although the true biological variances of the spikes in two conditions are very different. Non-spikes, from the same biological material across all samples, have common variance in two conditions. With sample size balanced, Student's test-statistics and Welch's test-statistics are identical and the difference in P-values comes only from the difference in degrees of freedom, which in turn come from the difference in variances. Since there are 12 samples in each group, Student's test uses 22 degrees of freedom for both spikes and non-spikes. The degrees of freedom for Welch's test are near the maximum value, 22, for all non-spikes due to homogeneity, and near the minimum possible value, 11, for all spikes due to heterogeneity. Therefore, the two tests control the Type I error equally but Welch's test has much less power.
5 DISCUSSION
In this article, we presented a way to account for both biological and technical variation in weighting by fitting a multi-level mixed effects model of bead-level intensities. We compared existing analysis methods for bead arrays, showing the conditions under which each method would be optimal. Theoretical results suggest that, when array-level biological variation is substantially less than bead-level technical variation, the MLM provides more accurate estimate than the unweighted method especially if the variation in number of beads is large across samples. When biological variation is close to or greater than technical variation, the difference between two methods becomes small. On the contrary, when biological variation is substantially greater than technical variation, the WLS provides inaccurate results compared with the unweighted method or the MLM. Given these theoretical considerations, our proposed method is based on the reasonable and realistic assumption that variance of the bead-level average is additive across the two levels of variation, technical and biological.
We confirmed these theoretical properties to be true in the spike-in data. We provided evidence that accuracy of differential expression analysis is improved by accounting for the bead-level variation with the multi-level model especially when biological variation is small. We also showed that when biological variation is large, weighted methods that ignore biological variation might even have lower accuracy than unweighted methods. The multi-level model, which accounts for both biological and technical variation in weighting, reduced the false discovery rate and increased the sensitivity in both settings.
We provide a software program to the research community for differential expression analysis using the multi-level model that analyzes tens of thousands of genes efficiently. The key to efficient programming was avoiding numerical inversion of tens of thousands of Fisher's information matrices.
We acknowledge the limitation of the spike-in data to answer questions about biological variability. Only spikes had real biological variability across samples, and non-spikes were biological replicates in all arrays. Type I error and specificity, which are estimated only by non-spikes, will be different from the reported values in real biological data. However, when biological variation exists in non-differentially expressed genes, we expect MLM to outperform methods that do not include biological variation in weights.
All differential expression analyses were performed for one gene at a time. There have been efforts, however, to combine these with empirical Bayesian method to move sample variance toward a pooled estimate across genes. These have shown to result in stable inference when the number of array is small (Smyth, 2004). For example, the empirical Bayesian method has often accompanied unweighted methods (Hageman et al., 2010; Iorns et al., 2010) and weighted methods (Fernando et al., 2009). It will be interesting to investigate the effect of variance modification in the multi-level mixed effects model.
Finally, on a practical note, we recommend researchers to keep bead-level data from Illumina BeadScan software. The same recommendation was made in multiple other reports (Dunning et al., 2008a; Stokes et al., 2007). Without bead-level data, for example, one cannot analyze expression intensities in log scale and consider bead-level variation at the same time. We repeated the analysis in this article using data in raw scale, and the performance of all seven tests were markedly poorer than that based on log2 scale, especially when biological variance were large among spike-ins. For example, top 874 genes detected by t-test did not include any spike-ins. To analyze data in log scale, researcher needs to use existing software, e.g., beadarray (Dunning et al., 2007), to convert bead-level data to bead summary data on log scale before applying the software provided in this article.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Prof. Melissa Fazzari for her helpful comments and proofreading of the manuscript.
Funding: National Cancer Institute (5P30CA013330-37 to R.K., 1UL1RR025750-0 to R.K.).
Conflict of Interest: none declared.
APPENDIX A
A FISHER'S SCORING ALGORITHM FOR ML AND REML
A.1 ML estimation
Here, we provide the technical details of Fisher's scoring algorithm we used in our program to maximise the likelihood of MLM to detect differential expression of K independent groups. The model has the following log-likelihood:
 |
Notice that 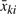 and ski2, the bead average and variance for each sample, are the sufficient statistics. Given the two variances, it is straightforward to show that
and ski2, the bead average and variance for each sample, are the sufficient statistics. Given the two variances, it is straightforward to show that
The first derivatives of the likelihood are
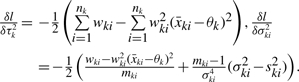 |
Although xki1,…, xkink are correlated, using the quadratic theorem of normal variable, one can show (mki − 1)ski2/σki2 still has χ2 distribution with the degrees of freedom mki − 1 and that ski2 is an unbiased estimator of σki2. By taking the expectation of second derivatives of the likelihood, and substituting 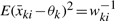 and Eski2 = σki2, we have all elements of the information matrix:
and Eski2 = σki2, we have all elements of the information matrix:
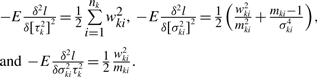 |
All other elements of the information matrix are zero. Taking the inverse of the information matrix, we have the following Fisher's scoring algorithm:
- Set initial values at
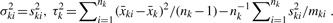
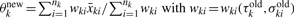
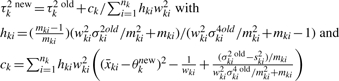
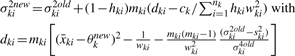
-
Repeat Steps (2)–(4) until convergence.
If we assume constant τ across K conditions, Steps (3) and (4) change to the following: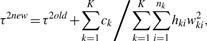
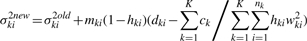
A.2 REML estimation
For our linear model, the REML estimator of τ2 is obtained by maximizing the following restricted likelihood (Laird, 2004):
Conveniently, one can modify Step (3) of the ML algorithm by adding the following term to the right-hand side of the equation (Laird, 2004):
If we assume constant τ across K conditions, the term changes to
A.3 Wald-type test
Once the parameters are estimated, one can perform a Wald-type test to compare K groups. Let 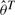 to be
to be  , Σ to be a diagonal matrix with i-th diagonal element being vk where
, Σ to be a diagonal matrix with i-th diagonal element being vk where 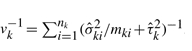 , and H to be a (k−1) × k matrix with i-th and (i + 1)-th elements of i-th row set as 1 and −1, and all other elements set as zero. With some algebraic work, one can derive the following Wald-type test statistic:
, and H to be a (k−1) × k matrix with i-th and (i + 1)-th elements of i-th row set as 1 and −1, and all other elements set as zero. With some algebraic work, one can derive the following Wald-type test statistic:
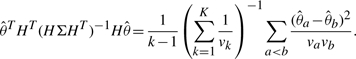 |
REFERENCES
- Becanovic K, et al. Transcriptional changes in Huntington disease identified using genome-wide expression profiling and cross-platform analysis. Hum. Mol. Genet. 2010;19:1438–1452. doi: 10.1093/hmg/ddq018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du P, et al. lumi: a pipeline for processing Illumina microarray. Bioinformatics. 2008;24:1547–1548. doi: 10.1093/bioinformatics/btn224. [DOI] [PubMed] [Google Scholar]
- Dunning MJ. beadarray: R classes and methods for Illumina bead-based data. Bioinformatics. 2007;23:2183–2184. doi: 10.1093/bioinformatics/btm311. [DOI] [PubMed] [Google Scholar]
- Dunning MJ, et al. Statistical issues in the analysis of Illumina data. BMC. Bioinformatic. 2008a;9:85. doi: 10.1186/1471-2105-9-85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunning MJ, et al. Spike-in validation of an Illumina-specific variance-stabilizing transformation. BMC Res. Notes. 2008b;1:18. doi: 10.1186/1756-0500-1-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fernando H, et al. Genome-wide analysis of a G-quadruplex-specific single-chain antibody that regulates gene expression. Nucleic Acids Res. 2009;37:6716–6722. doi: 10.1093/nar/gkp740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hageman RS, et al. High-fat diet leads to tissue-specific changes reflecting risk factors for diseases in DBA/2J mice. Physiol. Genomics. 2010;42:55–66. doi: 10.1152/physiolgenomics.00072.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iorns E, et al. The role of SATB1 in breast cancer pathogenesis. J. Natl Cancer Inst. 2010;102:1284–296. doi: 10.1093/jnci/djq243. [DOI] [PubMed] [Google Scholar]
- Kenward MG, Roger JH. Small sample inference for fixed effects from restricted maximum likelihood. Biometrics. 1997;53:983–997. [PubMed] [Google Scholar]
- Kuhn K, et al. A novel, high-performance random array platform for quantitative gene expression profiling. Genome Res. 2004;14:2347–2356. doi: 10.1101/gr.2739104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird N. NSF-CBMS Regional Conference Series in Probability and Statistics. Vol. 8. Beachwood, Ohio: Institute of Mathematical Statistics; 2004. Analysis of Longitudinal and Cluster-Correlated Data; p. 43. 91. [Google Scholar]
- Lin SM, et al. Model-based variance-stabilizing transformation for Illumina microarray data. Nucleic Acids Res. 2008;36:e11. doi: 10.1093/nar/gkm1075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson HD, Thompson R. Recovery of inter-block information when block sizes are unequal. Biometrika. 1971;58:545–554. [Google Scholar]
- Pinheiro JC, Bates DM. Mixed-effects Models in S and S-plus. New York: Spinger; 2000. [Google Scholar]
- Schaalje GB, et al. Adequacy of approximations to distributions of test statistics in complex mixed linear models. J. Agric. Biol. Environ. Stat. 2002;7:512–524. [Google Scholar]
- Smyth GK. Linear models and empirical bayes methods for assessing differential expression in microarray experiments. Stat. Appl. Genet. Mol. Biol. 2004;3 doi: 10.2202/1544-6115.1027. Article 3. [DOI] [PubMed] [Google Scholar]
- Stokes TH, et al. Conference Proceedings, IEEE Engineering in Medicine and Biology Society. Lyon, France: 2007. Extending microarray quality control and analysis algorithms to Illumina chip platform; pp. 4637–4640. [DOI] [PubMed] [Google Scholar]
- Tibshirani R. Outlier sums for differential gene expression analysis. Biostatistics. 2007;8:2–8. doi: 10.1093/biostatistics/kxl005. [DOI] [PubMed] [Google Scholar]
- Wong WC, et al. On the necessity of different statistical treatment for Illumina BeadChip and Affymetrix GeneChip data and its significance for biological interpretation. Biol. Direct. 2008;3:23. doi: 10.1186/1745-6150-3-23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu B. Cancer outlier differential gene expression detection. Biostatistics. 2007;8:566–575. doi: 10.1093/biostatistics/kxl029. [DOI] [PubMed] [Google Scholar]
- Young ARJ. Autophagy mediates the mitotic senescence transition. Genes Dev. 2009;23:798–803. doi: 10.1101/gad.519709. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.