Length bias correction for RNA-seq data in gene set analyses

Abstract

Motivation: Next-generation sequencing technologies are being rapidly applied to quantifying transcripts (RNA-seq). However, due to the unique properties of the RNA-seq data, the differential expression of longer transcripts is more likely to be identified than that of shorter transcripts with the same effect size. This bias complicates the downstream gene set analysis (GSA) because the methods for GSA previously developed for microarray data are based on the assumption that genes with same effect size have equal probability (power) to be identified as significantly differentially expressed. Since transcript length is not related to gene expression, adjusting for such length dependency in GSA becomes necessary.

Results: In this article, we proposed two approaches for transcript-length adjustment for analyses based on Poisson models: (i) At individual gene level, we adjusted each gene's test statistic using the square root of transcript length followed by testing for gene set using the Wilcoxon rank-sum test. (ii) At gene set level, we adjusted the null distribution for the Fisher's exact test by weighting the identification probability of each gene using the square root of its transcript length. We evaluated these two approaches using simulations and a real dataset, and showed that these methods can effectively reduce the transcript-length biases. The top-ranked GO terms obtained from the proposed adjustments show more overlaps with the microarray results.

Availability: R scripts are at http://www.soph.uab.edu/Statgenetics/People/XCui/r-codes/.

Contact: xcui@uab.edu

Supplementary information:Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Next-generation sequencing has been rapidly applied to measure gene expression levels (Marguerat and Bahler, 2010; Wang et al., 2009). The power of this application (RNA-seq) in quantifying and annotating transcriptomes is striking. By obtaining tens of millions of short sequence reads from the transcript population of interest and by mapping these reads to the reference genome, RNA-seq produces digital signals (counts) rather than analog signals (intensities) in microarrays, and thus leads to highly reproducible results with relatively little technical variation (Mortazavi et al., 2008). When enough reads are collected from a sample, it should be possible to detect and quantify RNAs from all biologically relevant classes including low and moderate abundance (Mortazavi et al., 2008).

Several methods have been proposed in the literature to calculate gene expression levels based on RNA-seq data. Cloonan et al. (2008) adjusted the gene read count data by the length of the transcript. Mortazavi et al. (2008) used the reads (or counts) per kilobase (kb) per million reads (RPKM) as the gene expression level, which adjusted the read counts by the sequencing depth (in units of million reads) in addition to the transcript length (in units of kb). The RPKM index facilitates comparison of expression measurements across different genes and different samples. Based on a Poisson model, Jiang and Wong (2009) proposed a more sophisticated method to measure the expression levels of a gene by taking into account all known isoforms of all genes. All above methods represent gene expression levels using normalized count data, which can be further processed and analyzed in a way similar to microarray data, such as empirical Bayes method (Cloonan et al., 2008; Smyth, 2004)

One of the unique features of RNA-seq data is that the number of reads obtained from a gene depends on the transcript length. Therefore, we have more power detecting differential expression for longer transcripts. It has been shown that, in RNA-seq data, the proportion of significantly differentially expressed genes increases with the transcript length, while such bias is not present in microarray data (Bullard et al., 2010; Oshlack and Wakefield, 2009). This length dependency can have major impact on gene set analysis (GSA), which tests sets of predefined genes based on existing knowledge for enrichment in a list of differentially expressed genes or for the treatment/condition effect on the gene set as a whole. GSA is commonly used in gene expression analysis for identifying pathways and Gene Ontology (GO) terms. The significant GO terms identified from the RNA-seq data using existing procedures established for the microarray data tend to be enriched for longer genes.

One purpose of conducting GSA is to rank predefined gene sets, such as pathways and GO terms, according to their relevance to the biological question under study. GSA typically is a two-step process. The first step is to summarize the data using a gene-level statistic describing the degree of differential expression of individual genes, and possibly obtaining a list of significantly differentially expressed genes based on the statistic. The second step is to test for the significant enrichment of a gene set based on the gene-level statistics or the list of significant genes (Barry et al., 2008). Ideally, the gene-level statistic used in GSA only depends on the gene expression levels, such as the fold change and/or the variation across replicates. However, for the RNA-seq data, the gene-level test statistic is also affected by the transcript length. If we use the gene-level statistics to test gene sets directly, for two gene sets with equal number of genes and equal effect sizes, the gene set with longer genes will likely be ranked higher than that with shorter genes. This will become problematic when researchers only select a few top-ranked gene sets in follow-up studies because the gene sets with shorter genes will tend to be overlooked. Therefore, some adjustments for this length dependency could be essential for ranking gene sets.

One of the commonly used gene-set-level tests in GSA is the Fisher's exact test, which is used to compare a list of significantly differentially expressed genes against all genes being analyzed to identify the gene sets that are enriched in the significant gene list. The null distribution of the Fisher's exact test is hypergeometric under the assumption that the probability of each gene entering the significant gene list is the same for genes with same effect size. However, this assumption does not hold for the RNA-seq data analysis because of the aforementioned length dependency. Thus, the hypergeometric distribution is no longer an appropriate null distribution for the Fisher's exact test in GSA for RNA-seq data. To address this problem, Young et al. (2010) estimated the probability of each gene to be included in the significant gene list by fitting a six-knot cubic spline model relating the empirical identification probability of a gene to its transcript length. This probability was then used in a random sampling procedure to estimate the null distribution for the Fisher's exact test. They showed that the random sampling procedure can be approximated using Wallenius' non-central hypergeometric distribution and the adjustment resulted in dramatic rank changes of the GO terms. This strategy is similar to the GSA method proposed for analyzing databases of regulating sequences although the latter used a non-central binomial distribution (Taher and Ovcharenko, 2009).

In this study, we proposed two approaches of adjusting GSA for RNA-seq data. In the first approach, we introduced the transcript-length adjustment for gene-level test statistics. The benefit of gene-level adjustment is that it is more general. It can adjust the transcript length bias in the identification of differentially expressed genes even if no GSA is conducted. For GSA, once genes are ordered by properly adjusted gene-level statistic, powerful non-parametric tests such as Wilcoxon rank-sum test can be applied at the gene set level. In the second approach, we used a transcript-length-based Wallenius' non-central hypergeometric distribution as the null distribution for the gene-set-level test. Using a transcript-length-based random sampling procedure as a gold standard, we showed that Wallenius' distribution is a closer approximation than the non-central binomial distribution. We also demonstrated that using transcript length directly (one parameter) for calculating the non-central parameter for Wallenius' distribution is an effective alternative to fitting a six-knot cubic spline function (six parameters) from the percentage of differentially expressed genes. Finally, we compared the effectiveness of all these adjustments using a real dataset.

2 METHODS

2.1 GSA with transcript-length adjustment at the gene-level test statistics

Since the RNA-seq data are counts in nature, the Poisson distribution has been used to model the number of reads obtained for each gene when no replicates or only technical replicates are present in the experiment (Marioni et al., 2008). If we denoted X₁, X₂ as the total counts of the same gene from two different tissues (or conditions), the gene is claimed to be significantly different in these two tissues if the absolute value of the (Wald-type) test statistic,

(1)

is larger than a chosen cut-off value. A P-value can also be obtained based on an approximate standard normal distribution. Here, Q is the ratio of the total sequence reads from the two tissues. Note that the Wald-type statistic is asymptotically the same as a likelihood ratio test used in Marioni et al. (2008). As pointed out previously (Bullard et al., 2010; Oshlack and Wakefield, 2009), the percentage of differentially expressed genes identified by this statistic has a positive correlation with the transcript length. Even averaging over the transcript length using RPKM does not eliminate this problem (Oshlack and Wakefield, 2009). To adjust for the effect of transcript length (L), we can subtract a length-dependent factor from the statistic in Equation (1) for each gene to obtain

(2)

where the read length d is 32 bp in the RNA-seq data from Marioni et al. (2008).

For comparison, we also tried to adjust for the length dependency using division in a similar way as Bullard et al. (2010) except the constant c.

(3)

Both Z₂ and Z₃ have an unknown constant, c, in the formula. How to determine the value of c and how much effect c has on GSA analysis results are important issues. Since it has been shown that the microarray data do not show transcript length bias, a good c should result in less variation among the differences between the two Z statistics above and the corresponding t statistics obtained from the microarray data. We chose the value of c by minimizing the variance of the differences between the statistics from the two data sources. This criterion is intended to minimize the difference between RNA-seq data and microarray data in transcript length dependency. This may not be the best criterion for determining the value of c. Interestingly, the best c values for Z₂ and Z₃ are very similar if not exactly the same using this criterion. The value obtained for c is around 0.031. In reality, most RNA-seq experiments do not have corresponding microarray data. Therefore, we also obtained the value of c by just fitting a linear regression through the origin to the total number of reads from each gene against the transcript length. The c value obtained based on regression (0.0436) is very similar to the one obtained using microarray data. Our examinations showed that the Wilcoxon rank-sum test-based GSA results are not very sensitive to the value of c and the two estimated c values gave very similar results. When Z₃ is used, the analysis is completely insensitive to the value of c because the change of c in Z₃ does not affect the rank of the gene-level statistics.

2.2 GSA with transcript-length adjustment at gene set level

Due to the length dependency of the gene-level statistics, we propose to use the Wallenius' non-central hypergeometric distribution instead of the central hypergeometric distribution to calculate the P-values for the Fisher's exact test. The former is a generalization of the hypergeometric distribution with items sampled in a biased fashion represented by a non-central parameter w, which is the odds ratio of the two groups to be sampled. This non-central parameter is estimated as 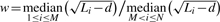where M, N, L_i, and d are the number of genes in a particular gene set, the total number of genes, the transcript length for each gene and the sequencing read length, respectively (See Supplementary Material for more details).

2.3 Simulations for comparison of methods at gene set level

We conducted some simulations to compare three distributions: the proposed Wallenius' non-central hypergeometric distribution, the non-central binomial distribution (Taher and Ovcharenko, 2009), and the central hypergeometric distribution, in respect to their suitability for serving as the null distribution for Fisher's exact test in GSA of RNA-seq data. Since the identification probability of a gene is approximately linear to the square root of its transcript length, we developed the following random sampling procedure to obtain the number of significant genes expected from a particular gene set under the null hypothesis.

1. Define 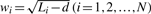as the weight for the identification probability for gene i.

2. Randomly pick a gene set of M genes from a particular quartile of the human transcript length distribution.

3. Randomly choose K genes without replacement from the total N genes expressed according to the weight defined in (1).

4. Record the number of genes among the K genes chosen in step (3) that are from the gene set.

5. Repeat steps (2) to (4) 1000 times to obtain the empirical distribution of number of genes from the gene set under the null hypothesis.

In our comparison, the total number of genes (N) was set to be 10 000. Although it is smaller than the number of genes in most tissues, the scale is in the right neighborhood. The gene set size (M) was set to be 10, 50, 100 and 500 because gene sets too small or too big are often excluded from analyses in practice. The number of significant genes (K) was set to be 50, 500 and 2000 to represent various proportions of significant genes in real data. The transcript length (L) was sampled from the human transcript length data downloaded from NCBI. To simulate gene sets with different transcript lengths, we randomly sampled transcript lengths from the first quartile, the fourth quartile and the middle two quartiles of the human transcript length distribution to represent sets of genes with short, long and average length, respectively. The sequencing read length was set to 32 bases to be consistent with the real data. We computed the mean and standard deviation for each distribution obtained from the simulation and used them for comparison.

The above simulation was for gene sets randomly sampled from particular quartiles of transcript length distributions, which is a good representation of the general trend. However, it does not reflect any true biological gene set. To examine the four distributions discussed above using a few true gene sets, we selected some GO terms that have various numbers of genes and various median transcript lengths. The GO terms were randomly selected from specific quartiles in the distribution of the median transcript length of all GO terms with genes expressed in the Marioni dataset. The number of genes in each GO term was also taken into consideration.

2.4 Real data analyses

To compare the proposed and available methods in the GSA analysis of RNA-seq data, we used a real dataset from the Marioni study (Marioni et al., 2008) to examine the reduction of length effect in the GO term enrichment test. Since this study has both RNA-seq data and microarray data from the same samples, we used the results obtained from the microarray data as the standards because results from microarray data are not found to be correlated with the transcript length (Oshlack and Wakefield, 2009).

2.4.1 Datasets

The RNA-seq dataset from Marioni et al. (2008) were generated for human liver and kidney samples with 7 runs per tissue, five runs for the 3 pM concentration and two runs for the 1.5 pM concentration. The microarray data from the same study were generated from the same kidney and liver samples with each sample profiled on three Affymetrix Human Genome U133 Plus 2.0 Arrays (GSE11045).

2.4.2 Data downloading and preprocessing

The RNA-seq dataset was obtained from the Supplementary Table 2 of Marioni et al. (2008). The gene ID in this dataset is Ensembl gene ID. GO terms mapped to the genes with Ensembl IDs were extracted using Bioconductor package biomaRt. The microarray dataset was downloaded from gene expression omnibus (GEO) (GSE11045). After downloading the raw microarray data, we applied the robust multiple-array analysis (RMA) procedure (Irizarry et al., 2003) with quantile normalization (Bolstad et al., 2003) for preprocessing the raw microarray data before identifying differentially expressed genes between kidney and liver using a t-test. For comparison purposes, the Affymetrix gene IDs were mapped to the Ensembl gene IDs using biomaRt. When multiple Affymetrix probe sets have the same Ensembl gene ID, the median expression of these probe sets was used as the expression level for the Ensembl gene ID.

We also applied three filters to select a set of genes and a set of GO terms to be used in the analysis:

1. We removed genes in the RNA-seq data that have less than 10 reads in total to avoid uncertain low counts.

2. We removed genes that are not on the Affymetrix U133 plus 2.0 microarray for comparison purpose.

3. We discarded GO terms with fewer than 5 and more than 500 genes in our final list of genes as commonly practiced in microarray data analysis.

Human transcript lengths were obtained from two databases. In our simulation study, we downloaded the human RefSeq as a flat file ‘human.rna.ghff.gz’ from NCBI (ftp://ftp.ncbi.nih.gov/refseq/) and calculated the transcript lengths accordingly. In the real data analysis, we extracted transcript lengths using Bioconductor package biomaRt (http://www.bioconductor.org/). The Ensembl gene ID in the RNA-seq data was used as the attribute to extract transcript lengths. The median transcript length was used for genes with multiple transcripts and genes were discarded if their transcript lengths are not available.

2.4.3 Identifying differentially expressed genes

For identifying differentially expressed genes from the microarray data, we first conducted a two-sample t-test to generate a list of significant genes with a false discovery rate (FDR; Benjamini and Hochberg, 1995) value of 0.05. For the RNA-seq data, we conducted a Wald-type test as shown in Equations (1–3) and obtained the corresponding P-values based on the standard normal distribution. Bonferroni correction was used to select the lists of significant genes at a significance level of 0.05. To evaluate the effect of gene-level adjustments on identifying differentially expressed genes, we divided the genes into bins of 247 genes with similar length and identified the percentage of differentially expressed genes within each bin for the RNA-seq data using the test statistics Z₁, Z₂ and Z₃.

2.4.4 GSA for GO terms

To examine the effect of our adjusted gene-level test statistics on the gene set enrichment analysis, gene-level test statistics Z₁, Z₂ and Z₃ were combined with the GO-term-level Wilcoxon rank-sum test. Significance level was set to 0.05 in the calculation. The results were compared with those from the microarray data analysis based on the t-test at gene level and the Wiconxon rank-sum test at GO-term level.

For comparing gene-set-level methods, GOseq package (version 0.1.5) (Young et al., 2010) was downloaded from the author's web site (http://bioinf.wehi.edu.au/software/goseq/). The GOseq Wallenius version was run with default parameter settings. The gene set enrichment P-values were directly used in our comparisons. Our gene set-level method was compared against GOseq, non-central binomial, central hyper geometric and reference null from our simulation.

3 RESULTS

3.1 Adjustment at the gene-level test statistics

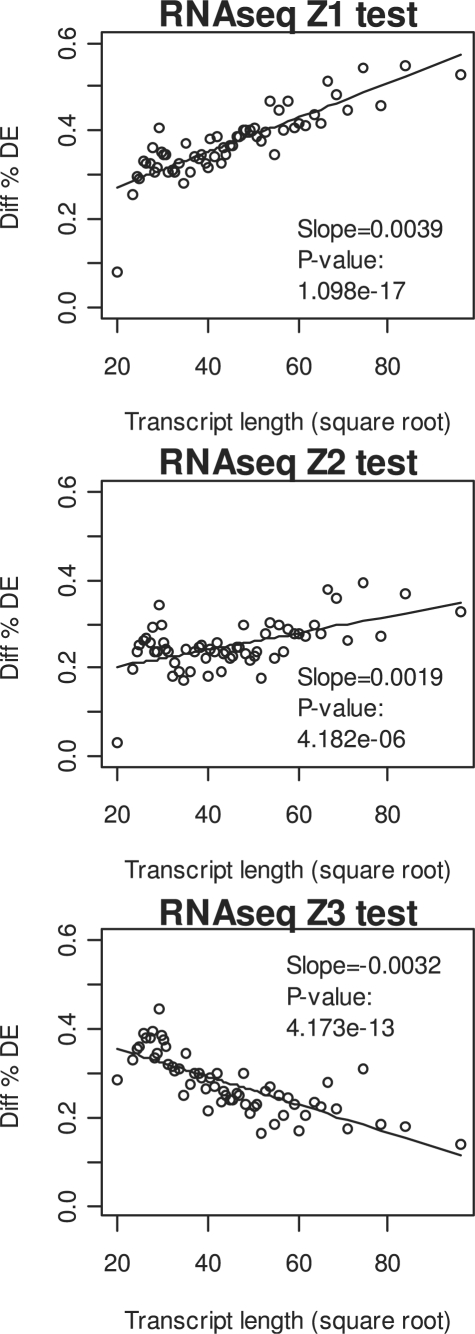
We proposed two ways to adjust for transcript length at the gene-level testing statistics as shown in Equations (2) and (3). These adjustment methods were compared with methods without such adjustments in analyzing the RNA-seq data from Marioni et al. (2008). The effects of the adjustments on identifying differentially expressed genes were evaluated by comparing with the results from the microarray data (Fig. 1 and Supplementary Fig. 2). Without adjustment, the difference of the proportions of significant genes between RNA-seq and microarray shows a positive dependency on transcript length (Fig. 1). This trend is substantially reduced although not completely eliminated by the adjustment in Z₂. However, over-adjustment of the length effect was observed from the adjustment in Z₃, which results in negative dependency on transcript length. Here, we used the significance level of 0.001 at nominal level for identifying differentially expressed genes to ensure the presence of substantial number of significant genes in the microarray results for comparison. The plots are in similar fashion at other significance levels (results not shown).

Fig. 1.

The differences between the RNA-seq data and the microarray data in the percentage of genes identified as significant using the three Z-tests. Each point represents a group of 247 genes with similar transcript length. Significance level was set to 0.001 to avoid the lack of significant genes from microarray data. Genes with zero or low counts (the sum of all counts is less than 10) were excluded from the analysis. The linear regression lines are shown.

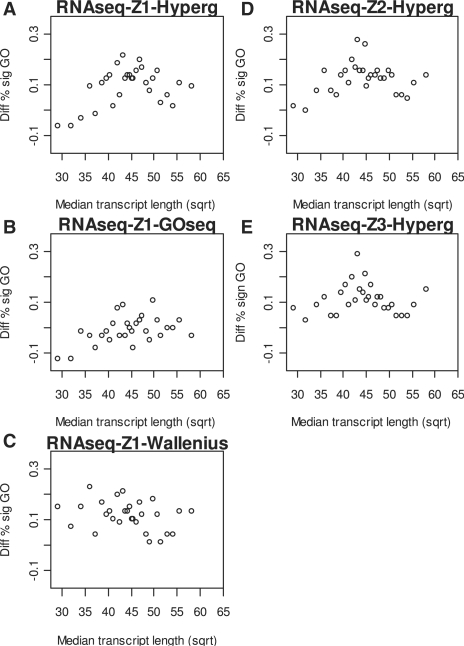
Fig. 2.

Effect of gene-level statistic adjustment in the GSA analysis. The differences between the percentages of significant GO terms from RNA-seq data and those from the microarray data are plotted against the median transcript length of the GO terms. GO terms are binned according to the median transcript length with 65 GO terms in each bin. Significance level for testing each GO term was set to 0.05. The linear regression lines are shown and the P-values from testing against the slope of 0 are shown as inserts.

For evaluating the effect of these two gene-level adjustment methods in GSA analysis, Z₁, Z₂ and Z₃ were combined with the Wilcoxon rank-sum test for GO term analysis. The results were also compared with those from the microarray data. The differences of the proportions of significant GO terms from RNA-seq and microarray are plotted against transcript length in Figure 2 and Supplementary Figure 3. A significant positive relation with the transcript length was observed when no adjustment was applied (with a P-value of 0.02 for the slope). The adjusted gene-level statistic, Z₂, can largely reduce such effect with a non-significant P-value of 0.11 for testing the slope. However, for the adjustment Z₃, the slope becomes significantly negative with a P < 0.04. In general, the transcript length dependency is less dramatic in the GO term analysis than that in the gene-level analysis as shown in Figure 1.

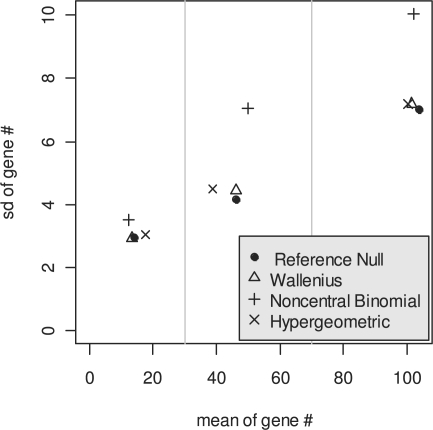
Fig. 3.

Comparison of different candidate null distributions for Fisher's exact test with the reference null distribution established by resampling simulations. ‘<Q1’, ‘Q1–Q3’ and ‘>Q3’ represent the genes in the gene set randomly sampled from less than the first, between the first and third and larger than the third quartiles of the transcript length distribution, respectively. Each gene set contains 50 genes. The non-central parameters were calculated based on the identification probability weight 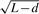for the relevant distributions. The Wallenius' distribution has similar mean and variance to the reference null distribution established by the simulations.

3.2 Adjustment of the null distribution for Fisher's exact test at gene set level

To correct the transcript length bias at the gene set level, we proposed a simple weight, 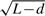, for the identification probability of each gene, with L and d representing the transcript length and the sequencing read length, respectively. This weight was then used to calculate the odds for Wallenius' non-central hypergeometric distribution (refer to Section 2), which was used as the null distribution for Fisher's exact test instead of the central hypergeometric distribution.

To evaluate Wallenius' distribution, the central hypergeometric distribution, and a non-central binomial distribution (Taher and Ovcharenko, 2009) for Fisher's exact test in GSA, we compared these three distributions with a reference null distribution obtained from a random sampling procedure based on the weight 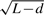for each gene. The results (Fig. 3) showed that the central hypergeometric distribution dramatically overestimates the expected number of significant genes from a gene set when the gene set consists of genes with short transcripts sampled from the first quartile of the length distribution of all human transcripts. In contrast, it dramatically underestimates the expected number of significant genes when the gene set consists of genes with longer transcripts sampled from the fourth quartile of the length distribution. The degree of difference did not seem to vary with the size of gene set. The expected numbers of genes from Wallenius and the non-central binomial distribution were close to the expected number in the reference null distribution established by the random sampling procedure (Fig. 3, top panel). However, the non-central binomial distribution shows inflated variation compared with the reference null distribution and Wallenius' distribution (Fig. 3, bottom panel). This inflation is more obvious when the genes are from the fourth quartile of the transcript length distribution. Figure 3 only shows results for gene sets with 50 genes. The general pattern is the same for gene sets of different sizes, such as 10, 100 and 500 genes, although the absolute values of the expected number of genes and the standard variation are different (Supplementary Fig. 4).

Fig. 4.

Comparison of the three candidate null distributions with the reference null distribution for three real GO terms. The three GO terms are: GO:0006120 with 37 expressed genes of median length 725.5 bp; GO:0008380 with 209 expressed genes of median length 1612.5 bp; and GO:0046777 with 81 expressed genes of median transcript length 2670 bp. They are separated by vertical gray lines. Wallenius' distribution has the best approximation to the reference null distribution at both mean and standard deviation (SD) for these GO terms.

The simulation results shown in Figure 3 are based on random sampling of genes from particular quartiles of the length distribution to form a gene set, which is a good representation of general trend, but it does not reflect any true biological gene set. To test a few true gene sets, we selected some GO terms with various numbers of genes and various median lengths to compare the four distributions discussed above. The results from three true gene sets that contain various numbers of genes and various median transcript lengths are shown in Figure 4. More results are shown in Supplementary Table 1. In general, the results are consistent with what we observed from Figure 3. The hypergeometric distribution overestimates the mean number of expected significant genes for gene sets with short genes but underestimates it for gene sets with longer genes. The non-central binomial distribution overestimates the variance. Both results showed that Wallenius' distribution is a good approximation for the reference null distribution based on random sampling, which is consistent with what was found recently (Young et al., 2010). The difference between our procedure and that of Young et al., which is implemented in GOseq package, is at the non-central parameter, where we used the square root of transcript length while they fitted a cubic spline to the percentage of differentially expressed genes.

3.3 Comparing methods for length effect adjustment in GSA

To compare the two categories of methods for reducing transcript length bias in GSA, we examined the trend of the difference between the proportions of significant GO terms along the median transcript length from the RNA-seq and that from the microarray data (Figs 2 and 5). The combination of unadjusted test Z₁ with hypergeometric distribution (Fig. 5A) shows positive correlation at shorter GO terms but slight negative at the longer GO terms. A perfect bias correction method would remove these trends along the transcript length and keep the percentage of significant GO terms high. For the GOseq method based on the Wallenius' distribution, the trends are largely reduced, but the percentage of significant GO terms decreases dramatically (Fig. 5B). In comparison, replacing the hypergeomentric distribution with the Wallenius' distribution using our parameterization, the positive correlation at the lower end is removed and the percentages of significant GO terms are kept high (Fig. 5C). When the gene-level adjustment statistics Z₂ (Fig. 5D) and Z₃ (Fig. 5E) are combined with the hypergeometric distribution, the effect is in between the combination of Z₁ with hypergeometric distribution (Fig. 5A) and the Wallenius distribution (Fig. 5C). For the Wilcoxon rank-sum based tests, results from Z₁ and Z₂ are similar except that Z₂ has a smaller and non-significant slope. The Z₃ test shows a slight negative trend (Fig. 2).

Fig. 5.

Comparison of different methods for adjusting transcript length bias based on the Fisher's exact test. Each point represents 65 GO terms with similar median transcript length. Significance level for GO terms is nominal P-value of 0.05. The significant gene list for microarray data is generated using significant level of FDR 0.025, while that for RNA-seq is generated using significant level of 0.05 with Bonferroni correction. Different significant levels are used to avoid extremely short gene list from microarray data.

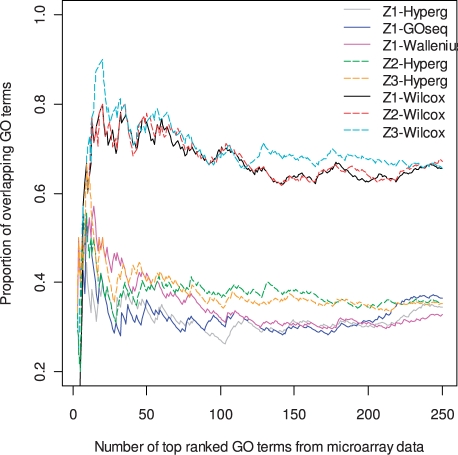
To examine the rank order of the results from all methods, we examined the ranking of the common GO terms that have 5–500 genes represented in both the microarray and the RNA-seq data. Figure 6 shows the overlaps of the top-ranked GO terms between RNA-seq and microarray from the two types of analysis methods, the Fisher's exact test methods and the Wilcoxon rank-sum test methods. In general, the results from the Fisher's exact test methods show much lower overlap than those from the Wilcoxon rank-sum test methods. This observation is consistent with the common understanding that the Wilcoxon rank-sum strategy is better than the Fisher's exact test strategy in GSA (Allison et al., 2006).

Fig. 6.

Comparison of the top-ranked GO terms generated by different methods. The GO terms were ranked based on the P-values from each method. The proportions of overlapping GO terms between the microarray data and the RNA-seq data are plotted. For the Fisher's exact test based methods, GO term ranks generated from RNA-seq data using central hypergeometric distribution (black), Wallenius' distribution parameterized in GOseq (blue) and Wallenius' distribution with our parameterization (magenta) were all compared with the microarray data analyzed based on central hypergeometric distribution. For the Wilcoxon rank-sum test-based global analysis, the GO term ranks generated from RNA-seq data using unadjusted (green) or adjusted (red) gene-level statistics were compared with the GO term ranks generated from microarray data based on Wilcoxon rank-sum global test without adjustment.

For the Fisher's exact test based method, our parameterization has a better overlap with microarray for the 100 top-ranked GO terms, but has very little improvement on the overlap when more top GO terms were considered. In contrast, the GOseq method showed less improvement at the top-ranked GO terms but show substantial improvement after top 200 GO terms (Supplementary Fig. 5). The combinations of the gene-level adjustments, Z₂ and Z₃, with the hypergeometric distribution show comparable levels of overlap with the combination of Z₁ and the Wallenius distribution at top-ranked GO terms but show substantial improvements for GO terms ranked between 100 and 200.

The GSA methods based on the Wilcoxon rank-sum test show high consistency in terms of the GO term ranks (70–80%) for the unadjusted Z₁ test. Minimal improvement on the rank overlap is observed from Z₂ over Z₁. For Z₃, substantial improvement is observed in some rank ranges, such as around the first 20 GO terms and between 100 and 200 GO terms. The lack of large difference among the three tests is consistent with the fact that the Spearman correlations between the three Z statistics from the RNA-seq data and the t statistics from microarray data are very similar, 0.753, 0.755 and 0.764 for Z₁, Z₂ and Z₃, respectively.

3.3.1 Summary

Similar to microarray data analysis, RNA-seq data analysis often has two steps, the gene-level analysis and the GSA. The second step can be based on the significant gene lists obtained from the first step using the Fisher's exact test or the statistics for each gene directly using the Wilcoxon rank-sum test (Fig. 7). Based on our analysis of the Marioni data, the Wilcoxon rank-sum test is preferred over the Fisher's exact test for its high overlap with microarray results. Transcript length adjustment at gene-level statistics followed by Wilcoxon rank-sum test has improvements but relatively small (Z₃ slightly better than Z₂). For gene-level testing, subtraction-based adjustment Z₂ shows better performance in reducing the dependency on transcript length, while the division-based Z₃ tends to over adjust the effect. For the Fisher's exact test, gene-set-level adjustments show relatively large improvement.

Fig. 7.

Flowchart for the analysis pipelines from preprocessed RNA-seq data to GSA. The two locations for correcting transcript length bias are highlighted with gray background. DE, differentially expressed.

4 DISCUSSION

RNA-seq is a rapidly growing technology that has the potential to replace microarray in profiling gene expression. However, when previously established methods for GSA were directly used on RNA-seq data, gene sets that consist of longer genes tended to be identified as significantly enriched. In this article, we proposed two strategies to reduce such length dependency. The first strategy is to adjust the gene-level statistics by removing transcript-length dependency before applying a standard Wilcoxon rank-sum test at the gene-set level. The second strategy is to adjust the gene set enrichment test by replacing the central hypergeometric distribution with Wallenius' non-central hypergeometric distribution in Fisher's exact test based on significant gene lists (Fig. 7). Our results showed that both strategies are effective in reducing length dependence in GSA analysis for RNA-seq data. However, the Wilcoxon rank-sum based strategy shows a substantial higher level of overlap with microarray results.

The RNA-seq technology is more sensitive to longer transcripts because it generates more reads from longer transcripts. Therefore, we have more statistical power to detect longer transcripts for differential expression. However, in this situation, the statistical power not only reflects the standardized effect size and sample size but also reflects the transcript length. To our knowledge, transcript length has not been found to be relevant to biological processes. The detection bias for longer transcripts is arguably a candidate to be corrected in identifying differentially expressed genes from RNA-seq data. Our adjustments of gene-level statistics modify the length effect substantially at gene-level tests. However, the two methods, Z₂ and Z₃, perform differently. Z₂ reduces the positive length effect substantially but not completely removing it, while Z₃ over adjusts the relationship to negative. Further, fine-tuning these formulas is necessary to achieve ideal effect.

Transcript length bias in RNA-seq is just one obvious bias to be corrected. Young et al. (2010) found that the percentage of differentially expressed genes also depends on gene expression levels (number of reads). They proposed to remove this dependency using the same method as for the length bias if the investigator desires. We also saw similar bias along the number of reads from the Marioni data. However, it is not clear to us that completely removing the expression intensity bias is biologically correct because there has been evidence showing that the level of stochastic expression of genes is associated with the level of gene expression (Bar-Even et al., 2006; Newman et al., 2006). Therefore, we decided not to pursue the adjustment for expression levels in the GSA analysis of RNA-seq data here. If the adjustment is desired, a similar strategy as described here can potentially be applied to remove the expression level bias.

In GSA, the transcript length dependency is also obvious. Since one of our goals of conducting GSA analysis is to rank the gene sets based on pathways and GO terms according to their relevance to the biological question under study for follow-up studies, the rank of gene sets identified from the GSA should only depend on biological relevant parameters, such as the fold change of the gene expression and/or the variation of the expression across samples. Therefore, we believe that some adjustment for the transcript length bias is beneficial.

The Fisher's exact test is a simple procedure for identifying over represented gene sets based on comparing a set of significantly differentially expressed genes against all genes under study. When a set of significantly differentially expressed genes is generated from the RNA-seq data, this method is a natural and common choice for the GSA (Allison et al., 2006). However, it has been demonstrated that the GO terms identified using this method tend to be the ones with longer transcripts (Oshlack and Wakefield, 2009) if no adjustment is applied to the gene-level statistics. One solution for this problem is adjusting the null distribution used in the Fisher's exact test for obtaining P-values. To take into account of the transcript length in the null distribution, we used a non-central hypergeometric distribution with a noncentral parameter determined by the transcript length. The non-central parameter represents the average detection power difference between the genes in the GO term and those outside the GO term. Some resampling procedures were used both by Young et al. (2010) and us to establish the null distribution. However, we both showed that Wallenius' non-central hypergeometric distribution, which can reduce the heavy computation demand of the resampling procedure, is a good approximation. The only difference between our method and Young et al.'s GOseq method lies in the parameterization of the non-central parameter for Wallenius' distribution. Young et al. (2010) used a six-knot spline to fit the percentage of differentially expressed genes against transcript length to determine the probability of each gene to enter the list of significantly differentially expressed genes. In our study, we simply used the square root of the transcript length based on the assumption that the number of reads obtained from each transcript is linear to its transcript length. Our parameterization is simpler and the performance of our method is better than the GOseq method for the high-ranked GO terms in our real data analysis (Fig. 6).

The non-central parameter for the Wallenius' distribution is based on the weighting factor 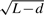. It depends on a few factors. One factor is the expressed genes in a dataset because only the genes that are expressed above certain level (e.g. total 10 reads in our analysis) in the dataset are used in calculating this non-central parameter. Therefore, the non-central parameters are dataset specific. There is not a universal value for a given gene set that can be used for the analysis of any dataset. Another factor is the sequence depth. As the sequencing depth increases the power for detecting differential expression increases. When the power increases to a certain level, the difference of identification probability among genes will be reduced to a negligible size and the non-central parameter for Wallenius' distribution will be close to 1. Wallenius' distribution approaches the central hypergeometric distribution. Therefore, the transcript length-based adjustment is only necessary when the sequencing depth is not high enough for the power of detecting differential expression approaching 1. The third factor is the read length determined by the sequencing technology. Since the non-central parameter was calculated based on 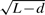, when d is long enough, for example, longer than the transcript length of all genes, there will be no length dependency because the number of reads will only be dependent on the number of transcripts. These are just some of the factors that influence the non-central parameter. Other factors, such as mapability and sequence accuracy, also potentially affect the non-central parameter. Further improving the parameterization can be achieved using more complex relationships between transcript length and number of reads by incorporating all these factors mentioned above.

It is important to point out that this study is based on the RNA-seq experiments with only technical replicates, which is seen in many of the published RNA-seq experiments. The technical replicates are modeled as independent Poisson distributions. It has been shown recently that negative binomial distribution is a better model to incorporate larger variance for handling biological replicates or replicated libraries (Anders and Huber, 2010; Robinson and Smyth, 2007, 2008). The transcript length bias issue also needs to be evaluated for these models.

One potential problem of transcript length bias correction at the gene level is the change of statistical power and FDR. With length bias adjustment, both FDR and power could increase for short genes but both could decrease for the long genes depending on methods. The overall net change is unknown. Evaluating the gain and loss as well as how to tweak the adjustment in order to minimize the FDR and maximize the power is some immediate future work to consider.