Dynamic Stability of Human Walking in Visually and Mechanically Destabilizing Environments

Abstract

Understanding how humans remain stable during challenging locomotor activities is critical to developing effective tests to diagnose patients with increased fall risk. This study determined if different continuous low-amplitude perturbations would induce specific measureable changes in measures of dynamic stability during walking. We applied continuous pseudo-random oscillations of either the visual scene or support surface in either the anterior-posterior or mediolateral directions to subjects walking in a virtual environment with speed-matched optic flow. Floquet multipliers and short-term local divergence exponents both increased (indicating greater instability) during perturbed walking. These responses were generally much stronger for body movements occurring in the same directions as the applied perturbations. Likewise, subjects were more sensitive to both visual and mechanical perturbations applied in the mediolateral direction than to those applied in the anterior-posterior direction, consistent with previous experiments and theoretical predictions. These responses were likewise consistent with subjects’ anecdotal perceptions of which perturbation conditions were most challenging. Contrary to the Floquet multipliers and short-term local divergence exponents, which both increased, long-term local divergence exponenets decreased during perturbed walking. However, this was consistent with specific changes in the mean log divergence curves which indicated that subjects’ movements reached their maximum local divergence limits more quickly during perturbed walking. Overall, the Floquet multipliers were less sensitive, but reflected greater specificity in their responses to the different perturbation conditions. Conversely, the short-term local divergence exponents exhibited less specificity in their responses, but were more sensitive measures of instability in general.

INTRODUCTION

Our ability to remain stable while walking is challenged during many daily activities like walking on an uneven sidewalk, or stepping off a curb or over an obstacle. Clinically, some have measured gait variability as a possible indicator of stability. However, there is as yet no universally accepted measure to directly quantify stability in terms of how people respond to (either small or large) perturbations. Techniques from nonlinear dynamics provide direct quantitative assessments of local dynamic stability and have demonstrated measurable differences between healthy young and elderly people (Granata and Lockhart 2008; Kang and Dingwell 2008) and between patient populations and healthy individuals (Dingwell and Cusumano 2000; Dingwell et al. 2007; Yakhdani et al. 2010) during unperturbed walking. However, how these measures of stability change when people are subjected to external perturbations has not yet been determined.

Floquet multipliers (FM) and local divergence exponents (LDE) have been used to assess orbital and local dynamic stability in humans during unperturbed walking (Donelan et al. 2004; Kang and Dingwell 2006; Dingwell et al. 2008; Kang and Dingwell 2008). FM generally indicate that humans are orbitally stable (i.e. FM < 1) whereas LDE indicate that humans are locally unstable (LDE > 0) during unperturbed walking (Dingwell et al., 2007). However, it is not yet known to what extent either measure can be appropriately used to assess gait. First, human gait is neither strictly periodic (a requirement of FM calculations) nor strongly aperiodic (an assumption of LDE calculations). Second, FM and LDE are strictly defined only for deterministic systems and all biological systems are inherently stochastic. However, the finite-time modifications used to calculate FM and LDE do provide reasonable estimates of the stability human walking even in the presence of these limitations. It is yet to be determined if these measures of stability can quantify changes in stability within a given individual, such as may be experienced with aging or when exposed to a challenging ambulatory environment.

Virtual reality (VR) systems provide a safe environment in which to apply perturbations during human gait, but still allow for a variety of types of perturbations to be applied (e.g., visual or somatosensory, in particular directions, etc). Changing aspects of the VR environment such as the angle of visual projection or optical flow speed can induce gait characteristics that are generally associated with more cautious walking, such as shorter and wider steps (Nyberg et al. 2006; Hollman et al. 2007; Lamontagne et al. 2007). These studies indicate the promise of using VR as a tool for studying changes in dynamic stability during perturbed gait. Recently, O’Connor and Kuo (2009) exposed subjects to sinusoidal oscillations of the visual scene and found that subjects were more sensitive in the ML than the AP direction during walking. Their study focused on changes in variability rather than direct measures of dynamic stability and left open the question of how stability measures change when exposed to similar perturbations during walking.

We recently exposed individuals to continuous pseudo-random oscillations of either the visual scene or support surface in a virtual environment with speed appropriate optical flow. We knew these oscillations would make our subjects qualitatively more unstable. This was confirmed by the fact that when our subjects were exposed to these perturbing environments, they exhibited “cautious” gait characteristics, like shorter wider steps, and they also exhibited increased movement variability (McAndrew et al. 2010). Our purpose here was to determine if these same qualitatively destabilizing oscillations could also evoke measureable changes in dynamic stability, as quantified by Floquet multipliers and local divergence exponents, during walking. We hypothesized that participants would be: 1) more dynamically unstable when walking during continuous, pseudo-random perturbations than without and 2) more dynamically unstable during mediolateral (ML) than during anterior-posterior (AP) perturbations.

METHODS

A complete description of our experiment is given in McAndrew et al. (2010). In brief, we collected data on 12 healthy young adults walking in a Computer Assisted Rehabilitation ENvironment (CAREN) system (Motek, Amsterdam, Netherlands). While walking, participants were exposed to continuous, pseudorandom oscillations of the support surface or visual field. The 5 experimental conditions consisted of unperturbed walking (NOP), anterior-posterior platform (APP) or visual (APV) oscillations, and mediolateral platform (MLP) or visual (MLV) oscillations. The order in which each condition was presented was randomized across subjects to minimize potential learning effects. Subjects walked at the same speed for all conditions. Perturbations were applied as a pseudo-random sum of sines equation with 4 incommensurate frequencies (0.16, 0.21, 0.24 and 0.49 Hz). Subjects completed five 3-minute walking trials for each experimental condition.

A 24-camera Vicon motion capture system was used to collect kinematic data at 60 Hz. Subjects wore 22 reflective markers (McAndrew et al. 2010). Four markers were placed on each foot, the head and pelvis. The remaining 6 markers were placed on the acromium processes, the C7 and T8 vertebrae, the sternum, xyphoid process.

Delay embedded state spaces (Gates and Dingwell 2009) were constructed for the AP, ML and vertical (VT) velocities of the C7 vertebral marker using the original data and their time delayed copies (Dingwell and Marin, 2006):

$$\mathbf{S}(t)=[v(t),v(t+\tau ),\dots ,v(t+(d_E-1)\tau )]$$ (1)

where S(t) is the d_E-dimensional state vector, v(t) is the original 1-dimensional data, τ is the time delay and d_E is the embedding dimension. Time delays were determined from the first minimum of the Average Mutual Information function (Fraser 1986), yielding average time lags of 15, 20 and 10 samples for the AP, ML and VT directions, respectively. An embedding dimension of d_E = 5 (Dingwell and Cusumano 2000) was used for all trials, such that S (t) ∈ ℛ⁵. For orbital stability analyses, C7 marker data from each entire trial were used to construct the state spaces. For local stability analyses, 150 continuous strides of data were re-sampled to 15,000 total data points, or approximately 100 data points per stride (England and Granata 2007; Bruijn et al. 2009) prior to being delay embedded.

Floquet multipliers (FM) estimated orbital stability of the system, based on well-established techniques (Hurmuzlu and Basdogan 1994; Nayfeh and Balachandran 1995; Hurmuzlu et al. 1996; Kuo 1999; Donelan et al. 2004). First, state spaces used to calculate FM (described above) were divided into individual strides and then each stride was time normalized to 101 samples, corresponding to 0 – 100% of the gait cycle (Dingwell and Kang 2007). Poincaré maps were then defined for each percent of the gait cycle as

$${\mathbf{S}}_{k+1}=\mathbf{F}({\mathbf{S}}_k)$$ (2)

where S is the state of the system at stride k at each given Poincaré section (i.e., at each % of the gait cycle). Fixed points for each Poincaré map were defined from the average trajectory across all strides in a given trial, yielding:

$${\mathbf{S}}^{*}=\mathbf{F}({\mathbf{S}}^{*})$$ (3)

The orbital stability of the system was then estimated from a linearized approximation of equation (2).

$$[{\mathbf{S}}_{k+1}-{\mathbf{S}}^{*}]\approx J({\mathbf{S}}^{*})[{\mathbf{S}}_k-{\mathbf{S}}^{*}]$$ (4)

Where for S ∈ ℛ⁵, J(S*) ∈ℛ^5×5 is the Jacobian matrix for the system for each Poincaré section (percent of the gait cycle). The first 4 eigenvalues of J (S*)defined the FM which quantify how small perturbations grow or diminish for a given Poincaré section between one cycle and the next (Hurmuzlu and Basdogan 1994; Nayfeh and Balachandran 1995; Hurmuzlu et al. 1996; Kuo 1999; Donelan et al. 2004; Kang and Dingwell 2008). The last (i.e., 5^th) eigenvalue of J (S*) had a value of ~0 and was thus spurious (Kang & Dingwell, 2008). The magnitude of the maximum FM (maxFM) for each percent of the gait cycle was then calculated. These maxFM were then averaged for each trial for statistical comparisons. If maxFM < 1, perturbations on average shrink by the next cycle and the system is considered stable. If maxFM > 1, perturbations on average grow by the next cycle and the system is considered unstable.

Local dynamic stability was assessed by calculating local divergence exponents (LDE). LDE quantify how neighboring trajectories in a state space evolve over time (Rosenstein et al. 1993; Dingwell and Cusumano 2000). After finding the nearest neighbors, the average logarithmic separation (i.e., divergence) between neighbors is calculated. LDE are then calculated by using a least-square fit to estimate the slope of the mean log divergence (MLD) curve:

$$y(i)=\frac{1}{\mathrm{\Delta }t}\langle \text{ln}\left[d_j(i)\right]\rangle =[{\lambda }^{*}]i+c$$ (5)

where d_j is the Euclidean distance between the j^th pair of nearest neighbors after i discrete time steps and 〈 〉 indicates the average over all j. Short-term $\left({\lambda }_S^{*}\right)$ and long-term $\left({\lambda }_L^{*}\right)$ LDE were calculated as the slope of y(i) vs. i between 0 and 1 strides and between 4 and 10 strides, respectively (Kang and Dingwell 2008). Positive LDE indicate local instability.

Max FM and LDE values were computed independently for C7 marker velocities in the AP, ML and vertical (VT) directions. Two-way analyses of variance (ANOVA) (Condition × Subject) and Tukey post-hoc analyses were used to assess statistical significance between conditions for maxFM, ${\lambda }_S^{*}\text{ and }{\lambda }_L^{*}$. A p-value of 0.05 was considered significant.

RESULTS

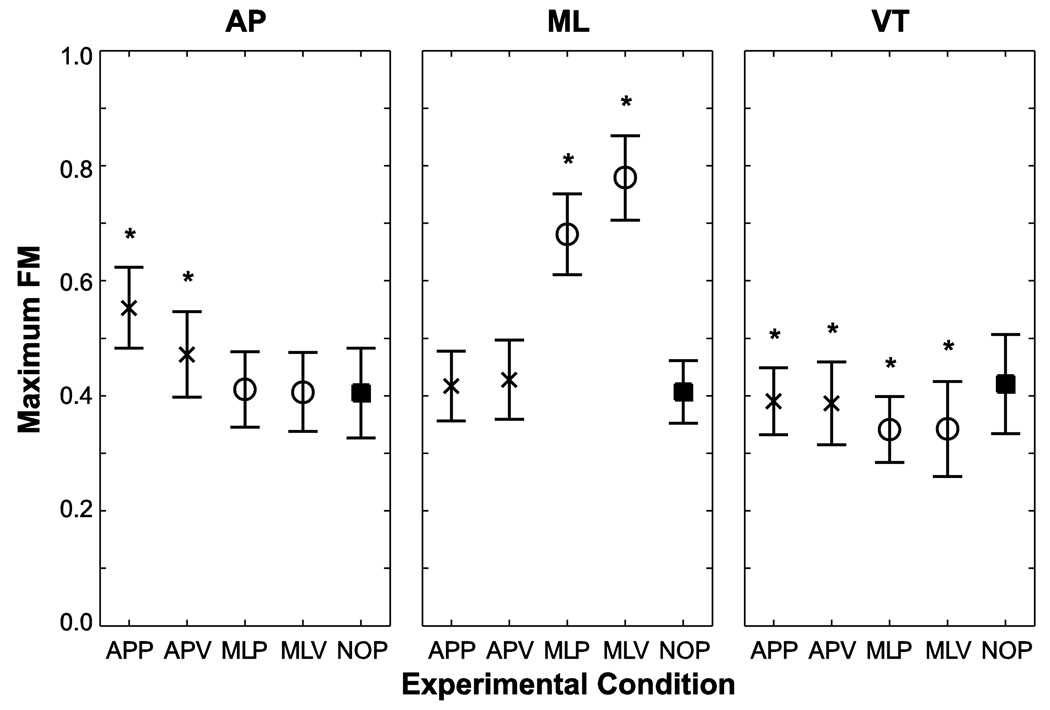
Subjects’ C7 movements in the AP direction were orbitally more unstable during AP perturbations than during the NOP condition (p < 0.001; Fig. 1 Left). There were no significant changes in orbital stability during the ML perturbations relative to NOP (p = 0.963 for MLP; p = 1.000 for MLV). APP perturbations caused the greatest increases in maxFM relative to all other conditions (p < 0.001). Subjects’ C7 movements in the ML direction were orbitally more unstable during the ML perturbations than during the NOP condition (p < 0.001; Fig. 1 Middle). There were no significant changes in orbital stability during AP perturbations (p = 0.753 for APP; p = 0.104 for APV). MLV perturbations caused the greatest increases in maxFM relative to all other conditions (p < 0.001). Subjects’ C7 movements in the VT direction were slightly but significantly more orbitally stable during all perturbation conditions than during NOP (APP, p = 0.032; APV, p = 0.009; MLP, MLV, p < 0.001; Fig. 1 Right). Subjects were also more orbitally stable during MLP relative to APP (p < 0.001) and during MLV relative to APV (p < 0.001). Overall, subjects exhibited orbitally stable (i.e., all maxFM < 1) C7 marker movements in all directions for all conditions.

Figure 1.

Floquet multipliers for each test condition for C7 marker movements in the AP, ML and VT directions. Each “*” indicates a statistically significant difference from the NOP condition at p < 0.05. Symbols are as follows: “×” indicates perturbations in the AP direction; “○” indicates perturbations in the ML direction and “■” indicates NOP.

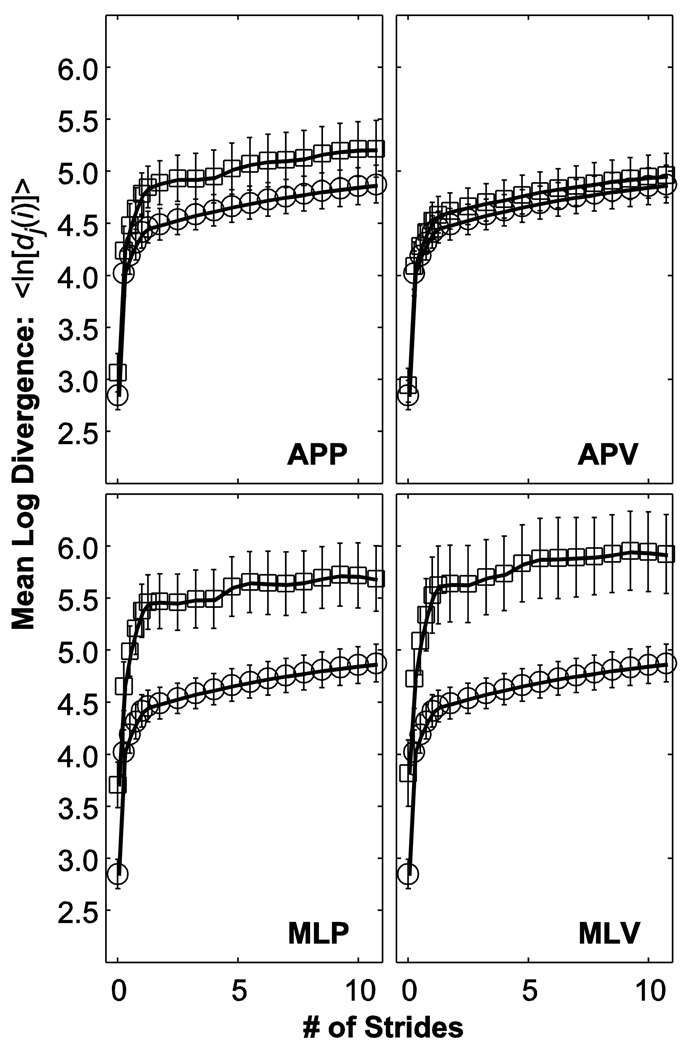
MLD curves for C7 movements in the ML direction generally shifted up and to the left for all perturbation conditions relative to NOP (Fig. 2). Thus, the slopes of these plots between 0 and 1 strides tended to be steeper during perturbation trials. Between 4 and 10 strides, individual MLD curves became more variable and less “smooth” during the perturbation conditions relative to NOP. On average, however, these MLD curves tended to be slightly flatter (i.e., lower slope) in this 4–10 stride region. MLD curves for C7 movements in the AP and VT directions (not shown) showed similar trends.

Figure 2.

Average mean log divergence (MLD) curves for ML movements of the C7 marker for all perturbation conditions. In each sub-panel, squares (“□”) indicate the specified perturbed condition. For comparison, circles (“○”) indicate the unperturbed (NOP) condition, which is the same in each panel. Error bars indicate between-subject ±1 standard deviations.

For C7 movements in all 3 directions, subjects demonstrated decreased short-term local stability (increased ${\lambda }_S^{*}$) during all perturbation conditions relative to NOP (p < 0.001; Fig. 3). C7 movements in the AP and VT directions were more unstable during APP than the MLP perturbations (p < 0.001), whereas C7 movements in the ML direction were more unstable during MLP than APP perturbations (p < 0.001). Subjects exhibited greater ${\lambda }_S^{*}$ during MLV than APV (p < 0.001) for C7 movements in all 3 directions. For C7 movements in both the AP and VT directions, subjects exhibited the greatest instability in response to APP perturbations (p < 0.001; Fig. 3 Left and Fig. 3 Right). Conversely, C7 movements in the ML direction were most unstable during the MLV perturbations (p < 0.001; Fig. 3 Middle).

Figure 3.

Short-term local divergence exponents $\left({\lambda }_S^{*}\right)$ for each test condition for C7 marker movements in the AP, ML and VT directions. Each “*” indicates a statistically significant difference from the NOP condition at p < 0.05. Symbols are as follows: “×” indicates perturbations in the AP direction; “○” indicates perturbations in the ML direction and “■” indicates NOP.

Subjects’ C7 movements in the AP direction were more stable long-term (decreased ${\lambda }_L^{*}$) during all perturbation conditions than during NOP (p < 0.001; Fig. 4 Left). Subjects exhibited significantly greater ${\lambda }_L^{*}$ during MLP perturbations relative to APP perturbations (p = 0.013) and during APV perturbations relative to MLV perturbations (p < 0.001). Subjects’ C7 movements in the ML direction exhibited lower ${\lambda }_L^{*}$ during ML perturbations than NOP (p < 0.001; Fig. 4 Middle). However, the AP perturbations yielded no significant changes in ${\lambda }_L^{*}$ (APP, p = 1.000; APV, p = 0.337). Subjects exhibited greater ${\lambda }_L^{*}$ during APP than during MLP perturbations (p < 0.001) and during APV than during MLV perturbations (p < 0.001). Subjects’ C7 movements in the VT direction exhibited decreased ${\lambda }_L^{*}$ during all perturbation conditions relative to NOP (APP, MLP, MLV, p < 0.001; APV, p = 0.038; Fig. 4 Right). There were no significant differences between ${\lambda }_L^{*}$ during APP and MLP conditions (p = 0.570). Subjects exhibited decreased ${\lambda }_L^{*}$ during MLV relative to APV perturbations (p < 0.001).

Figure 4.

Long-term local divergence exponents $\left({\lambda }_L^{*}\right)$ for each test condition for C7 marker movements in the AP, ML and VT directions. Each “*” indicates a statistically significant difference from the NOP condition at p < 0.05. Symbols are as follows: “×” indicates perturbations in the AP direction; “○” indicates perturbations in the ML direction and “■” indicates NOP.

DISCUSSION

Understanding how humans remain stable during challenging locomotor activities is critical to developing effective tests to diagnose patients with increased fall risk. Imposing carefully structured locomotor challenges in contexts like virtual environments may also provide effective training interventions to reduce fall risk in these patients. The purpose of this study was to determine if exposing subjects to different types of continuous pseudo-random perturbations which destabilized their walking movements would evoke measureable changes in proposed measures of dynamic stability (i.e., Floquet multipliers and local divergence exponents). In general, subjects exhibited direction-specific responses in dynamic stability to these perturbations. Subjects were always orbitally stable (maxFM < 1) and locally unstable (λ^* > 0), consistent with previous results from unperturbed walking (Dingwell and Kang 2007; Dingwell et al. 2007). These findings also directly extend those of (McAndrew et al. 2010), who demonstrated that these same subjects also exhibited “cautious” gait characteristics (e.g., shorter wider steps) and increased movement variability when exposed to these perturbations.

Subjects exhibited direction-specific responses to perturbations in all stability measures quantified. For example, subjects had significantly larger maxFM in the AP direction during the AP perturbations but not during ML perturbations and significantly larger maxFM in the ML direction during ML perturbations but not during AP perturbations (Fig. 1). In addition, subjects appeared to be more sensitive to ML perturbations than to AP perturbations. For example, maxFM for AP movements during APP perturbations increased by only ~ 0.2 above NOP, whereas maxFM for ML movements during ML perturbations increased by ~ 0.4 above NOP. Thus, subjects’ stability changed more in response to a ML perturbation than an AP perturbation. These results are consistent with the mean standard deviation (meanSD) position results from this dataset, which indicated that in the ML direction, subjects had significantly greater position variability than during the ML perturbations than during the AP or NOP conditions (McAndrew et al. 2010). Moreover, these results are consistent with both modeling predictions (Kuo 1999; Bauby and Kuo 2000) that suggested humans are more unstable in the ML than the AP direction, and also with experimental work that indicated increased metabolic cost for maintaining ML stability (Donelan et al. 2004; Dean et al. 2007).

Hobbelen and Wisse noted that one drawback to the ability of FM to reflect disturbance rejection, or the ability to not fall, is that FM look only at very small perturbations to a walker’s state space as opposed to the effects of real world disturbances (Hobbelen and Wisse 2007). While their study focused on modeling and robotic applications, their observation is also relevant to our study. Our FM results indicate that even small perturbations to our subjects during the perturbed walking conditions would cause their maxFM to increase significantly, particularly in the direction in which the perturbation was applied (Fig. 1). Thus, it appears that in humans being exposed to real world perturbations, FM do reflect an increased capacity to be disturbed during walking, or that they are more unstable. While we do presume that decreased stability leads to increased risk of falling, we did not test that directly in this study, since we did not apply perturbation large enough to induce falls. The direct connections to actual falls should be explored in future research.

Su and Dingwell (2007) demonstrated that a 2-dimensional biped model walking down a bumpy slope exhibited no significant changes in orbital stability as the irregularity of the walking surface was varied across the range of feasible perturbations. The present study is the first study to expose human subjects to similar continuous perturbations. Unlike Su and Dingwell (2007) however, we found that while humans did not become orbitally unstable while walking, they did experience significant increases in maxFM for C7 movements in the same directions in which the perturbations were applied, indicating that human stability was significantly affected by the perturbations (Fig. 1).

MaxFM results for ML movements demonstrated that the ML perturbations induced decreased orbital stability relative to NOP, while AP perturbations induced no changes in orbital stability (Fig. 1). This was anecdotally consistent with subjects’ perceptions, which were that the ML perturbations were more challenging conditions in which to walk. This is noteworthy because it further supports the possibility of maxFM as a clinically relevant measure of walking stability. Previous work suggests that maxFM measures might detect differences between age groups (Granata and Lockhart 2008; Kang and Dingwell 2008), but otherwise my not be sensitive enough for clinical use. The effective ‘dose-response’ relationship between perturbation magnitude and stability responses was not determined in this study, however. Such relationships should be explored in future studies for rehabilitation applications.

Subjects were locally unstable during all experimental conditions in this study including NOP. The ${\lambda }_S^{*}$ (Fig. 3) indicated direction-specific responses that were similar to those observed in the orbital stability results (Fig. 1), with the greatest responses being to those perturbations acting in the same directions as the movements analyzed. However, ${\lambda }_S^{*}$ indicated de creased stability during all perturbations relative to NOP. This finding supports previous work indicating that ${\lambda }_S^{*}$ is more sensitive than maxFM to changes in stability in both humans (Dingwell and Kang 2007) and dynamic walking models (Su and Dingwell, 2007). It is also consistent with the variability and gait parameter results of this study which indicated that gait parameters were affected during all perturbation conditions relative to NOP (McAndrew et al. 2010).

The increased maxFM and ${\lambda }_S^{*}$ indicated greater instability of participants during perturbed walking. However, during the perturbed walking trials, relative to walking normally, these subjects also exhibited decreased ${\lambda }_L^{*}$ (Fig. 4). One reason for this is that during the perturbed walking conditions, the MLD curves (Fig. 2) from which ${\lambda }_S^{*}\text{ and }{\lambda }_L^{*}$ are derived, generally shifted up and to the left. Because no subject fell down, the total magnitude of the divergence is expected to remain bounded. Therefore, as the MLD curves become steeper over the ${\lambda }_S^{*}$ range, it is no surprise that they also become flatter over the ${\lambda }_L^{*}$ range. Together, both changes indicate that subjects’ movements reached their maximum local divergence limits more quickly during perturbed walking. This is precisely what we observed.

This also suggests that choosing ranges other than 0–1 and 4–10 strides for calculating ${\lambda }_S^{*}\text{ and }{\lambda }_L^{*}$, respectively, might be more appropriate for the perturbed walking conditions. However, changing the ranges over which ${\lambda }_S^{*}\text{ and }{\lambda }_L^{*}$ are calculated would potentially confound attempts to make appropriate comparisons across conditions. Likewise, we emphasize that these ${\lambda }_S^{*}\text{ and }{\lambda }_L^{*}$ do not represent true “Lyapunov exponents” (Dingwell and Cusumano, 2000) and so assessing the degree of linearity of the fits to the MLD curves (Fig. 2) is less critical for our analyses. These ${\lambda }_S^{*}\text{ and }{\lambda }_L^{*}$ exponents calculated here still provide valid estimates of the average local instability observed over the ranges indicated. Our results thus imply that changes in ${\lambda }_S^{*}\text{ and }{\lambda }_L^{*}$ may exhibit an inverse relationship during perturbed walking.

The trends in the VT direction results for this study were notably different from those in the AP and ML directions. MaxFM and ${\lambda }_L^{*}$ both indicated increased stability for VT C7 movements during all perturbation conditions relative to NOP (Figs. 1 and 4). With respect to the latter, the results are similar to the AP direction ${\lambda }_L^{*}$ results. However, in this study we did not apply comparable perturbations in the VT direction and so the physical interpretation of these results is not immediately obvious. These changes likely resulted in some way from the mechanical coupling between the AP, ML, and VT movements of the C7 marker.

Defining an appropriate state space for performing orbital and local stability calculations is important (Gates and Dingwell 2009). Here, we used delay embedding (Dingwell and Cusumano, 2000) of the C7 velocity data. The perturbations applied in this study caused subjects to move around on the treadmill significantly. This introduced nonstationarities into their movements that made it inappropriate to use displacement coordinates as state variables (Dingwell and Marin 2006). Computing accelerations numerically from raw position data introduces significant noise, which is also problematic. Thus, for this experiment, using delay embedding of the velocity time series achieved the best balance between stationarity and noise in the resulting state spaces.

In conclusion, subjects experienced decreased orbital and short-term local dynamic stability in a direction-specific manner when walking during the continuous pseudo-random perturbations applied in the present study. Our results indicate that orbital dynamic stability can be influenced in humans by applying pseudo-random perturbations during walking and that these changes are consistent with subjects’ perceptions of which perturbation conditions are the most challenging in which to walk. Short-term local stability $\left({\lambda }_S^{*}\right)$ measures were more sensitive than orbital stability measures, but also detected strong direction-specific responses to perturbations. Conversely, long-term local dynamic stability $\left({\lambda }_L^{*}\right)$ appeared to improve during perturbations. However, this was consistent with the idea that when subjects do not overtly fall, their movements will remain at least loosely bounded and therefore so will the magnitudes of their resulting MLD curves (Fig. 2).