Anisotropic Elastic Network Modeling of Entire Microtubules

Abstract

Microtubules are supramolecular structures that make up the cytoskeleton and strongly affect the mechanical properties of the cell. Within the cytoskeleton filaments, the microtubule (MT) exhibits by far the highest bending stiffness. Bending stiffness depends on the mechanical properties and intermolecular interactions of the tubulin dimers (the MT building blocks). Computational molecular modeling has the potential for obtaining quantitative insights into this area. However, to our knowledge, standard molecular modeling techniques, such as molecular dynamics (MD) and normal mode analysis (NMA), are not yet able to simulate large molecular structures like the MTs; in fact, their possibilities are normally limited to much smaller protein complexes. In this work, we developed a multiscale approach by merging the modeling contribution from MD and NMA. In particular, MD simulations were used to refine the molecular conformation and arrangement of the tubulin dimers inside the MT lattice. Subsequently, NMA was used to investigate the vibrational properties of MTs modeled as an elastic network. The coarse-grain model here developed can describe systems of hundreds of interacting tubulin monomers (corresponding to up to 1,000,000 atoms). In particular, we were able to simulate coarse-grain models of entire MTs, with lengths up to 350 nm. A quantitative mechanical investigation was performed; from the bending and stretching modes, we estimated MT macroscopic properties such as bending stiffness, Young modulus, and persistence length, thus allowing a direct comparison with experimental data.

Introduction

The microtubule (MT) is a long protein filament composed of hundreds or thousands of tubulin dimers; together with actin and intermediate filaments, MTs make up the cell cytoskeleton, and strongly affect cell mechanical properties. Of all the cytoskeleton filaments, MTs exhibit the largest bending stiffness (1,2). A quantitative characterization of the role played by MT mechanical properties could strongly enhance the understanding of its biological functions.

At the molecular level, flexural rigidity depends on both the mechanical properties of the MT building blocks, i.e., the tubulin dimers, and on the intermolecular interactions holding dimers together in the MT lattice. While several experimental studies with atomic resolution have been carried out to better understand the relationship between tubulin structure and the monomers’ organization in the MT, there is still uncertainty over a number of issues, such as the dependency of bending stiffness and persistence length on the molecular structure (1,3–6).

To better understand MT mechanics and its implications in determining MT dynamics instability or cytoskeleton features, several approaches based on analytical or computational modeling have been applied, such as mechano-chemical models (7,8), molecular dynamics (MD) (9–14), finite elements approaches (3,4,11,15–17), and vibrational analysis (10,18–25).

In particular, MD is a powerful method which has been successfully employed to investigate the physical features of protein systems (10,26,27); however, at present, the computational cost of MD simulations limit their applicability to relatively small protein complexes (typically comprising ∼10⁵ atoms), hence much smaller than realistic MT fragments (comprising ∼10⁶ atoms). Fortunately, the spatio-temporal limitations of standard MD can be overcome by alternative simplified strategies. In particular, the elastic network model (ENM) (28) approach, in either the form of a Gaussian network model (29) or anisotropic network model (ANM) (30), has proved remarkably effective. Recent studies have demonstrated that methods based on ENM are particularly useful to: 1), explore the structural dynamics of biomolecules and their complexes; and 2), to extract the dominant modes of motion, thus determining the key functional sites (31–38) and investigate the mechanical properties of proteins (39–43). However, the application of the ENM approach to large molecular systems (such as MTs) can also become prohibitively expensive in terms of computational cost, so that more-efficient strategies are required. In the ENM framework, the representation of the molecular structure by the rotation-translation of blocks (RTB), i.e., the so-called block normal mode analysis (44–46), makes it possible to treat large molecular systems characterized by hundreds of thousands of residues, like the MTs.

In this study, a coarse-grain model of entire MTs, represented by an ENM, was developed. By combining data from MD and normal mode analysis (NMA) molecular modeling, we carried out a systematic investigation of MT mechanical properties. In particular, MD simulations were used to refine and optimize the conformation of tubulin monomers and their packing into the MT lattice. Then, NMA was performed to investigate vibrational properties of the MT modeled as an elastic network. MT mechanical properties, such as bending stiffness k_f (i.e., flexural rigidity), stretching stiffness k_s, torsional stiffness k_t, bending modulus, Y_f, stretching modulus, Y_x (i.e., Young's or normal modulus), and persistence length, l_p, were estimated on the basis of the bending and the stretching modes, and results were directly compared with experimental data (4–6,47,48). The model developed in this work provides:

• 1.A description of a significant fragment of MT (up to 1,000,000 atoms and hundreds of interacting tubulin monomers in the MT macrostructure);
• 2.A realistic evaluation of MT macroscopic mechanical properties, obtained considering the atomic structure at the molecular level, and directly comparable with experimental data.

Methods

Preparation of the microtubule structure

Tubulin dimers associate to build the microtubule structure (1) as depicted in Fig. 1 a. It is expected that the conformation of each dimer is influenced by interactions with surrounding dimers in the MT lattice. One should consider the MT (Fig. 1, a–c) as a periodic structure where

• 1.Sequences of αβ-tubulin monomers are repeated along each protofilament in longitudinal direction; and
• 2.Sequences of αα- or ββ-tubulin monomers are repeated along the MT circumferential direction (Fig. 1 b).

Figure 1.

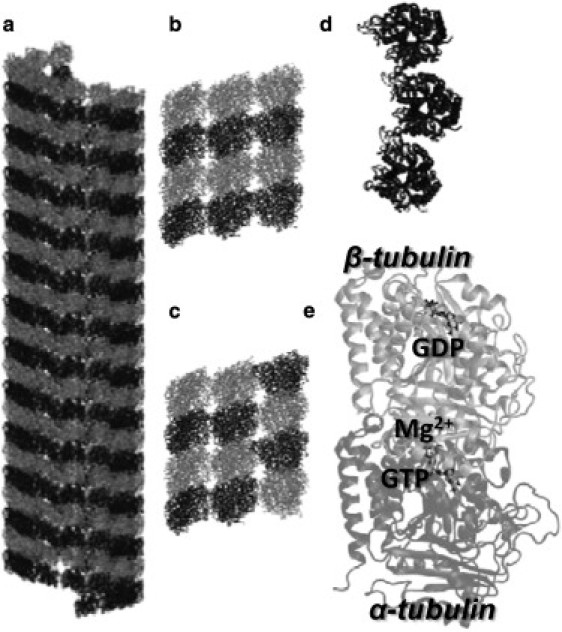
13:3 MT B-lattice. (a) Front view of an entire MT, where sequences of α-tubulin (dark shaded) and β-tubulin (light shaded) repeat along each protofilament in a longitudinal direction. (b and c) Atomistic tubulin-sheets: the standard tubulin-sheet models the standard interaction surfaces found in the MT lattice (b), while the seam tubulin-sheet models, specifically, the interaction in the seam region of the MT wall (c). (Note that, for a better view of the molecular systems, water molecules are not shown, even if present in the simulations.) Each all-atom tubulin-sheet consists of 12 monomers and ∼300,000 atoms. (d) Being representative of the MT wall, tubulin-sheets are curved following the curvature of the MT wall. (e) The αβ-tubulin dimer together with GTP, GDP, and Mg²⁺; this atomistic structure has been used as basic unit to model the tubulin-sheets for MD simulations.

The structure is completed by the presence of the MT seam, which is characterized by an αβ-interface for a B-lattice 13:3 MT (Fig. 1 c), i.e., an MT with 13 protofilaments and three start helices (2,49–51).

We have taken advantage of the MT structural symmetries and have performed MD simulations of MT wall cell units (Fig. 1, b and c), consisting of a central tubulin dimer completely surrounded by adjacent monomers, in both longitudinal and circumferential directions.

Each of these molecular systems, called the tubulin-sheet in the following, is representative of the MT wall, and will be used to optimize the atomic structure of the tubulin dimer.

The name “tubulin-sheet” recalls in some way the Zinc-sheet, a two-dimensional crystalline structure in which tubulin monomers polymerize in the presence of Zn²⁺ ions, when stabilized with a taxomere such as Taxol. The Zinc-sheet is flat and composed of antiparallel protofilaments resulting in a structure which is markedly different with respect to the MT arrangement. For their high stability during crystallographic analyses, Zinc-sheets were used for determining the atomic structure of the αβ-tubulin (52). The tubulin-sheets considered in this work strongly differ from the Zinc-sheet structures in two main conformational characteristics:

• 1.Tubulin-sheets are curved (Fig. 1 d) following the curvature of the MT wall (2); and
• 2.Tubulin monomers in tubulin-sheets are arranged in parallel protofilaments, thus representing a periodic cell of the MT wall.

Given that tubulin-sheets are systems of tubulin monomers, the first step of this study has been the choice of the αβ-tubulin atomic structure. The αβ-tubulin atomic structure was obtained with a resolution of 3.7 Å by Nogales et al. (52) using electron crystallography; the structure is available on the RCSB Protein DataBank (1TUB code). Several initial refinements of the 1TUB tubulin atomic structure were carried out. Specific details and motivations for choosing 1TUB with respect to other available tubulin dimer atomic structures and the followed refinement procedure are reported in the Supporting Material. The refined tubulin dimer atomic structure (Fig. 1 e) contained atomic coordinates for: α-tubulin monomer, guanosine-5′-triphosphate (GTP), Mg²⁺ ion, β-tubulin monomer, and guanosine-5′-diphosphate (GDP).

Despite containing a complete description of the tubulin dimer, the 1TUB crystallographic structure from the Protein DataBank (either plain or refined by removing taxol and adding Mg²⁺ ion) is not suitable to be docked in an MT lattice (53). In particular, when forming the MT lattice (2), 1TUB α-monomers showed interlocking loops between adjacent monomers in the lateral surface. The interlocking loops are identified as the M-loop of one monomer and the H1-B2 loop in the adjacent monomer. Given that the interaction between the M-loop and the H1-B2 loop represents the most important interaction surface for the lateral contacts between α-monomers, the entire α-tubulin H1-B2 loop was remodeled using the software MODELLER (54) combined with a simulated annealing procedure. A detailed description of the H1-B2 loop remodeling is reported in the Supporting Material.

To obtain a correct positioning of tubulin monomers in the MT lattice structure, and thus a proper curved conformation of the tubulin-sheets, the remodeled (see the Supporting Material) tubulin dimer has been docked onto a 13:3 MT model (2). From this starting MT structure, composed of dimer structures, we were able to extract all the tubulin-sheet conformations.

In particular, two different configurations of the tubulin-sheet were built:

• 1.The standard tubulin-sheet (Fig. 1 b), i.e., the periodic unit of tubulin monomers taken from a generic part of the MT lattice, far from the seam area; and
• 2.The seam tubulin-sheet (Fig. 1 c), which models the seam area. Given that the tubulin-sheets represent part of the MT wall, they are curved following the MT curvature (Fig. 1 d) (2).

The tubulin-sheets consisting of 12 tubulin monomers each were then assembled and surrounded by water molecules and counterions; the final sheet models comprise ∼300,000 atoms each.

Given that the tubulin dimer is a compact ellipsoid of ∼4.6 × 40 × 65 nm (width, height, and depth, respectively) (51) and assuming a cutoff distance for the nonbonded interactions of 1.2 nm, the central dimer of the tubulin-sheet models will experience the same interactions as inside the MT lattice (Fig. 1, b and c) while the surrounding monomers will be affected by direct interaction with the solvent.

Equilibrium MD simulations on both standard and seam tubulin-sheets were run for 10 ns at 300K in the NVT ensemble. During the MD equilibration, a constraint was applied to the center-of-mass of each of the monomers surrounding the central dimer. Details on the MD scheme carried out are reported in the Supporting Material.

The output structures of the central dimer from the atomistic MD simulations of the standard and the seam tubulin-sheet have been used to create the whole atomic structure of the 13:3 MT (Fig. 1 a and Fig. 2 a), subsequently employed in the NMA.

Figure 2.

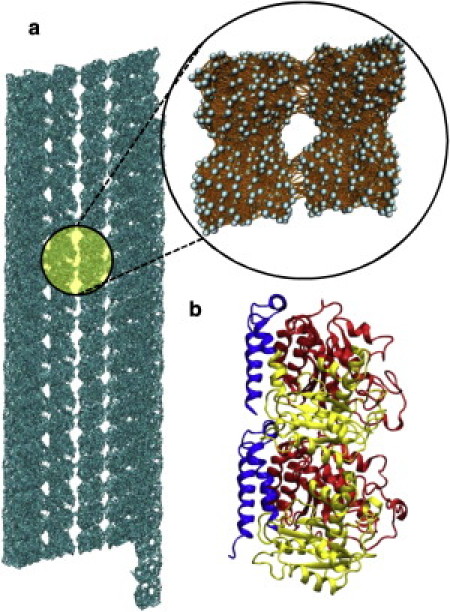
(a) Elastic network model of the MT. A whole MT is shown (left); MT geometry corresponds to the 13:3 MT B-lattice structure (2). The detail highlighted (circle, and zoomed on the right), shows two interacting tubulin dimers belonging to adjacent protofilaments. (Spheres) C_α-atoms. (Sticks) Bonds among the atoms, which are closer than the cutoff distance set equal to 1.2 nm. (b) Three main functional domains in the tubulin monomers: the Rossmann fold, the intermediate domain, and the C-terminal domain (52). Each domain is considered as a rigid block in the RTB approach.

Normal mode analysis of entire microtubules

For NMA to be carried out, the whole MT has been modeled as an anisotropic ENM (29). Each tubulin residue is represented by a node located at the position of each C_α-atom. Nodes closer than the cutoff distance (1.2 nm) were connected by springs (Fig. 2 a). Standard anisotropic ENM cutoff distances reported in literature, determined by comparison with experimental data (55), vary between 1.2 and 1.5 nm.

The total potential energy V_MT of the MT structure was expressed using the anisotropic network model (ANM) formulation (55),

$$V_{MT}=\frac{1}{2}\mathbf{\Delta }{r}^T\mathbf{H}\mathbf{\Delta }r\text{,}$$ (1)

where Δr is the 3N-dimensional vector describing the fluctuations Δr_i of the position vector r_i for the node i (1 ≤ i ≤ N), and H is the Hessian matrix, the 3N × 3N matrix of the second derivatives of V_MT with respect to the mass-weighted coordinates. N is the number of particles (C_α-atoms) in the molecular system.

In standard methods, the normal modes of a system are obtained by diagonalizing the Hessian matrix H. The large number of C_α-atoms (>50,000) in the ENM of the MT requires the use of the RTB approach for a cost-effective treatment of H (44–46). In this method, the system is divided in n_b rigid blocks; each block is made of a certain number of residues (each represented by C_α-atoms) considered as a rigid body. The deformation of the whole system is given by rotation-translation movements of the rigid blocks (45). A more detailed explanation of the RTB method is reported in the Supporting Material.

To reduce the number of blocks in the whole MT structure, three rigid domains were identified in each tubulin monomer, representing the three functional domains of the protein as determined by Nogales and co-workers (52) (Fig. 2 b): the Rossmann fold, from the N-terminal (residue 1) to residue 205; the intermediate domain, from residue 206 to 381; and the C-terminal domain, from residue 382 to the C-terminal (residue 440 for α-tubulin and residue 427 for β-tubulin). A correspondence between the functionally defined domains and their dynamics has been also confirmed by a further computational study (10).

The eigenvectors, e_vi, obtained by using the RTB approach, describe the modes of free vibration accessible to the structure in its own native conformation, while the eigenvalues, λ_n, determine the frequency of the mode. To investigate the dependency of the MT mechanical properties on MT length, we assembled MTs with lengths ranging from 100 nm (ENM composed by roughly 150,000 C_α-atoms) to 350 nm (ENM composed by roughly 450,000 C_α-atoms). The trajectory for each mode was generated starting from λ_n and e_vi by means of an in-house FORTRAN77 code. For each mode n, a sinusoidal oscillation around the equilibrium position, r_i,min, was generated to obtain the new positions r_i of every i^th C_α-atom. The oscillation was modulated by e_vi with a selected amplitude (B) using the equation

$$r_i\left(t\right)=r_{i,\min }+B{e}_{vi}\sin \left({\omega }_{n}t\right)\text{,}$$ (2)

where ω_n is the angular frequency, directly related to the eigenvalue λ_n of a specific mode as

$${\omega }_n=\sqrt{\gamma {\lambda }_n}\text{,}$$ (3)

where γ is the elastic constant of the springs connecting the C_α-atoms in the ENM, equal to 1 kcal/(mol Ų) (55). The calculated vibration normal modes and the related frequencies can be related to the filament mechanical properties by applying the linear elastic beam theory (40,41,43).

Details and main formulas used to derive the mechanical properties from the normal modes have been reported in the Supporting Material.

Results

Molecular dynamics on curved standard and seam tubulin-sheets

A measure of the conformational changes of a structure is given by the root-mean-square deviation (RMSD). Fig. 3 a displays the RMSD time history of the central tubulin dimer in both standard and seam tubulin-sheets; equilibration of the tubulin dimer is achieved at ∼4000 ps, when the value of the RMSD reaches an approximately constant value of ∼0.25 nm for both the tubulin-sheets.

Figure 3.

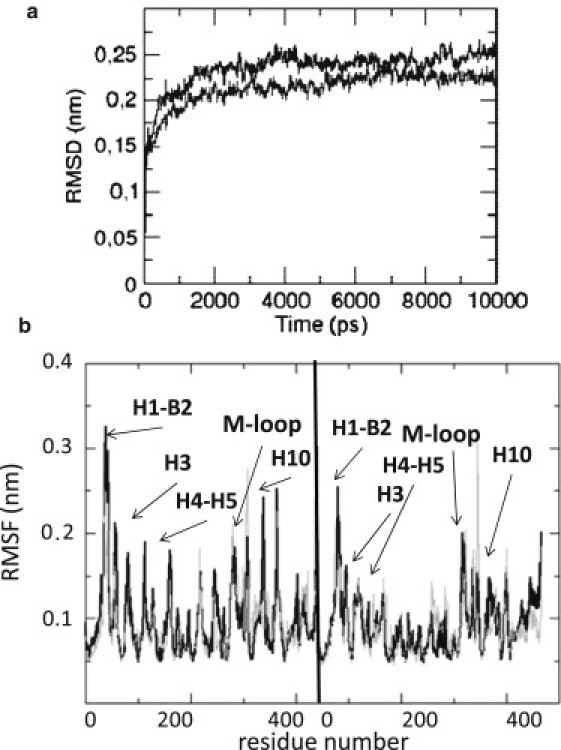
(a) RMSD of the C_α-atoms of the central tubulin dimer for the standard tubulin-sheet (dark shaded) and the seam tubulin-sheet (dashed). An equilibrium value of ∼0.25 nm is reached after 4000 ps in both cases. (b) RMSF of C_α-atoms of the central tubulin dimer in the case of standard sheet (dark shaded curve) and seam sheet (dashed shaded curve). The main differences are noticeable in specific regions involving lateral interactions (which are different in standard and seam sheet) for both α- and β-tubulin.

Root-mean-square fluctuation (RMSF) plots show differences mainly in peripheral areas of the central tubulin dimer of both tubulin-sheets (Fig. 3 b). In particular, considering the α-tubulin monomer, the H1-B2 loop (residues 35–45 and 50–60) and H4-H5 loop (residues 150–170), which are involved in lateral contacts, show marked peaks for both standard and seam tubulin-sheets. The first part of helix H3 (residues 110–120), involved in longitudinal contacts, shows RMSF values in the standard sheet (at ∼0.2 nm) higher than those obtained in the seam sheet (at ∼0.1 nm). Again, helix H10 (residues 330–340), which is involved in longitudinal and lateral contacts, shows a peak at ∼0.3 nm only in the case of the standard tubulin-sheet. No differences between standard and seam tubulin-sheets are detected for the M-loop. Concerning the β-monomer, the same behavior is detected for H1-B2 loop, while helix H3 and the H4-H5 loop results more stable, showing lower RMSF values, with respect to the α-monomer. Moreover, the M-loop shows a higher stability in the β-monomer rather than the α-monomer. A peak in the region around residues 300–310 is detected in both the α- and β-monomer of the central dimer of the seam tubulin-sheet, which is not present in the standard tubulin-sheet (Fig. 3 b).

Normal mode analysis of entire microtubules

From the generated trajectories, four main modes are identified (Fig. 4, a–d): stretching (Fig. 4 a), longitudinal bending (Fig. 4 b), torsion (Fig. 4 c), and circumferential bending (Fig. 4 d). All the other observed trajectories can be considered as a composition of these four main modes.

Figure 4.

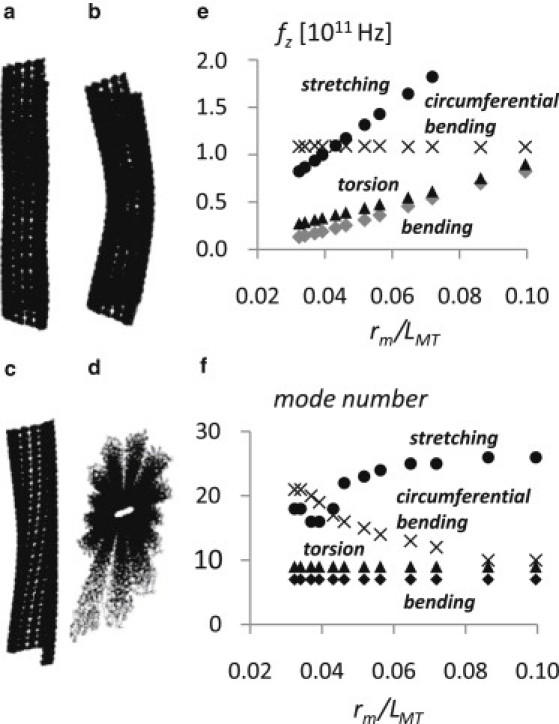
Major modes detected by means of NMA simulations for the MT. Stretching (a), longitudinal bending (b), torsion (c), and circumferential bending (d). (e) Frequency as a function of the ratio between the mean radius with respect to the length of the MT, r_m/L_MT, for longitudinal bending (shaded diamonds), stretching (solid circles), torsion (solid triangles), and circumferential bending (crosses) modes. In each case the mode frequency is found in the range 1 × 10¹⁰–2 × 10¹¹ Hz. The circumferential bending is characterized by a roughly constant value with respect to L_MT. (f) Mode number (i.e., frequency rank) with respect to r_m/L_MT. For each length the longitudinal bending mode is the seventh mode; the torsion mode is the ninth mode independently of the MT length. The mode number changes for the stretching modes, increasing as the ratio r_m/L_MT increases (i.e., MT length decreasing), while the mode number for the circumferential bending shows an opposite trend. At approximately a r_m/L_MT value of 0.5 the mode number curve of stretching modes crosses that of circumferential modes, indicating that as the MT length increases, the circumferential bending frequency becomes higher, and, thus, its amplitude reduces. Conversely, as r_m/L_MT approaches zero, amplitude for stretching modes becomes more important.

It is noticeable that in the case of the bending, stretching, and torsion modes, the mode frequencies decrease as a function of the length, while in the case of circumferential bending, the mode frequency shows to be almost constant, just slightly increasing (Fig. 4 e). Mode frequencies are calculated in the order of 10¹⁰–10¹¹ GHz (<10 cm⁻¹), in accordance with previous computational studies on MT vibrations (18–20,56).

The mode number is assigned according to its frequency (Fig. 4 f). Note that the seventh mode is the first nonrigid mode. Our results obtained from NMA simulations show that the longitudinal bending oscillation mode corresponds to the first nonrigid mode (seventh mode) for each simulated MT length, L_MT. Torsion modes are found at the ninth mode, independent of the L_MT value. In turn, in the case of the stretching and the circumferential bending oscillations, the mode number shows marked dependency on the ratio r_m/L_MT and consequently on the MT length. In the case of circumferential bending, the mode number decreases as the ratio r_m/L_MT increases.

The mode number for stretching modes (the one at highest frequency among the four main modes under investigation) decreases with the increase of L_MT (Fig. 4 f).

From longitudinal bending, stretching, and torsion modes, mechanical parameters such as bending stiffness k_f, bending modulus Y_f, persistence length l_p, stretching stiffness k_s, stretching modulus Y_x, shear modulus G, and torsion stiffness k_t, are estimated.

The k_f value estimated from NMA analyses ranges between 4 × 10⁻²⁴ and 9 × 10⁻²⁴ Nm² (Fig. 5 a) increasing with L_MT (Fig. 5 a).The l_p values are calculated in the range from 0.8 to 2 mm, showing a strong dependence on L_MT (Fig. 5 b).

Figure 5.

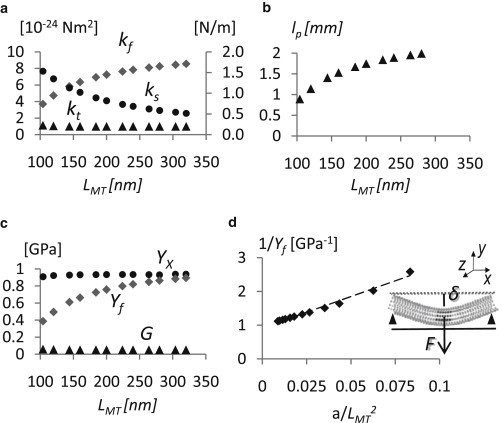
(a) Data showing the relationship among the bending stiffness k_f (diamonds), stretching stiffness k_s (circles), torsion stiffness k_t (triangles), and the MT length, L_MT. The values k_t remain constant with respect to L_MT, while k_f increases and k_s decreases when MT length rises. (b) Relation between the persistence length l_p (triangles) and L_MT. A strong dependence of l_p on the MT length is noticeable. (c) Bending modulus Y_f (diamonds), stretching modulus Y_x (circles), and shear modulus G (triangles), directly obtained by torsion stiffness versus L_MT. The Y_f values markedly increase with the MT length, approaching the value of Y_x (∼1 GPa) for L_MT at ∼300 nm. The G-value is constant and roughly equal to 0.05 GPa, i.e., two-orders-of-magnitude less than the Young's modulus Y_x. (d) Inverse of the bending modulus 1/Y_f, with respect to the constant a/L_MT², where a is equal to 12f(I/A) and f is a geometric factor equal to 1.38 in case of a hollow cylinder. The linear regression gives directly the value of Y_x as the inverse of the y intercept of the fitting curve (Y_x = 1.1 GPa), while G is the inverse of the slope of the curve (G = 0.05 GPa). A graphical description of the MT bending test is also reported; the MT is supported at the free ends and deflected, δ, by a concentrated force, F, acting in the middle.

The k_s values show an opposite behavior with respect to k_f, decreasing with L_MT from 1.5 N/m to 0.5 N/m, while k_t versus L_MT showed a constant value of ∼1 × 10⁻²⁴ Nm² (Fig. 5 a).

The behavior of Y_f, Y_x, and G, as a function of L_MT, are shown in Fig. 5 c. While Y_x and G values show a clearly constant behavior at ∼1 GPa and 0.05 GPa, respectively, the Y_f values depend markedly on the L_MT values ranging from 0.3 to 1 GPa, approaching the Young's modulus value for MTs longer than 250 nm. The Y_f behavior follows the same trend shown for k_f (Fig. 5, a and c).

Discussion

Molecular dynamics on curved standard and seam tubulin-sheets

The results of the MD simulations show similar RMSD curves for tubulin dimer inserted in standard or seam tubulin-sheet. However, it should be remembered that the RMSD of a protein (throughout the MD simulation) gives information about the changes of the overall protein fold. If no major fold changes happen, the RMSD value is quite stable and converges quickly to an equilibrium value. This behavior does not exclude local changes during the simulation.

In particular, tubulin monomers are proteins with a very stable central core, while external surfaces are mainly composed by high flexible loops (as H1-B2 loop) and α-helices (9,12). While the tubulin structure is just slightly modified in its overall conformation, the greatest fluctuations concern the outer surfaces, which are composed of only a few amino acids. These outer-surface regions are known to be associated with monomer-to-monomer interactions that affect the overall MT mechanical properties and play a role in MT dynamic instability (4,9,20,21,57–60).

Indeed, results from RMSF analysis show differences between standard and seam tubulin-sheet. In particular, large fluctuations are detected in regions involved in lateral contacts (e.g., H1-B2 loop and M-loop). These findings are in agreement with experimental evidences (53) and previous computational investigations (9,36). Concerning the M-loop, we found a RMSF value lower than that reported by Keskin et al. (36). This difference is reasonably due to the boundary conditions applied for analyzing the tubulin dimer, which in the Keskin work (36) is not surrounded by neighbor monomers. In our case, where the tubulin monomer is constrained by the presence of other monomers, the fluctuations of the M-loop are limited and also driven by the movements of other interacting regions, such as the H1-B2 loop. Finally, fluctuation results highlight a remarkable peak in RMSF only in a well-defined region of the tubulin dimer in the seam sheet, between the M-loop and helix H10, which is located on the external lateral surfaces of the monomer. Interestingly, this region is stable in the standard tubulin-sheet in agreement with previous works (9,36). These previous studies were focused on standard lateral interactions (αα, and ββ), so the marked peak detected in our MD simulations for the seam tubulin-sheet could not have been highlighted before. The position of this loop suggests a possible mechanism caused by the change of the lateral interface at the seam, which could have a role in determining the greater instability of the seam with respect to the other regions of the MT wall. Further investigations are needed to better elucidate the reasons for this instability mechanism.

Based on the above observations, it is clear that equilibrium MD simulations of tubulin-sheets (periodic regions of the MT wall) resulted in local changes of the topology that affect the definition of the elastic network used to model the entire MT.

Normal mode analysis of entire microtubules

The vibrational frequencies predicted for bending, stretching, torsion, and circumferential bending are in agreement with previous studies (17–19,21,56) investigating the vibrational properties of MTs. In particular, in all cases, a dependence of the vibrational modes on the MT length has been noted (Fig. 4 e). In particular, the frequency for longitudinal bending, stretching, and torsion linearly decreases as the ratio r_m/L_MT decrease. This means that as the MT becomes longer, the longitudinal bending, stretching, and torsion modes present larger amplitudes and become dominant in the MT dynamics. This behavior is particularly noticeable for the frequency of the stretching modes, which show the greatest slope.

Conversely, the frequency for circumferential bending slightly increases (Fig. 4 e) as the r_m/L_MT decreases. In Fig. 4 f, the same information is given by plotting the mode number (the rank of vibrational mode in order of frequency) as function of r_m/L_MT. The opposite frequency tendency for stretching and circumferential bending modes makes the two curves intersect for a ratio r_m/L_MT of ∼0.5, which corresponds to an MT length of ∼250 nm.

Circumferential bending is controlled by the circumferential bending stiffness that is directly dependent on the weak lateral interactions (4,9,20,21,24,57–60). Previously, circumferential vibration has been extensively studied by Wang and co-workers (23,24), who developed an orthotropic elastic shell model for studying MT buckling. Our results are in close agreement with their findings, showing that the frequency of circumferential modes specifically depends on the MT radius; the frequency increases as the MT radius decreases.

Moreover, our results are in line with findings of de Pablo et al. (15) and Schaap et al. (16). By means of radial indentation AFM experiments (supported also by computational modeling investigations), it was demonstrated how MT mechanics, and in particular the response to deformations given by longitudinal bending and radial indentation, is dominated by different parts of the MT structure. Response to bending is dominated by protofilaments, while response to radial indentation is dominated by localized connection between protofilaments. Our results suggest that when MTs are very short, longitudinal bending can be strongly influenced by circumferential bending (large amplitude modes are detected for high r_m/L_MT ratios), which causes localized or uncontrolled buckling.

Concerning stretching modes, it is interesting to note that stretching stiffness is length-dependent, as expected, decreasing as the MT length increases. If we think of the MT as a structure composed of rings of tubulin dimers arranged in a head-to-tail fashion to form the whole MT lattice, we can understand this behavior. Each tubulin ring can be modeled as a spring showing a certain stretching stiffness. By modeling the entire MT as a harmonic oscillator (a single spring), its elastic constant, k, will be given by the series of the springs representing each ring (11–13). The same example can also be used to justify our findings regarding the stretching vibration mode, which changes rank as the MT length increases (Fig. 4 f). When the MT length increases, the MT mass, m, increases. Considering the MT as a harmonic oscillator, its vibration frequency will be related to the square-root of k/m value.

Concerning the bending modes, the results obtained in terms of k_f (4 × 10⁻²⁴ and 9 × 10⁻²⁴ Nm²) and l_p (0.8–2 mm) are consistent with previous experimental data (4–6,47,48) describing MTs as very stiff rods with an l_p of approximately millimeters (0.5–8 mm obtained for taxol-stabilized MTs). For nonstabilized MTs, k_f ranges from 4.7 10⁻²⁴ (61) to 3.4 10⁻²³ Nm² (62), while k_f of taxol-stabilized MTs is between 1.9 × 10⁻²⁴ (61) and 2.15 × 10⁻²³ Nm² (6).

Owing to the ability of NMA to separate vibration modes, values of Y_x and G are directly obtained by stretching and torsion modes. Calculated values for Y_x ≈ 1 GPa and G ≈ 0.05 GPa corroborate the experimental evidence that MTs are highly anisotropic structures. Given their cylindrical shape and their structural organization in protofilaments, MTs might be better modeled as transversely isotropic structures (5), thus implying that the transverse Young's moduli (in the cross-section plane) are equal, and are different from the longitudinal Young's modulus, Y_x. The bent structure of the MT as obtained by the trajectory of the first bending mode can be considered as a beam supported at the free ends and deflected (bent in a plane) by a concentrated load acting in the middle (Fig. 5 d).

Following the Timoshenko beam theory, the bending deflection, δ, is given by the sum of the contribution due to the pure bending, determined by Y_x, and the pure shear, governed by G (4,5). Thus, the inverse of the longitudinal bending modulus, Y_f, calculated from the bending modes is

$$\frac{1}{Y_f}=\frac{\left(12f\frac{I}{A}\right)}{L_{MT}}\frac{1}{G}+\frac{1}{Y_x}\text{.}$$ (4)

Fig. 5 d displays 1/Y_f as a function of a/L_MT², where a is the constant factor depending on the MT geometry equal to the term in brackets in Eq. 4, and f is equal to 1.38 in the case of a hollow cylinder. I is the moment of inertia of the cross-sectional area with respect to the corresponding axis of deflection, which is ∼1 × 10⁻³² m⁴ for a 13:3 MT; A is the cross-sectional area of the filament (which in the case of 13:3 MT is ∼1.8 × 10⁻¹⁶ m²), and L_MT is the filament length.

By using the approximation of a transversely isotropic structure for the MT, a value of Y_x of ∼1.1 GPa, and a value of G of 0.05 GPa are obtained.

The dependency of Y_f, k_s, and hence l_p on the MT length, and our results about Y_x and G characterized by a difference of two orders of magnitude, are findings in agreement with previous investigations of MT mechanical properties (3,4,17). The results indicating a length-dependent k_f and consequently a length-dependent l_p are interesting, although this is certainly a still-controversial issue in the literature. In particular, the low G-value has been attributed to the weak lateral interaction among protofilaments. For short MTs (hundreds of nm), the sliding between adjacent protofilaments is relevant during MT bending (4). Conversely, very long MTs (several μm) are more rigid and Y_x completely dominates the mechanical behavior because only a slight sliding occurs between adjacent protofilaments during bending (6). This mechanism has been used to explain results coming from the numerous experimental and computational investigations, where a ratio between Y_x and G between 10² (4) and 10⁶ (5) was found. In particular, in the study of Kis et al. (4), the elastic deformation of MTs bound to a surface with holes of different sizes was directly measured with AFM. The results, obtained using the Timoshenko approach and measuring the deflection of an indented MT simply supported at its ends, showed a significant difference between Y_x (100 MPa) and G (1.4 MPa), as a consequence of the MT anisotropy. Even if the Timoshenko approach has been adopted, the effective Y_x value seems to be far from the values widely associated to the MT in literature (Y_x ≈ 1–2 GPa (5,6,23)). On the basis of our results we can infer that for MTs with a very short contour length (as for the ones investigated by Kis et al. (4)), circumferential bending should not be neglected given that, at this MT length, it strongly affects the overall mechanics of the MT.

A high Y_x/G ratio (∼10⁶) is reported by Pampaloni et al. (5), who adopted a single-particle tracking method to investigate thermal fluctuations of grafted MTs. The MT has been modeled as a beam curved in a plane with constant curvature and deflection calculated on the basis of this hypothesis. However, this is a rude approximation given that, for an MT filament vibrating under thermal motion, we expect more-complex three-dimensional deformations. Even though the MT is deflected on a plane, MT fluctuations under thermal forces should be seen as a composition of deformations given by bending, stretching, and torsion modes, which altogether are responsible for the accounted deflection. Overestimations of the deflection values could yield an excessive Y_x/G ratio.

In our study, the vibration analysis gave us the possibility to

• 1.Separate modes, avoiding interferences given by superposition of vibration modes.
• 2.Apply the Timoshenko approach considering the MT as a beam constrained at the free ends and bent in a plane.

In this way we were able to obtain results in terms of Y_x at ∼1 GPa and G of ∼0.05 GPa, with different methods (e.g., directly from the stretching and torsion modes or by using the Timoshenko approach). It is also important to notice that under the assumption of transverse isotropy, Y_x and G are not linked by the Poisson relationship G = Y_x/2(1+ν). Hence, a large Y_x/G ratio does not imply a value of the Poisson number ν > 1/2, which would reveal a collapse of the cross-section in bending condition, and would assume a nonphysical meaning (5).

A last observation is related to many recent findings suggesting that proteins or molecules interacting with tubulin dimers (as tau proteins) assembled in the MT lattice, can influence the overall MT mechanics. This was demonstrated for Taxol generally used to stabilize MTs in the in vitro experiments (6,9,16,53,64), which binds β-tubulin in a region close to M-loop and strengthens the interaction between adjacent protofilaments. In this study the effects of Taxol has not been taken into consideration. Given that our ANM models are very simple, just including extra interaction sites to capture the effect of Taxol is unlikely to make much difference. However, the Taxol might affect the tubulin monomers arrangement and their packing in the MT structures. These features are captured by MD simulations (9,65), and hence, they could also have an influence on the mechanical properties at the level of the ENM of the whole MT. Effects of Taxol have been investigated by Sept and MacKintosh (65). In their work, a coarse-grain method for connecting MD simulations to continuum mechanics was developed and applied to MT mechanics. Although a relatively small simulated molecular system (six interacting monomers modeling a portion of two interacting filaments), their coarse-grain model was able to provide significant information on dimer-dimer spacing in the presence of the Taxol molecule, and data on MT mechanical properties in term of bending stiffness, Young's modulus, and shear modulus, in good agreement with experimental observations (65). Further developments could be addressed by considering other MT binding molecules and by better describing the molecular aspects of these interactions and their effects on MT mechanical behavior (based, for example, on the approach applied in this article).

Conclusions

In this work, a highly coarse-grained model of the entire MT built as an ENM has been developed. Starting from the atomic structure of the tubulin dimer, and from information available on the tubulin hierarchical organization in the MT lattice wall, a whole MT with length of approximately hundreds of nanometers has been modeled. MD simulations were conducted to refine the molecular conformation and the packing of the tubulin dimers (the MT building blocks) inside the MT lattice structure. The vibrational normal modes have been calculated by means of NMA, considering the MT as an ENM where only C_α-atoms are considered. Owing to the significant computational effort required, the Hessian matrix representing the whole MT has been treated by means of the RTB approach. In particular, each tubulin monomer has been considered as composed of three rigid domains, each representing one of the well-known functional domains of the tubulin monomer. By analyzing the modes of vibration, we calculated fundamental mechanical properties, such as the flexural rigidity, the bending modulus, the stretching stiffness, the elastic normal modulus (i.e., the Young modulus), and the persistence length. The close agreement with previous experimental data and computational studies allowed us to infer some points of discussion on the still open debate about MT anisotropy.

As a final remark, it is necessary to point out one of the most important novelties of this work with respect to previous investigation: contrary to other computational studies (generally modeling at continuum level the MT) (3,4,7,8,15–25), this MT coarse-grain approach is able to provide a detailed description of the MT mechanics based just on the knowledge of the atomic coordinates of the tubulin dimers and their arrangement into the MT lattice being able to reproduce mechanics of the MT with a very high degree of accuracy.