Multiscale Complexity in the Mammalian Circadian Clock

Summary of Recent Advances

The field of systems biology studies how the interactions among individual components (e.g. genes and proteins) yield interesting and complex behavior. The circadian (daily) timekeeping system in mammals is an ideal system to study complexity because of its many biological scales (from genes to animal behavior). A wealth of data on each of these scales has recently been discovered. At each scale, modeling can advance our understanding of challenging problems that arise in studying mammalian time-keeping. However, future work must focus on bridging the multiple spatial and temporal scales in the modeling of SCN network. Here we review recent advances, and then delve into a few areas that are promising research directions. We also discuss the flavor of modeling needed (simple or detailed) as well as new techniques that are needed to meet the challenges in modeling data across scales.

Introduction

Circadian (∼24-hour) rhythms are universally found in almost all living organisms, with proper circadian timekeeping being essential for survival. Circadian malfunctioning has been linked with many diseases including heart attacks, cancer, diabetes and sleep disorders [1]. An interesting example of how circadian timekeeping can affect human health is Familial Advanced Sleep Phase Syndrome, where a change in a single nucleotide in the individual's genes can cause members of certain families to rise early in the morning [2,3]. This connection from genes to behavior has been seriously studied ever since the PERIOD (PER) locus was discovered [4] as a regulator of the daily rhythms of Drosophila. Thus, for the past 40 years, circadian research has been a model system for studying how cellular and genetic events can regulate behavior of entire organisms.

From its inception, circadian timekeeping has been an interdisciplinary field, including geneticists, on one end, to psychologists on the other (with nearly every biological discipline in between). Many theorists and quantitative modelers have also contributed to the field [5]. At least two of the three founders of the field (Aschoff and Pittendrigh) collaborated with modelers who used differential equations (the mathematical descriptions of how systems behave with time). This connection continues in the present day. Theorists have written and contributed at least 600 papers in this field. A casual review of the literature clearly indicates that there is now a renewed interest in theoretical chronobiology [6]. Thus it is not difficult to extrapolate a large role for theorists in the future of circadian biology.

At its inception, chronobiology defined the key principles of circadian rhythms including autonomous rhythmicity (the fact that rhythms were endogenous), entrainment (the ability to match rhythms in the external world) and temperature compensation (the ability to keep accurate time at different temperatures). The earliest mathematical models of circadian clocks were simple and reflected the dearth of experimental knowledge at the cellular level. Thus, most modeling focused on ‘phase-only’ models whose behavior can be described by a phase response curve (PRC). Winfree [7] later showed how mathematical models of time-keeping should also consider amplitude.

These ideas are still relevant today. However, the discovery of PER launched the beginning of the molecular age of circadian rhythms research. This molecular approach is of particular interest for systems biologists since it promises a potential mechanistic explanation for the 24-hour rhythms of life.

And then things got complicated …

Drosophila PER lead to the discovery of mammalian PER1, PER2 and PER3. These bind with CRYPTOCHROME (CRY) 1 and CRY2 to repress transcription activated by heterodimers of BMAL1 or BMAL2 and CLOCK (CLK) or NPAS2. While some of these proteins were initially considered redundant, later work showed each having a distinct function(e.g. PER1 KO mice can show circadian rhythms while PER2 KO mice do not; CRY1 KO mice have an short period phenotype whereas CRY2 KO mice have a long period phenotype). The behavior of the complexes of these proteins is highly dependent on phosphorylation (not to mention acetylation, methylation, and sumolation). The key kinases including Casein Kinase I (CKI) ε and CKIδ trigger degradation by proteins like F-box/LRR-repeat protein 3 or β-transducin repeat-containing protein and other cellular events [1]. Phosphorylation sites are numerous [2,8] and single nucleotide changes can have dramatic effects. Furthermore, modeling has barely touched the combinatorial complexity resulting from molecular interactions. For example, figure 1 illustrates this complexity in PERIOD protein phosphorylation: this phosphorylation can occur in a specific sequential manner as shown in figure 1a, or independently as shown in figure 1b.

Figure 1.

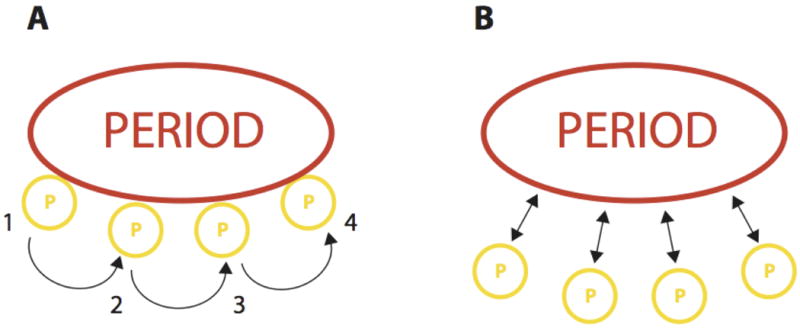
A key regulator of circadian (∼24-hour) rhythms is the phosphorylation of the PERIOD proteins. There are many possible phosphorylation sites on PERIOD,. Moreover we do not know whether phosphorylation occurs sequentially (as in A, where each site has a specific order in which it is phosphorylated on the PERIOD protein, i.e. ordering is important) or independently (as in B where any site can equally be phosphorylated since there is no ordering or preference to the phosphorylation sites on the PERIOD protein). The latter case illustrates the combinatorial complexity which may require serious consideration in the modeling of circadian rhythms.

A quick estimate of the possible complexes (some of which are pictorially represented in figure 2) among these aforementioned twelve core clock proteins, is 2¹² = 4096. While this number includes several complexes that do not occur experimentally, it underestimates the total number of relevant complexes when the various phosphorylation states of the proteins are considered, reinforcing this motif of combinatorial complexity. Moreover, we do not count the additional feedback loops (e.g. Rev-erbα) which interact with the main clock loop. Furthermore, this estimate does not begin to consider other important cellular processes that interact with the circadian clock, as illustrated in the top panel of figure 3: transcription regulation, translation, degradation, cell division, electrophysiology and metabolism. All these processes have been shown to have a strong influence on the circadian clock [9-18] and some have argued strongly that they are an integral part of the timekeeping mechanism.

Figure 2.

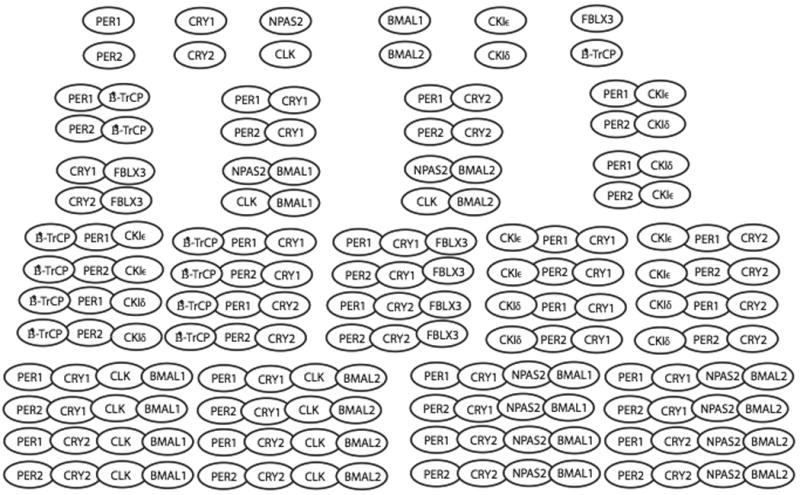
The following key proteins in the mammalian circadian clock (PER1, PER2, CRY1, CRY2, NPAS2, CLK, BMAL1, BMAL2, CKIε, CKIδ, FBXL3 and β-TrCP) can be formed to form many macromolecular complexes, some of which are illustrated here.

Figure 3.

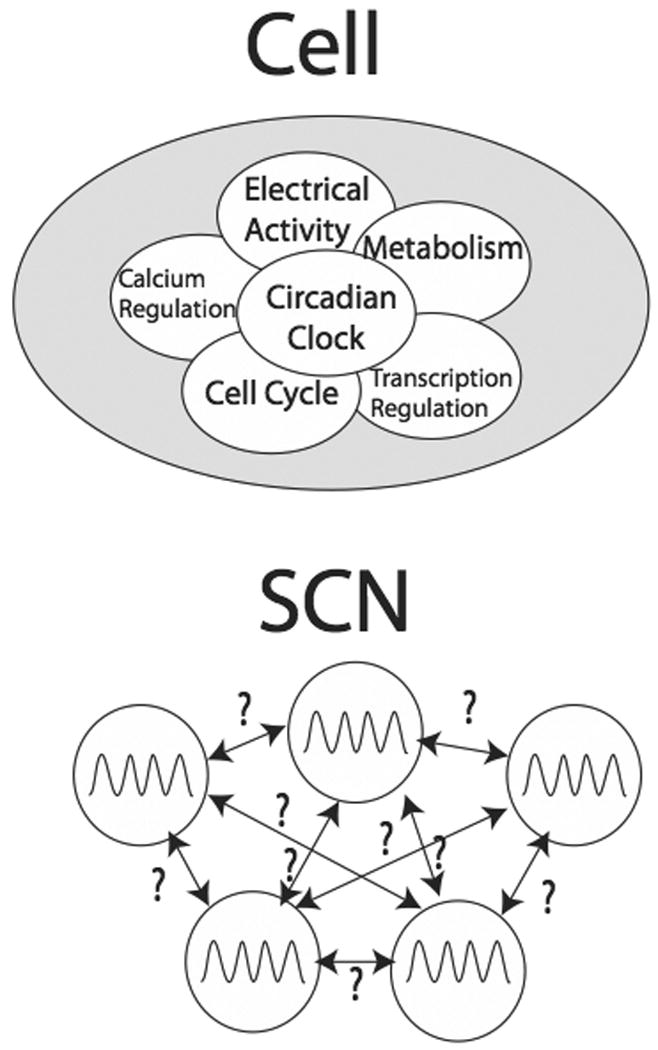
Circadian rhythms within a cell are intracellularly linked to many other cellular systems and processes, including but not limited to: transcription regulation, cell cycle, metabolism, calcium regulation, and electrical physiological activity (Top). Many details of the interaction between individual cells within the suprachiasmatic nucleus (SCN), which acts as the central circadian pacemaker in mammals, are important but unknown (Bottom)

And it gets more complex …

Individual cells within the SCN do not act alone and must communicate with one another, as illustrated in the bottom panel of figure 3. In fact, rhythms within the network are much more robust than individual cellular rhythms [19]. The SCN must interact with many other systems within the organism to properly function. For example, rhythms are constantly being regulated by hormone release. Moreover, the SCN receives information about time in its external world through a direct pathway from the retina via a dedicated photic system [1].

We now review each level of complexity, discussing key results and identifying possible research challenges.

From Protein Modification to Protein Function

Circadian rhythms are very carefully regulated by post-translational modifications. Several important genetic mutations, affecting whole organism behavior, have been linked to changes in post-translational modification. However, though many possible phosphorylation sites have been identified, little is known about their specific function [20]. We also do not know whether these phosphorylation events act sequentially, combinatorially or independently as shown in figure 1. Here molecular dynamics simulations will play a very important role into a research area which has barely been explored. Likewise, simple mechanistic models could be used to make predictions about the interplay between individual phosphorylation sites [21,22].

From Genes to Genetic Network

In recent years, this area has received a considerable amount of attention. In a landmark paper [23], Goodwin showed that a simple genetic negative feedback loop could sustain biochemical oscillations. While the Goodwin model was not developed exclusively as a mathematical model for circadian rhythms, Goldbeter [24] realized that with modifications, the model could predict what was then known about the PER gene. Detailed single cell models, focusing on the underlying biochemical dynamics of cellular physiology, were investigated [25-28] and represented a significant shift from those models where Goodwin or Van der Pol oscillators were used to represent individual cells. These models attempt to incorporate all relevant experimental data about core clock components; later models also investigated the significance of molecular noise [29-32,33•]. Recent work has focused on the role of transcription regulation of activators and repressors. In particular, several predictions regarding the mutations of core clock proteins have been verified in recent published work [34]. Furthermore, single cell models have been successful in studying the role of post-translation processes, and have yielded predictions that have been confirmed experimentally [21].

From Genetic Networks to Cellular Systems

Recent research has shown that circadian timekeeping is intricately linked to other cellular processes. The circadian clock is intricately linked with the electrical behaviour of neurons. Mathematical modeling has successfully predicted unexpected circadian electrical activity, which was verified experimentally [35-36,37••]. Similar links now exist with metabolic regulation, cell cycle, and transcription regulation [38-40, 41•,42]. The future will involve the development of mathematical models to understand the connection between these various physiological processes with mammalian time-keeping, with careful attention to the results of experimental data [43•,44,45].

Synthetic biology also offers an ideal approach to understanding complexity at the cellular level. Recent work in this area has focused on how interacting feedback loops can increase robustness [46•] in addition to understanding the dynamics of coupled oscillators [47••]. These studies have relied on mathematical modeling which can be particularly predictive in synthetic biology since the components of synthetic systems are often well characterized.

From Cells to Tissues

Moreover, individual cellular timekeeping is different from that seen in an organism [48,49]. Individual cells with rhythms whose amplitude decays over time can show sustained rhythms when coupled together[34]. Moreover, individual cellular oscillators can become desynchronized from each other. This can lead to the appearance of multiple rhythms in the organism's behavior [50•]. The bottom panel of figure 3 illustrates that the intercellular communication mechanism is unknown; key questions include the following. How can the theory of coupled oscillators help us understand SCN network behavior? (Much progress has been made in this area [51-58], but most inter-cellular mechanisms are ‘all-to-all’, where every cell is connected with every other cell.) What happens when we use a different network topology [59]? How can different inter-cellular coupling mechanisms affect network physiology [60-61]? Furthermore, what happens when we incorporate both chemical and electrical inter-cellular coupling [62]?

An additional, yet physiologically interesting consideration at this level, is the role of molecular noise in coupled SCN oscillators. This approach was first suggested and investigated by Enright in 1984 [63]. He reached the conclusion that a collection of coupled noisy oscillators recovered sustained rhythms; his model did not incorporate the molecular details that have since appeared in the literature [25-28]. Given our advance in understanding of the molecular clock, what will we discover when we re-visit Enright's hypothesis? What role does noise contribute to the physiology of the entire network [64-66]?

Minimal or Detailed Models

To answer this question, we appeal to a musical metaphor. Some listeners like nothing more than the beauty of a simple melody for which one can quickly feel comfortable knowing intuitively all that is going on. Other listeners prefer a complex Bach fugue where a detailed understanding of the interplay between voiceparts is rarely appreciated by the listener, but a beautiful picture emerges nonetheless. Examples exist where intuitive mathematical models lead to important experimental advances [67]. Likewise, complex models that account for many of the “parts”and lead to unintuitive predictions [21,37,68] For example, a detailed model predicted a gain of function for the tau mutation, initially thought to be incorrect, which was later verified [21].

Thus we find a place for both simple and complex models. Just as we do not support modeling whose simplifications, while leading to clean mathematical expressions, leave out key biology, we also do not support complexity for complexity's sake. If the model equations can be simplified further to 2 variables, analytic methods from nonlinear dynamics (phase plane analysis, bifurcations) [69] and stochastic differential equations [70] can be applied to study the system further. More detailed models accurately reflect the physiology of the underlying process, though they are computationally more expensive.

However, an alternate view of simple vs. complex models is provided by two key results from mathematical analysis. Forger and Kronauer found that many complex mathematical models easily reduce to a small region (e.g. 2-dimenional) of phase space [71-72]. This dimensional reduction of model phase space is illustrated in Figure 4. Each variable in this subspace is a combination of many other model variables (e.g. those variables representing the various molecules shown in figure 2). However the dynamics on this small subspace can be very similar to those found in simple models. Similar analysis has been shown by others [73-74].

Figure 4.

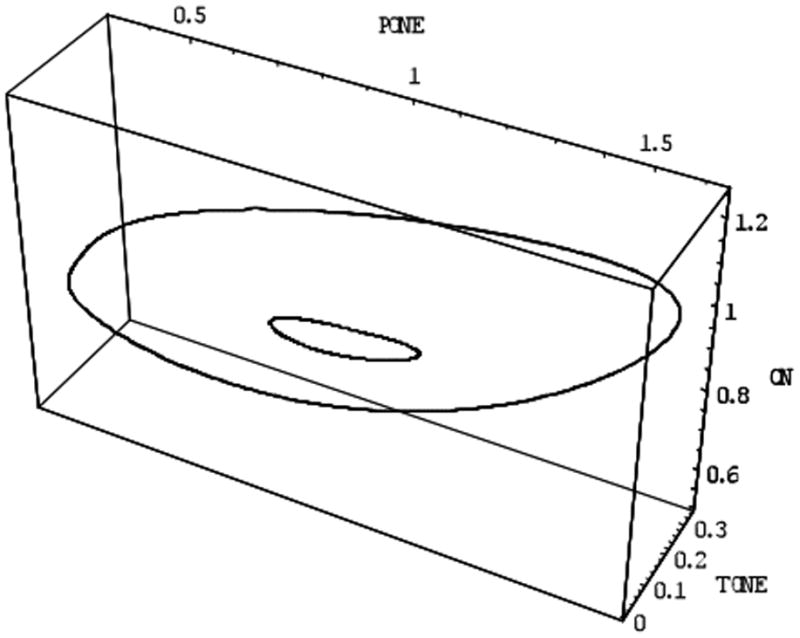
Simulations of a circadian clock model by Leloup and Goldbeter, which can display two modes of oscillations (both shown as circles). Here we plot three of the variables in the model: the axis labeled ‘Pone’ is the first phosphorylated state of the Per repressor protein, the axis labeled ‘Tone’ is the first phosphorylated state of the Tim repressor protein, and the last axis (labeled ‘CN’) is the Per-Tim complex in the nucleus. Notice the two oscillatory solutions lie on a 2-dimensional plane where the system spends most of its time. This illustrates how high dimensional models, which initially seem complex, may have a hidden but simple structure [85].

Likewise, criticisms of the use (or abuse) of parameters have been leveled on both types of models. Simple models have parameters (e.g. oscillator stiffness or period) which are difficult to relate with biophysical rate constants. On the other hand, detailed models that use biophysical rate constants are oftentimes criticized since the numerical values of these rate constants may not be known. However, recent work indicates that only a few key combinations of parameters may be essential [75••] in models containing many parameters. Again, we stress the possibility that detailed models may actually be simple models in disguise, occupying a low dimensional region of phase space and depending only on a few key combinations of parameters.

A recent experimental study [18] illustrates the use of complex and simple models. The authors observed that reducing transcription regulation leads to a shorter period experimentally, while predictions from a detailed model hint at an opposite result. For example, a recent detailed model [26] provides a specific mechanism of transcription regulation (specifically the co-ordinated action of several E-boxes), while other published models use Hill-type terms (whose biophysical mechanism is either known to be wrong or used without any biophysical justification [76]). Thus the detailed model is based on experimental results which explores a specific biochemical mechanism, whereas mechanism is not the focus of the simple model. We find this observation very useful, not to further the unscientific debate about whether a detailed or simple model is better, but as an indication that further thinking is required on how transcription regulation actually occurs.

Development of new analytical techniques

Associated with the development of any mathematical model is the accurate and efficient search for unknown model parameters values. For example, these values may be reaction rates, whose values are not available in the published literature. To date, most searches for parameters have been ad hoc. Recent advances, including Bayesian parameter analysis [77] and iterative evolutionary strategies [78•], are promising approaches. However, a systematic approach to finding these parameters must be pursued and developed.

The complexities posed by detailed models can only be studied using computational methods. Once the biochemical network of the underlying process has been constructed, the reactions between all the species in this network can be delineated. The two most widely used modeling approaches to study reaction networks are deterministic and stochastic [70,79]. The deterministic framework uses the law of mass action, which allows this reaction network to be translated into a set of coupled differential equations. On the other hand, a stochastic (or noisy) model allows for random fluctuations in the chemical species. From a physiological standpoint, these fluctuations need to be considered because the copy numbers of protein and mRNA are low. What is now needed are efficient computational algorithms that can simulate complex cellular models from smaller sub-cellular parts [80]. As more cellular details emerge, existing models will become more complex with more components. However, current methods are computationally slow and expensive. Finally, mathematical techniques must be developed to determine how to optimally perturb oscillator models [81•,82-83].

Conclusion

Mammalian time-keeping is a complex process; in order to sort through the myriad experimental data, collected at various temporal and spatial scales, we need multiscale mathematical modeling [84]. We would like to stress that a multi-scale mathematical model will achieve its greatest efficacy when it will contribute to the design of future experiments. The large output of experimental data challenges the modeler to build models whose utility is to “predict”, rather than “post-dict” experimental phenomena. Thus these models must be continually revised until a satisfactory model for mammalian time-keeping prediction is achieved. In closing, it will be increasingly important for experimentalists and modelers to continue working closely together to optimize this iterative process.