Prediction of the human thoracic and lumbar articular facet joint morphometry from radiographic images

Abstract

The articular facet joints (AFJ) play an important role in the biomechanics of the spine. Although it is well known that some AFJ dimensions (e.g. facet height/width or facet angles) play a major role in spinal deformities such as scoliosis, little is known about statistical correlations between these dimensions and the size of the vertebral bodies. Such relations could allow patient-specific prediction of AFJ morphometry from a few dimensions measurable by X-ray. This would be of clinical interest and could also provide parameters for mathematical modeling of the spine. Our purpose in this study was to generate prediction equations for 20 parameters of the human thoracic and lumbar AFJ from T1 to L4 as a function of only one given parameter, the vertebral body height posterior (VBHP). Linear and nonlinear regression analyses were performed with published anatomical data, including linear and angular dimensions of the AFJ and vertebral body heights, to find the best functions to describe the correlations between these parameters. Third-order polynomial regressions, in contrast to the linear, exponential and logarithmic regressions, provided moderate to high correlations between the AFJ parameters and vertebral body heights; e.g. facet height superior and interfacet width (R², 0.605–0.880); facet height inferior, interfacet height and sagittal/transverse angle superior (R², 0.875–0.973). Different correlations were found for facet width and transverse angle inferior in the thoracic (R², 0.703–0.930) and lumbar (R², 0.457–0.892) regions. A set of 20 prediction equations for AFJ parameters was generated (P-values < 0.005, anova). Comparison of the AFJ predictions with experimental data indicated mean percent errors < 13%, with the exception of the thoracolumbar junction (T12–L1). It was possible to establish useful predictions for human thoracic and lumbar AFJ dimensions based on the size of the vertebral bodies. The generated set of equations allows the prediction of 20 AFJ parameters per vertebral level from the measurement of the parameter VBHP, which is easily performed on lateral X-rays. As the vertebral body height is unique for each person and vertebral level, the predicted AFJ parameters are also specific to an individual. This approach could be used for parameterized patient-specific modeling of the spine to explore the clinically important mechanical roles of the articular facets in pathological conditions, such as scoliosis.

Introduction

The articular facet joints (AFJ) play an important role in the biomechanics of the spine; they transmit a significant percentage of spinal loading, and provide translational, rotational and axial stability in the spine (Lorenz et al. 1983; Adams & Hutton, 1983; Onan et al. 1998). The shape, position and orientation of the AFJ strongly regulate the physiological motion of the spine (Taylor & Twomey, 1986; White & Panjabi, 1990). A patient-specific prediction of vertebral morphometric data (e.g. size and orientation of the AFJ) could be of clinical interest in the evaluation of operative and non-operative spinal treatments. For example, during clinical or radiographic examination of a patient with a spinal deformity such as scoliosis, the physicians are faced with the problem that it is not possible to know what the original anatomical dimensions of this spine were before deformity started. Most procedures for spinal deformity corrections are based on the average values of vertebral dimensions of a healthy spine, without taking into account that each patient has a specific morphometry. One possibility would be to use an X-ray of a patient and, from direct measurement of a dimension of an intact vertebra (e.g. vertebral body height), predict other dimensions (e.g. articular facet size or orientation) by using the relationships between them.

Another important issue for such predictions of vertebral morphometry is to provide parameters for mathematical modeling of the spine. Shirazi-Adl (1991, 1994), Zander et al. (2003) and Schmidt et al. (2008a,b, 2009) investigated the AFJ in normal and pathological conditions using finite element models. The geometry of these models often comes from 3D reconstruction of computed tomography, which requires a considerable processing time and computational power. Finite element models with a simple but parameterized geometry could be an alternative to these complex models because they would allow different vertebral geometries to be fitted.

The human vertebral morphometry has been measured in a number of studies (Table 1) and using patient-specific stereoradiographic reconstruction techniques (Aubin et al. 1997; Petit et al. 1998; Pomero et al. 2004). Previous investigations of statistical correlations between dimensions of vertebral structures have been used to predict vertebral dimensions. However, the relationships between the geometrical parameters describing the different parts of a given vertebra and the vertebral body height are only well known for the anterior structures and some posterior structures (e.g. pedicles) (Scoles et al. 1988; Kunkel et al. 2010).

Table 1.

Summary of in vitro measurements of geometric parameters of the human articular facets reported for thoracic and lumbar vertebrae.

Reference	Technique	Vertebral level	Facet geometric parameters
van Schaik et al. (1985)	CT	L3–5	Transverse plane angle
Cotterill et al. (1986)	CT	T6, T12, L3	Interfacet height/width
			Transverse plane angle
Berry et al. (1987)	DM	T2, T7, T12, L1–5	Interfacet height
Scoles et al. (1988)	DM	T1, T3, T6, T9, L1, L3, L5	Inferior facet pedicle distance
			Inferior facet/mid-pedicle length
Ahmed et al. (1990)	CT	L2–5	Facet angle/depth/length
Panjabi et al. (1993)		T1–12, L1–5	Facet height/width
			Interfacet height/width
			Facet area
			Transverse/sagittal plane angle
Boszczyk (1997)	DM	T12, L1–5	Facet height/width
			Transverse/Sagittal plane angle
Ebraheim et al. (1997)	DM	T1–12	Facet thickness
			Facet height/width
			Sagittal plane angle
Laporte et al. (2000)	DM	T1–12	Transverse/Sagittal plane angle
			Facet height/width
			Facet area
			Distance from facet centers
Dai (2001)	CT/MRI	L4–5	Transverse/Sagittal plane angle
Masharawi et al. (2004)	DM	T1–12, L1–5	Transverse/sagittal plane angle
			Interfacet height/width
Masharawi et al. (2005)	DM	T1–12, L1–5	Facet height/width
Masharawi et al. (2007a)		L1–5	Facet height/width
			Interfacet height/width
			Facet concavity/convexity
Masharawi et al. (2007b)	DM	L1–5	Transverse plane angle
Wang & Yang (2009)	CT	L4–5	Sagittal plane angle

CT, computed tomography; DM, direct measurement; MRI, magnetic resonance imaging.

Although it is well known that some AFJ parameters, such as facet height and width or facet angles, play a major role in spinal deformities such as scoliosis due to pathological changes in the anatomy of the posterior structures (Parent et al. 2002; Aebi, 2005), little is known about vertebral relationships between AFJ parameters and vertebral heights. Breglia (2006) investigated only two AFJ parameters and found a poor correlation between them and the vertebral body height posterior (VBHP). Other studies investigated statistical correlations of AFJ parameters not only with VBHP but with all other vertebral parameters; in these cases, 6–15 initial parameters were necessary for the prediction of some AFJ parameters (Lavaste et al. 1992; Skalli et al. 1993; Maurel et al. 1997; Laporte et al. 2000). A quantitative analysis of the relationship between the AFJ parameters and VBHP allowing patient-specific predictions has not yet been investigated.

The purpose of the current study was to generate prediction equations for 20 parameters of the human thoracic and lumbar AFJ as a function of only one given parameter measurable by X-ray, the VBHP.

Materials and methods

Study population

Vertebral anatomical data were collected from Panjabi et al. (1991, 1992, 1993) and were included in this study. To carry out statistical analyses, measurements of the VBHP and 20 anatomical measurements were selected to describe the size and orientation of the human thoracic (T1–12) and lumbar (L1–4) AFJ (Fig. 1).

Fig. 1.

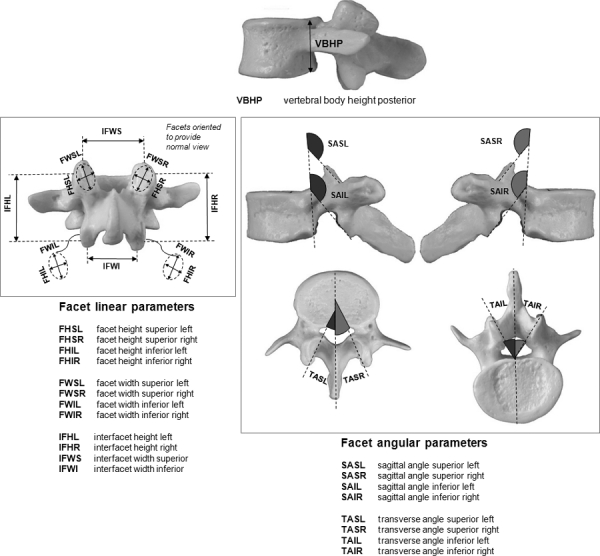
Schematic representation of the anatomical parameters that were considered for linear and nonlinear regression analyses. Vertebral body height posterior and linear and angular dimensions of the articular facet joints. The facet surfaces were approximated by a plane. The orientation of the planes was defined by two angles made by the facet plane with the sagittal and transverse anatomic planes.

Statistical analysis

To perform linear and nonlinear regression with these data, the same methodology used by Kunkel et al. (2010) was adopted. The parameter VBHP was used as the predictor variable, and the values of the parameters related to the vertebral level L5 were not included in the analysis. However, due to the existence of a considerable difference between the morphometry of the articular facets in the thoracic and lumbar regions, a modification was introduced to achieve a better prediction of the AFJ parameters. It refers to separate regressions using thoracic (T1–12) and lumbar (L1–4) data together, thoracic data alone, and lumbar data alone. A brief description of the implemented methodology in this study follows.

Correlation and regression analyses with AFJ parameters and VBHP

Each AFJ parameter selected for this study from T1–12 and L1–4 was correlated with VBHP. A least-squares regression analysis was performed to find linear and nonlinear functions to describe the relationship between each pair of parameters. These functions represented prediction equations which take the forms y = C₁ + C₂x for linear, y = C₁+ C₂ln(x) for logarithmic,

for exponential, and

for polynomial equations, where y was the value of the articular facet parameter to be predicted, x was the value of the VBHP on each vertebral level, and C₁, C₂, C₃, C₄…C_n were the regression coefficients. The fraction of the overall variance of each facet parameter that was reduced by a specific regression, R² value, was used to assess the best function of the set of generated prediction equations. For the polynomial equations, the number of coefficients was continually increased until adding another higher-order term did not significantly increase R².

Identification of the best prediction equation

An anova was performed to define the significance of each prediction equation that fits a given facet parameter. The respective residual plots were examined to assess the quality of these equations. The identification of the best prediction equations was based on the following criteria: values of R²> 0.5 associated with a probability level of P-value < 0.05 and a standard error of the estimate (SE) < 30% of the standard deviations of the experimental data of Panjabi et al. (1993).

Evaluation of the predictability of the prediction equation

For each AFJ parameter, the theoretical predictions were plotted against the corresponding known experimental data of Panjabi et al. (1993) and Cotterill et al. (1986) considering their respective confidence limits. The dataset of Cotterill et al. (1986) included three AFJ parameters (interfacet height and width, and transverse angle superior) of two thoracic (T6 and T12) and one lumbar (L3) vertebrae. As these three parameters provided in this dataset did specify where the measurements were obtained (right or left side, superior or inferior), the predictions of these parameters in our study were performed considering all possibilities.

Results

Third-order polynomial regressions, in contrast to the linear, exponential, logarithmic and polynomial regressions with other orders, provided the best results with significant correlations between each of the AFJ parameters and VBHP. The inclusion of more than four polynomial coefficients increased the R² values; however, anova S indicated that the obtained correlations did not significantly improve parameter predictions. For this reason, only the results of third-order polynomial predictions are provided (Table 2 for thoracic and Table 3 for lumbar regions).

Table 2.

Polynomial coefficients (C₁, C₂, C₃ and C₄) for prediction equations of 20 articular facet joint parameters per vertebral level of the human thoracic spine. Refer to Fig. 1 for abbreviations.

Parameter	Abbreviation	C1	C2	C3	C4	SE	R2	P-value
Facet dimensions
Height	FHSL	−4.775	4.189	−0.309	0.007	1.18	0.647	0.0046
	FHSR	33.916	−2.520	0.068	0.001	0.87	0.751	0.0006
	FHIL	62.954	−6.484	0.235	−0.002	0.68	0.910	1.49E-06
	FHIR	82.879	−10.102	0.444	−0.006	0.64	0.924	5.61E-07
Width	FWSL	381.760	−59.777	3.175	−0.056	0.7	0.771	0.0061
	FWSR	244.770	−36.675	1.890	−0.032	0.46	0.850	0.0011
	FWIL	383.000	−61.279	3.325	−0.059	0.60	0.788	0.0045
	FWIR	314.610	−50.508	2.763	−0.050	0.60	0.703	0.0164
Interfacet height	IFHL	45.467	−5.543	0.329	−0.005	0.79	0.970	2E-06
	IFHR	−56.782	11.697	−0.628	0.013	0.76	0.973	1.35E-06
Interfacet width	IFWS	744.410	−111.100	5.625	−0.094	1.47	0.880	0.0005
	IFWI	620.110	−95.960	5.0701	−0.088	0.89	0.868	0.0007
Facet orientations
Transverse angle	TASL	−629.850	106.150	−5.322	0.089	2.09	0.922	5.71E-07
	TASR	−468.340	81.873	−4.122	0.070	1.70	0.938	1.65E-07
	TAIL	−772.290	131.960	−6.800	0.116	1.40	0.930	5.73E-05
	TAIR	−294.800	53.407	−2.529	0.040	1.98	0.785	0.0047
Sagittal angle	SASL	998.880	−149.700	8.0381	−0.143	1.04	0.952	1.31E-05
	SASR	−1084.000	160.740	−8.4545	0.147	1.41	0.904	0.0002
	SAIL	−2549.600	463.78	−27.063	0.521	8.47	0.849	0.0012
	SAIR	2375.500	−434.840	25.490	−0.493	8.20	0.862	0.0084

SE in mm (for facet linear parameter) or in degree (for facet angular parameters).

The basic form of the prediction equations is y = C₁ + C₂x + C₃x² +C₄x³, where y is the value of the facet parameter to be predicted and x is the value of the VBHP on each vertebral level. S, superior; I, inferior; L, left; R, right. Values in bold indicate facet parameters that show the same polynomial coefficients for thoracic and lumbar vertebrae.

Table 3.

Polynomial coefficients (C₁, C₂, C₃ and C₄) for prediction equations of 20 articular facet joint parameters per vertebral level of the human lumbar spine. Refer to Fig. 1 for abbreviations.

Parameter	Abbreviation	C1	C2	C3	C4	SE	R2	P-value
Facet dimensions
Height	FHSL	−4.775	4.188	−0.309	0.007	1.18	0.647	0.0046
	FHSR	33.916	−2.519	0.068	0.001	0.87	0.751	0.0006
	FHIL	62.954	−6.484	0.235	−0.002	0.68	0.910	1.49E-06
	FHIR	82.879	−10.102	0.444	−0.006	0.64	0.924	5.62E-07
Width	FWSL	240.180	−35.123	1.759	−0.029	1.49	0.457	0.0416
	FWSR	177.180	−25.063	1.233	−0.020	1.07	0.516	0.0283
	FWIL	109.750	−14.135	0.647	0.010	1.10	0.556	0.0255
	FWIR	70.833	−8.667	0.396	−0.006	1.09	0.559	0.0168
Interfacet height	IFHL	135.720	−20.994	1.201	−0.021	1.16	0.950	4.11E-08
	IFHR	97.381	−14.658	0.856	−0.015	1.33	0.942	1.06E-07
Interfacet width	IFWS	595.510	−85.587	4.185	−0.067	1.78	0.818	9.80E-05
	IFWI	312.070	−43.273	2.100	−0.033	2.50	0.605	0.0091
Facet orientations
Transverse angle	TASL	−629.850	106.150	−5.322	0.089	2.09	0.922	5.71E-07
	TASR	−468.340	81.873	−4.122	0.070	1.70	0.938	1.65E-07
	TAIL	−578.400	98.978	−4.951	0.082	1.65	0.892	4.45E-06
	TAIR	−394.580	70.418	−3.485	0.057	3.24	0.526	0.0254
Sagittal angle	SASL	−1384.100	260.400	−15.230	0.292	10.44	0.875	1.02E-05
	SASR	895.720	−180.630	10.957	−0.217	10.08	0.876	9.99E-06
	SAIL	24.358	24.433	−2.355	0.064	14.45	0.808	0.0001
	SAIR	−88.384	−14.160	1.824	−0.055	13.93	0.829	6.74E-05

SE in mm (for facet linear parameter) or in degree (for facet angular parameters).

The basic form of the prediction equations is y = C1 + C₂x + C₃x² + C₄x³, where y is the value of the facet parameter to be predicted and x is the value of the VBHP on each vertebral level. S, superior; I, inferior; L, left; R, right. Values in bold indicate facet parameters that show the same polynomial coefficients for thoracic and lumbar vertebrae.

Considering the previously established criteria, the polynomial regressions using the thoracic and lumbar data together (T1–12 and L1–4) showed variable correlations with VBHP (R² 0.516–0.950), providing significant prediction equations for all selected AFJ parameters from VBHP (an exception was FWSL).

The polynomial regressions considering only the thoracic data (T1–12) resulted in improvements for predictions of 70% of the thoracic AFJ parameters such as an increase of R² (from 0.650 to 0.973), an increase in the significance and a decrease of SE (Table 2). In the case of the other thoracic AFJ parameters, such as facet heights (FHSL, FHSR, FHIL and FHIR) and transverse plane angles (TASL and TASR), where no improvement was achieved, the polynomial coefficients obtained from the regressions using the thoracic and lumbar data together were accepted.

Polynomial regressions considering only lumbar data (L1–4) did not satisfy the minimum criteria required for the selection of the prediction equations. This was probably due to the low number of observations in the lumbar region (just four parameter values per vertebrae). Therefore, the polynomial coefficients obtained from the regressions using the thoracic and lumbar data together were used to predict the lumbar AFJ parameters (Table 3).

Facet linear parameters predictions

High correlations were found for inferior facet heights (FHIL and FHIR) with VBHP (R², 0.910–0.924). Superior facet heights (FHSL and FHSR) showed moderate correlations (R², 0.647–0.751). Comparisons with experimental data of Panjabi et al. (1993) showed that the best predictions were found for FHIR with a mean percent error of approximately 14% in T12 and a maximal error of 7% in all other levels (Fig. 2A). The largest error of approximately −17% was found for FHSL predictions in the lumbar level (Fig. 2D). For facet widths (FWSL, FWSR, FWIL, FWIR), no significant difference was found between the correlations of the widths of the superior and inferior facets with VBHP. The best correlations with VBHP were achieved on the thoracic levels (R², 0.703–0.850) where a mean percent error < 10% was found (e.g. Fig. 2B,E). Although these parameters showed poor correlation for lumbar levels (R², 0.457–0.559) good predictions could be achieved with the largest error of 28.4% in the FWSL (L1) prediction (Fig. 2E). The interfacet heights and widths (IFHL, IFHR, IFWS and IFWI) exhibited high correlations with VBHP (R², 0.818–0.973) with the exception of thoracic IFWI (R²= 0.605). Independent of thoracic or lumbar levels, the best correlations were found for interface heights. Predictions of these parameters showed a mean percent error < 11% for all vertebral levels (e.g. Fig. 2C). The mean percent errors were < 12% (for thoracic) and < −18% (for lumbar) for the IFWS and IFWI (e.g. Fig. 2F).

Fig. 2.

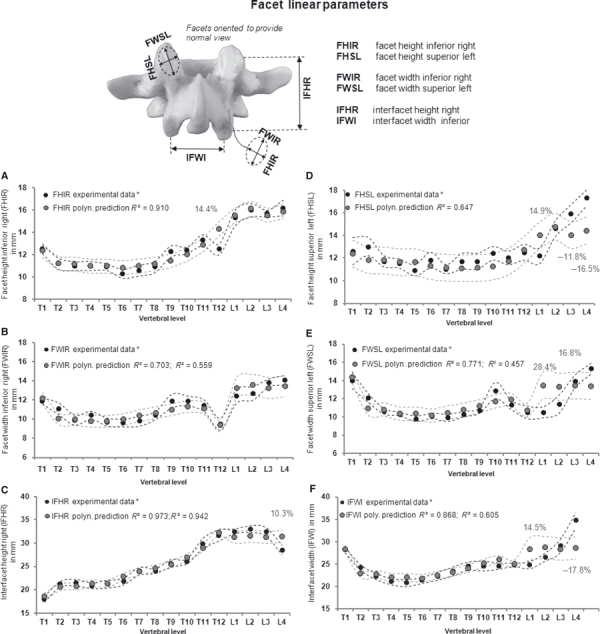
Polynomial predictions of parameters related to dimensions of the human thoracic and lumbar articular facet joints (FHIR, FWIR, IFHR, FHSL, FWSL and IFWI) from VBHP, superimposed on experimental data of Panjabi et al. (1993)*. Dotted curves indicate standard deviation of both the predictions and experimental data. R² is provided for thoracic and for lumbar levels. Only mean percent errors > 5% for all vertebral levels are shown. Best predictions (left); worst predictions (right).

Facet angular parameters predictions

The transverse angles showed high correlations for TASL, TASR and TAIL with VBHP for all levels (R², 0.785–0.938). TAIR displayed a poor correlation (R² = 0.526) for the lumbar levels. For the predictions with data of Panjabi et al. (1993) the largest mean percent error found was approximately 10% (TAIR, L4). All other predictions including lumbar levels showed an error < 6% (e.g. Fig. 3A,C). The sagittal angles superior and inferior (SASL, SASR, SAIL and SAIR) also showed high correlations with VBHP, with R² ranging from 0.808 to 0.952. For SASR and SASL, very good predictions using the data of Panjabi et al. (1993) were found for thoracic levels, with a mean percent error < 4%; the lumbar predictions for these parameters showed variable errors of −0.6 to −9.3% (e.g. Fig. 3B). SAIL and SAIR predictions in the T11 level showed a considerable mean percent error of approximately 27%; all other thoracic levels displayed an error < 9%. The lumbar predictions showed errors of 5–20% (e.g. Fig. 3D).

Fig. 3.

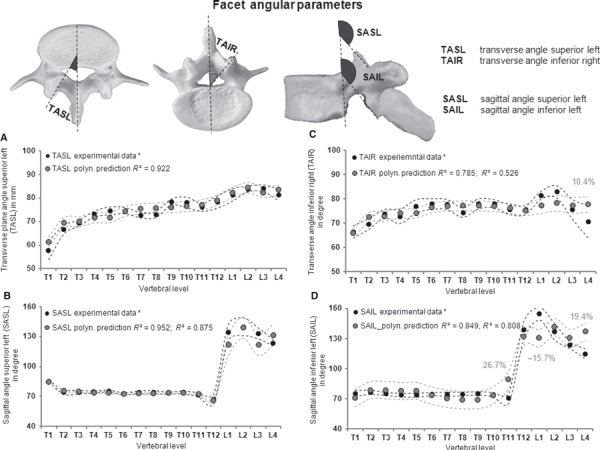
Polynomial predictions of parameters related to orientations of the human thoracic and lumbar articular facet joints (TASL, SASL, TAIR and SAIL) from VBHP, superimposed on experimental data of Panjabi et al. (1993)*. Dotted curves indicate standard deviation of both the predictions and experimental data. R² is provided for thoracic and for lumbar levels. Only mean percent errors > 5% for all vertebral levels are shown. Best predictions (left); worst predictions (right).

Evaluation of the prediction equations

The third-order polynomial predictions were generally within or close to the regions of the 95% confidence intervals of the experimental data of Panjabi et al. (1993) (Fig. 4). Using the dataset of Cotterill et al. (1986), the comparisons with experimental and predicted thoracic IFHR and IFHL showed a mean percent error of approximately 13% (T6) and an error of approximately 0.22 mm (< 2%) (T12) (Fig. 5A,D). The L3 prediction showed the largest error of approximately 2.6 mm (9%) for IFHL (Fig. 5D). The predictions of the IFWS and IFWI exhibited a mean percent error < 16% for the thoracic level and better results for L3, respectively 1.7 mm (6.3%) and 1.01 mm (3.8%) (Fig. 5B,E). The predictions of the facet orientation, TASR and TASL, showed very similar results to experimental data values, with mean percent errors of approximately −11% (T6), −5% (T12) and −9% (L3) (Fig. 5C,F).

Fig. 4.

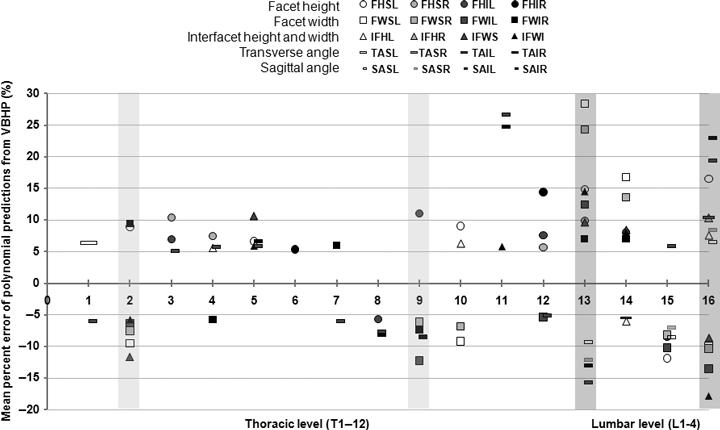
Mean percent errors > 5% for polynomial predictions of 20 articular facet joint parameters from VBHP of experimental data of Panjabi et al. (1993). Error per vertebral level of the human thoracic (T1–12) and lumbar (L1–4) spine. Refer to Fig. 1 for abbreviations. Polynomial predictions were satisfactory for all AFJ parameters with a few exceptions of some thoracic facet linear dimensions (T2 and 9, light gray highlighted bars) and some lumbar facet orientations (L1 and 4, dark gray highlighted bars).

Fig. 5.

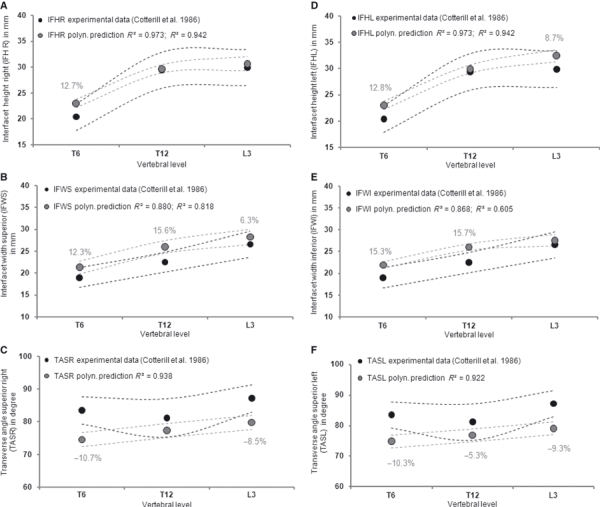
Comparison of some predicted articular facet joint parameters (IFHR, IFWS, TASR, IFHL, IFWI and TASL) with corresponding experimental data from Cotterill et al. (1986) in selected vertebral levels (T6, T12 and L3). Refer to Fig. 1 for abbreviations. R² is provided for thoracic and for lumbar levels. The means and 95% confidence intervals (dotted lines) of both the experimental and the predicted values are shown. Only mean percent errors > 5% for all vertebral levels are shown.

Discussion

In this study, the morphological relationships between anatomical characteristics of the human AFJ and VBHP were described by linear and nonlinear regression analyses. A set of prediction equations for AFJ parameters of the thoracic (T1–12) and lumbar (L1–4) spine was generated as a function of the VBHP (Tables 2 and 3).

SEs indicates that, with few exceptions, polynomial predictions were satisfactory for all AFJ parameters. The exceptions were in the facet dimensions in the thoracic region (T2 and 9) and facet orientation in the lumbar region (L1 and 4) (Fig. 4). The best predictions of facet orientations were found for the transverse angles. Excluding the level T1, no errors > 5% were found in the prediction of the transverse angles of the thoracic or lumbar regions, probably because these parameters show very little variability within the vertebrae from T1 to L4. Notably in the midthoracic region (i.e. T3–8), excellent predictions with errors < 10% could be achieved for most parameters of the AFJ. In contrast, predictions with errors of up to −15% were found for all sagittal angles in the thoracolumbar junction (T12–L1) (Fig. 4). This was due to the large variability of this region within individuals, with the AFJ being either frontally oriented, as in the thoracic vertebrae, or sagittally oriented, as in the lumbar vertebrae. This is in accordance with Goel & Weinstein (1990) and Masharawi et al. (2004) who showed that the morphology of the first lumbar vertebra is distinct from the other vertebrae, with a transition from the typically thoracic to the lumbar vertebra.

Our results were compared, when possible, with existing published experimental measurements of AFJ geometry (Table 1). However, it was not possible to carry out the evaluation of the predictability of all best-fitting equations using experimental data from more datasets. This was due to a lack of availability of measurements in the literature, including values of VBHP and facet parameters in the same dataset. Berry et al. (1987) provided data on the values of VBHP and interfacet height in some vertebral levels but a reference system different to Panjabi et al. (1993) was used. The dataset of Boszczyk (1997) provides accurate experimental measurements of VBHP and the main AFJ parameters, but these were obtained using different landmarks to Panjabi et al. (1993). Ebraheim et al. (1997) provided a large quantity of data on facet parameters but no information about the size of the vertebral bodies. Masharawi et al. (2004, 2005, 2008) performed direct measurement on normal spine of facet and vertebral body parameters but the values of VBHP of these studies were not provided.

All correlation coefficients generated in the current study were considerably better than those obtained by Breglia (2006). He correlated interfacet width and inclinations with VBHP by simple linear regression, finding a poor or even no correlation. Our results showed high correlations for these AFJ parameters after nonlinear regressions. The advantages of using nonlinear regressions to fit vertebral data were described in a previous study (Kunkel et al. 2010). Comparisons of the theoretical predictions with the dataset of Cotterill et al. (1986) indicated that the predictions closely agreed with the experimental data. Although the differences in the predictions of lumbar facet parameters were moderate, an excellent correlation between the thoracic facet parameters and VBHP was found (Fig. 5).

It should be emphasized that the predictions using the set of equations generated in the current study are an approximation and should not be extrapolated beyond the limits of the data of Panjabi et al. (1991, 1992). Furthermore, the AFJ show individual and segmental variation (Bernick & Cailliet, 1982; Taylor & Twomey, 1986; Wang & Yang, 2009; Ahmed et al. 1990; Diacinti et al. 1995). Moreover, the facet surfaces that were described here as planar are usually curved (Taylor & Twomey, 1986). Nevertheless, as the two datasets used in this study were provided from in vitro measurements, further investigations are necessary to evaluate the predictability of the regression equations with a dataset from patients.

The advantage of using the generated set of prediction equations (Tables 2 and 3) is the capability to obtain size and orientations of the AFJ considering individual variability from only a single parameter per vertebrae (VBHP) measurable on lateral X-ray. Direct measurement of the main AFJ parameters, considering each vertebral level, cannot be performed in X-rays due to the superposition of several anatomical structures, specifically in the sagittal thoracic region of the spine. Moreover, the lumbar AFJ are difficult to image with X-rays because they are both curved and oblique to the sagittal plane.

Another advantage of using the prediction equations is that they can provide data for parameterized finite element modeling considering patient-specific AFJ morphometry. Thus the geometric congruence between adjacent articular facets could be ensured, and the AFJ changes both between subjects and between vertebral levels maintained. This could avoid the practice adopted in the construction of some models where the AFJ are redirected to force the lower facet of a vertebra to become congruent with the upper facet of the one below (e.g. Maurel et al. 1997;Breglia 2006). Such approximations could produce errors in the modeling of facet contact at different spinal levels.

Conclusion

The present study shows that it is possible to establish useful predictors for human thoracic and lumbar AFJ parameters based on the size of the vertebral body. The generated set of prediction equations enables fast acquisition of geometrical parameters of the AFJ as a function of a single parameter (VBHP), which is measurable in X-rays. As the VBHP is unique for each person and vertebral level, the predicted size and orientations of the AFJ are also specific to an individual. It may be applied for parameterized patient-specific modeling of the spine based on X-ray images alone. Such models make it possible to explore the clinically important mechanical roles of the articular facets in spinal deformities, including scoliosis.

Conflict of interest statement

The authors of this study did not and will not receive benefits in any form from a commercial party related directly or indirectly to the content of this study.