Abstract
Micro-computed tomographic analyses of trabecular bone architecture have been used to clarify the link between positional behavior and skeletal anatomy in primates. However, there are methodological decisions associated with quantifying and comparing trabecular anatomy across taxa that vary greatly in body size and morphology that can affect characterizations of trabecular architecture, such as choice of the volume of interest (VOI) size and location. The potential effects of these decisions may be amplified in small, irregular-shaped bones of the hands and feet that have more complex external morphology and more heterogeneous trabecular structure compared to, for example, the spherical epiphysis of the femoral head. In this study we investigate the effects of changes in VOI size and location on standard trabecular parameters in two bones of the hand, the capitate and third metacarpal, in a diverse sample of nonhuman primates that vary greatly in morphology, body mass and positional behavior. Results demonstrate that changes in VOI location and, to a lesser extent, changes in VOI size had a dramatic affect on many trabecular parameters, especially trabecular connectivity and structure (rods vs. plates), degree of anisotropy, and the primary orientation of the trabeculae. Although previous research has shown that some trabecular parameters are susceptible to slight variations in methodology (e.g. VOI location, scan resolution), this study provides a quantification of these effects in hand bones of a diverse sample of primates. An a priori understanding of the inherent biases created by the choice of VOI size and particularly location is critical to robust trabecular analysis and functional interpretation, especially in small bones with complex arthroses.
Keywords: body size, cancellous bone, carpal, homology, metacarpal, volume of interest
Introduction
The morphometric study of trabecular (cancellous) bone is an expanding area of research among biological anthropologists, following on from the long-accepted idea that bone adapts dynamically to mechanical loading and thus can inform our understanding of primate habitual behavior (e.g. Turner, 1992; Ruff et al. 2006). Interspecific studies across different primate taxa have found that trabecular architecture distinguishes different locomotor repertoires (e.g. Fajardo & Müller, 2001; MacLatchy & Müller, 2002; Ryan & Ketcham, 2002a; Fajardo et al. 2007; Scherf & Hublin, 2007; Scherf, 2008; Scherf et al. 2009) and manipulative behaviors (Lazenby et al. 2008a,b;), providing novel insight into the functional interpretation of both extant and fossil primate morphology (Ryan & Ketcham, 2002b; Scherf, 2008). The majority of these studies have investigated trabecular bone using noninvasive micro-computed tomography (micro-CT) in large, spherical epiphyses of long bones such as the femur or humerus (e.g. Fajardo & Müller, 2001; MacLatchy & Müller, 2002; Scherf & Hublin, 2007; Scherf et al. 2009).
However, comparisons of trabecular structure among different primates (e.g. Fajardo & Müller, 2001; MacLatchy & Müller, 2002; Ryan & Ketcham, 2002a) and in anatomical areas of the skeleton in which joint surfaces are more complex and trabecular bone less homogeneous than that of the femoral head (Zylstra & Ketcham, 2004; Maga et al. 2006; Griffin, 2008; Griffin et al. 2010; Lazenby et al. 2010a), have highlighted several methodological challenges that have not arisen in traditional clinical studies of human trabecular structure. In one of the first comparative micro-CT studies on nonhuman primate trabecular bone, Fajardo & Müller (2001) raised several concerns about quantifying and comparing trabecular architecture across taxa of varying body sizes. In particular, they discussed possible allometric effects associated with trabecular structure and the impact of the size of the volume of interest (VOI). In comparative analyses, it is common for study samples to include taxa that are an order of magnitude different in body size (e.g. Ryan & Ketcham, 2005; Maga et al. 2006; Fajardo et al. 2007) and thus identifying allometric affects on trabecular architecture is important. For example, trabecular thickness has been shown to scale negatively or not at all with body size and thus trabeculae are relatively much larger in smaller-bodied taxa than in larger-bodied ones (Swartz et al. 1998; Fajardo & Müller, 2001). Trabecular structure and number are also size-dependent, such that in smaller-bodied taxa the trabeculae are fewer and connect primarily to cortical bone, whereas in larger-bodied taxa there are more trabeculae that connect primarily to other trabeculae (Swartz et al.1998).
A second issue raised by Fajardo & Müller (2001) concerned the use of a standardized VOI and the problem of over-sampling in comparative studies. Placing a similarly sized VOI in both large and small animals will result in either a proportionately greater amount of trabeculae being sampled in smaller taxa or, because trabecular size does not scale with body size, a proportionately greater amount of trabeculae being sampled in larger taxa. In either case, use of a standardized VOI size in taxa of varied body sizes may yield biased results. Lazenby et al. (2010b) provide a formal test of standardized vs. scaled VOI size, showing that, indeed, some trabecular parameter values change when VOI size is scaled to a dimension of bone size (as a surrogate for body size). Measures of trabecular connectivity and structure (rods vs. plates) are particularly sensitive.
A third issue is the effect of variation in VOI location within the arthrosis of the bone being analyzed. The percentage of bone volume has been shown to vary between 12 and 37% depending on the position of a region of interest and that a slight shift (i.e. a few millimeters) in the position of the region of interest can change relative bone volume by 1–13% (Whitehouse & Dyson, 1974). Trabecular thickness and degree of anisotropy have been shown to similarly vary depending on the ROI position (Whitehouse & Dyson, 1974). In a 3D analysis of human lumbar vertebrae and the epiphyses of two long bones, Nägele et al. (2004) showed that movement of the VOI up to 4 mm significantly altered values for trabecular number, separation and thickness in some anatomical regions. These studies reveal that testing the effects of varying VOI location is important for determining anatomically and/or biomechanically homologous VOIs across study specimens and for meaningful intra- and interspecific comparisons of trabecular architecture. This is particularly true when analyzing the trabecular structure of bones in which the anatomy is more complex and the trabeculae more heterogeneous than that of the spherical epiphyses of long bones, such as the bones of the hands and feet (Maga et al. 2006; Griffin et al. 2010). The morphology of such bones can be highly informative for understanding function and positional behavior (e.g. Tocheri et al. 2005; Maga et al. 2006) as the hands and feet are the biomechanical link between the substrate and the rest of the skeleton during locomotion. This leads to a fourth issue in that it is unclear whether standard approaches to analyzing trabecular architecture are appropriate for such bones. Specifically, it is uncertain whether the influence of methodological decisions, such as those listed above, is inherently greater in small, complex bones than in long bones whose epiphyses are spherical and generally contain more homogenously distributed trabeculae. For example, in their analysis of trabecular architecture of human and extant great ape calcanei, Maga et al. (2006) purposely altered VOI size and location to quantify trabeculae that they considered functionally, rather than anatomically, homologous. In doing so, they found substantial differences in some parameters (e.g. degree of anisotropy) highlighting the implications of such methodological decisions.
In this paper we examine the effects of altering VOI size and location in irregularly shaped bones of the hand in a sample of nonhuman primates. This sample comprises hominoids, cercopithecoids and New World monkeys, which differ substantially in their positional behavior, morphology and body size (Table 1). We examine trabecular structure in four anatomical areas of the capitate and third metacarpal using scaled VOIs of various sizes and locations. We investigate the potential effects of varying VOI size and location within each individual. In this analysis we address methodological issues concerning robust quantification of trabecular structure in irregular-shaped bones and explore theoretical issues of allometry and the use of anatomically vs. biomechanically homologous VOI locations. Although we expect interspecific differences in trabecular structure across our study sample given that the hands are used for a diverse range of positional and manipulative behaviors, our focus is on the effect of the methodological approach rather than on the functional signal.
Table 1.
Sample of articulated hands used in this study (n= 1 for each species).
| Scan resolution (relative resolution2) (μm) | |||||
|---|---|---|---|---|---|
| Taxon | Sex | Positional behavior | Mean body mass (kg)1 | Capitate/MC3 base | MC3 head |
| Pan troglodytes | ♀ | Arboreal knuckle-walker3 | 33.2 | 31.95 (7.53) | 31.94 (5.71) |
| Gorilla gorilla | ♀ | Terrestrial knuckle-walker | 97.7 | 38.65 (7.22) | 40.33 (6.15) |
| Pongo pygmaeus | ♀ | Torso-orthograde suspensory4 | 37.8 | 29.43 (8.61) | 44.53 (4.84) |
| Symphalangus syndactylus | ? | Brachiator | 10.6-10.9 | 20.19 (11.91) | 24.39 (7.26) |
| Macaca fascicularis | ♀ | Arboreal palm-/plantigrade quadruped | 3.1 | 15.98 (11.57) | 21.03 (6.20) |
| Papio anubis | ♂ | Terrestrial digitigrade quadruped | 25.1 | 28.59 (7.35) | 31.94 (5.26) |
| Ateles sp. | ? | Torso-orthograde suspensory | 7.7–8.9 | 19.35 (10.69) | 21.03 (8.25) |
Mean sex-specific body mass given when sex of the specimen is known and range is given for both sexes when sex is unknown. All body mass data derived from Plavcan & van Schaik (1997).
The relative resolution is given to normalize for variation in trabecular thickness and scan resolution across taxa that vary greatly in overall size. This is a measure of the average trabecular thickness divided by the resolution (see Methods).
We use the terms ‘arboreal knuckle-walker’ for Pan and ‘terrestrial knuckle-walker’ for Gorilla as a brief description that reflects both the most frequent positional behavior (both knuckle-walk 85% of their locomotor time; Tuttle & Watts, 1985) and the most common ecological context (Hunt, 1992; Remis, 1995).
Describes both torso-orthrograde clambering and brachiation which make up 35–60% of arboreal locomotion (Cant et al. 2001; Thorpe & Crompton, 2006).
Methods
We investigate intra-individual variation in trabecular parameters as a consequence of varying VOI size and location in one specimen each of seven different primate taxa. All primate hands were complete articulated specimens housed in the osteology collection of the Berlin Museum für Naturkunde, except for that of Pan troglodytes, which was loaned from the Frankfurt Senckenberg Museum (Table 1). All specimens were obtained from wild-shot adults (based on the presence of an erupted third molar and complete epiphyseal fusion throughout the skeleton). All specimens were deemed relatively young adults based on limited dental attrition and the absence of any osseous pathology, obviating concern about age-related changes to skeletal tissue. The hands had dried naturally with various amounts of soft tissue preservation.
The hands were scanned with a BIR ACTIS 225/300 high-resolution micro-CT scanner at the Department of Human Evolution, Max Planck Institute for Evolutionary Anthropology (Leipzig, Germany). All specimens were scanned with an acceleration voltage of 130 kV and 100 μA using a 0.25 brass filter. Because scan resolution is dependent on the geometry of the object and the hands varied greatly in size and morphology, resolutions ranged from 15.98 to 44.53 μm. Several studies have shown that certain trabecular parameters (e.g. trabecular thickness or degree of anisotropy, see below) can be highly dependent on scan resolution (Kothari et al. 1998; Sode et al. 2008; Isaksson et al. 2010). Therefore, we have provided a relative resolution (mean trabecular thickness/pixels) for each taxon and anatomical area in Table 1, following Sode et al. (2008). The relative resolution is a measure of the number of pixels assigned to an average trabecular thickness and provides a normalized resolution to more easily compare values across taxa that vary greatly in body size (∼ 3–98 kg) and scan resolution (16–45 μm). The relative resolution ranges between 6.2 (Macaca) and 11.6 (Ateles), the smallest-bodied taxa with the thinnest average trabeculae and highest resolution, and between 4.8 (Gorilla) and 8.6 (Pongo), the largest-bodied taxa with the thickest average trabeculae and lowest scan resolution). These resolution values are equal to or higher than those found in clinical, high-resolution scans of humans (4.3) and mice (6.1) (Sode et al. 2008).
Each image was reconstructed as a 2048 × 2048 16-bit TIFF image stack from 2500 projections (angular positions) with two-frame averaging. Segmentation of bone from each image stack was accomplished using the ray casting algorithm (RCA; Scherf & Tilgner, 2009). RCA is an edge-detection-based segmentation method that differentiates bone from non-bone based on the gray-level gradient of the image, rather than the absolute gray-level values commonly used by global or iterative thresholding procedures (Scherf & Tilgner, 2009). Following segmentation, data were converted into 8-bit binarized image stacks (TIFF format).
Trabecular mass and architecture were quantified in the capitate head (proximal) and base (distal) and the articulating third metacarpal (MC3) base (proximal) and head (distal). To test for effects of VOI size and location, multiple VOIs were created in each anatomical region (Fig. 1). The effect of variation in VOI size was examined in the head of both the capitate and MC3 (both of which are roughly spherical). VOIs measuring 20, 35 and 50% of the minimum diameter of the capitate/MC3 head articular facet (mediolateral in all specimens) were positioned in the approximate center of the head of each bone. Deriving all three VOIs from the same anatomical origin ensured that differences in measured architectural properties did not accrue from variation in placement of the VOI within the trabecular mass of the head.
Fig. 1.
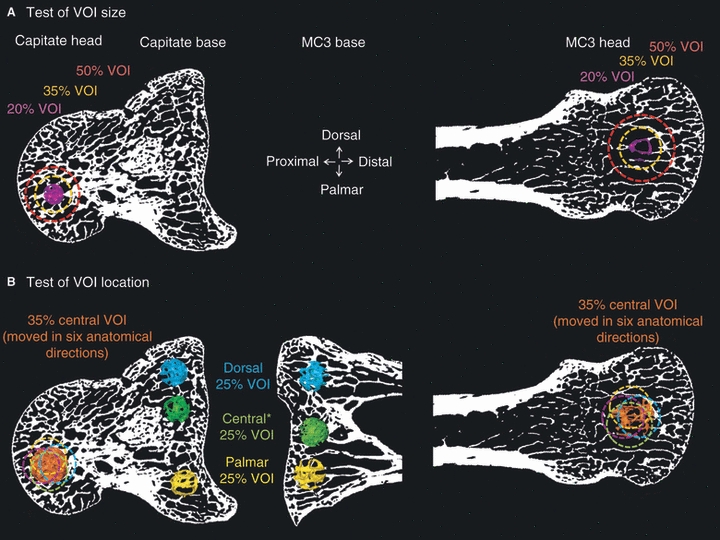
An example of volumes of interest (VOI) placed in the Gorilla capitate head and base (lateral view) and MC3 base (lateral view) and head (dorsal view) to test for effects of VOI size (A) and location (B). (A) Test of VOI size was conducted only in the spherical heads of the capitate and MC3 (B) Test of VOI location was conducted in the capitate and MC3 heads by shifting the VOI in six anatomical directions (not all are depicted). The test of VOI location in the capitate and MC3 bases was conducted by placing a VOI in dorsal, central and palmar positions (see Methods for details). *The central VOI is not ‘centered’ in the capitate base in Gorilla because of anatomical constraints of the invaginated medial side. However, in other taxa, this VOI was placed more centrally. The CT slice depicted is not necessarily ideal for all VOIs. Images not to scale.
To evaluate the effect of VOI location we used two methods to accommodate the morphological differences between the roughly spherical head and the more complex, blocky base of each bone. In the capitate and MC3 heads we created six spherical VOIs scaled at 35% (in addition to the central VOI), which were shifted 10% of the maximum mediolateral breadth of the articular facet from the original centered position in six anatomical directions: dorsal/palmar, medial/lateral and distal/proximal (Fig. 1A). As specimens were desiccated, articulated whole hands, individual elements could not be oriented in a consistent position during scanning; therefore the shifted VOI position approximates that of the above-mentioned anatomical directions. In the capitate and MC3 bases we placed three spherical VOIs (scaled arbitrarily to 25% of mediolateral breadth of the base in all specimens) in dorsal, palmar and central positions of the subarticular area (Fig. 1B).
The positioning of each VOI was determined in avizo 6.1® (Mercury Systems) using both a transparent surface model of the specimen as well as three orthogonal slices through the CT volume. All VOIs comprised trabecular bone only. The following commonly used trabecular morphometric parameters were then quantified for each VOI using CTan® (skyscan™, 2007): bone volume fraction (BV/TV), trabecular number (Tb.N), trabecular separation (Tb.Sp), trabecular bone pattern factor or connectivity (Tb.Pf), structure model index (SMI), trabecular thickness (Tb.Th), and degree of anisotropy (DA). These parameters characterize relative bone mass, organization and orientation and have been shown to be significant determinants of tissue-level mechanical properties (e.g. Young's modulus, failure strength) as well as indicators of bone/joint function such as direction and magnitude of loading (e.g. Mittra et al. 2005; Ryan & Rietbergen, 2005; Bevill et al. 2006; Pontzer et al. 2006; Fajardo et al. 2007; Sran et al. 2007).
Degree of anisotropy quantifies the relative degree of alignment among trabeculae in a VOI, while the primary orientation of that alignment is determined by the first eigenvector. In CTan, DA was determined by calculating the mean intercept length, or the distance between bone intercepts found by projecting a series of lines through a 3D volume of trabeculae. A high DA value (closer to 1) means fewer bony intercepts and thus a relatively more aligned or anisotropic trabecular pattern, whereas a lower DA value (closer to 0) means more bony intercepts and a more isotropic trabecular pattern (Skyscan™, 2007). Note that throughout this paper we use a ratio of the degree of anisotropy: DA = 1 − [min. eigenvalue/max. eigenvalue]. This ratio bounds the DA values between 0 (total isotropy) and 1 (total anisotropy), as opposed to the more cumbersome raw DA values, which range from 1 (total isotropy) to infinity (total anisotropy). The primary directionality of trabecular orientation within the VOI can be determined using the first eigenvector, which is the angle of the long axis of a 3D ellipsoid that is fitted to the trabecular matrix based on the mean intercept length analysis. We analyzed the influence of VOI size and location on the angle of the first eigenvector in the capitate and MC3 heads, whereas the effect on DA was assessed in all anatomical locations.
Our study sample consists of a taxonomically diverse range of primates of varying body size, morphology and positional behavior in order to assess intra-individual variation in taxa whose carpal/metacarpal structure differs substantially in form. A single specimen represents each taxon, resulting in total of 26 VOIs examined in each individual and 182 VOIs in the study overall. Although it is possible that a larger sample would yield specimens with less (or more) variation and allow for intra- and interspecific comparisons, our aim here is to show how variation in VOI size and location in each individual can affect trabecular parameters. Because statistical analysis of a small sample is problematic, we illustrate the potential variation in trabecular architecture due to differences in VOI size and location using the coefficient of variation and descriptive statistics, including the mean, minimum and maximum values and standard deviation (see Appendices 1–3). The coefficient of variation [CV; CV = 100 × (standard deviation/mean)] is an effective way of comparing variation across taxa with vastly different mean values (Cope & Lacy, 1995). For clarity, we considered parameters with a CV of 10.0 or greater to be highly variable. When a trabecular parameter yielded both positive and negative values, the CV was not reported. In such cases (i.e. Tb.Pf and SMI in the capitate head), the mean is close to zero and the standard deviation relatively high, which renders the CV misleading and inappropriate (Zar, 1984). Thus, comparisons of these parameters can only be assessed graphically (Figs 2 and 3) and via the mean and standard deviation (Appendices 1 and 2).
Fig. 2.
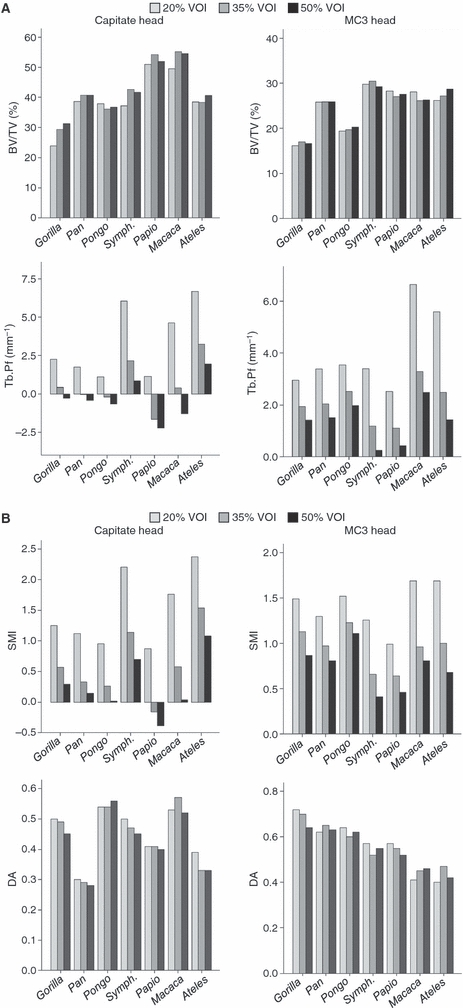
Variation in selected trabecular parameters due to changes in scaled VOI size (20, 35 and 50%) in the capitate head and MC3 head. (A) Bone volume fraction (BV/TV) and trabecular connectivity (Tb.Pf), (B) structure model index (SMI) and degree of anisotropy. Note: Trabecular connectivity (Tb.Pf) and structure (SMI) are both based on the relative proportion of convex (quantified as positive values) and concave (quantified as negative values) trabecular surfaces. In bone that is particularly well-connected (i.e. many enclosed concavities) Tb.Pf and SMI values can be negative, as is seen in Papio, for example.
Fig. 3.

Variation in selected trabecular parameters due to changes in VOI location (distal/proximal, medial/lateral, dorsal/palmar) relative to the central VOI in the capitate and MC3 heads (see Methods). Trabecular parameters include (A) bone volume (BV/TV) and trabecular connectivity (Tb.Pf; lower values indicated more connected trabecular structure); (B) trabecular thickness (Tb.Th) and degree of anistropy (DA; values closer to 0 are more isotropic and values closer to 1 are more anisotropic).
Results
Test of VOI size in the capitate and MC3 heads
Variation in VOI size (scaled to 20, 35 and 50%) does not result in high variability in the quantification of bone volume fraction (BV/TV), trabecular thickness (Tb.Th), number (Tb.N), or orientation (DA) in either the capitate or MC3 heads (Table 2, Fig. 2, Appendix 1). However, trabecular separation (Tb.Sp) exhibits substantial variability (i.e. CV > 10.0) in Symphalangus, Ateles and Macaca. The use of the CV to assess connectivity (Tb.Pf) and structure (SMI) was not appropriate in the capitate head (see Methods). However, Fig. 2 demonstrates graphically that in moving from a smaller to a larger VOI size, connectivity increases and the structure (SMI) becomes more plate-like in all taxa (as reflected in lower values in these parameters, see also Appendix 1). The same pattern is found in the MC3 head across all taxa, with connectivity and SMI varying greatly in several taxa (e.g. Symphalangus, Papio, Ateles; Table 2). Overall, these results suggest that the majority of parameters are robust against changes in VOI size, with the notable exceptions of trabecular connectivity and the structure model index.
Table 2.
Variation in trabecular parameters, expressed as the coefficient of variation (CV), attributable to changes in VOI size (20, 35 and 50% scaled VOIs) in the capitate head and MC3 head.
| Taxon | Location | Bone volume BV/TV | Connectivity Tb.Pf | Structure SMI | Thickness Tb.Th | Number Tb.N | Separation Tb.Sp | Anisotropy DA |
|---|---|---|---|---|---|---|---|---|
| Gorilla | Cap head | 13.7 | – | – | 9.9 | 4.4 | 4.6 | 5.5 |
| Pan | Cap head | 3.1 | – | – | 5.1 | 3.2 | 9.0 | 3.5 |
| Pongo | Cap head | 2.5 | – | – | 1.4 | 3.1 | 5.9 | 2.1 |
| Symph | Cap head | 7.2 | – | – | 7.4 | 7.2 | 19.4 | 5.3 |
| Papio | Cap head | 3.1 | – | – | 7.5 | 5.7 | 8.8 | 1.4 |
| Macaca | Cap head | 5.8 | – | – | 6.9 | 2.5 | 6.3 | 4.9 |
| Ateles | Cap head | 3.3 | – | – | 10.0 | 7.2 | 28.7 | 9.9 |
| Gorilla | MC3 head | 2.6 | 36.8 | 26.8 | 1.2 | 2.6 | 8.6 | 6.1 |
| Pan | MC3 head | 0.1 | 41.5 | 24.3 | 1.2 | 1.5 | 5.1 | 2.4 |
| Pongo | MC3 head | 2.3 | 29.5 | 16.4 | 2.8 | 2.2 | 5.5 | 3.2 |
| Symph | MC3 head | 2.1 | 100.1 | 56.3 | 0.1 | 3.3 | 8.3 | 4.6 |
| Papio | MC3 head | 2.3 | 79.0 | 38.7 | 2.7 | 2.5 | 7.6 | 4.6 |
| Macaca | MC3 head | 4.1 | 53.4 | 40.8 | 2.0 | 2.0 | 15.8 | 6.0 |
| Ateles | MC3 head | 4.7 | 68.2 | 46.0 | 4.3 | 1.9 | 14.0 | 8.4 |
Note: CVs greater than 10.0 are given in bold. The coefficient of variation (CV) is not provided for Tb.Pf and SMI because both parameters yielded both positive and negative values (Zar, 1984). See Fig. 2 for a graphic depiction of the variation in these parameters. Cap, capitate; MC3, third metacarpal; Symph., Symphalangus.
Test of VOI location in the capitate and MC3 heads
In each specimen, six scaled (to 35% of the minimum diameter of the articular facet) VOIs were shifted along orthogonal axes from the position of the central VOI anywhere from 0.39 to 1.36 mm (in Ateles and Gorilla, respectively) in the capitate head and from 0.48 to 1.53 mm (in Macaca and Gorilla, respectively) in the MC3 head, depending on the size of the element. The effects of changing VOI location in the capitate and MC3 heads are summarized in Table 3 and Fig. 3 (see also Appendix 2). Compared to altering VOI size, varying VOI location in the capitate and MC3 heads resulted in greater variability of the measured trabecular parameters in most taxa. Bone volume fraction (BV/TV) varies to a greater degree in the MC3 head than in the capitate head (with the exception of Symphalangus, Table 3). In the capitate head, the approximate distal and proximal VOI locations in particular demonstrate the greatest variability (Fig. 3A).
Table 3.
Variation in trabecular parameters. expressed as the coefficient of variation (CV), attributable to changes in VOI location in the capitate head and MC3 head.
| Taxon | Location | Bone volume BV/TV | Connectivity Tb.Pf | Structure SMI | Thickness Tb.Th | Number Tb.N | Separation Tb.Sp | Anisotropy DA |
|---|---|---|---|---|---|---|---|---|
| Gorilla | Cap head | 4.6 | – | 17.3 | 3.5 | 3.3 | 4.4 | 11.2 |
| Pan | Cap head | 4.9 | – | 28.8 | 3.2 | 2.3 | 3.2 | 13.5 |
| Pongo | Cap head | 3.6 | – | 32.2 | 5.5 | 2.7 | 4.1 | 6.7 |
| Symph | Cap head | 10.5 | – | 8.9 | 8.1 | 6.2 | 11.6 | 8.5 |
| Papio | Cap head | 5.0 | – | – | 5.5 | 1.5 | 5.1 | 13.6 |
| Macaca | Cap head | 5.7 | – | 21.1 | 11.3 | 8.6 | 9.8 | 6.9 |
| Ateles | Cap head | 7.5 | – | 13.0 | 7.9 | 7.9 | 14.0 | 19.0 |
| Gorilla | MC3 head | 12.4 | 18.6 | 14.2 | 2.4 | 12.7 | 8.1 | 3.7 |
| Pan | MC3 head | 3.2 | 15.0 | 9.2 | 0.7 | 3.4 | 2.7 | 4.9 |
| Pongo | MC3 head | 13.7 | 19.5 | 10.7 | 10.1 | 8.1 | 7.8 | 12.4 |
| Symph. | MC3 head | 10.2 | 35.7 | 14.6 | 4.6 | 9.2 | 10.4 | 4.9 |
| Papio | MC3 head | 10.5 | 46.5 | 19.6 | 2.7 | 10.7 | 8.1 | 8.4 |
| Macaca | MC3 head | 13.1 | 22.6 | 13.7 | 2.7 | 12.2 | 13.7 | 9.4 |
| Ateles | MC3 head | 9.3 | 30.1 | 17.4 | 1.8 | 9.3 | 10.3 | 17.5 |
Note: CVs greater than 10.0 in bold. The coefficient of variation (CV) is not provided for Tb.Pf because it yielded both positive and negative values (Zar, 1984). See Fig. 3 for a graphic depiction of the variation in Tb.Pf. Abbreviations the same as in Table 2.
Trabecular thickness (Tb.Th) and number (Tb.N) are relatively robust to shifting VOI location in both the capitate and MC3 heads (Table 3). Trabecular thickness is the only parameter to vary more in the capitate head than in the MC3 head and, interestingly, the pattern of results (i.e. taxa distributed by body size; Fig. 3B) suggests that there may be a positive allometric effect (contraSwartz et al. 1998). Generally, the distal and proximal VOI locations within each head are more variable compared to the other four locations. On the other hand, trabecular connectivity (Tb.Pf) and structure (SMI) are highly influenced by VOI position. Connectivity and structure are remarkably variable in the MC3 head in all VOI positions and slightly less variable in the capitate head (Table 3; CV for Tb.Pf. is unreliable but see Fig. 3A).
The degree of trabecular anisotropy (DA) is also variable in the capitate head and is only slightly less so in the MC3 head (Table 3, Fig. 3B). In other words, shifting VOI position can have a dramatic impact on the degree to which trabeculae evince a preferred orientation. In the Ateles capitate head, for example, trabeculae may be relatively isotropic (DA = 0.23) or more anisotropic (DA = 0.44), depending of VOI location (Appendix 2). Trabecular separation (Tb.Sp) exhibited a similar pattern of variation due to change in VOI location.
Figure 4 illustrates the angular difference between the reference eigenvector (calculated for the central VOI and depicted graphically as 0°) and the first eigenvector for each of the six additional VOIs in both the capitate and MC3 heads. The amount of variation in the angle of orientation differs between anatomical regions, among VOI locations and among taxa. In general, trabecular orientation in Pongo (2–9°), Gorilla (1–8°) and Macaca (1–5°) is relatively robust to changes in VOI location in the capitate head, compared to Ateles (5–56°), Papio (3–24°) and Symphalangus (7–31°). In the MC3 head, variation in the primary orientation of trabeculae is greatest in Ateles (6–89°), Papio (1–36°) and Gorilla (3–30°), and moderate in the remaining taxa (Fig. 4).
Fig. 4.

Angular differences (in degrees) in the primary orientation of trabeculae (i.e. first eigenvector) that results from shifting the VOI location in six anatomical directions. The 0° line represents the value of the first eigenvector of the central VOI to which all other VOIs are compared in the capitate head (A) and MC3 head (B). Each colored line represents the difference (in degrees) from the central VOI eigenvector by shifting the VOI distally (red), proximally (blue), medially (green), laterally (orange), dorsally (purple) and palmarly (black). For example, the first eigenvectors of the six VOIs in the Pan capitate head vary from that of central VOI by 4° in the proximal VOI and up to 19° in the dorsal VOI.
Test of VOI location in capitate and MC3 bases
Variation in the VOI location (i.e. dorsal, central and palmar) in the base of both the capitate and MC3 has dramatic effects on all parameters in most, but not all, taxa (Table 4, Fig. 5). It is perhaps not surprising that these effects are generally more exaggerated in the more complex morphology of the base than in the spherical arthroses of the corresponding heads. For example, variation in measured bone volume fraction (BV/TV) in the capitate base is substantial in some taxa (e.g. Pongo, Ateles and Symphalangus; Table 4). In Pongo, such variation translates into a 30% difference in bone volume depending on the VOI location, with a BV/TV of only 13.6% in the central VOI but of 46.2% in the palmar VOI (Appendix 3). BV/TV is even more variable in the MC3 base (Table 4).
Table 4.
Variation in trabecular parameters. expressed as the coefficient of variation (CV), attributable to changes in VOI location in the capitate base and MC3 base.
| Taxon | Location | Bone volume BV/TV | Connectivity Tb.Pf | Structure SMI | Thickness Tb.Th | Number Tb.N | Separation Tb.Sp | Anisotropy DA |
|---|---|---|---|---|---|---|---|---|
| Gorilla | Cap base | 33.3 | 55.5 | 13.0 | 22.2 | 12.0 | 12.9 | 38.7 |
| Pan | Cap base | 3.0 | 3.0 | 1.8 | 2.4 | 0.3 | 4.0 | 8.1 |
| Pongo | Cap base | 63.9 | 78.9 | 44.9 | 33.5 | 30.6 | 23.3 | 7.8 |
| Symph | Cap base | 40.1 | 60.0 | 25.9 | 30.4 | 9.3 | 6.2 | 29.9 |
| Papio | Cap base | 26.6 | 55.3 | 24.1 | 17.6 | 10.6 | 17.8 | 17.5 |
| Macaca | Cap base | 6.2 | 10.4 | 11.6 | 14.7 | 19.3 | 26.9 | 3.4 |
| Ateles | Cap base | 51.1 | 42.8 | 14.3 | 16.2 | 40.8 | 42.7 | 29.5 |
| Gorilla | MC3 base | 7.8 | 33.3 | 9.4 | 9.3 | 10.8 | 5.7 | 27.3 |
| Pan | MC3 base | 31.4 | 49.5 | 22.0 | 13.7 | 19.8 | 14.0 | 9.5 |
| Pongo | MC3 base | 29.5 | 26.6 | 14.4 | 6.0 | 25.4 | 9.7 | 3.1 |
| Symph | MC3 base | 79.2 | 58.3 | 9.7 | 33.9 | 64.4 | 45.5 | 14.1 |
| Papio | MC3 base | 6.1 | 38.8 | 20.1 | 2.7 | 8.5 | 6.1 | 30.8 |
| Macaca | MC3 base | 43.5 | 35.7 | 14.8 | 9.3 | 39.2 | 49.0 | 8.8 |
| Ateles | MC3 base | 81.5 | 29.5 | 17.8 | 10.0 | 83.2 | 21.1 | 24.0 |
Note: CVs greater than 10.0 are given in bold. Abbreviations are the same as in Table 2.
Fig. 5.
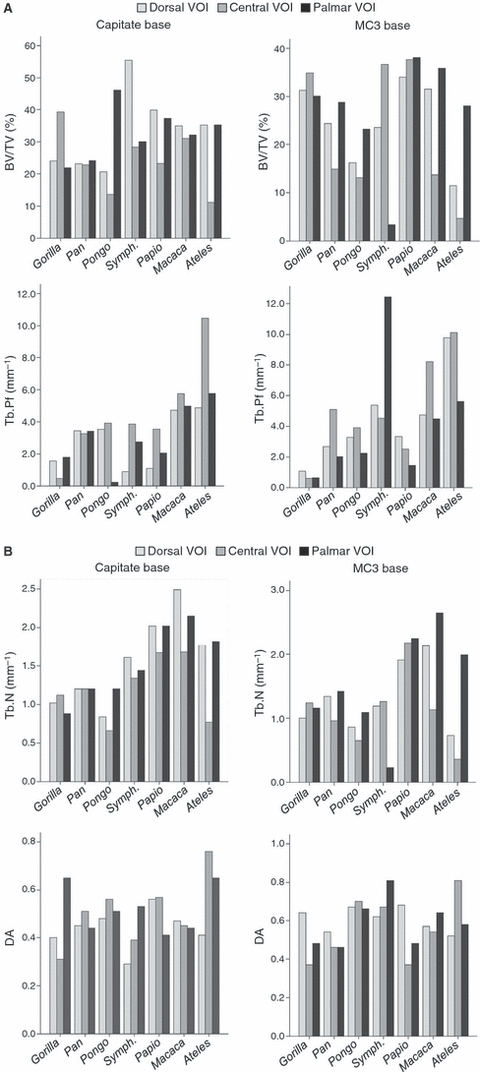
Variation in selected trabecular parameters due to changes in VOI location (dorsal, central and palmar) in the capitate base and MC3 base. (A) Bone fraction number (BV/TV) and trabecular connectivity (Tb.Pf), (B) trabecular number (Tb.N) and degree of anisotropy (DA). See Fig. 3 for description of trabecular parameters.
Parameters quantifying trabecular organization are affected by VOI location differently depending on the taxon but for each parameter the majority of taxa exhibit considerable variation. For example, in the capitate base, at least six of seven parameters exhibit CVs greater than 10.0 in Gorilla, Pongo, Papio and Ateles (Table 4). As found in the anatomical heads, trabecular connectivity (Tb.Pf) is remarkably variable, with high CV values in all taxa except Pan in both the capitate and MC3 bases (Table 4). Degree of anisotropy (DA) varies greatly as well across most taxa in both the capitate and MC3 bases (Table 4 and Fig. 5). In the capitate base, trabecular parameters in Pan appear uniquely robust to shifts in VOI location, indicating a relatively homogeneous trabecular structure in that taxon, but all other taxa are substantially more variable.
In summary, trabecular parameters are more susceptible to changes in VOI location than to changes in VOI size. Trabecular connectivity (Tb.Pf) and structure (SMI) are the notable exceptions, being strongly affected by changes both in VOI size and in location in all anatomical areas and in most taxa. In contrast, trabecular thickness and number are relatively robust to all changes in the VOI in both the capitate and MC3 heads. Varying the VOI location in the capitate and MC3 heads also strongly affects the degree of anisotropy (DA), trabecular separation (Tb.Sp) and trabecular orientation (i.e. first eigenvector). All trabecular parameters are substantially affected by changes in VOI location in the more complex arthroses of the capitate and MC3 bases in all taxa except Pan.
Discussion
Previous trabecular studies discussed caveats regarding potential biases created by the size and location of the volume of interest (VOI) in interspecific studies in which body size varies greatly (Fajardo & Müller, 2001) and/or morphology is complex (Maga et al. 2006). This analysis investigated the potential influence of VOI size and location on trabecular parameters in the capitate and third metacarpal (MC3) in a taxonomically diverse sample of primates that vary greatly in body mass and morphology. We found that changes in VOI location in particular and, to a lesser extent, changes in VOI size, had a dramatic affect on the majority of trabecular parameters in all four anatomical regions examined and in almost all taxa. Figure 6 presents 3D isosurface reconstructions from the central MC3 head VOI illustrating the variation in trabecular anatomy across the study sample. This study demonstrates and formally quantifies that certain trabecular parameters (i.e. degree of anisotropy, trabecular connectivity, structure and orientation) are particularly sensitive to choice of VOI, whereas other parameters (i.e. bone volume fraction, trabecular number and thickness) are generally more robust. These results exemplify the difficulty in intra- and interspecific studies of determining VOIs that are anatomically and/or functionally homologous (e.g. Maga et al. 2006). Informed consideration of the VOI location and size is critical for the robust analysis of trabecular architecture.
Fig. 6.
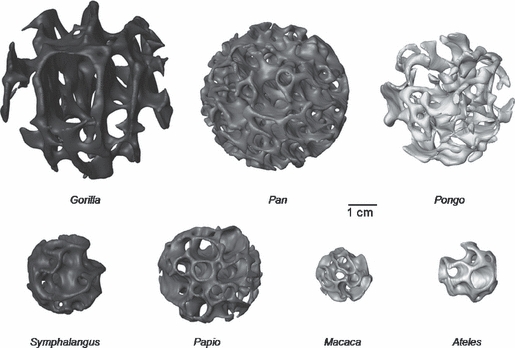
An example of variation in trabecular anatomy in the third metacarpal head of each taxon. The 3D isosurface models of the scaled (to 35% of articular facet width), central volume of interest are depicted, illustrating the variation in size and trabecular anatomy across the study sample. All images are to 1-cm scale.
In the capitate and MC3 heads, most trabecular parameters were more robust to changes in VOI size than to changes in VOI location, although trabecular connectivity and structure (SMI) were strongly affected in both cases. The capitate and MC3 heads are both generally spherical in shape, but the trabeculae of the MC3 are typically more heterogeneous and do not extend as far proximally (i.e. towards the shaft of the metacarpal) as they do towards the body (distally) in the capitate. This difference may reflect the fact that, unlike the capitate, which develops from a single ossification center, the MC3 head is an epiphysis, and the adult trabecular architecture may be influenced by developmental factors (e.g. endochondral ossification of the growth plate). As such, shifting of the VOI location distally and proximally generally produced more variable results compared to the central VOI. This pattern of variability was found in both elements and suggests that researchers should be mindful of VOI placement in these anatomical areas, particularly with regard to proximodistal directions.
Placing VOIs in complex arthroses
Trabecular organization in the capitate and MC3 bases was more susceptible to changes in VOI location than the roughly spherical anatomical heads, demonstrating that informed placement and size of the VOI is especially important in bones with complex anatomy (Maga et al. 2006). The capitate and MC3 bases share an articulation and both bones also form multiple articulations with other carpals and metacarpals. However, in cercopithecoids this anatomical area is roughly square and, in the smaller species, placement of a single, central VOI is reasonable to quantify the trabecular architecture in each base. Conversely, the large, more complex (i.e. beveled and palmarly elongated) capitates–MC3 articulation of great apes would intuitively require both a dorsal and palmar VOI to capture regional variation and potentially yield a more detailed understanding of loading at this joint. Furthermore, the medial side of the hominoid capitate is invaginated by the deep ligamentous attachment site, making placement of a central VOI difficult and the trabecular architecture in this region more heterogeneous. The question then remains, are homologous VOIs attainable in interspecific studies where size, shape and trabecular morphology vary substantially (Maga et al. 2006; see below)?
The results of this study show that, especially in analyses of complex arthroses, trabecular parameters are influenced by VOI location. For example, bone volume fraction and degree of anisotropy are known to be two of the main determinants of the mechanical properties of trabecular bone (e.g. Rice et al. 1988; Ulrich et al. 1999). In the capitate base, placing the VOI in a central vs. dorsal or palmar position can alter the relative bone volume by roughly 30% and the degree of anisotropy by up to 0.3 (on a scale of 0 to 1). Knowledge of potential bias in quantifying the bone volume fraction is especially important when one considers that BV/TV can predict > 80% of overall bone strength as measured by Young's modulus (Odgaard, 1997; Stauber et al. 2006).
Appropriate parameters for small and/or complex arthroses
In studies of trabecular bone, the direction of the first eigenvector is commonly interpreted as representing the primary direction of load or force through a bone (Maga et al. 2006; Ryan & Krovitz, 2006). Given the variation in the degree of anisotropy already discussed, it is not surprising that the first eigenvector is strongly influenced by VOI position as well. For example, shifting the VOI by < 1 mm in the MC3 head can change the primary direction of orientation by as much as 30°. Such differences in trabecular orientation can have a substantial effect on the functional interpretation of a joint or bone, especially in interspecific studies including fossil taxa for which we can rely only on preserved bone to interpret positional behavior (Ryan & Ketcham, 2002b; Maga et al. 2006; Scherf, 2008; Scherf et al. 2009).
With regards to VOI size, Lazenby et al. (2010b) demonstrated the importance of using VOIs that are scaled to some measure of bone/body size rather than a standardized VOI size in interspecific trabecular analyses. They recommended using scaled VOIs to avoid oversampling bias (see Fajardo & Müller, 2001) but caution that the scaling criterion in their study and in previous analyses (e.g. Ryan & Ketcham, 2002a; Maga et al. 2006) is chosen arbitrarily. Our study similarly demonstrates that the scaling criterion can influence some trabecular parameters, especially trabecular connectivity (Tb.Pf) and structure (SMI).
Trabecular connectivity and structure are calculated in a similar way and are highly correlated (Lazenby et al. 2008a), thus it is not unexpected that they are equally affected by changes to the VOI. Connectivity and structure are sensitive to changes in volume, especially in highly connected bone, and a smaller VOI may truncate some trabeculae (e.g. cutting a rod in half) that are complete in a larger VOI, demonstrating the importance of making informed decisions about VOI size. For example, connectivity and structure were dramatically influenced by shifting a 35% scaled VOI either distally or proximally from the central position in the capitate head (Fig. 2). A VOI scaled to 50% incorporates these more distal and proximal regions of the capitate head and, consequently, trabecular connectivity and structure change relative to a smaller VOI (Fig. 4). The sensitivity of these parameters to variation in the VOI is not trivial. Loss of connectivity is a significant predictor of structural failure in, for example, studies of skeletal aging and osteoporosis (Riggs et al. 2008; Recker et al. 2009). The relative proportion of rods vs. plates has been shown to be a major determinant of trabecular stiffness and yield strength (Stauber et al. 2006; Sran et al. 2007). The structure of a trabecular mass is thought to reflect relative magnitude of loading, with plates accommodating higher functional strains and rods preferentially located in a region of lower strain (Ding et al. 2001; Ryan & Ketcham, 2005). Although all parameters were influenced by changes in VOI size and location in at least some individuals, trabecular connectivity and structure were substantially affected by these changes in all anatomical regions and the majority of taxa, and therefore may not necessarily yield informative values in small, complex arthroses.
Limitations and recommendations
Several studies have shown that some trabecular parameters, particularly trabecular thickness, structure model index and degree of anisotropy, can be highly sensitive to changes in scan resolution (Kothari et al. 1998; Sode et al. 2008; Isaksson et al. 2010). For example, Isaksson et al. (2010) recently showed that anisotropy values increase (because thinner, connecting trabeculae disappear first) and the SMI error increases as resolution decreases. Thus, we cannot rule out that differences in scan resolution across taxa in this study may account for some of the variation found in trabecular parameters. Although it is especially important to acknowledge such a bias in intra- or interspecific comparative studies, in an intra-individual study such as this, all VOIs within each individual will be equally biased (if at all) by the scan resolution and thus it is not considered to have a substantial impact on our results.
This study demonstrates that VOI size and location can affect the trabecular parameters within an individual in all of our sampled taxa, regardless of their differences in morphology, body size and positional behavior. However, with only one specimen per taxon, we are unable to evaluate how these trabecular parameters may vary within a species or across species. Larger sample sizes of each taxon may reveal patterns in the affects of VOI choice that permit more predictable quantification of bias or reveal some parameters as being more (or less) robust to changes in VOI size and location than the current study suggests. However, this study reveals that even among taxa with similar positional behaviors, such as Pan and Gorilla (knuckle-walkers) or Symphalangus and Ateles (brachiators), the differences in (1) the trabecular parameter values and, (2) how the trabecular parameters are affected by varying VOI size and location are still profound. Some parameters seem to be more influenced by body size and thus allometry must also be considered with functional interpretations. It is interesting to note that trabecular thickness, which is said to scale negatively or not at all with body size (Swartz et al. 1998; Fajardo & Müller, 2001), appears to shows a positive allometric relationship in this study (Fig. 3B).
The susceptibility of some trabecular parameters to be strongly influenced by relatively minor changes in VOI size and especially VOI location suggests that we must use caution when interpreting the functional significance of intra- and interspecific differences in trabecular parameters. Furthermore, these results demonstrate that we must be equally cautious when comparing results across different studies that may have used different VOI sizes or locations. Even measures of relative bone volume, anisotropy and the primary orientation of the trabeculae (i.e. first eigenvector) that are considered the most direct measures of bone strength and loading pattern are substantially influenced by variation in the VOI location. We recommend that researchers try to understand the inherent bias in their study sample by testing a priori the influence of differently scaled VOI sizes and variation in VOI location in each taxon, and subsequently using appropriate caution in interpreting the functional significance of interspecific variation. Trabecular analyses of irregular-shaped bones (e.g. carpal bones) are inherently constrained by anatomy and thus we support the aim of Maga et al. (2006) to determine biomechanically, rather than anatomically, homologous VOIs (although these are not necessarily mutually exclusive). Ultimately, the goal of trabecular analyses is a more comprehensive understanding of function (e.g. loading) of a joint or bone; thus choice of VOI size/location, especially in interspecific studies, should be guided by how the bone functions within the joint and the anatomical region in each species. Our analysis reveals clearly that informed choice of scaled VOI size and location is critical for robust trabecular analyses, especially in anatomical regions with complex and varying arthrosis morphology.
Acknowledgments
We are grateful to Frieder Mayer and Saskia Jancke (Berlin Museum für Naturkunde) and Virginie Volpato (Frankfurt Senckenberg Museum) for access to specimens. We thank Andreas Winzer for help with scanning the material, Rico Tilgner for helpful advice during the analysis and Philipp Gunz for help with the figures. We are also grateful to all participants of the Max Planck Institute for Evolutionary Anthropology Trabecular Workshop for an informative discussion that helped in the initial stages of this project. We thank two anonymous reviewers for their constructive comments that greatly improved this manuscript. This research is funded by the Max Planck Society (M.M.S. and T.L.K.) and the Natural Sciences and Engineering Research Council of Canada Discovery Grant 183660-03 (R.L.).
Appendix 1
Raw summary statistics for each trabecular parameter from the three scaled (20, 35 and 50%) VOIs in the capitate head (a) and MC3 head (b). SD, standard deviation; min-max, minimum and maximum values; Symph., Symphalangus.
| Taxon | Variable (unit) | BV/TV (%) | Tb.Pf (mm−1) | SMI (–) | Tb.Th (mm) | Tb.N (mm−1) | Tb.Sp (mm) | DA (–) |
|---|---|---|---|---|---|---|---|---|
| (a) Capitate head | ||||||||
| Gorilla | Mean | 28.13 | 0.79 | 0.70 | 0.27 | 1.04 | 0.75 | 0.48 |
| SD | 3.86 | 1.30 | 0.49 | 0.03 | 0.05 | 0.03 | 0.03 | |
| Min–max | 23.81–31.24 | −0.28 to 2.24 | 0.29–1.25 | 0.24–0.29 | 1.00–1.09 | 0.71–0.77 | 0.45–0.50 | |
| Pan | Mean | 39.99 | 0.42 | 0.53 | 0.27 | 1.46 | 0.51 | 0.29 |
| SD | 1.22 | 1.15 | 0.52 | 0.01 | 0.05 | 0.05 | 0.01 | |
| Min–max | 38.58–40.7 | −0.42 to 1.73 | 0.14–1.12 | 0.26–0.29 | 1.41–1.49 | 0.46–0.55 | 0.28–0.30 | |
| Pongo | Mean | 36.85 | 0.07 | 0.41 | 0.26 | 1.40 | 0.59 | 0.55 |
| SD | 0.91 | 0.90 | 0.48 | 0.00 | 0.04 | 0.03 | 0.01 | |
| Min–max | 36.02–37.83 | −0.66 to 1.08 | 0.02–0.95 | 0.26–0.27 | 1.37–1.45 | 0.55–0.61 | 0.54–0.56 | |
| Symph. | Mean | 40.46 | 2.99 | 1.35 | 0.24 | 1.67 | 0.41 | 0.47 |
| SD | 2.90 | 2.72 | 0.78 | 0.02 | 0.12 | 0.08 | 0.03 | |
| Min–max | 37.15–42.58 | 0.81–6.04 | 0.70–2.21 | 0.23–0.26 | 1.58–1.81 | 0.32–0.47 | 0.45–0.50 | |
| Papio | Mean | 52.39 | −0.93 | 0.11 | 0.23 | 2.27 | 0.29 | 0.41 |
| SD | 1.63 | 1.79 | 0.67 | 0.02 | 0.13 | 0.03 | 0.01 | |
| Min–max | 51.00–54.19 | −2.23–1.11 | −0.39 to 0.87 | 0.21–0.24 | 2.16–2.41 | 0.26–0.31 | 0.40–0.41 | |
| Macaca | Mean | 53.06 | 1.23 | 0.79 | 0.21 | 2.55 | 0.24 | 0.54 |
| SD | 3.06 | 3.04 | 0.88 | 0.01 | 0.06 | 0.02 | 0.03 | |
| Min–max | 49.54–55.13 | −1.29 to 4.61 | 0.04–1.76 | 0.19–0.22 | 2.48–2.60 | 0.23–0.26 | 0.52–0.57 | |
| Ateles | Mean | 39.10 | 3.94 | 1.66 | 0.23 | 1.69 | 0.40 | 0.35 |
| SD | 1.30 | 2.45 | 0.65 | 0.02 | 0.12 | 0.12 | 0.03 | |
| Min–max | 38.27–40.60 | 1.93–6.67 | 1.08–2.37 | 0.21–0.26 | 1.58–1.82 | 0.27–0.48 | 0.33–0.39 | |
| (b) MC3 head | ||||||||
| Gorilla | Mean | 16.55 | 2.10 | 1.16 | 0.25 | 0.66 | 1.05 | 0.69 |
| SD | 0.43 | 0.77 | 0.31 | 0.00 | 0.02 | 0.09 | 0.04 | |
| Min–max | 16.11–16.96 | 1.42–2.94 | 0.87–1.49 | 0.25–0.25 | 0.64–0.67 | 0.99–1.15 | 0.64–0.72 | |
| Pan | Mean | 25.81 | 2.31 | 1.03 | 0.18 | 1.42 | 0.50 | 0.63 |
| SD | 0.02 | 0.96 | 0.25 | 0.00 | 0.02 | 0.03 | 0.02 | |
| Min–max | 25.78–25.82 | 1.52–3.38 | 0.81–1.30 | 0.18–0.18 | 1.40–1.44 | 0.47–0.52 | 0.62–0.65 | |
| Pongo | Mean | 19.77 | 2.68 | 1.29 | 0.22 | 0.92 | 0.69 | 0.62 |
| SD | 0.45 | 0.79 | 0.21 | 0.01 | 0.02 | 0.04 | 0.02 | |
| Min–max | 19.37–20.25 | 1.98–3.54 | 1.11–1.52 | 0.21–0.22 | 0.90–0.94 | 0.65–0.72 | 0.60–0.64 | |
| Symph. | Mean | 29.80 | 1.61 | 0.78 | 1.69 | 0.18 | 0.49 | 0.55 |
| SD | 0.62 | 1.61 | 0.44 | 0.07 | 0.01 | 0.04 | 0.03 | |
| Min–max | 29.2–30.44 | 0.25–3.39 | 0.41–1.26 | 1.62–1.75 | 0.17–0.18 | 0.45–0.53 | 0.52–0.57 | |
| Papio | Mean | 27.57 | 1.36 | 0.70 | 0.17 | 1.63 | 0.53 | 0.55 |
| SD | 0.64 | 1.07 | 0.27 | 0.00 | 0.04 | 0.04 | 0.03 | |
| Min–max | 26.98–28.25 | 0.43–2.53 | 0.46–0.99 | 0.17–0.17 | 1.59–1.67 | 0.49–0.57 | 0.52–0.57 | |
| Macaca | Mean | 26.80 | 4.14 | 1.15 | 0.13 | 2.04 | 0.38 | 0.44 |
| SD | 1.09 | 2.21 | 0.47 | 0.00 | 0.04 | 0.06 | 0.03 | |
| Min–max | 26.09–28.06 | 2.49–6.65 | 0.81–1.69 | 0.13–0.13 | 2.01–2.09 | 0.32–0.44 | 0.41–0.46 | |
| Ateles | Mean | 27.31 | 3.17 | 1.12 | 0.17 | 1.59 | 0.48 | 0.43 |
| SD | 1.27 | 2.16 | 0.52 | 0.01 | 0.03 | 0.07 | 0.04 | |
| Min–max | 26.14–28.66 | 1.43–5.59 | 0.68–1.69 | 0.16–0.18 | 1.56–1.62 | 0.40–0.52 | 0.40–0.47 | |
Appendix 2
Raw summary statistics for each trabecular parameter from the centrally placed scaled VOI (central VOI) and the six additional VOIs in varied anatomical positions (see text) in the capitate head (a) and MC3 head (b). Abbreviations are the same as in Appendix 1.
| Taxon | Variable (unit) | BV/TV (%) | Tb.Pf. (mm−1) | SMI (–) | Tb.Th (mm) | Tb.N (mm−1) | Tb.Sp (mm) | DA (–) |
|---|---|---|---|---|---|---|---|---|
| (a) | ||||||||
| Gorilla | Central VOI | 29.35 | 0.41 | 0.57 | 0.28 | 1.03 | 0.77 | 0.49 |
| Mean | 30.02 | 0.33 | 0.56 | 0.28 | 1.07 | 0.76 | 0.48 | |
| SD | 1.38 | 0.25 | 0.10 | 0.01 | 0.04 | 0.03 | 0.05 | |
| Min–max | 28.36–31.88 | −0.16 to 0.57 | 0.37–0.64 | 0.27–0.30 | 1.02–1.11 | 0.72–0.80 | 0.41–0.55 | |
| Pan | Central VOI | 40.70 | −0.04 | 0.33 | 0.27 | 1.49 | 0.52 | 0.29 |
| Mean | 40.43 | 0.14 | 0.42 | 0.28 | 1.46 | 0.53 | 0.29 | |
| SD | 1.98 | 0.25 | 0.12 | 0.01 | 0.03 | 0.02 | 0.04 | |
| Min–max | 37.85–42.75 | −0.12 to 0.48 | 0.28–0.62 | 0.26–0.29 | 1.41–1.49 | 0.51–0.55 | 0.23–0.33 | |
| Pongo | Central VOI | 36.02 | −0.20 | 0.26 | 0.26 | 1.38 | 0.61 | 0.54 |
| Mean | 36.83 | −0.18 | 0.26 | 0.26 | 1.41 | 0.60 | 0.55 | |
| SD | 1.31 | 0.19 | 0.08 | 0.01 | 0.04 | 0.02 | 0.04 | |
| Min–max | 35.59–39.37 | −0.49 to 0.03 | 0.14–0.36 | 0.24–0.28 | 1.35–1.46 | 0.34–0.48 | 0.50–0.60 | |
| Symph. | Central VOI | 42.58 | 2.13 | 1.14 | 0.24 | 1.81 | 0.44 | 0.47 |
| Mean | 41.59 | 2.22 | 1.19 | 0.24 | 1.70 | 0.42 | 0.46 | |
| SD | 4.37 | 0.42 | 0.11 | 0.02 | 0.10 | 0.05 | 0.04 | |
| Min–max | 37.08–49.84 | 1.56–2.86 | 0.04–1.04 | 0.22–0.28 | 1.58–1.81 | 0.34–0.48 | 0.41–0.52 | |
| Papio | Central VOI | 54.19 | −1.66 | −0.16 | 0.24 | 2.23 | 0.29 | 0.41 |
| Mean | 52.83 | −1.38 | −0.01 | 0.24 | 2.23 | 0.30 | 0.41 | |
| SD | 2.62 | 0.34 | 0.18 | 0.01 | 0.03 | 0.02 | 0.06 | |
| Min–max | 49.67–57.35 | −1.96 to −0.90 | −0.33 to 0.25 | 0.22–0.26 | 1.35–1.46 | 0.29–0.33 | 0.35–0.60 | |
| Macaca | Central VOI | 55.13 | 0.38 | 0.58 | 0.21 | 2.60 | 0.24 | 0.57 |
| Mean | 54.19 | 0.42 | 0.61 | 0.21 | 2.58 | 0.25 | 0.53 | |
| SD | 3.09 | 0.44 | 0.13 | 0.02 | 0.22 | 0.02 | 0.04 | |
| Min–max | 48.65–57.96 | −0.27 to 1.05 | 0.41–0.78 | 0.18–0.25 | 2.29–2.99 | 0.22–0.29 | 0.48–0.57 | |
| Ateles | Central VOI | 38.27 | 3.23 | 1.54 | 0.23 | 1.67 | 0.46 | 0.33 |
| Mean | 39.56 | 3.44 | 1.55 | 0.24 | 1.67 | 0.43 | 0.34 | |
| SD | 2.96 | 0.56 | 0.20 | 0.02 | 0.13 | 0.06 | 0.06 | |
| Min–max | 36.3–43.92 | 2.74–4.20 | 1.24–1.83 | 0.21–0.26 | 1.49–1.91 | 0.32–0.49 | 0.23–0.44 | |
| (b) | ||||||||
| Gorilla | Central VOI | 16.96 | 1.94 | 1.13 | 0.25 | 0.67 | 1.00 | 0.70 |
| Mean | 16.55 | 1.97 | 1.10 | 0.25 | 0.67 | 1.07 | 0.68 | |
| SD | 2.05 | 0.37 | 0.16 | 0.01 | 0.08 | 0.09 | 0.03 | |
| Min–max | 13.86–19.93 | 1.47–2.55 | 0.89–1.37 | 0.24–0.26 | 0.54–0.81 | 0.95–1.21 | 0.64–0.71 | |
| Pan | Central VOI | 25.82 | 2.04 | 0.97 | 0.18 | 1.43 | 0.50 | 0.65 |
| Mean | 25.86 | 2.08 | 0.97 | 0.18 | 1.42 | 0.51 | 0.63 | |
| SD | 0.83 | 0.31 | 0.09 | 0.00 | 0.05 | 0.01 | 0.03 | |
| Min–max | 24.46–27.34 | 1.52–2.58 | 0.81–1.11 | 0.18–0.18 | 1.34–1.50 | 0.49–0.53 | 0.58–0.67 | |
| Pongo | Central VOI | 19.69 | 2.53 | 1.23 | 0.21 | 0.94 | 0.71 | 0.60 |
| Mean | 20.62 | 2.36 | 1.20 | 0.22 | 0.92 | 0.72 | 0.59 | |
| SD | 2.83 | 0.46 | 0.13 | 0.02 | 0.07 | 0.06 | 0.07 | |
| Min–max | 17.60–26.09 | 1.55–2.91 | 0.96–1.36 | 0.20–0.27 | 0.81–1.04 | 0.63–0.80 | 0.45–0.66 | |
| Symph. | Central VOI | 30.44 | 1.19 | 0.66 | 0.18 | 1.69 | 0.48 | 0.52 |
| Mean | 29.79 | 1.19 | 0.69 | 0.18 | 1.68 | 0.51 | 0.54 | |
| SD | 3.03 | 0.43 | 0.10 | 0.01 | 0.15 | 0.05 | 0.03 | |
| Min–max | 25.15–32.87 | 0.49–1.91 | 0.52–0.85 | 0.17–0.19 | 1.42–1.93 | 0.46–0.61 | 0.52–0.58 | |
| Papio | Central VOI | 26.98 | 1.11 | 0.64 | 0.17 | 1.59 | 0.53 | 0.55 |
| Mean | 27.04 | 1.15 | 0.64 | 0.17 | 1.62 | 0.54 | 0.55 | |
| SD | 2.84 | 0.54 | 0.13 | 0.00 | 0.17 | 0.04 | 0.05 | |
| Min–max | 23.41–32.42 | 0.28–1.70 | 0.44–0.78 | 0.16–0.17 | 1.36–1.94 | 0.46–0.60 | 0.49–0.62 | |
| Macaca | Central VOI | 26.09 | 3.28 | 0.96 | 0.13 | 2.03 | 0.38 | 0.45 |
| Mean | 26.68 | 3.46 | 1.01 | 0.13 | 2.06 | 0.39 | 0.44 | |
| SD | 3.48 | 0.78 | 0.14 | 0.00 | 0.25 | 0.05 | 0.04 | |
| Min–max | 22.76–31.50 | 2.33–4.49 | 0.81–1.17 | 0.13–0.14 | 1.74–2.45 | 0.31–0.46 | 0.40–0.52 | |
| Ateles | Central VOI | 27.14 | 2.49 | 1.00 | 0.17 | 1.56 | 0.51 | 0.47 |
| Mean | 28.23 | 2.58 | 1.01 | 0.17 | 1.62 | 0.49 | 0.44 | |
| SD | 2.62 | 0.78 | 0.17 | 0.00 | 0.15 | 0.05 | 0.08 | |
| Min–max | 24.11–32.5 | 1.56–3.86 | 0.77–1.29 | 0.17–0.18 | 1.39–1.86 | 0.43–0.55 | 0.32–0.51 | |
Appendix 3
Raw summary statistics for each trabecular parameter from the three scaled (25%) VOIs located in dorsal, central and palmar positions of the capitate base (a) and MC3 base (b). Abbreviations are the same as in Appendix 1.
| Taxon | Variable (unit) | BV/TV (%) | Tb.Pf (mm−1) | SMI (–) | Tb.Th (mm) | Tb.N (mm−1) | Tb.Sp (mm) | DA (–) |
|---|---|---|---|---|---|---|---|---|
| (a) Capitate base | ||||||||
| Gorilla | Mean | 28.39 | 1.28 | 0.93 | 0.28 | 1.01 | 0.74 | 0.45 |
| SD | 9.46 | 0.71 | 0.12 | 0.06 | 0.12 | 0.10 | 0.18 | |
| Min–max | 21.92–39.25 | 0.47–1.8 | 0.81–1.05 | 0.24–0.35 | 0.88–1.12 | 0.65–0.84 | 0.31–0.65 | |
| Pan | Mean | 23.36 | 3.38 | 1.31 | 0.19 | 1.20 | 0.58 | 0.47 |
| SD | 0.69 | 0.10 | 0.02 | 0.00 | 0.00 | 0.02 | 0.04 | |
| Min–max | 22.8–24.13 | 3.26–3.45 | 1.28–1.32 | 0.19–0.20 | 1.2–1.2 | 0.55–0.59 | 0.44–0.51 | |
| Pongo | Mean | 26.84 | 2.56 | 1.16 | 0.28 | 0.90 | 0.71 | 0.52 |
| SD | 17.15 | 2.02 | 0.52 | 0.09 | 0.27 | 0.17 | 0.04 | |
| Min–max | 13.64–46.22 | 0.24–3.92 | 0.56–1.48 | 0.21–0.39 | 0.66–1.20 | 0.56–0.89 | 0.48–0.56 | |
| Symph. | Mean | 37.95 | 2.50 | 1.21 | 0.26 | 1.46 | 0.52 | 0.40 |
| SD | 15.21 | 1.50 | 0.31 | 0.08 | 0.14 | 0.03 | 0.12 | |
| Min–max | 28.32–55.48 | 0.89–3.86 | 0.94–1.55 | 0.21–0.35 | 1.34–1.61 | 0.48–0.54 | 0.29–0.53 | |
| Papio | Mean | 33.45 | 2.23 | 0.93 | 0.17 | 1.90 | 0.41 | 0.51 |
| SD | 8.90 | 1.23 | 0.23 | 0.03 | 0.20 | 0.07 | 0.09 | |
| Min–max | 23.28–39.83 | 1.09–3.54 | 0.71–1.16 | 0.13–0.20 | 1.67–2.02 | 0.36–0.49 | 0.41–0.57 | |
| Macaca | Mean | 32.66 | 5.15 | 1.55 | 0.16 | 2.11 | 0.36 | 0.45 |
| SD | 2.02 | 0.54 | 0.18 | 0.02 | 0.41 | 0.10 | 0.02 | |
| Min–max | 31.01–34.92 | 4.72–5.75 | 1.41–1.75 | 0.14–0.18 | 1.68–2.49 | 0.27–0.46 | 0.44–0.47 | |
| Ateles | Mean | 27.21 | 7.03 | 1.97 | 0.18 | 1.45 | 0.43 | 0.61 |
| SD | 13.90 | 3.01 | 0.28 | 0.03 | 0.59 | 0.18 | 0.18 | |
| Min–max | 11.16–35.24 | 4.87–10.47 | 1.71–2.27 | 0.15–0.20 | 0.77–1.82 | 0.30–0.64 | 0.41–0.76 | |
| (b) MC3 base | ||||||||
| Gorilla | Mean | 32.10 | 0.77 | 0.80 | 0.29 | 1.13 | 0.63 | 0.50 |
| SD | 2.49 | 0.26 | 0.08 | 0.03 | 0.12 | 0.04 | 0.14 | |
| Min–max | 30.11–34.90 | 0.61–1.07 | 0.72–0.87 | 0.26–0.31 | 1.00–1.24 | 0.59–0.66 | 0.37–0.64 | |
| Pan | Mean | 22.67 | 3.27 | 1.18 | 0.18 | 1.24 | 0.56 | 0.49 |
| SD | 7.12 | 1.62 | 0.26 | 0.02 | 0.25 | 0.08 | 0.05 | |
| Min–max | 14.87–28.83 | 2.03–5.10 | 0.98–1.47 | 0.15–0.20 | 0.96–1.42 | 0.51–0.65 | 0.46–0.54 | |
| Pongo | Mean | 17.50 | 3.15 | 1.22 | 0.20 | 0.87 | 0.72 | 0.68 |
| SD | 5.16 | 0.84 | 0.17 | 0.01 | 0.22 | 0.07 | 0.02 | |
| Min–max | 13.09–23.18 | 2.25–3.91 | 1.07–1.41 | 0.19–0.21 | 0.65–1.09 | 0.65–0.79 | 0.66–0.70 | |
| Symph. | Mean | 21.19 | 7.45 | 2.15 | 0.21 | 0.89 | 0.72 | 0.70 |
| SD | 16.78 | 4.35 | 0.21 | 0.07 | 0.58 | 0.33 | 0.10 | |
| Min–max | 3.37–36.69 | 4.53–12.45 | 1.91–2.30 | 0.15–0.29 | 0.23–1.26 | 0.42–1.07 | 0.62–0.81 | |
| Papio | Mean | 36.61 | 2.43 | 1.09 | 0.17 | 2.11 | 0.34 | 0.51 |
| SD | 2.22 | 0.94 | 0.22 | 0.00 | 0.18 | 0.02 | 0.16 | |
| Min–max | 34.05–38.09 | 1.45–3.33 | 0.85–1.28 | 0.17–0.18 | 1.91–2.25 | 0.32–0.36 | 0.37–0.68 | |
| Macaca | Mean | 27.04 | 5.81 | 1.53 | 0.14 | 1.97 | 0.44 | 0.58 |
| SD | 11.76 | 2.07 | 0.23 | 0.01 | 0.77 | 0.22 | 0.05 | |
| Min–max | 13.69–35.88 | 4.49–8.20 | 1.32–1.77 | 0.12–0.15 | 1.13–2.65 | 0.28–0.69 | 0.54–0.64 | |
| Ateles | Mean | 14.70 | 8.51 | 2.06 | 0.14 | 1.03 | 0.69 | 0.64 |
| SD | 11.98 | 2.51 | 0.37 | 0.01 | 0.85 | 0.15 | 0.15 | |
| Min–max | 4.67–27.96 | 5.62–10.13 | 1.64–2.3 | 0.13–0.16 | 0.36–1.99 | 0.54–0.83 | 0.52–0.81 | |
Author contributions
T.L.K., M.M.S., R.L. and J.-J.H. contributed to the research design. T.L.K. micro-CT scanned specimens. M.M.S., R.L. and T.L.K. did the data analysis and wrote the manuscript. J.J.H. provided research support.
References
- Bevill G, Eswaran SK, Gupta A, et al. Influence of bone volume fraction and architecture on computed large-deformation failure mechanisms in human trabecular bone. Bone. 2006;39:1218–1225. doi: 10.1016/j.bone.2006.06.016. [DOI] [PubMed] [Google Scholar]
- Cant JGH, Youlatos D, Rose MD. Locomotor behavior f Lagothrix lagothricha and Ateles belzebuth in Yasuni National Park, Ecuador: general patterns and nonsuspensory modes. J Hum Evol. 2001;41:141–166. doi: 10.1006/jhev.2001.0485. [DOI] [PubMed] [Google Scholar]
- Cope DA, Lacy MG. Comparative application of the coefficient of variation and range-based statistics for assessing the taxonomic composition of fossil samples. J Hum Evol. 1995;29:549–576. [Google Scholar]
- Ding M, Odgaard A, Danielsen C, et al. Mutual associations among microstructural, physical, and mechanical properties of human cancellous bone. J Bone Joint Surg. 2001;84B:900–907. doi: 10.1302/0301-620x.84b6.11994. [DOI] [PubMed] [Google Scholar]
- Fajardo RJ, Müller R. Three-dimensional analysis of nonhuman primate trabecular architecture using micro-computed tomography. Am J Phys Anthropol. 2001;115:327–336. doi: 10.1002/ajpa.1089. [DOI] [PubMed] [Google Scholar]
- Fajardo RJ, Müller R, Ketcham R, et al. Nonhuman anthropoid primate femoral neck trabecular architecture and its relationship to locomotor mode. Anat Rec. 2007;290:422–436. doi: 10.1002/ar.20493. [DOI] [PubMed] [Google Scholar]
- Griffin N. Bone architecture of the hominin second proximal pedal phalanx: a preliminary investigation. J Hum Evol. 2008;54:162–168. doi: 10.1016/j.jhevol.2007.09.008. [DOI] [PubMed] [Google Scholar]
- Griffin NL, D’Août K, Ryan TM, et al. Comparative forefoot trabecular bone architecture in extant hominids. J Hum Evol. 2010;59:202–213. doi: 10.1016/j.jhevol.2010.06.006. [DOI] [PubMed] [Google Scholar]
- Hunt KD. Positional behavior of Pan troglodytes in the Mahale Mountains and Gombe Stream National Parks, Tanzania. Am J Phys Anthropol. 1992;87:83–105. doi: 10.1002/ajpa.1330870108. [DOI] [PubMed] [Google Scholar]
- Isaksson H, Töyräs J, Hakulinen M, et al. Structural parameters of normal and osteoporotic human trabecular bone are affected differently by microCT image resolution. Osteoporos Int. 2010 doi: 10.1007/s00198-010-1219-0. doi: 10.1007/s00198-010-1219-0. [DOI] [PubMed] [Google Scholar]
- Kothari M, Keaveny TM, Lin JC, et al. Impact of spatial resolution on the prediction of trabecular architecture parameters. Bone. 1998;22:437–443. doi: 10.1016/s8756-3282(98)00031-3. [DOI] [PubMed] [Google Scholar]
- Lazenby R, Angus S, Cooper DML, et al. A three-dimensional microcomputed tomographic study of site-specific variation in trabecular microarchitecture in the human second metacarpal. J Anat. 2008a;213:698–705. doi: 10.1111/j.1469-7580.2008.00991.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazenby R, Cooper DML, Angus S, et al. Articular constraint, handedness, and directional asymmetry in the human second metacarpal. J Hum Evol. 2008b;54:875–885. doi: 10.1016/j.jhevol.2007.12.001. [DOI] [PubMed] [Google Scholar]
- Lazenby R, Skinner M, Hublin J-J, et al. Metacarpal trabecular architecture variation in the chimpanzee (Pan troglodytes): Evidence for locomotion and tool-use? Am J Phys Anthropol. 2010a doi: 10.1002/ajpa.21390. doi: 10.1002/ajpa.21390. [DOI] [PubMed] [Google Scholar]
- Lazenby R, Skinner M, Kivell TL, et al. Scaling VOI size in 3D μCT studies of trabecular bone: a test of the over-sampling hypothesis. Am J Phys Anthropol. 2010b doi: 10.1002/ajpa.21385. doi: 10.1002/ajpa.21385. [DOI] [PubMed] [Google Scholar]
- MacLatchy L, Müller R. A comparison of the femoral head and neck trabecular architecture of Galago and Perodicticus using micro-computed tomography (μCT) J Hum Evol. 2002;43:89–105. doi: 10.1006/jhev.2002.0559. [DOI] [PubMed] [Google Scholar]
- Maga M, Kappelman J, Ryan T, et al. Preliminary observations on the calcaneal trabecular microarchitecture of extant large-bodied hominoids. Am J Phys Anthropol. 2006;129:410–417. doi: 10.1002/ajpa.20276. [DOI] [PubMed] [Google Scholar]
- Mittra E, Rubin C, Qin Y-X. Interrelationship of trabecular mechanical and microstructural properties in sheep trabecular bone. J Biomech. 2005;38:1229–1237. doi: 10.1016/j.jbiomech.2004.06.007. [DOI] [PubMed] [Google Scholar]
- Nägele E, Kuhn V, Vogt H, et al. Technical considerations for microstructural analyses of human trabecular bone sites from specimens excised from various skeletal sites. Calcif Tissue Int. 2004;75:15–22. doi: 10.1007/s00223-004-0151-8. [DOI] [PubMed] [Google Scholar]
- Odgaard A. Three-dimensional methods for quantification of cancellous bone architecture. Bone. 1997;20:315–328. doi: 10.1016/s8756-3282(97)00007-0. [DOI] [PubMed] [Google Scholar]
- Plavcan JM, van Schaik CP. Interpreting homonid behavior on the basis of sexual dimorphism. Am J Phys Anthropol. 1997;103:37–68. doi: 10.1006/jhev.1996.0096. [DOI] [PubMed] [Google Scholar]
- Pontzer H, Lieberman D, Momin E, et al. Trabecular bone in the bird knee responds with high sensitivity to changes in load orientation. J Exp Biol. 2006;209:57–65. doi: 10.1242/jeb.01971. [DOI] [PubMed] [Google Scholar]
- Recker R, Ste-Marie L-G, Langdahl B, et al. Oral ibandronate preserves trabecular microarchitecture: micro-computed tomography findings from the oral ibandronate osteoporosis vertebral fracture trial in North America and Europe study. J Clin Densitom. 2009;12:71–76. doi: 10.1016/j.jocd.2008.10.006. [DOI] [PubMed] [Google Scholar]
- Remis M. Effects of body size and social context on the arboreal activities of lowland gorillas in the Central African Republic. Am J Phys Anthropol. 1995;97:413–433. doi: 10.1002/ajpa.1330970408. [DOI] [PubMed] [Google Scholar]
- Rice JC, Cowin SC, Bowman JA. On the dependence of the elasticity and strength of cancellous bone on apparent density. J Biomech. 1988;21:155–168. doi: 10.1016/0021-9290(88)90008-5. [DOI] [PubMed] [Google Scholar]
- Riggs BL, Melton LJ, Robb RA, et al. A population-based assessment of rates of bone loss at multiple skeletal sites: evidence for substantial trabecular bone loss in young adult women and men. J Bone Miner Res. 2008;23:205–214. doi: 10.1359/JBMR.071020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruff CB, Holt B, Trinkhaus E. Who's afraid of the big bad Wolff?: ‘Wolff's Law’ and bone functional adaptation. Am J Phys Anthropol. 2006;129:484–498. doi: 10.1002/ajpa.20371. [DOI] [PubMed] [Google Scholar]
- Ryan TM, Ketcham RA. The three-dimensional structure of trabecular bone in the femoral head of strepsirrhine primates. J Hum Evol. 2002a;43:1–26. doi: 10.1006/jhev.2002.0552. [DOI] [PubMed] [Google Scholar]
- Ryan TM, Ketcham RA. Femoral head trabecular bone structure in two omomyid primates. J Hum Evol. 2002b;42:241–263. doi: 10.1006/jhev.2002.0575. [DOI] [PubMed] [Google Scholar]
- Ryan TM, Ketcham RA. Angular orientation of trabecular bone in the femoral head and its relationship to hip joint loads in leaping primates. J Morphol. 2005;265:249–263. doi: 10.1002/jmor.10315. [DOI] [PubMed] [Google Scholar]
- Ryan TM, Krovitz G. Trabecular bone ontogeny in the proximal human femur. J Hum Evol. 2006;51:591–602. doi: 10.1016/j.jhevol.2006.06.004. [DOI] [PubMed] [Google Scholar]
- Ryan TM, Rietbergen B. Mechanical significance of femoral head trabecular bone structure in Loris and Galago evaluated using micromechanical finite element models. Am J Phys Anthropol. 2005;126:82–96. doi: 10.1002/ajpa.10414. [DOI] [PubMed] [Google Scholar]
- Scherf H. Locomotion-related femoral trabecular architecture in primates: high resolution computed tomographies and their implications for locomotor preferences in fossil primates. In: Endo H, Frey R, editors. Anatomical Imaging towards a New Morphology. Tokyo: Springer; 2008. pp. 39–60. [Google Scholar]
- Scherf H, Hublin J-J. Habitual loading conditions of the shoulder joint in Pan troglodytes and Homo sapiens and its implications on humeral trabecular architecture. J Morphol. 2007;268:1129–1130. [Google Scholar]
- Scherf H, Tilgner R. A new high-resolution computed tomography (CT) segmentation method for trabecular bone architectural analysis. Am J Phys Anthropol. 2009;140:39–51. doi: 10.1002/ajpa.21033. [DOI] [PubMed] [Google Scholar]
- Scherf H, Tilgner R, Hublin J-J. Effects of locomotion: morphological differences in humeral cancellous bone of hominids and their relation to habitual loading conditions of the shoulder joint. Am J Phys Anthropol. 2009;138(S48):229. [Google Scholar]
- Sode M, Burghardt AJ, Nissenson RA, et al. Resolution dependence of the non-metric trabecular structure indices. Bone. 2008;42:728–736. doi: 10.1016/j.bone.2007.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sran MM, Boyd SK, Cooper DML, et al. Regional trabecular morphology assessed by micro-CT is correlated with failure of aged thoracic vertebrae under a posteroanterior load and may determine the site of fracture. Bone. 2007;40:751–757. doi: 10.1016/j.bone.2006.10.003. [DOI] [PubMed] [Google Scholar]
- Stauber M, Rapillard L, van Lenthe GPZ, et al. Importance of individual rods and plates in the assessment of bone quality and their contribution to bone stiffness. J Bone Miner Res. 2006;21:586–595. doi: 10.1359/jbmr.060102. [DOI] [PubMed] [Google Scholar]
- Swartz SM, Parker A, Huo C. Theoretical and empirical scaling patterns and topological homology in bone trabeculae. J Exp Biol. 1998;201:573–590. doi: 10.1242/jeb.201.4.573. [DOI] [PubMed] [Google Scholar]
- Thorpe SKS, Crompton RH. Orangutan positional behavior and the nature of arboreal locomotion in hominoidea. Am J Phys Anthropol. 2006;131:384–401. doi: 10.1002/ajpa.20422. [DOI] [PubMed] [Google Scholar]
- Tocheri MW, Razdan A, Williams RC, et al. A 3D quantitative comparison of trapezium and trapezoid relative articular and nonarticular surface areas in modern humans and great apes. J Hum Evol. 2005;49:570–586. doi: 10.1016/j.jhevol.2005.06.005. [DOI] [PubMed] [Google Scholar]
- Turner CH. On Wolff's law of trabecular architecture. J Biomech. 1992;25:1–9. doi: 10.1016/0021-9290(92)90240-2. [DOI] [PubMed] [Google Scholar]
- Tuttle RH, Watts DP. The positional behaviour and adaptive complexes for Pan Gorilla. In: Kondo S, editor. Primate Morphophysiology, Locomotor Analysis and Bipedalism. Tokyo: University of Tokyo Press; 1985. pp. 261–288. [Google Scholar]
- Ulrich D, van Rietbergen B, Laib A, et al. The ability of three-dimensional structural indices to reflect mechanical aspects of trabecular bone. Bone. 1999;25:55–60. doi: 10.1016/s8756-3282(99)00098-8. [DOI] [PubMed] [Google Scholar]
- Whitehouse WJ, Dyson ED. Scanning electron microscope studies of trabecular bone in the proximal end of the human femur. J Anat. 1974;118:417–444. [PMC free article] [PubMed] [Google Scholar]
- Zar JH. Biostatistical Analysis. 2nd edn. Englewood Cliffs, NJ: Prentice Hall, Inc; 1984. [Google Scholar]
- Zylstra M, Ketcham RA. Three-dimensional modeling of cancellous bone architecture: comparison of primate and human carpal bones. The FASEB Journal. 2004;18:A413. [Google Scholar]


