A Bayesian Hierarchical Model for Classification with Selection of Functional Predictors

Abstract

Summary

In functional data classification, functional observations are often contaminated by various systematic effects, such as random batch effects caused by device artifacts, or fixed effects caused by sample-related factors. These effects may lead to classification bias and thus should not be neglected. Another issue of concern is the selection of functions when predictors consist of multiple functions, some of which may be redundant. The above issues arise in a real data application where we use fluorescence spectroscopy to detect cervical pre-cancer. In this paper, we propose a Bayesian hierarchical model which takes into account random batch effects and selects effective functions among multiple functional predictors. Fixed effects or predictors in non-functional form are also included in the model. The dimension of the functional data is reduced through orthonormal basis expansion or functional principal components. For posterior sampling, we use a hybrid Metropolis-Hastings/Gibbs sampler, which suffers slow mixing. An Evolutionary Monte Carlo algorithm is applied to improve the mixing. Simulation and real data application show that the proposed model provides accurate selection of functional predictors as well as good classification.

1. Introduction

Classification with functional data is a challenging problem due to the high dimensionality of the observational space and the high correlation between adjacent points of the functional observations. One solution is to reduce the dimension and use the reduced features for classification, as done in Hall, Poskitt and Presnell (2001), Zhao, Marron and Wells (2004), and Ferré and Villa (2006). Another way is to use generalized linear regression, which was proposed by James (2002) and Müller and Stadtmüller (2005) and was applied to practical problems by Ratcliffe, Heller and Leader (2002) and Leng and Müller (2005).

In real data analysis, there are often practical issues that are not handled by the approaches mentioned above. One is the presence of systematic effects that are significant enough to bias classification, such as the artificial differences caused by measuring with different devices. In the Web Appendix A, an example is constructed to show how the device difference can mislead the classification in an unbalanced design. A similar issue is addressed in Baggerly et al. (2004). Another practical concern arises with multiple functional predictors. In this case, some functions are usually redundant or contain no information, therefore selecting a subset of the functions can reduce the cost of data collection for future observations, and may improve classification accuracy.

Our work is motivated by the investigation of fluorescence spectroscopy for cervical pre-cancer diagnosis (Ramanujam et al., 1996). In our clinical study, several different fluorescence spectra have been collected and used simultaneously for a single diagnosis. It is known that some spectral curves contain more disease related information hence are more “important” than others (Chang et al., 2002). Therefore it is beneficial to find those spectral curves that are best for diagnosis and to remove the unnecessary ones.

The fluorescence spectroscopy data analyzed here are collected in the following way. An excitation light at a fixed wavelength illuminates the cervical tissue. During illumination, the endogenous fluorescent molecules in tissue absorb the excitation light and emit fluorescent light. The emitted light is then captured by an optical detector which produces the spectrum as a smooth curve. In each measurement, the excitation light is varied at 16 different excitation wavelengths, ranging from 330 nm to 480 nm with increments of 10 nm. This produces 16 spectral curves for each measurement. In each curve, the spectral intensities are recorded at emission wavelengths ranging between 385 nm and 700 nm. During data preprocessing, the curves are truncated so that some intensity points at the smallest and largest emission wavelengths are removed.

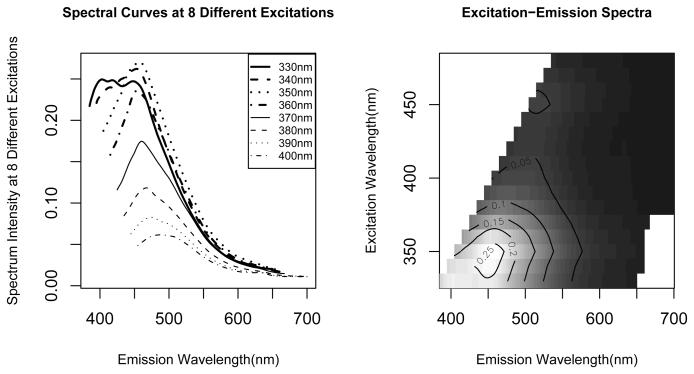
Figure 1 illustrates one observation. The left panel shows the first 8 of the total 16 spectral curves from this observation. The right panel shows a heat plot of the intensities, by stacking up all the 16 spectra in the order of their excitation wavelength. We call such a set of fluorescence spectroscopy curves an excitation-emission matrix (EEM).

Figure 1.

Left panel: spectral curves at 8 different excitation wavelengths ranging from 330nm to 400nm. Right panel: heat plot of an excitation-emission matrix (EEM).

One purpose of this study is to select a few excitation curves out of a total of 16 for diagnosis. The selected curves can then be measured in the future to reduce the device cost and measurement time. Several factors that are brought in by the experimental design need to be considered in this study. First, the data are obtained using two instruments with four optical probes located at three clinics. A preliminary study shows that there exist significant differences among the data from different device-probe-clinic combinations, which will put the classification at risk since the diseased cases are rare and distributed inhomogeneously across these combinations, like the example shown in the Web Appendix A. Second, in addition to device-clinic differences, it is believed that other factors, such as tissue type of the sample and menopausal status of the patient, will be confounded with the disease information. These factor effects are shown through box-plots in Web Figure 1.

This paper proposes a Bayesian hierarchical model with selection of functional predictors for complex functional data classification problems, where multiple functional predictors are influenced by random batch effects and fixed effects. We extend the idea of Bayesian variable selection to generalized functional linear regression with binary responses. Details on Bayesian variable selection can be found in George and McCulloch (1993, 1997) and Brown, Vannucci and Fearn (1998, 2002). We use a Bayesian hierarchical model to take into account random batch effects. Fixed effects or predictors in non-functional form are also included in the model. The dimension of the functional data are reduced through orthonormal basis expansion or functional principal component analysis. A Hybrid Gibbs/Metropolis-Hasting sampler is used for posterior sampling, which we find mix slowly. An Evolutionary Monte Carlo (EMC) algorithm (Liang and Wong, 2000) is then applied for better mixing. Similarly to most variable selection methods, our proposed model can serve for both predictor selection and prediction(with model averaging). In our current application, we are mainly interested in selecting functional predictors to be measured in the future at a reduced cost. However, the model may also be applied to classification problems with redundant functional predictors simply to improve prediction.

The rest of the paper is organized as follows. We introduce the Bayesian hierarchical model with functional predictor selection in Section 2, discuss the selection of parameters in Section 3, and describe the proposed MCMC algorithms in Section 4. Simulation results are shown in Section 5. The application of the proposed model to the fluorescence spectroscopy data is given in Section 6, followed by discussion in Section 7. More discussion on setting priors and parameters in MCMC algorithms can be found in Web Appendix C.

2. The Bayesian hierarchical model with selection of functional predictors

2.1 The proposed model

Suppose that we obtain functional observations from L exchangeable batches, in which the lth batch contains n_l observations and each observation contains J functions. For l = 1, …, L, i = 1, …, n_l and j = 1, …, J, let $x_{\mathit{ij}}^l\left(t\right)$ be the jth function observed from the ith observation in batch l, which takes values in L²[T_j], with T_j the compact domain of $x_{\mathit{ij}}^l\left(t\right)$. In addition to the functional observations, there are also non-functional observations ${\mathbf{s}}_i^l$, which is assumed to be a vector of length q. We treat the observations $\{{\mathbf{s}}_i^l,x_{\mathit{ij}}^l\left(t\right),j=1,\dots ,J\}$ as predictors and assume the binary responses $y_i^l$ to be conditionally independent given the predictors. We introduce univariate latent variables $z_i^l$ which link the responses $y_i^l$ to the predictors as follows:

$$y_i^l=\{\begin{array}{cc}1\hfill & \text{if}{z}_i^l<0,\hfill \\ 0\hfill & \text{if}{z}_i^l\ge 0.\hfill \end{array}\phantom{\}}$$

$$z_i^l={\left({\mathbf{s}}_i^l\right)}^T\alpha +\underset{j=1}{\overset{J}{\Sigma }}{\int }_{T_j}{x}_{\mathit{ij}}^l\left(t\right){\beta }_j^l\left(t\right)\mathit{dt}+{∊}_i^l.$$ (1)

Here we take the first component of ${\mathbf{s}}_i^l$ to be 1 to include the intercept term. For all i and l, we assume ${∊}_i^l$ to be i.i.d. with distribution N(0, 1), and assume that ${\beta }_j^l\left(t\right)\in L^2\left[T_j\right]$ for all j. See Albert and Chib (1993) for the use of latent variables to analyze binary response data.

In many cases, some functional predictors do not contribute to the the classification, and selecting a subset of them may actually improve the classification accuracy. In our application introduced in Section 1, there are also economic reasons for using a subset of the J functional predictors. To this end, we introduce a hyper-parameter τ to the priors of ${\beta }_j^l\left(t\right)$, where τ = (τ₁, …, τ_J)^T and each component takes values either 1 or 0, indicating whether or not the corresponding functional predictor is selected. The proposed priors for α and ${\beta }_j^l\left(t\right)$ are as follows:

$$\begin{array}{cc}\hfill \alpha ~& N(0,{\sigma }_1^2{I}_q),\hfill \\ \hfill {\beta }_j^l\left(t\right)\mid {\beta }_j^0\left(t\right),{\tau }_j,{\sigma }_b^2~& \mathit{GP}({\beta }_j^0,{\sigma }_b^2{\gamma }_{\tau j}),\hfill \\ \hfill {\beta }_j^0\left(t\right)\mid {\tau }_j~& \mathit{GP}(0,{\sigma }_0^2{\gamma }_{\tau j}),\hfill \\ \hfill {\tau }_j\mid {\omega }_j~& \text{Bernoulli}\left({\omega }_j\right),\hfill \\ \hfill {\sigma }_b^2\mid d_1,d_2~& \text{Inv-gamma}(d_1,d_2),\hfill \end{array}$$ (2)

where ${\sigma }_1^2,{\sigma }_0^2$, d₁, d₂, ω_j are pre-specified prior parameters. GP(μ, γ) denotes a Gaussian process with mean μ(t) and covariance function γ(s, t). We let γ_τj depend on τ_j by

$${\gamma }_{{\tau }_j}(s,t)=[v_1^2{\tau }_j+v_0^2(1-{\tau }_j)]\underset{k=1}{\overset{\infty }{\Sigma }}{w}_k^j{\varphi }_k^j\left(s\right){\varphi }_k^j\left(t\right),$$ (3)

where ${\left\{{\varphi }_k^j\right\}}_{k=1}^{\mathrm{\infty }}$ is a complete orthonormal basis of L²[T_j]. Note that the infinite sum in equation (3) is a perfectly general form for a covariance function; it is simply the spectral representation of a covariance function (Ash and Gardner, 1975). We will treat ${\left\{{\varphi }_k^j\right\}}_{k=1}^{\mathrm{\infty }}$ and ${\left\{w_k^j\right\}}_{k=1}^{\mathrm{\infty }}$ as prior parameters and make specific choices of them. In equation (3), we let ν₁ >> ν₀ > 0 and set ν₀ to be close to 0. Under this setting, both ${\beta }_j^l\left(t\right)$ and ${\beta }_j^0\left(t\right)$ will have covariances function close to 0 when τ_j = 0 (i.e., the jth functional predictor is not selected), and have relatively large variances when τ_j = 1(i.e., the jth functional predictor is selected). This type of prior is motivated by George and McCulloch (1993, 1997) where they used mixture-normal priors for variable selection. The $w_k^j$'s in equation (3) are pre-specified positive weight parameters subject to ${\Sigma }_{k=1}^{\mathrm{\infty }}{w}_k^i<\mathrm{\infty }$ for all j. For simplicity, we assume that the Gaussian process priors for ${\beta }_j^l\left(t\right)$ are independent for all j and l, and that priors for τ_j are independent for all j. In order to do practical posterior inference, it will be necessary to construct finite dimensional approximations to the functional predictors and coefficients. This will be described in detail in Section 2.2 below.

2.2 The posterior inference

From equation (1) and the standard normal assumption of ${∊}_i^l$, it is easy to see that the conditional distribution of $z_i^l$ given $y_i^l$, α and ${\beta }_j^l\left(t\right)$ is a truncated normal

$$z_i^l\mid y_i^l,\alpha ,{\beta }_j^l\left(t\right)~\mathit{TN}({\mu }_z,1)\{I_{\{z_i^l<0\}}{I}_{\{y_i^l=1\}}+I_{\{z_i^l\ge 0\}}{I}_{\{y_i^l=0\}}\},$$ (4)

where ${\mu }_z={\left({\mathrm{s}}_i^l\right)}^T\alpha +{\Sigma }_{j=1}^J{\int }_{T_j}{x}_{\mathit{ij}}^l\left(t\right){\beta }_j^l\left(t\right)\mathit{dt}$ and I_{·} is the indicator function. Since ${\left\{{\varphi }_k^j\right\}}_{k=1}^{\mathrm{\infty }}$ is a complete orthonormal basis of L²[T_j], we can expand $x_{\mathit{ij}}^l\left(t\right)$ and ${\beta }_j^l\left(t\right)$ by

$$x_{\mathit{ij}}^l\left(t\right)=\underset{k=1}{\overset{\infty }{\Sigma }}{c}_{\mathit{ijk}}^l{\varphi }_k^j\left(t\right),{\beta }_j^l\left(t\right)=\underset{k=1}{\overset{\infty }{\Sigma }}{b}_{\mathit{jk}}^l{\varphi }_k^j\left(t\right),$$ (5)

and use the truncated versions of (5) to approximate $x_{\mathit{ij}}^l\left(t\right)$ and ${\beta }_j^l\left(t\right)$. Note that the orthonormal basis can be chosen to be a known basis such as Fourier or wavelet basis. If assuming that $x_{\mathit{ij}}^l\left(t\right)$ has zero mean and ${\int }_{T_j}E\left[x_{\mathit{ij}}^l{\left(t\right)}^2\right]\mathit{dt}<\mathrm{\infty }$, Mercer's theorem and Karhunen-Loève theorem (Ash and Gardner, 1975) suggest taking the eigenfunctions of the covariance operator K_j as the orthonormal basis, where K_j is defined by

$${\mathbf{K}}_j{x}_{\mathit{ij}}^l\left(t\right)=\int x_{\mathit{ij}}^l\left(s\right)k_j(s,t)\mathit{ds},k_j(s,t)=\mathrm{Cov}(x_{\mathit{ij}}^l\left(s\right),x_{\mathit{ij}}^l\left(t\right)).$$

In this case, the coefficients ${\left\{c_{\mathit{ijk}}^l\right\}}_{k=1}^{\mathrm{\infty }}$ are called functional principal component (FPC) scores of $x_{\mathit{ij}}^l\left(t\right)$. Note that using the FPC method is different from using fixed basis expansions in that the eigenfunctions need to be estimated. Various estimating methods have been proposed in Ramsay and Silverman (1997) and Hall, Müller and Wang (2006).

Once the orthonormal basis coefficients or the FPC scores have been estimated, we can reduce (1) by applying the truncated approximations in (5), which gives

$$z_i^l={\left({\mathbf{s}}_i^l\right)}^T\alpha +\underset{j=1}{\overset{J}{\Sigma }}\underset{k=1}{\overset{p_j}{\Sigma }}{c}_{\mathit{ijk}}^l{b}_{\mathit{jk}}^l+{∊}_i^l,$$ (6)

where p_j is the truncation parameter for the jth functional predictor. The notation of the above equation can be simplified by concatenating coefficients of the J functions to make one vector b_l. The simplified form of equation (6) is

$${\mathbf{Z}}_l={\mathbf{S}}_l\alpha +{\mathbf{C}}_l{\mathbf{b}}_l+{∊}_l,$$ (7)

where ${\mathbf{Z}}_l={(z_1^l,\dots ,z_{n_l}^l)}^T$ and ${∊}_l={({∊}_1^l,\dots ,{∊}_{n_l}^l)}^T$. S_l is a matrix of size n_l × q with the ith row equals ${\left({\mathbf{s}}_i^l\right)}^T$, and C_l is a matrix of size $n_l\times p(p={\Sigma }_{j=1}^J{p}_j)$ with the ith row equals ${(c_{i11}^l,\dots ,c_{i1p_1}^l,\dots ,c_{iJ1}^l,\dots ,c_{iJ{p}_j}^l)}^T$. Similarly, ${\mathbf{b}}_l={(b_{11}^l,\dots ,b_{1p_1}^l,\dots ,b_{J1},\dots ,b_{J{p}_J}^l)}^T$. Based on (7), the conditional distribution of the latent variables in (4) becomes

$${\mathbf{Z}}_l\mid \alpha ,{\mathbf{b}}_l,{\mathbf{Y}}_l~\mathit{TN}({\mu }_l,{\mathbf{I}}_{n_l})\prod _{i=1}^{n_l}(I_{\{z_i^l<0\}}{I}_{\{y_i^l=1\}}+I_{\{z_i^l\ge 0\}}{I}_{\{y_i^l=0\}}),$$ (8)

where μ_l = S_lα + C_lb_l and ${\mathbf{Y}}_l={(y_1^l,\dots ,y_{n_l}^l)}^T$. The truncated orthonormal basis expansion or FPC analysis also reduce the Gaussian process priors for ${\beta }_j^l\left(t\right)$ and ${\beta }_j^0\left(t\right)$ to multivariate normal priors

$$\begin{array}{cc}\hfill {\mathbf{b}}_l\mid {\mathbf{b}}_0,{\sigma }_b^2,\tau ~& N({\mathbf{b}}_0,{\sigma }_b^2{\Sigma }_{\tau }),\hfill \\ \hfill {\mathbf{b}}_0\mid \tau ~& N(0,{\sigma }_0^2{\Sigma }_{\tau }),\hfill \end{array}$$ (9)

where Σ_τ = D_τ W^1/2RW^1/2D_τ. Here R is the prior correlation matrix of b_l and b₀. In our setup, R = I_p, an identity matrix since in Section 2.1 we assumed that ${\beta }_j^l\left(t\right)$'s are independent for all j's. W is also a diagonal matrix of size p, with positive diagonal components $(w_1^1,\dots ,w_{p_1}^1,\dots ,w_1^J,\dots ,w_{p_J}^J)$. In other words, the diagonal of W concatenates the first p_j components of the weight sequence ${\left\{w_k^j\right\}}_{k=1}^{\mathrm{\infty }}$, for j = 1, …, J. D_τ is another diagonal matrix with diagonal components

$$(u_1^1,\dots ,u_{p_1}^1,\dots ,u_1^J,\dots ,u_{p_J}^J),$$

where $u_k^j={\nu }_1{\tau }_j+{\nu }_0(1-{\tau }_j)$, for k = 1, …, p_j, j = 1, …, J. Note that $u_k^j$ does not depend on k.

With the conditional distribution (8), the priors for α, τ and ${\sigma }_b^2$ in (2), and the reduced multivariate priors for b_l and b₀ in (9), we get the joint conditional posterior distribution of α, b_l's, b₀, ${\sigma }_b^2$, τ given Z_l's and Y_l's by

$$\begin{array}{cc}\hfill & \pi (\alpha ,{\mathbf{b}}_1,\dots ,{\mathbf{b}}_L,{\mathbf{b}}_0,{\sigma }_b^2,\tau \mid {\mathbf{Z}}_l,{\mathbf{Y}}_l,l=1,\dots ,L)\hfill \\ \hfill & \propto \pi \left(\alpha \right)\pi \left({\sigma }_b^2\right)\pi (b_0\mid \tau )\pi \left(\tau \right)\prod _l\pi ({\mathbf{Z}}_l\mid \alpha ,{\mathbf{b}}_l,{\mathbf{Y}}_l)\pi ({\mathbf{b}}_l\mid {\mathbf{b}}_0,{\sigma }_b^2,\tau ).\hfill \end{array}$$ (10)

The parameters α, b_l's and b₀ can all be integrated out sequentially from (10), which gives the marginal conditional posterior distribution

$$\pi ({\sigma }_b^2,\tau \mid {\mathbf{Z}}_l,{\mathbf{Y}}_l,l=1,\dots ,L).$$ (11)

See the Web Appendix B for details of the integration. Based on (8), (10) and (11), MCMC algorithms can be designed to obtain posterior samples of the parameters. Using the posterior samples of b_l's, we can estimate ${\beta }_j^l\left(t\right)$'s. For new observations, we can use the estimated ${\beta }_j^l\left(t\right)$'s and posterior estimate of α for prediction.

3. Setting parameters

It is important to determine the truncation parameters p_j used in basis expansion (see equation (6)). One could set up priors for each p_j and adopt reversible jump MCMC (Green, 1995) for posterior sampling. This strategy is reasonable but will introduce extra complications for MCMC. Another strategy of determining the p_j's is through cross-validation. A test set can be used and the p_j's can be determined through maximizing the prediction performance on test set. This method is straightforward but prohibitive unless one assumes p_j ≡ p. It is also computationally expensive since it requires the model to be trained on all possible choices of p. For this paper, we propose a simple practical method for determining p_j's. Since the truncated basis expansion is used to approximate the original functional predictors, we set an approximation criterion to determine p_j. For example, if using FPC analysis, we set the criterion to be $\widehat{f}\left(p_j\right)={\Sigma }_{k=1}^{p_j}{\widehat{\lambda }}_k∕{\Sigma }_{k=1}^K{\widehat{\lambda }}_k\ge c_1$, for 0 < c₁ ≤ 1, 1 ≤ p_j ≤ K. Here λ̂_k's are the estimated eigenvalues, and K is the maximum number of eigenvalues that are non-zero. Here f̂(p_j) represents the proportion of variability accounted using the first p_j FPC's. We usually set c₁ above 0.99 in this paper. If using a known orthonormal basis, we suggest to let f̂(p_j) = 1 − Σ_i∥x_ij(t) − x̂_ij(t)∥²/∥x_ij(t)∥² ≥ c₂, where x̂_ij(t) is the estimated function of x_ij(t) after truncating at p_j, and ∥·∥ is the L² norm. We also suggest setting c₂ above 0.99.

The weight sequences ${\left\{w_k^j\right\}}_{k=1}^{\mathrm{\infty }}$ in equation (3) will determine the weight matrix W in (9). We discuss the choices of ${\left\{w_k^j\right\}}_{k=1}^{\mathrm{\infty }}$ here. We know that $w_k^j>0$ and ${\Sigma }_{k=1}^{\mathrm{\infty }}{w}_k^j<\mathrm{\infty }$. The main effect of $w_k^j$ is to weight higher orders of the orthonormal basis $\left\{{\varphi }_k^j\left(t\right)\right\}$ toward zero so that the series in (3) converges. In this paper, we always set $1=w_1^j>w_2^j>\cdots >0$ so that all the weights are between 0 and 1. We determine ${\left\{w_k^j\right\}}_{k=1}^{\mathrm{\infty }}$ by another parameter m such that $w_k^j=m^{(k-1)}$ for all k = 1, …, ∞ and all j. Smaller value of m will make ${\left\{w_k^j\right\}}_{k=1}^{\mathrm{\infty }}$ decay to zero faster. The values of ${\left\{w_k^j\right\}}_{k=1}^{\mathrm{\infty }}$ are truncated at p_j to form the weight matrix W. We usually take m between 0.5 and 0.9. The setting of other MCMC parameters and priors is discussed in Web Appendix C.

4. Markov Chain Monte Carlo

Based on the model constructed in Section 2, we propose two MCMC algorithms for posterior sampling. The first one is a hybrid Metropolis-Hastings/Gibbs sampler, and the second one is a modified version of Algorithm 1 which uses the EMC algorithm to improve the mixing when the number of functional predictors is relatively large.

4.1 MCMC Algorithm 1 (Hybrid Metropolis-Hastings/Gibbs Sampler)

• Step 0. Set initial values for b_l's, α, τ and ${\sigma }_b^2$.

• Step 1. For l = 1, …, L, conditional on Y_l and current values of b_l and α, update Z_l from the truncated normal distribution described in equation (8) of Section 2.2.

• Step 2. Update ${\sigma }_b^2$ based on $\pi ({\sigma }_b^2\mid \tau ,{\mathbf{Z}}_l,{\mathbf{Y}}_l,l=1,\dots ,L)$. Sample a proposal ${\tilde{\sigma }}_b^2$ by $\log {\tilde{\sigma }}_b^2=\log {\sigma }_b^2+∊$, with ε ~ N(0, δ²). δ is an adjustable step size. Compute the ratio

  $$R_{\sigma }=\frac{\pi ({\tilde{\sigma }}_b^2\mid \tau ,{\mathbf{Z}}_l,{\mathbf{Y}}_l,l=1,\dots ,L){\tilde{\sigma }}_b^2}{\pi ({\sigma }_b^2\mid \tau ,{\mathbf{Z}}_l,{\mathbf{Y}}_l,l=1,\dots ,L){\sigma }_b^2}$$

  and update ${\sigma }_b^2={\tilde{\sigma }}_b^2$ with probability min(1, R_σ).
• Step 3. Update τ based on $\pi (\tau \mid {\sigma }_b^2,{\mathbf{Z}}_l,{\mathbf{Y}}_l,l=1,\dots ,L)$. First generate a proposal τ̃ using “switch/swap”, i.e., provided that τ does not contain all 1's or all 0's, with probability ξ, randomly swap one 1 term with one 0 term; and with probability 1 − ξ, randomly pick one position and switch it. Then let

  $$R_{\tau }=\frac{\pi (\tilde{\tau }\mid {\sigma }_b^2,{\mathbf{Z}}_l,l=1,\dots ,L)}{\pi (\tau \mid {\sigma }_b^2,{\mathbf{Z}}_l,l=1,\dots ,L)}$$

  and update τ = τ̃ with probability min(1, R_τ).

• Step 4. Update α conditional on current values of ${\sigma }_b^2$, τ and Z_l through the conditional distribution $\alpha \mid {\sigma }_b^2,\tau ,{\mathbf{Z}}_l~N({\mu }_{\alpha },{\mathbf{V}}_{\alpha })$, where μ_α and V_α are defined as in Web Appendix B.

• Step 5. Conditional on current values of α, ${\sigma }_b^2$, τ and Z_l, update b₀ by b₀|α, ${\sigma }_b^2$, τ, Z_l ~ N(μ₀, V₀), where μ₀ and V₀ are defined as in Web Appendix B.

• Step 6. Conditional on current values of b₀, α, ${\sigma }_b^2$, τ and Z_l, update b_l by b_l|b₀, α, ${\sigma }_b^2$, τ, Z_l ~ N(μ_l, V_l) for all l, where μ_l and V_l are defined as in Web Appendix B.

Repeat step 1 – 6 until the maximum number of iterations is reached.

The “switch/swap” proposal used in step 6 is similar to the methods used in Brown et al. (1998, 2002). Our simulation shows that if the number of functional predictors is small, this type of proposal can locate the correct value of τ within a few iterations. However, when the number of functional predictors become large, the number of possible values of τ increases at an exponential rate. The “switch/swap” proposal can hardly find successful proposals because of the discrete nature of the large state space, which results in extremely low acceptance rate (e.g., acceptance rate less than 0.1%).

In order to obtain better mixing for τ, we construct a more effective EMC algorithm based on Algorithm 1. The EMC algorithm is a MCMC scheme that inherits the attractive features of both simulated annealing and genetic algorithms. It simulates a population of I Markov chains in parallel, each chain with a different “temperature”. The temperatures are ordered decreasingly to form a “ladder”. If π(θ) denotes the target posterior distribution and t_i denotes the temperature for the ith chain, then the transformed posterior for the ith chain is π_i(θ) ∝ π(θ)^1>/t_i. Such transformations have the effect of making the unnormalized target posterior density more flat or more spiky. The EMC algorithm improves on Metropolis-Hastings updates by introducing three operations: mutation, crossover and exchange. These operations allow both independent updates for each chain and interactions between neighboring chains. More details on EMC algorithm can be found in Liang and Wong (2000), Liu (2001), Goswami and Liu (2007) and Bottolo and Richardson (2008).

In the EMC algorithm, the choice of temperatures for the temperature ladder is important. We adopt a simple method suggested in Bottolo and Richardson (2008), which uses a geometric sequence and adjusts the common ratio in a burn-in period so that the acceptance rate for the exchange operation is between 10% and 60%. The number of chains I and the maximum temperature are pre-specified. Based on our experiences, we suggest choosing I to be around J/2, and the maximum temperature between 10 and 10³. The Algorithm 2 stated below gives details of the EMC algorithm.

4.2 MCMC Algorithm 2 (EMC)

• Step 0. Set initial values for b_l's, α, τ and ${\sigma }_b^2$. And set up an initial temperature ladder: t₁ > t₂ > … > t_I > 0, where t_i+1/t_i = a (i = 1, …, I) denotes the initial ratio of the geometric sequence. We re-adjust the temperature ladder so that t₁ is bounded by the maximum temperature and one chain has temperature exactly 1. We also set the step-size for adjusting temperature to be δ_a = log₂(a)/(3ñ), where and ñ is the ratio of the burn-in period a block size(usually 100). We also set the parameter ζ, the probability of mutation and crossover, and ξ, the probability of switch and swap within the mutation step.

• Step 1. Run step 1 – 2 in Algorithm 1 independently for each chain, obtaining samples of Z_l's and ${\sigma }_b^2$.

• Step 2. Conditional on current values of Z_l's and ${\sigma }_b^2$ in each chain, update τ according to step 2.1 and 2.2. For convenience, here we denote $\pi (\tau \mid \cdot )=\pi (\tau \mid {\sigma }_b^2,{\mathbf{Z}}_l,{\mathbf{Y}}_l,l=1,\dots ,L)$, and denote π_i(τ|·) the similar expression when plugging in the samples of ${\sigma }_b^2$ and Z_l's from the ith chain.

  • Step 2.1. (mutation/crossover) With probability ζ, perform a mutation step independently for each chain, i.e., “switch” or “swap” with probability ξ, as in step 3 of Algorithm 1. In particular, denote the mutated value for the ith chain to be τ̃ and compute the log ratio log $\log r_m^i=[\log {\pi }_i(\tilde{\tau }\mid \cdot )-\log {\pi }_i(\tau \mid \cdot )]∕t_i$. Update τ = τ̃ with probability $\min (1,r_m^i)$.
  • With probability 1−ζ, perform the crossover step [I/2] times, where [I/2] denotes the integer part of I/2. The crossover is conducted as follows: randomly select a pair of chains (i, j) and exchange the right segment of τ's from a random point. Denote the old values to be (τⁱ, τ^j), and the crossed values to be (τ̃ⁱ, τ̃^j), we then compute the log ratio: log r_c = [log π_i(τ̃ⁱ|·) − log π_i(τⁱ|·)]/t_i + [log π̃^j|·) − log π_j(τ^j|·)]/t_j. The (τ̃ⁱ, τ̃^j) are accepted with probability min(1, r_c).
  • Step 2.2. (exchange) Exchange the τ samples from two adjacent chains I times, i.e., randomly choose τⁱ and τ^j from neighboring chains, and compute the log ratio: log r_e = [log π_j(τ^j|·) − log π_i(τⁱ|·)]/t_i + [log π_j(τⁱ|·) − log π_j(τ^j|·)]/t_j, and exchange τⁱ with τ^j with probability min(1, r_e).

• Step 3. Conditional on current values of Z_l's, ${\sigma }_b^2$, and the current samples of τ, run step 4 – 6 in Algorithm 1 independently for each chain, obtaining samples of α, b₀ and b_l's.

• Step 4. For every block of iterations within the burn-in period, we adjust the temperature ladder according to the acceptance rate of exchange operations within this block. A new geometric ratio ã is computed by log₂ ã = log₂ a ± δ_a, where the “+” sign is used when we would like to reduce the acceptance rate of exchange. The new temperature ladder is applied to the next block of iterations.

Repeat step 1 – 4 until the maximum number of iterations is reached.

5. Simulation results

Two simulation studies were conducted to evaluate the performance of the proposed model for functional data classification. In both simulations, we generate data that contain both random and fixed effects. Simulation 1 uses 4 functional predictors, and thus τ is a binary vector of length 4. Since the number of functional predictors is small, the MCMC Algorithm 1 works well. Simulation 2 increases the number of functional predictors to 20, in which case the Algorithm 1 suffers slow mixing. Algorithm 2 is used, which improves the mixing for posterior samples of τ.

5.1 Simulation 1

We generate n = 1000 i.i.d. observations, using 2 non-functional predictors and 4 functional predictors. For the non-functional predictors, one of them is generated from a uniform distribution on [0, 1], the other is a binary variable. The 4 functional predictors are generated using the first 10 orthonormal cosine bases on the interval [0, 1], i.e., using bases ${\varphi }_0\left(t\right)=1,{\varphi }_k\left(t\right)=\sqrt{2}\cos \left(k\pi t\right)$, k = 1, …, 9 (see Eubank (1999) for details of cosine series). The random effect has two levels, i.e., L = 2. We set the true value of τ to be (0, 1, 0, 1), indicating that the first and the third function do not contribute to the model, i.e., ${\beta }_1^l\left(t\right)={\beta }_3^l\left(t\right)\equiv 0,\forall l$. Other parameters that are used to generate the data are ${\sigma }_0^2=10,{\sigma }_1^2=10,{\sigma }_b^2=5$. The weights ${\left\{w_k^j\right\}}_{k=1}^{\mathrm{\infty }}$ used for the prior covariance are determined by parameter m = 0.51. The binary responses are generated based on (1) using numerical integration. To evaluate classification results, the data are randomly split into a training set(with 800 observations) and a test set(with 200 observations).

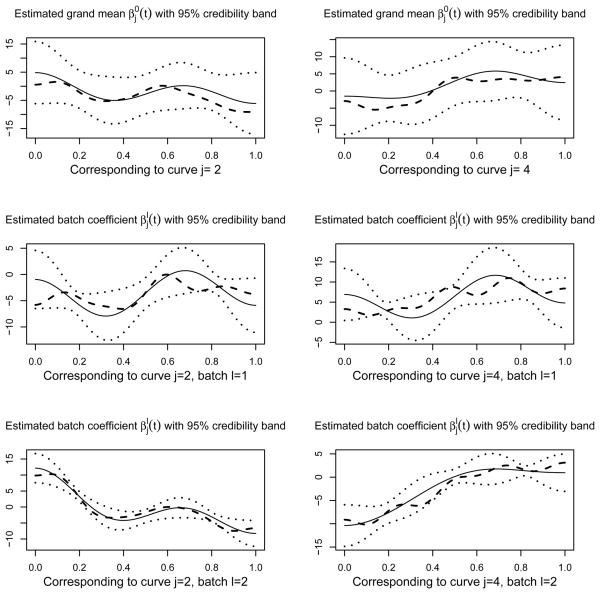
The proposed model in Section 2 is applied to the training data. We use FPC to construct the orthonormal basis and set the approximation criterion described in Section 3 to be c₁ = 0.99, which results in p_j = 4 for all j. Note that the computation of FPC scores for the test set is based on the eigenfunctions estimated from the training set in order to avoid possible bias. Based on the FPC scores, the model is trained using the MCMC Algorithm 1 with the following priors: ${\sigma }_0^2={\sigma }_1^2=20$, d₁ = 4.3, d₂ = 16, ω_j ≡ 0.5, ${\nu }_1^2=1,{\nu }_0^2={10}^{-6}$. The prior parameters for the weight matrix W is set to be such that m = 0.98. We set ζ = ξ = 0.5 and δ = 1.4. We performed 30,000 iterations with a burn in period of 15,000. It turns out that the posterior samples of τ converge to the true τ within 10 iterations. The estimated marginal posterior probability (Pr{τ_j = 1}, j = 1, …, 4) = (0, 1, 0, 1), indicating that our algorithm has correctly selected the second and the fourth functional predictor with high accuracy. Web Figure 2 shows the autocorrelation plot of the posterior samples of ${\sigma }_b^2$ and the corresponding histogram plot. The Geweke convergence diagnostic test (Geweke, 1992) for ${\sigma }_b^2$ using the first 10% and last 50% of the samples gives Z-score −0.57, indicating the convergence of the posterior sample means. The posterior median for ${\sigma }_b^2$ is 5.7, and the 95% credible interval for ${\sigma }_b^2$ is (3.0, 12.4). Note that since we are using a different orthonormal basis (FPC) than that used to generate data, the posterior estimates of b_l's and b₀ will not be comparable with the true values. However, we can estimate coefficient function ${\widehat{\beta }}_j^l\left(t\right)$'s from b_l and compare them with the true coefficient functions. Figure 2 shows the posterior b means of the coefficient functions and the corresponding simultaneous 95% credibility bands for the non-zero cofficient functions, along with the true functions. The simultaneous credibility band is obtained by finding a constant M, such that 95% of the simulated posterior functions fall in the interval ${\widehat{\beta }}_j^l\left(t\right)\pm M{\widehat{\sigma }}_j^l\left(t\right),\forall t$, where ${\widehat{\beta }}_j^l\left(t\right)$ and ${\widehat{\sigma }}_j^l\left(t\right)$ denotes the posterior mean and standard deviation of the cofficient functions. From Figure 2, we see that the true coefficient functions lie in the 95% credibility bands.

Figure 2.

The posterior estimation of the non-zero coefficient functions ${\beta }_j^l\left(t\right)$ and their 95% simultaneous credibility band, compared with the true coefficient functions used to generate the data. Here j is the the index for mutiple functional predictors, and l is the index for batch. ${\beta }_j^0\left(t\right)$'s are the grand means of all batch coefficients. The solid lines denote the posterior mean; the dotted lines denote the 95% credibility bands; the dashed lines denote the true coefficient functions. We only listed the estimations for j = 2, 4 since the functional predictors at j = 1 and 3 are unselected and thus the associated coefficient estimations are close to zero.

After the training step, the estimated coefficient functions are applied to the test set to get the posterior predictive probability. Treating y_i = 1 as diseased and y_i = 0 as normal, the predictions on the test set gives sensitivity 92% and specificity 99%, with the total misclassification rate 4.5%. Note that the sensitivity and specificity we reported here are obtained by finding a point on the empirical ROC curve that maximizes the sum of sensitivity and specificity (see Zweig (1993) for introduction of ROC Curves).

As mentioned in Section 4, in Algorithm 1, we use a Metropolis-Hastings step with a “switch/swap” proposal to update the parameter τ. In this simulation, the space for τ only has 2⁴ possible values. The trace of posterior samples of τ shows that when Algorithm 1 starts from a random value, it only updates 3 times before reaching the correct value, which never changes afterward. However, as the length of τ increases, the size of the state space of τ increases exponentially, and the “switch/swap” proposal takes a long time to find a ”good” proposal. Our experiments show that when the length of τ goes beyond 8, Algorithm 1 suffers extremely low acceptance rate for τ and mixes very slowly. Therefore we suggest using Algorithm 2 when the number of functional predictors is large (e.g., greater than 8).

5.2 Simulation 2

To evaluate the performance of Algorithm 2 when there are a relatively large number of functional predictors, we generate n = 1000 i.i.d. observations similarly as in Simulation 1 using the first 10 cosine bases functions, but increase the number of functional predictors per observation to 20. We set the true τ to be such that 8 out of the 20 components are 1's. Other parameters are set to be the same as in Simulation 1. We also split the data to training and test set as in Simulation 1.

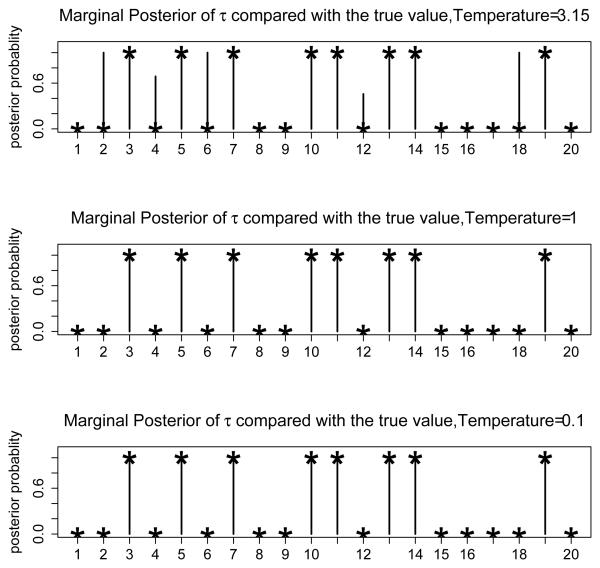
Similarly to Simulation 1, we set approximation criterion c₁ = 0.99 as we approximate the functional predictors using FPC, which results in p_j = 4 for all j. Seven parallel chains are used in Algorithm 2 with a maximum temperature of 18 for the temperature ladder and the geometric ratio for the ladder starting at 3. Other prior parameters are set similarly as in Simulation 1. We perform 20, 000 MCMC iterations with a burn-in period of 5, 000 in which the temperature ladder is adjusted. In addition to this burn-in period, an extra 5, 000 iterations are used as a second-stage burn-in period(with the fixed temperature ladder obtained from the first period). Therefore the posterior inference is based on the last 10, 000 iterations. It takes around 3 hours to complete the job using a computer server with dual 3.4 GHz Intel Xeon processors and 4 GB of memory. The MCMC algorithm is coded using R. The final temperature ladder after the burn-in period adjustment is (18, 7.53, 3.15, 1, 0.55, 0.23, 0.1). The acceptance rates of ${\sigma }_b^2$ for different chains are (56, 41, 33, 23, 17, 12, 9) × 10⁻², and the acceptance rates of τ in the mutation operation step are (23, 13, 4, 0, 0.5, 1, 0) × 10⁻⁴, in the same order of the temperature ladder. The acceptance rates for crossover and exchange operations are 15.3% and 45.8%, respectively. We plot the estimated marginal posterior probability Pr{τ_j = 1}, j = 1, …, 20, under three selected temperatures in Figure 3, compared with the true value of τ. Figure 3 shows that at temperature 3.15, more components in τ than the true are selected. The chains with temperature 1 and 0.1 show similar marginal posterior probabilities. They both pick out the correct functional predictors. The estimated regression coefficient functions are obtained from the chain with temperature 1 and applied to the test set for prediction, with a resulting sensitivity of 94.3%, specificity of 95.8% and misclassification rate of 5%.

Figure 3.

The marginal posterior probabilities Pr{τ_j = 1, j = 1}, …, J, at 3 selected temperatures. The symbol ★ indicates the true value of each component of τ. The vertical lines are the marginal posterior probabilities.

6. Application to fluorescence spectroscopy data

The proposed model is applied to the fluorescence spectroscopy data introduced in Section 1. In this data set, an EEM measurement corresponds to an observation with 16 functional predictors. Using our approach, we aim to select a subset of the 16 curves in the EEM to reduce the cost of data collection.

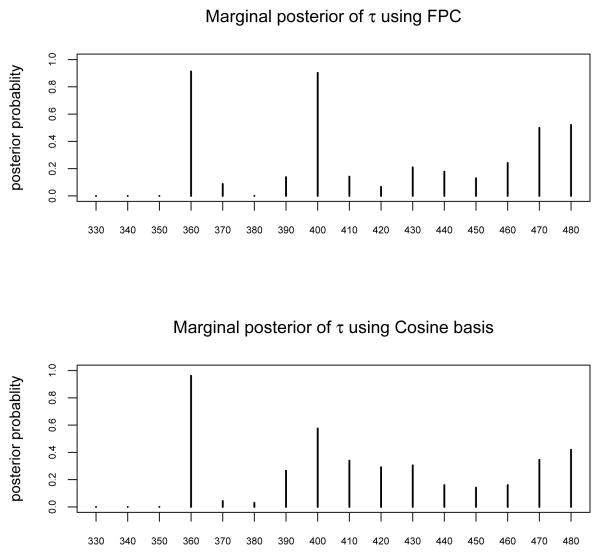
There are a total of 2414 measurements taken from 1006 patients. Each patient has 1 or more (up to 6) sites that were measured and there exists repeated measurements (although not for every patient). The data were pre-processed by procedures such as background correction and smoothing. All measurements come from 6 device-clinic combinations, which we treat as the sources of random effects. Two fixed effects are considered and treated as non-functional predictors in the proposed model: tissue-type, coded as 1, 2, and menopausal status, coded as 1, 2, 3. The 2414 measurements are randomly split into training and test set, with 1353 observations in the training set and 1061 in the test set. The split is conducted at the patient level, i.e., measurements from each patient either all fall in training set or all fall in test set. The proportion of diseased observations in the training and test sets are 10% and 9%, respectively. Both cosine basis expansion and FPC are used to approximate the functional predictors. We determine the number of basis functions used for each curve by setting the approximation criterion c₁ = 0.998 for FPC, and c₂ = 0.992 for cosine basis expansion. The resulting p_j's for the functional predictors range from 2 to 4. The priors are set as: ${\sigma }_0^2={\sigma }_1^2=20$, d₁ = 3.6, d₂ = 22.9, ω_j ≡ 0.5, ν₁ = 1, ν₀ = 10⁻³. The weight matrix W is determined by setting the parameter m = 0.81, using the way described in Section 3. In both cases, we perform 20,000 MCMC iterations with 5, 000 burn-in iterations for temperature ladder adjustment. Similary as in Simulation 2, an extra 5, 000 iterations are used as a second-stage burn-in period. Nine parallel chains are used in Algorithm 2 for both sets of basis functions. The maximum temperature used in Algorithm 2 is 10 in both the FPC case and the cosine expansion case. Both cases use an initial geometric ratio a = 3. Other parameters used in Algorithm 2 are: δ = 1.2, ζ = ξ = 0.5. The acceptance rates in both cases are listed in Web Table 1. The posterior mean estimate for ${\sigma }_b^2$ is 3.10 using FPC, and is 3.52 using cosine basis expansion. In Figure 4, we plot the estimated marginal posterior probabilities Pr{τ_j = 1}, j = 1, …, 16, for both cases. Figure 4 shows that the two basis expansion methods provide similar marginal posterior probabilities for τ. Both methods show high probabilities of selection for functions at excitation 360 and 400nm, followed by functions at excitation 480nm and others. The marginal posterior probabilities suggest an order of selection for the functional predictors, with higher quantities having higher priority of being selected. The decision of selection can be made by setting the total number of functions to select, and choose the functions by the marginal posterior probabilities. For example, if we would like to select 3 functional predictors, both methods of basis expansion suggest to select functions at excitation 360, 400 and 480nm. One can also make decisions based on the joint posterior probabilities of τ(e.g., selecting the most frequently visited model.)

Figure 4.

The marginal posterior probabilities Pr{τ_j = 1}, j = 1, …, 16, for both cases of basis expansions. The top panel is based on FPC, and the bottom panel is based on Cosine basis expansion.

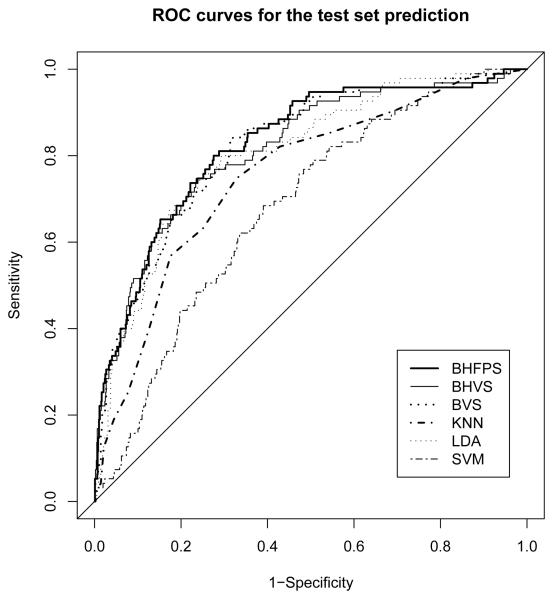
The estimated regression coefficients are applied to the test set for prediction. The prediction results are listed in Table 1 and are compared with 5 other classifiers. Here we denote our proposed model “BHFPS”, an abbreviation of Bayesian Hierarchical Functional Predictor Selection. Note that all the classifiers in Table 1 use both the non-functional and all 16 functional predictors. In particular, the BVS model is a regular Bayesian variable selection method which does not consider the random effects and functional predictor selection. It selects variables among the pooled scores obtained from orthonormal basis expansion of the 16 curves (Zhu, Vannucci and Cox, 2007). The Bayesian hierarchical variable selection (BHVS) is an extension of the BVS model which includes the random effects with a hierarchical setup. From Table 1, we see that the proposed method (BHFPS) obtains slightly higher area under the ROC curve(AUC) than BHVS and BVS. Table 1 also shows that the two orthonormal basis expansion methods are comparable in their prediction ability, although the cosine basis expansion method shows slightly lower AUC's than the FPC method. In Figure 5, we compare the empirical ROC curves for models listed in Table 1 using the results of the FPC method.

Table 1.

Results of test set prediction using the proposed model (BHFPS) compared with 5 other methods. Two methods of basis expansions are used: cosine basis expansion and functional principal components.

	Using Cosine basis expansion				Using FPC
Method	AUC	MisR	Sens	Spec	AUC	MisR	Sens	Spec
BHFPS	0.824	26.7%	81.1%	72.6%	0.826	26.9%	80.0%	72.5%
BHVS	0.808	25.4%	74.7%	74.6%	0.814	23.7%	74.7%	76.5%
BVS	0.802	28.1%	76.8%	71.4%	0.819	30.5%	84.2%	68.0%
KNN	0.697	27.7%	62.1%	73.3%	0.718	32.1%	71.8%	74.7%
LDA	0.796	27.3%	74.7%	72.5%	0.804	25.0%	75.8%	74.9%
SVM	0.657	56.6%	85.3%	39.2%	0.679	38.4%	68.4%	61.0%

AUC: Area under ROC curve; MisR: misclassification rate; Sens: sensitivity; Speci: specificity; BHFPS: the proposed Bayesian hierarchical functional predictor selection model; BHVS: Bayesian hierarchical variable selection model; BVS: regular Bayesian variable selection model; KNN: K-nearest neighbor; LDA: linear discriminant analysis; SVM: linear support vector machine. See text for explanation of BVS and BHVS models

Figure 5.

ROC curves obtained by test set prediction using the proposed model compared with 5 other classifiers, where BHFPS, BHVS, BVS, KNN, LDA and SVM are defined in Table 1.

Based on the functional predictors selected from the proposed model, classification algorithms can be trained independently using only the selected curves. For example, trained on the first 3 functional predictors selected by the proposed model, the BHVS model gives sensitivity 73.7% and specificity 70%, with corresponding AUC 0.80 and misclassification rate 29%. Compared with Table 1, these prediction results are comparable with those using all 16 curves(which are based on model averaging over the different posterior selections of τ). Hence it is possible to use a smaller number of curves and retain a high prediction power. Using the selected curves, a new device can be constructed which reduces cost and saves measurement time.

7. Discussion

Motivated by a practical problem in functional data classification, we have proposed a Bayesian hierarchical model to deal with situations when functional predictors are contaminated by random batch effects. Inferences based on this model help to select a subset of functional predictors for classification. This model is applied to a real application of using fluorescence spectroscopy for cervical pre-cancer diagnosis. The results suggest that it is possible to build more cost-effective device with fewer spectral curves.

When setting the priors for the coefficient functions in (2), we have assumed that ${\beta }_j^l\left(t\right)$ are independent for all j and l, which leads to the prior correlation matrix R = I_p in (9) after approximation with basis expansion. This is just a simple and convenient choice of prior. It is possible to allow the priors for ${\beta }_j^l\left(t\right)$ to be correlated, such as assuming that $({\beta }_1^l\left(t\right),\dots ,{\beta }_J^l\left(t\right))$ is a multivariate Gaussian process, as done in Morris and Carroll (2006). However, determining prior correlations can be difficult and the resulting posterior computation can be complex.

Another concern arises over the necessity of using a hierarchical structure to adjust for batch effects. As we have pointed out in Section 1 and the Web Appendix A, for data obtained from an unbalanced experimental design, classification can be easily biased by batch effects. Algorithms that do not adjust for batch effects may result in classification based on batch difference, rather than disease information. Using a hierarchical model is a natural way to model the batch structure. In our real data application, although the hierarchical models (BHFPS and BHVS) did not improve prediction significantly over models like BVS (see Table 1 and Figure 5), they are more suitable as they adjust for the batch effects. In fact, we should not always expect that adjusting for batch effect can improve the prediction, since with a bad experimental design, a classification algorithm can get prediction as good as 100% sensitivity and specificity, by simply using batch information (see, e.g., discussions of Baggerly et al. (2004)).

In our simulation and real data applications, the proposed model was trained using data from all batches, and predictions were made on observations from the same batches. Like many other hierarchical models, our proposed model can also predict observations from new batches. However, it is natural to expect that the prediction will be worse when predicting on new batches, since the random effect of the new batch is unknown when training the model.

Finally, like many other regression problems, when there exists collinearity between the functional predictors, a unique solution for the “best” subset may not be guaranteed. In this case, our proposed model may provide nearly equal posterior probabilities of selecting one or the other functional predictors.