FCS Diffusion Laws in Two-Phase Lipid Membranes: Determination of Domain Mean Size by Experiments and Monte Carlo Simulations

Abstract

Many efforts have been undertaken over the last few decades to characterize the diffusion process in model and cellular lipid membranes. One of the techniques developed for this purpose, fluorescence correlation spectroscopy (FCS), has proved to be a very efficient approach, especially if the analysis is extended to measurements on different spatial scales (referred to as FCS diffusion laws). In this work, we examine the relevance of FCS diffusion laws for probing the behavior of a pure lipid and a lipid mixture at temperatures below, within and above the phase transitions, both experimentally and numerically. The accuracy of the microscopic description of the lipid mixtures found here extends previous work to a more complex model in which the geometry is unknown and the molecular motion is driven only by the thermodynamic parameters of the system itself. For multilamellar vesicles of both pure lipid and lipid mixtures, the FCS diffusion laws recorded at different temperatures exhibit large deviations from pure Brownian motion and reveal the existence of nanodomains. The variation of the mean size of these domains with temperature is in perfect correlation with the enthalpy fluctuation. This study highlights the advantages of using FCS diffusion laws in complex lipid systems to describe their temporal and spatial structure.

Introduction

Since Singer and Nicolson (1) first proposed the mosaic fluid model, in which lipids are considered as a type of sea in which proteins are embedded, the description of biological lipid membranes has evolved to reflect a spatiotemporal heterogeneous mixture of components. It is now widely accepted that biological membranes are organized in domains of different compositions and sizes, including nano- and microscale organization. Membrane heterogeneity may be of various types. Several lipid lamellar phases have been identified in model systems. Basically, the lipid bilayer can exist in gel (or solid) phases g, fluid (or liquid disordered) phases f, and liquid ordered phases, which are often enriched in cholesterol (see Table 1 for a summary of the symbols used in this work). In a complex lipid mixture, these different phases may coexist, leading to the formation of domains (2). This is the basis for the concept of rafts as functional domains existing within biological membranes (3). Because this is of great interest in terms of cell biology, much work has been done on rafts over the past 10 years (4–7). The results led to the current view that rafts are highly dynamic, heterogeneous membrane structures that are rich in cholesterol and sphingomyelin, are ∼10–200 nm in diameter, and are present in the lipid membranes of all eukaryotic cells (8). However, since their sizes are below the diffraction limit, there are no images of these structures.

Table 1.

Definitions of symbols used in the text

Symbol	Definition
g	Gel phase (equivalent to s solid phase)
f	Fluid phase (equivalent to ld liquid disordered phases)
w	Waist of the laser
τd	Diffusion time
Deff	Effective diffusion coefficient
${\tau }_{d_0}$	Linear asymptotic extrapolation of the diffusion time (τd at $w^2=0$)
$l.u.$	Lattice unit: $1{(\text{l}.\text{u})}^2=$1 lipid
$w_0^2$	Linear asymptotic extrapolation of the probed area (w2 at ${\tau }_d=0$)
$l_c$	Coherence length (defined in section 1.8 of the Supporting Material)
ag	Area occupied by one lipid in the gel state
af	Area occupied by one lipid in the fluid state
${\tau }_d^f$	Diffusion time in fluid state
${\tau }_d^g$	Diffusion time in gel state
α	Anomalous exponent of the diffusion process $0<\alpha <2$

As noted above, domains in complex mixtures are dynamic structures; therefore, it seems relevant to use diffusion as a spatiotemporal probe of the local environment. This approach has been developed with such techniques as fluorescence recovery after photobleaching (FRAP) (9–11), fluorescence correlation spectroscopy (FCS) (12–15), and single particle tracking (SPT) (16). Each of these dynamic microscopic techniques has advantages and disadvantages with respect to its timescale and statistics. For example, FCS is sensitive on the millisecond–second timescale, corresponding to the characteristic diffusion time in fluid or ordered lipid mixtures of a fluorescently labeled molecule through a focus with a waist of ∼200 nm.

Recently, Wawrezinieck et al. (17) showed that direct fitting of the autocorrelation function was inaccurate for discriminating between these complex diffusions, but exploration at different space scales provides a more detailed view of the environmental structure. They developed a variable-waist FCS experiment and observed deviation from pure Brownian motion in live cell membranes (18), which was recently confirmed at different space scales down to 50 nm (15,19). Numerical simulations in arbitrarily controlled geometries were used to reassign these FCS diffusion laws to heterogeneous probed environments such as rafts or a mesh of partially permeable barriers. A good correspondence was observed between these simulations and the experimental data in cell membranes. However, although the system investigated was very complex, the geometries and parameters used for the simulations were quite simple. Therefore, investigations are strongly needed to further explore the accuracy of these quantitative FCS diffusion laws to reveal domains in a well-defined system where the molecular motions are driven only by the thermodynamic parameters of the system itself.

In this work, we investigated the use of FCS diffusion laws in well-defined lipidic systems, such as DMPC/DSPC mixtures or DMPC alone. DMPC and DMPC/DSPC lipid mixtures have been studied extensively for some time. Their thermodynamic behavior has been deciphered by many different techniques, including differential scanning calorimetry (DSC), neutron scattering, NMR, electron spin resonance, Raman spectroscopy, Fourier transform infrared spectroscopy (20), and atomic force microscopy (AFM) (21). Pure DMPC is known to exhibit a phase transition from the gel to the fluid phase at $296.5K$, whereas the DMPC/DSPC (8:2 mol/mol) mixture is characterized by two main transition temperatures: one for the first transition from totally gel to a gel-fluid mixture ($gg:gf$) at $299\text{K}$ and one for the second transition from a gel/fluid mixture to totally fluid ($gf:ff$) at $308\text{K}$ (22). Studies have shown that DMPC/DSPC mixtures form nonideal, two-phase mixtures with small clusters of the minor phase in a continuum of the major phase. The nonideal mixing properties of this system make the DMPC/DSPC binary mixture a good model for investigating phase separation and lipid domain formation. FRAP studies that examined the structural characteristics of this mixture (10,23) revealed the existence of solid domains in a sea of fluid lipids surrounded by a fluctuating shell at temperatures within the two transition temperatures ($gg:gf$ and $gf:ff$). Using this approach, Schram et al. (23) described the gel phase domains as being ramified in the case of highly miscible lipids, or large and compact phases in the case of poorly miscible lipids. The topology and size were shown to vary across the phase diagram.

Determination of thermodynamic parameters resulted in the development of numerical simulations. Various investigators have used Monte Carlo (MC) methods to simulate the lateral distribution of each component in the pure gel or fluid phase of the DMPC/DSPC mixture, first by assuming one state and two components (24), and more recently by computing a two-phase, two-component triangular lattice model (25). This model has been successfully used to predict the size, shape, and number of gel(g)/fluid(f) clusters (26) and was recently used to simulate FCS experiments (27).

The accuracy of the thermodynamic microscopic description of DMPC/DSPC mixtures makes this an ideal model system for exploring the relevancy of FCS diffusion laws. Our goal in this study was to extend the results of previous works (24–27) both theoretically and experimentally. The experimental FCS diffusion laws in both DMPC/DSPC (8:2 mol/mol) mixtures and pure DMPC at different temperatures spanning the range of the phase transitions show clear deviations from a pure Brownian motion. To elucidate the origin of this deviation and quantitatively characterize it, we performed numerical simulations on these lipids. In this study, both approaches (numerical and experimental) revealed striking similarities regarding the obtained FCS diffusion laws in terms of the effective diffusion coefficient and deviation from pure Brownian motion as a function of the lipid states. Furthermore, our results confirm that FCS diffusion laws can be used to distinguish the existence of domains and determine their mean size.

Materials and Methods

The materials and methods used in this work are detailed in the Supporting Material, including the lipids and fluorescent dyes used, preparation of multilamellar vesicles, the FCS setup, fit of the experimental autocorrelation functions for the experimental part of the study, and MC numerical simulations, thermodynamic model and parameters, reconstruction of autocorrelation functions in the simulations, and analysis of image generated in the simulations using image correlation spectroscopy (ICS) or morphometry for the numerical part of the study.

Results

FCS at variable radii and temperatures in DMPC and DMPC/DSPC samples

FCS diffusion laws were acquired in pure DMPC lipid multilamellar vesicles and vesicles made of DMPC/DSPC (8:2 mol/mol), both labeled with C5-Bodipy-PC (see sections 1.1 and 4 in the Supporting Material for more information about the choice of this dye) at different temperatures below, within, and above the phase transitions. Fig. 1 A shows a typical correlogram obtained from pure DMPC at 297 K with a transversal waist w = 218 μm. Fig. 1 B shows the same type of experimental correlogram obtained from the DMPC/DSPC 8:2 mol/mol mixture at 302 K with a transversal waist w = 210 μm. In both parts of the figure, the line is the fit of the correlogram obtained using Eq. S1, which allows determination of a characteristic diffusion time τ_d. The residual (upper part of Fig. 1, A and B) assesses the quality of the fit. FCS diffusion laws were obtained from experiments made at different waists for different temperatures. These are depicted in Fig. 1, C and D, for pure DMPC and the DMPC/DSPC mixture, respectively.

Figure 1.

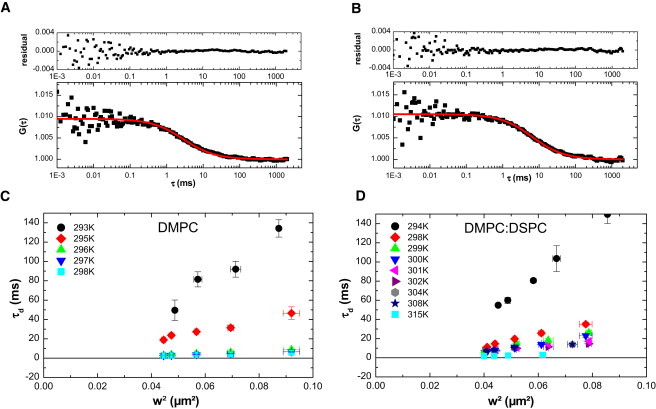
Experimental correlograms and FCS diffusion laws obtained in lipid mixtures. (A and B) Correlograms obtained on multilamellar vesicles of (A) DMPC and (B) DMPC/DSPC 8:2 mol/mol (square dots indicate experimental data) fitted with Eq. S1. Residuals are plotted in the upper part of the figure, showing the accuracy of the fit. (C and D) Experimental FCS diffusion laws obtained for (C) DMPC and (D) DMPC/DSPC 8:2 mol/mol at different temperatures. (Color version online.)

FCS diffusion laws can be approximated at different temperatures by the following equation:

$${\tau }_d=\frac{w^2}{4D_{eff}}+{\tau }_{d_0},$$ (1)

where τ_d is the experimentally determined values of diffusion time at different waist w, and ${\tau }_{d_0}$ is the extrapolated diffusion time at $w^2=0$. These FCS diffusion laws also allow the determination of an effective diffusion coefficient D_eff. Fig. S1, A and B, show the increase of this diffusion coefficient D_eff with temperature for both samples.

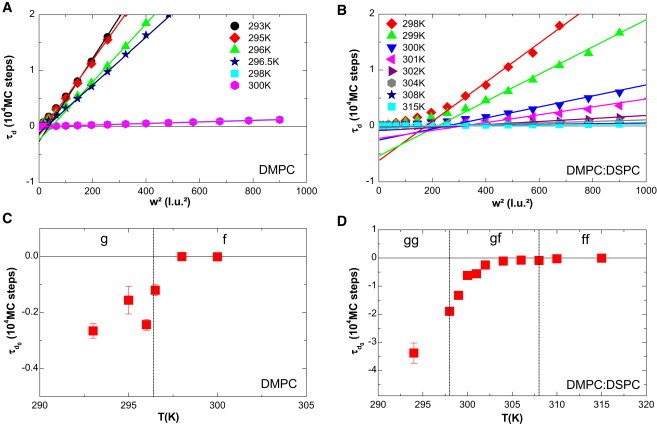
As illustrated in Fig. 2, A and B, the fit of the experimental FCS diffusion laws exhibits a negative ${\tau }_{d_0}$ for temperatures below the phase transition in the case of DMPC ($T<297\mathrm{K}$; Fig. 2 A), and below the second transition ($gf:ff$) in the case of the DMPC/DSPC mixture ($T<310\mathrm{K}$; Fig. 2 B). When the FCS laws are acquired in the pure fluid phase, they exhibit ${\tau }_{d_0}$ values close to zero, indicating a pure Brownian behavior of the diffusing molecules as expected ($T>298\text{K}$ for DMPC alone (Fig. 2 A), and $T>310\text{K}$ for the DMPC/DSPC mixture (Fig. 2 B)). The plot of ${\tau }_{d_0}$ as a function of temperature shows that in both cases (DMPC alone or lipid mixture; Fig. 2, C and D) the more the system is in the gel phase (or the more the temperature decreases), the more ${\tau }_{d_0}$ becomes negative.

Figure 2.

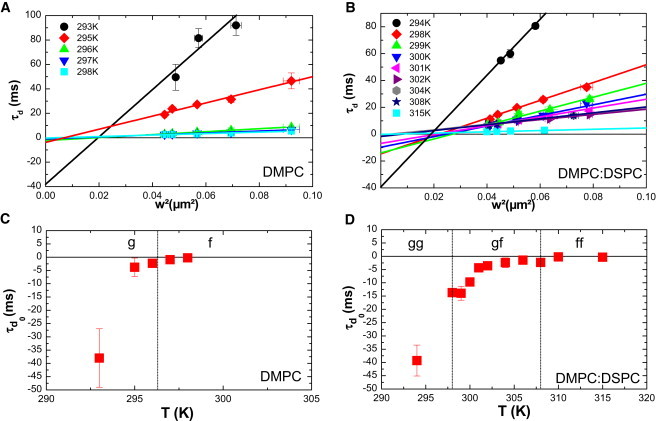
Variation of experimental ${\tau }_{d_0}$ as a function of temperature. (A and B) Fit of the asymptotic part of the experimental FCS diffusion laws using Eq. 1 for (A) DMPC and (B) DMPC/DSPC 8:2 mol/mol, allowing determination of ${\tau }_{d_0}$ for each set of data. (C and D) ${\tau }_{d_0}$ is plotted against temperature for (C) DMPC and (D)DMPC/DSPC 8:2 mol/mol. Square dots are obtained values with error bar. (Color version online.)

To determine the origin of a negative ${\tau }_{d_0}$ when gel domains are present in a fluid phase (see the Supporting Material), we performed MC simulations using a full set of thermodynamic parameters for DMPC and DMPC/DSPC lipid mixtures.

FCS at variable radii on MC numerical simulations: diffusion laws

MC simulations were performed at different temperature below, within, and above the two state transitions $(gg:gf:ff)$ of the DMPC/DSPC 8:2 (mol/mol) and below, within, and above the phase transition of DMPC alone ($g:f$). Fig. 3 A shows a snapshot of the DMPC/DSPC 8:2 mol/mol mixture at 304 K (g f state) as obtained from the MC simulation. Gel domains (in green or light gray) can be seen in a sea of fluid lipids (in red or dark gray; 60 × 120 lipid chains). MC simulated correlograms of this mixture are depicted for different waists at this temperature in Fig. 3 B, showing an increase of τ_d with increasing waists as expected. As seen from experiments (see Fig. 2), τ_d is also expected to increase with decreasing temperature at a given waist (illustrated in Fig. 3 C). At low temperature ($T<300\text{K}$) or large waist ($w>20\text{l}.\text{u}.$, where $\text{l}.\text{u}.$ is the lattice unit as defined in Table 1), the correlation function at long timescales shows higher noise due to the limited number of events arising at these times. Nevertheless, the determination of τ_d is still valid because the noise appears at much longer timescales than τ_d. Therefore, we can again establish the FCS diffusion laws by plotting τ_d as a function of the square of the waist w². FCS diffusion laws are depicted in Fig. 4 for different temperatures of the MC simulations for both the DMPC/DSPC mixture (Fig. 4 A) and DMPC alone (Fig. 4 B). As found experimentally in the case of the DMPC/DSPC mixture, above 310 K the FCS laws seem perfectly linear (Fig. 4 A), accounting for a pure Brownian diffusion of the lipids. Below 310 K (Fig. 4 A, inset), none of the FCS laws are linear, indicating a deviation from a pure Brownian diffusion as expected for inhomogeneous media. Even below the first transition temperature $gg:gf$ of the lipid mixture, these FCS laws still show a nonlinear behavior. As shown in Fig. 4 B, the same type of nonlinear FCS diffusion law was obtained in pure DMPC MC simulations below the transition temperature (296.5 K).

Figure 3.

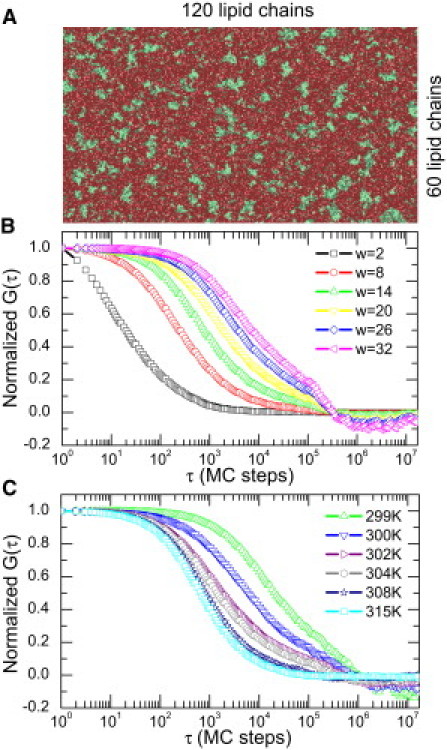
Images and correlograms obtained by MC simulation of a DMPC-DSPC 8:2 mol/mol mixture. (A) MC snapshot of a 60 × 60 lipid lattice 8:2 mol/mol DMPC-DSPC mixture at 304 K. Green (or light gray) domains correspond to gel lipids, and red or dark gray domains correspond to fluid lipids. (B) Normalized correlograms obtained from the MC simulation at 304 K for different waists. (C) Normalized correlogram obtained from the MC simulation at a given waist (w = 8 l.u.) at different temperatures from gel ($T<300\text{K}$) to liquid ($T>310\text{K}$) and within the melting regime ($300\text{K}<T<310\text{K}$).

Figure 4.

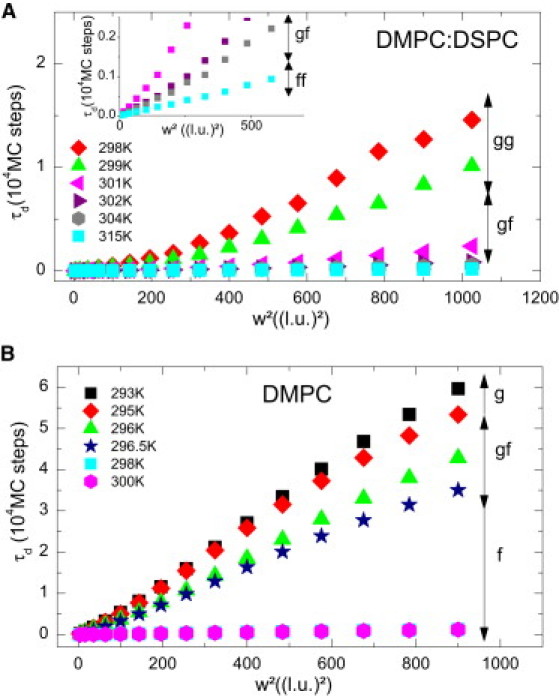
FCS diffusion laws obtained from MC simulation at different temperatures. (A) FCS diffusion laws obtained from MC simulations of the DMPC-DSPC 8:2 mol/mol mixture are represented for different temperatures below, within, and above the melting regime of the mixture. The inset shows an enlargement for low waists at high temperatures. These FCS diffusion laws exhibit two slopes at low temperature but start to be linear with a null origin at temperature above 310 K, indicating a pure Brownian diffusion process. (B) FCS diffusion laws obtained from MC simulations of pure DMPC are represented for different temperatures below and above the phase transition (296.5 K). Again the FCS diffusion laws exhibit two slopes below the phase transition and start to be linear with a null origin at temperature above 298 K.

The MC simulated FCS diffusion laws can be fitted using Eq. 1, as depicted in Fig. 5 A for DMPC alone and in Fig. 5 B for the DMPC/DSPC mixture.

Figure 5.

Variation of ${\tau }_{d_0}$ obtained by simulations as a function of temperature. (A and B) Fit of the asymptotic part of the MC FCS diffusion laws using Eq. 1 at different temperatures for (A) DMPC and (B) DMPC/DSPC 8:2 mol/mol. (C and D) ${\tau }_{d_0}$is plotted against temperature for (C) DMPC and (D) DMPC/DSPC 8:2 mol/mol. Square dots are obtained values with error bar. A sharp increase is seen around 300 K, close to the first melting temperature of the DMPC-DSPC 8:2 mol/mol mixture and around 296 K, close to the melting temperature for DMPC.

As in the experiments, the value of an effective diffusion coefficient D_eff can also be calculated and is plotted as a function of temperature in Fig. S1, C (DMPC/DSPC mixture) and D (DMPC alone). In both cases, it is important to note that the global shape of the curve $D_{eff}=f\left(T\right)$ is the same for the simulation and experiments, and is characterized by a sharp increase during the transition from gel to fluid medium. As in the experimental FCS diffusion laws, ${\tau }_{d_0}$ decreases with decreasing temperature as plotted in Fig. 5, C and D, for DMPC alone and the DMPC/DSPC mixture, respectively. ${\tau }_{d_0}$ also reaches values close to zero at $T\ge 310\text{K}$ for the DMPC/DSPC mixture and $T\ge 298\text{K}$ for DMPC alone, confirming a pure Brownian diffusion of the system above this temperature.

These observations are in agreement with our experimental results for both DMPC and DMPC/DSPC lipid mixtures. Both systems exhibit a deviation from pure Brownian motion as soon as they are not in a pure fluid state. These deviations can be detected with the use of FCS diffusion laws and are characterized by a negative ${\tau }_{d_0}$.

Determination of domain size

The FCS diffusion laws obtained from MC simulations in this study can be described by two linear laws crossing over each other at a given waist, exhibiting a crossover regime that is a putative function of the domain size. Wawrezinieck et al. (17) previously showed that deviations from a single linear regime in the FCS diffusion laws were a signature of heterogeneities in the probed environment. They also showed, using numerical simulations, that the crossover regime in the FCS diffusion laws is a function of the relative size of both the probing waist and the domain size. In the case of restriction to diffusion in a mesh of partially permeable barriers, Eq. S10 shows that the FCS diffusion law can be described by two linear laws crossing over each other close to the mesh size, allowing its measurement.

In the experimental FCS diffusion laws obtained here, only the linear law corresponding to high values of w² is accessible. Nevertheless, a surface $w_0^2$ can be introduced as the intercept between the linear fit at high waists and the abscissa axis of the FCS diffusion laws. This surface relates to the extrapolated negative diffusion time at origin τ_d0. Equation 1 shows that $w_0^2=-4D_{eff}{\tau }_{d_0}$. Equation S12 suggests that the crossover regime occurs proportionally to this surface $w_0^2$. Because $w_0^2$ is a parameter that can be easily determined from both simulations and experiments, we sought to determine the extent to which it is related to the size of domains. For this purpose, we determined $w_0^2$ in the numerical simulations by fitting with Eq. 1 the second part (between $300\text{l}.\text{u}{.}^2<w^2<1200\text{l}.\text{u}{.}^2$) of the FCS diffusion laws. The obtained values were then compared with those obtained by ICS and by direct space morphoanalysis (see section 1.8 in the Supporting Material for detailed explanations) performed on images of the simulations (such as the one depicted in Fig. 3 A). These comparisons were made at different temperatures for the DMPC/DSPC lipid mixture.

In the case of the ICS analysis, all images between the two main phase transitions were analyzed using a biexponential function with two characteristic coherence lengths ($l_{c_1}$ and $l_{c_2}$; Eq. S8). It appeared that, in that case, $l_{c_1}$ varied between 0.5 and 1 ${(\text{l}.\text{u}.)}^2$, which is a value equivalent to one chain or one lipid, and indeed is the smallest pattern the image can contain. Finally, for the direct space morphology analysis, domains representing less than two lipids were not taken into consideration. We compared the values obtained with each method by measuring the number of lipids in the domains (see Fig. 6 A). This comparison shows that the mean number of lipids obtained by our FCS diffusion laws is close to that revealed by both the morphoanalysis and the ICS analysis. This clearly shows that the $w_0^2$ is a direct indication of the number of lipids in the domains. This number of lipids is directly obtained from the morphoanalysis and estimated by FCS and ICS in supposed circular domains of area $\pi l_{c_2}^2$ or $\pi \sqrt{w_0^2}/2$. There are no fundamental reasons for choosing circular domains except to facilitate a direct comparison the analyses. However, this assumption of circular domains was made in several dynamic studies on this and other lipid mixtures (9,23,28).

Figure 6.

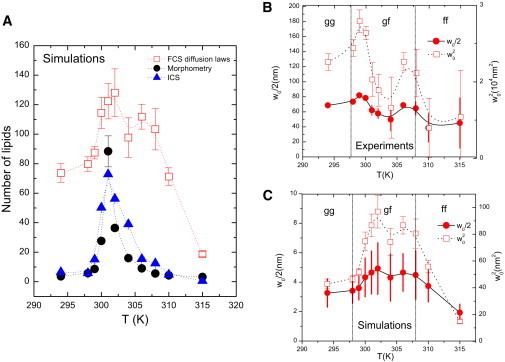
Changes in the lipid domain size as a function of temperature. (A) Comparison of the number of lipids present in the domains as obtained by three different methods (see section 1.8 of the Supporting Material for details). The methods were used to determine the number of lipids in the domains by MC simulation of the DMPC/DSPC 8:2 mol/mol mixture, and the results are compared as a function of temperature. Open squares are the values obtained by determination of $w_0^2$ in FCS diffusion laws. Note that the variation of the domain size revealed by ICS of the FCS diffusion laws shows striking similarities with the heat capacity profile (c.f. Fig. 8.6 of Heimburg (22). (Experimental points are linked by a dashed curve polynomial fit to guide the eye.) (B and C) Variation of $w_0^2$ and $w_0/2$ as a function of temperature for the DMPC/DSPC mixture. Plots of $w_0^2$ (right scale) and $w_0/2$ (left scale) are depicted as a function of temperature, determined (B) experimentally or (C) numerically from a DMPC/DSPC 8:2 mol/mol mixture. This shows two different scales of domain size for experiment and numerical simulation. (Experimental points are linked by a solid curve (for $w_0/2$) or a dashed curve (for $w_0^2$) polynomial fit to guide the eye.)

Using a surface area of a_f = 63Ų and a_g = 45Ų for PC lipids in the fluid phase or gel phase (9,29), respectively, we were able to calculate the mean radius of the domains in nanometers. Fig. 6 B and C, show changes in the experimental (Fig. 6 B) and simulated (Fig. 6 C) $w_0^2$ and the subsequent mean radii ($w_0/2$) found by FCS diffusion laws as a function of temperature. It can be seen that the shape of the $w_0^2=f\left(T\right)$ curve is similar to the heat capacity profile of the DMPC/DSPC (8:2 mol/mol) lipid mixture (for comparison, see Fig. 8.6 of Heimburg (22)). Indeed, these figures clearly show that the mean domain radii observed vary with temperature and exhibit a main change between 301 and 302 K (close to the first maximum increase in enthalpy observed in this mixture by DSC) and a smaller shoulder around 306 K (close to the second maximum increase in enthalpy observed in this mixture by DSC). This was also seen in the FCS diffusion laws of DMPC alone (data not shown). In that case, $w_0^2$ (equivalently $w_0/2$) showed an increased at 296 K, close to the $g:f$ phase transition temperature of DMPC (30). Whereas radii $\left(w_0/2\right)$ of domains revealed by FCS diffusion laws in MC simulations were found to be <5 nm, experimental FCS diffusion laws show values of $w_0/2$ > 50 nm and < 80 nm.

Discussion

Various techniques have been used for a long time to study diffusion in lipid mixtures. Vaz et al. (10) performed FRAP experiments on DMPC/DSPC 8:2 mol/mol at different temperatures using NBD-DLPE as the fluorescent dye, and found values ranging from $D_{eff}=0.25\mu {\text{m}}^2.{\text{s}}^{-1}$ at T = 293 K to $D_{eff}=7.5\mu {\text{m}}^2.{\text{s}}^{-1}$ at T = 308 K. The experimental FCS diffusion laws obtained in this study exhibit effective diffusion coefficients between 0.12 $\mu {\text{m}}^2.{\text{s}}^{-1}$ at 294 K and 5.6 $\mu {\text{m}}^2.{\text{s}}^{-1}$ at 310 K.

The global increase of D_eff obtained by FCS diffusion laws as a function of temperature is in accord with that observed by FRAP. In complex media, FRAP measurements generally do not show total fluorescence recovery. This is described by fitting FRAP recovery curves with a so-called immobile fraction. This immobile fraction reflects the incapacity for nonbleached molecules to enter the photodestructed area during the time of the experiment, and therefore provides indirect information on the restriction to diffusion. The immobile fraction ranges between zero (free diffusion) and one (no diffusion). In a previous study, Vaz et al. (10) showed that the immobile fraction varied from 0.52 at 293 K to 0 at 308 K, with a sharp transition in between that was closely linked to the phase transitions $gg:gf:ff$ of the lipid mixture. The FCS diffusion laws observed in our study exhibit nonzero and negative ${\tau }_{d_0}$ below the second transition $gf:ff$. We note that the shape of the evolution of the immobile fraction as a function of the temperature of the lipid mixture in Vaz et al. (10) is strikingly similar to the evolution of our ${\tau }_{d_0}$ parameter. In a pure gel phase, one would expect to recover a pure Brownian behavior of the molecules with a (much) longer characteristic diffusion time, in which case the immobile fraction, as well as our ${\tau }_{d_0}$ parameter, should go back to the zero value. However, this was not the case here, nor was it the case for the immobile fraction in the study by Vaz et al. (10). One simple explanation could be that the system is not in a pure gel state at a temperature close to 294 K. However, the MC simulation shows that >99% of the system is in the gel state. When this amount of gel is present in the mixture, percolation is not expected to occur and long-range diffusion in the fluid phase should stop, this fluid phase diffusion being the main component observed in our FCS experiments. Therefore, other explanations are needed.

It has been suggested that even in the gel state, some defects can occur along the lipid bilayer (ripple phase formation) that allows fast diffusion along these defects (31). This would lead to fast fluctuations within the observed area and therefore a higher effective diffusion coefficient (D_eff) than expected. For example, using FCS, Hac et al. (27) also found diffusion coefficients in the gel phase in the range of 0.05–0.1 $\mu m^2.s^{-1}$, which is significantly higher than that reported by other methods. Nevertheless, ripple phase formation is certainly not the only explanation for the high D_eff values found in the gel phase, since our MC simulations exhibit exactly the same behavior of the ${\tau }_{d_0}$ parameter observed in the experiments, regardless of the fact that ripple phases do not exist in the simulations.

A change in the lipid state can also be a source of fluorescence fluctuations within a given area and therefore lead to a new correlation time. The system studied here exhibits three different timescales: one characteristic of diffusion in a pure liquid environment (${\tau }_d^f$), one characteristic of a pure gel environment (${\tau }_d^g$), and one proportional to the rate of change from liquid to solid state (or inversely) for each lipid chain. It has been shown that the latter timescale has an influence on the apparent diffusion (26,27). If the change of lipid state occurs more rapidly than the time needed for a tracer to diffuse into a gel obstacle, the obstacle itself will be able to fluctuate and to change its shape and size. This is equivalent to diffusion in smooth obstacles, where it is known that percolation occurs even at a high concentration of obstacles (32). The FCS diffusion laws obtained here exclude the possibility that the domains were totally impermeable, since it has been shown that in this case, D_eff is decreased but the diffusion is still Brownian (${\tau }_{d_0}=0$) (33).

Finally, the timescale of the method is also very important. Both FCS and FRAP experiments are conducted over tenths of seconds, which precludes measurement at diffraction-limited spots ($w<400\text{nm}$) of D_eff < ${10}^{-4}$ or ${10}^{-5}\mu {\text{m}}^2.{\text{s}}^{-1}$. It is therefore clear that if D_eff in the pure gel phase is lower than this value, it will be overestimated by FCS. In the same manner, limited computation time prevents one from running simulations over 10¹⁵ MC steps, and can therefore lead to incorrect measurement of the diffusion time.

All of these possibilities could explain the finding of a higher D_eff than expected and a nonzero ${\tau }_{d_0}$ in the pure gel phase at 294 K.

Another parameter of interest in our FCS diffusion laws is the value of the intercept of the asymptotic linear extrapolation of the diffusion law with the abscissa axis. This parameter is empirically defined as the zero diffusion time characteristic waist (value of w² at ${\tau }_d=0$). It was analyzed as a function of temperature and exhibited a very good correlation to the DSC curve, with two maxima located at the same temperature (2 K accuracy) for DMPC/DSPC 8:2 mol/mol and one maximum at 296 K for DMPC alone. Liquid or solid domains are known to be maximal in size at the maximum enthalpy (34,35); therefore, it seemed reasonable to analyze this $w_0^2$ parameter as a function of the domain size. Using classical random walk simulations, Wawrezinieck et al. (17) showed that in given geometries, this parameter allows one to estimate the exact size of the mesh or the domain. Destainville (36) confirmed these numerical simulation results by analytically solving the problem in the case of restricted motion by a mesh of partially permeable barriers. The geometry of the system studied here is totally unknown and depends only on the thermodynamic properties of it. Therefore, it is difficult to obtain an analytical model that precisely defines the size of the domains as a function of $w_0^2$. Nevertheless, by using ICS or direct morphometry analysis of the images obtained from the MC simulation, we found that the radius of the circular-like domains revealed in the images is close to the size of those estimated by means of the $w_0^2$ parameter obtained from the FCS diffusion laws. This clearly shows that $w_0^2$ is a good estimator of the size of the domains in the lipid mixture.

In the experimental study, circular-like domains had a mean radius ranging from 50 to 80 nm. AFM studies on a 50:50 mol/mol DMPC/DSPC supported bilayer lipid mixture revealed the coexistence of domain sizes between 50 (circular) and 150 × 300 nm (rectangular) in the g f phase (37). These values are consistent with those we determined experimentally using FCS diffusion laws in our 80:20 mol/mol DMPC/DSPC lipid mixtures. Gliss et al. (38) also showed the existence of nanoscale domains in a DMPC/DSPC mixture. AFM imaging allowed them to measure gel domains of 10 nm, and neutron diffraction led to identification of gel domains of 7 nm. These sizes are comparable to those we observed in our MC simulations by ICS analysis, direct morphometry analysis, or estimation of the $w_0^2$ parameter in the simulated FCS diffusion laws (2.5–5 nm). The results obtained here show the existence of domains on two different types of spatial scales. They should be compared with those found using other dynamic methods, such as FRAP or numerical simulation of diffusion. Using free area theory for diffusion in lipid bilayers to analyze their FRAP results, Almeida et al. (9) extrapolated the existence of domains within the range of 8 nm in LigGalCer/DPPC 2:8 mol/mol mixtures. In the same study, using percolation theory, they showed that liquid domains as large as 400 nm could exist in the vicinity of the percolation threshold in DMPC/DSPC/cholesterol ternary mixtures. Schram et al. (23) failed to correctly estimate the domain size in a DMPC/DSPC mixture similar to ours (8:2 mol/mol) based on numerical simulation; however, they obtained gel size domains of 8 nm using FRAP data acquired from $C_{18}{C}_{10}\text{PC}:\text{DSPC}$. Finally, using ESR, Sankaram et al. (28) demonstrated the existence of gel domains of 6 nm separated by a center-to-center distance of 20 nm in a 75:25 mol/mol DMPC/DSPC mixture, but emphasized the fact that “direct imaging by electron microscopy has revealed that some domains in two-component lipid systems may have considerably larger sizes than the mean values reported here”. This has been confirmed by AFM imaging (37). Finally, using confocal microscopy, Bagatolli et al. (39) showed the existence of micrometer-sized domains within giant unilamellar vesicles made of DMPC/DSPC 1:1 mol/mol. Therefore, it seems reasonable to accept the notion that domains can coexist at different spatial scales. Although MC simulations cannot reveal the existence of domains of ∼100 nm due to the limited time calculation, FCS experiments should be able to reveal domains of ∼10 nm. However, it can be seen that, based on a simple assumption, a rapid calculation of the time needed to diffuse through a 10 nm domain close to the first transition gg:gf is <100 μs. It is always difficult to measure a diffusion time within this range using FCS, even when a model with two diffusion times is used to fit the autocorrelation function.

One could also argue that using C5-Bodipy-PC as the fluorescent indicator can lead to misleading results because this dye is known to partition poorly in gel domains or liquid order domains (40). However, Fig. S3 refutes this hypothesis because it shows that when the head-labeled dye atto647-PE (15) is used, the same scale of sizes is found for the domains in the DMPC/DSPC 8:2 mol/mol mixture.

The fact that the system exhibits different space and timescale confinements raises a question about the fractality of the system. Previous studies described the fractal geometry of a DMPC/DSPC lipid mixture (23,41,42). The snapshots of our simulations clearly show that the domains are not circular or square, but have a very complex geometry. Sugar et al. (43) studied this issue in detail using numerical simulation, but without experimental proofs.

Anomalous diffusion has been extensively used to describe many different types of dynamic behaviors of biological molecules in complex media (for review, see Dix and Verkman (44)). Large classes of diffusion processes in which fractal scaling properties play an important part are known to display anomalous diffusion (45). Basically, it can be seen as a general case for diffusion. The relation between time and space can be generalized as $\langle r^2\rangle \propto t^{\alpha }$, with $0<\alpha <2$. If $\alpha =1$, the diffusion is normal and described by pure Brownian motion, whereas if $\alpha <1$, the system is subdiffusive, indicating that the molecular motions are restricted. DMPC/DSPC two-phase, two-component lipid mixtures have been described by means of anomalous diffusion in both MC simulations (26) and experiments (27). In this case, α was found to be systematically less than one, except in the f f region and the far gg region (very low temperature), where the molecular motion again became Brownian. FCS diffusion laws obtained in both MC simulations and experiments have also been fitted by anomalous diffusion. In this study, α was found to vary between 0.5 and 1 in both cases (MC simulations and experiments), and exhibited two minima at the phase transitions $gg:gf$ and $gf:ff$ (see Fig. S4). Anomalous diffusion can therefore clearly describe the molecular motion in two-phase, two-component lipid mixtures or during phase transition in a pure lipid. However, even if it gives information on the heterogeneity of the system, it fails to quantitatively interpret the structure of this heterogeneous medium.

Finally, there is no real consensus on the size of membrane heterogeneities in model systems (23,26,43) or living cells (7,8). AFM, neutron scattering, Förster resonant energy transfer, FRAP, and FCS have all been used to measure these domains, and the observed discrepancies may be due to the range of spatial scales probed by the different experimental techniques, as well as the inherent nature of membrane heterogeneities. Indeed, different reports have shown that membrane heterogeneities can exhibit fractal geometry and self-similarity (23,41,42). Our results indicate that the apparent characteristic size of membrane heterogeneities in the DMPC/DSPC 8:2 mol/mol lipid mixture and in DMPC alone is dependent on the spatial scale probed, and that diffusion in these systems is self-similar and anomalous. We speculate that MC simulations run for larger systems would exhibit other sizes of domains, and therefore it would be interesting to explore whether other transitions at scales far below the diffraction limit can be observed experimentally by means of FCS diffusion laws.

Conclusions

In this work, we studied a two-phase, two-component DMPC/DSPC 8:2 mol/mol lipid mixture and a pure DMPC lipid system using FCS diffusion laws both experimentally and by MC simulation with a complete thermodynamic description. The results clearly show that these FCS diffusion laws, whether in MC simulation or experiment, allow quantitative characterization of the system in terms of diffusion, phase transition, and mean size of the gel or fluid domain present in the lipid mixture. It was previously shown that the domain size and transient confinement times can be predicted by the use of FCS diffusion laws on defined geometries and a pure random walk model (17). Here, we have shown that this can be generalized to a more complex model in which the geometry is unknown and the molecular motions are driven only by the thermodynamic parameters of the system itself. Indeed, the fractal nature of the DMPC/DSPC lipid mixture shows the existence of domains at different scales. However, we were able to clearly identify these domains by FCS diffusion laws and correctly estimate their mean size, as confirmed by the use of other approaches such as ICS and direct morphoanalysis.

This work clearly confirms that FCS diffusion laws provide a powerful means of quantitatively analyzing molecular motions in heterogeneous media and obtaining structural information.