Interactions of a Charged Nanoparticle with a Lipid Membrane: Implications for Gene Delivery

Abstract

We employ self-consistent field theory to study the thermodynamics of membrane-particle interactions in the context of gene delivery systems, with the aim to guide the design of dendrimers that can overcome the endosomal escape barrier by inserting into membranes and creating pores. We consider the interaction between a model polyamidoamine dendrimer and a membrane under controlled tension as a function of the separation between the dendrimer and the membrane. In all the cases we have studied, the lowest free energy state corresponds to the membrane partially wrapping the dendrimer. However, with moderate tension, we find that a G5 (or larger) generation dendrimer, through thermal fluctuation, can induce the formation of metastable pores. These metastable pores are subsequently shown to significantly lower the critical tension necessary for membrane rupture, thus possibly enhancing the release of the trapped genetic material from the endosome.

Introduction

Polymer-based synthetic vectors hold great promise as gene delivery vehicles. They afford immense flexibility in design, are easy to manufacture, and allow repeated administration without adverse immune responses. The synthetic vectors rely on the ability of the positively charged polymers to electrostatically bind and condense the genetic material into nanoparticles, termed “polyplexes”. Rational design of an efficient gene delivery vehicle requires a mechanistic understanding of each step during the gene delivery process, including the formation and stability of the polyplexes; the systemic delivery and targeting; the cellular internalization, endosomal escape, cytoplasmic trafficking, and nuclear transport; and finally the unpackaging of the nucleic acid from the polyplex and incorporation into the genome (1). In this work, we focus on the endosomal escape mechanism.

As the polyplex is trafficked from the endosome to the lysosome, acidification activates enzymes that degrade the trapped genetic material. In the proton sponge hypothesis (2–4), it is believed that cationic polymers are able to avoid this fate by absorbing the protons as they are pumped into the endosome. This causes a swelling of the polymer and an influx of counterions. The resulting increase in osmotic pressure eventually ruptures the membrane and releases the trapped polyplexes into the cytosol.

In addition to the proton sponge effect of the polymers, it has been experimentally shown that nonspecific interactions between free polyamidoamine dendrimers and lipid membranes enhance membrane permeability and hole formation, depending on dendrimer size (generation, G) and charge (terminal functional groups) (5–8). Specifically, G7 amine-terminated dendrimers induce the formation of holes, whereas G5 amine-terminated dendrimers primarily expand preexisting defects, and G5 acetamide-terminated (charge neutral) dendrimers do not cause hole formation. With respect to overcoming the endosomal escape barrier, these observations, together with results indicating that the presence of excess free polycations can increase the transfection efficiency by two orders of magnitude (9,10), suggest that a molecular understanding of the membrane-particle system can provide a foundation for the design of dendrimers as efficient gene delivery vehicles (in what follows, we will use the terms “dendrimer” and “particle” interchangeably).

Toward this end, recent advances in computation power and simulation methodologies have produced interesting observations that both complement the experimental findings and provide useful molecular-level insight (11). In particular, Lee and Larson (12) have performed coarse-grained molecular-dynamics simulations of G3–G7 dendrimers on a DPPC (dipalmitoylphosphatidylcholine) bilayer. Their results suggest that the dendrimer is more efficient in inducing membrane permeability, as compared to flexible linear polymers, because its rigid spherical structure prefers to gain favorable electrostatic interactions from both leaflets, thus facilitating the formation of a pore.

In this work, we use self-consistent field (SCF) theory (13) to explore the structural and energetic properties of metastable and unstable states involved in dendrimer-induced pore formation and membrane rupture. In comparison to direct molecular simulation, the SCF theory allows access to both true equilibrium and metastable states without limitations due to short simulation times. Furthermore, thermodynamic variables such as the membrane tension are easily and directly controlled. We seek to understand how the effect of the dendrimer is coupled to the effect of the tension in the membrane, with the aim to find conditions favoring the formation of a metastable pore, which we show can nucleate membrane rupture.

Throughout this work, we take care to properly treat the electrostatics and excluded volume interactions. We account for the spatially varying dielectric constant and include the Born energy of the ions (14). Although SCF theory has been applied to similar systems, electrostatic effects from charged species were not included (15,16). With respect to understanding the role of the dendrimers in facilitating endosomal escape, it is critical that the long-ranged electrostatic interactions are accounted for (12).

Model

Our system consists of a membrane bilayer assembled from double-tailed lipids in solvent with added salt ions. The lipids are represented as graft copolymers, which we model as discrete Gaussian chains, consisting of a head segment of N_H negatively charged head monomers with volume υ_H and two identical tail segments, each consisting of N_T tail monomers with volume υ_T (see Fig. 1). We note that in using the discrete Gaussian chain as our model, we have ignored bending rigidity. Indeed, real lipid molecules have bonds with limited flexibility; in particular, unsaturated lipids contain double bonds, or kinks. However, bond order parameters calculated from similar lattice models (17–19) in the same spirit as our discrete Gaussian chain model have shown good qualitative agreement with experimental findings (20–22) and even excellent agreement with molecular dynamics simulations (23–25). We use the Gaussian model primarily for convenience, as it is the simplest model that captures the conformational degrees of freedom of the lipid molecules. Similar models have been used to study other membrane processes, for example fusion (26).

Figure 1.

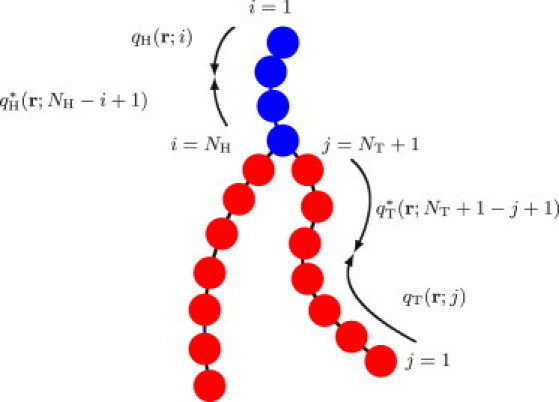
A double-tailed lipid model consisting of head (blue) and tail (red) monomers. The values q_I and q_I^∗, where I = H, T, are the chain propagator and complementary chain propagator, respectively, used for calculating the single chain statistics (see Appendix).

In addition to the lipids, there are solvent monomers with volume υ_S, and salt ions taken as point charges of elementary electron charge e and valency z_±. We work mostly in the grand canonical ensemble, where the number of lipid, solvent, and ion molecules is controlled by the chemical potentials obtained from the homogeneous bulk phase. For a range of dendrimer generations and charge densities, we calculate the free energy of the system as a function of the dendrimer position with respect to the membrane. Therefore, we include a fixed dendrimer in the system, whose position and density profile we specify, and solve for the remaining density profiles of the lipids, solvents, and ions.

We begin with a particle-based Hamiltonian for our system, given by

$$\mathcal{H}=\sum _{\mathrm{i}=1}^{n_{\mathrm{L}}}{h}_{\mathrm{i}}\left(\left\{\mathbf{r}\right\}\right)+\frac{1}{2}\sum _{\mathrm{J}\ne \mathrm{K}}\int d\mathbf{r}\mathit{d}{\mathbf{r}}^{\mathbf{\prime }}{\widehat{\varphi }}_{\mathrm{J}}\left(\mathbf{r}\right)u_{\mathrm{JK}}\left(\mathbf{r}\mathrm{,}{\mathbf{r}}^{\mathbf{\prime }}\right){\widehat{\varphi }}_{\mathrm{K}}\left({\mathbf{r}}^{\mathbf{\prime }}\right)+\frac{e^2}{2}\int d\mathbf{r}\mathit{d}{\mathbf{r}}^{\mathbf{\prime }}{\widehat{\rho }}_{\text{c}}\left(\mathbf{r}\right)C\left(\mathbf{r}\mathrm{,}{\mathbf{r}}^{\mathbf{\prime }}\right){\widehat{\rho }}_{\text{c}}\left({\mathbf{r}}^{\mathbf{\prime }}\right).$$ (1)

The first term accounts for the connectivity of the n_L lipids. The second term accounts for the pairwise energetic interaction potentials among species, where the summation is over the instantaneous volume fraction of solvent, head, and tail monomers, defined, respectively, as

$$\begin{array}{l}{\widehat{\varphi }}_{\text{S}}\left(\mathbf{r}\right)={\upsilon }_{\text{S}}\stackrel{n_{\text{S}}}{\sum _{\text{j}=1}}\delta \left(\mathbf{r}-{\mathbf{r}}_{\text{j}}\right),\hfill \\ {\widehat{\varphi }}_{\text{H}}\left(\mathbf{r}\right)={\upsilon }_{\text{H}}\stackrel{n_{\text{L}}}{\sum _{\text{i}=1}}\stackrel{N_{\text{H}}}{\sum _{\text{a}=1}}\delta \left(\mathbf{r}-{\mathbf{r}}_{\text{ia}}\right),\hfill \\ {\widehat{\varphi }}_{\text{T}}\left(\mathbf{r}\right)=2{\upsilon }_{\text{T}}\stackrel{n_{\text{L}}}{\sum _{\text{i}=1}}\stackrel{N_{\text{T}}}{\sum _{\text{b}=1}}\delta \left(\mathbf{r}-{\mathbf{r}}_{\text{ib}}\right).\hfill \end{array}$$

The hard-core excluded volume between the species is accounted for by a local incompressibility constraint

$${\widehat{\varphi }}_{\text{S}}\left(\mathbf{r}\right)+{\widehat{\varphi }}_{\text{H}}\left(\mathbf{r}\right)+{\widehat{\varphi }}_{\text{T}}\left(\mathbf{r}\right)=1$$

that applies at all r. The third term in Eq. 1 is the Coulomb energy of the system, where C(r,r′) is the Coulomb operator satisfying

$$-\nabla \cdot \left[\epsilon \left(\mathbf{r}\right)\nabla C\left(\mathbf{r},{\mathbf{r}}^{\prime }\right)\right]=\delta \left(\mathbf{r}-{\mathbf{r}}^{\prime }\right).$$

It accounts for the long-ranged electrostatic interactions from the total charge density of all charged species,

$$e{\widehat{\rho }}_c\left(\mathbf{r}\right)=c_{\text{F}}{\varphi }_{\text{F}}\left(\mathbf{r}\right)-\frac{c_{\text{H}}}{{\upsilon }_{\text{H}}}{\widehat{\varphi }}_{\text{H}}\left(\mathbf{r}\right)+z_{+}e{\widehat{c}}_{+}\left(\mathbf{r}\right)-z_{-}e{\widehat{c}}_{-}\left(\mathbf{r}\right),$$

where c_F is the magnitude of the charge density on the fixed dendrimer and c_H is the magnitude of the charge per head monomer (and is dimensionless). ${\widehat{c}}_{\pm }\left(\mathbf{r}\right)$is the instantaneous number density of the ions. Note that the density profile ϕ_F(r) for the dendrimer is specified by us. Any reasonable function may be used. We choose a hyperbolic tangent function with a characteristic width for the interface (27) so that the dielectric constant $\epsilon \left(\mathbf{r}\right)$, which is spatially varying and depends on the volume fractions of the different species, will be smooth and continuous in r. However, with respect to the lipids, the dendrimer is impenetrable and the density profile of the fixed particle is essentially a step function.

The grand canonical partition function Ξ is obtained by summing over all particle degrees of freedom, including the position of each solvent and ion molecule, as well as the position and conformation of each lipid chain:

$$\Xi =\sum _{n_{\left\{\text{L},\text{S},+,-\right\}}=0}^{\infty }\frac{e^{\left({\mu }_{\text{L}}{n}_{\text{L}}+{\mu }_{\text{S}}{n}_{\text{S}}+{\mu }_{+}{n}_{+}+{\mu }_{-}{n}_{-}\right)}}{n_{\text{L}}!n_{\text{S}}!n_{+}!n_{-}!{\upsilon }_{\text{L}}^{n_{\text{L}}}{\upsilon }_{\text{S}}^{n_{\text{s}}}{\upsilon }_{+}^{n_{+}}{\upsilon }_{-}^{n_{-}}}\times \int \prod _{\text{i}=0}^{n_{\text{L}}}\mathcal{D}{\mathbf{r}}_{\text{i}}\int \prod _{\text{j}=0}^{n_{\text{S}}}d{\mathbf{r}}_{\text{j}}\int \prod _{\text{k}=0}^{n_{+}}d{\mathbf{r}}_{\text{k}}\int \prod _{\text{l}=0}^{n_{-}}d{\mathbf{r}}_{\text{l}}\times \prod _{\mathbf{r}}\delta \left[1-{\widehat{\varphi }}_{\text{H}}\left(\mathbf{r}\right)-{\widehat{\varphi }}_{\text{T}}\left(\mathbf{r}\right)-{\widehat{\varphi }}_{\text{S}}\left(\mathbf{r}\right)-{\varphi }_{\text{F}}\left(\mathbf{r}\right)\right]e^{-\mathcal{H}}.$$

In this work, we scale all energies by k_BT. The solvent volume υ_S and the lipid volume ${\upsilon }_{\text{L}}=N_{\text{H}}{\upsilon }_{\text{H}}+2N_{\text{T}}{\upsilon }_{\text{T}}$ are used as the volume scales instead of the cube of the de Broglie wavelength. This only shifts the chemical potential by a constant, and does not affect any of the thermodynamics of interest. The δ-functional accounts for the incompressibility of the head, tail, and solvent monomers at all positions within the system volume.

In SCF theory, the first step is to replace the above particle-based model with a field-theoretic model, using a series of techniques related to Hubbard-Stratonovich transformations (13). This decouples the interactions among particles and replaces them with interactions between single particles and effective fields. The final result for the field-theoretic partition function can be generically written in the form $\Xi =\int D\omega \exp \left(-F\left[\omega \right]\right)$, where F is an effective Hamiltonian that is complex and depends on the (multidimensional) field variable ω.

In general, the field-theoretic partition function cannot be evaluated in closed form. The mean-field, or self-consistent field approximation, amounts to assuming that a single field configuration ${\omega }^{\ast }$ dominates the functional integral, i.e., $\Xi \approx \exp \left(-F\left[{\omega }^{\ast }\right]\right)$, where $F\left[{\omega }^{\ast }\right]$ in our model is given by

$$F=-\frac{e^{{\mu }_{\text{L}}}}{{\upsilon }_{\text{L}}}{Z}_{\text{L}}\left({\xi }_{\text{H}},{\xi }_{\text{T}}\right)-\frac{e^{{\mu }_{\text{S}}}}{{\upsilon }_{\text{S}}}{Z}_{\text{S}}\left({\xi }_{\text{S}}\right)-\frac{e^{{\mu }_{\pm }}}{{\upsilon }_{\pm }}{Z}_{\pm }\left(\psi \right)+\int d\mathbf{r}[\sum _{\mathrm{J}\ne \mathrm{K}}\left({\chi }_{\text{JK}}{\varphi }_{\text{J}}{\varphi }_{\text{K}}-{\xi }_{\text{J}}{\varphi }_{\text{J}}+\frac{{\kappa }_{\text{J}}}{2}{\left[\nabla {\varphi }_{\text{J}}\right]}^2\right)+\psi \left(c_{\text{F}}{\varphi }_{\text{F}}-\frac{c_{\text{H}}}{{\upsilon }_{\text{H}}}{\varphi }_{\text{H}}\right)-\frac{\epsilon }{2}{\left(\nabla \psi \right)}^2].$$ (2)

Here, we have assumed the energetic interactions to be short-ranged so that local interactions are captured by the terms containing the Flory χ-parameters and nonlocal interactions are captured by the gradient terms (28). We comment that in modeling systems involving long polymers, such gradient terms are usually not included, as the chain connectivity is sufficient to capture the nonlocal effects on length scales of interest. Because we are treating shorter chains, we include these terms to account for nonlocal effects at shorter length scales. In Eq. 2, and in what follows, we recognize the imaginary nature of the potential field variables at the saddle point and redefine the conjugate chemical potential fields iξ → ξ, and the electrostatic potential field −iψ → ψ. The summation ∑_J≠K is once again over heads, tails, and solvents, while we have dropped the r dependence for notational conciseness. The incompressibility constraint has been invoked to eliminate ϕ_S in favor of ϕ_H and ϕ_T.

The partition functions that arise in the above expression are for a single molecule in its respective field(s) and are given by

$$Z_{\text{S}}\left({\xi }_{\text{S}}\right)=\int d\mathbf{r}\exp \left\{-{\upsilon }_{\text{S}}{\xi }_{\text{S}}\right\},$$

$$Z_{\pm }\left(\psi \right)={\int }^{}d\mathbf{r}\exp \left\{\mp \psi e{z}_{\pm }-u_{\pm }^b\right\},$$

$$Z_{\text{L}}\left({\xi }_{\text{H}},{\xi }_{\text{T}}\right)={\int }^{}d\mathbf{r}{q}_{\text{H}}\left(\mathbf{r};N_{\text{H}}\right)q_{\text{T}}^2\left(\mathbf{r};N_{\text{T}}+1\right)e^{2{\upsilon }_{\text{H}}{\xi }_{\text{H}}},$$

for the solvents, ions, and lipids, respectively. The form of Z_S(ξ_S) is simple enough; Z_±(ψ) and Z_L(ξ_H,ξ_T) require some explanation. Firstly, Z_±(ψ) contains the Born self-energy of the ions

$$u_{\pm }^b=z_{\pm }^2{e}^2/8\pi a_{\pm }\epsilon ,$$

where ε is the spatially varying dielectric constant. We note that although the volume of the salt ions does not enter into the incompressibility, with respect to the self-energy of an ion, we specify a_± = 0.3 nm as the radius. The value $u_{\pm }^b$ cannot be absorbed into a redefinition of the chemical potential for a spatially varying dielectric medium. The derivation of the expression for the Born energy of a spatially varying dielectric medium is rather involved and we refer the interested reader to a complete derivation by Wang (14). Secondly, we have introduced the chain propagator q_I (r; i) for I = H, T, where i is the monomer index, to obtain the single-chain statistics of the lipid. The propagator accounts for the chain connectivity and the Boltzmann weight due to the self-consistent potential field. Calculation of the propagator for our discrete Gaussian chain is described in the Appendix, with the initial condition (for placing the end monomers) $q_{\text{I}}\left(\mathbf{r};1\right)=\exp \left\{-{\upsilon }_{\text{I}}{\xi }_{\text{I}}\left(\mathbf{r}\right)\right\}$ for I = H, T. The total partition function for a single chain follows naturally by joining the chain propagators at the branch point, where an extra exponential factor $e^{2{\upsilon }_{\text{H}}{\xi }_{\text{H}}}$ is included in the partition function to correct for overcounting the joined monomer.

The mean-field configuration that gives $F\left[{\omega }^{\ast }\right]$ is obtained by requiring that Eq. 2 is stationary with respect to variations in the fields. Variation with respect to the volume fraction fields ϕ_H and ϕ_T gives

$$\begin{array}{l}{\xi }_{\text{H}}={\xi }_{\text{S}}+{\chi }_{\text{SH}}\left(1-2{\varphi }_{\text{H}}-{\varphi }_{\text{T}}-{\varphi }_{\text{F}}\right)+\left({\chi }_{\text{HT}}-{\chi }_{\text{ST}}\right){\varphi }_{\text{T}}-{\kappa }_{\text{H}}\Delta {\varphi }_{\text{H}}-\frac{c_{\text{H}}}{{\upsilon }_{\text{H}}}\psi -\left({\epsilon }_{\text{H}}-{\epsilon }_{\text{S}}\right)\left(\frac{{\left(\nabla \psi \right)}^2}{2}+\frac{z_{\pm }^2{e}^2{c}_{\pm }}{8\pi a_{\pm }{\epsilon }^2}\right),\hfill \\ {\xi }_{\text{T}}={\xi }_{\text{S}}+{\chi }_{\text{ST}}\left(1-{\varphi }_{\text{H}}-2{\varphi }_{\text{T}}-{\varphi }_{\text{F}}\right)+\left({\chi }_{\text{HT}}-{\chi }_{\text{SH}}\right){\varphi }_{\text{H}}-{\kappa }_{\text{T}}\Delta {\varphi }_{\text{T}}-\left({\epsilon }_{\text{T}}-{\epsilon }_{\text{S}}\right)\left(\frac{{\left(\nabla \psi \right)}^2}{2}+\frac{z_{\pm }^2{e}^2{c}_{\pm }}{8\pi a_{\pm }{\epsilon }^2}\right).\hfill \end{array}$$ (3)

Here, $c_{\pm }=e^{\mu \pm }{\upsilon }_{\pm }^{-1}\exp \left\{\mp z_{\pm }e\psi -u_{\pm }^b\right\}$ is the ion distribution. Variation with respect to ψ gives

$$-\nabla \left(\epsilon \nabla \psi \right)=c_{\text{F}}{\varphi }_{\text{F}}-\frac{c_{\text{H}}}{{\upsilon }_{\text{H}}}{\varphi }_{\text{H}}\pm \left\{z_{\pm }e{c}_{\pm }\right\};$$ (4)

with respect to ξ_S, gives

$$1-{\varphi }_{\text{H}}-{\varphi }_{\text{T}}-{\varphi }_{\text{F}}=e^{{\mu }_S}\exp \left\{-{\upsilon }_{\text{S}}{\xi }_{\text{S}}\right\};$$ (5)

and with respect to ξ_H and ξ_T, gives

$$\begin{array}{l}{\varphi }_{\text{H}}\left(\mathbf{r}\right)=\frac{{\upsilon }_{\text{H}}{e}^{{\mu }_{\text{L}}}}{{\upsilon }_{\text{L}}}\stackrel{N_{\text{H}}}{\sum _{\text{i}=1}}{q}_{\text{H}}\left(\mathbf{r};i\right)e^{{\upsilon }_{\text{H}}{\xi }_{\text{H}}}{q}_{\text{H}}^{\ast }\left(\mathbf{r};N_{\text{H}}-i+1\right),\hfill \\ {\varphi }_{\text{T}}\left(\mathbf{r}\right)=2\frac{{\upsilon }_{\text{T}}{e}^{{\mu }_{\text{L}}}}{{\upsilon }_{\text{L}}}\stackrel{N_{\text{T}}}{\sum _{\text{i}=1}}{q}_{\text{T}}\left(\mathbf{r};i\right)e^{{\upsilon }_{\text{T}}{\xi }_{\text{T}}}{q}_{\text{T}}^{\ast }\left(\mathbf{r};N_{\text{T}}+1-i+1\right).\hfill \end{array}$$ (6)

Here we have introduced the complementary chain propagator $q_{\text{I}}^{\ast }$ (r;i), which also satisfies a similar equation to that for q_I (r; i), but with the initial conditions

$$\begin{array}{l}{q}_{\text{H}}^{\ast }\left(\mathbf{r};1\right)=e^{{\upsilon }_{\text{H}}{\xi }_{\text{H}}}{q}_{\text{T}}\left(\mathbf{r};N_{\text{T}}+1\right)q_{\text{T}}\left(\mathbf{r};N_{\text{T}}+1\right),\hfill \\ q_{\text{T}}^{\ast }\left(\mathbf{r};1\right)=e^{{\upsilon }_{\text{H}}{\xi }_{\text{H}}}{q}_{\text{T}}\left(\mathbf{r};N_{\text{T}}+1\right)q_{\text{H}}\left(\mathbf{r};N_{\text{H}}\right).\hfill \end{array}$$

Again, to correct for overcounting the monomer when the propagators are joined, we include an extra exponential factor $e^{{\upsilon }_{\text{I}}{\xi }_{\text{I}}}$. Equation 4 is the Born-energy augmented Poisson-Boltzmann equation (14). Equation 5 can be trivially solved to yield ${\xi }_{\text{S}}=-{\upsilon }_{\text{S}}^{-1}\log \left(1-{\varphi }_{\text{H}}-{\varphi }_{\text{T}}-{\varphi }_{\text{F}}\right)$, where we have defined μ_S ≡ 0 because the chemical potentials of the solvents and lipids are not independent for an incompressible system. Numerical SCF theory requires solving Eqs. 3–6, together with Eq. A2 for the chain propagators, iteratively until convergence. From these solutions, the free energy is obtained from Eq. 2.

Results

In this section, we study the thermodynamics of membrane-particle interactions and consider the implications to the endosomal escape, where, in addition to the proton sponge effect, another possible effect of the dendrimers is to insert into the endosomal membrane and form pores that can nucleate rupture at significantly lower tensions. As a reference, we first study the tension required to rupture a uniform membrane in the absence of the dendrimer.

Rupture of a uniform lipid membrane

Lipid membranes such as DPPC are often used as models for understanding the more complex and diverse biological membranes that define the boundaries of (and within) a cell. We begin by developing a coarse-grained model of a lipid membrane in a volume containing explicit solvent and mobile ion species at physiological salt concentration, $150\text{mM}$. For the lipid we choose N_H = 2 and N_T = 8 (per tail), with the monomer volumes υ_H = υ_T = 0.05 nm³. With these values, the total volume of our lipid is υ_L = 0.9 nm³, which is approximately the value for a lipid in a fully hydrated bilayer (υ_L = 1.232 nm³) as determined by Nagle and Wiener (29). The desired surface charge density is experimentally obtained by specifying the composition of lipid species in the membrane (30); for simplicity, we choose to distribute the charge evenly among the head monomers and set c_H = 0.25 for the (dimensionless) charge magnitude per head monomer.

The Flory and square gradient interaction parameters are chosen so that the model captures realistic features of a lipid membrane. Setting χ_HT = 75, χ_ST = 25, χ_SH = 0, and κ_H = κ_T = 2 (κ_S = 0), we obtain, in the tensionless state, an area per lipid of 0.74 nm² and a membrane width of ∼3.5 nm; see Fig. 2 a. Both values are similar to those obtained from experiments and molecular dynamics simulations (31). We choose ${\epsilon }_{\text{T}}=2$ and ${\epsilon }_{\text{H}}=50$ for the dielectric constants of the tail and head regions (32), respectively, and for the solvent we use ${\epsilon }_{\text{S}}=80$. Fig. 2 b shows an accumulation of cations in the head region due to the negatively charged head monomers, and a depletion of ions in the tail region due to the low value of the dielectric constant, ${\epsilon }_{\text{T}}$.

Figure 2.

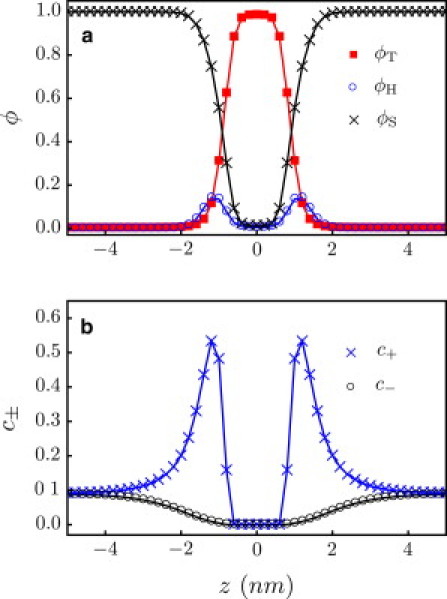
(a) Volume fractions and (b) ion number concentrations (nm⁻³) across the axis perpendicular to the membrane.

The above parameters are chosen based on experimental results for membranes in the tensionless state. The tension is defined by $\gamma ={\partial \mathcal{F}/\partial A|}_{n_{\text{L}}}$, where F is the appropriate free energy and A is the area. To study the limit of stability for a membrane under increasing tensions, we work in a semiopen system (open with respect to solvent and small ions but closed with respect to the number of lipids so that the number of lipids in the membrane is fixed) and obtain the free energy per unit area f as a function of the area per lipid σ. The tension is then evaluated according to

$$\gamma =f+{\sigma \frac{\partial f}{\partial \sigma }|}_{n_{\text{L}}}.$$

For a mechanically stable membrane, (∂γ/∂σ) > 0. Therefore, the condition (∂γ/∂σ) = 0 signals the onset of mechanical instability, which we identify with the point of rupture and term the value of tension at this point the critical tension. In Fig. 3, the rupture corresponds to the maximum of the tension-area curve, with a critical value of the areal expansion of ∼0.45, and critical tension γ_c ∼ 4.5 k_BT/nm². The same calculation is repeated in the grand canonical ensemble, which is open to all species. In this system, the excess grand potential (given by Eq. 2 relative to the uniform bulk solution) per unit area directly gives the tension up to the rupture value. The results from these two ensembles are identical. For convenience, particularly when a dendrimer is present, in what follows we work in the grand canonical ensemble.

Figure 3.

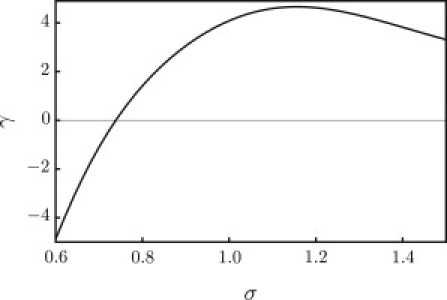
Membrane tension (k_BT/nm²) as a function of the area per lipid (nm²). The limit of metastability occurs where ∂γ/∂σ = 0.

We note that the rupture captured by this one-dimensional calculation is the limit of metastability for a uniform static membrane. In reality, thermal fluctuations and lipid rearrangements are responsible for regions of membrane thinning (33,34) that lead to rupture under much lower tensions. Therefore, it is not surprising that our value for the critical tension is higher than the values determined from micropipette aspiration experiments (0.75–2.5 k_BT/nm² depending on degree of saturation of the lipid tails (35)), and the areal expansion we obtain is an order-of-magnitude greater than the areal expansion obtained experimentally for lipid vesicles (36) (but comparable to the results for polymersome membranes (37)). We emphasize that these results do not suggest that our model is unphysical, but rather that the experimentally observed rupture is likely a nucleated event. In what follows, we study the effect of dendrimers on inducing different membrane structures and the energies associated with such inhomogeneities.

Thermodynamics of membrane-particle interactions

Properties of the fixed particle are chosen to capture the size and charge of different generations of polyamidoamine dendrimers (38). Because the outer surface of a high-generation dendrimer is highly congested and unlikely to be penetrated by lipids (see Zhang and Smith (5) and references within), we define a radius R_F, which excludes any lipids from within the volume of the particle. The total charge of the particle is given by the number of terminal amine groups, which are essentially all protonated at neutral pH (39). Due to significant backfolding of these amines (40), the charge can be assumed to be distributed evenly in the volume of the particle (see Fig. 7 later for a description of the dendrimer sizes and charge densities used in this work).

Figure 7.

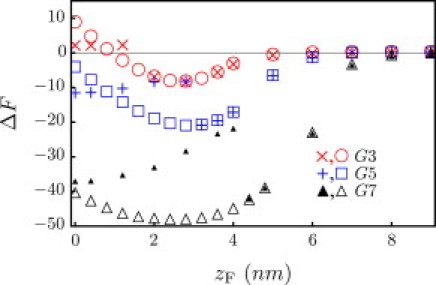
Free energy profile (k_BT) for a membrane with γ = 0.74 k_BT/nm² interacting with G3 (R_F = 1.8 nm, c_F = 1.30 nm⁻³), G5 (R_F = 2.7 nm, c_F = 1.55 nm⁻³), and G7 (R_F = 4.0 nm, c_F = 2.0 nm⁻³) dendrimers. Open symbols correspond to method 1; +, × and ▴ correspond to method 2 (see text for description).

We find the results insensitive to the dielectric constant chosen for the particle, and assign ${\epsilon }_{\text{F}}={\epsilon }_{\text{S}}=80$. Because the system is axially symmetric, we work in cylindrical coordinates, with the center of the particle defined as r_F = (r_F, z_F) = (0, z_F) and the membrane positioned at z = 0. The vertical position of the particle z_F then becomes a natural reaction coordinate for the system. In what follows, we constrain the position of the particle and numerically solve the set of SCF equations at each position. The solutions to the uniform membrane case are used as the boundary condition, holding the membrane at fixed tension and its outer edges at fixed position.

In general, the SCF equations can have multiple solutions, corresponding to different free energy minima, with one being the global minimum and the rest being the metastable minima. Capturing all the free energy minima is a nontrivial task. However, symmetry and simple physical intuition can often be used to limit the search. Here, we take advantage of the different ways of initializing the SCF equations as a means to access the stable and metastable minima. We consider two methods: 1), We begin with a noninteracting membrane-particle system and slowly move the particle along the path of decreasing z_F. At each step, the previous solutions are used to initialize the new equations. 2), We instantaneously place the particle at z_F, sometimes initializing the configurations with a hole in the membrane. This hole can be interpreted as a temporary defect caused by fluctuations.

Tensionless membrane

We first apply method 1 to a tensionless membrane and a fully protonated G5 dendrimer. Although the specific interactions are local, the electrostatic interactions are long-ranged and rearrangements of the lipid molecules allow the membrane to reach out and meet the particle, as shown in Fig. 5 a. At this point, the particle is within the attractive range of the membrane. This is depicted in Fig. 4, where the potential well in the free energy profile is due to a competition between satisfying the favorable electrostatic interactions and deforming the membrane. From the free energy profile, we see that the particle will continue toward z_F ∼ 0 nm, corresponding to a metastable, partially wrapped state.

Figure 5.

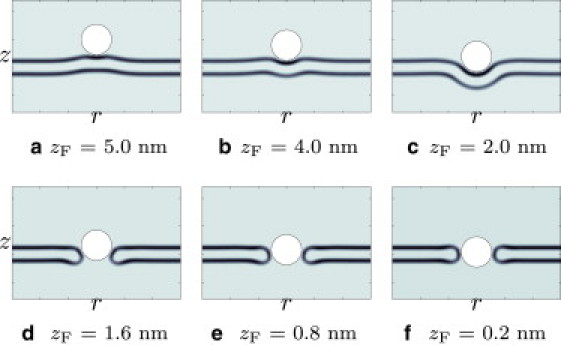
ϕ_H in cylindrical coordinates for a tensionless membrane and a fully protonated G5 dendrimer with c_F = 1.55 nm⁻³. (a–c) Solutions to both methods 1 and 2. (d–f) Solutions to method 2 only.

Figure 4.

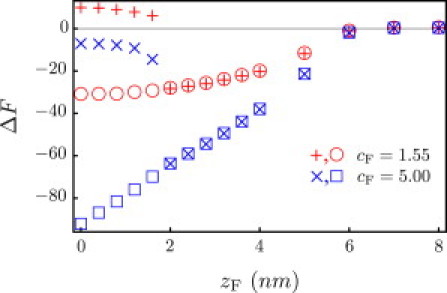
Free energy profile (k_BT) for the tensionless membrane. ΔF is relative to a noninteracting membrane-particle system, where z_F → ∞. The particle is a G5 dendrimer with radius R_F = 2.7 nm and charge density c_F = 1.55 nm⁻³ (all 128 surface amines are protonated). For comparison, we have also plotted the results for a hypothetical G5 dendrimer with c_F = 5.00 nm⁻³. Open symbols correspond to method 1; +and × correspond to method 2 (see text for description).

Interestingly, if we imagine an external force which continues to slowly push the particle, we find that the membrane does not rupture! Instead, it deforms until the two sides of the membrane trailing the leading edge of the particle fuse together, and a dendrimer-filled vesicle naturally pinches off from the membrane. Although beyond the scope of this article, further analysis of this process of pushing the particle through the membrane could provide information as to the energetics and forces required by the cell (in particular, the proteins recruited) to enforce shape transitions of the membrane involved in endocytosis.

We next solve the same SCF equations by method 2. Depending on the extent of the hole created by the particle and the parameters of the system (membrane tension, dendrimer charge, and dendrimer size), the system will fall into one of two solutions: either the membrane reseals the hole and partially wraps the particle, or the membrane forms a head-lined pore around the particle. This is observed from the density plots (Fig. 5) and from the free energy profile (Fig. 4), where the SCF solutions correspond to a partially wrapped particle until z_F ∼ 2.0 nm. Beyond this, if thermal fluctuations initiate a hole (as simulated by method 2), then the system will find the solutions to the higher energy path corresponding to a membrane pore. However, the particle must squeeze its way into the pore, as can be seen in Fig. 5 d and the free energy increases with decreasing z_F. This indicates that any pore induced into a tensionless membrane is highly unstable and will be short-lived.

In all of our calculations, it is important to remember that the particle position is fixed. In other words, we have constrained the SCF equations so that the membrane is forced to respond to a particle at fixed z_F. If we lift this constraint, the membrane will expel the particle and reseal the pore. The system will then find the metastable state corresponding to the partially wrapped particle.

From the above analysis for a fully protonated G5 dendrimer interacting with a tensionless membrane, it is clear that the pore state cannot exist without constraining the position of the particle. It is of interest to know whether the pore state can be stabilized by appropriately modifying the dendrimer. If the increase in free energy is due to the particle having to squeeze its way through the pore as it deforms the membrane, increasing the particle size is not the solution. Instead, suppose that we can increase the charge density on the dendrimer by chemically modifying the functional groups.

In Fig. 4 we compare the result for a hypothetical, highly charged G5 dendrimer (c_F = 5.00 nm⁻³) to the result for a fully protonated G5 dendrimer (c_F = 1.55 nm⁻³). Due to screening by the salt ions, increasing the charge density does not increase the range of electrostatic attraction. It increases the extent and stability of the wrapped state. If the system manages to reach the unstable pore state, it will be short-lived, according to the same explanation given in the preceding paragraph for c_F = 1.55 nm⁻³. From method 1, we find that electrostatic interactions alone are insufficient for a dendrimer to induce holes in a tensionless membrane. From method 2, even if thermal fluctuations assist by initiating temporary holes, we find that the dendrimer is unable to stabilize pores in a tensionless membrane.

Membrane under tension

In the proton sponge hypothesis, an increase in osmotic pressure is believed to rupture the endosome. We account for the osmotic pressure by applying a tension to the membrane, and explore the combined effects of the applied tension and the electrostatic interactions between the membrane and the particle. In Fig. 6, we continue with a fully protonated G5 dendrimer and plot the free energy profile for γ_c = 0.74 k_BT/nm². The cost of deforming a membrane under tension has shifted the metastable state from partially wrapped (z_F ∼ 0 nm) to surface-absorbed (z_F ∼ 2.8 nm). The membrane is also less successful at healing defects (e.g., those initialized by method 2) and transitions earlier to the pore state, which now corresponds to a second metastable state. It is also known that membrane permeability and hole formation are dependent on dendrimer generation and terminal functional groups (5–8). Therefore, we also consider G3–G7 dendrimers. Our results agree with experimental trends, where we find that G3 dendrimers do not stabilize pores, whereas G5 and G7 dendrimers do; see Fig. 7.

Figure 6.

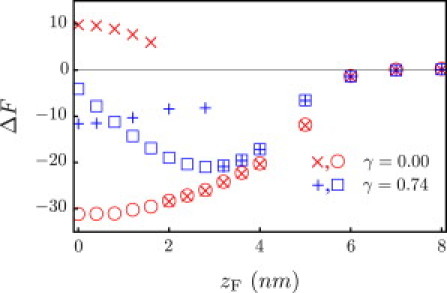
Free energy profile (k_BT) for a membrane with γ = 0.74 k_BT/nm², shown together with the tensionless membrane from Fig. 4. The particle is once again a fully protonated G5 dendrimer. Open symbols correspond to method 1; +and × correspond to method 2 (see text for description). Note that we are well below the limit of metastability for a homogeneous membrane, where rupture occurs at γ_c ∼ 4.5 k_BT/nm².

However, with respect to the endosomal escape, our interest lies in dendrimers that can nucleate rupture, not stabilize pores. Recall that rupture of a uniform membrane occurs at γ_c ∼ 4.5 k_BT/nm². Consider the membrane under tension with an inserted G5 dendrimer (c_F = 1.55 nm⁻³) shown in Fig. 6, where the pore state is metastable. If we slowly increase the tension from this state, we find that the limit of metastability occurs at γ_c ∼ 0.84 k_BT/nm² ; see Fig. 8. For tensions exceeding this value, the pore radius expands indefinitely and the membrane ruptures. Interestingly, even a highly charged particle, which should have strong adhesion to the head-lined pore periphery, lowers the rupture tension, where γ_c levels off at ∼1.3 k_BT/nm².

Figure 8.

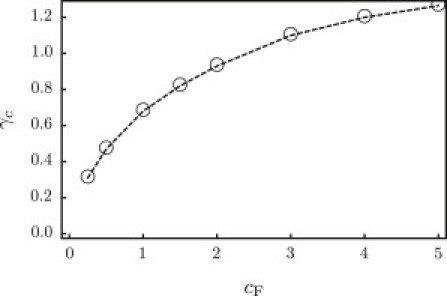
Rupture tension (k_BT/nm²) for a membrane containing a pore, plotted as a function of the charge density (nm⁻³) of the G5 dendrimer stabilizing the pore.

We should comment that increasing the charge on dendrimers makes the pore state energetically more favorable as compared to the wrapped state. So even though membranes containing higher-charged dendrimers require higher rupture tensions, the higher-charged dendrimers are more effective at stabilizing the pore state to begin with (see Fig. 7), and therefore more effective at facilitating rupture. The study of the actual nucleation barriers and pathways to pore formation and rupture are beyond the scope of this work. Nevertheless, these results show that highly charged dendrimers can greatly lower the rupture tensions. In terms of the endosomal escape, this dendrimer-induced rupture at significantly lower tensions is precisely what we seek.

Conclusion

In this work, we have used SCF theory to study the thermodynamics of membrane-particle interactions in the context of polymer-based gene delivery systems. We have focused on the endosomal escape mechanism, where our main goal is to understand the role of the dendrimer in nucleating membrane rupture (with the eventual release of the genetic material from the endosome). For different membrane tensions, dendrimer sizes and charge densities, we have explored the structural and energetic properties of the system. In what follows, we summarize our main findings and the implications for designing polymer-based gene delivery vectors.

For tensionless membranes, we find that the hydrophilic pore with an inserted dendrimer is unstable; the tensionless membrane prefers to satisfy the favorable electrostatic interactions by partially wrapping the dendrimer. Our results indicate that increasing the charge density of the dendrimer only increases the extent and stability of the wrapped state, whereas the pore state, if somehow created, remains unstable and short-lived. In other words, the tensionless membrane is so robust that even a highly charged particle is unable to insert into the membrane and stabilize a pore. This suggests that the osmotic pressure contribution from the proton sponge hypothesis is a necessary component if the endosomal escape is to be enhanced by particle insertion into the membrane.

To study the effect of the osmotic pressure, we apply a tension γ = 0.74 k_BT/nm² to the membrane. This value is well below the limit of metastability for a uniform membrane, for which γ_c ∼ 4.5 k_BT/nm². For G5 dendrimers and higher, we find that the pore corresponds to a metastable state, whereas for G3 dendrimers the pore is unstable. This agrees with experimental trends on the ability of the dendrimer to cause membrane permeability and hole formation (5–8). Lee and Larson (12), using molecular-dynamics simulations on similar membrane-particle systems, found that dendrimer-induced membrane disruption was dependent on generation and concentration. We believe that the apparent concentration dependence is related to local membrane tensions that are induced by nearby particles due to the fixed membrane area. This is in agreement with the effect of tension in our findings, where metastable pores exist only in combination with an applied tension. Finally, our results indicate that these same metastable pores can act as nucleation sites for rupture.

With respect to overcoming the endosomal escape barrier (one of many to consider in gene delivery systems), we have shown that there are at least two properties to consider into the design of the vector: 1), the dendrimer should be able to induce a tension on the membrane, e.g., by increasing the osmotic pressure through the proton sponge mechanism; and 2), the dendrimer should be sufficiently large and with enough charge so as to stabilize the pore state. Without the combined effect of the two, the membrane would prefer to satisfy the electrostatic interactions by partially wrapping around the dendrimer.

Finally, we comment on the limitations of this study. In all of our calculations, we have fixed the position of the dendrimer z_F so that the solutions we obtain are subject to this constraint. The free energy profile in this sense yields the potential of mean force between the particle and the membrane. The multiple unstable and metastable states are obtained from the behavior of the free energy as a function of z_F. However, the reaction coordinate for nucleating rupture most likely will not be z_F, but will involve the rearrangement of the lipids in the prepore state. This study does not address how the particle becomes inserted into the membrane from the partially wrapped state, nor does it address the subsequent nucleation event leading to rupture.

To study the pathways associated with these activated processes will require minimum energy path calculations using, e.g., the nudged elastic band (41,42) or the string method (43). We note that simpler calculations, where physical insight is used to impose one or more reaction coordinate constraints (in a similar spirit to our particle position z_F), have sometimes been used to study nucleation processes in membrane fusion (26). However, the structures associated with dendrimer-induced pore formation and membrane rupture are more complicated and it is not obvious that some simple constraints can be identified. We are currently applying minimum energy path calculations to dynamic SCF theory to address the actual nucleation events involved in the dendrimer-induced pore formation and membrane rupture.

Appendix: Propagator for a Single Chain in External Fields

We introduce the chain propagator by analogy to a Markovian process, where the monomer index i can be thought of as the analog of a discrete time variable in a stochastic process. In this way we seek to build up the configuration of the graft copolymer, from the free end of each arm to the branch point, beginning with the initial condition that

$$q_{\text{I}}\left(\mathbf{r},1\right)=e^{-{\upsilon }_{\text{I}}{\xi }_{\text{I}}\left(\mathbf{r}\right)}$$ (A1)

for I = H, T. Moving to subsequent monomers i corresponds to propagating forward in the time index:

$$q_{\text{I}}\left(\mathbf{r};i\right)=e^{-{\upsilon }_{\text{I}}{\xi }_{\text{I}}\left(\mathbf{r}\right)}\int d{\mathbf{r}}^{\prime }\Gamma \left(\left|\mathbf{r}-{\mathbf{r}}^{\prime }\right|\right)q_{\text{I}}\left({\mathbf{r}}^{\prime };i-1\right).$$ (A2)

Here i ∈ (2, N_I) and Γ denotes the transition probability from one monomer to the next, assumed to be Gaussian. For notational simplicity, in what follows drop the subscript I and denote q(r, i) as simply qⁱ(r). The above expression is essentially a reduced partition function for a chain beginning at r and ending anywhere. Rather than attempt to evaluate Eq. A2 directly by an integration scheme, we recognize that for a reasonably smooth external potential, the contributions are dominated by the transitions for which |r–r′| is approximately the range of (or less than) the Gaussian. Thus, following the usual practice in deriving a differential equation from the Chapman-Kolmogoroff equation, we expand r′ around r to quadratic order. Further representing the spatial derivatives by differences in cylindrical coordinates for our axially symmetric membrane-particle system, we get

$$q^{\text{i}+1}\left(r_{\text{j}},z_{\text{k}}\right)=e^{-\upsilon \xi \left(r_{\text{j}},z_{\text{k}}\right)}\left\{\left[1-4\gamma \right]q^{\text{i}}\left(r_{\text{j}},z_{\text{k}}\right)+\gamma q^{\text{i}}\left(r_{\text{j}},z_{\text{k}+1}\right)+\gamma q^{\text{i}}\left(r_{\text{j}},z_{\text{k}-1}\right)+\gamma \left(1+\frac{1}{2j}\right)q^{\text{i}}\left(r_{\text{j}+1},z_{\text{k}}\right)+\gamma \left(1-\frac{1}{2j}\right)q^{\text{i}}\left(r_{\text{j}-1},z_{\text{k}}\right)\right\}.$$ (A3)

Here we have defined γ = b²/6h², where b² is the variance of the transition probability and h is the grid spacing, and we have discretized space by a uniform grid:

$$\left(r_{\text{j}},z_{\text{k}}\right)=\left(jh,kh\right),j=0,\dots ,n_{\text{r}},k=-n_{\text{z}},\dots ,n_{\text{z}}.$$

From Eq. A3, we can identify the following transition probabilities on the discretized lattice:

$$\begin{array}{cc}\Gamma \left(r_{\text{j}},z_{\text{k}+1}\to r_{\text{j}},z_{\text{k}}\right)& =\gamma ,\\ \Gamma \left(r_{\text{j}},z_{\text{k}-1}\to r_{\text{j}},z_{\text{k}}\right)& =\gamma ,\\ \Gamma \left(r_{\text{j}+1},z_{\text{k}}\to r_{\text{j}},z_{\text{k}}\right)& =\gamma \left(1+\frac{1}{2j}\right),\\ \Gamma \left(r_{\text{j}-1},z_{\text{k}}\to r_{\text{j}},z_{\text{k}}\right)& =\gamma \left(1-\frac{1}{2j}\right),\\ \Gamma \left(r_{\text{j}},z_{\text{k}}\to r_{\text{j}},z_{\text{k}}\right)& =1-4\gamma ,\end{array}$$

where the last expression can be thought of as the survival probability. Equation A3 applies to j ≠ 0. For j = 0, we have

$$q^{\text{i}+1}\left(r_0,z_{\text{k}}\right)=e^{-\upsilon \xi \left(r_0,z_{\text{k}}\right)}\left\{\left[1-6\gamma \right]q^{\text{i}}\left(r_0,z_{\text{k}}\right)+\gamma q^{\text{i}}\left(r_0,z_{\text{k}+1}\right)+\gamma q^{\text{i}}\left(r_0,z_{\text{k}-1}\right)+4\gamma q^{\text{i}}\left(r_1,z_{\text{k}}\right)\right\},$$ (A4)

from which we similarly obtain the transition probabilities. Note that the positivity of the transition probabilities requires that γ < 1/6. Continuing with the analogy to a Markovian process, we can define an equivalent “master equation” for the chain propagator on our discrete grid, and Eq. A2 becomes

$$q^{\text{i}}\left(r_{\text{j}},z_{\text{k}}\right)=e^{-\upsilon \xi \left(r_{\text{j}},z_{\text{k}}\right)}\sum _{r_{\text{j}}^{\prime },z_{\text{k}}^{\prime }}\Gamma \left(r_{\text{j}}^{\prime },z_{\text{k}}^{\prime }\to r_{\text{j}},z_{\text{k}}\right)q^{\text{i}-1}\left(r_{\text{j}}^{\prime },z_{\text{k}}^{\prime }\right),$$

where it is understood that the summation is restricted to the nearest neighbors of (r_j,z_k). The discretization scheme we have used assumes that the range of a bond joining two monomers is on the order of (or less than) the grid spacing h. More precisely, $b<\sqrt{3/2}h$. For cases where we wish to lengthen the range of the bonds, we can include next-nearest neighbor transitions (and beyond) by inserting fictitious monomers at intermediate positions. These intermediate beads satisfy Eqs. A3 and A4, but without the Boltzmann weight associated with the external field. Finally, we comment that the discrete Gaussian chain given here, unlike the continuous Gaussian chain model, has finite range of bond lengths, which are specified by the grid spacing h and the number of intermediate beads.