Ultrasensitivity in Multisite Phosphorylation of Membrane-Anchored Proteins

Abstract

Cellular signaling is initially confined to the plasma membrane, where the cytoplasmic tails of surface receptors and other membrane-anchored proteins are phosphorylated in response to ligand binding. These proteins often contain multiple phosphorylation sites that are regulated by membrane-confined enzymes. Phosphorylation of these proteins is thought to be tightly regulated, because they initiate and regulate signaling cascades leading to cellular activation, yet how their phosphorylation is regulated is poorly understood. Ultrasensitive or switchlike responses in their phosphorylation state are not expected because the modifying enzymes are in excess. Here, we describe a novel mechanism of ultrasensitivity exhibited by multisite membrane-anchored proteins, but not cytosolic proteins, even when enzymes are in excess. The mechanism underlying this concentration-independent ultrasensitivity is the local saturation of a single enzyme by multiple sites on the substrate. Local saturation is a passive process arising from slow membrane diffusion, steric hindrances, and multiple sites, and therefore may be widely applicable. Critical to this ultrasensitivity is the brief enzymatic inactivation that follows substrate modification. Computations are presented using ordinary differential equations and stochastic spatial simulations. We propose a new role, to our knowledge, for multisite membrane-anchored proteins, discuss experiments that can be used to probe the model, and relate our findings to previous theoretical work.

Introduction

Cellular signaling relies on posttranslational modifications of proteins to integrate and shape the transmission of extracellular information into functional cellular outcomes. Phosphorylation and dephosphorylation of serine, threonine, or tyrosine residues on proteins by kinases and phosphatases, respectively, can impact signal transmission by altering the localization, enzymatic activity, and interaction partners of a protein. It is interesting to note that the phosphorylation state of proteins in individual cells can be very sensitive to upstream stimuli, so that small changes in stimulus (e.g., active kinase, receptor occupancy, etc.) can result in large changes in phosphorylation. Examples of such ultrasensitive or switchlike responses in the regulation of intracellular proteins are well documented (1–7), and are thought to be critical for cellular decision-making processes.

The processing of extracellular information is initially confined to the plasma membrane, where the cytoplasmic tails of receptors and other membrane-anchored proteins become phosphorylated, typically on multiple tyrosine residues. These phosphorylated residues serve as docking sites for enzymes that, when bound, propagate cellular signaling by catalyzing additional reactions. As an example, consider a class of cell-surface receptors that includes antigen, Fc, and other immune receptors that contain conserved tyrosine-containing motifs, such as immunoreceptor tyrosine-based activation, inhibitory, and switch motifs (ITAMs, ITIMs, and ITSMs, respectively) (8–10). In contrast to receptor tyrosine kinases (RTKs) (11), these receptors do not contain intrinsic catalytic domains and are regulated by extrinsic membrane-confined tyrosine kinases and phosphatases (10). We refer to these receptors as noncatalytic tyrosine-phosphorylated receptors (NTRs). As is the case with other receptors, the phosphorylation of NTRs directly impacts cellular decisions by initiating and regulating intracellular signaling cascades, yet how their phosphorylation is regulated by extrinsic enzymes is poorly understood.

As a representative NTR, consider the T-cell antigen receptor (TCR). The TCR is a multisubunit receptor on the surface of T-cells that contains 20 phosphorylation sites distributed on 10 ITAMs (12). Each ITAM contains two tyrosine residues that are phosphorylated by the Src family kinase Lck and dephosphorylated by the phosphatase CD45, both of which are also confined to the plasma membrane. The phosphorylation state of the TCR is thought to be tightly regulated, because the intracellular signaling cascade initiated by phosphorylated TCR ITAMs leads to T-cell activation, which, if inappropriate, can result in autoimmune disorders (12). Many NTRs contain multiple phosphorylation sites (8) and in the case of the TCR, the large number of sites is thought to be primarily required for signal amplification (12). A switchlike response at the level of individual NTRs can be useful for reducing noise and maintaining signal fidelity, and in the case of antigen receptors, it can contribute to the discrimination of antigens (13,14). In addition to NTRs, many nonreceptor membrane-anchored molecules, such as the adaptor linker for activated T-cells (LAT), contain multiple phosphorylation sites that are regulated by membrane confined enzymes.

The mechanisms underlying switchlike responses in the phosphorylation state of proteins are incompletely understood. For the case of a cytosolic protein containing a single phosphorylation site, Goldbeter and Koshland (15) mathematically showed that small changes in the active kinase or phosphatase concentrations can result in dramatic changes to the phosphorylation state of the protein. Since this sensitivity relies on the enzymes operating in the zero-order regime (where the concentrations of substrate are in excess of the enzyme concentrations), it was termed zero-order ultrasensitivity. Although it might provide an attractive explanation, zero-order ultrasensitivity has rarely been the mechanism for the observed switchlike response in cellular signaling, because enzymes often operate outside of the zero-order regime. In some cases, additional mechanisms (e.g., feedbacks (6), competition (4)) have been shown to be responsible for the switchlike response.

As for many cytosolic proteins, the enzymes acting on membrane-anchored proteins are also in excess of the substrate. For the case of the TCR, the phosphatase CD45 is the most abundant cell-surface protein on T-cells and the kinase Lck is at least twice as abundant as the TCR (2). Therefore, enzymatic modifications are expected to be operating outside of the zero-order regime. An important difference between cytosolic and membrane-anchored proteins is their respective mobilities: whereas diffusion coefficients of cytosolic proteins are in the range 1–10 μm²/s, the diffusion coefficients of membrane proteins are in the range 0.01–0.1 μm²/s. Therefore, it is commonly believed that the coupling of proteins in the membrane is limited by diffusion (16).

In this work, we report a novel mechanism of ultrasensitivity exhibited by multisite membrane-anchored proteins, but not cytosolic proteins, which operates in the first-order regime. Using detailed mathematical modeling, we examine the effect of changes in the kinase-phosphatase balance on the phosphorylation of multisite membrane-anchored proteins when enzymes operate in the first-order regime (i.e., enzymes are globally in excess of substrate) and find impressive ultrasensitivity that increases with the number of phosphorylation sites. Critical to this ultrasensitivity is the explicit modeling of diffusion-limited reactions and brief enzymatic inactivation that follows catalysis. All results are initially presented using a computationally efficient ordinary-differential-equation (ODE) model, but key results are recapitulated using a stochastic spatial simulator. We propose a new role for multisite membrane-anchored proteins (such as NTRs), discuss experiments that can be used to probe the model, and relate our findings to previous theoretical work.

Methods

Spatial simulations using Smoldyn

All spatial simulations are performed using Smoldyn (17), which is a discrete-time, continuous-space Monte Carlo agent-based simulation tool that accurately captures diffusion, chemical reactions, and spatial confinement (e.g., to a membrane). The algorithm for bimolecular reactions is an essential component of Smoldyn and is based on the Smoluchowsky theory of diffusion-limited chemical reactions (17). Binding reactions between an enzyme and substrate take place with a probability of 0.05 at each time step when the two molecules are within the binding radius (5 nm), and upon dissociation of an enzyme-substrate complex (via either $k_{off}$ or $k_{\text{r}}$), the molecules are placed at the binding radius (5 nm). Volume exclusion between enzymes is modeled as effective binary reactions that occur at a specific distance (default exclusion radius is 5 nm) and displaces the molecules to a larger distance (5.5 nm). Decreasing the displacement distance did not alter any of our conclusions but increased simulation times. The area of the simulation domain was taken to be 1 μm² with periodic boundary conditions, and a fixed time step of 5 × 10⁻⁶ s was used. Simulations of the full model (with volume exclusion) required 12 h of computations per data point using a 2.8-GHz central processing unit. The Smoldyn script used to generate our results is available upon request.

Results

A two-step model captures the effects of membrane diffusion

We begin exploring the effects of membrane diffusion on substrate phosphorylation using a two-step model (16–18) (Fig. 1, A and B),

$$S_j\underset{k_{-}}{\overset{X{k}_{+}}{\rightleftharpoons }}X\cdot \cdot S_j\underset{k_{off}}{\overset{\lambda k_{on}^{\ast }}{\rightleftharpoons }}X{S}_j$$ (1)

where S_j is the free substrate concentration having j sites phosphorylated and X is the free enzyme concentration (X = E for kinase, X = F for phosphatase). In this model, the enzyme and substrate must first form an encounter complex (X ⋅ ⋅ S_j) before binding (XS_j). The rate of forming an encounter complex is Xk₊ where k₊ is the diffusion-limited on-rate (see below). The encounter complex represents an approximate state where the enzyme and substrate are unbound but within physical proximity such that binding can take place. In this state, the molecules bind ($\lambda k_{on}^{\ast }$) or move apart ($k_{-}$) with first-order rates. In this model, $k_{on}^{\ast }$is the single-site on-rate and is multiplied by a factor (λ) that accounts for the number of available modification sites (λ = N − j for X = E and λ = j for X = F). When bound to the substrate, the enzyme may catalyze a reaction and dissociate ($k_{\text{r}}$, not shown in above scheme) or dissociate ($k_{off}$). Both $k_{\text{r}}$ and $k_{off}$ reactions result in an encounter complex, and therefore, the model locally captures conventional enzyme kinetics.

Figure 1.

Schematic of the two-step model coupled to multisite phosphorylation. (A) Interaction between membrane-anchored multisite proteins and membrane-anchored enzymes. The rate at which an enzyme forms an encounter complex (center) with the substrate is determined by the diffusion-limited on-rate ($k_{+}$) multiplied by the free-enzyme concentration (X). Within the encounter complex, the enzyme and substrate can bind or move apart with first-order rates $\lambda k_{on}^{\ast }$ and $k_{-}$, respectively. We assume a random phosphorylation scheme, and therefore, the effective binding rate is proportional to $k_{on}^{\ast }$, the single-site binding rate, multiplied by the number of (un)phosphorylated sites ($\lambda =N-j$ for the kinase and $\lambda =j$ for the phosphatase). Note that the microscopic rates, $k_{on}^{\ast }$ and $k_{-}$, are on the scale of a single substrate and enzyme but are directly proportional to the macroscopic rates $k_{on}^{\ast }=k_{on}/A$ and $k_{-}=k_{+}/A$, where $k_{on}$ is the bimolecular on-rate and A is the approximate area of the substrate. When in complex (right), the enzyme may catalyze a reaction and unbind ($k_{\text{r}}$, not shown) or unbind ($k_{off}$), and in both reactions, the enzyme and substrate return to the encounter complex (center). (B) Overhead view of the three states in A with approximate scales. (C) In the most general model we consider, upon catalysis the enzyme becomes inactive for a short period ($1/\mu$) before further catalysis can take place. Therefore, upon catalysis, the enzyme may diffuse away ($k_{-}$) or reactivate (μ).

When the substrate is free of enzyme (S_j), the rate at which enzyme binds (or couples) is $k_c=k_{+}\lambda k_{on}^{\ast }/\left(\lambda k_{on}^{\ast }+k_{-}\right)$, and when the substrate is bound to enzyme (XS_j), the rate at which it fully unbinds (or uncouples) from enzyme is $k_u=k_{off}{k}_{-}/\left(\lambda k_{on}^{\ast }+k_{-}\right)$. For the case of a substrate whose phosphorylation state does not change, we expect that $K_{\text{D}}=k_{off}/\left(\lambda k_{on}\right)$ at equilibrium and therefore, $k_{\text{u}}/k_{\text{c}}=k_{off}/\left(\lambda k_{on}\right)$. Assuming that $k_{on}^{\ast }=k_{on}/A$, where A is the encounter area (i.e., 1/A is the effective local concentration), it then follows that $k_{-}=k_{+}/A$. Therefore, the local rates ($k_{-}$, $k_{on}^{\ast }$) govern the interaction between a single enzyme and substrate but are directly related to the macroscopic bimolecular rates ($k_{+}$, $k_{on}$): $k_{-}=k_{+}/A$ and $k_{on}^{\ast }=k_{on}/A$. Note that the two-step ODE model includes both the diffusion and binding steps and therefore, the parameters k_c and k_u do not explicitly appear. Parameter definitions are summarized in Table 1.

Table 1.

Parameter definitions for the two-step ODE model

Parameter	Description	Units
$k_{+}$	Diffusion-limited on-rate	μm2 s−1
$k_{-}$	Local diffusion rate ($k_{-}=k_{+}/A$)	s−1
$k_{on}$	Bimolecular on-rate	μm2 s−1
$k_{on}^{\ast }$	Local on-rate ($k_{on}^{\ast }=k_{on}/A$)	s−1
$k_{off}$	Unbinding rate	s−1
$k_{\text{r}}$	Modification rate	s−1
μ	Reactivation rate	s−1
A	Encounter area ($A=\pi s^2$)	μm2
s	Binding radius	μm

The diffusion-limited on-rate on the membrane is $k_{+}=2\pi D/\log \left(b/s\right)$ (16–19), where $D=D_X+D_S$ is the sum of the diffusion coefficients for the enzyme (D_X) and substrate (D_S), b is the mean distance between enzyme ($b\approx 1/\sqrt{\pi X}$), and s is the reaction radius. A typical membrane protein is on the scale of 10 nm ($s=0.0056$ μm, $A=\pi s^2={10}^{-4}$μm²) and enzyme concentrations are in excess of 100 μm⁻² ($b=0.056$ μm). Taking the membrane diffusion coefficients to be $D_S=D_E=D_F=0.01$ μm²/s (20), we find that $k_{+}\approx 0.05$ μm²/s.

The model contains several assumptions. First, it is assumed that enzymes are in excess over substrate (i.e., enzymes operate far from the zero-order regime). Second, we initially assume that only a single enzyme can be within the encounter complex (e.g., due to steric effects), but we later relax this assumption. Third, we assume that enzymes act distributively, so that dissociation from the substrate occurs before subsequent catalytic modifications. Last, we present all results using a random phosphorylation scheme and identical parameter values for the kinase and phosphatase. The most general model we consider consists of 143 coupled ODEs that are generated using BioNetGen (21) and integrated in MATLAB (The MathWorks, Natick, MA). We include the BioNetGen file used to generate the ODE system in the Supporting Material. As output from the model, we compute the normalized total phosphorylation of the substrate at equilibrium,

$$\langle S\rangle =\sum _{j=0}^{N}j\left(S_j+E\cdot \cdot S_j+E{S}_j+F\cdot \cdot S_j+F{S}_j\right)/\left(N{S}_T\right),$$ (2)

where N is the number of sites and S_T is the total substrate concentration. The key advantage of using this approximate two-step model instead of explicit spatial simulations is that it is computationally efficient.

Effective processivity via membrane diffusion

In Fig. 2 A, we first show 〈S〉 as a function of the E/F ratio for substrates with 1–20 phosphorylation sites in the reaction-limited regime ($k_{on}=k_{+}/100$). In this limit, the two-step ODE model reduces to the classical well-mixed single-step model. We observe subsensitivity for the single-site substrate, which is reduced with increasing sites. This subsensitivity has been previously observed (22) and arises in the dilute substrate limit when enzymes interact with the substrate with high affinity. In this regime, the quasi-steady-state assumption is violated, and full-model calculations that explicitly track the substrate-enzyme complex (as we have performed) or the total quasi-steady-state approximation are required (22). Subsensitivity is reduced in substrates with multiple phosphorylation sites, but, as expected, ultrasensitivity is not observed (Fig. 2 A, inset) because enzymes are not saturated (i.e., enzymes are operating far from the zero-order regime and are in excess of substrate). Therefore, the addition of multiple sites does not produce ultrasensitivity in the total phosphorylation state of the substrate in this parameter regime (23,24). Additional details on subsensitivity can be found in the Supporting Material.

Figure 2.

Ultrasensitivity in multisite phosphorylation arising from diffusion-limited reactions and enzymatic inactivation. We compute the total phosphorylation state of the substrate (Eq. 2) at equilibrium as a function of the total kinase (E) and phosphatase (F) concentrations using the two-step model (Fig. 1 and main text) for 1–20 phosphorylation sites. Arrow indicates direction of increasing phosphorylation sites, and insets quantify the Hill number. All calculations are performed in the limit where enzymes saturate the substrate (enzymes are in excess of substrate). (A) In the reaction-limited regime ($k_{on}=k_{+}/100$), we obtain the established result of small Hill numbers and find that increasing the number of sites does not produce ultrasensitivity. (B) In the diffusion-limited regime ($k_{on}=100k_{+}$), local saturation effectively produces a processive scheme whereby local rebinding allows multiple modifications during a single enzyme-substrate encounter. (C and D) Introducing an enzymatic refractory state (μ = 1 s⁻¹) attenuates processivity by decreasing the probability of rebinding, but only in the diffusion-limited regime (D) is ultrasensitivity observed due to local enzymatic saturation. Parameters: k₊ = 0.1 μm²/s (diffusion-limited), k₊ = 10 μm²/s (reaction-limited), k_off = 1 s⁻¹, k_r = 0.1 s⁻¹, A = 0.01²μm² (encounter area), $k_{on}^{\ast }=k_{on}/A$, and $k_{-}=k_{+}/A$.

We reasoned that multisite substrates will provide local enzymatic saturation in the diffusion-limited regime ($k_{on}=100k_{+}$), since in the encounter complex there is a single enzyme and multiple phosphorylation sites. However, in this regime, the phosphorylation state of the substrate is not sensitive to large changes in the E/F ratio (Fig. 2 B). This follows from the observation that a single enzyme-substrate encounter leads to multiple modifications (via rebinding) (25) and therefore, diffusion-limited rates provide effective processivity (despite distributive enzyme kinetics), attenuating the dependence of substrate phosphorylation on enzyme concentrations. In other words, the dose-response curves for multisite substrates collapse onto the single-site substrate curve. Allowing multiple enzymes to form an encounter complex with the substrate reduces the effects of processivity (see section on volume exclusion and Fig. S3 in the Supporting Material).

Ultrasensivity by multisite phosphorylation and enzymatic inactivation

Processivity occurs because the rate of binding ($k_{on}^{\ast }$) is much larger than the local diffusive rate ($k_{-}$) for membrane reactions. On these fast timescales, which we approximate to be $1/k_{on}^{\ast }\sim 0.01$ ms and $1/k_{-}\sim 1$ ms (see Fig. 2), processes may take place that prevent the enzyme and substrate from rebinding. For example, the addition of a phosphate to the substrate leaves the kinase with an attached ADP that must be converted to ATP (directly or via release of ADP and reattachment of ATP) before the kinase can bind and catalyze an additional reaction (25–27). To model such processes, we include a short refractory period (Fig. 1 C) during which substrate and enzyme cannot bind by introducing a first-order rate μ capturing the rate of enzymatic reactivation. Repeating the computation with $\mu =1$ s⁻¹ we find no change in the reaction-limited regime (Fig. 2 C) but impressive ultrasensivity in the diffusion-limited regime (Fig. 2 D) that improves with the number of phosphorylation sites.

To further emphasize the relative role of diffusion, binding, and inactivation, in Fig. 3, we show the Hill numbers as a function of these parameters for a 20-site protein. In Fig. 3 A, we observe that longer refractory periods (smaller values of μ) and slower diffusion (i.e., smaller values of $k_{+}$, and therefore smaller values of $k_{-}$) lead to larger Hill numbers. We note that an optimum $k_{-}$ emerges (e.g., when $\mu =1$ s⁻¹) because when $k_{-}\lesssim \mu$, processivity is frequent, and when $k_{-}>1000$ s⁻¹, the reaction is no longer diffusion-limited. This latter point is illustrated in Fig. 3 B, where we observe large Hill numbers only in the diffusion-limited regime (lower right quadrant). Therefore, ultrasensivity is possible only when $k_{on}^{\ast }>k_{-}>\mu$. In other words, reactions must be limited by diffusion ($k_{on}^{\ast }>k_{-}$), but diffusion must be sufficiently large so that enzymes only reactivate after moving away from the substrate ($k_{-}>\mu$). In addition, we find that ultrasensitivity is possible over a wide range of $k_{off}$ and $k_{\text{r}}$, provided that the probability of an enzymatic modification ($k_{\text{r}}/(k_{\text{r}}+k_{off})$) is no smaller than ∼0.01 (Fig. 3 C).

Figure 3.

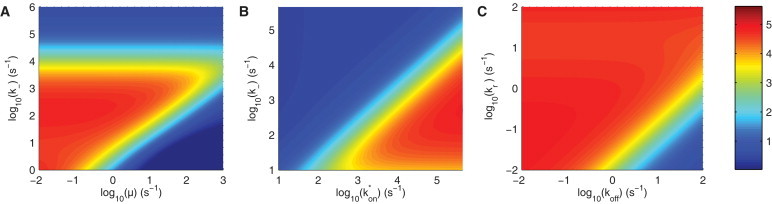
Parameter regimes supporting ultrasensivity. Heat maps of the Hill numbers are shown for a 20-site protein as a function of (A) μ versus $k_{-}$, (B) $k_{on}^{\ast }$ versus $k_{-}$, and (C) $k_{off}$ versus $k_{\text{r}}$. In A and B, note ultrasensivity in regimes where enzymes become locally saturated ($k_{-}<k_{on}^{\ast }$) and act distributively ($\mu <k_{-}$). Therefore, ultrasensivitity is supported when $k_{on}^{\ast }>k_{-}>\mu$. Default parameters are $k_{on}=10$μm²/s, $k_{+}=k_{on}/100$μm²/s, $k_{off}=1$ s⁻¹, $k_{\text{r}}=0.1$ s⁻¹, $A={0.01}^2$μm² (encounter area), $k_{on}^{\ast }=k_{on}/A={10}^5$s⁻¹, $k_{-}=k_{+}/A={10}^3$s⁻¹, and $\mu =1$ s⁻¹.

In summary, individual multisite proteins can act as switches even in the dilute substrate limit when reactions are diffusion-limited and when the short refractory period of enzymes is included. In what follows, we reproduce key results using a stochastic spatial simulator and explore the effects of volume exclusion.

Effects of volume exclusion in explicit spatial simulations

The above results are obtained with a computationally efficient but approximate ODE system based on the two-step model (16–19) (Fig. 1). To confirm that the observed ultrasensitivity is not an artifact of the approximative nature of the two-step ODE model, it is important to reproduce our results using explicit spatial simulations. To do this, we utilized Smoldyn, a Monte Carlo particle-based spatial simulator that captures local rebinding effects accurately (17) (see Methods). As in the ODE model, we implemented the enzymatic modification of a diffusing kinase and phosphatase acting on a multisite substrate (without any quasi-steady-state simplifications) and explicitly imposed volume exclusion between enzymes to account for steric effects (enzymes are modeled as hard discs with an “exclusion” radius of 5 nm, see Methods). In all simulations, we fix the binding radius to 5 nm. We note that complete enzyme exclusion is implicit in the two-step ODE model, because only a single enzyme can form an encounter complex with the substrate at any given time.

The Smoldyn simulations reproduced the results obtained with the two-step ODE model. We observe ultrasensitivity that is dependent on the number of phosphorylation sites (Fig. 4 A), and as expected, removing the refractory period or increasing the diffusion coefficient so that reactions are no longer limited by diffusion abolishes the observed ultrasensitivity (Fig. 4 B).

Figure 4.

Explicit spatial simulations recapitulate results obtained using the two-step ODE model and reveal the importance of volume exclusion. (A) The normalized total phosphorylation of the substrate (Eq. 2) at equilibrium as a function of the total kinase (E) and phosphatase (F) concentrations using spatial simulations in two dimensions with volume exclusion and enzymatic inactivation for the indicated number of phosphorylation sites. Each simulation is performed with one substrate and 100 enzymes in the simulation domain, and therefore, enzymes globally saturate the substrate. (B) Hill numbers as a function of the number of phosphorylation sites for the simulations in A (triangles), for the case when volume exclusion is removed (diamonds), for short refractory periods (squares), and for the reaction-limited regime (solid circles). (C) Dose-response curve for the 20-site substrate for different exclusion radii (fitted Hill numbers are indicated). Note that the binding radius is fixed at 5 nm and that, therefore, an exclusion radius >10 nm allows only a single enzyme to interact with the substrate. All simulations were performed using Smoldyn (17). Parameters: volume exclusion radius is 5 nm (default) or 0 nm without volume exclusion; binding radius is fixed at 5 nm; diffusion coefficient for enzymes and substrate is 0.01 μm²/s (default) or 10 μm²/s for the reaction-limited simulation; μ = 1 s⁻¹ (default) or μ = 10,000 s⁻¹ for the short-refractory-period simulation; k_r = 0.1 s⁻¹; k_off = 1 s⁻¹ (see Methods for additional details). The total phosphorylation state of the receptor is obtained by averaging the simulation for 1500 s at each E/F ratio.

We next investigated the effects of volume exclusion. We observed that removing volume exclusion, by setting the exclusion radius to 0 nm, increases the number of enzymes that can simultaneously interact with the substrate resulting in reduced ultrasensitivity (Fig. 4, B and C). In a similar way, in a modified two-step ODE model that allows more than one enzyme to form an encounter complex with the substrate, we also observed reduced ultrasensitivity (see Supporting Material, in particular Fig. S3). The presence of multiple enzymes within the reaction radius reduces the ratio of sites to enzymes and therefore locally decreases the saturation of enzymes by sites. Together with the observation that increasing the number of sites can compensate for multiple enzymes within the reaction radius (Fig. 4 B), we conclude that the observed ultrasensitivity critically depends on local enzymatic saturation. Indeed, increasing the exclusion radius to 25 nm in the Smoldyn simulations, so that only a single enzyme can interact with the substrate, we recover Hill numbers comparable to the ones obtained from the two-step ODE model (Fig. 4 C).

In summary, explicit spatial simulations in Smoldyn qualitatively reproduce both the ultrasensitivity observed in the approximate two-step ODE model and the conditions for such ultrasensitivity. Quantitative agreement is not possible, because the more realistic spatial simulations in Smoldyn, where both the exclusion and binding radii are set to 5 nm, allow multiple enzymes within the reaction radius of the substrate, whereas the two-step ODE model does not. We note that ultrasensitivity in multisite substrates does not come about from any concentration effects, because, for example, simulations with 20 single-site substrates do not produce ultrasensitivity (not shown), whereas simulations with a single 20-site substrate do (Fig. 4 A).

Discussion

In this work, we have shown that ultrasensitivity can arise in multisite proteins by local enzymatic saturation and enzyme inactivation. Local saturation of enzyme is established by purely passive processes that are independent of the global concentration of enzymes and substrate. Steric hindrances and slow membrane diffusion result in a situation where a single enzyme is locally saturated by multiple phosphorylation sites. Consistent with this mechanism, allowing multiple enzymes within the reaction radius, increasing the diffusion coefficient, or reducing the number of sites can decrease (and, in the appropriate limits, abolish) the observed ultrasensitivity. Brief enzymatic inactivation maintains distributive kinetics, which have been previously shown to be important for switchlike responses (28). It is important to note that all calculations have been performed in the limit where the global concentration of enzymes is larger than that of the substrate, and therefore, the observed ultrasensitivity is not a result of the classic zero-order mechanism.

Relation to previous work

Because the majority of studies use simple ODEs to model biochemical systems, they assume that the system is well-mixed. This assumption fails to capture the local spatiotemporal correlations present when the coupling rate between enzyme and substrate is, at least partially, dependent on diffusion. For example, Takahashi et al. (24) have recently shown that enzyme-substrate rebinding can convert a distributive mechanism into a processive mechanism, which can result in the loss of bistability. Since rebinding events are not captured by well-mixed ODE models, computationally expensive spatial simulations are thought to be required. Here, we have used a two-step ODE model that explicitly models the encounter complex (Fig. 1) to capture rebinding events. This model was previously shown to agree with spatial simulations in the dilute substrate limit (29), and we have repeated the findings of the two-step ODE model using spatial simulations in Smoldyn. The key advantage of the two-step ODE model over spatial simulations is that it can be used to rapidly explore parameter space (Fig. 3).

As reported by Takashi et al. (25), we find that the one-step diffusion-limited ODE model, which does not explicitly include the encounter complex, cannot approximate the effects of membrane diffusion, because it produces ultrasensitivity in the diffusion-limited regime even in the absence of enzymatic inactivation (see Supporting Material). This result is in contrast to the more accurate spatial simulations in Smoldyn and the two-step ODE model, where ultrasensitivity requires enzymatic inactivation.

In a recent study of the yeast mating pathway, Malleshaiah et al. (7) reported a novel mechanism of ultrasensitivity based on local enzymatic saturation that is achieved by two-stage binding. Enzymes in their cytosolic signaling module first bound the substrate using a binding domain (stage 1) and only then were able to bind one of the multiple phosphorylation sites to catalyze a reaction (stage 2). In this work, we show that slow membrane diffusion is able to effectively create two binding steps and that enzymes are therefore not required to have a second binding domain. In this way, our proposed ultrasensitivity mechanism should be applicable to a wide range of systems.

This mechanism of ultrasensitivity is robust to variations in protein concentrations (total substrate/enzyme ratio), because it can operate outside of the zero-order regime. In this first-order regime, multisite phosphorylation has been shown to support switchlike responses when including additional effects such as cooperativity between sites or between sites and the enzymes (30), nonessential sites (31), conformational changes (30), substrate sequestration (32), entropic mechanisms (33), and cascades of enzymes (34). We have shown that, at least for membrane-anchored proteins, multiple sites are sufficient to give switchlike responses. Previous reports of bistability (35) and multistability (36) in multisite phosphorylation rely, in part, on zero-order kinetics. Our work suggests that multistability may be possible even in the dilute substrate limit.

Model parameters

The ultrasensitivity we have described depends on the parameter regime of the system, namely, that $k_{on}^{\ast }>k_{-}>\mu$ (Fig. 3), and therefore, it is important to determine whether this regime is physiologically relevant. The first inequality implies that $k_{on}>k_{+}$ or, in other words, that the bimolecular reaction on-rate is larger than the diffusion-limited on-rate, which is directly proportional to the diffusion coefficient. Estimates of diffusion coefficients are available (e.g., D=0.05 μm²/s for the T-cell receptor (20)), but little information is available on the in situ reaction rates. Fluorescence recovery after photobleaching (FRAP) has been used previously to determine the reaction rates between cytosolic proteins (37), and a protocol has been proposed to determine reaction rates for membrane-confined proteins (38). In a similar spirit, fluorescence resonance energy transfer (FRET) has recently been used to determine reaction rates between membrane-confined receptors and ligands (39). These microscopy experiments can provide estimates of reaction parameters that can then be used to determine whether membrane-confined reactions are truly limited by diffusion.

The lifetime of the inactivation state of the enzymes ($1/\mu$) upon catalysis is also an important determinant of ultrasensitivity. Based on the above inequality ($k_{-}>\mu$), we have estimated that the inactive state should be >1 ms since $k_{-}\approx 1000$ s⁻¹. Detailed analysis of the mechanisms of phosphorylation and dephosphorylation reveals that kinases and tyrosine phosphatases do enter inactive states during catalysis. In the case of kinases, phosphorylation is accompanied by conversion of bound ATP to ADP, and the enzyme remains refractory until the ADP dissociates (25,26). For tyrosine phosphatases such as CD45, the phosphate group that is removed from the substrate is covalently coupled to a cysteine residue in the active site, and the phosphatase remains inactive until this phosphate is removed by hydrolysis (40). The duration of these refractory states is unknown, but because they have been shown to be rate-limiting for catalysis, some information about duration can be inferred from the turnover or $k_{cat}$, which is readily determined. Since $k_{cat}$ represents the overall rate of all the individual steps in catalysis, including the refractory period, it provides an upper limit for the lifetime of this state (41). Assuming two steps (phosphatase addition/removal followed by enzymatic reactivation), the overall catalytic rate is related to the rate constants of each individual step as $k_{cat}=k_{\text{r}}\mu /\left(k_{\text{r}}+\mu \right)$. Reported $k_{cat}$ values for Lck and CD45 acting on their natural substrates are ∼2 s⁻¹ (42) and ∼50 s⁻¹ (43), respectively, consistent with our assumption of inactive states lasting for >1 ms. However, further experimental work is needed to determine the precise lifetime of the inactive state.

Implications for membrane-anchored proteins

Regulation of the phosphorylation state of NTRs by extrinsic kinases and phosphatases is poorly understood. As an example, we considered the T-cell receptor, which contains 20 sites that are modified by a membrane-anchored kinase (Lck) and phosphatase (CD45). The large number of phosphorylation sites is thought to be important for signal amplification (12), but in this study, we show that multiple sites can also be critical for a switchlike response. A previously described synthetic system (44), whereby a kinase-phosphatase reaction scheme on the T-cell receptor has been reconstituted in a nonhematopoietic cell line, can be utilized to explore how multiple sites affect ultrasensitivity. This work predicts that the Hill coefficient of the kinase-phosphatase dose-response curve will decrease as the number of mutated phosphorylation sites increases, with, in addition, an overall decrease in the total phosphorylation. An early switchlike response at the level of individual T-cell receptors can be useful to discriminate foreign from self ligands and may contribute to the experimentally observed switchlike responses in downstream signaling molecules (2,6).

Future work

Switchlike responses are likely to be important for other NTRs and other nonreceptor membrane-anchored proteins that contain multiple phosphorylation sites. For example, the adaptor protein LAT contains nine sites that are phosphorylated by a Syk family kinase when it is recruited to the plasma membrane (45). A subset of these sites serve as docking sites for a cytosolic molecule known as Grb2, which protects these sites from dephosphorylation and through its interaction with SOS1 can cross-link the LAT. A recent theoretical study highlighted the importance of regulating the phosphorylated state of the LAT by showing that the total phosphorylation state of the LAT critically determines its oligomeric state (46). Our work has shown that the total phosphorylation state of LAT can be tightly regulated through multiple sites. In our model, we did not include the docking of cytosolic molecules and their potential to cross-link membrane-anchored proteins, and in the future, it will be important to extend our model to include these features.

We have focused on ultrasensitivity in the total phosphorylation of membrane-anchored proteins using an unstructured (random) phosphorylation scheme. However, some proteins are thought to signal only through specific phosphorylation profiles (e.g., when they are fully phosphorylated) and there are also examples of proteins that exhibit structured phosphorylation (e.g., sequential phosphorylation). Previous work has examined these effects (24,30,31,36), and in the future, it will be useful to examine how diffusion-limited reactions alter these results.