Fluctuation and response in biology

Abstract

In 1905, Albert Einstein proposed that the forces that cause the random Brownian motion of a particle also underlie the resistance to macroscopic motion when a force is applied. This insight, of a coupling between fluctuation (stochastic behavior) and responsiveness (non-stochastic behavior), founded an important branch of physics. Here we argue that his insight may also be relevant for understanding evolved biological systems, and we present a ‘fluctuation–response relationship’ for biology. The relationship is consistent with the idea that biological systems are similarly canalized to stochastic, environmental, and genetic perturbations. It is also supported by in silico evolution experiments, and by the observation that ‘noisy’ gene expression is often both more responsive and more ‘evolvable’. More generally, we argue that in biology there is (and always has been) an important role for macroscopic theory that considers the general behavior of systems without concern for their intimate molecular details.

Electronic supplementary material

The online version of this article (doi:10.1007/s00018-010-0589-y) contains supplementary material, which is available to authorized users.

Introduction

Modern biological research is primarily focused on dissecting molecular mechanisms, and as a result most theoretical analysis is also concerned with modeling the molecular details of a system [1]. In physics, on the other hand, there is a stronger culture of generalization, simplification, and abstraction. Much theoretical work in physics operates at a level that does not require knowledge of the precise molecular details of a system. Indeed, it is common to consider the behavior of systems in general, a level of abstraction that is quite rare in biology. Nonetheless, thermodynamics, fluid dynamics, and so forth are successful general theories that hold irrespective of each molecular player.

Historically, on the other hand, there have been proposals of macroscopic concepts in biology, the most important being Darwin’s theory of evolution via natural selection. Other examples include several concepts coined by Conrad Waddington in the 1940s, including the term ‘canalization’ to explain how robustness, i.e., the resistance of phenotypes to perturbation, is shaped through evolution [2]. Recently, with the advent of systems biology, qualitative concepts such as these have started to regain much attention [3–7].

Many important qualitative concepts in biology are concerned with the changeability of a system (see Box 1 in the supplementary material for a list of terms used in this paper). In addition to canalization, other examples include plasticity—how a biological system responds to environmental change—and evolvability—the feasibility of phenotypic change in response to mutation [5, 8]. Robustness, in contrast, refers to the insensitivity of a phenotype to environmental variation, noise in development, or genetic change [7].

In physics, the changeability of a system is studied as the response of a system against external force. Indeed, in thermodynamics a precise relationship exists that relates the response of a system to its fluctuations. This fluctuation–response relationship was pioneered by Einstein’s Brownian motion theory [9]. In both physics and biology, a great challenge is to reconcile the microscopic and macroscopic descriptions of a system. In his 1905 paper, Einstein proposed that the same random forces that cause the erratic Brownian motion of a particle also underlie the resistance to the macroscopic motion of that particle when a force is applied. This insight can be generalized to state that the response of a variable to perturbation should be proportional to the fluctuation of that variable in the absence of an applied force [10]. In short, the more something varies, the more it will respond to perturbation, irrespective of the precise molecular details.

We argue here that a generalized version of the fluctuation–response relationship can be applied to evolved, dynamical systems [11, 12]. We first present the proposal, and then the evidence from gene network simulations and genome-scale quantitative data that support it. Next we discuss how this quantitative relationship connects canalization to evolvability, and the implications for the idea of genetic assimilation. In short, we propose that fluctuation and responsiveness may be quite intimately connected in evolved, dynamical systems.

The fluctuation–response relationship

Consider a system characterized by a parameter a and a state variable x (x could, for example, be a phenotypic trait such as protein concentration, and a an environmental influence on x). The fluctuation–response relationship [9, 10] can be generalized (see [12] and Box 1 in the supplementary material for derivation and assumptions) to state that the change in the variable x in response to a change in a is proportional to the fluctuation in x under constant a:

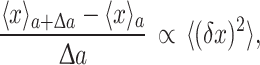1

If a is a parameter that characterizes the environmental condition, and x is the expression level of a gene (protein or mRNA concentration), then the relationship means that the change in expression in response to a change in the environment is proportional to the expression fluctuation (that is, the expression ‘noise’).

Alternatively, if a is a parameter that specifies the genotype (e.g., the number of substitutions in DNA sequence), then the relationship means that the rate of change of a phenotype is proportional to the level of isogenic fluctuation in that phenotype (i.e., variation in the absence of genetic variation). In other words, larger phenotypic fluctuations imply a faster speed of evolution. That is, a higher evolvability [8].

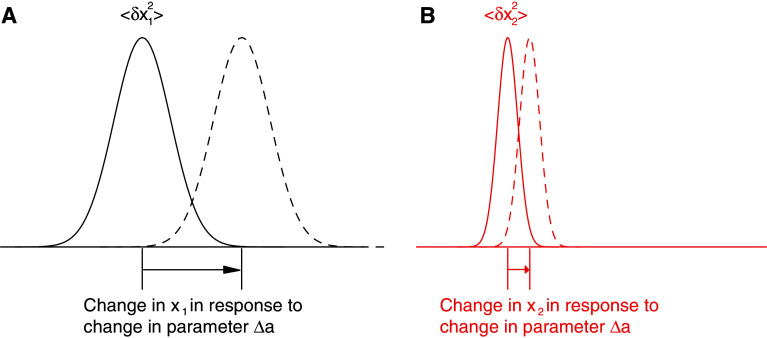
For any particular gene, therefore, the relationship proposes proportionality between the level of phenotypic noise, the responsiveness of the phenotype to perturbation, and the potential to evolve (Fig. 1).

Fig. 1.

Schematic representation of the fluctuation–response relationship. In response to a change in parameter a, the distribution of a phenotypic trait, x ₁ with large variance 〈(δx ₁)²〉 shifts more (a) than that of a phenotype x ₂ with a smaller variance 〈(δx ₂)²〉 (b). For example, x ₁ and x ₂ could be the expression levels of two genes, and a could be an environmental parameter that influences their expression. The relationship states that the response of each trait is proportional to its isogenic fluctuation

The relationship (Eq. 1) is derived under the assumption that the distribution of x is nearly Gaussian, and is controlled by a continuous parameter a, and the change ∆a is sufficiently small. If the distribution keeps a single-peaked structure, by suitable choice of the variable x, it is approximated by a Gaussian distribution. For example, if the distribution of the corresponding variable z is log-normal, we can use x = log(z) as a phenotype variable. When the distribution has several peaks, one could discuss the relationship (Eq. 1) for the distribution around each peak separately. Representation of genotype by a single continuous parameter a will be justified for gradual evolution under a single fitness condition (see below).

The fluctuation–response relationship in in silico evolved networks

If we take the assumption that genes are primarily influenced by a common source of variance, then proportionality between fluctuation and response is also expected when comparing across all of the genes in an organism. For systems where a common source of variance is not explicit, however, it is not obvious that this result should be true. However, as we present below, this behavior is indeed observed in evolved gene networks that do not take this assumption, and in quantitative data from model organisms (K.K., submitted manuscript).

Using a widely adopted gene regulatory network model [13–15] and in silico evolution experiments [16, 17], it is possible to investigate the relationship between fluctuation and response across all of the genes in an evolved regulatory network model. Using this approach, one indeed observes a striking proportionality between fluctuation and response, both for the expression of a single gene during the course of evolution (Fig. 2a), and when comparing across all genes at particular time-points after an initial period of evolution (Fig. 2b). Note that this proportionality relationship is achieved only after some generations of evolution towards a desired phenotype: gene regulatory networks randomly chosen do not satisfy the relationship. Selection under a given fitness condition allows ordering of genotypes, according to the distance between the genetic sequence in concern and that giving rise to the fittest phenotype. Then the genotype will be (approximately) represented by a single continuous parameter, as adopted in the distribution theory. Indeed, in an evolved dynamical system under a given fitness, fluctuation and response are coupled, as in our theoretical expectation. This is seen when considering the responses of individual genes, and also when comparing across all genes in the system.

Fig. 2.

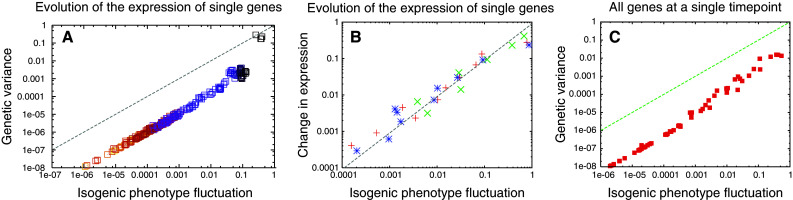
Proportionality between fluctuation and response in an in silico evolved gene regulatory network. a The relationship between the isogenic phenotype fluctuation [32] and genetic variance for a single gene during the course of an evolution experiment on a gene regulatory network model (see [16, 17] for details of the simulations). In the model, the gene expression level is normalized between −1 and 1, to remove any trivial dependence of expression variance on the average magnitude of expression level. Each data point is the measurement at a particular generation. Both the isogenic phenotype fluctuation and genetic variance reduce through the course of the experiment (from dark to light colors in the graph). The dashed line marks equality between the isogenic fluctuation and genetic variance. b The increase of average gene expression level versus the isogenic fluctuation for four target genes (with different colors) during the evolution experiment. The increase is computed per ten generations, for a total of 100 generations. Both the variance and speed decrease through the course of evolution. c The relationship between isogenic phenotype fluctuation and genetic variance across all genes at a single time-point. The data shown are computed from 200 individuals at the 300th generation of the experiment (see Kaneko [17] for details of the simulations)

The fluctuation–response relationship in an artificial selection experiment in bacteria

The coupling between fluctuation and response can also be investigated using experimental data. For example, the relationship for the response of a single gene has been observed in a bacterial selection experiment [12]. Here mutagenesis was performed on an artificial fluorescent protein expressed in Escherichia coli and individuals with the highest fluorescence were selected. Rounds of mutagenesis were repeated, and the increase in the fluorescence level between each generation of mutagenesis was measured. At each round of the experiment, the fluctuation in the fluorescence level was also measured as a variance of the fluorescence over many genetically identical cells. Strikingly, and consistent with the fluctuation–response relationship, the increase in the fluorescence level from one generation to the next was proportional to the isogenic fluctuation (noise) at that particular generation. Higher fluctuation was associated with a faster rate of evolution. The same behavior is seen in the network simulations (Fig. 2b).

The fluctuation–response relationship in yeast

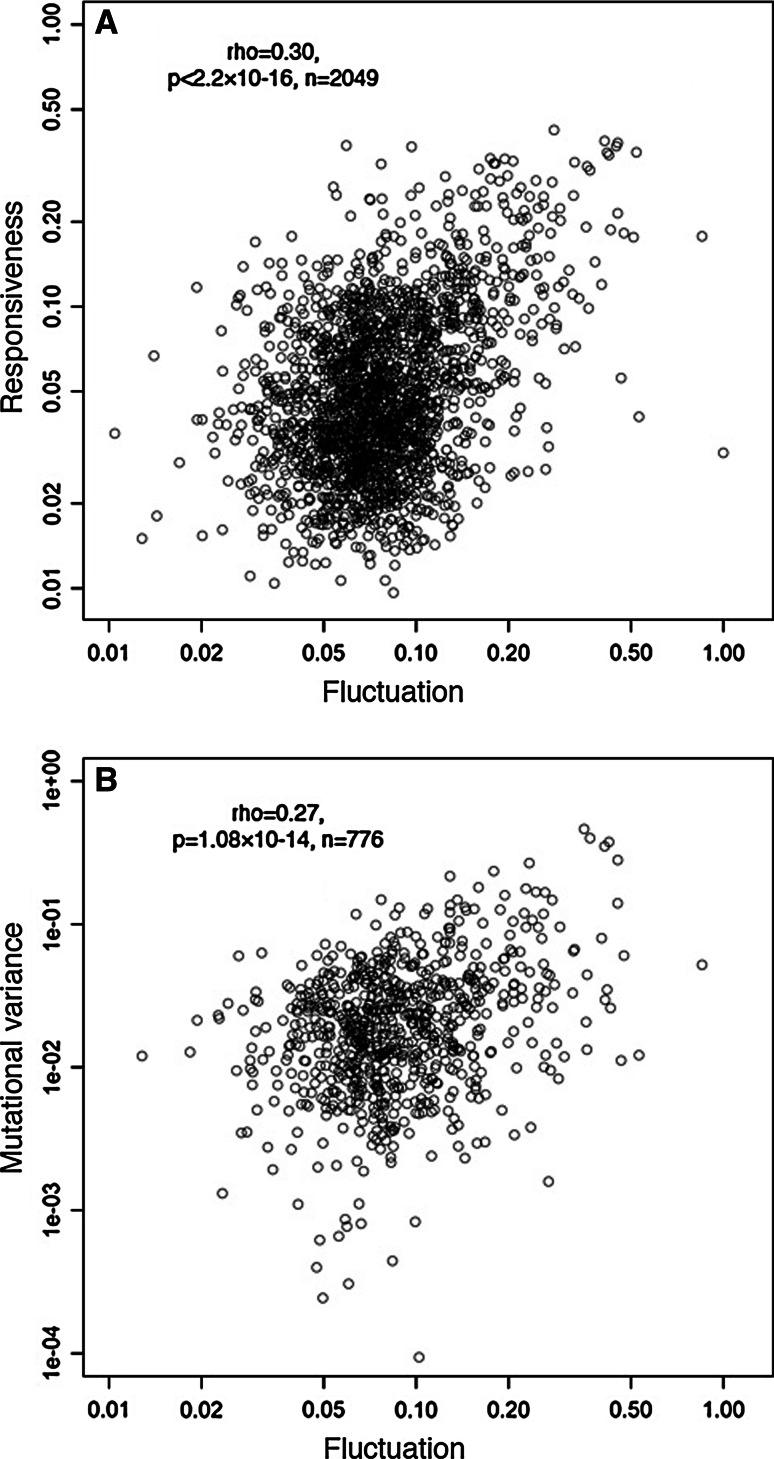
The fluctuation–response relationship across all genes is also rather consistent with global quantitative data from budding yeast. In yeast, global measurements have been made on the levels of isogenic expression fluctuation (expression ‘noise’ [18]), the responsiveness of expression to environmental change [19], and the change in expression following the accumulation of random mutations (‘mutational variance’) [20].

In yeast there is indeed quite a good correlation between the extent to which a gene’s expression changes across conditions (‘responsiveness’ or ‘plasticity’ [21]) and expression variation measured in a single condition (‘noise’ [18]) (Spearman rank correlation, rho = 0.30, p < 2.2 × 10⁻¹⁶, n = 2,049 genes, see also [20–23]). Genes with higher expression fluctuation are more responsive to changes in external conditions, and the relationship approaches proportionality across all genes (Fig. 3a, note that in all of these relationships, noise is measured using the ‘DM’ metric of Newman, where the coefficient of variation is quantified as the distance to a running median (DM) to correct for the relationship between coefficient of variation and the absolute level of expression [18]).

Fig. 3.

Coupling between fluctuation, response, and evolvability in yeast. a The relationship between isogenic expression fluctuation (‘noise’) and the environmental responsiveness of genes (‘plasticity’) in yeast across all genes. b The relationship between the isogenic expression fluctuation and the response to mutation (mutational variance) in yeast. Expression noise is quantified using the ‘DM’ measure of Newman et al. [18] that removes the confounding influence of protein abundance on coefficient of variation measurements. Environmental responsiveness is quantified from a compendium of gene expression profiling datasets compiled in [19] and reported in [21]. Mutational variance is estimated by comparing expression levels among lines in a mutation accumulation experiment under conditions in which selection is minimized using regular population bottlenecks [20]. Spearman correlation coefficients (rho) across genes are indicated

Also, as previously noted [20], across all genes in yeast there is also a correlation between expression noise and the responsiveness of expression to mutation (that is, variance across mutation accumulation lines (mutational variance), Fig. 3b, rho = 0.27, p = 1.08 × 10⁻¹⁴, n = 776 genes) or the expression divergence of genes between species (rho = 0.30, p < 2.2 × 10⁻¹⁶, n = 1,749 genes [23]). Consistent with the fluctuation–response relationship, noisy gene expression is more responsive to mutation, and noisy expression evolves faster between species.

Given their limitations, the genome-scale quantitative data are therefore intriguingly consistent with the proposed fluctuation–response relationship. Responsive gene expression is noisy, and noisy gene expression evolves faster. However, it should also be noted that noise and plasticity are not necessarily coupled in this way for all genes, and that during evolution selection may have disfavored coupling when there is a fitness conflict between the benefits of plasticity and the costs of noise [24].

The fluctuation–response relationship beyond gene expression

In this essay, we have only considered gene expression as a phenotypic trait. However, the fluctuation–response relationship may also apply to other traits beyond gene expression, and there is some evidence to support this. For example, in a series of experiments Stearns and colleagues [25] measured the variation of five life-history traits in inbred lines of Drosophila melanogaster. This quantifies the ‘environmental canalization’, or isogenic fluctuation of each trait (the traits were early fecundity, late fecundity, dry weight, age at eclosion, and lifespan). They also measured the variance of the same five traits among different genetic lines (‘genetic canalization’). Strikingly, they reported a strong proportionality between the isogenic variance (variance within a genotype) and the genetic variance (variance across genotypes) of each trait [25], suggesting that developmental mechanisms similarly buffer the phenotype against both genetic and environmental disturbance, and consistent with the fluctuation–response relationship.

Also in flies, a selection experiment to reduce morphological variation in a trait (i.e., to reduce stochastic variation) reduced the sensitivity to environmental change (i.e., reduced environmental variation) [26]. As in yeast, gene expression with higher variation among individuals may be more environmentally responsive in Drosophila [27]. In both flies [6] and plants [28] inactivation of a gene required for environmental robustness, the chaperone Hsp90, also has the effect of reducing robustness to mutation. In Caenorhabditis elegans inactivation of chromatin-modifying genes that reduce robustness to mutation also results in highly variable phenotypic outcomes in a constant environment [29]. However, much more quantitative phenotypic data is needed to assess how widespread correlations between trait fluctuation and trait response are in biology.

The connection between the fluctuation–response relationship, canalization, and genetic assimilation

In the 1940s, Conrad Waddington introduced the concept of canalization, the resistance of phenotypic traits to perturbation [2]. Waddington suggested (in a qualitative argument) that during evolution, phenotypes become more stable: that is, they become more robust to random variation, or, in his words, more ‘canalized’ [2]. His intuition was that genetic and non-genetic influences would similarly impact on a system, working through the same (at that time unknown) molecular mechanisms. This idea is indeed quite well supported by systematic genetic data in yeast, which show that genes that confer robustness to stochastic or environmental change also confer robustness to genetic change [30, 31]. Waddington proposed that more canalized traits would also be more stable in the face of genetic change, and so have a lower potential to evolve [2]. The fluctuation–response relationship outlined here can therefore be thought of as a quantitative statement of Waddington’s qualitative intuition, at least as applied to continuous traits. The relationship predicts that the potential of a trait to evolve should be proportional to its isogenic fluctuation.

A second important suggestion of Waddington’s was that initially environmentally induced change could later become fixed by mutation [2]. He called this process ‘genetic assimilation’, and it has remained a provocative idea ever since. The fluctuation–response relationship also provides a relevant insight into genetic assimilation. In the relationship, environmental and genetic responsiveness are coupled [11]. Therefore, if the fluctuation–response relationship holds for a trait, changes in phenotype can occur similarly through both environmental and genetic change, and genetic assimilation is a plausible mechanism of evolution.

Concluding remarks: a role for macroscopic theory in biology?

In summary, we have proposed here that in evolved, dynamical systems, we might expect levels of stochastic variation (noise or fluctuation) to be predictive of the responsiveness or plasticity of a system following environmental or genetic change. We have provided a theoretical argument for this relationship, and have shown its consistency with gene expression in evolved gene networks and to some extent with global quantitative measurements from yeast.

The relationship between fluctuation and response was first proposed by Albert Einstein in his Brownian motion theory [9]. In biology, such ‘macroscopic’ theory that ignores the precise molecular details might be considered quite rare. However, we would argue that ‘macroscopic’ theory has played an important role in biology, particularly in the pre-molecular era. Part of Einstein’s and Waddington’s success was the ability to step back and consider the general behavior of a system. Perhaps today, in an age of molecular details, we could all also benefit from sometimes stepping back, forgetting the details, and considering how biology works at this more macroscopic level.

Electronic supplementary material

Below is the link to the electronic supplementary material.