Estimation of semiparametric regression model with longitudinal data

Abstract

In a longitudinal study, an individual is followed up over a period of time. Repeated measurements on the response and some time-dependent covariates are taken at a series of sampling times. The sampling times are often irregular and depend on covariates. In this paper, we propose a sampling adjusted procedure for the estimation of the proportional mean model without having to specify a sampling model. Unlike existing procedures, the proposed method is robust to model misspecification of the sampling times. Large sample properties are investigated for the estimators of both regression coefficients and the baseline function. We show that the proposed estimation procedure is more efficient than the existing procedures. Large sample confidence intervals for the baseline function are also constructed by perturbing the estimation equations. A simulation study is conducted to examine the finite sample properties of the proposed estimators and to compare with some of the existing procedures. The method is illustrated with a data set from a recurrent bladder cancer study.

1 Introduction

We consider semiparametric modeling of covariate effects on a longitudinal response process based on repeated measurements observed at a series of sampling times. Suppose that there is a random sample of n subjects. For the ith subject, let Y_i (t) be the response process and let Z_i (t) be the possibly time-dependent covariates of dimensions p × 1 over the time interval [0, τ]. For example, Y_i (t) can be the response of the ith individual observed at time t, or the cumulative number of events that have occurred up to time t. We consider the following marginal proportional means model for Y_i (t), 0 ≤ t ≤ τ,

$${\mu }_i\left(t\right)=E\{Y_i\left(t\right)\mid Z_i\left(t\right)\}={\mu }_0\left(t\right)\exp \left\{{\beta }^{\mathrm{T}}{Z}_i\left(t\right)\right\},i=1,\dots ,n$$ (1)

where μ₀(t) is a completely unspecified function and β is a p-dimensional vector of unknown parameters. The notation β^T represents transpose of a vector or matrix β.

In longitudinal studies, subjects are followed over a period of time and the responses are taken at different time points. Suppose that the observations of Y_i (t) are taken at the sampling time points 0 ≤ t_i1 < t_i2 < … < t_ini ≤ τ, where n_i is the total number of observations on the ith subject. The sampling times are often irregular and depend on covariates. In addition, some subjects may drop out of the study early. Let $N_i\left(t\right)={\Sigma }_{j=0}^{n_i}I(t_{\mathit{ij}}\le t)$ be the number of observations taken on the ith subject by time t, where I (·) is the indicator function. Let C_i be the end of follow-up time or censoring time for the ith subject. Then the responses for the ith subject can only be observed at the time points before C_i. Thus N_i (t) can be written as $N_i^{\ast }(t\wedge C_i)$, where $N_i^{\ast }\left(t\right)$ is a counting process for sampling times.

Nonparametric and semiparametric modeling of longitudinal data have been studied extensively in recent years. These include semiparametric methods by Moyeed and Diggle (1994); Zeger and Diggle (1994); Liang et al. (2003), and nonparametric methods by Hoover et al. (1998); Wu et al. (1998); Wu and Zhang (2002), Wu and Liang (2004), Martinussen and Scheike (1999, 2000, 2001); Lin and Ying (2001); Scheike (2002); Sun and Wu (2005) and Fan and Li (2004). Most of the aforementioned works focus on additive time-varying coefficients regression models for the mean response.

When Y_i (t), 0 ≤ t ≤ τ, is a continuously observed counting process subject to right censoring, model (1) has been studied by Andersen and Gill (1982); Lawless and Nadeau (1995), and Lin et al. (2000) among others. Data collected on the individual response processes Y_i (t), 0 ≤ t ≤ τ, at a finite set of sampling times are also called panel data. Many authors have studied nonparametric estimation of panel count data in the absence of covariates; cf. Sun and Kalbfleisch (1995); Wellner and Zhang (2000); Lu et al. (2007); Hu et al. (2009). The semiparametric model (1) for the mean function allows the study of a treatment effect based on panel data, where the responses are not limited to the count data. Zhang (2002) proposed a semiparametric pseudolikelihood method for model (1) under the assumption that Y_i (t) is a nonhomogeneous Poisson process. For panel count data, model (1) has been studied by Sun and Wei (2000); Cheng and Wei (2000), and Hu et al. (2003). These works generally assume that the sampling times are independent of covariates or follow a proportional mean rate model to account for possible dependence on the covariates. However, mis-specification of the sampling model may mislead the inferences for the response process. Assuming time independent covariate processes, Hu et al. (2003, Sect. 2.2) proposed estimation procedure that does not require modelling of the observation process but assuming that the observation processes are discrete and that a subject has observations at some time points with positive probability. This approach is useful for situations where the panel count processes are observed at a fixed set of time points and would require discretizing the time scale in practice when the condition is not met.

We propose a sampling adjusted procedure for estimation of model (1) without having to specify a sampling model for observation times whether it is proportional, additive or transformation mean rate model, cf. Lin et al. (2000, 2001) and Scheike (2002). The proposed method applies to longitudinal response processes not limited to count data. Consider the following general mean rate model for sampling times:

$$E\{d{N}_i^{\ast }\left(t\right)\mid Z_i\left(t\right)\}=\alpha (t,Z_i\left(t\right))\mathit{dt}={\alpha }_i\left(t\right)\mathit{dt},$$ (2)

where, other than some imposed smooth conditions, the function α(t, z) is completely unspecified. We focus on the statistical analysis of model (1) for modelling the mean response without having to worry about the implications of model misspecification of the sampling times. Thus our estimator for β is robust to model misspecification of the sampling times. We also show that the proposed estimator for β is more efficient than the estimators proposed by Cheng and Wei (2000) and by Hu et al. (2003). In addition, a sampling adjusted estimator for the baseline function μ₀(t) is proposed and its pointwise confidence intervals are constructed using the perturbing method of Jin et al. (2001). In the case when some of the covariates may be time-dependent, an added advantage of the proposed method is that Z_i (t) need not to be observed at all time t. Only the values at sampling times are needed, which is practically convenient since the time-dependent covariates are usually observed at the sampling times.

The rest of the paper is organized as follows. In Sect. 2.1, we propose a sampling adjusted procedure for estimation of the proportional means model. Large sample properties are investigated. Pointwise confidence intervals for the baseline function is constructed in Sect. 2.2. The asymptotic efficiency of the proposed estimator is compared to the existing procedures in Sect. 2.3. A simulation study is presented in Sect. 3. An application of the proposed method to a recurrent bladder cancer study is given in Sect. 4. All proofs are given in the Appendix.

2 Estimation of proportional mean regression model

In this section, we propose an estimation procedure for model (1) based on the observations {(Y_i (t_ij), Z_i (t_ij)); j = 1, … , n_i, i = 1, … , n.}. These are the values of {(Y_i (t), Z_i (t)), 0 ≤ t ≤ τ} observed at sampling times or the jump time points of $N_i\left(t\right)=N_i^{\ast }(t\wedge C_i),i=1,\dots ,n$. Assume that the processes $N_i^{\ast }(\cdot )$ and Y_i (·) are independent given Z_i (·). The asymptotic results of the proposed estimators are proved. The asymptotic efficiency is discussed.

2.1 Estimation procedures and asymptotic properties

Under model (1) and Condition A given in the Appendix, Y_i (t) dN_i (t) − μ₀(t)exp {β^T Z_i (t)} dN_i (t) has mean zero for 0 ≤ t ≤ τ. The estimation of μ₀(t) for fixed β can be derived based on this property. Because of sparsity of the data at time t. we gather the data around a neighborhood of t through kernel smoothing. This motivates the following estimate for μ₀(t) when β is known:

$${\tilde{\mu }}_0(t;\beta )=\frac{{\Sigma }_{i=1}^n{\int }_0^{\tau }{K}_b(t-s)Y_i\left(s\right){\mathit{dN}}_i\left(s\right)}{{\Sigma }_{i=1}^n{\int }_0^{\tau }{K}_b(t-s)\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{\mathit{dN}}_i\left(s\right)},$$ (3)

where K_b(x) = K (x/b)/b, K (·) is a kernel function and b is the bandwidth. Let

$$\begin{array}{cc}\hfill {\tilde{S}}_y\left(t\right)& =n^{-1}\underset{i=1}{\overset{n}{\Sigma }}\underset{0}{\overset{\tau }{\int }}{K}_b(t-s)Y_i\left(s\right){\mathit{dN}}_i\left(s\right)\hfill \\ \hfill {\tilde{S}}^{\left(k\right)}(t;\beta )& =n^{-1}\underset{i=1}{\overset{n}{\Sigma }}{\int }_0^{\tau }{K}_b(t-s)Z_i^{\otimes k}\left(s\right)\exp \left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{\mathit{dN}}_i\left(s\right)\hfill \end{array}$$

for k = 0, 1, 2, where Z^⊗2 = ZZ^T, Z^⊗1 = Z and Z^⊗0 = 1. Define Z̃(t; β) = S̃⁽¹⁾ (t; β)/S̃⁽⁰⁾ (t; β). We can write μ̃₀(t; β) = S̃_y (t)/S̃⁽⁰⁾ (t; β).

A profile weighted least squares type estimator for β can be obtained by minimizing

$$l\left(\beta \right)=\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}{W}_i\left(s\right){(Y_i\left(s\right)-{\tilde{\mu }}_0(s;\beta )\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\})}^2{\mathit{dN}}_i\left(s\right),$$ (4)

where W_i (t) are weight processes and [t₁, t₂] is a subinterval of [0, τ]. The trimming of the boundary points is to avoid the complicated boundary problems involved in the proofs of the asymptotic properties. Our simulations have shown that t₁ and t₂ can be taken to be very close to 0 and τ, respectively, usually less than one bandwidth in difference. Note that ∂μ̃₀(t; β)/∂β = −μ̃₀(t; β) Z̃(t; β). By taking the partial derivatives of l(β) with respect to β, we have

$$\partial l\left(\beta \right)∕\partial \beta =\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}{W}_i\left(s\right){\tilde{\mu }}_0(s;\beta )\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}(Z_i\left(s\right)-\tilde{Z}(s;\beta ))(Y_i\left(s\right)-{\tilde{\mu }}_0(s;\beta )\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}){\mathit{dN}}_i\left(s\right).$$ (5)

Let W_i (t) = W (t)(μ̃₀(t; β)exp{β^T Z_i (t)})⁻¹ where W (t) is some weight process not depending on β and i. We obtain the following estimation function:

$$U\left(\beta \right)=\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}W\left(s\right)(Z_i\left(s\right)-\tilde{Z}(s;\beta ))(Y_i\left(s\right)-{\tilde{\mu }}_0(s;\beta )\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}){\mathit{dN}}_i\left(s\right).$$ (6)

Let β̂ be the estimator of β such that U(β̂) = 0. We show that β̂ is asymptotically consistent and has an asymptotic normal distribution. A estimator for the baseline mean function is given by μ̂₀(t) = μ̃₀(t; β̂).

As we shall see later in Sect. 2.3, the proposed estimator gains efficiency over the estimator of Hu et al. (2003) by centering Y_i (·) around its estimated mean, thus reducing variance, while Hu et al. (2003) avoided dealing with the baseline function μ₀(·) in their estimation of parametric components.

Let μ̃₁(t; β) = ∂μ̃₀(t; β)/∂β. Taking partial derivative of U (β) with respect to β, we have

$$\frac{\partial U\left(\beta \right)}{\partial {\beta }^{\mathrm{T}}}=-\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}W\left(s\right){(Z_i\left(s\right)-\tilde{Z}(s;\beta ))}^{\otimes 2}{\tilde{\mu }}_0(s;\beta )\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{\mathit{dN}}_i\left(s\right)-\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}W\left(s\right)\left(\frac{{\tilde{S}}^{\left(2\right)}(s;\beta )}{{\tilde{S}}^{\left(0\right)}(s;\beta )}-\tilde{Z}{(s;\beta )}^{\otimes 2}\right)(Y_i\left(s\right)-{\tilde{\mu }}_0(s;\beta )\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}){\mathit{dN}}_i\left(s\right).$$ (7)

By Lemma 1 given in the Appendix, the second term above is at the order of o_p(n). Let β₀ be the true value of β under model (1). By the first order Taylor expansion, we have

$$n^{1∕2}(\widehat{\beta }-{\beta }_0)={\left[-n^{-1}\frac{\partial U\left({\beta }^{\ast }\right)}{\partial {\beta }^{\mathrm{T}}}\right]}^{-1}{n}^{-1∕2}U\left({\beta }_0\right),$$ (8)

where β* is on the line segment between β̂ and β₀.

Let ξ_i (t) = I (C_i ≥ t), s_y(t) = E(ξ_i (t)α_i (t)Y_i (t)) and $s^{\left(k\right)}\left(t\right)=E\left[{\xi }_i\left(t\right){\alpha }_i\left(t\right)Z_i^{\otimes k}\left(t\right)\exp \left\{{\beta }^{\mathrm{T}}{Z}_i\left(t\right)\right\}\right]$, for k = 0, 1, 2. Let w(t) be a deterministic nonnegative function such that $W\left(t\right)\stackrel{P}{\to }w\left(t\right)$ uniformly in t. Define z̄(t) = S⁽¹⁾(t)/S⁽⁰⁾(t), $A={\int }_{t_1}^{t_2}w\left(s\right){\mu }_0\left(u\right)s^{\left(0\right)}\left(u\right)\left(s^{\left(2\right)}\left(u\right)∕s^{\left(0\right)}\left(u\right)-\stackrel{-}{z}{\left(u\right)}^{\otimes 2}\right)\mathit{du}$, and

$$\Sigma =E\left[{\left(\underset{t_1}{\overset{t_2}{\int }}w\left(s\right)(Z_i\left(s\right)-\stackrel{-}{z}\left(s\right))(Y_i\left(s\right)-{\mu }_0\left(s\right)\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}){\mathit{dN}}_i\left(s\right)\right)}^{\otimes 2}\right].$$ (9)

The following theorem presents the asymptotic consistency of the estimator β̂. By (8), the asymptotic normality of β̂ follows from the asymptotic consistency of β̂, uniform convergence of n⁻¹∂U (β)/∂β^T in a neighborhood of β₀ and asymptotic normality of n^−1/2U (β₀).

Theorem 1

Under Condition A given in the Appendix, $\widehat{\beta }\stackrel{P}{\to }{\beta }_0,n^{1∕2}(\widehat{\beta }-{\beta }_0)\stackrel{𝒟}{\to }N(0,A^{-1}\Sigma A^{-1})$ and ${\widehat{\mu }}_0\left(t\right)\stackrel{P}{\to }{\mu }_0\left(t\right)$ uniformly in t ∈ [t₁, t₂]. Consistent estimators for  = −n⁻¹ ∂U (β̂)/∂β^T and

$$\widehat{\Sigma }=n^{-1}\underset{i=1}{\overset{n}{\Sigma }}{\left(\underset{t_1}{\overset{t_2}{\int }}W\left(s\right)(Z_i\left(s\right)-\tilde{Z}(s;\widehat{\beta })){\widehat{∊}}_i\left(s\right){\mathit{dN}}_i\left(s\right)\right)}^{\otimes 2},$$

where ∈̂_i(S) = Y_i(S) − μ̂₀(S)exp{β̂^T Z_i(S)}.

From (9), we see that the weight process W (·) assigns the weight W (t_ij) to the difference Y_i (t_ij) − μ₀(t_ij)exp{β^T Z_i (t_ij)} at the sampling time t_ij. Taking W (·) = 1 implies that the longitudinal observations at all the times are equally weighted for the estimation of β, which is what we recommend for most applications. On the other hand, one can choose to emphasize the early or late observations by selecting W (·) to be decreasing or increasing. The optimal choice of W (·) for the observed data such that Σ defined in (9) is minimized is a challenge problem and needs further exploration.

In practice, the appropriate bandwidth can be selected using a leave-one-subject-out cross validation approach suggested by Rice and Silverman (1991). In particular, Let

$$\mathit{PE}\left(b\right)=n^{-1}\underset{i=1}{\overset{n}{\Sigma }}{\left[\underset{0}{\overset{\tau }{\int }}(Y_i\left(t\right)-{\widehat{\mu }}_{0\left(i\right)}\left(t\right)\mathit{exp}\left\{{\widehat{\beta }}_{\left(i\right)}^{\mathrm{T}}{Z}_i\left(t\right)\right\}){\mathit{dN}}_i\left(t\right)\right]}^2,$$ (10)

where, for a given bandwidth b, β_(i) and μ̂_0(I)(t) are the estimators of β and μ₀(t) based on the data without subject i. The data-driven bandwidth selection method is to choose the bandwidth b that minimizes the mean squares of fitted residuals PE(b). This data-driven bandwidth selection method is used in Sect. 4 for analyzing the bladder cancer data.

Next, we present an asymptotic result for the estimator μ̂₀(t) of the baseline function. The result is useful for constructing confidence intervals for the mean response curve given the covariates. Let μ₂ = ∫ u² K (u) du and η(t) = (s⁽⁰⁾(t))⁻¹[(s_y(t))″ − μ₀(t)(s⁽⁰⁾(^t))″], where ( f (t))″ denotes the second derivative of f (t) with respect to t.

Theorem 2

Under Conditions A and B given in the Appendix,

$${\left(\mathit{nb}\right)}^{1∕2}\{{\widehat{\mu }}_0\left(t\right)-{\mu }_0\left(t\right)-\frac{1}{2}{b}^2{\mu }_2\eta \left(t\right)\}\stackrel{𝒟}{\to }N\{0,{\left(s^{\left(0\right)}\left(t\right)\right)}^{-2}{\sigma }^2\left(t\right)\}$$

for t ∈ [t₁, t₂]. The asymptotic variance can be estimated consistently by (S̃⁽⁰⁾(t))⁻² σ̂²(t), where ${\widehat{\sigma }}^2\left(t\right)={\mathit{bn}}^{-1}{\Sigma }_{i=1}^n{\left[{\int }_0^{\tau }{K}_b(t-s){\widehat{∊}}_i\left(s\right){\mathit{dN}}_i\left(s\right)\right]}^2$.

2.2 Constructing confidence intervals for baseline function

The pointwise confidence intervals for the baseline function μ₀(t) can be constructed based on the asymptotic normality given in Theorem 2. However, since μ̂₀(t) has a slow convergence rate of (nb)^−1/2, the resampling-based method yields more accurate coverage probability. Here we present a method by perturbing the estimation equations. This method has been studied and shown to have good empirical properties by Jin et al. (2001) and by other authors. Let ζ₁, … ,ζ_n be iid random variables with mean 1 and variance 1, say, exponential random variables with mean 1. The perturbed estimating equation for μ₀(t) for fixed β is

$$\underset{i=1}{\overset{n}{\Sigma }}{\zeta }_i\left[Y_i\left(t\right){\mathit{dN}}_i\left(t\right)-{\mu }_0\left(t\right)\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(t\right)\right\}{\mathit{dN}}_i\left(t\right)\right]=0.$$ (11)

Similar to (3), we obtain the following smoothed estimator of μ₀(t) for given β:

$${\tilde{\mu }}_0^{\ast }(t;\beta )=\frac{{\Sigma }_{i=1}^n{\zeta }_i{\int }_0^{\tau }{K}_b(t-s)Y_i\left(s\right){\mathit{dN}}_i\left(s\right)}{{\Sigma }_{i=1}^n{\zeta }_i{\int }_0^{\tau }{K}_b(t-s)\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{\mathit{dN}}_i\left(s\right)}.$$ (12)

Perturbing the estimation Eq. 6 yields

$$U^{\ast }\left(\beta \right)=\underset{i=1}{\overset{n}{\Sigma }}{\zeta }_i\underset{t_1}{\overset{t_2}{\int }}W\left(s\right)(Z_i\left(s\right)-\tilde{Z}(s;\beta ))(Y_i\left(s\right)-{\tilde{\mu }}_0^{\ast }(s;\beta )\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}){\mathit{dN}}_i\left(s\right).$$ (13)

Let β̂* be the estimator of β such that U* (β̂*) = 0. Let ${\widehat{\mu }}_0^{\ast }\left(t\right)={\tilde{\mu }}_0^{\ast }(t;{\widehat{\beta }}^{\ast })$. Similar to Jin et al. (2001), the distributions of n^1/2(β̂ − β) and n^1/2(μ̂₀(t) − μ₀(t)) can be approximated by the distributions of n^1/2(β̂* − β̂) and $n^{1∕2}({\widehat{\mu }}_0^{\ast }\left(t\right)-{\widehat{\mu }}_0\left(t\right))$. A 100(1 − α)% confidence interval for μ₀(t), 0 ≤ t ≤ τ, can be constructed by (μ̂₀(t) − q_1−α/2(t), μ̂₀(t) − q_α/2(t)), where q_α/2(t), q_1−α/2(t) are the α/2 and 1 − α/2 quantiles of $\{{\widehat{\mu }}_0^{\ast k}\left(t\right)-{\widehat{\mu }}_0\left(t\right),k=1,\dots ,B\}$ based on B sets of perturbed estimation equations. Alternatively, the confidence interval for μ₀(t) can be obtained by μ̂₀(t) ± z_α/2SE*(t), where SE*(t) is the standard deviation of the estimators $\{{\widehat{\mu }}_0^{\ast k}\left(t\right),k=1,\dots ,B\}$ based on B sets of perturbed estimation equations. Our simulations show that the two approaches have similar performances, only the first is presented in Sect. 3.

2.3 Asymptotic efficiency considerations

Cheng and Wei (2000) studied model (1) by assuming that α_i (t) = λ₀(t) does not depend on Z_i (t). Their estimator of β has the asymptotic variance of A⁻¹Σ_CW A⁻¹, where

$${\Sigma }_{\mathit{CW}}=E{\left\{\underset{t_1}{\overset{t_2}{\int }}w\left(s\right)(Z_i\left(s\right)-\stackrel{-}{z}\left(s\right))[Y_i\left(s\right){\mathit{dN}}_i\left(s\right)-{\mu }_0\left(s\right){\lambda }_0\left(s\right)\exp \left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{\xi }_i\left(s\right)\mathit{ds}]\right\}}^{\otimes 2}.$$

Under noninformative censoring and the independence between Y_i (·) and $N_i^{\ast }(\cdot )$ given Z_i (·),

$${\Sigma }_{\mathit{CW}}=\Sigma +E{\left\{\underset{t_1}{\overset{t_2}{\int }}w\left(s\right)(Z_i\left(s\right)-\stackrel{-}{z}\left(s\right)){\mu }_0\left(s\right)\exp \left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}({\mathit{dN}}_i\left(s\right)-{\xi }_i\left(s\right){\lambda }_0\left(s\right)\mathit{ds})\right\}}^{\otimes 2},$$

where Σ is defined in (9). It is clear that our estimator β̂ has smaller asymptotic variance, thus more efficient than the estimator of Cheng and Wei (2000).

Hu et al. (2003) studied model (1) under the assumption that the observation process $N_i^{\ast }\left(t\right)$ follows the conditional proportional mean rate model

$${\alpha }_i\left(t\right)={\lambda }_0\left(t\right)\exp \left\{{\alpha }^{\mathrm{T}}{Z}_i\right\}$$ (14)

with λ₀(t) an unspecified baseline mean function, and that covariate Z_i is time independent. Hu et al. (2003, Sect. 2.3) obtained a joint estimator (β̂^M, α̂^M) for (β, α). Here we show that the HSW procedure is also applicable to time-dependent covariate and that our robust estimator is more efficient than the HSW estimator. We use a different parametrization, expressing the estimation equations as the functions of (β, α) instead of (β̃, α) as in Hu et al. (2003), where β̃ = β+α. Of course, the different ways of parametrization do not change the estimator for β or its asymptotic variance. Our parametrization only makes it easier to show that the proposed estimator β̂ is more efficient than the HSW estimator β̂^M.

Let

$$S_M^{\left(j\right)}(t;\beta ,\alpha )=n^{-1}\underset{i=1}{\overset{n}{\Sigma }}{\xi }_i\left(t\right)Z_i{\left(t\right)}^{\otimes j}\exp \{{(\beta +\alpha )}^{\mathrm{T}}{Z}_i\left(t\right),\text{for}j=0,1,2$$

and ${\stackrel{-}{Z}}_M(t;\beta ,\alpha )=S_M^{\left(1\right)}(t;\beta ,\alpha )∕S_M^{\left(0\right)}(t;\beta ,\alpha )$. The joint estimation equations of Hu et al. (2003) for (β, α) using data on [t₁, t₂] ⊂ [0, τ] are

$$\begin{array}{cc}\hfill U_1^M(\beta ,\alpha )& =\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}W\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{Z}}_M(s;\beta ,\alpha ))Y_i\left(s\right){\mathit{dN}}_i\left(s\right)\hfill \\ \hfill U_2^M\left(\alpha \right)& =\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}{W}_O\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{Z}}_M(s;0,\alpha )){\mathit{dN}}_i\left(s\right),\hfill \end{array}$$

where W(t) and W_O(t) are the weight processes. Hu et al. (2003) have focused the investigation on the unit weights of W(t) = 1 and W_O(t) = 1. Since W_O(t) = 1 is the optimal weight for estimating α, we let W_O(t) = 1.

Let Z̄_M(t; β, α) be the limit of Z̄_M(t; β, α) in probability. Let $M_i^O\left(t\right)={\int }_{t_1}^{\mathrm{T}}{\xi }_i\left(s\right)[{\mathit{dN}}_i\left(s\right)-\exp \left({\alpha }^{\mathrm{T}}{Z}_i\left(s\right)\right){\lambda }_0\left(s\right)\mathit{ds}]$, $M_i^M\left(t\right)={\int }_{t_1}^{\mathrm{T}}{\xi }_i\left(s\right)[Y_i\left(s\right){\mathit{dN}}_i\left(s\right)-{\mu }_0\left(s\right)\exp \left({(\beta +\alpha )}^{\mathrm{T}}{Z}_i\left(s\right)\right){\lambda }_0\left(s\right)\mathit{ds}]$ and $\Delta =E{\left\{{\int }_{t_1}^{t_2}{\xi }_i\left(s\right)w\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{z}}_M(s;\beta ,\alpha )){\mu }_0\left(s\right)\exp \left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{\mathit{dM}}_i^O\left(s\right)\right\}}^{\otimes 2}$. Let

$$\left[\begin{array}{cc}\hfill B_{11}\hfill & \hfill B_{12}\hfill \\ \hfill B_{21}\hfill & \hfill B_{22}\hfill \end{array}\right]=E\left\{{\left[\begin{array}{c}{\int }_{t_1}^{t_2}{\xi }_i\left(s\right)w\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{z}}_M(s;\beta ,\alpha )){\mathit{dM}}_i^M\left(s\right)\hfill \\ {\int }_{t_1}^{t_2}{\xi }_i\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{z}}_M(s;0,\alpha )){\mathit{dM}}_i^O\left(s\right)\hfill \end{array}\right]}^{\otimes 2}\right\}$$ (15)

where B₁₁ is the variance matrix of the top term in the square bracket, B₁₂ is the covariance matrix the top term and the bottom term, $B_{21}=B_{12}^{\mathrm{T}}$ and B₂₂ is the variance matrix of the bottom term in the square bracket.

The following Theorem shows that our estimator β̂ is more efficient than the HSW estimator β̂^M for β.

Theorem 3

Under the assumption that the observation process $N_i^{\ast }\left(t\right)$ has the conditional proportional mean rate model (14), the asymptotic variance of HSW estimator β̂^M for β is A⁻¹ΣA⁻¹+D, where $D=A^{-1}\Delta A^{-1}-A^{-1}{B}_{12}{A}_{\alpha }^{-1}-{\left(A^{-1}{B}_{12}{A}_{\alpha }^{-1}\right)}^{\mathrm{T}}+A_{\alpha }^{-1}{B}_{22}{A}_{\alpha }^{-1}$ is semi-positive definite and A_α is the usual information matrix associated with the proportional mean rate model defined in Condition (e) of Lin et al. (2000), which can be obtained by letting w(t) = 1, μ₀(t) = 1 and β = 0 in A.

Hu et al. (2003) have taken [t₁, t₂] to be [0, τ] while we take [t₁, t₂] to be a subinterval of [0, τ] to avoid dealing with boundary problems. This small[ trim] of data will not result in much efficiency loss in analyzing the data. In fact, t₁ and t₂ can be chosen arbitrarily close to 0 and τ , respectively.

When the observation process is a counting process, $M_i^O\left(t\right)$ is a martingale. It follows that B₂₂ = A_α and

$$\begin{array}{cc}\hfill B_{12}=& E\left\{\left[\underset{t_1}{\overset{t_2}{\int }}{\xi }_i\left(s\right)w\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{z}}_M(s;\beta ,\alpha )){\mu }_0\left(s\right)\exp \left({\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right){\mathit{dM}}_i^O\left(s\right)\right]\times {\left[\underset{t_1}{\overset{t_2}{\int }}{\xi }_i\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{z}}_M(s;0,\alpha )){\mathit{dM}}_i^O\left(s\right)\right]}^{\mathrm{T}}\right\}\hfill \\ \hfill =& E\left\{\left[\underset{t_1}{\overset{t_2}{\int }}{\xi }_i\left(s\right)w\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{z}}_M(s;\beta ,\alpha )){(Z_i\left(s\right)-{\stackrel{-}{z}}_M(s;0,\alpha ))}^{\mathrm{T}}\times {\mu }_0\left(s\right){\lambda }_0\left(s\right)\exp \left({(\beta +\alpha )}^{\mathrm{T}}{Z}_i\left(s\right)\right)\mathit{ds}\right]\right\}\hfill \\ \hfill =& E\left\{\left[\underset{t_1}{\overset{t_2}{\int }}{\xi }_i\left(s\right)w\left(s\right){(Z_i\left(s\right)-{\stackrel{-}{z}}_M(s;\beta ,\alpha ))}^{\otimes 2}{\mu }_0\left(s\right){\lambda }_0\left(s\right)\exp \left({(\beta +\alpha )}^{\mathrm{T}}{Z}_i\left(s\right)\right)\mathit{ds}\right]\right\}+E\left\{\left[\underset{t_1}{\overset{t_2}{\int }}{\xi }_i\left(s\right)w\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{z}}_M(s;\beta ,\alpha )){({\stackrel{-}{z}}_M(s;\beta ,\alpha )-{\stackrel{-}{z}}_M(s;0,\alpha ))}^{\mathrm{T}}\times {\mu }_0\left(s\right){\lambda }_0\left(s\right)\exp \left({(\beta +\alpha )}^{\mathrm{T}}{Z}_i\left(s\right)\right)\mathit{ds}\right]\right\}\hfill \\ \hfill =& E\left\{\left[\underset{t_1}{\overset{t_2}{\int }}{\xi }_i\left(s\right)w\left(s\right){(Z_i\left(s\right)-{\stackrel{-}{z}}_M(s;\beta ,\alpha ))}^{\otimes 2}{\mu }_0\left(s\right){\lambda }_0\left(s\right)\exp \left({(\beta +\alpha )}^{\mathrm{T}}{Z}_i\left(s\right)\right)\mathit{ds}\right]\right\}\hfill \\ \hfill =& A.\hfill \end{array}$$

By Theorem 3, the asymptotic variance of the HSW estimator β̂^M is $A^{-1}(\Sigma +\Delta )A^{-1}-A_{\alpha }^{-1}$. One can also see from the proof of Theorem 3 that β̂^M and α̂^M are asymptotically independent. In this case, the matrix $A^{-1}\Delta A^{-1}-A_{\alpha }^{-1}$ is semi-positive definite. This expression shows that the variance for the estimator β̂^M is reduced by modeling the observation process $N_i^{\ast }\left(t\right)$ using the proportional mean rate model as expected. However, the proposed estimator gains more efficiency by subtracting the mean of Y_i (t) in the estimation function U(β) in (6).

3 A simulation study

Some numerical simulation results are presented in this section to illustrate the feasibility and validity of the proposed methods. The responses are generated from the following model

$$Y_i\left(t\right)={\mu }_0\left(t\right)\exp ({\beta }_1{Z}_{1i}+{\beta }_2{Z}_{2i})+{∊}_i\left(t\right),i=1,\dots n,$$ (16)

over the time interval [0, τ] where β₁ = 1, β₂ = −0.5 and (Z_1i, Z_2i) are independent identically distributed. We take τ = 24. The Z_1i has a Bernoulli distribution with P(Z_1i = 1) = 0.4 and Z_2i is uniformly distributed on (0, 1). We consider two baseline functions μ₀(t) = 0.2 + 0.5t and μ₀(t) = 0.05t². The ∈_i (t) has a normal distribution conditional on the ith subject with mean ϕ_i and variance ${\sigma }_e^2=1$, and ϕ_i is normal with mean zero and variance ${\sigma }_{\varphi }^2=1$. The counting process $N_i^{\ast }\left(t\right)$ is set to be a Poisson process with intensity rate of α_i (t) over the interval [0, 24] . We consider two models for α_i (t). One is the proportional mean rate model with α_i (t) = 0.4 exp(0.3Z_1i + 0.6Z_2i). The other is the additive mean rate model with α_i (t) = 0.48Z_1i + 0.96Z_2i. We generate the censoring random variable C_i from the uniform distribution on (0,60). With this censoring distribution, about 36% of subjects have censored observations under both the proportional mean rate model and the additive mean rate model. The average uncensored observations per subject is about 12 under the proportional mean rate model and 13 under the additive mean rate model. Trimming away a little bit of boundary points, we take [t₁, t₂] = [1, 23]. For simplicity, the weight function W(t) = 1 and use the Epanechnikov kernel K(t) = 0.75(1 − t²)+.

Table 1 summarizes some simulation results from the estimators of β₁ and β₂ for n = 100, 200, 300 under the proportional mean rate sampling model α_i (t) = 0.4 exp(0.3Z_1i + 0.6Z_2i ) and for two different baseline functions. The bandwidths b = 1.5, 2.0 and 2.5 are used for the kernel smoothing. The simulation results based on the method of Hu et al. (2003) are indicated with HSW under the bandwidth column. The method of Hu et al. (2003) is developed under the proportional mean rate sampling model. In Table 2 we also list its simulation results under the misspecified additive mean rate sampling model α_i (t) = 0.48Z_1i + 0.96Z_2i , to show its sensitivity to the model specification and to demonstrate the robust property of the proposed estimator. Each entry in Table 1 and 2 is based on 1000 repetitions (samples), where, for k = 1, 2, under b = 1.5, 2.0 and 2.5, Bias(β_k) is the average of the estimation bias of β̂_k; SSE(β_k) is the sampling standard error of β̂_k; ESE(β_k) is the estimated standard error of β̂_k; CP(β_k) is the coverage probability of 95% confidence interval for β_k using β̂_k, and under b = HSW, they are corresponding summary statistics for the estimators of Hu et al. (2003).

Table 1.

Summary statistics for the estimators β̂ and β̂_HSW under the proportional mean sampling model α_i (t) = 0.4 exp(0.3Z_1i + 0.6Z_2i)

μ0(t)	n	b	Bias(β1)	Bias(β2)	SSE(β1)	SSE(β2)	ESE(β1)	ESE(β2)	CP(β1)	CP(β2)
0.2 + 0.5t	100	1.5	−0.0001	−0.0008	0.0391	0.0539	0.0370	0.0513	0.933	0.937
		2.0	−0.0003	−0.0000	0.0369	0.0532	0.0369	0.0510	0.947	0.935
		2.5	0.0025	0.0011	0.0377	0.0542	0.0369	0.0507	0.944	0.923
		HSW	−0.0010	0.0018	0.0548	0.1026	0.0522	0.0976	0.940	0.920
	200	1.5	−0.0004	−0.0003	0.0264	0.0366	0.0263	0.0364	0.946	0.947
		2.0	0.0013	0.0009	0.0268	0.0379	0.0263	0.0361	0.936	0.932
		2.5	0.0010	0.0003	0.0264	0.0372	0.0263	0.0360	0.949	0.935
		HSW	−0.0009	0.0015	0.0377	0.0713	0.0369	0.0694	0.942	0.930
	300	1.5	0.0004	0.0005	0.0222	0.0306	0.0216	0.0297	0.940	0.952
		2.0	0.0007	0.0002	0.0210	0.0301	0.0216	0.0296	0.960	0.946
		2.5	0.0002	−0.0001	0.0215	0.0294	0.0216	0.0296	0.948	0.952
		HSW	−0.0001	0.0027	0.0309	0.0570	0.0301	0.0568	0.943	0.952
0.05t2	100	1.5	−0.0001	−0.0005	0.0276	0.0381	0.0262	0.0364	0.932	0.939
		2.0	−0.0003	−0.0000	0.0261	0.0378	0.0261	0.0362	0.947	0.936
		2.5	0.0018	0.0008	0.0267	0.0385	0.0261	0.0360	0.942	0.925
		HSW	−0.0015	0.0032	0.0662	0.1284	0.0631	0.1230	0.939	0.928
	200	1.5	−0.0003	−0.0002	0.0187	0.0258	0.0186	0.0257	0.945	0.948
		2.0	0.0009	0.0006	0.0189	0.0268	0.0186	0.0256	0.938	0.933
		2.5	0.0006	0.0002	0.0187	0.0264	0.0186	0.0255	0.949	0.932
		HSW	−0.0011	0.0025	0.0462	0.0904	0.0447	0.0880	0.938	0.934
	300	1.5	0.0003	0.0003	0.0156	0.0216	0.0152	0.0209	0.940	0.951
		2.0	0.0004	0.0001	0.0149	0.0213	0.0152	0.0209	0.960	0.946
		2.5	0.0001	−0.0001	0.0151	0.0208	0.0152	0.0209	0.949	0.950
		HSW	−0.0006	−0.0036	0.0375	0.0708	0.0365	0.0723	0.938	0.947

Table 2.

Summary statistics for the estimators β̂ and β̂_HSW under the additive mean sampling model with α_i (t) = 0.48Z_1i + 0.96Z_2i.

μ0(t)	n	b	Bias(β1)	Bias(β2)	SSE(β1)	SSE(β2)	ESE(β1)	ESE(β2)	CP(β1)	CP(β2)
0.2 + 0.5t	100	1.5	0.0012	−0.0009	0.0446	0.0526	0.0431	0.0509	0.938	0.933
		2.0	0.0005	−0.0016	0.0443	0.0544	0.0428	0.0517	0.940	0.929
		2.5	0.0009	−0.0027	0.0433	0.0520	0.0427	0.0512	0.940	0.947
		HSW	0.048	−0.1956	0.0615	0.0984	0.0592	0.0955	0.861	0.490
	200	1.5	0.0006	−0.0008	0.0308	0.0379	0.0307	0.0366	0.938	0.938
		2.0	0.0007	−0.0014	0.0304	0.0366	0.0305	0.0366	0.951	0.946
		2.5	0.0002	0.0018	0.0304	0.0382	0.0305	0.0366	0.948	0.932
		HSW	0.0459	−0.1962	0.0414	0.0676	0.0418	0.0683	0.828	0.177
	300	1.5	0.0004	−0.0017	0.0248	0.0295	0.0251	0.0300	0.954	0.957
		2.0	0.0003	0.0013	0.0243	0.0308	0.0250	0.0300	0.946	0.936
		2.5	−0.0001	0.0006	0.0251	0.0307	0.0251	0.0298	0.952	0.929
		HSW	0.0459	−0.1959	0.0331	0.0549	0.0341	0.0559	0.750	0.055
0.05t2	100	1.5	0.0008	−0.0004	0.0316	0.0374	0.0305	0.0361	0.937	0.934
		2.0	0.0003	−0.0010	0.0313	0.0387	0.0302	0.0367	0.940	0.932
		2.5	0.0005	−0.0016	0.0306	0.0370	0.0301	0.0364	0.942	0.951
		HSW	0.0485	−0.1939	0.0692	0.1233	0.0668	0.1201	0.884	0.640
	200	1.5	0.0005	−0.0005	0.0217	0.0268	0.0217	0.0259	0.939	0.938
		2.0	0.0005	−0.0009	0.0214	0.0259	0.0215	0.0259	0.952	0.949
		2.5	0.0002	0.0014	0.0215	0.0271	0.0216	0.0259	0.946	0.934
		HSW	0.0463	−0.1951	0.0466	0.0856	0.0471	0.0860	0.854	0.392
	300	1.5	0.0003	−0.0011	0.0176	0.0208	0.0177	0.0212	0.954	0.959
		2.0	0.0003	0.0011	0.0172	0.0218	0.0177	0.0212	0.947	0.937
		2.5	−0.0001	0.0005	0.0177	0.0216	0.0177	0.0210	0.952	0.931
		HSW	0.0465	−0.1933	0.0380	0.0706	0.0384	0.0706	0.773	0.223

The biases for the proposed estimators are generally small and the coverage probabilities are close to 95% indicating appropriateness of the proposed estimation procedures for β. Under the proportional mean rate model, our estimator outperforms that of Hu et al. (2003) in terms of bias and standard error; see Table 1. When μ₀(t) = 0.2 + 0.5t, the ratios of the standard errors of the proposed estimator to those of the HSW estimator are around 0.72 for β₁ and 0.53 for β₂. When μ₀(t) = 0.05t², the ratios of the standard errors of the proposed estimator to those of the HSW estimator are around 0.42 for β₁ and 0.30 for β₂. Our estimators have similar performances under the additive mean rate model while the estimators of Hu et al. (2003) fall apart, see Table 2. These numerical results are consistent with the large sample results derived in Sect. 2.

The biases for the baseline function estimator μ̂₀(t), and the lengths and coverage probabilities of the 95% confidence intervals for μ₀(t) for n = 100 under the proportional mean rate sampling model α_i (t) = 0.4 exp(0.3Z_1i + 0.6Z_2i) and the additive mean rate sampling model α_i (t) = 0.48Z_1i + 0.96Z_2i at a number of the grid points are given Table 3. The perturbation method described in Sect. 2.2 is used to obtain the lengths and the coverage probabilities. The first numbers in parenthesis are biases, the second and third numbers are coverage probabilities and lengths of 95% confidence intervals for μ₀(t). Each entry in Table 3 is evaluated using 500 repetitions and 500 perturbation samples. We find in a simulation not presented here that using the perturbation method produces better results than using the bootstrap resampling at the subject level. Perhaps this is due to the variability in the number of observations across subjects. Table 3 shows that the biases are generally small, the coverage probabilities are close to 95% nominal level. The lengths of the 95% confidence intervals increase with t due to the increased variations in the estimator μ̂₀(t).

Table 3.

Summary statistics for the estimator μ̂₀(t) under the proportional mean sampling model (Cox) α_i (t) = 0.4 exp(0.3Z_1i + 0.6Z_2i) and the additive mean sampling model (Aalen) α_i (t) = 0.48Z_1i + 0.96Z_2i for n = 100. The first number in parenthesis is the bias, the second and third numbers the are coverage probability and length of a 95% confidence interval for μ₀(t)

αi(t)	b	t = 7	t = 10	t = 13	t = 16	t = 19
μi (t) = (0.2 + 0.5t) exp(Z1i − 0.5Z2i)
Cox	1.5	(−0.0009, 92.4, 0.683)	(0.0020, 94.4, 0.856)	(0.0016, 94.0, 1.037)	(−0.0013, 94.2, 1.228)	(0.0016, 93.4, 1.425)
	2.0	(−0.0036, 92.6, 0.668)	(−0.0012, 94.4, 0.843)	(−0.0026, 93.2, 1.026)	(−0.0054, 94.4, 1.217)	(−0.0037, 93.8, 1.416)
	2.5	(−0.0135, 93.2, 0.657)	(−0.0008, 95.0, 0.836)	(−0.0099, 94.8, 1.021)	(−0.0048, 95.8, 1.220)	(−0.0159, 94.8, 1.414)
Aalen	1.5	(−0.0097, 95.0, 0.748)	(−0.0070, 94.4, 0.979)	(−0.0058, 94.6, 1.217)	(−0.0051, 92.2, 1.465)	(−0.0069, 93.6, 1.713)
	2.0	(−0.0120, 94.2, 0.736)	(−0.0103, 94.0, 0.970)	(−0.0079, 94.8, 1.209)	(−0.0095, 92.2, 1.459)	(−0.0104, 93.8, 1.711)
	2.5	(−0.0092, 92.8, 0.734)	(−0.0113, 92.4, 0.962)	(−0.0191, 93.2, 1.199)	(−0.0211, 92.0, 1.446)	(−0.0212, 93.2, 1.700)
μi (t) = 0.05t2 exp(Z1i − 0.5Z2i)
Cox	1.5	(0.0191, 92.2, 0.526)	(0.0201, 92.4, 0.706)	(0.0158, 93.2, 0.992)	(0.0085, 95.2, 1.387)	(0.0191, 93.8, 1.881)
	2.0	(0.0327, 91.8, 0.510)	(0.0307, 92.8, 0.699)	(0.0232, 92.6, 0.993)	(0.0138, 95.2, 1.395)	(0.0138, 92.8, 1.895)
	2.5	(0.0427, 93.0, 0.502)	(0.0512, 94.6, 0.704)	(0.0322, 94.4, 1.010)	(0.0261, 95.6, 1.423)	(0.0003, 93.2, 1.927)
Aalen	1.5	(0.0115, 93.6, 0.526)	(0.0096, 94.0, 0.763)	(0.0059, 94.2, 1.142)	(0.0008, 92.8, 1.657)	(0.0006, 94.8, 2.290)
	2.0	(0.0252, 94.0, 0.513)	(0.0194, 94.2, 0.761)	(0.0162, 94.2, 1.145)	(0.0039, 94.4, 1.666)	(0.0020, 94.4, 2.305)
	2.5	(0.0503, 93.0, 0.513)	(0.0410, 92.4, 0.763)	(0.0173, 93.6, 1.144)	(0.0056, 93.2, 1.661)	(−0.0131, 93.4, 2.301)

4 An Application

In this section, we apply the proposed method to analyze a data set from the bladder caner study, conducted by the Veterans Administration Cooperative Urological Research Group of USA over four years of period. All the 121 subjects entered trial had superficial bladder tumors (Byar 1980). These tumors were removed transurethrally and then subjects were randomly allocated to one of the three treatments, placebo, thiotepa and pyridoxine. There were 47 subjects in the placebo group, 38 in the thiotepa group and the rest in the pyridoxine. Identical tablets were given daily by mouth to the subjects in the placebo and pyridoxine groups, while for the subjects in the thiotepa group, thiotepa was instilled into the bladder for 2 hours once a week for 4 weeks and once a month thereafter. Many subjects had multiple new tumors during the study. The new tumors were removed at the clinical visits of the subjects. One of the study objectives was to evaluate the effectiveness of thiotepa by comparing the placebo and the thiotepa groups in tumor accumulation. Thus the number of subjects of interest is n = 85 and the follow-up time is τ = 48 months.

Let Y_i(t) be the number of the accumulated new tumors for subject i by time t, t ∈ [0, τ]. The process Y_i (·) is only observable at the subject's finite number of clinical visits. The times of clinical visits varied among individuals and it has been noticed that the thiotepa group tended to visit the clinics more frequently than the placebo group. Let $N_i^{\ast }$ (·) be the counting process of the visiting times for subject i over the time period [0, τ]. Let Z_i be a 3-D vector with the first component indicating whether the subject was in thiotepa group, and the second and third component being the number of tumors observed at the beginning of the study and the size of the largest initial tumors, respectively. The average number of tumors observed at the beginning of the study is 1.936 for the placebo group and 2.316 for the thiotepa group. The average size of the largest initial tumors is 2.085 for the placebo group and 1.921 for the thiotepa group. The exact censoring time C_i for subject i is not available and is taken to be the subject's last visit time. The bladder cancer data set is published in Hu et al. (2003). The plots of the new tumor accumulations against entry time are given in Fig. 1(a) for subjects in the placebo group and in Fig. 1(b) for subjects in the thiotepa group.

Fig. 1.

The plots of the new tumor accumulations against entry time; (a) for the placebo group and (b) for the thiotepa group

The bladder cancer data has been analyzed by Hu et al. (2003) under the models (1) and (14) where they obtained an estimate of β̂^M = (−1.482, 0.285, −0.083) for β and the standard error of (0.329, 0.062, 0.105). To apply the proposed robust method, we first choose a bandwidth using the leave-one-subject-out cross validation method described in Sect. 2. The plot of the mean squares of fitted residuals PE(b) defined in (10) against different bandwidths are given in Fig. 2. The minimal value of PE(b) is found at the bandwidth b = 9.0.

Fig. 2.

The plot of the mean squares of fitted residuals against different bandwidths

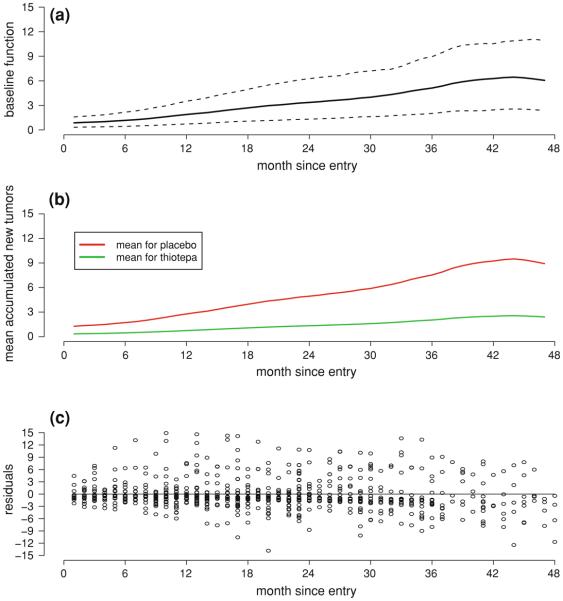
We trim a small part of boundary points and take [t₁, t₂] = [1, 47]. With b = 9.0, our method yields β̂ = (−1.310, 0.248, −0.067) and the standard error of (0.315, 0.062, 0.098). For this example, Hu et al. (2003) have shown that the proportional mean rate model (14) fits the clinical visit times well. The two methods produce similar estimates. We have tried different bandwidths ranging from 3.0 to 14.0, the results on the estimation are very similar, differ only on the thousand-th decimal place. We also estimate the baseline function in the model (1) and its 95% pointwise confidence intervals. The plot is given in Fig. 3(a). The plots of mean accumulated new tumors for the placebo group and the thiotepa group at the average number of tumors at the beginning of the study and the average size of largest initial tumors are given in Fig. 3(b), showing that the thiotepa group has much less accumulated new tumors on average. The residual plots of {∈̂_i (t), i = 1, …, 85} versus entry time are given in Fig. 3(c).

Fig. 3.

(a) The plot of the baseline function estimate μ̂₀(t) and 95% pointwise confidence intervals with the bandwidth b = 9.0 months; (b) The plots of mean accumulated new tumors for the placebo group and the thiotepa group at the average number of tumors (2.106) at the beginning of the study and the average largest initial tumors size (2.012); (c) The residual plots of {∈̂_i (t), i = 1, …, 85}

The plot shows that the distribution of ∈̂_i (t) for a given t is skewed to the right and is not symmetric around zero. The mean value of ∈̂_i (t) seems to be around zero. This is reasonable since the response process Y_i (t) here is the accumulated new tumor counts by time t, whose distribution exhibits similar pattern as that of a Poisson distribution.

5 Discussion

The procedure proposed here has several advantages over the existing methods. It is more flexible. The covariate processes need not to be observed at all the time, which is practically a useful feature when some of the covariates may change with time. It is robust to the assumptions of the sampling models since we do not need to specify a particular form for the conditional mean rate α(t, Z_i (t)). This is an important improvement and generalization of the existing methods. One does not need to know whether α(t, Z_i (t)) is of the proportional model (Lin et al. 2000), or the additive model (Scheike 2002), or the transformation model (Lin and Ying 2001). The proposed estimator is more efficient than the estimator of Cheng and Wei (2000) which assumes α(t, Z_i (t)) not depending on Z_i (t). It is also more efficient than the estimator of Hu et al. (2003) which assumes that α(t, Z_i (t)) is proportional.

In the situations where the response process is the number of recurrent events that have occurred by time t, it is expected that the baseline function μ₀(t) increases with time when covariate Z_i is time-independent. Although the proposed estimator μ̂₀(t) is still a valid estimator for μ₀(t), it is desirable to have a estimator that increases with time. Sun and Kalbfleisch (1995) proposed an estimator for the mean function of point processes of recurrent events based on isotonic regression, which is shown to be a pseudo-maximum likelihood estimator by Wellner and Zhang (2000). It would be interesting to construct a isotonic regression type estimator for μ₀(t).

6 Appendix

Large sample theory, such as presented by Van der Vaart (1998), together with an elegant technical lemma by Lin and Ying (2001), will be applied to prove the asymptotic results. We assume the following conditions throughout the paper:

Condition A. The censoring time C_i is noninformative in the sense that $E\{d{N}_i^{\ast }\left(t\right)\mid Z_i\left(t\right),C_i\ge t\}=E\{d{N}_i^{\ast }\left(t\right)\mid Z_i\left(t\right)\}$ and E{Y_i (t)|Z_i (t), C_i ≥ t} = E{Y_i (t)|Z_i (t)}; the censoring time C_i is allowed to depend on the covariate process Z_i (·); the process $N_i^{\ast }$ (·) is independent of Y_i (·) given Z_i (·); the processes Y_i (t), Z_i (t) and α_i (t), 0 ≤ t ≤ τ, are bounded and their total variations are bounded by a constant; E|N_i (t₂ − N_i (t₁)|² ≤ L (t₂ − t₁) for 0 ≤ t₁ ≤ t₂ ≤ τ, where L > 0 is a constant; the weight function W (t) can be written as a difference of two monotone functions, each of which converges in probability to a deterministic function, such that $W\left(t\right)\stackrel{P}{\to }w\left(t\right)$; the kernel function K (·) is symmetric with compact support on [−1, 1] and bounded variation; n → ∞, nb² → ∞ and nb⁴ → 0; s_y(t) and s^(k)(t), k = 0, 1, 2, are twice differentiable; (s⁽⁰⁾(t))⁻¹ are bounded over 0 ≤ t ≤ τ; and that A and Σ are positive definite.

Condition B. E|N_i (t + b) − N_i (t − b)|^2+ν = O(b), for some ν > 0; the limit ${\sigma }^2\left(t\right)={\lim }_{n\to \infty }bE{[{\int }_0^{\tau }{K}_b(t-s){∊}_i\left(s\right)d{N}_i\left(s\right)]}^2$ exists and is finite, where ∈_i (s) = Y_i (s) − μ₀(s) exp{β^TZ_i (s)}.

We remark that under the conditional independence of $N_i^{\ast }$ (·) and Y_i (·) given Z_i (·) and assuming noninformative censoring C_i, Condition B holds if $N_i^{\ast }$ (·) is Poisson process and if E{(∈_i (s))²ξ_i (s)α_i (s)} is continuous in s ∈ (t − b, t + b).

6.1 Technical lemmas

In the rest of the section, we drop β in the terms S̃^(k)(t; β) and Z̃(t; β) for ease of notation. Let $S^{\left(k\right)}\left(t\right)=n^{-1}{\Sigma }_{i=1}^n{\xi }_i\left(t\right){\alpha }_i\left(t\right)Z_i^{\left(k\right)}\left(t\right)\exp \left\{{\beta }^T{Z}_i\left(t\right)\right\},k=0,1,2$. Let Z̄(t) = S⁽¹⁾(t)/S⁽⁰⁾(t). Let $M_i\left(t\right)=N_i\left(t\right)-{\int }_0^t{\xi }_i\left(s\right){\alpha }_i\left(s\right)\mathit{ds}$. The process M_i (t) is a mean-zero process.

Lemma 1

Under Condition A, ${\tilde{S}}^{\left(k\right)}\left(t\right)\stackrel{P}{\to }{s}^{\left(k\right)}\left(t\right)\mathit{for}k=0,1,2,\tilde{Z}\left(t\right)\stackrel{P}{\to }\stackrel{-}{z}\left(t\right)$ and ${\tilde{\mu }}_0(t;\beta )\stackrel{P}{\to }{\mu }_0\left(t\right)$, uniformly in t ∈ [t₁, t₂] and β ∈ 𝒩 (β₀), a neighborhood of β₀.

Proof Similar to the proof given in the Appendix of Gilbert and Sun (2005), under Condition A, by Theorem 19.4 and 19.5 of Van der Vaart (1998), we have $n^{-1}{\Sigma }_{i=1}^n{\int }_0^t{Z}_i^{\otimes 2}\left(u\right)\exp \left\{{\beta }^T{Z}_i\left(u\right)\right\}d{N}_i\left(u\right)\stackrel{P}{\to }{s}^{\left(k\right)}\left(t\right)$ for k = 0, 1, 2, and $n^{-1}{\Sigma }_{n=1}^n{\int }_0^t{Y}_i\left(u\right)d{N}_i\left(u\right)\stackrel{P}{\to }{s}_y\left(t\right)$, uniformly in t × β ∈ [t₁, t₂] × 𝒩 (β₀). Since K (·) has bounded variation, nb² → ∞ and nb⁴ → 0, it follows ${\tilde{S}}^{\left(k\right)}\left(t\right)\stackrel{P}{\to }{s}^{\left(k\right)}\left(t\right)$ and ${\tilde{S}}_y\left(t\right)\stackrel{P}{\to }{s}_y\left(t\right)$, uniformly in t × β ∈ [t₁, t₂] × 𝒩 (β₀), by integrations by parts. Thus, $\tilde{Z}\left(t\right)\stackrel{P}{\to }\stackrel{-}{z}\left(t\right)$ and ${\tilde{\mu }}_0(t;\beta )\stackrel{P}{\to }{\mu }_0\left(t\right)$, uniformly in t × β ∈ [t₁, t₂] × 𝒩 (β₀). □

Lemma 2

Let η(t) = (s⁽⁰⁾(t))⁻¹[(s_y(t))″ − μ₀(t)(s⁽⁰⁾(t))″].

(a) Under Condition A and B, ${\left(nb\right)}^{1∕2}({\tilde{\mu }}_0(t;\beta )-{\mu }_0\left(t\right)-\frac{1}{2}{b}^2{\mu }_2\eta \left(t\right))\stackrel{𝒟}{\to }N(0,{\left(s^{\left(0\right)}\left(t\right)\right)}^{-2}{\sigma }^2\left(t\right))$;

(b) Under Condition A, ${\int }_{t1}^t{n}^{1∕2}({\tilde{\mu }}_0(s;\beta )-{\mu }_0\left(s\right))$ ds converges weakly to a mean-zero Gaussian process on [t₁, t₂], and $n^{-1∕2}{\Sigma }_{i=1}^n{\int }_{t1}^{t2}W\left(s\right)(Z_i\left(s\right)-\tilde{Z}\left(s\right))$ exp{β^TZ_i(s)} dM_i(s) converges weakly to mean-zero normal distribution.

Proof We begin with the proof of the assertion (a). Since μ₀(t) = s_y(t)/s⁽⁰⁾ (t), we have

$$\begin{array}{cc}\hfill n^{1∕2}({\tilde{\mu }}_0(t;\beta )-{\mu }_0\left(t\right))& =n^{1∕2}\left(\frac{{\tilde{S}}_y\left(t\right)}{{\tilde{S}}^{\left(0\right)}\left(t\right)}-\frac{s_y\left(t\right)}{s^{\left(0\right)}\left(t\right)}\right)\hfill \\ \hfill & ={\left({\tilde{S}}^{\left(0\right)}\left(t\right)\right)}^{-1}{n}^{1∕2}({\tilde{S}}_y\left(t\right)-s_y\left(t\right))-s_y\left(t\right){\left({\tilde{S}}^{\left(0\right)}\left(t\right)s^{\left(0\right)}\left(t\right)\right)}^{-1}{n}^{1∕2}({\tilde{S}}^{\left(0\right)}\left(t\right)-s^{\left(0\right)}\left(t\right)).\hfill \end{array}$$ (17)

Note that ${\int }_0^{\tau }{K}_b(t-s)s_y\left(s\right)\mathit{ds}=s_y\left(t\right)+\frac{1}{2}{b}^2{\mu }_2{\left(s_y\left(t\right)\right)}^{″}+o\left(b^2\right)$ and ${\int }_0^{\tau }{K}_b(t-s)s^{\left(0\right)}\left(s\right)\mathit{ds}=s^{\left(0\right)}\left(t\right)+\frac{1}{2}{b}^2{\mu }_2{\left(s^{\left(0\right)}\left(t\right)\right)}^{″}+o\left(b^2\right)$, uniformly in t ∈ [t₁, t₂]. Let $S_y\left(t\right)=n^{-1}{\Sigma }_{i=1}^n{\xi }_i\left(t\right){\alpha }_i\left(t\right)Y_i\left(t\right)$. We have

$$n^{1∕2}({\tilde{S}}_y\left(t\right)-s_y\left(t\right))={\int }_0^{\tau }{K}_b(t-s)n^{1∕2}(S_y\left(s\right)-s_y\left(s\right))\mathit{ds}+{\int }_0^{\tau }{K}_b(t-s)n^{-1∕2}\underset{i=1}{\overset{n}{\Sigma }}{Y}_i\left(s\right){\mathit{dM}}_i\left(s\right)+\frac{1}{2}{n}^{1∕2}{b}^2{\mu }_2{\left(s_y\left(t\right)\right)}^{\prime \prime }+o\left(n^{1∕2}{b}^2\right),$$ (18)

and

$$n^{1∕2}({\tilde{S}}^{\left(0\right)}\left(t\right)-s^{\left(0\right)}\left(t\right))={\int }_0^{\tau }{K}_b(t-s)n^{1∕2}(S^{\left(0\right)}\left(s\right)-s^{\left(0\right)}\left(s\right))\mathit{ds}+{\int }_0^{\tau }{K}_b(t-s)n^{-1∕2}\underset{i=1}{\overset{n}{\Sigma }}\exp \left\{{\beta }^T{Z}_i\left(s\right)\right\}{\mathit{dM}}_i\left(s\right)+\frac{1}{2}{n}^{1∕2}{b}^2{\mu }_2{\left(s^{\left(0\right)}\left(t\right)\right)}^{\prime \prime }+o\left(n^{1∕2}{b}^2\right).$$ (19)

By (17), (18), (19), the convergence of (S̃⁽⁰⁾ (t))⁻¹ in probability, the weak convergence of the processes n^½(S_y(t) − s_y(t)) and n^½(S⁽⁰⁾(t)) − s⁽⁰⁾(t)) on the interval [t₁, t₂], and Lemma 1 of Sun and Wu (2005), we have

$${\left(nb\right)}^{1∕2}({\tilde{\mu }}_0(t;\beta )-{\mu }_0\left(t\right))=n^{-1∕2}{b}^{1∕2}{\left(s^{\left(0\right)}\left(t\right)\right)}^{-1}{\int }_0^{\tau }{K}_b(t-s)\underset{i=1}{\overset{n}{\Sigma }}{\xi }_i\left(s\right){\alpha }_i\left(s\right){∊}_i\left(s\right)\mathit{ds}+n^{-1∕2}{b}^{1∕2}{\left(s^{\left(0\right)}\left(t\right)\right)}^{-1}{\int }_0^{\tau }{K}_b(t-s)\underset{i=1}{\overset{n}{\Sigma }}{Y}_i\left(s\right){\mathit{dM}}_i\left(s\right)-n^{-1∕2}{b}^{1∕2}{s}_y\left(t\right){\left(s^{\left(0\right)}\left(t\right)\right)}^{-2}{\int }_0^{\tau }{K}_b(t-s)\underset{i=1}{\overset{n}{\Sigma }}\exp \left\{{\beta }^T{Z}_i\left(s\right)\right\}{\mathit{dM}}_i\left(s\right)+\frac{1}{2}{n}^{1∕2}{b}^{5∕2}{\mu }_2{\left(s^{\left(0\right)}\left(t\right)\right)}^{-1}[{\left(s_y\left(t\right)\right)}^{\prime \prime }-{\mu }_0\left(t\right){\left(s^{\left(0\right)}\left(t\right)\right)}^{″}]+o_p(b+n^{1∕2}{b}^{5∕2}).$$ (20)

Let ${\varphi }_i\left(t\right)=b^{1∕2}{\int }_0^{\tau }{K}_b(t-s){∊}_i\left(s\right){\mathit{dN}}_i\left(s\right)$. It follows that

$${\left(\mathit{nb}\right)}^{1∕2}({\tilde{\mu }}_0(t;\beta )-{\mu }_0\left(t\right)-\frac{1}{2}{b}^2{\mu }_2\eta \left(t\right))={\left(s^{\left(0\right)}\left(t\right)\right)}^{-1}{n}^{-1∕2}\underset{i=1}{\overset{n}{\Sigma }}{\varphi }_i\left(t\right)+o_p\left(1\right).$$ (21)

Note that E(ϕ_i (t)) = 0. Let $B_n^2=n{\sigma }_n^2\left(t\right)$, where ${\sigma }_n^2\left(t\right)=\mathrm{Var}\left({\varphi }_i\left(t\right)\right)=\mathit{bE}{\left[{\int }_0^{\tau }{K}_b(t-s){∊}_i\left(s\right){\mathit{dN}}_i\left(s\right)\right]}^2\to {\sigma }^2\left(t\right)$. Under Condition A and B, for ν > 0,

$$\begin{array}{cc}\hfill \underset{i=1}{\overset{n}{\Sigma }}E{\left|{\varphi }_i\left(t\right)\right|}^{2+v}& ={\mathit{nb}}^{-(1+v∕2)}E{\left|\underset{0}{\overset{\tau }{\int }}K((t-s)∕b){∊}_i\left(s\right){\mathit{dN}}_i\left(s\right)\right|}^{2+v}\hfill \\ \hfill & =O\left(1\right){\mathit{nb}}^{-(1+v∕2)}b=O\left(1\right){\mathit{nb}}^{-v∕2}.\hfill \end{array}$$

Hence, ${\Sigma }_{i=1}^{n}E{\left|{\varphi }_i\left(t\right)\right|}^{2+v}∕B_n^{2+v}=O\left(1\right){\left(\mathit{nb}\right)}^{-v∕2}=o\left(1\right)$. It follows that $n^{-1∕2}{\Sigma }_{i=1}^n{\varphi }_i\left(t\right)\stackrel{𝒟}{\to }N(0,{\sigma }^2\left(t\right))$ by applying the Lindeberg-Feller central limit theorem for double arrays of random variables (cf. Serfling (1980), Corollary, page 32). Consequently,

$${\left(\mathit{nb}\right)}^{1∕2}({\tilde{\mu }}_0(t;\beta )-{\mu }_0\left(t\right)-\frac{1}{2}{b}^2{\mu }_2\eta \left(t\right))\stackrel{𝒟}{\to }N(0,{\left(s^{\left(0\right)}\left(t\right)\right)}^{-2}{\sigma }^2\left(t\right)).$$ (22)

Next, we prove the assertion (b). By Lemma 1, (S̃⁽⁰⁾(t))⁻¹ converges in probability uniformly on the interval [t₁, t₂]. By Lemma 1 of Sun and Wu (2005), the processes n^½(S_y(t) − s_y(t)), $n^{-1∕2}{\Sigma }_{i=1}^n{\int }_{t_1}^t{Y}_i\left(s\right){\mathit{dM}}_i\left(s\right)$ n^½(S⁽⁰⁾(t) − s⁽⁰⁾(t)) and $n^{-1∕2}{\Sigma }_{i=1}^n{\int }_{t_1}^t\exp \left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}$ dM_i(s) jointly converge in distribution to some mean-zero Gaussian processes on [t₁, t₂]. By (17), (18) and (19), applying Lemma 2 of Sun and Wu (2005) and Lemma A.1 of Lin and Ying (2001), we have

$$\begin{array}{cc}\hfill & n^{1∕2}(\underset{t_1}{\overset{t}{\int }}({\tilde{\mu }}_0(s,\beta )-{\mu }_0\left(s\right))\mathit{ds}\hfill \\ \hfill =& n^{-1∕2}\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t}{\int }}{\left(s^{\left(0\right)}\left(s\right)\right)}^{-1}\underset{0}{\overset{\tau }{\int }}{K}_b(s-u)(Y_i\left(u\right){\mathit{dN}}_i\left(u\right)-s_y\left(u\right)\mathit{du})\mathit{ds}-n^{-1∕2}\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t}{\int }}{s}_y\left(s\right){\left(s^{\left(0\right)}\left(s\right)\right)}^{-2}\underset{0}{\overset{\tau }{\int }}{K}_b(s-u)(\exp \left\{{\beta }^{\mathrm{T}}{Z}_i\left(u\right)\right\}{\mathit{dN}}_i\left(u\right)-s_0\left(u\right)\mathit{du})\mathit{ds}+o_p\left(1\right)\hfill \\ \hfill =& n^{-1∕2}\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t}{\int }}{\left(s^{\left(0\right)}\left(s\right)\right)}^{-1}(Y_i\left(s\right){\mathit{dN}}_i\left(s\right)-s_y\left(s\right)\mathit{ds})-n^{-1∕2}\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t}{\int }}{s}_y\left(s\right){\left(s^{\left(0\right)}\left(s\right)\right)}^{-2}(\exp \left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{\mathit{dN}}_i\left(s\right)-s_0\left(s\right)\mathit{ds})+o_p\left(1\right)\hfill \\ \hfill =& n^{-1∕2}\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t}{\int }}{\left(s^{\left(0\right)}\left(s\right)\right)}^{-1}(Y_i\left(s\right)-{\mu }_0\left(s\right)\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}){\mathit{dN}}_i\left(s\right)+o_p\left(1\right),\hfill \end{array}$$ (23)

which converges weakly to mean-zero Gaussian process by Lemma 1 of Sun and Wu (2005).

The weak convergence of $n^{-1∕2}{\Sigma }_{i=1}^n{\int }_{t_1}^{t_2}W\left(s\right)(Z_i\left(s\right)-\tilde{Z}\left(s\right))\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}$ dM_i(s), follows from the uniform convergence in probability of W(t) and Z̃(t), the weak convergence of $n^{-1∕2}{\Sigma }_{i=1}^n{\int }_{t_1}^{t_2}{Z}_i\left(s\right)\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{\mathit{dM}}_i\left(s\right)$ and $n^{-1∕2}{\Sigma }_{i=1}^n{\int }_{t_1}^{t_2}\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{\mathit{dM}}_i\left(s\right)$, and applications of Lemma A.1 of Lin and Ying (2001).

6.2 Proof of Theorem 1

Proof of the asymptotic consistency of β̂

We use a similar argument to the Appendix A.1 of Lin et al. (2001). By Lemma 1 and Theorem 19.4 of Van der Vaart (1998), we have $n^{-1}U\left({\beta }_0\right)\stackrel{P}{\to }0\text{as}n\to \infty$ Further, by (7), $-n^{-1}\partial U\left(\beta \right)∕\partial \beta \stackrel{P}{\to }A$ uniformly in a neighborhood of β₀. Note that A is continuous in β and is nonsingular in a neighborhood of β₀. Then, for any δ > 0, there exists an event J with P(J) < δ and a small neighborhood of β₀ inside of which the eigenvalues of −n⁻¹∂U(β)/∂β are bounded away from zero for all large n on J^c, the complement of J. Thus, by the inverse function theorem (Goffman 1965, p.92), we can find a small neighborhood of β₀, inside of which there exists a unique solution β̂ to U(β) = 0 for every sufficiently large n on J^c. Since δ can be arbitrarily small, it follows that unique β̂ exists in a neighborhood of β₀ with probability 1. The nonnegative definiteness of −n⁻¹∂U(β)/∂β in the entire domain of β implies the global uniqueness of β̂.

Considering an ∈ neighborhood of β₀ in the preceding arguments for any ∈ > 0, we see that β̂ converges to β₀ on J^c. This follows by P({β̂ ∈ 𝒩_∈(β₀)} ∩ J^c) → 1 as n → ∞. Thus, P(β̂ ∈ 𝒩_∈ (β₀)) → 1 since δ can be arbitrarily small, where 𝒩_∈ (β₀) is an ∈ neighborhood of β₀. This proves the consistency of β̂.

Proof of the asymptotic normality of β̂

Taking partial derivative of U(β) with respect to β and applying Lemma 1, we have

$$\begin{array}{cc}\hfill \frac{\partial U\left(\beta \right)}{\partial {\beta }^{\mathrm{T}}}=& -\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}W\left(s\right)\left[{\tilde{\mu }}_0(s;\beta )\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{Z}_i\left(s\right)+\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{\tilde{\mu }}_1(s;\beta )\right]{(Z_i\left(s\right)-\tilde{Z}\left(s\right))}^{\mathrm{T}}{\mathit{dN}}_i\left(s\right)+o_p\left(n\right)\hfill \\ \hfill =& -\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}W\left(s\right){(Z_i\left(s\right)-\tilde{Z}\left(s\right))}^{\otimes 2}{\tilde{\mu }}_0(s;\beta )\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{\mathit{dN}}_i\left(s\right)+o_p\left(n\right)\hfill \\ \hfill =& -\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}w\left(s\right){(Z_i\left(s\right)-\stackrel{-}{z}\left(s\right))}^{\otimes 2}{\mu }_0\left(s\right)\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{\mathit{dN}}_i\left(s\right)+o_p\left(n\right),\hfill \end{array}$$

It follows that

$$n^{-1}\frac{\partial U\left(\beta \right)}{\partial {\beta }^{\mathrm{T}}}\stackrel{P}{\to }-A.$$ (24)

Now, consider

$$\begin{array}{cc}\hfill n^{-1∕2}U\left(\beta \right)& =n^{-1∕2}\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}W\left(s\right)(Z_i\left(s\right)-\tilde{Z}\left(s\right))(Y_i\left(s\right)-{\mu }_0\left(s\right)\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}){\mathit{dN}}_i\left(s\right)\hfill \\ \hfill & -n^{-1∕2}\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}W\left(s\right)(Z_i\left(s\right)-\tilde{Z}\left(s\right))({\tilde{\mu }}_0(s;\beta )-{\mu }_0\left(s\right))\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{\mathit{dN}}_i\left(s\right).\hfill \end{array}$$ (25)

By Lemma 1, 2 and repeatedly applying Lemma A.1 of Lin and Ying (2001), the second term of (25) equals to

$$\begin{array}{cc}\hfill & n^{1∕2}\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}W\left(s\right)(\stackrel{-}{Z}\left(s\right)-\tilde{Z}\left(s\right))({\tilde{\mu }}_0(s;\beta )-{\mu }_0\left(s\right)){\stackrel{-}{S}}^{\left(0\right)}\left(s\right)\mathit{ds}\hfill \\ \hfill & +n^{-1∕2}\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}W\left(s\right)(Z_i\left(s\right)-\tilde{Z}\left(s\right))({\tilde{\mu }}_0(s;\beta )-{\mu }_0\left(s\right))\times \mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{\mathit{dM}}_i\left(s\right)=o_p\left(1\right).\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill n^{-1∕2}U\left(\beta \right)& =n^{-1∕2}\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}w\left(s\right)(Z_i\left(s\right)-\stackrel{-}{z}\left(s\right))(Y_i\left(s\right)-{\mu }_0\left(s\right)\mathit{exp}\left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}){\mathit{dN}}_i\left(s\right)+o_p\left(1\right)\hfill \end{array}$$ (26)

which converges in distribution to a normal random variable with variance equal to Σ.

By (8), (24) and (26), we have

$$n^{1∕2}(\widehat{\beta }-\beta )\stackrel{𝒟}{\to }N(0,A^{-1}\Sigma A^{-1}).$$ (27)

Proof of the uniform consistency of μ̂₀(t)

The uniform consistency ${\widehat{\mu }}_0\left(t\right)\stackrel{P}{\to }{\mu }_0\left(t\right)$ for t ∈ [t₁, t₂] follows by $\widehat{\beta }\stackrel{P}{\to }\beta$ and the uniform convergence of ${\tilde{\mu }}_0(t;\beta )\stackrel{P}{\to }{\mu }_0\left(t\right)$ on t ∈ [t₁, t₂] and β ∈ 𝒩(β₀)) in Lemma 1.

The consistency of  and Σ̂ follows from the consistency of β̂, the uniform consistency of μ̂₀(t) and by Lemma 1.

6.3 Proof of Theorem 2

Under Condition A, for t ∈ [t₁, t₂], ${\left(\mathit{nb}\right)}^{1∕2}({\tilde{S}}^{\left(0\right)}(t,\widehat{\beta })-{\tilde{S}}^{\left(0\right)}(t,\beta ))\stackrel{P}{\to }0$. We have ${\left(\mathit{nb}\right)}^{1∕2}({\tilde{\mu }}_0(t,\widehat{\beta })-{\tilde{\mu }}_0(t,\beta ))\stackrel{P}{\to }0$. Thus, by Lemma 2, for t ∈ [t₁, t₂],

$${\left(\mathit{nb}\right)}^{1∕2}({\tilde{\mu }}_0(t;\widehat{\beta })-{\mu }_0\left(t\right)-\frac{1}{2}{b}^2{\mu }_2\eta \left(t\right))\stackrel{𝒟}{\to }N(0,{\left(s^{\left(0\right)}\left(t\right)\right)}^{-2}{\sigma }^2\left(t\right)).$$

Since ${\tilde{S}}^{\left(0\right)}\left(t\right)\stackrel{P}{\to }{s}^{\left(0\right)}\left(t\right)$ by Lemma 1, to prove the consistency of the variance estimator, it suffices to show

$${\widehat{\sigma }}^2\left(t\right)={\mathit{bn}}^{-1}\underset{i=1}{\overset{n}{\Sigma }}{\left[\underset{0}{\overset{\tau }{\int }}{K}_b(t-s){\widehat{∊}}_i\left(s\right){\mathit{dN}}_i\left(s\right)\right]}^2\stackrel{P}{\to }{\sigma }^2\left(t\right).$$ (28)

The left hand side of (28) equals to

$${\mathit{bn}}^{-1}\underset{i=1}{\overset{n}{\Sigma }}{\left[\underset{0}{\overset{\tau }{\int }}{K}_b(t-s){∊}_i\left(s\right){\mathit{dN}}_i\left(s\right)+\underset{0}{\overset{\tau }{\int }}{K}_b(t-s)({\widehat{∊}}_i\left(s\right)-{∊}_i\left(s\right)){\mathit{dN}}_i\left(s\right)\right]}^2.$$

The (28) is implied by

$${\mathit{bn}}^{-1}\underset{i=1}{\overset{n}{\Sigma }}{\left[\underset{0}{\overset{\tau }{\int }}{K}_b(t-s){∊}_i\left(s\right){\mathit{dN}}_i\left(s\right)\right]}^2\stackrel{P}{\to }{\sigma }^2\left(t\right)$$ (29)

$${\mathit{bn}}^{-1}\underset{i=1}{\overset{n}{\Sigma }}{\left[\underset{0}{\overset{\tau }{\int }}{K}_b(t-s)({\widehat{∊}}_i\left(s\right)-{∊}_i\left(s\right)){\mathit{dN}}_i\left(s\right)\right]}^2\stackrel{P}{\to }0$$ (30)

Let ${\varphi }_i\left(t\right)=b^{1∕2}{\int }_0^{\tau }{K}_b(t-s){∊}_i\left(s\right){\mathit{dN}}_i\left(s\right)$. The limit (29) holds by using Chebychev's inequality because Eϕ_i(t)² → σ²(t) and $\mathrm{Var}\left\{n^{-1}{\Sigma }_{i=1}^n({\varphi }_i^2\left(t\right)-E{\varphi }_i^2\left(t\right))\right\}=n^{-1}\{E{\varphi }_i^4\left(t\right)-{\left(E{\varphi }_i^2\left(t\right)\right)}^2\}\le n^{-1}E{\varphi }_i^4\left(t\right)=O\left({\left({\mathit{nb}}^2\right)}^{-1}\right)$, under Condition A and B. To show (30), note that

$$\begin{array}{cc}\hfill & {\mathit{bn}}^{-1}\underset{i=1}{\overset{n}{\Sigma }}{\left[\underset{0}{\overset{\tau }{\int }}{K}_b(t-s)({\widehat{∊}}_i\left(s\right)-{∊}_i\left(s\right)){\mathit{dN}}_i\left(s\right)\right]}^2\hfill \\ \hfill & \le \underset{1\le i\le n}{\max }\underset{s\in [t-b,t+b]}{\sup }{|{\widehat{∊}}_i\left(s\right)-{∊}_i\left(s\right)|}^2{\mathit{bn}}^{-1}\underset{i=1}{\overset{n}{\Sigma }}{\left[\underset{0}{\overset{\tau }{\int }}{K}_b(t-s){\mathit{dN}}_i\left(s\right)\right]}^2.\hfill \end{array}$$

Under Condition A and B, $\mathit{bE}{\left[{\int }_0^{\tau }{K}_b(t-s){\mathit{dN}}_i\left(s\right)\right]}^2=O\left(1\right)$, we have ${\mathit{bn}}^{-1}{\Sigma }_{i=1}^n{\left[{\int }_0^{\tau }{K}_b(t-s){\mathit{dN}}_i\left(s\right)\right]}^2=O_p\left(1\right)$ by the Markov inequality. By the consistency of β̂ and the uniform consistency of μ̂₀(t) in Theorem 1, we have ${\max }_{1\le i\le n}{\sup }_{s\in [t-b,t+b]}|{\widehat{∊}}_i\left(s\right)-{∊}_i\left(s\right)|\stackrel{P}{\to }0$. Hence the limit (30) holds.

6.4 Proof of Theorem 3

By Hu et al. (2003),

$$U_1^M(\beta ,\alpha )=\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}{\xi }_i\left(s\right)w\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{z}}_M(s;\beta ,\alpha )){\mathit{dM}}_i^M\left(s\right)+o_p\left(n^{1∕2}\right)$$ (31)

$$U_2^M\left(\alpha \right)=\underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}{\xi }_i\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{z}}_M(s;0,\alpha )){\mathit{dM}}_i^O\left(s\right)+o_p\left(n^{1∕2}\right),$$

where z̄_M(t; β, α) is the limit of Z̄_M(tβ, α) in probability.

Taking the partial derivatives of $U_1^M(\beta ,\alpha )$ and $U_2^M\left(\alpha \right)$ with respective to β and α, Hu et al. (2003) showed that

$$\begin{array}{cc}\hfill \frac{\partial U_1^M(\beta ,\alpha )}{\partial {\beta }^{\mathrm{T}}}=-& \underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}W\left(s\right)\left(\frac{S_M^{\left(2\right)}(s;\beta ,\alpha )}{S_M^{\left(0\right)}(s;\beta ,\alpha )}-{\stackrel{-}{Z}}_M{(s;\beta ,\alpha )}^{\otimes 2}\right)\times Y_i\left(s\right){\mathit{dN}}_i\left(s\right)\stackrel{P}{\to }-A\hfill \\ \hfill \frac{\partial U_2^M\left(\alpha \right)}{\partial {\alpha }^{\mathrm{T}}}=-& \underset{i=1}{\overset{n}{\Sigma }}\underset{t_1}{\overset{t_2}{\int }}\left(\frac{S_M^{\left(2\right)}(s;0,\alpha )}{S_M^{\left(0\right)}(s;0,\alpha )}-{\stackrel{-}{Z}}_M{(s;0,\alpha )}^{\otimes 2}\right){\mathit{dN}}_i\left(s\right)\stackrel{P}{\to }-A_{\alpha },\hfill \end{array}$$ (32)

and that $\frac{\partial U_1^M(\beta ,\alpha )}{\partial {\alpha }^{\mathrm{T}}}=\frac{\partial U_1^M(\beta ,\alpha )}{\partial {\beta }^{\mathrm{T}}}\stackrel{P}{\to }-A$ and $\frac{\partial U_2^M\left(\alpha \right)}{\partial {\beta }^{\mathrm{T}}}=0$.

By (15), (31) and (32), the asymptotic covariance matrix of (β̂^M, α̂^M is

$$\begin{array}{cc}\hfill {\Sigma }_M& ={\left[\begin{array}{cc}A\hfill & A\hfill \\ 0\hfill & A_{\alpha }\hfill \end{array}\right]}^{-1}\left[\begin{array}{cc}{B}_{11}\hfill & B_{12}\hfill \\ B_{21}\hfill & B_{22}\hfill \end{array}\right]{\left[\begin{array}{cc}A\hfill & 0\hfill \\ A\hfill & A_{\alpha }\hfill \end{array}\right]}^{-1}\hfill \\ \hfill & =\left[\begin{array}{cc}{A}^{-1}\hfill & -A_{\alpha }^{-1}\hfill \\ 0\hfill & A_{\alpha }^{-1}\hfill \end{array}\right]\left[\begin{array}{cc}{B}_{11}\hfill & B_{12}\hfill \\ B_{21}\hfill & B_{22}\hfill \end{array}\right]\left[\begin{array}{cc}{A}^{-1}\hfill & 0\hfill \\ -A_{\alpha }^{-1}\hfill & A_{\alpha }^{-1}\hfill \end{array}\right]\hfill \\ \hfill & =\left[\begin{array}{cc}{\Sigma }_M^{11}\hfill & {\Sigma }_M^{12}\hfill \\ {\Sigma }_M^{21}\hfill & {\Sigma }_M^{22}\hfill \end{array}\right],\hfill \end{array}$$ (33)

where

$${\Sigma }_M^{11}=A^{-1}{B}_{11}{A}^{-1}-A^{-1}{B}_{12}{A}_{\alpha }^{-1}-{\left(A^{-1}{B}_{12}{A}_{\alpha }^{-1}\right)}^{\mathrm{T}}+A_{\alpha }^{-1}{B}_{22}{A}_{\alpha }^{-1}$$ (34)

is the asymptotic variance matrix of β̂^M, ${\Sigma }_M^{21}=A_{\alpha }^{-1}{B}_{21}{A}^{-1}-A_{\alpha }^{-1}{B}_{22}{A}_{\alpha }^{-1}$ is the asymptotic covariance matrix of α̂^M and β̂^M, ${\Sigma }_M^{12}={\left({\Sigma }_M^{21}\right)}^{\mathrm{T}}$ and ${\Sigma }_M^{22}=A_{\alpha }^{-1}{B}_{22}{A}_{\alpha }^{-1}$ is the asymptotic variance matrix of α̂^M.

Note that

$$M_i^M\left(t\right)=\underset{t_1}{\overset{t}{\int }}{\xi }_i\left(s\right)[Y_i\left(s\right)-{\mu }_0\left(s\right)\exp \left({\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right)]{\mathit{dN}}_i\left(s\right)+\underset{t_1}{\overset{t}{\int }}{\xi }_i\left(s\right){\mu }_0\left(s\right)\exp \left({\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right){\mathit{dM}}_i^O\left(s\right).$$ (35)

We have the following decomposition for the top term in the square bracket in (15):

$$\underset{t_1}{\overset{t_2}{\int }}{\xi }_i\left(s\right)w\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{Z}}_M(s;\beta ,\alpha )){\mathit{dM}}_i^M\left(s\right)=\underset{t_1}{\overset{t_2}{\int }}{\xi }_i\left(s\right)w\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{Z}}_M(s;\beta ,\alpha ))[Y_i\left(s\right)-{\mu }_0\left(s\right)\exp \left({\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right)]{\mathit{dN}}_i\left(s\right)+\underset{t_1}{\overset{t_2}{\int }}{\xi }_i\left(s\right)w\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{Z}}_M(s;\beta ,\alpha )){\mu }_0\left(s\right)\exp \left({\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right){\mathit{dM}}_i^O\left(s\right).$$ (36)

Since the two terms in (36) are uncorrelated, we have

$$\begin{array}{cc}\hfill B_{11}& =\Sigma +E{\left\{\underset{t_1}{\overset{t_2}{\int }}{\xi }_i\left(s\right)w\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{z}}_M(s;\beta ,\alpha )){\mu }_0\left(s\right)\exp \left\{{\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right\}{\mathit{dM}}_i^O\left(s\right)\right\}}^{\otimes 2}\hfill \\ \hfill & =\Sigma +\Delta .\hfill \end{array}$$ (37)

Hence we can write

$$\begin{array}{cc}\hfill {\Sigma }_M^{11}& =A^{-1}\Sigma A^{-1}+A^{-1}\Delta A^{-1}-A^{-1}{B}_{12}{A}_{\alpha }^{-1}-{\left(A^{-1}{B}_{12}{A}_{\alpha }^{-1}\right)}^{\mathrm{T}}+A_{\alpha }^{-1}{B}_{22}{A}_{\alpha }^{-1}\hfill \\ \hfill & =A^{-1}\Sigma A^{-1}+D.\hfill \end{array}$$ (38)

Note that the first term is asymptotic variance matrix of our estimator β̂. It remain to show that the matrix D is semi-positive definite.

Because the first term in (36) is uncorrelated to the second term in (36) and is also uncorrelated to the bottom term in in the square bracket in (15), replacing the top term in (15) by the second term of its decomposition in (36), we have

$$\begin{array}{cc}\hfill & E\left\{{\left[\begin{array}{c}{\int }_{t_1}^{t_2}{\xi }_i\left(s\right)w\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{z}}_M(s;\beta ,\alpha )){\mu }_0\left(s\right)\exp \left({\beta }^{\mathrm{T}}{Z}_i\left(s\right)\right){\mathit{dM}}_i^O\left(s\right)\hfill \\ {\int }_{t_1}^{t_2}{\xi }_i\left(s\right)(Z_i\left(s\right)-{\stackrel{-}{z}}_M(s;0,\alpha )){\mathit{dM}}_i^O\left(s\right)\hfill \end{array}\right]}^{\otimes 2}\right\}\hfill \\ \hfill & =\left[\begin{array}{cc}\Delta \hfill & B_{12}\hfill \\ B_{21}\hfill & B_{22}\hfill \end{array}\right].\hfill \end{array}$$ (39)

Now replacing the middle matrix of (33) by the above matrix, we have that the matrix

$${\left[\begin{array}{cc}A\hfill & A\hfill \\ 0\hfill & A_{\alpha }\hfill \end{array}\right]}^{-1}\left[\begin{array}{cc}\Delta \hfill & B_{12}\hfill \\ B_{21}\hfill & B_{22}\hfill \end{array}\right]{\left[\begin{array}{cc}A\hfill & 0\hfill \\ A\hfill & A_{\alpha }\hfill \end{array}\right]}^{-1}$$

is semi-positive definite. Hence, its first block matrix $D=A^{-1}\Delta A^{-1}-A^{-1}{B}_{12}{A}_{\alpha }^{-1}-{\left(A^{-1}{B}_{12}{A}_{\alpha }^{-1}\right)}^{\mathrm{T}}+A_{\alpha }^{-1}{B}_{22}{A}_{\alpha }^{-1}$ is also semi-positive definite.