Shape Priors for Segmentation of the Cervix Region Within Uterine Cervix Images

Abstract

The work focuses on a unique medical repository of digital uterine cervix images (“cervigrams”) collected by the National Cancer Institute (NCI), National Institute of Health, in longitudinal multiyear studies. NCI together with the National Library of Medicine is developing a unique web-based database of the digitized cervix images to study the evolution of lesions related to cervical cancer. Tools are needed for the automated analysis of the cervigram content to support the cancer research. In recent works, a multistage automated system for segmenting and labeling regions of medical and anatomical interest within the cervigrams was developed. The current paper concentrates on incorporating prior-shape information in the cervix region segmentation task. In accordance with the fact that human experts mark the cervix region as circular or elliptical, two shape models (and corresponding methods) are suggested. The shape models are embedded within an active contour framework that relies on image features. Experiments indicate that incorporation of the prior shape information augments previous results.

Introduction

The purpose of this work is to embed prior shape information into the task of cervix region segmentation within uterine cervix images (“cervigrams”). The images in this work were collected by the National Cancer Institute (NCI) in order to study the evolution of cervical cancer¹⁴. A multistage system is being developed in order to automatically analyze the content of the cervigrams within this database^5,6. Such a system should provide an accurate delineation of the different tissues within the cervix and enable the extraction of various features from the segmented tissues. Features such as: size, color, shape, and relative position within the cervix can then be used for cervical cancer research and for indexing of cervigrams within the archive.

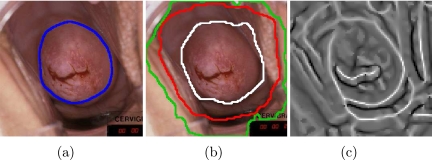
The current work is focused on the automated segmentation of the cervix region. The cervix region is an important landmark that defines the region of medical and anatomical interest within the cervigram. Its detection enables further analysis to focus within the cervix region itself. Typical cervigrams with the cervix region marked are presented in Figure 1. The cervix region is located in the central part of the image, with surrounding vaginal walls and parts of clinical equipment intruding in the image. A dark surrounding frame can be seen containing lines and text that are overlaid on the image at time of the photographic development. The cervix region within these images was marked by a medical expert with specialized experience in gynecological oncology (blue line). It exhibits a large variability in size, color, shape, and position across the different cervigrams, which constitute a challenging automated segmentation task.

Fig 1.

Cervix region examples marked by a medical expert with specialized experience in gynecological oncology.

In previous works, the detection of the cervix region was performed based on features derived from the input image. An initial rough region of interest (ROI) was initially extracted using features of color and position⁵. A more accurate delineation of the boundary was then enabled using an active contour framework based on curvature and color features¹⁵. The current work extends the active contour framework by integrating prior shape information into it. The anatomical region features of the cervix (as marked by the medical experts) can be characterized by their elliptical or circular shapes; hence, the ellipse and the circle are chosen for the shape models. Embedding shape information into the cervix region segmentation process is shown in the current work to improve the segmentation quality.

A vast amount of work had been done to embed prior-shape information into a segmentation task. A popular approach is to use prior models based on allowable deformation of a template shape. In this approach, the shape model is generated from an aligned training set, and different tools are used for its representation. Cootes et al.³ presented the Active Shape Model, which uses the statistics of a large set of points, sampled at meaningful locations along the object boundary. The generated high-dimensional model requires a vast amount of computational power; thus, dimensionality reduction is desired. Leventon et al. used principle component analysis in order to extract the mean shape and the eigenshapes and represented them with a Gaussian distribution⁸. In a different work of that group, the model is represented by a levelset function, using intensity and curvature as a function of the signed distance from the object boundary⁷. Following model generation, there are works that use an active contour framework in a levelset implementation for the segmentation task^2,13. In these works, registration and segmentation are performed simultaneously to align a new image to the prior model. Methods, such as those mentioned above, are inappropriate for the cervix region segmentation task due to the large variability of cervix shapes that exist across the database. Such variability leads to a model with a large range of allowable deformations that has a minor effect on the resulted segmentation. In addition to that, cross-image registration of cervices from different patients is a question that was not addressed thus far; thus, a model learned from a registered training set is currently not available.

The objective of the current work is to propose a method that can cope with the large variability of shapes and can incorporate elliptical or circular shapes information in a straightforward and a low-complexity scheme. Two methods are presented:

• A method that utilizes the distribution of shape features and a circular shape prior.

• A novel method that uses an implicit shape representation via levelsets and an elliptical shape prior.

Method

In an active contour framework, the image is considered as a function I:Ω→R⁺ where Ω∈R² is the image domain. The segmentation problem is mathematically formulated as searching for a contour C:[0,L]→R² in the image, which is optimal with respect to some predefined integral measure, E(C), also called the energy functional. Formally, this problem is stated as: C = argmin_cE(C). In the current work, the energy functional consists of two terms: a data term and a shape prior term:

1

The data term, developed in a former work¹⁵, is activated first and evolves the curve according to the input image region and curvature-based edge properties. The shape term is added next and better aligns the contour to a predefined model of the cervix’s shape. The α parameter is a time-dependant parameter that controls the activation sequence of the two terms.

Embedding a Circular Prior using the Distribution of Shape Features

The first method for embedding shape information in the active contour framework is based on the distribution of shape features⁹. The shape energy term in this method penalizes the difference between the feature distributions of a given curve and of a prior reference curve. It can be shown that such distributions can capture the intuitive similarity of shapes in a flexible way, while being invariant to shape transformations¹¹. This method is applied here with a circular shape prior and is hereon termed the circular prior.

We start with a brief description of the method. We then present specific modifications used for the cervix region segmentation task. The shape distribution is defined as the cumulative distribution function (CDF) of feature values measured uniformly along the shape boundary. Let Φ be a continuously defined feature along the curve C, and λ be a variable spanning the range of values Λ of the feature. The CDF of Φ, H(λ), is defined as:

2

Here, h(x) is an indicator function, which is 1 when the inequality is satisfied and 0 otherwise. When it is meaningful to exhibit the particular curve C for which H(λ) is computed, we will write H(C, λ).

The shape energy term, E_prior(C), is defined as:

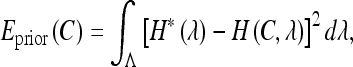3

where H(C,λ) is the feature distribution function of the curve C, and the prior shape information is captured in the target distribution H*(λ).

The shape descriptor used in the current work to describe the circular shape prior is termed the “internode distances” descriptor. This descriptor captures the CDF of the normalized distances between all nodes within the set of nodes S, sampled uniformly along the curve. The curve evolution minimization equation for the internode distances feature is⁹:

4

where Γ is the parameterized curve as a function of the arc length {X(s),Y(s)} with s ε {0,1}, 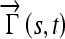is a vector with coordinates {X(t) − X(s), Y(t) − Y(s)} and n(s) is the outwards normal at {X(s),Y(s)}. The normalized internode distance between nodes (s,t), is defined as:

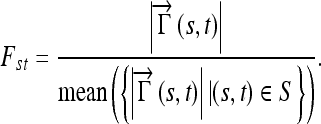5

In the current work, the levelset formulation for the shape term is implemented as follows:

6

where is computed for pixels along the zero levelset (the evolving curve C) and is diffused using a simple Gaussian filter ( in Eq. 6) of size 5 × 5 and σ = 0.5.

This method has various advantages that serve the current application: There is no need for registration and alignment of the prior-shape model and the evolving curve as the method is based on the distance between normalized feature distributions. These distributions are invariant to scale and rotation. On the other hand, the method is based on a nonparametric sampled curve, and its levelset implementation is not straightforward. Considering an image of size M × N pixels, and assuming a sampled curve of size O(x) where x < M × N, the algorithm complexity is O(x²). Originally, this method was designed to deal with much more complex shapes, and as such when applied to the cervigram region segmentation with a prior shape of a simple circle, it might seem too complex.

Combining Data and Shape Terms in the Curve Evolution Process

A two-stage procedure is used to combine the data and shape terms: The first stage uses the data term to evolve the initial approximate ROI to better fit the cervix region and outputs a curve hereon termed the datadriven curve. In the second stage, the detected boundary is further refined by combining the data and shape terms. This results in a smoother, more circular shape for the output boundary.

Experiments on a large set of images have indicated the importance of a two-stage procedure⁶. In a single-stage procedure, using the two terms simultaneously results in a cervix boundary that is larger than desired. The dataterm is attracted to local concavities which are present between the initial ROI and the actual cervix boundary. The shape term tries to generate the optimal bounding circle that includes these concavities, thus, preventing the curve from following the data inwards in favor of a more circular shape.

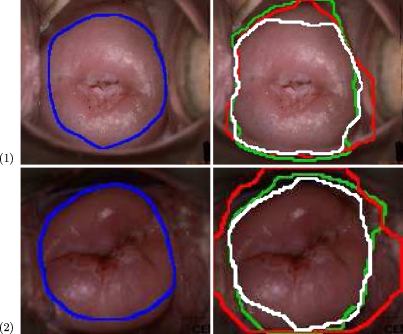
A comparison between the two-stage procedure and the simultaneous activation of the data and shape terms, in a single stage, is presented in Figure 2. Figure 2a shows the medical expert-marked boundary (blue). Figure 2b shows the initial ROI (green), along with the boundary detected using data and shape terms in a single-stage procedure (red) and the boundary detected using the two-stage procedure (white). Local concavities can be found between the initial ROI curve and the desired cervix boundary (bright values in Fig. 2c). The curve generated by the single-stage procedure (red) is attracted to the concavities that are closest to the initial ROI, with the shape term enforcing a circular shape based on these concavities. It was empirically found that parameter tuning of within-term forces and between the two terms does not improve this outcome. The suggested two-stage procedure (white curve) results in a curve that matches more closely with the expert markings.

Fig 2.

Incorporating prior shape information in the curve evolution functional. a Manual marking of the expert (blue); b cervix boundary results: initial ROI (green); boundary detected using data and shape terms in a single-stage procedure (red); boundary detected using the two-stage procedure (white); c curvature feature map (bright regions correspond to local concavities)⁶.

In the second stage of the curve evolution process, the relative weighting of the data and shape terms needs to be considered. Experiments have shown that equally weighing the two terms causes the datadriven contour to overinflate as it tries to match the circular prior model. In order to avoid this undesirable effect, the contour is restricted from evolving outwards beyond a predefined distance limit from the datadriven curve (which is in good proximity to the desired cervix boundary). This is done by using the following equation:

7

where is the levelset formulation of the data term¹⁵, is defined by Eq. 6 and the parameter, w_d(x,y), locally weights the shape term per pixel. The local weights, w_d(x,y), are defined using the signed distance transform, d(x,y), that computes the minimal distance between a pixel (x,y) and the datadriven curve (positive distances interior to the curve and negative distances exterior to the curve). The weighting function, w_d(x,y), is defined as:

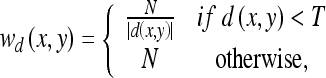8

where T specifies the distance limit and is assigned a small value of T = –3 pixels, and N is a parameter that controls the general influence of the shape term. The proposed weighting function suppresses the influence of the shape term on pixels positioned outside the datadriven curve. Note that the weights are computed once per datadriven curve.

The effect of the local weights on the boundary detection quality is illustrated in Figure 3. The manual markings of the expert are presented in blue. The datadriven curve is marked in green. The result for equally weighing the shape term is marked in red and the result for locally weighing the shape term is marked in white. The results demonstrate that the equally-weighted curve (red) inflates the input datadriven curve (green) whereas the locally weighted curve (white) is smoother and matches more closely to the expert markings.

Fig 3.

Effect of local weights on boundary detection quality. Left image—manual markings of the expert (blue). Right image—boundary detection results: Datadriven curve (green); Equally weighted shape term (red); Locally weighted shape term (white).

Embedding an Elliptical Prior Using an Implicit Shape Representation Via Levelsets

In this section, a second novel method that incorporates the prior shape of an ellipse into the active contour framework is presented. As the parameters of the ellipse are not known in advance, the method simultaneously estimates the prior model and performs the segmentation. This is done by alternating between the two steps of elliptical model estimation and cervix boundary segmentation. The method is hereon termed the elliptical prior.

The elliptical prior is generated using the bounding and bounded ellipses of the evolving curve. It is computed using the following procedure: (1) the bounding ellipse is computed using the Geometric Bounding Toolbox of Matlab. (2) The bounded ellipse is computed using the covariance matrix of the coordinates along the evolving curve. An initial bounded ellipse is generated using a 2D projection of the covariance matrix onto the image plain at a fixed sigma. This initial projection is enlarged until an intersection with the curve is reached. (3) A set of shortest paths (lines) between the pixels of the bounding and bounded ellipses is extracted. (4) The elliptical prior is defined as the centerline crossing the lines within this set.

The shape energy term of the active contour framework within the segmentation step minimizes the integral of the nonoverlapping areas between the elliptical prior and the evolving curve. This is done implicitly, as suggested in¹², using the levelset representations of the two curves:

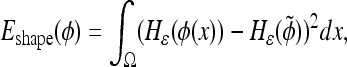9

In this equation, 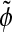is the levelset of the prior model, H is the Heaviside function of a given levelset, and 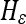is its smoothed approximation¹:

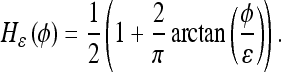10

The Heaviside function is an indicator function for object and background and is used in that case to define the nonoverlapping areas between the evolving curve and the prior.

The shape term within the curve evolution equation is obtained by minimizing E with respect to Φ:

11

where 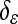is approximated by:

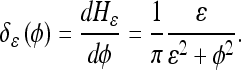12

This method is much simpler to implement (as compared to the method of the circular prior) due to its levelset formulation. For an image of size M × N pixels and curve of size O(x), the algorithm complexity is O(x). This complexity is attained by using a narrow band implementation of the levelset function. The model estimation procedure described above is simpler as compared to other methods that estimate general-shape priors¹². The elliptical-shape prior can be computed directly from the curve coordinates; thus, the complex search for optimal model transformation parameters is unnecessary.

Experiments and Results

The curve evolution framework presented in this work was evaluated using two sets of cervigrams for which the manual markings of a medical expert with specialized experience in gynecological oncology are available (120 cervigrams in Set₁ and 158 in Set₂). The cervigrams were randomly selected out of the NCI database (containing 100,000 images), without any restricting rules.

Experiments were conducted following preprocessing in which initial ROI was extracted and specularities were removed^5,16. Quantitative evaluation was carried out by comparing the generated contours to the expert-based markings. Several overlap metrics were used, including the Dice metric: 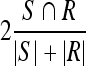, the Sensitivity metric: 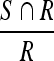and the False Positives (FP) metric: 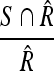, with S being the area of the automatically segmented region, R the expert segmentation and its complement (the area outside the expert-marked boundary). The Hausdorff distance, a maximum surface distance⁴, was used as well. The Hausdorff distance defines the largest difference between two contours (measured in pixels) and is a good indicator for shape resemblance, with a smaller Hausdorff distance corresponding to more similar contours.

Circular Prior Performance Evaluation

In the first experiment, the influence of the circular prior on the segmentation performance is examined and the refinement of the initial datadriven curve is evaluated. Tuning the different parameters within the active contour framework was performed on a small training set of five cervigrams that were randomly selected out of Set₁. Once defined, the parameters were kept constant across all images in the test sets.

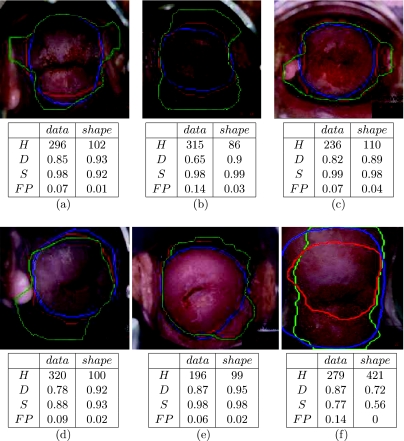
Figure 4 displays examples of cervix boundary detection. The datadriven contour generated in the first step of the curve evolution process is marked in green and the final result, following the refinement with the circular prior, is marked in red. Manual markings of the expert are imposed in blue. Corresponding overlap and Hausdorff measures are listed under each example. It is important to note when examining the Hausdorff results that the images are of approximately 1,500 × 2,500 pixels.

Fig 4.

Cervix boundary detection. Datadriven contour, based on color and curvature features—marked in green; final contour, following refinement with a circular prior—marked in red; expert markings imposed in blue. Hausdorff (H), Dice (D), Sensitivity (S) and False Positives (FP), for the datadriven (data) and the circular shape prior (shape) contours are listed under corresponding cervigrams.

The following observations can be made from the results in Figure 4: The contours are smoother and more convex when the shape term is added, as desired. They exclude more irrelevant regions within the cervix. Good similarity to the expert markings can be seen in most of the cases. These facts are reflected by the quantitative evaluation, where a significant improvement in the FP and the Hausdorff metrics is achieved. The sensitivity results of examples (a)–(e) attain high values, as they include most of the expert’s markings. These sensitivity results are similar for the two contours being compared. Example (f) shows an extreme case, where the sensitivity decreases due to the shape prior constraint. In this example, the datadriven curve is already close or located within the markings of the expert. Advancing the curve further using the circular shape prior generates a final smaller contour, as there are no color or curvature features that can prevent the curve from shrinking.

Table 1 presents the average cervix boundary segmentation results with (circle) and without (no prior) the shape priors, computed for the images of Set₁ and Set₂. The Dice metric reflects a small improvement when using the circular prior. Sensitivity values are similar. These results indicate that the datadriven curve is already in good proximity to the desired contour and that regions within the cervix are handled well. The Hausdorff metric reflects a substantial improvement when applying the circular prior, thus, indicating on a better shape resemblance of the generated contours to the expert’s markings. The FP metric reflects a considerable improvement, corresponding to a strong reduction of nonrelevant tissues (outside the cervix region). This reinforces the addition of the circular prior to the curve evolution process. Results analysis is similar for both sets.

Table 1.

Average Results of Cervix Boundary Segmentation with and without the Shape Priors

	Set1			Set2
	No prior	Circle	Ellipse	No prior	Circle	Ellipse
Dice	0.79 (0.10)	0.81 (0.10)	0.82 (0.09)	0.73 (0.12)	0.75 (0.13)	0.76 (0.12)
Sensitivity	0.95 (0.05)	0.94 (0.08)	0.92 (0.09)	0.96 (0.07)	0.95 (0.09)	0.93 (0.1)
FP	0.28 (0.13)	0.13 (0.12)	0.11 (0.1)	0.33 (0.15)	0.16 (0.14)	0.13 (0.11)
Hausdorff	254 (105)	216 (91)	210 (87)	300 (125)	231 (115)	224 (101)

Mean value and standard deviation (within parentheses) are presented over the two datasets used for evaluation (Set₁, Set₂).

Elliptical Prior Performance Evaluation

The second experiment examines the performance of the elliptical prior. Tuning the different parameters within the active contour framework was performed on a small training set of five cervigrams, as in the former experiment, and the parameters were kept constant across all images in the test sets.

Figure 5 shows example results of the two shape priors. Manual markings are imposed in blue, results of the circular prior are imposed in red and results of the elliptical prior are imposed in white. Examples (a) and (b) show cases where cervix boundary detection by the circular prior is more accurate. In these cases, there is a high visual resemblance of the manual markings to a circle and the circular model is more appropriate. The cervix boundary in examples (c) and (d) has a high resemblance to an ellipse. The elliptical prior achieved better results in these cases. Average results of the elliptical prior, computed over the images of Set₁ and Set₂, are presented in Table 1 (Ellipse). A comparison between the results of the elliptical prior and the circular prior reveals similar Dice and Sensitivity values. The FP and the Hausdorff metrics show a slight improvement when using the elliptical prior as compared to the circular prior. Overall, the results computed over the entire datasets are similar.

Fig 5.

Cervix boundary segmentation with different shape priors. Manual markings imposed in blue; circular prior results imposed in red and elliptical prior results, imposed in white.

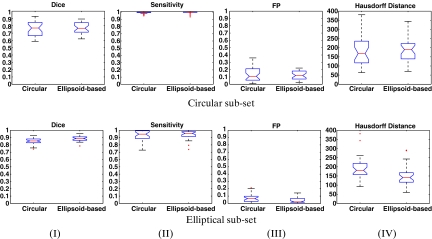
In the final experiment, we pursue a more thorough investigation of the two shape priors. We try to isolate the influence of the shape prior term on the evolving curve and reduce the effect of other factors that might interfere with the curve evolution process. Two special subsets of cervigrams were generated for this experiment, each containing 31 images. The first subset includes cervigrams in which the manual expert markings resemble a circle (the circular subset). The second subset includes cervigrams in which the markings resemble an ellipse (the elliptical subset). The datadriven curve obtained in the selected images, is already in good proximity to the manual markings of the expert; thus, a good initialization for the second step of the curve evolution process is enabled. This good initialization prevents the curve from converging into local optimum, which are related to the image features and are located outside the actual cervix boundaries. The curve evolution process in the selected cases is mainly driven by the shape prior term, as desired.

In order to accurately reflect the distribution of the different results over the dataset, notched box-and-whisker plots¹⁰ (hereon termed box plots) are used. The boxes within the plot have lines at the lower quartile, median, and upper quartile values of the data. The whiskers are lines extending outward from the boxes to show the extent of the rest of the data, with the extent set to 1.5 the interquartile range (IQR) of the samples. Outliers are data with values beyond the ends of the whiskers (marked as +). The notches around the median line define a robust estimate of the uncertainty about the median and are used for box-to-box comparison. Boxes whose notches do not overlap indicate that the medians of the two datasets differ at the 5% significance level. When comparing between different box plots, the following rules are set in order to specify the best results: (1) The box plot should have the highest (lowest) median, significantly different from the other medians (as indicated by the notch). (2) The interquartile range should be relatively narrow as it includes 75% of the data. (3) The values of the lower and upper quartiles should be as high (low) as possible. (4) The amount of outliers should be small.

Figure 6 presents a comparison via box plots between the results of the circular (left box plot) and elliptical (right box plot) shape priors for each of the subsets. The results for the circular subset are presented in the top row, and results for the elliptical subset are presented in the bottom row. Columns (I)–(IV) show results for: Dice, Sensitivity, False-Positive (FP), and Hausdorff distance, in respective order.

Fig 6.

A comparison between circular (left box plot) and elliptical (right box plot) shape priors. Top row: Circular subset results. Bottom row: elliptical subset results. Presented are box plot results for: (I) Dice, (II) Sensitivity, (III) FP and (IV) Hausdorff Distance.

The box plot results of the circular subset are similar for the two shape priors. The IQR obtained by the different quality measures for the elliptical prior is narrower than this obtained for the circular prior, but the median value is not significantly different between the two methods. This observation indicates that the elliptical prior can capture well a circular cervix region, as the ellipse is a generalization of a circle. In the box plots obtained for the elliptical subset the elliptical prior obtained significantly better results, as expected.

Conclusions and Future Work

This work concentrates on embedding shape information for cervix boundary segmentation. Two methods are presented: the first method is based on shape features distribution using a circular prior. The second method is a novel method for embedding an elliptical prior, which uses an implicit shape representation via a levelset function. Experiments are conducted on two test sets of cervigrams, and compared to human-expert markings. The incorporation of the prior shape information in the segmentation framework is shown to improve former datadriven segmentation results.

The results obtained with the two shape priors on the entire test set are similar, as there are other factors that influence the curve evolution process. One of these factors is the initial, datadriven curve and its position relative to the true cervix boundary. This position varies considerably across the cervigram images due to their large content variability. The position of the initial curve has a strong influence on the active contour process, as the process tends to converge into local optimum.

A more focused experiment that isolates the effect of the shape prior term on the segmentation quality, indicates the superiority of the elliptical prior over the circular prior. The elliptical prior (using the levelset framework) is also shown to have a reduced order of complexity, O(x), as compared to the complexity, O(x²), of the circular prior (and the corresponding curve-based functional).

The matching of the shape model to the problem at hand is an additional issue that should be considered. Although the manual ground truth markings have a clear tenancy to resemble a circular or elliptical shape, this is not the case for all images. In part of the images, the segmentation quality, when using the presented shape model, will suffer from lack of resemblance to the ground truth. There are also cases where one prior overestimates the cervix region while the other prior underestimates it. Future work will include the combination of the two methods in order to produce better results. In addition, different ways for per-image parameter tuning will be investigated as a single set of parameters for the active contour framework might be inadequate for the current large and diverse database.