Spine Localization in X-ray Images Using Interest Point Detection

Abstract

This study was conducted to evaluate a new method used to calculate vertebra orientation in medical x-ray images. The goal of this work is to develop an x-ray image segmentation approach used to identify the location and the orientation of the cervical vertebrae in medical images. We propose a method for localization of vertebrae by extracting the anterior—left—faces of vertebra contours. This approach is based on automatic corner points of interest detection. For this task, we use the Harris corner detector. The final goal is to determine vertebral motion induced by their movement between two or several positions. The proposed system proceeds in several phases as follows: (a) image acquisition, (b) corner detection, (c) extracting of the corners belonging to vertebra left sides, (d) global estimation of the spine curvature, and (e) anterior face vertebra detection.

Introduction

Digital image segmentation plays a crucial role in many medical imaging applications by automating or facilitating the delineation of anatomical structures and other regions of interest. In medical applications, image segmentation is used to classify different anatomy features, such as vertebrae, bones, and soft issues. As the biomedical images of the same class are highly similar, low-level image features of the object of interest, e.g., shape of vertebra body in case of spine images, have to be identified for efficient medical diagnostic. This information can be also used for medical image indexing. Most of the existing work on medical image segmentation has been focused on magnetic resonance (MR) or computed tomography (CT) images. Much less work has been done on the segmentation of x-ray images. That is why, in this work we propose a framework of vertebral mobility analysis applied to x-ray images, and based on an original approach using only faces and corner vertebra detection. We want to provide a computer vision tool for medical x-ray images that enable measurement of vertebra movements and determine the mobility of each vertebra compared to others in the same image.

Classical image segmentation algorithms assume that the regions to be segmented contain homogeneous features. With this assumption, the segmentation algorithms attempt to segment the input image into regions based on feature homogeneity criteria. Unfortunately, such homogeneity criteria are not satisfied for large and complex x-ray images. So, the segmentation of the spine x-ray images is generally addressed using a hierarchical procedure. The distinctive region of the image, including the general spine region, is first being segmented at a gross level of detail. This is followed by a fine-grained segmentation of the spine region into individual vertebra. Much research in this direction has been carried out by The Lister Hill National Center for Biomedical Communications, a research and development division of the National Library of Medicine (NLM).¹ Another approach consists of the boundaries detection. A large set of contour detection methods have been proposed in the literature to analyze and to extract vertebra from x-ray images.^2,3 In literature, two main solutions are proposed to the problem of vertebra segmentation in digitized spine x-ray images.

The first class of solutions presents deformable models⁴ such as active contour⁵, active shape⁶, and level set methods^7,8. These methods are contour-based instead of region-based. As such, they have the potential of extracting contours of body parts that do not contain homogeneous features. Deformable templates of global object appearance are widely used for image segmentation.⁹ Active shape model (ASM) and Active appearance model (AAM) were first proposed by Cootes.¹⁰ In these works, the shape is defined as the remaining information after alignment (rotation, translation, scaling) between two objects. An extension of ASM introduces a model of the underlying distribution of intensity around landmark; it becomes AAM. AAM uses the classical model of shape, but adds a model of the profile intensity perpendicular to the object contour.

These techniques can produce correct results even in the case of missing or locally ambiguous boundary evidence. However, entirely global models can be too constrained to adhere to new images adequately. Deformable models sometimes fail in the extraction of boundaries with significant gaps. Moreover, an important weakness of these approaches is that they typically require good initialization of the model contour, near the final solution, and thus need manual intervention¹¹ or automatic object recognition.¹² If the model is poorly initialized, these approaches can be easily affected by noise and extraneous edges in the image, resulting in incorrect segmentation of the regions.

The second class of solutions presents the techniques exploiting Hough Transform.^13,14 These methods use a large set of templates to capture the great variability in the shape of the vertebra. But, although the Hough transform gives fairly good results on synthetic and real images, the computational cost is high. The success of the Hough transform-based techniques depends on three parameters: (1) gradient information, (2) representativeness of the template, and (3) reckoning of the votes in the accumulator structure. It is common to find great variability in the shape of the cervical vertebrae across a large set of images.¹⁵ This is the major drawback of the Hough transform-based techniques.

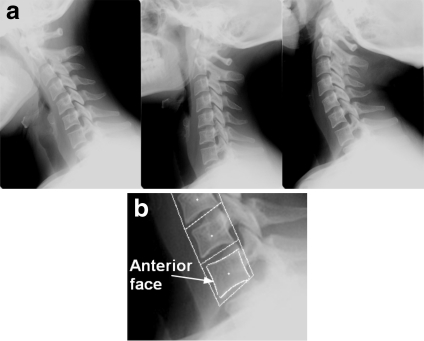
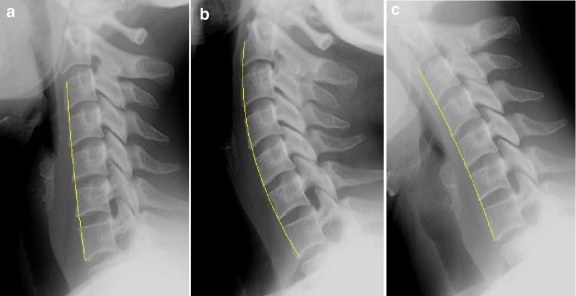
In this paper, we propose an alternative method for spine localization and vertebral mobility analysis in medical x-ray images. This method presents a semiautomatic computer-based technique used to detect vertebra orientations and intervertebral angles. The proposed approach is based on anterior face extraction and spine localization using automatic vertebra corner detection through the Harris corner detector. The extraction of some quantitative measures of particular changes between images acquired at different moments allows determining vertebral mobility. For instance, to measure and compare the corresponding vertebrae between several images, we analyze vertebra anterior faces extracted from some images corresponding to the cervical vertebra of the same person, in flexion, neutral, and extension positions, Figure 1a.

Fig 1.

(a) Flexion, neutral, and extension position of the cervical spine; (b) vertebra anterior face extracted using a contour detection process³.

This paper is organized in the following way: In the “Background” section, we present some theoretical background describing the basis of the Harris corner detector used in this paper. In the “Material and Methods” section, we present the proposed method of anterior face detection and global spine estimation using the corner faces extracted by the Harris detector. In the “Results” section, we describe the numerical segmentation results given by this method and presented by the angular measures of each vertebra and, a global estimation of the spine using polynomial fitting. We present also the analysis of the angular variation between several positions using the proposed method.

Background

Corner Detection

Corners in digital images are the robust features that provide important information of objects; they give important clues for shape representation and analysis. Generally, object information can be represented in terms of its corners. Precise detection of corner points can play a very important role in various applications like object capturing, shape perception, scale space theory, and polygonal approximation.¹⁶ In our work, we propose to use the Harris corner detector, which is a very popular corner detector widely used in the literature. In the following paragraph, we introduce the basis of this detector.

Harris Detector

The Harris corner detector is a popular interest point detector proposed by Harris and Stephen.¹⁷ They described what has become known as the Plessey feature point detector. The most advantage of this operator is its strong invariance to rotation, scale, illumination variation, and image noise.¹⁸ This detector is based on the local autocorrelation function of a signal, where the local autocorrelation function measures the local changes of the signal with patches shifted by a small amount in different directions. We can see the outline of how it works if we consider the following matrix:

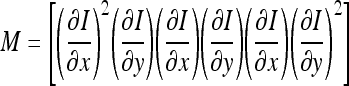1

where 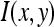is the gray level intensity. If at a certain point the two eigenvalues of the matrix 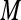are large, then a small motion in any direction will cause an important change of gray level. This indicates that the point is a corner. The corner response function is given by:

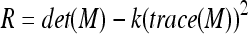where 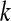is a parameter set to 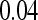(a suggestion of Harris).

Corners are defined as local maxima of the corner function 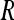. Subpixel precision is achieved through a quadratic approximation of the neighborhood of the local maxima. To avoid corners generated because of image noise, we smooth the images with a Gaussian filter. However, this should not be done on the input images, but on images containing the squared image derivatives, i.e., .

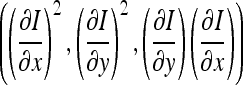Material and Methods

In this paper, we propose the use of the corner points of interest to extract the spine position and to calculate the orientation angles belonging to each vertebra to estimate their mobility. The goal of our work is to extract the angular variation along the cervical spinal column and its global curvature by computing the orientation angles corresponding to each vertebra, and the global orientation of the spine. In this section, we propose to calculate vertebra orientation angles by extracting their anterior faces, Figure 1b. To this aim, we propose the use of corner points of interest. For this task, we first apply the Harris corner detector for extracting the corners of each vertebra and especially those corresponding to their anterior faces.

The process of corner extraction is described in the “Corner Detection” subsection. In practice, often far too much corners are extracted. In this case, we first restrict the number of corners. This process consists of only selecting the corners with a value 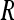above a certain threshold. This threshold can be tuned to yield the desired number of features. We define a high threshold to keep only interesting points. Also, as for some scenes, most of the strongest corners are located in the same area. We refine this scheme further to ensure that in every part of the image a sufficient number of corners are found. For this purpose, we limit the number of corner points detected in each neighborhood of 8 pixels to the once having the higher value of .

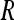We also notice that for our developed application, we had given to the user the possibility to change at each time the values of 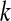and 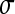in the step of corner extraction. Therefore, the application shows in real time the new corners detected. This real-time feedback allows accurate corner detection according to user preferences.

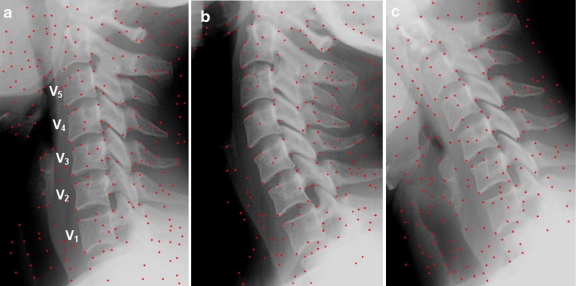
In Figure 2, we present the results given by the process of corner detection applied to three x-ray images corresponding to the cervical spinal column of a patient in neutral, extension, and flexion positions (Fig. 1b).

Fig 2.

Corner detection results using the Harris detector, applied to three images of the same patient, in three different positions, (a): neutral, (b): extension, (c): flexion.

After the corner detection process, we first extract each vertebra anterior face by detecting the points corresponding to vertebra corners. So, the corners kept are those corresponding to the left sides. The anterior face of each vertebra is therefore characterized by two corner points (Fig. 1).

Proposed Method: Vertebral Mobility Analysis Using Corner Detection

It is difficult to achieve fully automatically the segmentation of x-ray spinal images with current computer vision methods because of the specific structure of vertebra and the dense context with ribs and other organs. We propose using vertebra corners as points of interests for vertebral mobility analysis. However, it is very difficult to decide if a corner is corresponding to a specified vertebra without a hard preprocessing step, like edge or region detection. That is why, we propose a semiautomatic method—using only one landmark—based on a supervised process, where the user has to click just one time around the corner’s area belonging to the anterior face of one vertebra. This process of anterior face localization and spine localization is described in the next paragraph.

Anterior Face Detection

We noticed that the curve passing by all the anterior faces takes a parabolic form. That is why we propose to consider a linear model curve: 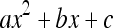passing through the corners belonging to vertebra left borders. For this purpose, we use a least squares polynomial fitting method. To this aim, we build iteratively a second degree linear model by using all detected corners—of the anterior faces—at each step. We continue this treatment until detecting all vertebra anterior faces. We thus preferred to start by extracting the corners from the left border instead of those of right-hand side, because there is less noise on the left side of vertebra borders. This is explained by the fact that in this area, there is less anatomic noise and no presence of other anatomical structures.

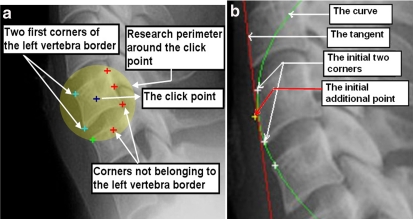
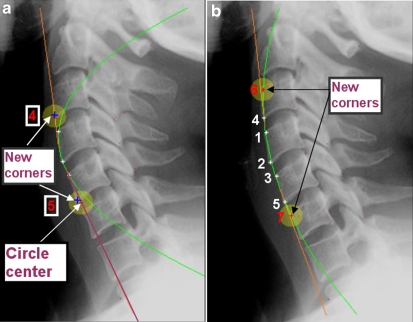
To extract valid corners, the algorithm takes the corners contained in a circle one by one; see Figure 3a. The perimeter of this circle is fixed experimentally according to image size.

Fig 3.

(a) Detection of the two first anterior face corners using the click point position; (b) the first line established and the tangent at mid line used to iterate the research at the two directions: up and bottom.

The first step is to detect two anterior face corners belonging to one vertebra situated on the image center. Using only one click point placed by the user on one of the vertebrae, we extract at least two corners of the nearest vertebra left border. The first research circle zone is centered on this click point; Figure 3a. If we find more than two corners—on the left side of the click point in the research circle area; Figure 3a—we keep the two having the maximum gradient value and which are closer to the circle center. It is obvious that the task would be much easier if the user had given more than one click. The interest here is to implement a robust algorithm that gives acceptable results with only one click by image.

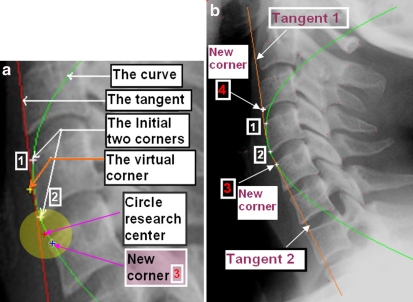
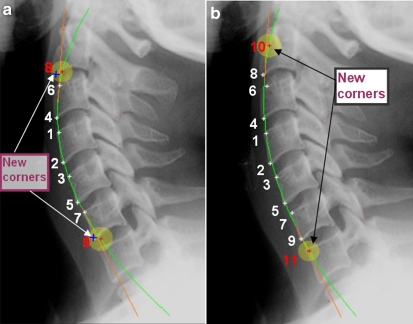
As we have at least two corners belonging to the anterior face of one vertebra, we can detect the remaining corners of each anterior face on the image. We add to these first two corners a virtual point in the medium, to obtain an acceptable parabola between the first two corners, and not a line; Figure 3b. Then we trace the tangent of the curve at this point. We displace the research zone according to the tangent direction on the two directions: top and bottom. Hence, we define one circular research perimeter at each direction. The distance between the two older founded corners and this two-circle research center is experimentally fixed according the average vertebra and intervertebral length area. We initially select all the corners intercepted by each of these two research perimeters. The perimeter is a circle whose ray and center are selected according to image size and vertebra sizes. The ray of this circle is equal to half of the distance between the two previous corners, and the center of this circle is located on the line extracted from this two previous corners. We ensure that one corner is located inside the circle close to the perimeter to get all the research area in the neighborhood of this corner; Figure 4a. We compare the distances between all these selected corners and the center of the circle of research, and will keep as left side corner the point corresponding to the smallest distance. We reiterate the process with the last two corners found on the bottom and above by tracing the tangent passing through these two corners to extract two new ones by using a new circle research perimeter near each corner found. Extracting new anterior face corners will provide better curve, which will be used to find another corner and so on, by creating a new tangent passing through each new founded corner. Figures 5 and 6 illustrate the progress of this fitting operation.

Fig 4.

(a) The research circle used to extract the third corner through the first tangent; (b) the third and the fourth corners extracted using the first tangent. A tangent is traced through each of these new corners for extracting new ones in the two directions: bottom and up.

Fig 5.

Anterior faces corner extraction progress, (a): extraction of new corner 4 and 5, (b): extraction of new corners 6 and 7.

Fig 6.

Anterior faces corner extraction progress, (a): extraction of new corner 8 and 9; (b): extraction of new corners 10 and 11.

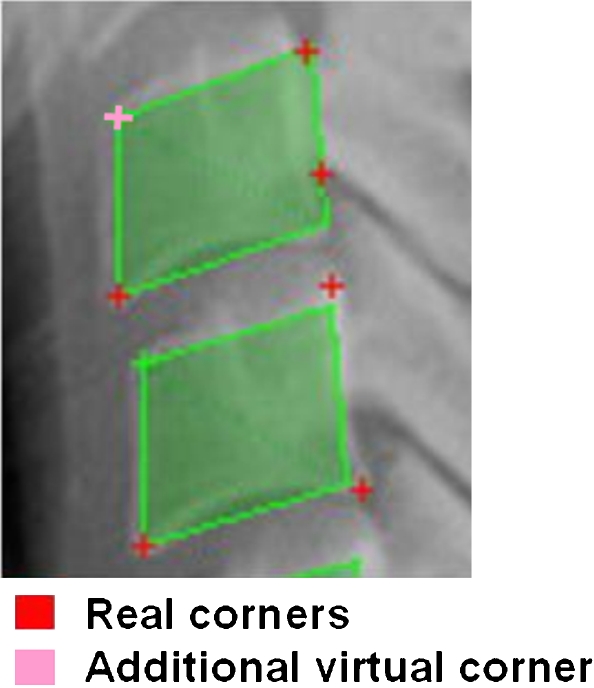
When a corner misses, the proposed algorithm could stop for lack of new corners. To solve this problem, we reiterated it using a virtual corner, which comes to replace the real corner. The position of this virtual corner is easily founded if at least three corners are known. Indeed, the distances between the corners of the vertebrae are generally repeated with identical values throughout vertebra borders. The first distance separating two close vertebrae is called the small distance, and the other representing the average length of these vertebrae is called the long distance. Using this characteristic, we can estimate the corner position, when the corner detector used fails to detect it; Figure 7.

Fig 7.

Adding a virtual anterior face corner—if this one is not detected.

On the other hand, if the process cannot retrieve the three first anterior face corners, we can deduce that there is no significant corner in the research area. In this case, we apply an additional pretreatment step consisting of a contrast enhancement process.¹⁹ This preprocessing step is a solution, which can be proposed to ensure a better recognition of each corner. This pretreatment is motivated by the connection observed between the contrast of a grayscale image and the magnitude of intensity edge-based contrast where the contrast is measured.²⁰ This contrast enhancement step provides very good results and a better corner recognition when applied to x-ray image of the spinal column.¹⁹

Results

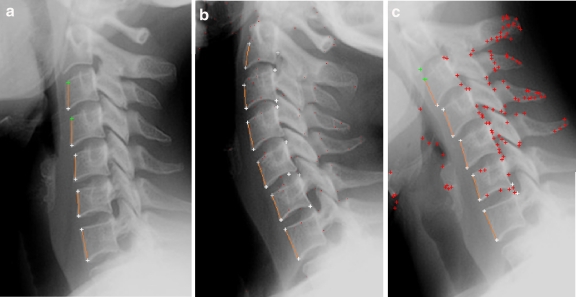
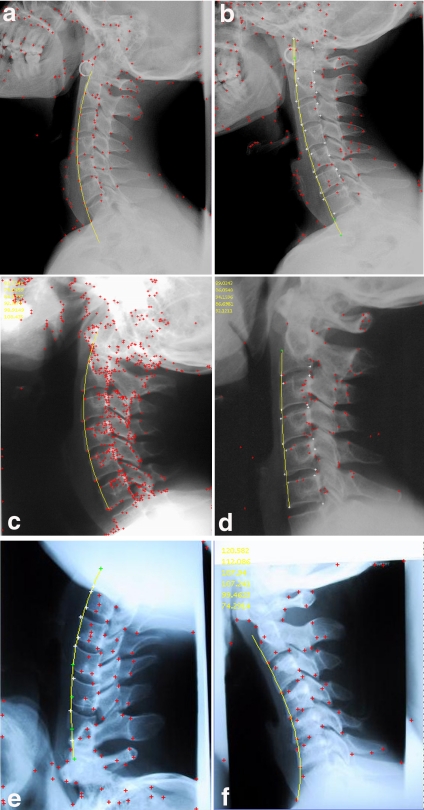
We applied the proposed method of face detection to a set of x-ray images of the cervical spinal column. We have tested the algorithm on a set of 100 images chosen from the archive maintained by the National Library of Medicine (NLM)¹ and also some x-ray images belonging to real patients. Figure 8 shows the results obtained by applying the proposed method to three x-ray images corresponding to the neutral, flexion, and extension positions of the spinal column belonging to the same patient. The main advantage of the proposed approach is to allow an estimation of the overall curvature of the cervical spinal column. These results are presented in Figure 9. This step is very useful for a second processing like fine-grained vertebra segmentation, which can be used to determine the necessary points for x-ray images indexing.

Fig 8.

Anterior face detection results —using the proposed method— applied to three images of the cervical spinal column, corresponding to Figure 2. (a): neutral position, (b): extension position, (c): flexion position.

Fig 9.

The global curvature of the cervical spinal column, (a): neutral position, (b): extension position, (c): flexion position.

Vertebral mobility was estimated by computing the orientation angles belonging to each face of the contour. In Tables 1, 2, and 3 we present some quantitative measurements of the orientation angles belonging to vertebra anterior faces. So, we present the orientation angles for the five vertebrae belonging to the images (a), (b), and (c) of Figure 2. This allows motion head estimation and vertebral mobility computation.

Table 1.

The Angles Corresponding to the Frontal Face in Reference Position, Figure 8a

	Manual Detection	Proposed Method
V1	101.0	101.0
V2	95.1	91.7
V3	90.0	90.0
V4	93.5	89.8
V5	92.6	90.04

Table 2.

the Angles Corresponding to the Frontal Face in Extension Position, Figure 8b

	Manual Detection	Proposed Method
V1	111.4	114.7
V2	111.3	110.0
V3	107.1	108.4
V4	98.8	102.52
V5	92.7	95.5

Table 3.

The Angles Corresponding to the Frontal Face in Flexion Position, Figure 8c

	Manual Detection	Proposed Method
V1	112.1	113.6
V2	106.3	105.3
V3	103.9	104.03
V4	111.0	113.8
V5	116.4	119.8

To check the validity of these measurements, we compared them with the results obtained manually. A group of 15 people have selected with the greatest precision possible the anterior face for each vertebra, then we have determined the average values; Table 3. This procedure that normally must be done by the specialist, will maybe give the best results, but it is time consuming.

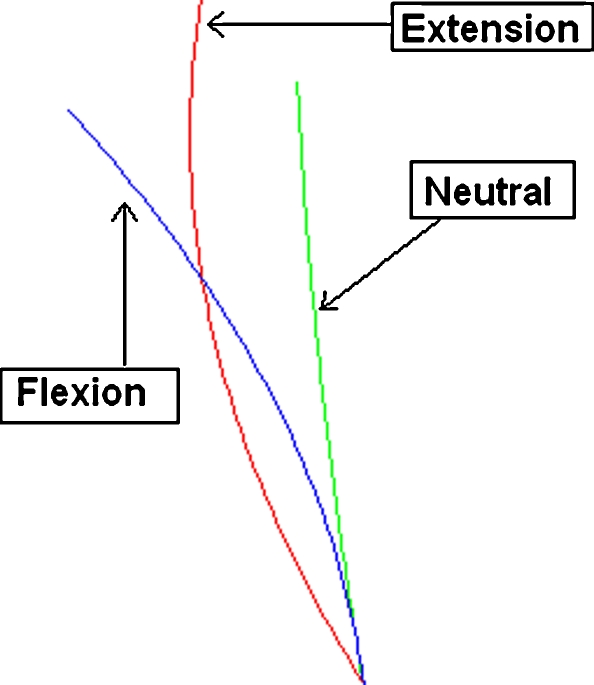
Once all the segments that represent anterior faces are found, we compute the orientation angle for each vertebra and the angular variation for the same vertebra in two different positions. A graphical representation of this variation using the faces detection method is shown in Figure 10. It is necessary also to know the general curve that contains all the vertebrae that we are analyzing; Figures 9 and 10.

Fig 10.

Angular variation between the positions of extension and flexion using the proposed method.

The numerical data presented in Tables 1, 2, and 3 and Figure 10 confirm the poor mobility in the flexion-extension movement for vertebrae 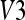, , 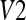and 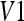. This would mean a problem of mobility from 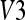to 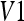. The comparison was done on several images. The angle difference between the proposed method and the manual results is in the range 0–4 degrees; it seems thus acceptable. During our experiments, the proposed technique has proven to give repetitive and reproducible results on a large set of images. We can deduce that the proposed method gives precise results and allows accurately detection of the anterior face of each vertebra.

The main advantage of this method is that it is very fast compared to the whole contour detection methods, and need only one landmark—given by the user on one vertebra—for the whole process. On the other hand, the results of this method did not depend strongly on this clicks point, with an acceptable error margin, and very accurate results. In Figure 11, we present other results of six x-ray images of the cervical spinal column. These results are presented by the curve representing the curvature of the spine. The corners used to trace this curve using the proposed method are also used to extract the anterior face for each vertebra. By examining all results in Figure 11, we can deduce that the proposed method produces very good estimation of the spine curvature for all the positions. Finally, we notice that our method is very fast and can produce the expected results in less than 1 s.

Fig 11.

Other examples of the global spine curvature detection. These images are representing the cervical spinal column of different patients: (a), (c), and (e): extension positions, (b), and (d) neutral positions, (f): extension position.

Conclusion

In this paper, a new segmentation approach applied to x-ray images of the spinal column was developed. Our goal was to determine the variation between the positions of vertebrae in the flexion-extension movements and to measure their mobility. Another specific goal of the proposed application was to create an efficient semiautomated method for identifying the overall angle of curvature of the spine. This approach presents a new method of anterior face extraction using the Harris corner detector, and an iterative fitting process using the extracted corners of every anterior face.

We have applied, with successful results, this method to a set of 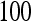real images. We can notice that our approach gives satisfactory results with more stability. Finally, we can deduce that for vertebral mobility analysis, the proposed method allows an accurate and precise analysis.

The applied technique has given acceptable results to measure the mobility of cervical vertebrae, but also this technique can be applied for dorsal and lumbar regions. However, future enhancements should include the superior and inferior face detection and the ability to measure more variables than the angular variations, e.g., the intervertebral distances. Currently, we are developing a content-based image retrieval system by using the results presented in this paper.