Comparative Performance Analysis of State-of-the-Art Classification Algorithms Applied to Lung Tissue Categorization

Abstract

In this paper, we compare five common classifier families in their ability to categorize six lung tissue patterns in high-resolution computed tomography (HRCT) images of patients affected with interstitial lung diseases (ILD) and with healthy tissue. The evaluated classifiers are naive Bayes, k-nearest neighbor, J48 decision trees, multilayer perceptron, and support vector machines (SVM). The dataset used contains 843 regions of interest (ROI) of healthy and five pathologic lung tissue patterns identified by two radiologists at the University Hospitals of Geneva. Correlation of the feature space composed of 39 texture attributes is studied. A grid search for optimal parameters is carried out for each classifier family. Two complementary metrics are used to characterize the performances of classification. These are based on McNemar’s statistical tests and global accuracy. SVM reached best values for each metric and allowed a mean correct prediction rate of 88.3% with high class-specific precision on testing sets of 423 ROIs.

Introduction

Interpreting high-resolution computed tomography (HRCT) images of the chest showing patterns associated with interstitial lung diseases (ILDs) is time-consuming and requires experience. ILDs are a heterogeneous group of around 150 illnesses of which many forms are rare and, thus, many radiologists have little experience with. The diagnosis of ILDs is often established through the collaborations of the clinicians, radiologists, and pathologists. Images play an important role and patients may not require surgical lung biopsy when the clinical and radiographic (HRCT) impression is consistent with a safe diagnosis of ILD.¹ The first imaging examination used is the chest radiograph because of its low cost and weak radiation dose. When the chest x-ray does not carry enough elements to finalize the diagnosis, HRCT is used to provide an accurate assessment of lung tissue patterns.² Computerized HRCT analysis can provide quick and precious information for emergency radiologists and other non-chest specialists.^3,4 Whereas the radiologists’ ability to interpret HRCT data is likely to change based on the domain-specific experience, human factors, and time of the day, computerized classification of lung tissue patterns is 100% reproducible. The computer-aided detection (CAD) system can be used as first reader in order to improve the radiologist’s productivity and reduce reading fatigue.^5,6 One approach for building image-based computerized diagnostic aid for ILDs is to imitate the radiologists’ human vision system. This latter can be schematized into two main parts:

• the eyes, which act as captors and aims at extracting relevant features from the observed scene⁷ and

• the visual cortex, which takes decisions based on the pre-processed information provided by the eyes as input as well as the knowledge and experience of the radiologist as information processor.

In pattern recognition, these two tasks can be respectively identified as feature extraction and supervised machine learning. In this work, the feature extraction part is based on texture properties and gray-level analysis (gray-level histograms) along with complementary analysis of spatial variations in the image through discrete wavelet frames with a quincunx subsampling scheme.^8–10 The two are described in “Texture Features”. Texture properties have been shown to have high importance for medical image analysis in CADe systems.¹¹ In this paper, the supervised machine learning part is studied.

Supervised Learning

Since the outputs of the CADe are the detected classes of lung tissue patterns, the machine learning task involved is a classification task. Once the feature space is built, algorithms have to be used to detect and create boundaries among the several classes of lung tissue patterns. This process is called supervised learning.

In order to classify unknown regions of interest (ROIs) of lung tissue, a model has to be built from known labeled data through the training phase. The training is challenging, as it is partly based on the experience of the radiologists. The goal is to find the functions 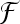which model best the boundaries among the distinct classes of lung tissue patterns represented in the feature space. The best functions are those that achieve classification of a test set with the lowest error rate. The test set is composed of labeled ROIs, which have not been used to train the classifier. It simulates future unknown instances and thus allows measuring the generalization performance. Indeed, the objective is to minimize the error rate on the training set while avoiding overfitting of the training instances. Several approaches are available to implement 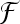. Three general approaches including five classifier families are studied in this paper:

• Learning by density estimation with naive Bayes and k-nearest neighbor (k-NN) classifiers;

• Recursive partitioning of the feature space with J48 decision trees; and

• Nonlinear numerical approaches with the multilayer perceptron (MLP) and kernel support vector machines (SVM).

In practice, the choice of a classifier family is a difficult problem and it is often based on the classifier which happens to be available or best known to the user.^12,13

Classifier Families

Naive Bayes

The naive Bayes classifier is based on a probability model and assigns the class, which has the maximum estimated posterior probability, to the feature vector extracted from the ROI. The posterior probability 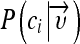of a class c_i given a feature vector 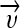is determined using Bayes’ theorem:

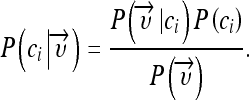1

This method is optimal when the attributes are orthogonal. However, in practice, it performs well without this assumption. The simplicity of the method allows good performance with small training sets.¹⁴ Indeed, by building probabilistic models, it is robust to outliers (i.e., feature vectors that are not representative of the class to which they belong). Moreover, it creates soft decision boundaries, which has the effect of avoiding overtraining. However, the arbitrary choice of the distribution model for estimating the probabilities P(x) along with the lack of flexibility of the decision boundaries results in limited performance for complex multiclass configurations.

k-Nearest Neighbor

The k-nearest neighbor classifier cuts out hyperspheres in the space of instances by assigning the majority class of the k-nearest instances according to a defined metric (e.g., Euclidean distance).¹⁵ It is asymptotically optimal and its straightforward implementation allows rapid tests, for example for evaluating features. However, several shortcomings are inherent to this method. It is very sensitive to the curse of the dimensionality. Indeed, increasing the dimensionality has the effect to sparse the feature space, and local homogeneous regions that represent the prototypes of the diverse classes are spread out. The classification performance strongly depends upon the used metric.¹⁴ Moreover, a small value of k results in chaotic boundaries and makes the method very sensitive to outliers.

J48 Decision Trees

The J48 decision trees algorithm divides the feature space successively by choosing primarily features with the highest information gain.¹⁶J48 is an implementation of the C4.5 algorithm. In medicine, it is in correspondence to the approach used by clinicians to establish a diagnosis by answering successive questions. This is nevertheless only partially true when radiologists interpret HRCT images. This method is robust to noisy features, as only attributes with high information gain are used. However, it is sensitive to the variability of data. The structure of the tree is likely to change completely when a new instance is added to the training set. Another drawback is its incapability to detect interactions between features, as it treats them separately. This results in decision boundaries that are orthogonal to dimensions, which is not accurate for highly nonlinear problems. Two main parameters influencing the generalization performance require optimization:

• N_instances: the minimum number of instances per leaf, which determines the size of the tree; and

• C_pruning: the feature confidence factor used for pruning the tree, which consists of removing branches that are deemed to provide little or no gain in statistical accuracy of the model.

Multi-layer Perceptron

MLPs are inspired by the human nervous system where information is processed through interconnected neurons.¹⁷ The MLP is a feed-forward neural network, which means that the information propagates from input to output. The inputs are fed with values of each feature and the outputs provide the class value. With one layer of neurons, the output is a weighted linear combination of the inputs. This network is called the linear perceptron. By adding an extra layer of neurons with nonlinear activation functions (the hidden layer), a nonlinear mapping between the input and output is possible.¹⁸ The training phase consists of iterative optimization of the weights connecting the neurons by minimizing the mean squared error rate of classification. The learning rate, R_learn, which controls the adjustments of the weights during the training phase, must be chosen as a trade-off between error on the training set and overtraining. Another critical parameter is the number of units, N_hidden, of the hidden layer. Indeed, the MLP is subject to overfitting and requires an optimal choice of the parameters for regularization. The MLP can create models with arbitrary complexity by drawing unlimited decision boundaries. It is also robust to noisy features, as these will obtain a low weight after training.

Kernel Support Vector Machines

Kernel SVMs implicitly map input feature vectors 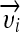to a higher dimensional space by using the kernel function 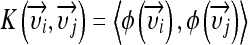. For example, the Gaussian kernel is defined by:

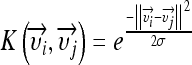2

with σ being the width of the Gaussian to determine. In the transformed space, a maximal separating hyperplane is built considering a two-class problem. Two parallel hyperplanes are constructed symmetrically on each side of the hyperplane that separates the data. The goal is to maximize the distance between the two external hyperplanes, called the margin.^19,20 An assumption is made that the larger the margin is, the better the generalization error of the classifier will be. Indeed, SVMs were developed according to the structural risk minimization principle which seeks to minimize an upper bound of the generalization error, while most of the classifiers aims at minimizing the empirical risk, the error on the training set.²¹ The SVM algorithm aims at finding a decision function 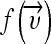, which minimizes the functional:

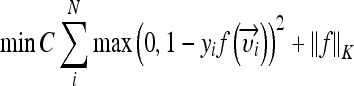3

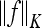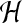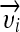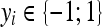where N is the total number of feature vectors, is a norm in a reproducing kernel Hilbert space, , defined by the positive definite function K, which means that the functionals f are bounded. y_i is the label of with (two-class problem). The parameter C determines the cost attributed to errors and requires optimization. For the multiclass configuration, several SVM models are built using one versus one combinations. Finally, the majority class is attributed.

In summary, SVMs allow training generalizable, nonlinear classifiers in high-dimensional spaces using a small training set. This is enabled through the selection of a subset of vectors (called the support vectors) which characterizes the true boundaries between the classes well.

Classifiers Used for Lung Tissue Categorization in HRCT Data

A brief review of the recent techniques used for the categorization of lung tissue patterns in HRCT data is given in this section.

Shyu et al.³ describe a physician-in-the-loop content-based image retrieval system in which the physician delineates a suspicious ROI. The system classifies ROIs using decision trees that minimize the entropy over all distributions associated with lung tissue classes and matches the ROI against reference images in JPEG (and not DICOM) that are already indexed in the database. The hierarchical organization of the features imposed by the structure of decision trees assigns too much importance to the first selected attributes and is not adapted to integrate information from a set of complementary attributes such as gray-level histogram bins.

In Caban et al.,²² normal versus fibrotic patterns are classified using SVMs with gray-level histograms, co-occurrence, and run-length matrices. No details about the choices of the parameters of the SVMs are communicated. The small dataset used (nine HRCT image series) leads to a biased classification task, since training and testing using series from the same patient create instances artificially close together in the feature space.

Nonlinear binning of gray-level values for co-occurrence matrices is proposed in²³ in order to qualify lung tissue fibrosis in HRCT data. A minimum Mahalanobis distance classifier is used. This extended naive Bayes classifier relies on the assumption that the probability density functions of the classes are Gaussian, leading to non-flexible decision boundaries.

Two classifiers along with two feature selection techniques are evaluated in²⁴ through their ability to detect fibrosis in HRCT images using co-occurrence matrices. The two are naive Bayes and J48 decision trees. The feature selection technique showed improvement of classification accuracy, whereas two classifier families achieved equivalent performance. Still, the dataset used for testing is fairly small and the classifiers may not be flexible enough for multiclass problems. Information about the localization of the lung tissue patterns within a lung atlas is integrated as an additional feature in,²⁵ which allow a classification accuracy improvement.

In Uppaluri et al.,²⁶ six lung tissue patterns are classified using an adaptive multiple texture feature method. Correlated features are removed and a Bayesian classifier is used. The latter may not be accurate for classifying any type of lung tissue, as it is sensitive to the choice of the probability density function of the features.

Optimization of the parameters of SVMs with Gaussian kernels using a gradient descent is carried out in Shamsheyeva and Sowmya.²⁷ Quincunx wavelet frames are used as texture features. The dataset used is small, containing 22 images for four lung pattern classes. The optimization of the cost C of the errors, as well as the width σ of the Gaussian kernel, is carried out for each two-class combination. The use of an anisotropic Gaussian kernel is tested in Shamsheyeva and Sowmya²⁸ and did not lead to significant improvement of the classification accuracy.

In Depeursinge et al.,¹⁰ gray-level histograms with discrete wavelet frame features were evaluated using a k-NN classifier. In this paper, we evaluate the ability of five optimized common classifier families to discriminate among six lung tissue patterns characterized by improved quincunx wavelet frame texture features.

The paper is structured as follows. In “Method(s)”, the dataset used for evaluating the classifier families is described. “Results” is divided into two parts. “Texture Features” studies the composition of the feature space, whereas “Classifier Family Evaluation” carries out the comparison of the classifier performances. Results are interpreted in “Interpretation” and final conclusions are drawn in “Conclusions.”

Method(s)

The dataset used is part of an internal multimedia database of ILD cases^29,30 containing HRCT images created in the Talisman project at Geneva University Hospitals and University of Geneva. Approval of the ethics commission was obtained ahead of the official start of the project to allow for a collection of retrospective cases. The slice thickness of the images is limited to 1 mm. Annotation of regions is performed by two radiologists. Around 100 clinical parameters related to the 15 most frequent ILDs are acquired with each case. A graphical user interface implemented in Java was developed in order to meet the needs of the radiologists for the various annotation tasks. It allows high-quality annotations in 3D HRCT data. Eight hundred forty-three ROIs from healthy and five pathologic lung tissue patterns commonly found in HRCT images of the chest are selected for training and testing the classifiers (see Table 1). The selected patterns are healthy, emphysema, ground glass, fibrosis, micronodules, and macronodules. Distributions of the classes are highly imbalanced, as the largest class, fibrosis, contains 312 ROIs and the smallest class, macronodules, only 22 ROIs. There is a mean of 140.5 ROIs per class.

Table 1.

Distribution of the ROIs Per Class of Lung Tissue Pattern

Classifier implementations were taken from the open source Java library Weka.^31,32 The feature extraction and the optimization of the classifier parameters were implemented in Java. Quincunx wavelet frames are implemented in Java.⁹LIBSVM library is used for the SVMs’ C-support vector machine classification.³³

Results

Texture Features

The construction of the feature space is detailed in this section. It is composed of image texture features, as the taxonomy used by radiologists to interpret patterns in HRCT images often relates to texture properties.¹⁰ The two feature groups are gray-level histograms, air components and quincunx wavelet frame coefficients with B-spline wavelets.

Full-resolution (12-bit gray values) HRCT images contain values in Hounsfield units (H.U.) in the interval [−1,500;1,500]. These values correspond univoquely to densities of the anatomic organs and thus allow the identification of lung tissue components. In order to take advantage of this, histograms of pixel values are computed over each ROI. Each bin value is integrated into the feature space, and the optimal number was investigated in Depeursinge et al.¹⁰ where 40 bins constituted the best trade-off between classification accuracy and dimensionality of the feature space. Twenty-two bins corresponding to pixel values in [−1,050;600] were kept, as the bins outside this interval were very sparsely populated. The air component value given by the number of pixels with value less than −1,000 H.U. is computed as an additional feature.

In order to study the spatial organization of the pixels, quincunx wavelet frame (QWF) coefficients are extracted from the ROIs. Discrete wavelet frames have shown to perform well for texture analysis.⁸ Compared to the wavelet transform, wavelet frames are redundant and offer more flexibility for image analysis: they enable translation invariance by removing the subsampling part of the algorithm. A quincunx subsampling scheme is used in order to allow a finer scale progression compared to classical dyadic wavelet transform⁹ (images are downsampled by a factor of 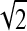instead of 2 at each iteration). Moreover, its isotropy is suitable for analysis of axial images of the lung tissue, as we made the assumption that no information is contained in directionality of patterns. The mean, μ_i, and variance, σ_i, of the coefficients of eight iterations of QWF are computed over each ROI, resulting in 16 QWF features.

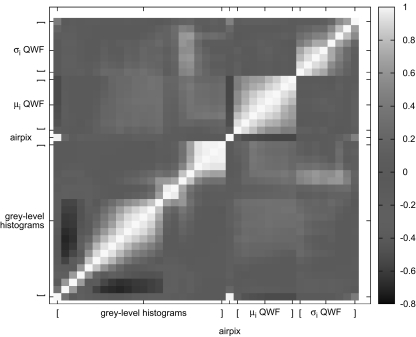
The feature space contains a total of 39 attributes that are normalized in order to give equivalent weight to each of them. The correlation of the values is shown in Figure 1.

Fig. 1.

Correlation matrix of the feature space.

Classifier Family Evaluation

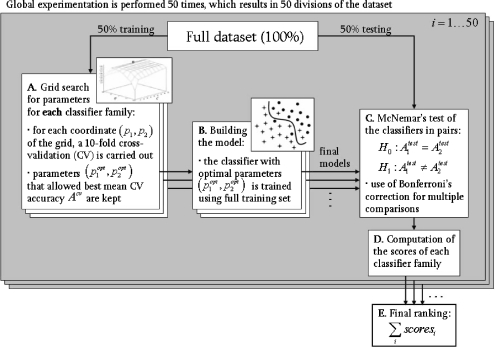
The methodology utilized to compare the performance of each classifier family is described in this section. The full dataset (843 ROIs) is divided into two equal parts: 50% for training and 50% for testing. Training means both search for optimal parameters and creation of the model (i.e., adjustments of the decision boundary). The methodology is detailed in Figure 2 and in “Grid Search for Optimal Parameters” and “Ranking.”

Fig. 2.

Methodology for benchmarking the classifiers.

Grid Search for Optimal Parameters

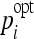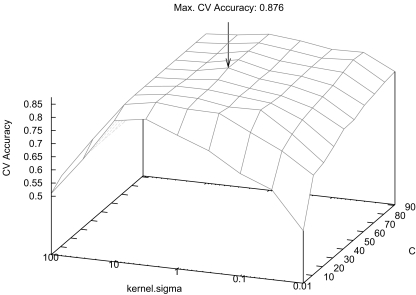
In order to determine the optimal parameters p_i, a grid search is performed for each classifier family. When required, exponential grid steps were used for coarse search. For every coordinate of the grid, a tenfold cross-validation (CV) is carried out on the training set. Optimal parameters that allowed best mean CV accuracy 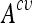are used to train the final model on the entire training set. Optimized parameters are detailed in Table 2. An example of grid search for best 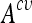is shown in Figure 3 where the cost C and the σ value of the Gaussian kernel of the SVM are optimized. A preliminary coarse grid search is performed to locate regions of the space with high 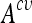values.

Table 2.

Grid Search for Optimal Parameters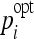

Classifier family	Parameters	Ranges	Step
Naive Bayes	–	–	–
k-NN	k	[0; 100]	linear
J48	Ninstances, Cpruning	[0; 5], [0.02; 0.24]	lin, lin
MLP	Rlearn, Nhidden	[10−10 ; 105], {0, 6, 22, 45}	log, –
SVM	C, σ	[1; 100], [102; 10−2]	lin, log

The values for the number of hidden layer units, N_hidden, of the MLP are chosen as {none, number of classes, (number of attributes + number of classes)/2, number of attributes + number of classes}

Fig. 3.

Grid search for SVM optimal parameters C and σ.

Ranking

Instances of the test set are classified by each classifier family, and McNemar’s test is applied to the classifiers in pairs with the hypothesis:

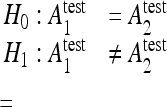with 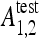the testing accuracy of the classifiers 1,2 computed as the number of correctly classified instances divided by the total number of instances in the test set. Compared to other statistical tests for comparing supervised classification learning algorithms, McNemar’s test showed to be the only test with acceptable type I error rate in Dietterich.³⁴ Type I errors correspond to a false detection of difference in performance between two algorithms. Bonferroni’s correction for multiple comparisons is used to adjust the threshold of the test. When H₀ is rejected and 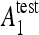is greater than 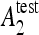, the score of the classifier 1 is incremented. When H₀ is accepted, 0.5 is added to the scores of both classifiers. The global experimentation is repeated 50 times and a final ranking based on the total of the scores is performed. As distribution of the classes are highly imbalanced, the geometric mean, A^geom, of each class-specific accuracy, A^ci, on the test set are computed for every classifier as follows:

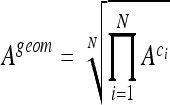4

with N as the number of classes. A^geom gives the same importance to each class even if the classes are imbalanced.³⁵ Two classification configurations are investigated. First, classifiers are evaluated on a multiclass configuration using all six classes of lung tissue. Similarly, a two-class configuration opposing healthy versus pathological tissues is investigated. In this configuration, the classes emphysema, ground glass, fibrosis, micronodules, and macronodules are grouped together to form the class pathologic containing 730 ROIs versus 113 for the class healthy. 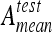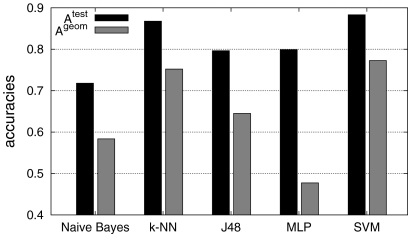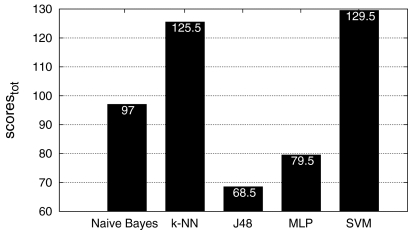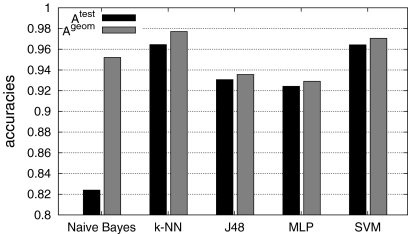Final rankings, mean testing accuracies , and mean geometric accuracies 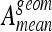are shown in Figures 4, 5, 6, and 7. The class-specific accuracies achieved by each classifier family are presented in Tables 3 and 4.

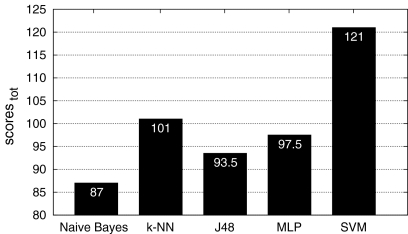
Fig. 4.

Final ranking based on the total of the scores of the classifiers with the six-class configuration. SVM reached the best score with 121.

Fig. 5.

Overall mean testing accuracies 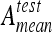and 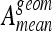with six classes. SVM reached best accuracies with 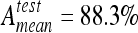and .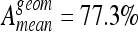

Fig. 6.

Final ranking with the two-class configuration. Again, SVM reached the best score with 129.5.

Fig. 7.

Overall mean testing accuracies with two classes. k-NN reached best accuracies with 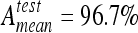and 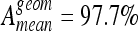and is closely followed by SVM.

Table 3.

Class-specific Accuracies for Each Classifier Family

	Healthy	Emphysema	Ground glass	Fibrosis	Micronodules	Macronodules
Naive Bayes	0.9161	0.8753	0.7873	0.7454	0.3778	0.3076
k-NN	0.9104	0.9978	0.7369	0.8926	0.91	0.3605
J48	0.7568	0.9419	0.6803	0.8821	0.7555	0.3054
MLP	0.7290	0.9707	0.6756	0.8751	0.8035	0.2461
SVM	0.9242	0.9874	0.7731	0.9218	0.8907	0.4250

Best performances are highlighted in bold. SVM reached three times the best accuracy and is no more than 2% behind the best performance over all classes

Table 4.

Class-specific Accuracies for Each Classifier Family with Two-Class Configuration

	Healthy	Pathological
Naive Bayes	0.922	0.8087
k-NN	0.8923	0.9764
J48	0.6985	0.9675
MLP	0.711	0.958
SVM	0.8535	0.9818

Naive Bayes performs well for classifying healthy tissue.

Stability

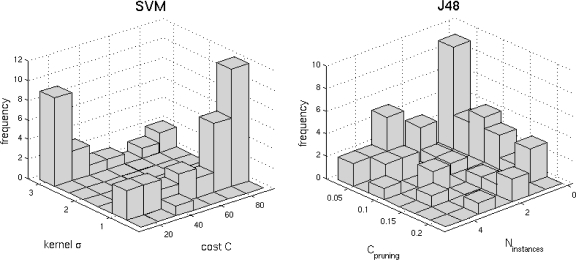
Optimal parameters of each classifier family were stored for every 50:50 division. In order to study the stability, histograms of the values of (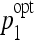, 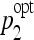) are built for SVMs and J48 as shown in Figure 8.

Fig. 8.

Bivariate histograms of the optimal parameters (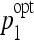, 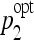) for SVM and J48.

Interpretation

Feature Space

In the correlation matrix (see Fig. 1) of the feature space, three groups of features clearly appear as little correlated: the gray-level histograms, the mean μ_i of QWF, and the variance σ_i of QWF. Bins of gray-level histograms are highly correlated in pairs, which is in accordance with the assumption that the density of the tissue extracted from the same ROI is roughly homogeneous. However, one can differentiate two subgroups: the 14 first bins with values in [−1050;0] corresponding to various lung tissue patterns, the 15th to 22nd bins with values in [0;600] corresponding to higher density tissue (i.e., vascular tissue). Features in this second subgroup are highly correlated due to sparsity. It is not surprising that the first bin is highly correlated with air pixels. Means of QWF are anti-correlated with air pixels, which is in accordance with the fact that regions with air are homogeneous (i.e., emphysema and interior of bronchus). Little correlation among the three groups of features suggests that the feature space contains little redundancy and is adapted to describe lung tissue texture.

Classifier Performances

All scores are shown in Figures 4 and 6 resulting in strong variations among the classifiers. Moreover, the variations can be decreased by the use of Bonferroni’s correction, which makes the tests more permissive (i.e., McNemar’s test rejects more easily H₀). Two classifier families reach scores out of the lot: k-NN and SVM. These performances are confirmed by their respective accuracies in Figures 5 and 7. Overall scores and mean testing accuracies, 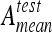, show to be complementary metrics. For example, with the six-class configuration, the MLP reaches high global accuracy of 79.9% with a low score of 97.5. Those discordances can be understood by looking at the mean geometric accuracies, 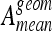. The latter is very low for MLP with a value of 47.7%, which indicates that the MLP has a very low class-specific accuracy, and thus a low precision for each class, which is not suitable for the characterization of lung tissue. Therefore, the SVM that reached best score and global accuracy is able to classify tissue of each class accurately even from those that are little represented. Beyond the fact that the k-NN classifier reached a slightly lower score and global accuracy compared to SVM with six classes, one problem occurs with this classifier. The optimal number k of nearest neighbors for each of the 50 training/testing splits was 1. This strong tendency can be explained by the fact that for some classes, the number of patients is low, and thus, many ROIs are extracted from the same image series. Training and testing with images from the same image series can result in a biased classification, as images are similar as they belong to the same patient. Two such instances are artificially close in the feature space and will facilitate the classification task while attributing the class of the closest neighbor, which probably belongs to the same image series. In that sense, the k-NN classifier carries out overfitting of the training instances, which is not suitable for classifying ROIs from new ILD cases.

The complementarity of the classifiers is studied in Tables 3 and 4. Naive Bayes performs surprisingly well for classifying healthy tissue in the two-class configuration. However, the low accuracy achieved on the majority class pathological suggests that Naive Bayes tends to favor the class healthy. Again, the competition between k-NN and SVM is tight with an advantage for SVM. For the six-class configuration, SVM reached three times the best accuracy and is no more than 2% behind the best performance over all classes. On the difficult class macronodules, SVM outperforms all other classifier families by more than 6% of accuracy.

Distributions of the optimal parameters (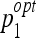, 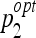) represented in Figure 8 show distinct behavior for SVM and J48. Coupled parameters are more uniformly distributed for J48 compared to SVM: σ of the Gaussian kernel of SVM is characterized by a bimodal distribution. This means that two values of σ allow a convenient mapping of the feature space to higher dimensions for accurate separation of the classes. These values affect the optimal value of cost C. Indeed, the organization of the classes in the transformed space is fixed by the value of σ, which requires a corresponding readjustment of the optimal cost C. The most frequent pair of values of J48 occurs nine times over 50, while the second most frequent pair occurs five times. For the SVM, the most frequent pair occurs 12 times over 50, while the second most frequent pair occurs nine times. In that sense, the SVM classifier offers more stability. The stability has an important influence on the generalization performance: a classifier that frequently obtained identical pairs of optimal parameters has a high probability to be optimal for classifying new data.

Conclusions

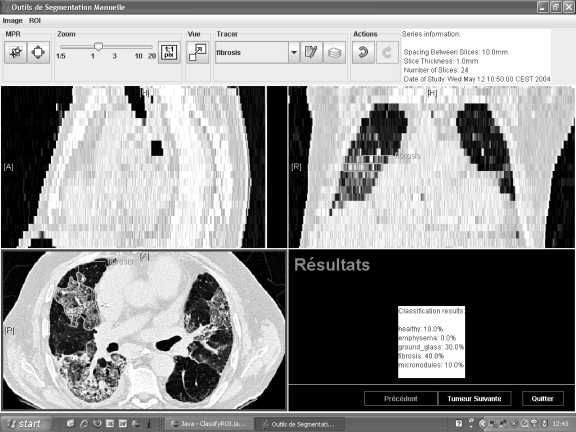
In this paper, five common classifier families were tested to discriminate six classes of lung tissue patterns in HRCT data from healthy cases and cases affected with ILDs. Evaluation of the classifiers is based on a high-quality dataset taken from clinical routine. The classifiers were optimized in order to compare their best performance. The SVM classifier constitutes the best trade-off between the error rate on the training set and generalization, the ability to classify ROIs correctly from images of new patients. Since SVMs were designed to avoid overfitting of training samples, using them to classify medical images with much heterogeneity is adapted. The SVM classifier was able to correctly classify 88.3% of the instances into the six classes and 96.4% when discriminating healthy tissue versus all other pathological classes. Two metrics were used to characterize the performances of the classifiers: scores based on McNemar’s test along with global accuracy on the test set. The two metrics have shown to be complementary. The optimal classification algorithms were integrated into a software for classification of ROIs directly in three-dimensional DICOM images (Fig. 9). The diagnostic aid tool is easy to integrate into the PACS having the same user interface and offers the possibility to add clinical data from the electronic patient record. The classifier belongs to the core of a computer-aided diagnosis system involved in the decision-making process.

Fig. 9.

A screenshot of the DICOM viewer for the classification of image regions.