Abstract
There are lots of work being done to develop computer-assisted diagnosis and detection (CAD) technologies and systems to improve the diagnostic quality for pulmonary nodules. Another way to improve accuracy of diagnosis on new images is to recall or find images with similar features from archived historical images which already have confirmed diagnostic results, and the content-based image retrieval (CBIR) technology has been proposed for this purpose. In this paper, we present a method to find and select texture features of solitary pulmonary nodules (SPNs) detected by computed tomography (CT) and evaluate the performance of support vector machine (SVM)-based classifiers in differentiating benign from malignant SPNs. Seventy-seven biopsy-confirmed CT cases of SPNs were included in this study. A total of 67 features were extracted by a feature extraction procedure, and around 25 features were finally selected after 300 genetic generations. We constructed the SVM-based classifier with the selected features and evaluated the performance of the classifier by comparing the classification results of the SVM-based classifier with six senior radiologists′ observations. The evaluation results not only showed that most of the selected features are characteristics frequently considered by radiologists and used in CAD analyses previously reported in classifying SPNs, but also indicated that some newly found features have important contribution in differentiating benign from malignant SPNs in SVM-based feature space. The results of this research can be used to build the highly efficient feature index of a CBIR system for CT images with pulmonary nodules.
Key words: Feature selection, content-based image retrieval, classification, CT images, lung diseases
Introduction
Solitary pulmonary nodules (SPNs) are common findings in thoracic imaging. The volumetric computed tomography (CT) technique has introduced spiral scans which shorten the scan time and, when used in thoracic imaging, reduce the artifacts caused by partial volume effects, cardiac motion, and unequal respiratory cycles. For these reasons, spiral CT is useful in identifying and characterizing SPNs.
However, it is still difficult for radiologists to distinguish malignant from benign nodules. Differentiating malignant nodules from benign ones by visual examination is subjective and the results vary between different observers and in different cases. In general, experienced radiologists classify nodules more accurately than resident radiologists. The necessity for reliable and objective analysis has prompted the development of computer-aided systems.
It is reported that two radiologists working together outperform any independent radiologist. The computer-assisted diagnosis and detection (CAD) system can provide a “second opinion,” which might improve the radiologist’s performance. One study has demonstrated that radiologists more accurately classified SPNs (as measured by area under the receiving operating characteristic (ROC) curve (AUC)) with CAD assistance.1 Recent studies have focused on the role of CAD in differentiating and characterizing pulmonary nodules. These reports discuss characteristics of nodules demonstrated to be relevant to their classification.2–8 For example, the presence of calcification and/or fat indicates that the nodule is likely to be benign, while irregular margins and heterogeneous attenuation are signs of malignancy.9 Another way to improve accuracy of diagnosis on new images is to recall or find images with similar features from archived historical images which already have confirmed diagnostic results,10 and content-based image retrieval (CBIR) technology is now proposed for this purpose in digital imaging and management environment.11,12
Selecting the right features and constructing the higher performed classifier of pulmonary nodules are very important in developing the qualified CAD and CBIR systems. For example, most of the CAD systems consist of two steps: feature extraction and classification. In CBIR, the large amount of visual features such as shape, texture, and granulometry are usually included to build the searching index.13
Some studies have been done on finding and selecting features and evaluating the performance of classifiers of lung nodule and tissues for CAD and CBIR purposes.14–20 In feature selection studies, most researches focused on differentiating the visual features of pulmonary nodules and tissues, and there were few considerations about the differentiating features for classifying benign from malignant SPNs. In classifier construction studies for lung CAD, linear discriminant analysis (LDA) and artificial neural networks (ANN) were studied intensively.2–8 However, in LDA, the complex decision surface might not be linear. In ANN, it was difficult to determine the number of units in the hidden layer and its gradient-based algorithm might be trapped in local minima.
In this paper, we present a method for selecting pattern features of pulmonary nodules of CT images and evaluate the performance of support vector machine (SVM)-based classifiers in differentiating benign from malignant SPNs. We constructed the SVM-based classifier with the selected features using a genetic generation procedure and evaluated the performance of the classifier by comparing the classification results of the SVM-based classifier with two groups of senior and junior radiologists′ observations, as well as the results of the neural-network-based classifier. The results of this research are not only helpful to improve CAD for diagnosis on SPNs but also useful to build the highly efficient feature index of a CBIR system for CT images with pulmonary nodules. We discussed the impacts of nodule segmentation results and kernel function selection on the performances of SVM-based classifier in differentiating benign from malignant SPNs.
Materials and Methods
Materials
High-resolution scans of 77 patients with solitary pulmonary nodules mostly less than 3 cm performed between October 1999 and December 2006 were included in our study. The selection criteria included the following: nodules were solitary, and there was no calcification or artifacts from cardiac motion or beam hardening from adjacent bone. Definitive diagnoses were obtained in each case by cytological or histopathological examination of surgical specimens and CT-guided transthoracic needle aspiration biopsy or based on clinical data such as no radiological evidence of nodular growth during two or more years of follow-up.
Among the 77 patients, 48 were men and 29 were women (age range, 27–86 years; mean, 57.97 years). There were 43 malignant cases (27 adenocarcinoma, nine squamous cell carcinoma, four small cell carcinoma, and three adenosquamous carcinoma). Thirty-four cases were benign (17 pulmonary hamartomas, eight cases of pulmonary tuberculosis, five cases of inflammatory pseudotumor, and four cases of pneumonia). Four of the 77 cases were larger than 3 cm. The largest was 4.48 cm; the smallest was 0.54 cm and the mean diameter was 1.90 cm. Among the 77 cases, 31 were larger than 2 cm, while seven out of the 31 cases were benign and 24 were malignant. Large nodules were inclined to be malignant, which dovetailed with the radiologists’ knowledge.
The images were obtained by Somatom Plus (Siemens AG, Germany) and Somatom 16 (Siemens AG, Germany) CT scanners with the following parameters: 120 kV, 100 mA, 1-s scanning time, and a standard reconstruction algorithm for the Somatom Plus scanner and 120 kV, 250 mA, 0.5-s scanning time, and a standard reconstruction algorithm (B41f) for the Somatom 16 scanner. Some patients had additional scans covering the tumors.
Nodule Segmentation
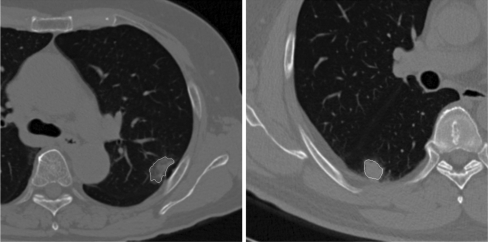
We used two methods to perform nodule segmentation in our study: the region-grow and the snake techniques. First, we can identify the boundary of most nodules by using the region-grow method from a user-specified seed point inside the nodule with adjustable thresholds. This region-grow method has also been used in other lung nodule segmentation applications.2,7 However, the region-grow technique could not be applied if the nodule contacted with vessels or the chest wall. In those cases, we applied the snake approach after using region grow. We have 77 cases of images; 61 of these case images can be segmented by using region grow, and 14 should be segmented by using both region-grow method and snake approach, and only two cases of images must be segmented by user interactively. The times required to segment a nodule with our region-grow software program were about 4 s averagely. Figure 1 shows two examples of nodules for which the borders were identified by each of these two techniques.
Fig 1.
The segmentation results of two pulmonary nodules.
Due to partial volume averaging effects, the spikes of some nodules had much lower attenuations than the center of the nodule. As a result, the border of the spikes identified by the region-grow method was not sharp. The snake method depended on its initial border and did not trace the exact border of the nodule in some cases, but, in such cases, we reinitialized the process to get a satisfied result. The segmentation results covered most of the nodule area and captured most characteristics of the borders. In our study, the segmentation results were all approved by an experienced radiologist.
Feature Extraction
In image pattern recognition, feature extraction is the first step in image classification. The visual features of lung nodules, such as the size, shape, and internal texture, were considered in our study, as such characteristics would be considered by the radiologist when classifying a nodule as malignant or benign. For example, nodules with calcification or fat are more likely to be benign, whereas irregular borders suggest malignancy. To characterize nodules, we also tried to capture other features that may suggest malignancy, such as attenuation statistics, Gabor filter responses, wavelet decomposition features, multiscale Hurst parameters, and so on.
We performed specific feature extraction of lung CT images with nodules based on the following parameters: the first-order statistics features (feature 1 to feature 14) describe the attenuation distribution and the shape of the histogram; the second-order statistics features (feature 15 to feature 34) describe the spatial dependency of pixel values, particularly, entropy features represent the smoothness of the region of interest (ROI); the Gabor features (feature 35 to feature 46) capture the directional information at different scales; the wavelet frame decomposition features (feature 47 to feature 55) represent the energy of the decomposed image; the multiscale Hurst features (feature 56 to feature 61) describe the roughness of the ROI at different scales; and shape features represent the area, perimeter, irregularity of the border, and size of the ROI. A complete list of the features is provided in Table 1. Some features have good discriminant power, while other features contribute little to the classification. Therefore, the extracted features must be subjected to an optimal selection procedure before being used in classification. This selection procedure is further described in the next section.
Table 1.
A Complete List of Features Extracted for Lung Nodules in CT Images
| Feature extraction methods | Feature no. | Feature name |
|---|---|---|
| First-order statistics | 1∼10 | HIST1, HIST2,…HIST10 |
| 11 | MEANV | |
| 12 | STDV | |
| 13 | KURT | |
| 14 | SKEW | |
| Second-order statistics | 15∼19 | ASM1, CONT1, CORR1, IDM1, ENTR1 |
| 20∼24 | ASM2, CONT2, CORR2, IDM2, ENTR2 | |
| 25∼29 | ASM3, CONT3, CORR3, IDM3, ENTR3 | |
| 30∼34 | ASM4, CONT4, CORR4, IDM4, ENTR4 | |
| Gabor filters | 35∼46 | GAB1, GAB2, …GAB12 |
| Wavelet frame decomposition | 47∼55 | WF1, WF2, …WF9 |
| Fractal parameters | 56∼58 | HM1, HM2, HM3 |
| 59∼61 | HS1, HS2, HS3 | |
| Shape features | 62 | AREA |
| 63 | PERI | |
| 64 | COMP | |
| 65 | MEAND | |
| 66 | MIND | |
| 67 | MAXD |
Algorithms of Feature Selection, Statistical Classification, and Analysis
We enrolled 77 cases of SPNs in this study and extracted 67 features for each image. Thus, there was a high possibility of overfitting during the classification step due to the low number of samples relative to the number of features extracted. For this reason, it was necessary to reduce the high dimensionality of the input feature vectors.
In this study, we employed a genetic-algorithm-based feature selection technique to recreate multiple groups of feature subsets with different numbers of features (between five and 30 of the total 67 features were used in each analysis). This allows us to evaluate the performance of each classifier built by different groups of feature subsets. We also introduced the support-vector-machine-based classifier in this section to classify the SPNs as well and its related algorithm. In order to evaluate the performance of the classifiers in differentiating the malignant nodules from SPNs, the ROC analysis was also included in this section.
Genetic Algorithm for Feature Selection
Feature selection is a combinational optimization approach to a problem that is difficult to solve directly. The genetic algorithm is a general optimization method that is useful especially for computation-intensive applications. It mimics the evolution process in biology by representing the solution of the problem as genomes. The crossover of good genomes (indicated by small fitness value) tends to yield better results, and a certain probability of mutation allows for exploration of the whole solution space. After many generations of crossover and mutation, the algorithm yields an acceptable solution.
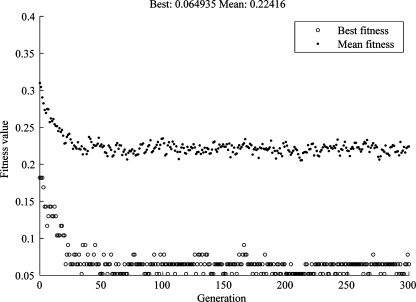
In this study, each generation had the same number of features, and the fitness function was defined as the misclassification rate of a tenfold cross-validation procedure. In this procedure, the samples were divided randomly into ten groups, while one group was used as test data; the rest of the samples were used to fit a multivariate normal-density function. The test data were classified based on likelihood ratios. After each group had acted as test group exactly once, the fitness function was calculated as the misclassification rate. The smaller the value was, the better the was fitness of the genome. Figure 2 showed an evolution process of mean fitness and best fitness with the increasing of generations, in which the number of features was fixed to 25, and the number of genomes in each population was 100, and the number of generations was 300. It demonstrates that both the mean fitness and the best fitness values drop drastically after about 50 generations.
Fig 2.
The evolution of best fitness and mean fitness value with increasing numbers of generations, in which the number of features was fixed to 25; the number of genomes in each population was 100, and the number of generations was 300.
Support Vector Machine
Support vector machine is based on the structural risk minimization principle. It is reported that SVM outperforms other classifiers in many studies.21,22 The SVM approach enjoys many attributes. It is less computationally intense in comparison to artificial neural networks. It performs well in high-dimensional spaces and also well on both training data and testing data but does not suffer from the small size of training dataset as do other kinds of classifiers since the decision surface of SVM-based classifier is determined by the inner product of training data.
The basic idea of SVM is to construct a hyperplane that maximizes the margin between negative and positive examples. The hyperplane is determined by the examples called support vectors that are closest to the decision surface. The decision surface is determined by the inner product of training data, which enables us to map the input vectors through function Φ into a higher-dimensional inner product space called feature space. The feature space could be implicitly defined by kernel K(x, y). To tolerate noise and outliers and to avoid overfitting, slack variables ξi are introduced which allows the margin constraints to be violated.23
Consider the training samples (xi, yi), i = 1,…,m, where each point xi is an input vector with label yi ∈ {−1, 1}. The decision surface has the form:23
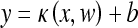 |
1 |
The decision surface is the solution of the following optimization problem:
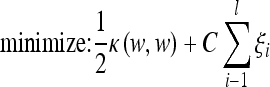 |
2 |
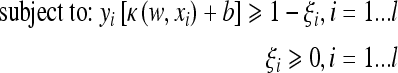 |
3 |
where C > 0 is a parameter chosen by the user to penalize decision errors and ϕ is the mapping determined by the kernel function. The most popular kernel is the Gaussian kernel function which is defined by:
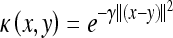 |
4 |
where γ is also chosen by the user.
In our study, the value of C was chosen to be 50 and the value of γ was chosen to be 1, and those values had good performance in the application. We will discuss in more detail why we choose Gaussian kernel function in “Reliability of Nodule Segmentation and Its Impact on the SVM-Based Classifier.”
ROC Analysis
An ROC graph is a technique for visualizing the performance of classifiers and is useful to compare the performance of different classifiers in medical decision-making systems. The graph depicts the tradeoff between the true-positive and false-positive rates. While an ROC graph is a two-dimensional description of classifier performance, it is often useful to reduce it to one scalar value. The AUC is largely adopted to represent the expected performance of a classifier. The AUC of a classifier is equivalent to the probability that the classifier will rank a randomly chosen positive instance higher than a randomly chosen negative instance.24
Results
Feature Selection of CT Images with SPN
We enrolled 77 cases in this study as described in “Materials” and extracted 67 features for each SPN. Since the dimensionality of the feature space is comparable to the number of samples, feature selection was carried out using a genetic algorithm as mentioned in “Genetic Algorithm for Feature Selection.” The results of some selected feature subsets are shown in Table 2. There are about 30 subsets and each of the subset contains the number of selected features from five to 30. The next step is to determine the relevance of each selected feature to the process of differentiating benign and malignant nodules.
Table 2.
The Subsets of Feature Selection Carried Out by Using a Genetic Algorithm Mentioned in “Genetic Algorithm for Feature Selection” with The Evolution of Best Fitness and Mean Fitness Value of Genetic Generations as Indicated by Fig. 2
| Subset num. | Label num. (#) of selected features |
|---|---|
| 5 | 1, 6, 10, 15, 36 |
| 6 | 10, 11, 23, 32, 33, 36 |
| 7 | 1, 4, 6, 10, 14, 18, 31 |
| 8 | 2, 3, 10, 11, 17, 23, 33, 36 |
| 9 | 1, 4, 10, 13, 29, 33, 34, 45, 64 |
| 10 | 4, 10, 11, 13, 20, 29, 34, 36, 62, 65 |
| … | … |
There are about 30 subsets and each of subset contains the number of selected features from five to 30. The no. of subsets means that there are five features in this subset if the no. is five, and the selected features in each subset means that the kinds of the features listed in Table 1 are contained in this subset
During the evaluation process by using the genetic algorithm, some features may be selected many times as the number of generation increases. The more times it was selected, the more important it contributed to the final generation of selected features. The number of times each feature was selected is provided in Table 3. From Table 3, we see that HIST1, HIST4, HIST10, ENTR3, ENTR4, GAB2, COMP, and MEAND were present in more than half of the feature subsets. The feature selection results were consistent with the knowledge of the radiologists. For example, the fourth histogram feature which indicated the presence of fat existed in most feature subsets. This is consistent with radiologists’ knowledge that the presence of fat suggests that a SPN is benign. We will discuss the selected features and compare them with previous reported studies further in “Discussion.”
Table 3.
The Number of Times each Feature Was Selected in the 300 Genetic Generation Procedure
| Feature name | HIST1 | HIST2 | HIST3 | HIST4 | HIST5 | HIST6 | HIST7 | HIST8 | HIST9 | HIST10 | MEANV | STDV | KURT | SKEW | ASM1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Selected times | 18 | 3 | 4 | 22 | 6 | 3 | 2 | 2 | 5 | 25 | 13 | 2 | 21 | 10 | 3 |
| Feature name | CONT1 | CORR1 | IDM1 | ENTR1 | ASM2 | CONT2 | CORR2 | IDM2 | ENTR2 | ASM3 | CONT3 | CORR3 | IDM3 | ENTR3 | ASM4 |
| Selected times | 2 | 11 | 7 | 11 | 7 | 2 | 8 | 7 | 12 | 2 | 5 | 5 | 4 | 18 | 3 |
| Feature name | CONT4 | CORR4 | IDM4 | ENTR4 | GAB1 | GAB2 | GAB3 | GAB4 | GAB5 | GAB6 | GAB7 | GAB8 | GAB9 | GAB10 | GAB11 |
| Selected times | 6 | 5 | 10 | 21 | 3 | 17 | 2 | 4 | 2 | 2 | 1 | 3 | 3 | 3 | 5 |
| Feature name | GAB12 | WF1 | WF2 | WF3 | WF4 | WF5 | WF6 | WF7 | WF8 | WF9 | HM1 | HM2 | HM3 | HS1 | HS2 |
| Selected times | 11 | 5 | 1 | 4 | 3 | 3 | 1 | 3 | 0 | 3 | 2 | 2 | 3 | 3 | 3 |
| Feature name | HS3 | AREA | PERI | COMP | MEAND | MIND | MAXD | ||||||||
| Selected times | 11 | 11 | 13 | 18 | 20 | 4 | 1 |
SVM-Based Classifiers for CT Images with SPN
The basic idea of using SVM to classify the patterns in SVM-based feature space is to construct a hyperplane that maximizes the margin between negative and positive examples. The hyperplane is determined by the examples called support vectors that are most close to the decision surface. We employed the SVM-KM toolbox25 as the SVM implementation based on the decision surface solution given by Eqs. 1 to 4 and the features selected in “Feature Selection of CT Images with SPN” to construct SVM-based classifier. The parameter C was set to be 50 and γ set to be 1 throughout this study.
Figure 3 showed the decision surface of SVM-based classification by using HIST1 and HIST10 in SVM-based feature space. The upper-right part in Fig. 3 indicates that the output of the classifier is positive, and down-left part indicates that the output of the classifier is negative. The circle symbol “o” indicates true-positive samples and plus symbol “+” represents true-negative samples, the features of which were used to train the SVM-based classifier. All the features are scaled to the range [0, 1]. The HIST1 feature represents the percentage of pixels in the nodule that are less than −185 HU, and the feature is scaled to the range [0, 1]. Higher values of HIST1 mean that a higher percentage of pixels are in a single bin of the histogram. The HIST10 represented the percentage of pixels above 136 HU which was in the range of calcification and indicated that high percentage of calcification and low attenuation pixels suggested that the nodule was benign.
Fig 3.
The decision surface of SVM is indicated in feature space by using HIST1 and HIST10. The upper-right part in the figure indicates that the output of the classifier is positive, and down-left part indicates that the output of the classifier is negative. The circle symbol indicates true-positive samples and plus symbol represents true-negative samples, the features of which were used to train the SVM-based classifier. This figure indicated that the high percentage of calcification and low attenuation pixels suggested that the nodule was benign.
Performance Evaluation of SVM-Based Classifiers for Differentiating SPNs
Comparison of SVM- and BP-ANN-Based Classifiers
In classifier construction studies for lung CAD, the ANN was usually used,3,4 so we compared the performance of SVM-based classifier with ANN-based in the following. We employed a two-layered feedforward neural network which contained one input layer, one hidden layer, and one output layer. The number of inputs in the input layer equaled the dimensionality of the input vector. The output layer contained one unit to output a score that indicated the malignancy of an input nodule, and the number of units in the hidden layer was chosen from three to 18 so that the area under the ROC curve was maximized. The neural network toolbox of Matlab® was used in this study
Now, we compared the performance of SVM and back propagation (BP)-ANN in differentiating solitary pulmonary nodules in terms of AUC using the selected feature subsets with leave-one-out procedure.
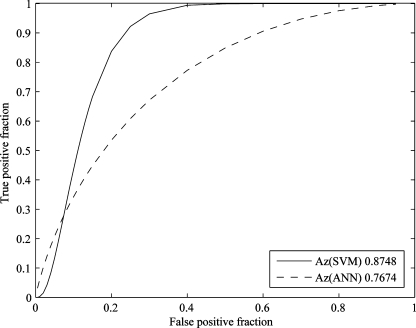
A leave-one-out procedure was carried out in which one nodule was used for test purpose and the others were used for training the SVM- and ANN-based classifiers until each example was used for test only once. For a subset of features, the AUCs of SVM and ANN could be calculated using ROCKET.26 Thus, the AUCs of SVM and ANN using different feature subsets were calculated. We selected 26 subsets of features, which contained different number of features, ranging from five to 30. Each subset of features was used to train the SVM and ANN classifiers and differentiate nodule(s) by a leave-one-out procedure, and the AUCs of the two classifiers were calculated and listed in Table 4, and the related bar graph was shown in Fig. 4 and Fig. 5 illustrated the ROC curves of SVM and ANN with ten selected features. From Figs. 4 and 5, we see that the performance of SVM-based classifier in differentiating SPNs is better than that of the ANN-based classifier.
Table 4.
The AUC of SVM and ANN by Leave-one-out Procedure Using Different Feature Subsets
| Subset num. | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|
| SVM | 0.8714 | 0.8208 | 0.8721 | 0.8639 | 0.8865 | 0.8673 | 0.868 |
| ANN | 0.7825 | 0.7839 | 0.7592 | 0.8406 | 0.8406 | 0.7975 | 0.7613 |
| Subset num. | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| SVM | 0.8953 | 0.814 | 0.8598 | 0.8345 | 0.8871 | 0.8693 | 0.8748 |
| ANN | 0.8865 | 0.764 | 0.8256 | 0.7661 | 0.7497 | 0.7811 | 0.7674 |
| Subset num. | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| SVM | 0.8194 | 0.8632 | 0.8385 | 0.8433 | 0.7886 | 0.7879 | 0.8549 |
| ANN | 0.7661 | 0.7462 | 0.7763 | 0.7654 | 0.8358 | 0.7531 | 0.7798 |
| Subset num. | 26 | 27 | 28 | 29 | 30 | ||
| SVM | 0.8296 | 0.8310 | 0.7968 | 0.8091 | 0.7393 | ||
| ANN | 0.7832 | 0.7558 | 0.71 | 0.8187 | 0.816 |
Fig 4.
The ROC curves of SVM- and BP-ANN-based classifiers using ten selected features by the leave-one-out method.
Fig 5.
The AUCs of SVM- and BP-ANN-based classifiers by the leave-one-out method using different feature subsets.
Comparison of SVM-Based Classifier with the Radiologists’ Observation
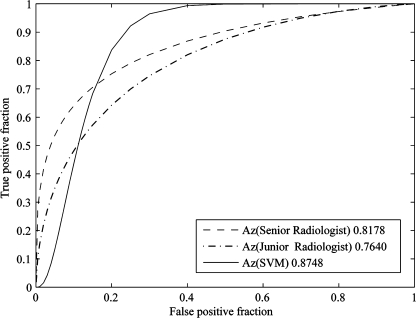
In order to evaluate the performance of SVM-based classifier in differentiating SPNs compared to radiologists’ observation, we set up an experiment to let two groups of radiologists read the 77 cases of CT images with SPNs. Group one had three senior radiologists who had more than 20 years of experience in reading lung CT images in radiology department of Huadong Hospital in Shanghai; group two had three junior radiologists who had 2 to 5 years in reading lung CT images. All of these two groups of radiologists had never read these images before. They used PACS diagnostic workstations with high-resolution monitors to read these images and marked the pathology of nodules as benignancy with −1 and malignancy with 1 independently. The senior radiologists had better performance in differentiating SPNs than juniors. To represent the performance of senior and junior radiologists respectively, we used the averaged results of senior radiologists and junior radiologists, respectively, as the likelihood of malignancy to generate the ROC curves for them. Figure 6 illustrated the ROC curves of senior and junior radiologists’ performance, as well as the SVM-based classifier with 17 selected features. From Fig. 6, we see that the SVM-based classifier had better performance in differentiating SPNs than radiologists.
Fig 6.
The ROC curves of radiologists′ average performance and the SVM-based classifier with 13 selected features. The SVM-based classifier had better performance in differentiating SPNs than average of radiologists.
Discussion
Comparison of the Selected Features with Other Reported Results
CAD studies have offered insight in differentiating benign and malignant SPNs. For example, McNitt-Gray et al.2 considered density distribution, area, and texture to classify 31 nodules by means of linear discriminant analysis, achieving an accuracy of 90.3%. As presented in “Feature Selection of CT Images with SPN,” these most frequently selected features in our research are the characteristics most commonly considered by radiologists in distinguishing benign from malignant nodules and also are consistent with data in the published literature.3,5,6,9 Except for these, we found that seven new features (GAB2, CORR1, HS2, CORR2, CORR4, GAB12, and HM3) represented in SVM-based feature space also have important impact on differentiating SPNs, and these newly found features should be included in feature index of a CBIR system for SPNs. Table 5 gives the comparison of the features selected (including times selected in evaluation process by using the genetic algorithm) in our research with the published literature.
Table 5.
The Comparison of the Features Selected in SVM-based Space in Evaluation Process by Using the Genetic Algorithm in our Research with Published Literature. Seven New Features Represented in SVM-based Feature Space have been Found to be Important on Differentiating SPNs, and these Features should also be Included in Feature Index of a CBIR System for SPNs
| Feature name | Times selected | Literature published | Description | Significance |
|---|---|---|---|---|
| HIST10 | 24 | Matsuki et al.1 | Pixel range [136 HU, ∼] | Calcification |
| KURT | 23 | Matsuki et al.,1 McNitt-Gray et al.,2 Nakamura et al.,3 Kawata et al.,5 Shah et al.7 | Kurtosis of the nodule | Shape |
| HIST4 | 22 | Nakamura et al.,3 Kawata et al.5 | Pixel range [−104 HU, −65 HU] | The range of fat |
| ENTR4 | 21 | McNitt-Gray et al.2 | The entropy of averaged concurrence matrix, step = 4 | Uniformity or complexity of the texture |
| MEAND | 19 | Matsuki et al.1, McNitt-Gray et al.,2 Nakamura et al.,3 Kawata et al.,5 Shah et al.7 | Mean diameters of the nodule | Shape |
| HIST1 | 18 | McNitt-Gray et al.,2 Shah et al.7 | Pixel range [∼, −185 HU] | Low attenuation pixels |
| ENTR3 | 18 | McNitt-Gray et al.2 | The entropy of averaged concurrence matrix, step = 3 | Uniformity or complexity of texture |
| GAB2 | 17 | Small Gabor filter responses at 45° | The spectrum of local image | |
| COMP | 16 | Nakamura et al.3 | Compactness of nodule | Roundness of the nodule |
| ENTR1 | 13 | McNitt-Gray et al.2 | The entropy of averaged concurrence matrix, step = 1 | Uniformity or complexity of the texture |
| PERI | 12 | Matsuki et al.,1 McNitt-Gray et al.,2 Nakamura et al.,3 Kawata et al.,5 Shah et al.7 | Perimeter of the nodule | Shape |
| ENTR2 | 11 | McNitt-Gray et al.2 | The entropy of averaged concurrence matrix, step = 2 | Uniformity or complexity of the texture |
| MEANV | 10 | Matsuki et al.,1 McNitt-Gray et al.,2 Nakamura et al.3 | Mean of the nodule pixels | Mean of nodule density |
| CORR1 | 10 | The correlation of averaged concurrence matrix, step = 1 | Correlation of local image | |
| HS2 | 10 | The standard deviation of Hurst parameters, scale = 2 | Roughness of an image | |
| CORR2 | 8 | The correlation of averaged concurrence matrix, step = 2 | Correlation of local image | |
| CORR4 | 8 | The correlation of averaged concurrence matrix, step = 4 | Correlation of local image | |
| GAB12 | 8 | Small Gabor filter responses at 135° | The spectrum of local image | |
| HIST3 | 7 | Nakamura et al.,3 Kawata et al.5 | Pixel range [−144 HU, −105 HU] | Nodule density |
| HIST5 | 7 | Nakamura et al.,3 Kawata et al.5 | Pixel range [−64 HU, −25 HU] | Nodule density |
| IDM2 | 7 | Nakamura et al.3 | The inverse difference moment of averaged concurrence matrix, step = 2 | Homogeneity of the texture |
| IDM3 | 7 | Nakamura et al.3 | The inverse difference moment of averaged concurrence matrix, step = 3 | Homogeneity of the texture |
| HM3 | 7 | The mean of Hurst parameters, scale = 3 | Roughness of an image |
Kernel Function Selection in SVM Classifier Construction
Although we chose the Gaussian kernel function to construct the SVM-based classifier in “ROC Analysis,” the feature distributions of selected features in SVM-based feature space depend on the kernel functions which map the selected features to SVM feature space. So, the performance of SVM-based classifier in differentiating SPNs may rely on selected kernel function. In this section, we will select the different kernel functions to construct and evaluate the SVM-based classifiers to see whether there is significant difference between these kernel functions in differentiating SPNs. Usually, there are multiple kernels that can be selected, and the potential candidate kernels can be linear, multiple polynomial, Gaussian, and sigmoid, such as:
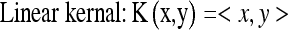 |
5 |
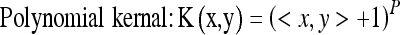 |
6 |
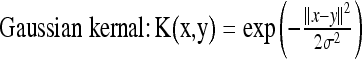 |
7 |
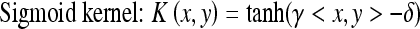 |
8 |
We used these kernel functions one by one to construct the SVM-based classifiers with different selected feature sets and then used these classifiers to classify the SPNs.
We used a leave-one-out procedure to carry out the evaluation in which one nodule was used for test purpose and the others were used for training the SVM-based classifiers until each example was used for test only once, same as Comparison of SVM- and BP-ANN-Based Classifiers. For a subset of features, the AUCs of SVM could be calculated using ROCKET.26 Table 6 gives the evaluation results of AUCs of SVM-based classifiers with different kernel functions on six subsets with feature numbers from five to 30. From Table 6, we can see that there is no significant difference between these kernel functions in differentiating SPNs since the average AUCs of SVM-based classifiers with different kernel functions are almost the same.
Table 6.
The AUCs of SVM-based Classifiers with Different Kernel Functions by Leave-one-out Procedures Using Different Feature Subsets
| Feature num. in a subset | AUCs of SVM with Gaussian | AUCs of SVM with linear | AUCs of SVM with polycon (power = 2) | AUCs of SVM with polycon (power = 3) |
|---|---|---|---|---|
| 5 | 0.825581395 | 0.870725034 | 0.856361149 | 0.893296854 |
| 10 | 0.859097127 | 0.863885089 | 0.834473324 | 0.892612859 |
| 15 | 0.856361149 | 0.831737346 | 0.744186047 | 0.865253078 |
| 20 | 0.868673051 | 0.831053352 | 0.800273598 | 0.881668947 |
| 25 | 0.807797538 | 0.765389877 | 0.794801642 | 0.79753762 |
| 30 | 0.819425445 | 0.883036936 | 0.764021888 | 0.763337893 |
| Average | 0.830106282 | 0.844286015 | 0.801720509 | 0.832789645 |
The reasons of selecting Gaussian kernel function in our research are: (1) the Gaussian model only has one parameter, and it is easy to construct the Gaussian SVM classifier compared to polynomial model which has multiple parameters; (2) the linear kernel function is a specific example of Gaussian model; (3) although both Gaussian and sigmoid models can realize the nonlinear mapping in high-dimensional space, there is less limitation in using Gaussian kernel function, but sigmoid may have invalidation values in some parameters. So, it is reasonable to choose Gaussian kernel function in constructing SVM-based classifier.
Reliability of Nodule Segmentation and Its Impact on the SVM-Based Classifier
Since the segmentation results of lung CT images with nodules would impact the feature extraction and selection for constructing SVM- or ANN-based classifiers, we should investigate the reliability of segmentation methods used in our research. In the following, we will perform some steps to evaluate whether our segmentation methods are reliable and how they impact on the SVM-based classifier.
In region-grow method, the threshold 800 was used as common value to perform the segmentation, but a user can adjust the threshold on individual case of image a little bit based on his or her visual evaluation on the results of segmented nodules. We chose four users to perform the segmentation on 77 cases of images, respectively. These four users can identify the boundary of most nodules by using the region-grow method from a user-specified seed point inside the nodule with adjustable thresholds or apply snake approach to refine the segmentation results on some (14 images) nodule images. So, we got four groups of segmented 77 cases of images which may have different segmentation results on these images. We performed feature extraction and feature selection on each of these four groups of images and used the selected features from each of the four groups to construct SVM-based classifier, respectively, then used leave-one-out procedure to calculate AUCs of these four SVM-based classifiers to evaluate their performance on differentiating SPNs. Table 7 shows the results of the comparison between four feature groups related to four user nodule segmentation results with region-grow and snake methods.
Table 7.
The AUCs of SVM-based Classifiers Constructed from Four Groups the Features of which were Extracted and Selected Based on Four Users′ Nodule Segmentation Results, Respectively
| Feature num. in a subset | User 1 | User 2 | User 3 | User 4 |
|---|---|---|---|---|
| 5 | 0.870041 | 0.863885 | 0.762654 | 0.825581 |
| 10 | 0.881669 | 0.889193 | 0.857729 | 0.859097 |
| 15 | 0.876197 | 0.856361 | 0.810534 | 0.856361 |
| 20 | 0.844733 | 0.853625 | 0.844049 | 0.868673 |
| 25 | 0.79959 | 0.850889 | 0.861833 | 0.807797 |
| 30 | 0.80301 | 0.790698 | 0.759234 | 0.819425 |
| Average | 0.837762 | 0.851705 | 0.82545 | 0.830106 |
From Table 7, we can see that our nodule segmentation methods are reliable for different qualified users to segment the SPNs on most lung CT images since the differences of segmentation results from different users with region-grow and snake segmentation methods have no significant impact statistically on the results of differentiating SPNs by using the SVM-based classifier.
Selected Features Potentially Used in CBIR System
In a medical CBIR system, the large amount of visual features and low-level image character features such as shape, texture, and granulometry are usually included to build the image-searching index,13 which is a multiple-dimension feature vector database and is linked to an image database storing related historical images with confirmed diagnostic results. The working principle of CBIR is to look for candidate images from the CBIR image database, the features of which are similar with that of an input image. As the numbers of character features of an image are usually very large such as more than hundreds or thousands, some of features are useful to label the image characters, and some are not. The image-searching efficiency (iteration times and costs of similarity calculation of every searching) of finding the right images from CBIR system are mostly dependent on the dimension numbers of feature vectors and selected correct features used to label image characters.10 The fewer the dimension numbers of feature vectors are, the less are the costs of similarity calculation of every searching. The more correct the features used to label image characters are, the more few are the itinerate searching times in CBIR searching procedure. So, it will greatly improve the performance of a CBIR system if we used more correct features to label image characters with fewer numbers of the features in building image-searching index.
With the results of this paper, we can use selected pattern features of SPNs to build searching index in a CBIR system for lung cancer CT images, which would have more searching efficiency than that without optimally selecting pattern features of SPNs from CT images,12 as the number of selected features are reduced from 67 to 17 without sacrificing the performance of classifiers in differentiating lung nodules.
Conclusions
In this paper, we presented a method for optimally selecting pattern features of SPNs from CT images, determined the usefulness of various selected pattern features for a CAD in differentiating SPNs or for a CBIR system in searching similar feature nodules, and evaluated the performance of support-vector-machine-based classifier in differentiating lung nodules.
Seventy-seven biopsy-confirmed CT cases of SPNs were included in this study. A total of 67 features were extracted by a feature extraction procedure, and 25 features were finally selected from these 67 features after 300 genetic generations. We constructed the SVM-based classifier with the selected features and evaluated the performance of the classifier by comparing the classification results of the SVM-based classifier with six radiologists’ observations and ANN-based classifier. The evaluation results showed that the SVM-based classifier had good performance in differentiating the benign from malignant SPNs compared to an average performance of radiologists in our research and was more accurate than the ANN-based classifier in distinguishing benign from malignant SPNs. This study results not only showed that most of the selected features are characteristics frequently considered by radiologists in classifying SPNs which are also consistent with the finding of CAD analyses previously reported but also indicated that some newly found features have important contribution to differentiating benign from malignant SPNs in SVM-based feature space.
The results of this research are not only helpful to improve CAD for diagnosis on SPNs but also useful to build the highly efficient feature index of a CBIR system for CT images with pulmonary nodules. We discussed the impacts of nodule segmentation results and kernel function selection on the performances of SVM-based classifier in differentiating benign from malignant SPNs.
Acknowledgements
The project was supported by the grants from the National Nature Science Foundation of China (grant no. 30570512) and Shanghai Science and Technology Committee (grant no. 064119658, 06SN07111). The authors would like to thank Dr. Xiaojun Ge for providing the CT images used in this study.
References
- 1.Matsuki Y, Nakamura K, Watanabe H, Aoki T, Nakata H, Katsuragawa S, Doi K. Usefulness of an artificial neural network for differentiating benign from malignant pulmonary nodules on high-resolution CT: evaluation with receiver operating characteristic analysis. Am J Roentgenol. 2002;178(3):657–663. doi: 10.2214/ajr.178.3.1780657. [DOI] [PubMed] [Google Scholar]
- 2.McNitt-Gray MF, Hart EM, Goldin JG, Yao CW, Aberle DR. A pattern classification approach to characterizing solitary pulmonary nodules imaged on high resolution computed tomography. Proc SPIE. 1996;2710:1024–1034. doi: 10.1117/12.237911. [DOI] [Google Scholar]
- 3.Nakamura K, Yoshida H, Engelmann R, MacMahon H. Computerized analysis of the likelihood of malignancy in solitary pulmonary nodules with use of artificial neural networks. Radiology. 2000;214:823–830. doi: 10.1148/radiology.214.3.r00mr22823. [DOI] [PubMed] [Google Scholar]
- 4.Shiraishi J, Abe H, Englemann R, Aoyama M. Computer-aided diagnosis to distinguish benign from malignant solitary pulmonary nodules on radiographs: ROC analysis of radiologists′ performance–initial experience. Radiology. 2003;227:469–474. doi: 10.1148/radiol.2272020498. [DOI] [PubMed] [Google Scholar]
- 5.Kawata Y, Niki N, Ohmatsu H, Kusumoto M, et al: Hybrid classification approach of malignant and benign pulmonary nodules based on topological and histogram features. In: Proc MICCAI 297–306, 2000
- 6.Silva AC, Paiva AC, Oliveira ACM. Comparison of FLDA, MLP and SVM in diagnosis of lung nodule. Lect Notes Comput Sci. 2005;3587:285–294. doi: 10.1007/11510888_28. [DOI] [Google Scholar]
- 7.Shah SK, McNitt-Gray MF, Rogers SR. Computer aided characterization of the solitary pulmonary nodule using volumetric and contrast enhancement features. Acad Radiol. 2005;12(10):1310–1319. doi: 10.1016/j.acra.2005.06.005. [DOI] [PubMed] [Google Scholar]
- 8.Yamashita K, Matsunobe S, Tsuda T, Nemoto T. Solitary pulmonary nodule: preliminary study of evaluation with incremental dynamic CT. Radiology. 1995;194:399–405. doi: 10.1148/radiology.194.2.7824717. [DOI] [PubMed] [Google Scholar]
- 9.Siegelman SS, Khouri NF, Leo FR. Solitary pulmonary nodules: CT assessment. Radiology. 1986;160:307–312. doi: 10.1148/radiology.160.2.3726105. [DOI] [PubMed] [Google Scholar]
- 10.Müller H, Michoux N, Bandon D. A review of content-based image retrieval system in medical applications-clinical benefits and future directions. Int J Med Informatics. 2004;73(1):1–23. doi: 10.1016/j.ijmedinf.2003.11.024. [DOI] [PubMed] [Google Scholar]
- 11.Fisher B, Deserno T, Ott B, et al. Integration of a research CBIR system with RIS and PACS for radiological routine. Proc SPIE. 2008;6919:691914–1–691914-10. doi: 10.1117/12.770386. [DOI] [Google Scholar]
- 12.Tan Y, Zhang J, Hua Y, Zhang G. Content-based image retrieval in picture archiving and communication system. Proc SPIE. 2006;6145:614515–1–614515-8. doi: 10.1117/12.652671. [DOI] [Google Scholar]
- 13.Deserno T, Antani S, Long RL: Ontology of gaps in content-based image retrieval. J Digit Imaging (in press), 2007 [DOI] [PMC free article] [PubMed]
- 14.Depeusinge A, Lavindrasana J, Hidki A, et al. A classification framework for lung tissue categorization. Proc SPIE. 2008;6919:69190C1–69190C12. [Google Scholar]
- 15.Silva AC, Carvalho PCP, Gattass M. Diagnosis of lung nodule using semivariogram and geometric measures in computerized tomography images. Comput Methods Programs Biomed. 2005;79:31–38. doi: 10.1016/j.cmpb.2004.12.008. [DOI] [PubMed] [Google Scholar]
- 16.Haralick RM. Statistical and structural approaches to texture. Proc IEEE. 1979;67:786–804. doi: 10.1109/PROC.1979.11328. [DOI] [Google Scholar]
- 17.Clausi DA, Jernigan ME. Designing Gabor filters for optimal texture separability. Pattern Recogn. 2000;33:1835–1849. doi: 10.1016/S0031-3203(99)00181-8. [DOI] [Google Scholar]
- 18.Manjunath B, Ma W. Texture features for browsing and retrieval of image data. IEEE Trans Pattern Analysis Mach Intell. 1996;18(8):837–842. doi: 10.1109/34.531803. [DOI] [Google Scholar]
- 19.Unser M. Texture classification and segmentation using wavelet frames. IEEE Trans Image Processing. 1995;4:1549–1560. doi: 10.1109/83.469936. [DOI] [PubMed] [Google Scholar]
- 20.Kaplan LM, Murenzi R. Texture segmentation using multiscale Hurst features. IEEE Int Conf Image Process. 1997;3:205–208. [Google Scholar]
- 21.Joachims T: Text categorization with support vector machines. In: Proceedings of European Conference on Machine Learning (ECML), 1998
- 22.Brown M, Grundy W, Lin D, Cristianini N, Sugnet C, Furey T, Ares M, Haussler D: Knowledge-based analysis of microarray gene expression data using support vector machines. 1999. http://www.cse.ucsc.edu/research/compbio/genex/genex.html. Santa Cruz, University of California, Department of Computer Science and Engineering
- 23.Shawe-Taylor J, Cristianini N. Kernel methods for pattern analysis. Cambridge: Cambridge University Press; 2004. [Google Scholar]
- 24.Fawcett T: ROC graphs: notes and practical considerations for data mining researchers. Technical report HPL-2003-4 HP Labs, 2003.
- 25.Canu S, Grandvalet Y, Guigue V, Rakotomamonjy A. SVM and kernel methods Matlab toolbox. Rouen: Perception Systèmes et Information, INSA de Rouen; 2005. [Google Scholar]
- 26.Metz CE: ROCKIT software. http://xray.bsd.uchicago.edu/krl/index.htm, 2006