Tamper Detection and Restoring System for Medical Images Using Wavelet-based Reversible Data Embedding

Abstract

Over the past few years, the billows of the digital trends and the exploding growth of electronic networks, such as worldwide web, global mobility networks, etc., have drastically changed our daily lifestyle. In view of the widespread applications of digital images, medical images, which are produced by a wide variety of medical appliances, are stored in digital form gradually. These digital images are very easy to be modified imperceptively by malicious intruders for illegal purposes. The well-known adage that “seeing is believing” seems not always a changeless truth. Therefore, protecting images from being altered becomes an important issue. Based on the lossless data-embedding techniques, two detection and restoration systems are proposed to cope with forgery of medical images in this paper. One of them has the ability to recover the whole blocks of the image and the other enables to recover only a particular region where a physician will be interested in, with a better visual quality. Without the need of comparing with the original image, these systems have a great advantage of detecting and locating forged parts of the image with high possibility. And then it can also restore the counterfeited parts. Furthermore, once an image is announced authentic, the original image can be derived from the stego-image losslessly. The experimental results show that the restored version of a tampered image in the first method is extremely close to the original one. As to the second method, the region of interest selected by a physician can be recovered without any loss, when it is tampered.

INTRODUCTION

Due to the explosive expansion of the Internet and the extensive development of multimedia technologies, we have stepped into the digital worldwild web age. The higher bandwidth and better quality of service (QoS) for both wired and wireless networks and lower cost and more familiar digital recording and storage devices have made it possible to create an efficient and convenient environment of e-health care. Among these applications of the Internet, electronic patient records (EPRs), which can be easily transmitted or received via e-mail by hospitals or clinics and exchanged through health care providers, play a decisive role. Typically, an EPR contains the personal information and health history of a patient, including name of the patient, physical examinations, prescriptions, historic pathology, laboratory examination reports, treatment procedure, diagnostic images, and so on.¹ The disclosure of an EPR may cause an individual some unexpected psychical, physical, and even financial losses and troubles. Therefore, the transmission of EPRs should be protected and provided in a secure manner. In this paper, we only focus on the diagnostic images of the EPR.

Diagnostic images, also called medical images, are obtained by computerized radiography, computed tomography (CT), ultrasound (US), magnetic resonance imaging (MRI), and so on. In comparison with the conventional analog imaging systems, the digital imaging systems nowadays provide more excellent processing capabilities, higher flexibility, and better cost-effectiveness. As a result, digital images are increasingly taking the place of their classical analog counterparts. Inspired by the current trend, more and more medical images are now stored in digital form. On the other hand, as a result of the availability of powerful image processing software packages such as Photoshop (Adobe Systems, USA) or PhotoImpact (Ulead Systems, Taiwan), anyone can easily modify such digital media for any desire and create unconscious forgeries. For this reason, how to prevent a medical image from being maliciously altered, that is, detecting the tampered parts and restoring the original image, becomes an important issue.

In order to safeguard digital images, various kinds of image protection mechanisms have been employed so far. Among these mechanisms, the image authentication schemes are the best known and the most widely used method by the contemporary computer systems. The existing image authentication systems may be classified into two categories: hard authentication and soft authentication. Both of them serve to ensure the integrity of the digital images. In the conventional image authentication,^2,3 also known as hard authentication, a sender creates a message authentication code (MAC) and encrypts it using an encryption algorithm. After that, he delivers the digital images and the encrypted MAC to the receiver. The receiver can obtain the digital images and the MAC when he decomposes the received package. By comparing the decrypted MAC and the generated MAC from the received images, the receiver can determine whether the received digital images are modified or not.

Another approach for image authentication is soft authentication.^4–6 Watermarking techniques are mostly used to achieve this goal. Generally, the authentication codes are usually derived from the prominent features of the original image and are embedded into the image directly. At the receiver, the embedded authentication codes are extracted to get the original feature vector and this vector is then compared with the feature vector calculated from the doubtful image. If the original image is tampered, these two feature vectors will be different.

However, the methods mentioned above not only modify but also distort the original image in an irreversible manner. The distortion, no matter how small, may cause that the modified medical images could not be used for further diagnosis because of the possibility of misdiagnosis. Recently, some lossless, also called reversible, data-embedding techniques have been reported in the literature.^7–9 These techniques, like their loss counterparts, embed the authentication messages by modifying the original image and making some degree of distortion. Nevertheless, they also have the capability of removing the embedded information and restoring the original content after the extraction of embedded data.

In this paper, we proposed two wavelet-based lossless data-embedding schemes for detecting and restoring a tampered medical image. The first scheme divides the image into several non-overlapped blocks of equal size. The average pixel value of each block is calculated and encoded by a symmetric key cryptosystem¹⁰ in terms of the recovery information and authentication message for the original image. Through the discrete wavelet transform (DWT),¹¹ the original image is changed from the spatial domain into the frequency domain. After the transform, the recovery information and authentication message will be hidden in the frequency domain. Finally, the inverse DWT is used to transform the image from the frequency domain to the spatial domain and then to build a stego-image, which can be publicized in its spatial domain. Once tampering has been detected, the tampered areas could be recovered with visually acceptable qualities by extracting the special characteristic features concealed in the stego-image. The second scheme allows the physicians to select a region of interest (ROI) for protection. Instead of using the average pixel values of blocks as the recovery features, the second scheme adopts all the pixel values of ROI. If this particular region is tampered, then it could be recovered without any loss.

The remainder of this paper is organized as follows. In the “Preliminaries” section, we will briefly describe the related techniques in this system. In the “Tamper Detection and Restoration” section, we will introduce our novel approach of tamper detection and restoration by using the lossless data-embedding technique. Then, the experimental results and performance analysis will be presented in the “Experimental Results” section. Finally, the conclusions and the directions of our future works will be given in the “Conclusions” section.

PRELIMINARIES

In this section, techniques involved in our method such as the symmetric key cryptosystem, Haar wavelet transform, and lossless data embedding will be introduced. Particularly, we will aim for the reversible watermarking by using a difference expansion.

Symmetric Key Cryptosystem

Cryptography is the art or science of keeping messages secret. If a single private key is used in the encryption and decryption processes, then the cryptographic algorithm is called the symmetric cryptography algorithm. One famous representation of the symmetric cryptography algorithm is the Advanced Encryption Standard (AES).¹⁰ Symmetric cryptography algorithms are typically fast and are suitable for processing large streams of data. In this technique, both the sender and the receiver must share the same secret key for data exchange. The sender applies the encryption function using the key to encrypt the plaintext and to produce the ciphertext. The ciphertext is sent to the receiver who then applies the decryption function using the same secret key. Because the plaintext cannot be derived from the ciphertext without knowledge of the key, the ciphertext can be sent over public networks such as the Internet. Obviously, the key distribution is the soul of the primary security concerns for data exchange using this algorithm. To achieve better security, it is necessary to protect the private key from disclosure of the third party and to change frequently. Furthermore, an appropriate key size is also required to ensure a greater security. Generally, a key of 512 bits is considered an acceptable size.

Haar Wavelet Transform

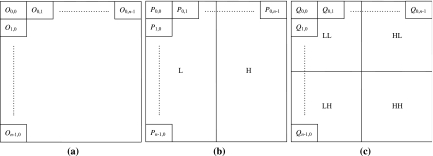
DWT is a common image processing skill of transforming an image in the spatial domain into its frequency domain. In this paper, we choose the well-known DWT, Haar wavelet transform, to cope with the images. The basic idea of the Haar wavelet transform is calculating the average and difference values for each pair of pixel values and is illustrated as follows. Generally, there are two steps in the Haar wavelet transform for an image, the horizontal division and the vertical division. In the horizontal division, as shown in Figure 1a, we choose each pair of pixel values from left to right and compute the addition

1

and the subtraction

2

where O is the image in the spatial domain with size of n × n, P is derived from O after the horizontal phase, and O_i,j and P_i,j denote the pixel values of location (i,j) for images O and P, respectively as shown in Figure 1b. As to the vertical division, we choose each pair of pixel values from top to bottom and compute the addition

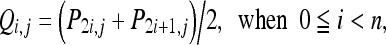3

and the subtraction

4

where P is derived from O after the horizontal phase, Q is derived from P after the vertical phase, both of them with size n × n, and P_i,j and Q_i,j denote the pixel values of location (i, j) for images P and Q, respectively, as shown in Figure 1c. The image Z now is decomposed into four parts, low, middle, and high frequencies denoting LL₁, LH₁, HL₁, and HH₁. The subbands labeled LH₁, HL₁, and HH₁ represent the finest scale wavelet coefficients. On the contrary, the subband LL₁, which contains most of the energy in the image, is the coarse overall shape. To obtain the next coarser scaled wavelet coefficients, the subband LL₁ alone is further decomposed into LL₂, LH₂, HL₂, and HH₂. This process may be repeated several times until some final scale is reached, if necessary.

Fig 1.

Two steps of DWT: (a) spatial domain; (b) horizontal channel; (c) vertical channel.

Lossless Data-embedding Technique

One common drawback of most data-embedding techniques is the fact that the original image has the unavoidable embedding distortion and this distorted image cannot be recovered to the original one, pixel by pixel. The main reason why this distortion cannot be removed completely is the loss of image fidelity owing to the quantization, bit replacement, or integer bounding at the boundaries of the gray levels, 0 and 255 for the 8-bit grayscale images. Although the distortion is often very slight and various kinds of perceptual models are used to minimize its visibility, the distortion may be unacceptable for medical images for obvious legal reasons and a potential risk of misinterpretation of an image by a physician. Therefore, the need for lossless data-embedding techniques has recently been highlighted to solve this problem.

The concept of lossless data-embedding technique first appeared in the authentication patent of Honsinger et al¹² at the Eastman Kodak company. The authors employ the additive spread spectrum techniques in which the addition has been replaced with modulo 256 to embed data in the spatial domain. Although the modulo addition prevents the potential problems associated with the limited range of pixel values in the digital representation of the original image, for instance, overflows and underflows during addition and subtraction, it may introduce some distortion into the watermarked image when pixel values with grayscales close to zero are flipped to values close to 255, or pixel values with grayscales close to 255 are mapped to values close to zero. Thus, the visual quality of a watermarked image is degraded because of the appearance of annoying salt-and-pepper noise. To overcome this problem, J. Fridrich et al⁷ adopted the JBIG lossless compression scheme¹³ to compress the least significant bit (LSB) planes. In this method, they decompose an image into bit planes and then replace the LSB planes of the image with a bit stream containing the authentication information obtained by calculating the whole image hash bits and the compressed form of the original LSBs. Because of the lossless compression of the LSBs, they not only create an additional space to fill up the watermarked payload, but also make it possible to allow for the reconstruction of original image. Later, they utilized other schemes such as the RS-embedding scheme and an order-2 function (whose inverse function is itself) to improve the hiding capacity or reduce the embedding distortion. Vleeschouwer et al⁸ proposed a reversible data-embedding algorithm by the circular interpretation of objective transformations that fulfills all quality and functionality requirements of lossless watermarking.

Tian’s Difference Expansion

The main idea of Tian’s method⁹ is performing the integer Haar wavelet transform in a row-by-row or column-by-column manner. Given a grayscale image O with size m × n, where m and n denote the number of rows and columns, respectively, without losing generality, we can assume that n is even. For a grayscale-valued pair (x, y), where x and y are adjacent to each other, x and y are integers and are bounded in [0, 255]. The row-by-row integer-valued Haar wavelet transform maps the pair (x, y) onto another pair (l, h) given by

5

where the symbol ⌊.⌋ is the floor function meaning “the greatest integer less than or equal to.” For example, ⌊3.5⌋ = 3, ⌊−4.7⌋ = −5. The inverse integer Haar wavelet transform of Eq. (5) is

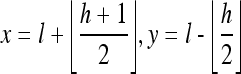6

The integer Haar wavelet transform in Eq. (5) maps the original image O onto a low-pass band L with L(i, j) = l and a high-pass band H given by H(i, j) = h in a row-by-row manner. Therefore, the sizes of L and H are both m × n/2. By modifying the values of high-pass band H, for instance, shifting left one bit in its binary representation and adding a new bit, which you like to embed, in the least significant bit, the data embedding can be carried out easily. Owing to the limit of grayscale value, it must be bounded in the range of [0, 255], such that

7

As both l and h are integers, one can derive that the above inequalities are equivalent to

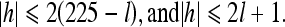8

To prevent the overflow and underflow problems, the difference value h after data embedding must satisfy constraint (8). As long as h is in such range, it is guaranteed that x and y computed from equality (6) will still be in the range of [0, 255]. It is easy to see the constraint (8) is equivalent to

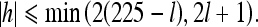9

The algorithm can be explained with the running steps and be simulated through a simple example below.

Embedding Procedure

• Step 1:

  Assume that we have two grayscale values x = 206, y = 201, and we would like to embed one bit b, with b ∈ {0, 1} into (x, y).

• Step 2:
  Compute the average and difference values of x and y,

  

  The integer Haar wavelet transform maps the pair (x, y) = (206, 201) onto another pair (l, h) = (203, 5).
• Step 3:

  Expand the difference number h into its binary representation, h = 5 = 101₂.

• Step 4:

  Add b = 1 into the binary representation of h at the location right after the least significant bit (LSB), and we can get h′, h′ = 101b₂ = 1,011₂ = 11.

• Step 5:
  Compute the new grayscale values by l and h′,

  

  The inverse integer Haar wavelet transform maps the pair (l, h′) = (203, 11) onto another pair (x′, y′) = (209, 198).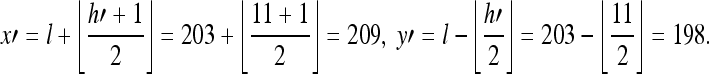

Extracting Procedure:

• Step 1:
  Compute the average and difference values of the embedded pair (x′, y′),

  

  The integer Haar wavelet transform maps the pair (x′, y′) = (209, 198) onto another pair (l′, h′) = (203, 11).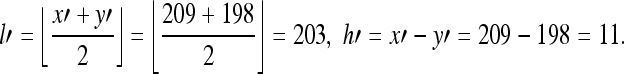
• Step 2:

  Expand the difference number h′ into its binary representation, h′ = 11 = 1,011₂ = 101b₂, and extract the LSB, which is “1” in this case, as the embedded bit b.

• Step 3:

  Remove the embedded bit b from the binary representation of h′, we can get h″, h″ = 101₂ = 5.

• Step 4:

  With the average vaule l′ and difference value h″, we can restore exactly the original grayscale values.Since both x and y are integers, we can get only one solution that x = 206 and y = 201, when 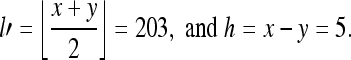The inverse integer Haar wavelet transform maps the pair (l′, h″) = (203, 5) onto another pair (x, y) = (206, 201).

Unfortunately, medical images often have large amounts of pixel value with grayscales close to zero or 255, which cannot satisfy the constraint (9). To overcome this problem, we will give a solution in the next section.

TAMPER DETECTION AND RESTORATION

In this section, two wavelet-based lossless data-embedding methods are proposed to detect tampering and to recover the original image from a tampered medical image. One method is able to recover the whole blocks of the image and another method enables to recover only a particular region where a physician will be interested in, with a better visual quality.

The Method with Ability to Recover the Whole Image

In this method, the tamper detection and restoring system can be carried out for the whole image. First, we divide the host image into several blocks of equal size. The recovery information and the authentication message are generated from each block by counting its average pixel value. After encrypting and scattering, these features will be concealed into the original image by a modified Tian’s lossless data-embedding scheme. Then, we can get the stego-image. By comparing the embedded features beforehand with the calculated features in hand, a physician can perceive whether an image is tampered or not easily, when he receives the stego-image from the public networks. If any modifications are detected, the tampered positions will be pointed out and the previous concealed features will be extracted to recover the tampered areas. On the contrary, if all blocks of the stego-image are authentic, it can be announced that the stego-image is not tampered. Furthermore, the original image can be derived from the stego-image by removing the embedded information. This method consists of two procedures, the embedding procedure and the verification procedure.

Embedding Procedure

The embedding procedure includes three components: the feature extraction, encryption, and embedding. The algorithms of these processes are described step by step as follows.

Feature Extraction The first step of the embedding procedure is to generate the recovery features. Certainly, the more recovery features extracted, the better visual quality the recovery image will have; on the other hand, however, more recovery features collected also brings about more distortion to the original image. To give careful consideration to both visual quality of the stego-image and the recovery image, it is necessary to limit the amount of recovery features. In our scheme, the original image O is divided into non-overlapping blocks of 4 × 4 pixels, where O = {o₁, o₂, ..., o_x} and x = n/4 × n/4. Later, we count the average pixel value of each block as the recovery feature F. Consequently, every block has a possession of 8 bits storage space, and the total size of recovery features are t = 8 × x bits so that F = {f₁, f₂, ..., f_t}, where f_i ∈ {0, 1}, for i = 1, 2, ..., t.

Feature Encryption If someone can take out the embedding features and modify them easily to pass the verification procedure for illegal purpose, the embedding features will become suspect and unreliable. For this reason, the embedding features need to be encrypted. Hence, in this paper, we sequentially use two secret keys, K₁ and K₂, as the seeds of pseudorandom number generators to disperse the features twice. By this way, it would increase the degree of security with low computational time.A pseudo-random number generator with a secret key K₁ as the seed of random number is employed to generate a series of binary strings B with size t, where B = {b₁, b₂, ..., b_t}. An encrypted binary string C = {c₁, c₂, ..., c_t} can be obtained by performing the Excusive OR (XOR) computation for each element between F and B.

10

Then, the second secret key K₂ is the seed of pseudorandom number generator H to disperse C and get C′ = {c₁′, c₂′, ..., } before embedding. The hash formula is as follows.

11

Feature Embedding As mentioned before, the key point of Tian’s difference expansion for each pair of pixel values is to create an additional hiding space from expanding the difference value without changing the average value. To hold out the average value invariably and losslessly in the future, the injury of difference value in the frequency domain adopts a concept of “share injury equally” in the spatial domain.⁹ That is, one half of injury is added by one pixel value and one half of injury is subtracted by the other pixel value in the spatial domain. For example, a grayscale-valued pair (206,201) with average equals to 203 and the difference equals to 5. After embedding 1 bit into the difference in the frequency domain, the difference changes from 5 to 11, and the injury of difference equals to 6. By sharing the injury equally in the spatial domain, the grayscale-valued pair (206,201) is turned into (209,198). Unfortunately, this method cannot show the same excellent performance when it is applied in medical images. By virtue of large amount of grayscale values close to zero or 255 in medical images, most of pixel pairs will encounter overflow or underflow problems when they execute the embedding procedure of Tian’s difference expansion. Namely, only a few of difference values in the medical images could be expandable to embed the information. To solve this problem, we can do only one operation, addition or subtraction. For instance, we only do addition for a grayscale value exactly equal to zero or do subtraction for a grayscale value exactly equal to 255, instead of doing both of them, as the value of addition and subtraction is the same. Take a block with size 2 × 2 for example. Through the integer Haar wavelet transform, if we want to embed something in the frequency domain, the element of the spatial domain must be changed as follows:

1. When the injury of embedding in the upper right element in the frequency domain is “hl”, two elements in Tian’s algorithm should be changed for the corresponding block in the spatial domain. It is necessary to subtract “hl/2” from the upper left element and add “hl/2” to the upper right element. Instead of it, we keep the upper left element unchanged, add “hl/2” to the upper right element if the upper right element exactly equals to zero or subtract “hl/2” to the upper right element when the upper right element exactly equals to 255.

2. When the injury of embedding in the lower left element in the frequency domain is “lh,” two elements in Tian’s algorithm should be changed for the corresponding block in the spatial domain. It is necessary to subtract “lh/2” from the upper left element and add “lh/2” to the lower left element. Instead of it, we keep the upper left element unchanged, add “lh/2” to the lower left element if the lower left element exactly equals to zero or subtract “lh/2” to the lower left element when the lower left element exactly equals to 255.

3. As to the injury of embedding in the lower right element in the frequency domain, let it be “hh.” Four elements in the Tian’s algorithm should be changed for the corresponding block in the spatial domain. There is a need to add “hh/4” to the upper left and the lower right elements; at the same time, “hh/4” should be subtracted from the upper right and the lower left elements. Instead of it, we keep the upper left, the upper right, and the lower left elements unchanged, add “hh/4” to the lower right element if the lower right element exactly equals to zero or subtract “hh/4” to the lower right element when the lower right element exactly equals to 255.

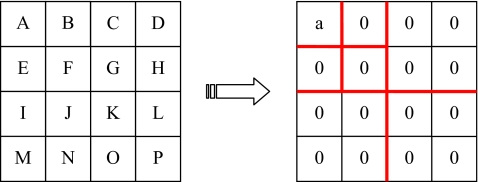
Our alternative method needs to find out all the smooth blocks first. The definition of smooth block in our system is that after performing the wavelet transform, only low pass band has nonzero value; the coefficients of the remainder high subbands must be zero, as shown in Figure 2. In our scheme, smooth block with size 4 × 4 is preferable, because it has more space for hiding the information. A 4 × 4 smooth block will have 15 elements to embed, but only 12 elements from four 2 × 2 smooth blocks can be used to embed. When embedding, we always keep the upper leftmost element in the smooth block unchanged. If the upper leftmost element exactly equals to zero, we do addition to those elements that need to be changed; conversely, we do subtraction to those elements that need to be changed when the upper leftmost element exactly equals to 255. To prevent erroneous judgment from a stego-image in the verification procedure, the lower rightmost element in the smooth block is wasted to embed a specific nonzero value, and the specific nonzero value only be kept by the sender and receiver. After embedding all recovery features, we will get a stego-image O′ and this image can be open in public.

Fig 2.

A smooth block with size of 4 × 4.

The Verification Procedure

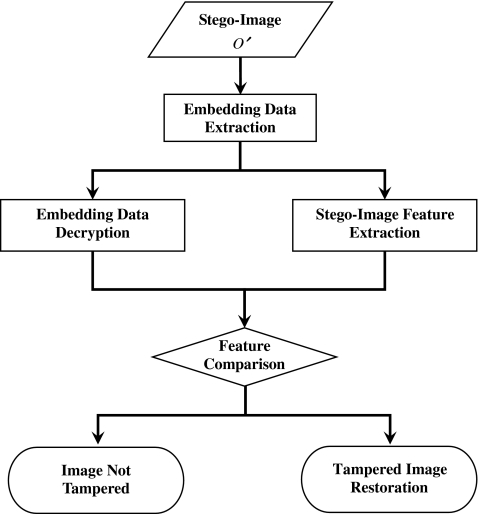
The verification procedure is to check whether a stego-image O′ is tampered or not. If the image is tampered, the restoring system will start. Otherwise, the original image will be derived from stego-image without any loss. The process of the verification procedure is shown in Figure 3.

Fig 3.

The flowchart of verification procedure.

Embedding Data Extraction To verify the integrity of a stego-image, the embedding features concealed in the image must be extracted first. Because the elements in the low pass band of the 4 × 4 smooth block remain unchanged during the previous embedding procedure, the specific nonzero value embedded in the lower rightmost element, and the range of injury of difference is limited, we can find the blocks with embedding features easily. Through the second secret key K₂, the scattered embedding features can be returned to the encrypted recovery features E = {e₁, e₂, ..., e_t} by the following formula,

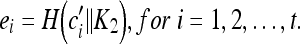12

Here H is a pseudorandom number generator. Although an intruder can extract the embedding features, he can only acquire a meaningless and useless sequence of features without K₂.

Embedding Data Decryption When the physician gets the encrypted recovery features E, he has to use the sender’s secret key K₁ for decryption. The pseudorandom number generator with secret key K₁ as the seed of random number can produce the same series of binary strings B = {b₁, b₂, ..., b_t} with size t. By performing the XOR computation for each element between E and B, the physician can obtain the original embedding recovery features D = {d₁, d₂, ..., d_t}. To the intruder, without K₁, he has no chance to erase or add something meaningful.

13

Here, e_i and b_i denote the ith element in E and B, respectively.

Stego-image Feature Extraction After extracting the embedding data E from stego-image O′, the same way of extraction in the embedding procedure may repeat for O′ to get a series of compared features F′ = .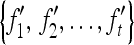

Feature Comparison It is easy to know whether a stego-image O′ is tampered or not by comparing the features D derived from the embedding procedure and the other features F′ obtained from the verification procedure. If they are identical, undoubtedly, O′ is considered to be authentic and the original image O can be acquired from O′. Oppositely, if there is any disagreement between the features, O′ must be tampered and would be restored using the feature D. Each 4 × 4 block has its corresponding recovery value represented by 8 successive binary bits in feature D. While the block is tampered, the recovery bits would be acquired. Then, all the pixel values within the tampered block would be restored by the recovery value.

The Method with Ability to Recover ROI

Because of the limit of embedding capacity, the recovery image may be unperceptive by the human eyes although it loses some slight information. However, if such slight information is the most important part of medical images, it may cause the possibility of misdiagnosis. Therefore, for more precise diagnosis, a physician must concern himself with some particular regions in some cases; for instance, the microcalcifications of an x-ray mammography image. The areas containing microcalcifications can be called the region of interest (ROI). To recover the ROI with better visual quality, the method mentioned in “The Method with Ability to Recover the Whole Image” subsection needs to be modified slightly.

To begin with, a physician needs to select any block as the ROI block. The main difference from the previous method is that only the recovery information of ROI is embedded in this method. Namely, only the most important recovery information will be hidden in the stego-image; consequently, instead of using the average pixel values of blocks with size 4 × 4, we have enough space to embed all the pixel values of ROI block.

EXPERIMENTAL RESULTS

In this section, we will describe the experiments in detail and discuss the experimental results. The operating environment used for our experiments includes a personal computer with Pentium IV 2.8 G MHz CPU, 512 MB RAM, and the platform Windows XP. Two grayscale medical images, x-ray mammograms with image size 512 × 512 pixels and 256 gray levels (8 bits/pixel), as shown in Figure 4a and Figure 5a, have been the target for testing the ability of tamper detection and restoration. The experimental results are discussed in two aspects. One is the ability to recover the whole image and the other is the ability to recover the ROI. This study was approved by the local ethics committee and informed consent was obtained from all included patients.

Fig 4.

(a) Original image; (b) stego-image; (c) tampered image; (d) positions of tampered area; (e) recovered image.

Fig 5.

(a) Original image; (b) stego-image; (c) tampered image; (d) positions of tampered area; (e) recovered image.

In general, except for human eyes, the common tool to estimate an image quality is the peak signal-to-noise ratio (PSNR) value. The PSNR formula is defined as follows:

14

15

where n and m are the width and height of an image, and O_ij and denote the original pixel values and the processed pixel values, respectively.

Whole-image Recovery

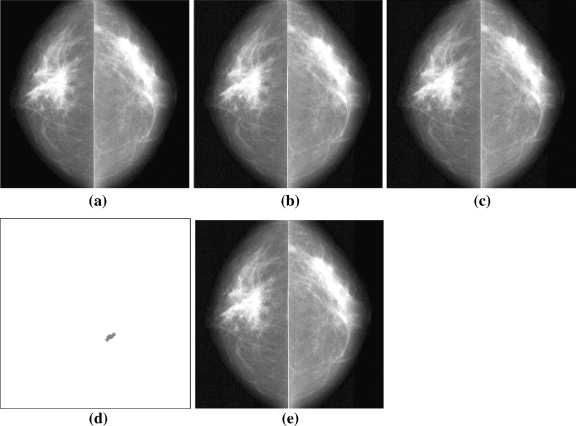
In the embedding phase, the lossless data embedding technique is executed to obtain the stego-images, as shown in Figure 4b and Figure 5b. The PSNR values of this watermarked image are 40.54 and 39.45 dB, and all the authors confirmed it is not perceivable on the sense of sight. Then, we produce the tampered images, as shown in Figure 4c and Figure 5c, respectively. The artificial distortions in Figure 4b are changing the letter “R” of upper left part to “P”, adding a black spot in the left half part, and blurring a small block in the right half part. As to Figure 5b, we add some microcalcifications in it. In the verification phase, if the concealed features are not identical to the calculated features, the image must be tampered. The tampered areas for Figure 4c and Figure 5c are shown clearly in Figure 4d and Figure 5d. When the verification scheme confirms an image has been tampered with, the restoration is then performed. Our system can successfully recover the previous tampered areas to get a recovery image with PSNR value 39.90 and 39.43 dB, as shown in Figure 4e and Figure 5e, respectively.

However, in some cases, owing to the limitation of recovery features, the recovered image may not be satisfied. For instance, small but important pieces, like the microcalcifications, are wiped out, as shown in Figure 6a. The tampered area can also be detected by our system correctly, as shown in Figure 6b; nevertheless, the recovered image, as shown in Figure 6c, still loses the information of microcalcifications and is too obscure to recognize, although its PSNR value is up to 38.55 dB.

Fig 6.

(a) Tampered image; (b) positions of tampered area; (c) recovered image.

ROI Recovery

From the second experiment in the “Whole-image Recovery” section, there are some important regions for diagnosis; for instance, the microcalcifications of an x-ray mammography image, that should be recovered with a better visual quality. Because microcalcifications are an early sign of breast cancer and the microcalcification detection is one of the key issues for breast cancer screening¹⁴, the region containing the microcalcifications should be highly protected. This particular region could be called the region of interest (ROI).

In the second method, a physician could select any important block as the ROI block, as shown in Figure 7a. After embedding the recovery information of ROI, the stego-image with PSNR value 36.38 dB is produced, as shown in Figure 7b, and the tampered image with wiped off microcalcifications is shown in Figure 7c. Figure 8 illustrates the tampering process within the ROI image. Figure 8a is the original ROI image, Figure 8b indicates the positions of the tampered area, and Figure 8c shows the tampered result. Finally, the recovery result is shown in Figure 7d, and we can see that the areas containing microcalcifications are visibly clearly.

Fig 7.

(a) To select the ROI with the microcalcifications; (b) stego-image; (c) tampered image (the microcalcifications are wiped off); (d) recovered image with microcalcification.

Fig 8.

Comparison between original ROI and tampered ROI of Figure 7(a). (a) Original ROI; (b) positions of tampered area; (c) tampered ROI.

CONCLUSIONS

In this paper, we have proposed two wavelet-based lossless data-embedding methods to detect tampering and to recover the original image from a tampered medical image. Our system not only can detect the tampered positions of the stego-image, but also can recover the content of the modified image. Furthermore, once a watermarked image is announced authentic, the original image can be derived from the stego-image losslessly.

Our first method can recover the whole image by the concealed features, the average pixel value of each 4 × 4 block, in the stego-image. Obviously, the recovered image in this method may be obscure in some cases. To solve this problem, our second method is proposed to let physicians select a particular region as ROI to protect the crucial information such as the microcalcifications of an x-ray mammography in regular follow-up and differential diagnosis of breast malignancy. Instead of using the average pixel values of blocks with size 4 × 4 as the recovery features, the second method adopts all the pixel values of ROI. Hence, we are able to have a recovered image with high image quality while comparing series of x-ray films in clinical practice. It is also impossible for anyone to exert himself trying to decode the embedding features or to pass the verification procedure, without the secret keys. It seems quite reasonable for medical images to adopt the ROI concept in our second method because the physicians and the malicious intruders are always devoting their attention to those regions.

The results presented in this paper are preliminary, and more validation and further expansion are required. In future work, we expect to expand the proposed methods to accommodate mammograms with greater bits per pixel, such as 12 or 16 bits, and the ROI to be selected more flexibly, such as more than one region could be considered or any type of shapes. Besides, the issue of recovery feature selection for better image quality also attracts us.