Power Spectral Analysis of Mammographic Parenchymal Patterns for Breast Cancer Risk Assessment

Abstract

Purpose: The purpose of the study was to evaluate the usefulness of power law spectral analysis on mammographic parenchymal patterns in breast cancer risk assessment. Materials and Methods: Mammograms from 172 subjects (30 women with the BRCA1/BRCA2 gene mutation and 142 low-risk women) were retrospectively collected and digitized. Because age is a very important risk factor, 60 low-risk women were randomly selected from the 142 low-risk subjects and were age matched to the 30 gene mutation carriers. Regions of interest were manually selected from the central breast region behind the nipple of these digitized mammograms and subsequently used in power spectral analysis. The power law spectrum of the form 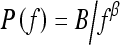was evaluated for the mammographic patterns. The performance of exponent β as a decision variable for differentiating between gene mutation carriers and low-risk women was assessed using receiver operating characteristic analysis for both the entire database and the age-matched subset. Results: Power spectral analysis of mammograms demonstrated a statistically significant difference between the 30 BRCA1/BRCA2 gene mutation carriers and the 142 low risk women with an average β values of 2.92 (±0.28) and 2.47(±0.20), respectively. An A_z value of 0.90 was achieved in distinguishing between gene mutation carriers and low-risk women in the entire database, with an A_z value of 0.89 being achieved on the age-matched subset. Conclusions: The BRCA1/BRCA2 gene mutation carriers and low-risk women have different mammographic parenchymal patterns. It is expected that women identified as high risk by computerized feature analyses might potentially be more aggressively screened for breast cancer.

Introduction

Mammography is a valuable tool for the early detection of breast cancer^1,2 and has been regularly used for breast cancer screening. An estimated 178,480 new cases of invasive breast cancer are expected to occur among women in the USA in 2007.³ Many factors increase a woman’s risk of developing breast cancer,^4,5 with the inherited susceptibility genes, most notably BRCA1 and BRCA2, accounting for approximately 5–10% of all cancer cases. Approximately 50% of these gene mutation carriers will develop breast cancer by the age of 50 years.^6–9 Therefore, a woman at high risk of developing breast cancer is expected to benefit from close surveillance and aggressive screening for breast cancer.

Mammographic parenchymal patterns have been studied extensively^10–25 to demonstrate the relationship between breast density and the risk of developing breast cancer. Wolfe¹⁰ described the mammographic parenchymal patterns with four categories (N1, P1, P2, and DY) based on the radiographic appearance of prominent ducts and dysplasia. Visual estimation of the percentage of fibroglandular tissue on the mammogram as breast density has also been used to characterize the breast parenchymal patterns.^12,13 Quantitative breast density estimation and mammographic pattern characterization based on computerized texture analyses^14–25 have been also investigated using digitized mammograms. Numerous studies^13,18–20 have shown that increased mammographic breast density yields as high as a five- to sixfold increase in risk of developing breast cancer.

In our earlier studies,^21,22 regions of interest (ROIs) were selected from the central breast region behind the nipple, and then computerized radiographic features were extracted from the ROIs to characterize both breast density and the parenchymal texture patterns of the breast. Our results showed that women at high risk of developing breast cancer tended to have dense breasts with mammographic patterns that were coarse and low in contrast. Our results also suggested that there was a statistically significant decrease in the performance of the computerized texture features in the task of distinguishing between high-risk and low-risk women groups, as the ROI location was varied from the central region behind the nipple.²³

Power law spectrum of the form 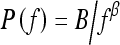has recently been shown by Burgess et al. to be related to the background parenchymal pattern of breast structure on mammography.^26,27 Thus, in our current study, we investigate such power law spectral analysis on the digitized mammograms of two groups of women—BRCA1/BRCA2 gene mutation carriers and low-risk women. Power spectral analyses were performed on selected ROIs, and the performance of the individual image β value, as the decision variable in the task of differentiating between BRCA1/BRCA2 gene- mutation carriers and low-risk women, was evaluated using receiver operating characteristic (ROC) analyses.^28,29

Materials and Methods

Database

The cases used in this study are summarized here and have been described in detail elsewhere.²² Women with known BRCA1 and BRCA2 gene mutations were recruited from the Cancer Risk Clinic at the University of Chicago and the University of Pennsylvania Cancer Center where genetic counseling is available for women at high risk of developing breast cancer. The gene mutation carriers were tested at the Clinical Laboratory Improvement Amendments-approved laboratories under the institution review board-approved protocols at both institutions. For women known to have breast cancer, we only used mammograms that were obtained before the cancer diagnosis. These prior mammograms were reviewed by an expert mammographer and were included only if they were free of any detectable abnormalities. The 30 BRCA1 and BRCA2 gene mutation carriers had ages 33 to 55 years, with a mean age of 42.7 years.

The mammograms of 142 low-risk women from the screening mammography program at the University of Chicago Hospitals were also obtained. These mammograms were of women who had no family history of breast or ovarian cancer and no prior history of breast cancer or benign breast disease. These women had a less than 10% lifetime risk of developing breast cancer based on the Gail model.³⁰ Because age is one of the most important risk factors, 60 low-risk women were randomly selected and age matched to the 30 BRCA1 and BRCA2 mutation carriers at 5-year intervals for the study.

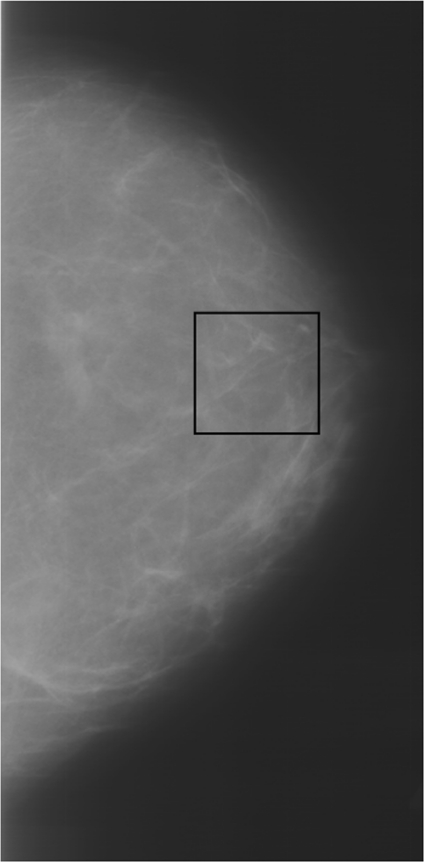
All mammograms were digitized using a laser film digitizer (Konica LD 4500; Konica Medical, Wayne, NJ) at 100 × 100-μm² pixel size and 10-bit quantization level. The laser film digitizer was routinely calibrated to assure that film optical density in the range of 0.0 to 3.5 is linearly translated into digital pixel values. ROIs, 256 by 256 pixels in size, were manually selected from the central breast region behind the nipple,²³ as they usually include the most dense part of the breast. These ROIs were used for subsequent power law spectral analyses. An example of a selected ROI from a breast image is shown in Fig 1.

Fig. 1.

A selected ROI from central breast region behind nipple on a digitized mammogram.

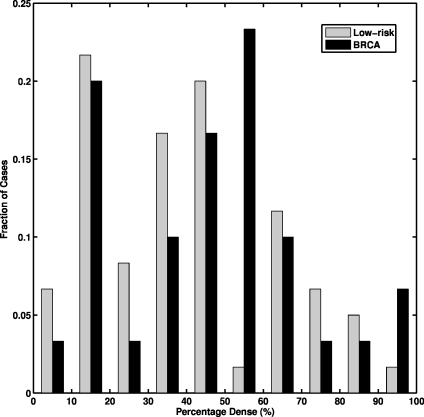
The breast percentage dense was estimated by an expert breast radiologist for the age-matched data set. The histogram of the percentage dense distribution is shown in Fig. 2. The 30 gene mutation carriers have breast percentage dense ranging from 5 to 90%, with a mean of 43%, and the 60 age-matched low-risk women have breast percentage dense ranging from 3 to 90%, with a mean of 37% (p = 0.22 from a two-tailed t test for the difference between the two groups).

Fig. 2.

The histogram of breast percentage dense for the 30 BRCA1/2 gene mutation carriers and the 60 age-matched low-risk women.

Power Law Spectral Analysis

Power law spectral analysis performed in this study is based on the power spectrum from the discrete Fourier transformation (DFT) of the ROI image data. The discrete Fourier transform³¹ of an ROI image, f(m, n), of size M by N is given by

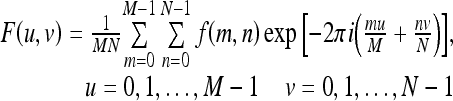1

where u and v are the spatial frequencies in the x and y directions, respectively.

The ROI image used in our study has a finite number of data samples, which can be represented by the two-dimensional Rect function in spatial domain and results in a two-dimensional sinc² function in the spatial frequency domain.²⁶ To reduce the discontinuity in the spatial domain, a window function is applied on the ROI image before the DFT.²⁶ The radial window function is based on a Hanning window function,^26,32,33h(r), which is given by

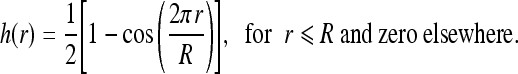2

The power spectrum, P(f) (also called spectral density), is given by

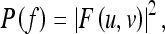3

where 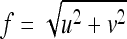is radial frequency.

The power law spectrum²⁶ is defined by

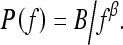4

This power law spectrum was calculated using selected ROI images. The algorithm used for estimating the exponent β for an ROI image is as follows: (1) Compute the power spectrum of the ROI image, (2) average the power spectrum along a radial slice, and (3) estimate the exponent β from the least squares fit of the power law spectrum up to the Nyquist frequency.^26,34

Computer-extracted Feature

As noted earlier, mammograms from both BRCA1 and BRCA2 gene mutation carriers and low-risk women were included in this study. The exponent β was estimated for each image and was used as a computer-extracted feature (i.e., the mathematical descriptor) to characterize the mammographic parenchymal pattern of the specific mammogram. The usefulness of the exponent β as a decision variable in the task of differentiating between the BRCA1 and BRCA2 gene mutation carriers and the women at low-risk of developing cancer was evaluated using ROC analysis.^28,29

Results

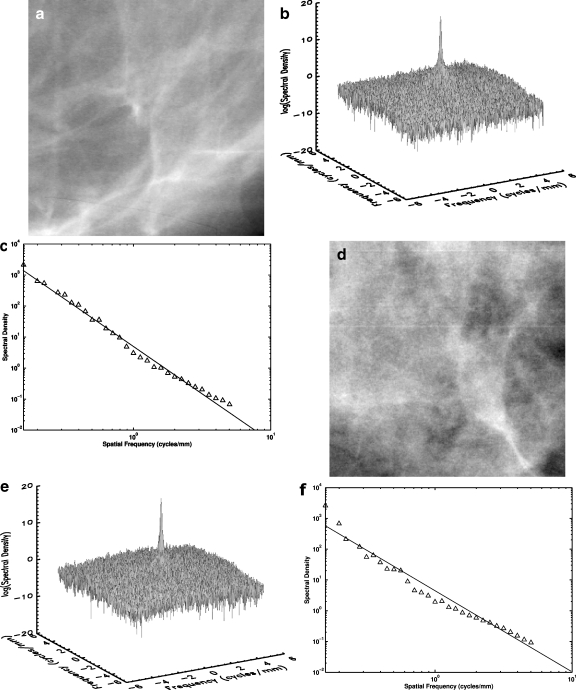
The power spectrum (spectral density), which is based on the discrete Fourier transform method with a radial Hanning window, was calculated for each ROI image in the data set. Figure 3a shows an example of an ROI image selected from the BRCA1/BRCA2 mutation carrier group. The spectral density surface plot for the same ROI image is shown in Fig. 3b. This spectral density surface plot is sharply peaked at zero frequency and has little angular dependence. The relationship between spectral density and spatial frequency (log–log plot) is shown in Fig. 3c for the same ROI. The least squares fit from the log–log plot yields a β value of 2.90 and a coefficient of determination R² value of 0.99 for the linear fit.

Fig. 3.

a A selected ROI image from a digitized mammogram of a BRCA1 gene-mutation carrier. b The surface plot of the power spectrum of the ROI image in a. c The log–log plot of spectral density vs spatial frequency of the ROI image in a. The coefficient of determination R² value for the linear fit is 0.99. d A selected ROI image from a digitized mammogram of a low-risk woman. e The surface plot of the power spectrum for the ROI image in d. f The log–log plot of spectral density vs spatial frequency of the ROI image in d. The coefficient of determination R² value for the linear fit is 0.97.

An ROI image selected from a woman at low risk for breast cancer is shown in Fig. 3d. The surface plot of the 2D spectral density for the same ROI image is shown in Fig. 3e, and the log–log plot between spectral density and spatial frequency is shown in Fig. 3f. A β value of 2.58 is estimated from the linear regression line with a coefficient of determination R² value of 0.97 for the linear fit.

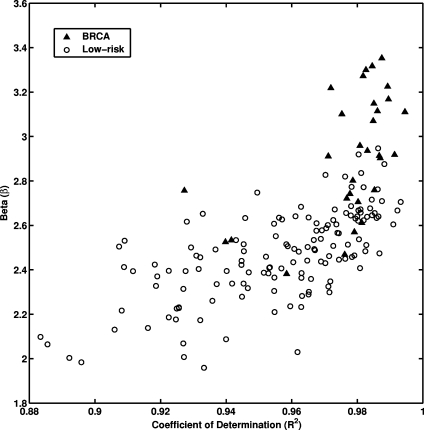
The least-squares fits were performed between log spectral density and log spatial frequency on each mammographic image for the entire database. Figure 4 shows the relationship between individual β value and the coefficient of determination R² value of the corresponding linear regression line for all the ROI images. A relatively high R² value was observed for the entire data set (average R² value of 0.96 with a standard deviation of 0.02). Such high R² value suggests that indeed there is a linear relationship between log spectral density and log spatial frequency for the mammographic patterns of breast structure. The mammographic parenchymal patterns appear to have an approximately isotropic power law spectrum of the form 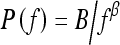, as noted earlier by Burgess.²⁶

Fig. 4.

The distribution between the exponent β values of power law spectrum and coefficient of determination R² values for the entire database.

Larger β values (Figure 4) were obtained for the database of 30 gene mutation carriers with an average value of 2.92 ± 0.28. Whereas, an average β value of 2.47 ± 0.20 was obtained for the database of 142 low-risk women. The p value was less than 0.0001 with 95% confidence interval of 0.36–0.53 for the difference of the two means from an unpaired t test. The usefulness of the β value as a decision variable in the task of differentiating between the gene mutation carriers and the low-risk women can be indicated in terms of area under the ROC curve, A_z. Using this single feature, ROC analysis yielded an A_z value of 0.90 in differentiating between gene mutation carriers and low-risk women in the entire database. For the age-matched subset, an A_z value of 0.89 was achieved. The estimated standard error for A_z value was 0.04, both for the entire database and in the age-matched subset.

Discussion

In this study, we investigated the power law spectrum, of the form 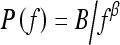, of the mammographic parenchymal patterns of BRCA1 and BRCA2 gene mutation carriers as well as of women at low risk for developing breast cancer. Our results demonstrate that in general, the mammographic parenchymal patterns appears to have an isotropic 2D power law spectrum of the form 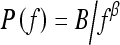, with β in the range from 2.0 to 3.3 for the entire database. Similar observations on mammographic images, in general, have been reported by others.^32,35

An important issue is the understanding of the effect of high frequency noise on the power spectral analysis. In our study, we chose to include frequencies—up to the Nyquist frequency in the estimation of the exponent β value, as the purpose of our study was to differentiate between gene mutation carriers and low-risk women for breast cancer risk assessment, rather than to characterize the parenchymal patterns for human observer detection tasks. Others have shown that human observer detection performance depends on the statistical characteristics of the image noise.³⁶

Understanding the image noise properties is useful in evaluating the effect of image noise on the visual signal detection performance. From Fig. 3c and f, it is apparent that image noise is present at high frequencies in the mammographic images, as indicted by the slight change in slopes of the log–log plots at frequencies around one cycle per millimeter.

BRCA1 and BRCA2 gene mutation carriers and low-risk woman have different mammographic patterns, which are indicated by the β value as a computer-extracted feature (Figure 4). On average, the larger β values were obtained for mutation carriers, and the smaller β values were obtained for low-risk women. As indicated by the A_z value, the high-level performance in differentiating between mammographic patterns of gene mutation carriers and low-risk women was achieved by using the exponent β value as the single feature.

It is interesting to note that as observed in Fig. 4, the goodness of the fitting, as indicated by the coefficient of determination R² value, is higher for the gene carrier database as compared to the low-risk database. While the reason for this is still under investigation, it may be that women at high risk for breast cancer have a parenchymal texture pattern that is more statistically self-similar over a range of spatial scales than that of women at low risk, or it may be that because of the coarser nature of the parenchymal texture pattern of women at high risk, spectral analysis yields more accurate calculations within the spatial limitations of the 0.1-mm pixel size.

To further elaborate the relationship between the exponent β and mammographic parenchymal patterns, the exponent β can be transformed to the fractal dimension, which is defined by

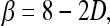5

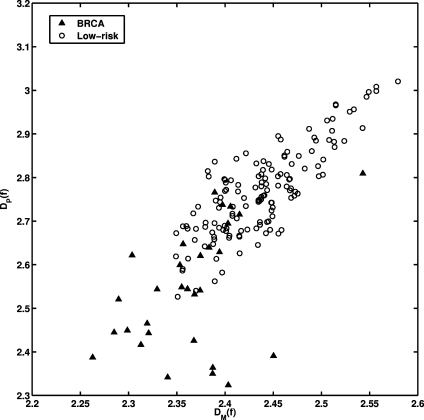
where D is fractal dimension.^26,37 For the gene mutation carriers, their mammographic images appear to have a coarser texture, as reflected by a lower fractal dimension (larger β value). The texture pattern from the low-risk women yields higher fractal dimension (smaller β value). These observations agree with our previous studies on fractal analysis of mammograms.²⁵ As seen in Fig. 5, we obtained a correlation coefficient of r = 0.80 (P value less than 0.0001) between the fractal dimension estimated using the β value and the fractal dimension estimated using the Minkowski algorithm from our earlier studies.²⁵

Fig. 5.

The distribution between the fractal dimension estimated from the power spectral analysis (D_P(f)) and from the Minkowski fractal dimension (D_M(f)) for the entire database. The correlation coefficient (r) between D_M(f) and D_P(f) is 0.80 (P < 0.0001).

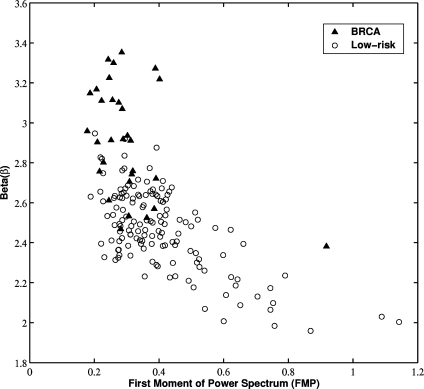
The exponent β value indirectly characterizes the frequency content of the texture pattern with a large β value reflecting a low spatial frequency component. The exponent β value was compared with our previous investigations of the first moment of power spectrum (FMP).²⁴ FMP is derived from the two-dimensional Fourier transform and is used to characterize the texture pattern’s spatial frequency content. For the gene mutation carriers, their mammographic patterns appear to be dominated by low-frequency content (larger β value), which is in good agreement with their FMP features (smaller FMP value). From Fig. 6, a correlation coefficient of r = 0.62 (P value less than 0.0001) was obtained between β value and FMP.

Fig. 6.

The distribution between the exponent β from the power spectral analysis and FMP for the entire database. The correlation coefficient (r) between β and FMP is 0.62 (P < 0.0001).

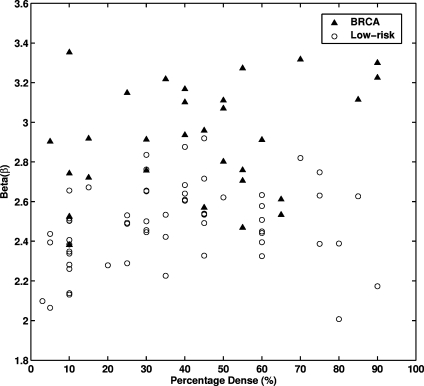
A relatively low correlation coefficient (r = 0.26) was observed between β value and breast density (Figure 7). Mammograms from both the gene mutation carriers and the women at low risk spanned the range of densities. Thus, breast density and parenchymal patterns may act as risk factors in a complementary way.

Fig. 7.

The distribution between the exponent β from the power spectral analysis and breast percentage dense for the entire database. The correlation coefficient (r) between β and percentage dense is 0.26 (P = 0.013).

In summary, the results from this study agree with prior research in that mammographic parenchymal patterns have an isotropic 2D power law spectrum of the form 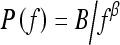. Furthermore, we have found that the mammographic images of BRCA1 and BRCA2 gene mutation carriers present a coarser texture (i.e., larger β value) than those of women at low risk for breast cancer. Such a radiographic marker may aid clinicians in assessing an individual’s risk of developing breast cancer and for monitoring the effectiveness of preventive and therapeutic treatments.