Content-based Retrieval of Mammograms Using Visual Features Related to Breast Density Patterns

Abstract

This paper describes part of content-based image retrieval (CBIR) system that has been developed for mammograms. Details are presented of methods implemented to derive measures of similarity based upon structural characteristics and distributions of density of the fibroglandular tissue, as well as the anatomical size and shape of the breast region as seen on the mammogram. Well-known features related to shape, size, and texture (statistics of the gray-level histogram, Haralick’s texture features, and moment-based features) were applied, as well as less-explored features based in the Radon domain and granulometric measures. The Kohonen self-organizing map (SOM) neural network was used to perform the retrieval operation. Performance evaluation was done using precision and recall curves obtained from comparison between the query and retrieved images. The proposed methodology was tested with 1,080 mammograms, including craniocaudal and mediolateral-oblique views. Precision rates obtained are in the range from 79% to 83% considering the total image set. Considering the first 50% of the retrieved mages, the precision rates are in the range from 78% to 83%; the rates are in the range from 79% to 86% considering the first 25% of the retrieved images. Results obtained indicate the potential of the implemented methodology to serve as a part of a CBIR system for mammography.

INTRODUCTION: BREAST CANCER AND MAMMOGRAPHY

Breast density has been shown to be a risk factor in the development of breast cancer. Wolfe¹ presented the first study relating the density and structure of breast tissues as seen on mammograms to the characteristics of breast disease: he described and illustrated cases associating patterns of parenchymal distortion with the risk of development of breast cancer. Since then, several other researchers have studied the relation between the structural composition of breast tissue and the abnormalities found in the related regions.² A consequence of the understanding of this relationship has been the development of systems for the description and analysis of the density patterns found in mammograms: the Breast Imaging Reporting and Data System (BI-RADS),³ developed by the American College of Radiology, is the most important of such systems. BI-RADS contains recommendations for standardization of terms used in image-based diagnosis of breast diseases, the division of breast composition and mammographic findings into categories, and suggestions for further actions by the radiologist.

Visual analysis of mammograms takes into consideration the shape and size of the breast, the conditions of the breast contour and the nipple position, and the distribution of fibroglandular tissue (degree of granularity, amount, and distribution of breast density). Notwithstanding the developments mentioned above, visual analysis of mammograms by radiologists remains subjective and suffers from a high degree of interobserver variability.⁴ A given mammogram may be categorized into different classes by various radiologists. With the aim to reduce such variability, systems have been proposed for content-based image retrieval (CBIR) and computer-aided diagnosis (CAD) based upon objective measures that represent, in a quantitative manner, mammographic features related to breast structure, diseases, and diagnosis.^4–8

Computer-aided Diagnosis Systems

Systems for CAD have been designed with the aim of assisting radiologists in the analysis of mammograms. The purpose of CAD is to increase the accuracy of diagnosis, as well as to improve the consistency of interpretation of images via the use of the computer’s results as a reference.⁵ The results of computer-based image processing and CAD could also be useful in addressing other limitations in visual interpretation of mammograms due to poor quality and low contrast of the images, superposition of breast structures due to the projection nature of mammograms and the compression of the breast for imaging, visual fatigue in the screening context, and environmental distraction. It has been shown that double reading (interpretation of each mammographic exam by two radiologists) can increase the accuracy of diagnosis:⁵ the suggested use of CAD systems also includes the role as a second reader.

CAD systems have well-defined objectives, such as the detection of suspicious lesions, characterization of lesions as benign or malignant, analysis of bilateral asymmetry in breast parenchymal patterns, and analysis of breast density. An example of the application of a CAD system for the classification of breast density is the work of Zhou et al.,⁴ which includes an automated system to obtain measures of breast density in accordance with BI-RADS. Classification was realized based upon features extracted from the gray-level histogram and peaks corresponding to fatty and fibroglandular tissues. Nevertheless, it is difficult to achieve high accuracy in deriving measures of breast tissue density due to intrinsic difficulties with mammographic images; furthermore, the estimates provided by radiologists based upon visual analysis are subjective.

An approach to address the problems mentioned above is to realize unsupervised and automatic classification of images through the characterization of similarity based upon breast tissue density. Such a classification permits quantitative evaluation of the similarity of images independent of subjective factors. Classification of images as above may be realized with a CBIR system, the results of which could be evaluated and improved upon via a system of relevance feedback (by expert radiologists specialized in mammography).⁶ In this manner, a CAD system can contribute effectively toward the reduction of interobserver variability in the classification of images. Li et al.⁷ present an example of applying CBIR as a tool to aid in radiological diagnosis.

Content-based Image Retrieval Systems

Similar to CAD systems, CBIR systems use information extracted from images to represent or describe them; however, the main purpose of CBIR is application related to semantic description of knowledge extracted from the images. Such items of information could be referred to as “visual features”.⁸

Initial systems for image retrieval were text-based, using textual descriptors to represent images such as annotations, key words, and visual characteristics of color, texture, and shape. In the medical context, textual characteristics appear in the form of data related to patient records. In an automatic system, image characteristics could be extracted in the form of features.^8,9 In a CBIR system, images are indexed by vectors of characteristic features extracted from the images. To retrieve images from a database in response to a query, a comparison is performed between the feature vector of the query image and the corresponding vectors of the images in the database. The comparison is made using measures of similarity in the space of metrics related to the features. Several functions exist for use as measures of similarity of vectors. The most commonly used measure is the Euclidian distance. Müller et al.¹⁰ have provided a detailed review of CBIR.

A query or search of similarity could be made in two ways: “range query” and “k-nearest-neighbor (k-NN) query”. A range query uses a limit for the distance from the query sample or a reference point to retrieve images: all images in the database having a distance less than the specified limit are retrieved and presented to the user. In a k-NN query, the k-nearest images to the query image are retrieved: in a practical medical application, the user may be interested in only a small number of images (3, 5, 7, etc.) for comparative analysis with the current image on hand (query case).

Observe that a CBIR system possesses a structure similar to that of CAD systems, except for the difference in the final objective. A CBIR system uses quantitative features for indexing, comparative analysis, and retrieval of images based upon a similarity measure. A CAD system may use similar measures and methods, but with the aim of leading toward a diagnostic decision. Regardless, both CBIR and CAD systems may be used as diagnostic aids.

In the context of mammography and breast cancer, some works have explored the use of CBIR. Azevedo-Marques et al.⁸ developed a mammographic image retrieval system for use as a diagnostic aid; they proposed the use of visual features obtained from Haralick’s measures of texture for the characterization of regions of interest (ROIs) containing microcalcifications. Alto et al.⁹ proposed the use of texture, gradient (edge-sharpness), and shape measures as indices for quantitative representation of breast masses in mammograms, and studied their application for CBIR. They suggested that features that can give high accuracy in pattern classification experiments could also be used as efficient indices for CBIR. El-Naqa et al.¹¹ proposed an approach to the retrieval of digital mammograms using microcalcification clusters. They explored the use of neural networks and support vector machines in a two-stage hierarchical learning network for predicting the perceptual similarity from similarity scores collected in human-observer studies. Muramatsu et al.¹² proposed a psychophysical measure based on neural networks for evaluation of similar images with mammographic masses. For other related previous works, see Tao and Sklansky,¹³ Ornes et al.,¹⁴ El-Naqa et al.,¹⁵ and Nakagawa et al.^16,17

Kohonen Self-organizing Map Networks for Content-based Image Retrieval

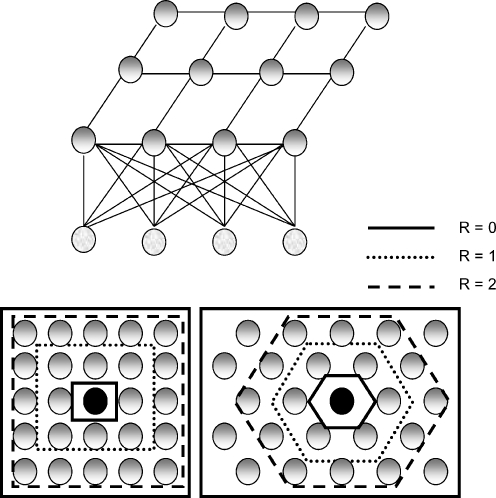
In the self-organizing map (SOM) architecture of neural networks, neurons are organized in the form of rectangular or hexagonal grids, and are usually arranged in two-dimensional layers. Figure 1 presents the topology of a SOM network and the grids showing the neighborhood of a “winner neuron”. In the basic scheme of the SOM network, the neurons of the output layer compete for the information presented at the neurons of the input layer.¹⁸ If a winner neuron emerges, that neuron is readjusted to respond in a stronger manner to the same stimulus. Within this unsupervised model, not only the winner neuron gets adjusted, but its neighbors are also adjusted.

Fig. 1.

The architecture of the Kohonen self-organizing map (SOM) network and neighborhoods in rectangular and hexagonal grids. The winner neurons are shown in black and the neighbors are shown in gray. Neighborhoods of radius R = 0, 1, and 2 are also shown for the rectangular and hexagonal grids.

In brief, a SOM network functions as follows: the synaptic weights are initialized with small random values. An input signal x = [x₁, x₂, ..., x_n], with its values representing an item of information, is provided to the network, without any desired output being specified (unsupervised training). Given an input x, an output neuron j will provide the highest response; this neuron is then considered to be the winner. This neuron is always activated with a high response whenever the same input pattern is applied to the neurons in the input layer. The winner neuron j and its neighbors V_j have their synaptic weights adjusted so as to provide a stronger response to the input x. The network is considered to be trained after all of the training data have been presented to the network, and the training criteria have been satisfied. After the training phase, the network may be used for query and retrieval purposes. This phase is essentially the same as the training phase, except that the weights of the neurons are not altered any more. When the test entries are recognized correctly, the network is considered to have been successfully trained.

The adaptation of the neurons is crucial for the orderly training of the SOM because despite the fact that each neuron is modified independently of the others, it is the whole set of neurons that represents the information conveyed by the input. The adjustment of the synaptic weights takes place in the following manner: initially, the winner neuron is found for the input presented; this is the neuron having the least distance between its weight vector w_j and the input vector x. In each step of the training phase, the neuron with the highest response is adjusted so as to provide an even larger response for the same input; simultaneously, the neurons in the neighborhood V_j are also adjusted.

The neurons that are outside the subset of the neighborhood as defined above are not adjusted. The adaptation of the neurons is simple: once the winner neuron is selected, the weights of the neuron and its neighbors are updated as

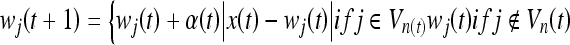1

where t is the stage of iteration, V_n is the range of the neighborhood, and α(t) is the rate of learning.

Kohonen¹⁸ proposed that, in practical computation, the training process could be stopped when there is no further change in the weights of the selected neuron. The process may also be stopped after a certain number of iterations (epochs).

Laaksonen et al.¹⁹ described the use of the SOM as a CBIR system for the retrieval of multimodality images. In their work, a SOM network is trained in the unsupervised mode with a set of features. The similarity between images depends upon the characteristics of the input features and the measure of similarity used. Then, similar images are grouped together in classes according to a threshold applied to the selected measure of similarity. For every image provided as the query case, the features of the image point toward one of the classes of images. If the image cannot be grouped with any of the classes, it is used to form a new class.

METHODS

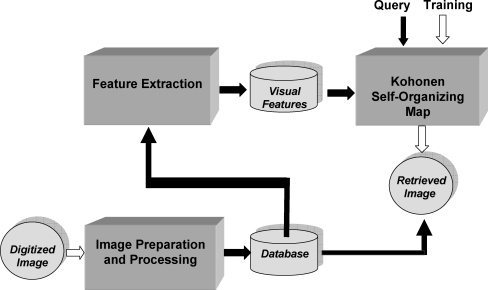
The following subsections provide the details of the methods developed, including preprocessing of the images to remove noise, and procedures for the extraction of shape and texture features. The training and testing steps of the SOM developed for CBIR are also described. Figure 2 presents a schematic representation of the procedures.

Fig. 2.

Schematic block diagram of the proposed CBIR system.

Database

A database of 1,080 mammograms, including 270 pairs of craniocaudal (CC) views and 270 pairs of mediolateral-oblique (MLO) views from the database of the Clinical Hospital of the Faculty of Medicine, University of São Paulo, Ribeirão Preto, Brazil, was prepared for the study (see Table 1). Approval was obtained from the Research Ethics Committee. Films were digitized using a Vidar DiagnosticPro scanner with a resolution of 300 dpi (pixel size of 85 μm) and 12 bits per pixel.

Table 1.

Numbers of Images that were Categorized by the Radiologists of the Hospital Using BI-RADS Categories 1, 2, 3, or 4 for Tissue Composition

View	BI-RADS Composition				Total
	1	2	3	4
CC right	90	112	50	18	270
CC left	91	111	50	18	270
MLO right	90	112	50	18	270
MLO left	91	111	50	18	270
Total	362	446	200	72	1,080

This information was used as the “gold standard” for judgment of relevant images for a given query in evaluation of the results of CBIR.

CC Craniocaudal, MLO mediolateral-oblique

Films of two sizes were included in the database: 24 × 30 cm and 18 × 24 cm; the digitized image matrices were of size 2,835 × 3,543 and 2,126 × 2,835 pixels, respectively. Images were cropped to remove patient and imaging markers. To reduce computational requirements, images were down-sampled to matrices of size 1,024 × 1,024 pixels by the bilinear method. Information about breast density, size, and shape were preserved, and an effective resolution of 279 and 223 micrometers per pixel was obtained for the two film sizes mentioned above.

Mammograms were categorized by radiologists of the hospital using BI-RADS categories 1, 2, 3, or 4 for tissue composition. This classification for tissue composition was used as the “gold standard” for judgment of relevant images for a given query in evaluation of the results of CBIR (see Table 1). CC and MLO views were manually separated for the analysis of retrieval.

Preprocessing of Images

Some images contained a significant amount of noise. We applied the anisotropic diffusion equation²⁰ combined with the Wiener filter to remove noise while simultaneously performing edge enhancement.²¹

Segmentation of the breast region was performed as follows. Several thresholding methods were applied to each image, including maximum entropy,²² moment-preserving method,²² Otsu’s method,²² the method of Ridler and Calvard,²³ the method of Reddi et al.,²⁴ and a method based upon the spatial gray-level dependence (SGLD) matrix.²² The best result among the above was selected for each image by one of the radiologists involved in the study. Figure 3 shows two examples of binarized breast regions with different shapes.

Fig. 3.

Two examples of binarized mammographic images with different shapes of the breast region.

A straight-line approximation to the pectoral muscle (in MLO views) was detected as follows.²¹ The Canny method²⁵ was applied to detect the edges in the image. The result was binarized, and the Radon transform²⁶ was used to search for the longest line nearest to the thoracic edge of the image.

To detect the nipple, the following procedures were applied to determine the point of convergence of breast tissue patterns.²¹ The Top-Hat morphological filter was applied to the mammogram to enhance lobular and ductal structures. The location of the maximum intensity in the Radon transform of the result was used to detect the nipple.

The fibroglandular disc was segmented by using the following thresholding methods: maximum entropy,²² moment-preserving method,²² and Otsu’s method.²² The best result among the above was selected for each image by one of the radiologists involved in the study.

Extraction of Visual Features

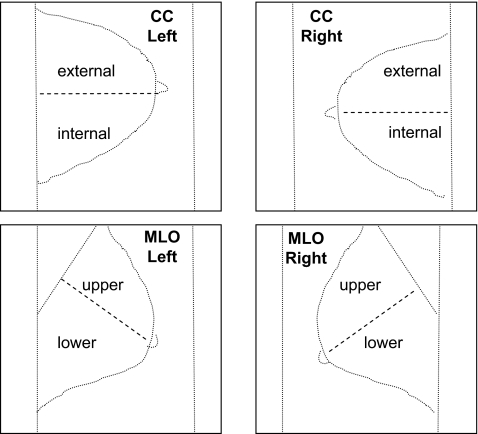
A total of 88 features were computed for each mammogram. Table 2 lists the features and the regions of the mammographic image used to derive them. Shape factors were extracted from the contour of the binarized breast region. Texture features were computed from the gray-level image of the breast region. Granulometric features were derived from the segmented fibroglandular tissue (disc). The breast region was divided into two parts using the nipple as a reference (see Fig. 4): in the case of CC views, the horizontal line through the nipple was used, whereas in the case of MLO views, the perpendicular to a straight-line approximation to the pectoral muscle edge that passed through the nipple was used. Additional measures of texture and moments were derived from the internal/external parts of CC views and the upper/lower parts of MLO views (see Fig. 4). This division was performed to incorporate the procedure followed by radiologists in the visual interpretation of mammograms.

Table 2.

Number of Features Extracted in each Group Per Region of Interest (ROI) and Mammogram

Features	ROI	Number of features per ROI	Number of features per mammogram
Shape	Binary breast region	3	3
Texture	Subregion*	14	28
Moments	Subregion*	7	14
Histogram	Subregion*	5	10
Radon	Subregion*	10	20
Granulometric	Fibroglandular disc	13	13

Texture Haralick’s texture features, Histogram statistics of gray-level histogram, Moments Hu’s moment-based features, Radon Radon-domain features, Granulometric granulometric features.

*Internal or external region for craniocaudal (CC) views, and upper or lower region for mediolateral-oblique (MLO) views.

Fig. 4.

The breast region in each mammogram was divided in two subregions. Each craniocaudal (CC) view was divided into external and internal regions; each mediolateral-oblique (MLO) view was divided into upper and lower regions.

The methods developed for feature extraction are described in detail in the following paragraphs.

Shape Features

The goal of shape features is to find other breast images with the same size and shape (in terms of being elongated, rounded, and rough) of the query image in the retrieval process. Because a mammogram is a two-dimensional representation of the three-dimensional interaction phenomenon between the X-rays and breast tissue, some bias and error can be introduced in density evaluation. For instance, women with large breasts may have a substantial amount of glandular breast tissue, and yet have an appearance of low breast density in the mammograms. On the other hand, women with small breasts and low amounts of glandular tissue may have the appearance of higher density in the mammograms. Therefore, shape and size features can have an important complementary role in density evaluation. In this study, three shape and size features are used: area, ratio of diameters, and compactness.

The area A of each segmented breast region was estimated in pixels and normalized with respect to the total number of pixels in the image. A correction factor was applied to take into account the two sizes of mammograms in the database and the related pixel sizes.

The ratio of diameters D_R was defined as the ratio D_y/D_x. The distance D_y was measured as the distance from the nipple to the chest wall in CC views, and as the perpendicular distance from the pectoral muscle edge to the nipple in the case of MLO views (see Fig. 5). The distance D_x was defined as the length of the perpendicular bisector of the line related to D_y (within the breast region), as shown in Figure 5. The feature D_R characterizes the elongation of the breast.

Fig 5.

The distances D_x and D_y used to derive the ratio of diameters measure D_R.

Compactness is a commonly used measure of shape roughness, defined as the ratio of the squared perimeter P² to the area A of a contour. The normalized version of compactness, given by

2

was used to derive a shape factor for the binarized breast region.

Granulometric Features

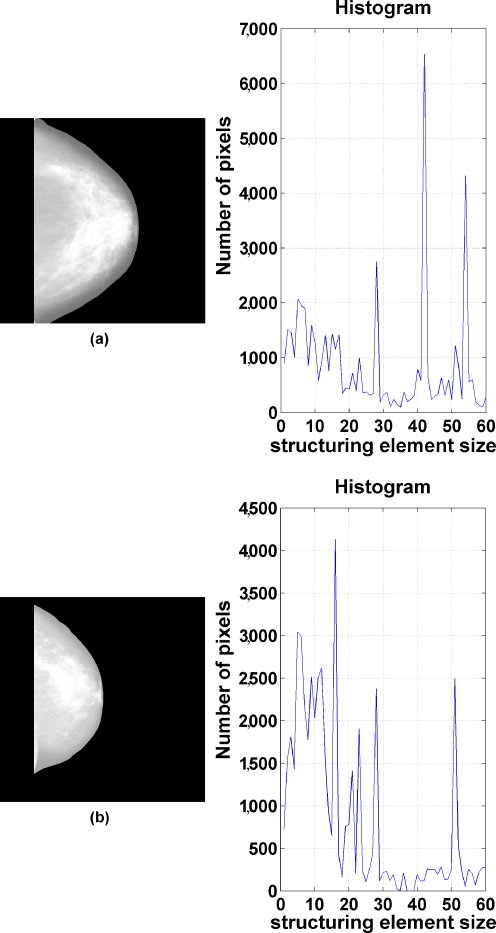
Granulometry provides measures that characterize the distribution of size of objects in an image.²⁷ To obtain granulometric features, the morphological opening filter was applied to the segmented fibroglandular discs. The structuring element was defined as a circle with a radius varying between 5 and 60 pixels (in steps of one pixel). For each structuring element, a difference image was computed between the original and the filtered versions. A histogram was created to represent the number of nonzero (fibroglandular tissue) pixels in the difference images against the size of the structuring element (see Fig. 6). The mean, variance, skewness, kurtosis, and entropy of the histogram were computed for each mammogram.

Fig 6.

Two examples related to the extraction of granulometric measures showing the original images and the corresponding histograms of the number of nonzero pixels in the difference images (after morphological filtering) versus structuring element size.

Radon-domain Features

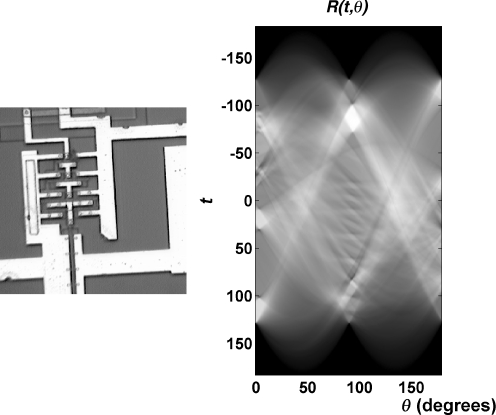
The Radon transform²⁶ expresses the projections of a given image f(x, y) at various ray angles θ and ray positions t as

3

Figure 7 shows a simple test image and its Radon transform. Figure 8 shows a CC mammogram as well as the corresponding fibroglandular disc segmented into its external and internal subregions; the radon transforms of the subregions and functions derived thereof are also shown. As evident from the examples in Figures 7 and 8, the Radon transform displays large values at ray angles and positions that correspond to strong linear features in the image.²⁶

Fig 7.

A simple test image and its Radon transform (image obtained from http://www.mathworks.com/company/newsletters/news_notes/images/circuit1.gif).

Fig 8.

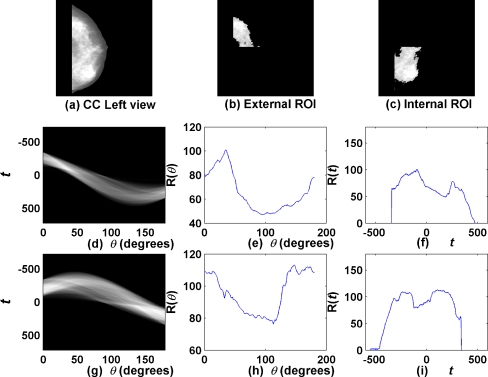
Example of Radon-domain functions: (a) a CC mammogram; (b) external ROI of segmented fibroglandular disc; (c) internal ROI of segmented fibroglandular disc; (d) Radon transform (R(t,θ)) of external ROI; (e, f) functions R(θ) and R(t) for external ROI; (g) Radon transform (R(t,θ)) of internal ROI; (h, i) functions R(θ) and R(t) for internal ROI.

The Radon transform R(t,θ) may be integrated to obtain two one-dimensional functions of t and θ as R(t) and R(θ) to facilitate analysis of angles at which high densities are present in the given image. Figure 8 shows examples of the functions R(t) and R(θ) for the two subregions of the fibroglandular disc of a mammogram. It is seen from the plots in Figure 8 (e) and (h) that the image possesses high density at about θ = 40° and θ = 120°. We computed the mean, variance, skewness, kurtosis, and entropy of the functions R(t) and R(θ) for each segmented subregion as shown in Figure 4 for each mammogram for use as features in CBIR.

Texture Features

Haralick et al.²⁸ proposed 14 measures of texture derived from the SGLD matrices of the given image. The 14 measures represent variations in gray levels and pairs of gray levels that relate to smoothness, regularity, heterogeneity, and contrast in the image. We use the 14 texture measures of texture computed for the segmented subregions as shown in Figure 4 of each mammogram as features for CBIR. The features were derived from an averaged SGLD matrix computed for a distance of one pixel and 0, 45, 90, and 135 degrees for each image.

Moment-based Features

Hu²⁹ defined seven normalized moment-based features that are invariant to position, scaling, and rotation. We derived the seven moment-based features for each segmented subregion as shown in Figure 4.

Statistics of Gray-level Histograms

To characterize the gray-scale distribution in a given image, we computed the mean, variance, skewness, kurtosis, and entropy of its histogram. These five features were computed for each segmented subregion as shown in Figure 4 for each mammogram.

Feature Selection

Principal component analysis (PCA) was applied to reduce the dimensionality of features. Table 3 lists the dimensionality reduction achieved for various combinations of features. The condition applied in PCA was to preserve at least 90% of the variance of the original set of features. Although 88 features (in total) were computed for each mammogram, PCA led to a feature dimension of 18 for efficient image representation for CBIR.

Table 3.

Number of Features Extracted in each Group and Dimension of Features Reduced by Principal Component Analysis (PCA)

Features	Number of Features	Number of PCA
Shape	3	3
Histogram	10	8
Texture	28	8
Moments	14	7
Radon	20	13
Granulometric	13	9
Shape, histogram	13	10
Shape, texture	31	9
Shape, moments	17	8
Shape, Radon	23	14
Shape, granulometric	16	11
Shape, histogram, texture	41	13
Shape, histogram, moments	27	14
Shape, histogram, Radon	33	16
Shape, histogram, granulometric	26	15
Shape, texture, moments	45	12
Shape, texture, Radon	51	16
Shape, texture, granulometric	44	13
Shape, moments, Radon	37	15
Shape, moments, granulometric	30	13
Shape, Radon, granulometric	36	17
Shape, histogram, texture, moments	55	15
Shape, histogram, texture, Radon	61	17
Shape, histogram, texture, granulometric	54	16
Shape, histogram, moments, Radon	47	16
Shape, histogram, moments, granulometric	40	17
Shape, histogram, Radon, granulometric	46	18
Shape, texture, moments, Radon	65	17
Shape, texture, moments, granulometric	58	14
Shape, texture, Radon, granulometric	64	17
Shape, moments, Radon, granulometric	50	19
Shape, histogram, texture, moments, Radon	75	18
Shape, histogram, texture, moments, granulometric	68	17
Shape, histogram, moments, Radon, granulometric	60	18
Shape, histogram, texture, Radon, granulometric	74	18
Shape, texture, moments, Radon, granulometric	78	18
Shape, histogram, texture, moments, Radon, granulometric	88	18

Texture Haralick’s texture features, Histogram statistics of gray-level histogram, Moments Hu’s moment-based features, Radon Radon-domain features, Granulometric Granulometric features.

Training and Testing of the SOM for CBIR

The structure of the Kohonen SOM network used in the experiments conducted varied as follows. The number of input neurons was set to be equal to the number of features used to represent a mammogram, as listed in Table 3 for the various feature combinations evaluated. A rectangular grid was used for creating a 17 × 17 neighborhood matrix of neurons for the output layer (289 neurons). The distance D between two neurons is the magnitude of the maximum element in the vector obtained by subtracting the neurons’ coordinates as

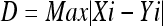4

Therefore, it is possible to select neighboring neurons of radius from 0 to 16 around the winning neuron. The neighborhoods of radius R = 0, 1, and 2 are shown in Figure 1. A maximum of 8,000 cycles was used in the training process. The learning rate was not fixed, but did not exceed 0.0001 in any of the tests.

The leave-one-out method was used to create the training and testing cases from the available database of mammograms. The database used was manually divided in four groups of 270 images each (left CC, right CC, left MLO, and right MLO). In this procedure, for each group, a query image is separated from the data set containing 270 images and the SOM network is trained with the 269 remaining images. Then, the query image is used as the system input. This procedure is repeated until all images are used as the query. Because of the use of an output layer layout with 289 neurons, every image can be classified as a single class.

To evaluate the performance of the CBIR system, measures of precision and recall were obtained according to the rules given in Table 4 for comparing the BI-RADS categorization (performed by the radiologists) between the query and retrieved mammograms, as follows:

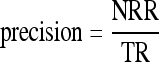5

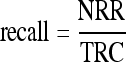6

where NRR is number of relevant images retrieved, TR is total number of images retrieved, and TRC is total number of relevant images in the database. For each CBIR experiment, a range query was applied for image retrieval using SOM radius distance from R = 0 to R = 16, and the average and standard deviation values of precision were computed.

Table 4.

Rules Used for the Verification of the Precision of Retrieval, Taking into Consideration the Potential Variability in Evaluation of Breast Tissue Composition Using BI-RADS Categorization

BI-RADS Category of Query Image	Acceptable BI-RADS Categories of Retrieved Images
1	1 and 2
2	1, 2, and 3
3	2, 3, and 4
4	3 and 4

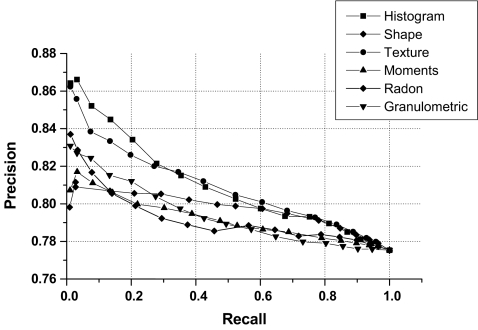
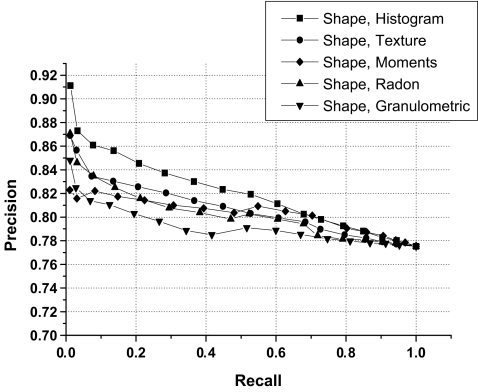
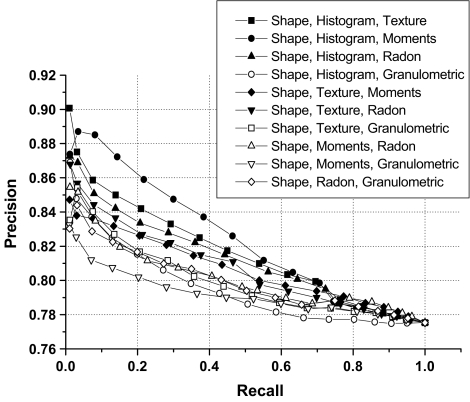
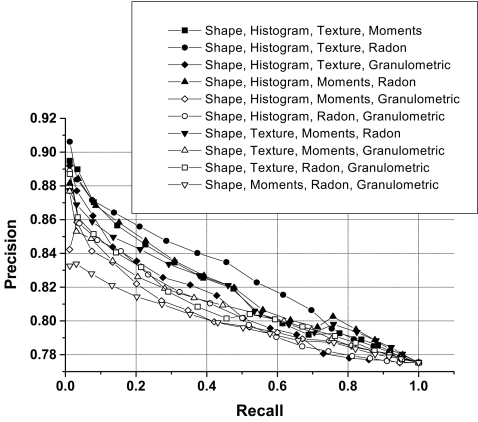
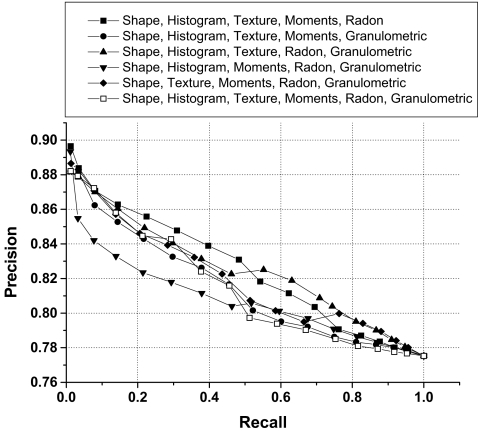
Figures 9, 10, 11, 12, and 13 show precision and recall curves for several feature combinations used in the CBIR experiments.

Fig 9.

Precision versus recall curve for individual groups of features.

Fig 10.

Examples of precision versus recall curve for selected combinations of two groups of features.

Fig 11.

Examples of precision versus recall curve for selected combinations of three groups of features.

Fig 12.

Examples of precision versus recall curve for selected combinations of four groups of features.

Fig 13.

Examples of precision versus recall curve for selected combinations of five and six groups of features.

RESULTS AND DISCUSSION

Table 5 lists the precision (mean and standard deviation) obtained for different feature combinations considering the whole set of images, precision considering that 25% of images are retrieved, and precision when 50% of images are retrieved. Features combinations provided average precision rates in the range from 79% to 83%. The results obtained indicate that the proposed features can facilitate CBIR of mammograms with good levels of accuracy. However, the nature of similarity represented by the various features and their combinations differ significantly, and an appropriate set of features needs to be selected based upon the desired results. Good feature selection can facilitate the clustering of images into the different categories of interest. Though the PCA provided an indication for the “good features”, other feature selection method could be used as well.

Table 5.

Average Precision (Mean and Standard Deviation), the Precision with the First 25% of the Images Retrieved, and Precision with the First 50% of the Images Retrieved, Obtained for the Various Groups and Selected Combinations of Features

Features	Precision (%) (μ ± σ)	P(0.25) (%)	P(0.5) (%)
Shape	79.15 ± 1.11	80.55	79.93
Histogram	81.20 ± 3.02	82.77	80.45
Texture	81.01 ± 2.64	82.33	80.68
Moments	79.16 ± 1.30	79.92	79.00
Radon	79.35 ± 1.82	79.66	78.66
Granulometric	79.56 ± 1.95	80.75	78.93
Shape, histogram	82.28 ± 3.76	84.17	82.10
Shape, texture	80.86 ± 2.78	82.33	80.55
Shape, moments	80.15 ± 1.58	81.33	80.48
Shape, Radon	80.45 ± 2.68	81.29	80.04
Shape, granulometric	79.43 ± 1.99	79.86	78.96
Shape, histogram, texture	81.77 ± 3.76	83.84	81.37
Shape, histogram, moments	82.27 ± 4.11	85.55	82.10
Shape, histogram, Radon	81.29 ± 3.21	83.10	81.07
Shape, histogram, granulometric	79.96 ± 2.95	80.98	78.71
Shape, texture, moments	80.66 ± 2.32	82.35	80.39
Shape, texture, Radon	80.84 ± 2.96	82.50	80.56
Shape, texture, granulometric	80.14 ± 2.49	81.43	79.26
Shape, moments, Radon	80.26 ± 2.45	81.08	79.59
Shape, moments, granulometric	79.38 ± 1.68	79.90	78.96
Shape, Radon, granulometric	80.10 ± 2.11	81.26	79.48
Shape, histogram, texture, moments	81.97 ± 3.94	84.31	81.48
Shape, histogram, texture, Radon	82.67 ± 4.04	85.22	82.93
Shape, histogram, texture, granulometric	81.32 ± 3.80	83.01	80.31
Shape, histogram, moments, Radon	82.06 ± 3.60	84.52	81.69
Shape, histogram, moments, granulometric	80.50 ± 2.59	81.61	79.72
Shape, histogram, Radon, granulometric	80.78 ± 3.42	82.65	80.23
Shape, texture, moments, Radon	81.72 ± 3.28	83.90	81.45
Shape, texture, moments, granulometric	81.00 ± 2.97	82.27	80.68
Shape, texture, Radon, granulometric	81.14 ± 3.25	82.65	80.29
Shape, moments, Radon, granulometric	80.01 ± 1.99	81.17	79.63
Shape, histogram, texture, moments, Radon	82.44 ± 3.99	85.41	82.83
Shape, histogram, texture, moments, granulometric	81.60 ± 3.70	83.96	80.76
Shape, histogram, moments, Radon, granulometric	82.45 ± 3.46	84.67	82.35
Shape, histogram, texture, Radon, granulometric	81.04 ± 3.14	82.14	80.50
Shape, texture, moments, Radon, granulometric	82.14 ± 3.67	84.29	81.10
Shape, histogram, texture, moments, Radon, granulometric	81.62 ± 3.92	84.03	80.32

Shape Shape features, Haralick Haralick’s texture features, Histogram statistics of gray-level histogram, Moments Hu’s moment-based features, Radon Radon-domain features, Granulometric granulometric features

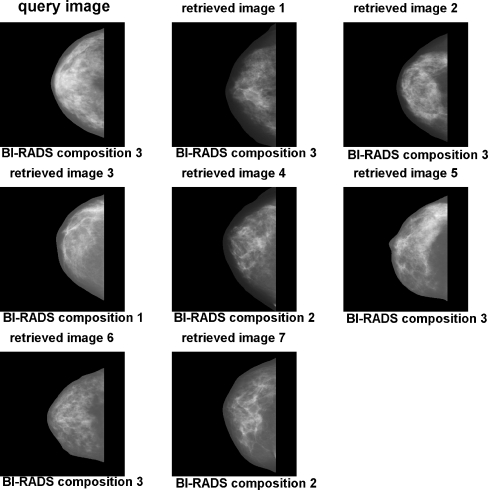
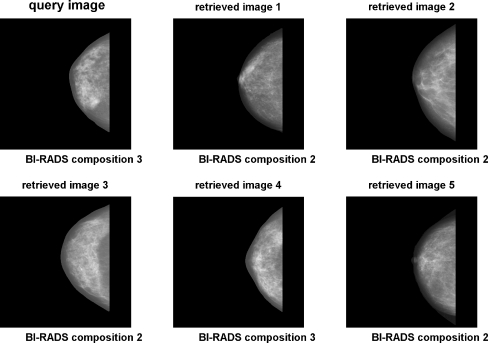
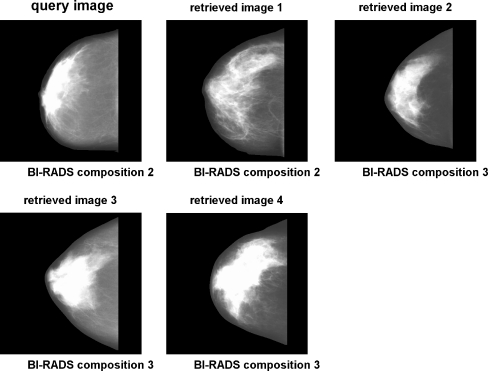
Figure 14 shows an example of a query image and retrieved images based upon the combination of shape, histogram, and moment-based features. Figure 15 shows an example using the combination of shape, histogram, texture, and granulometric features. Figure 16 shows an example using the combination of shape, histogram, moment-based, Radon-domain, and granulometric features. The feature combinations mentioned above provided average precision values of 82.27%, 81.32%, and 82.45%, respectively. It can be observed that the retrieved images match in size and shape with the query images, which was expected because of the effectiveness of shape features for CBIR. The SOM average training time for each leave-one-out cycle was 62.6 s. Testing time (retrieval time) was directed related with the range query applied, with a variation from 0.1 ms for radius equal 0 to 562.3 ms for radius equal 16.

Fig 14.

Example of CBIR using the combination of shape, histogram, and moment-based features. Range query with radius R = 0.

Fig 15.

Example of CBIR using the combination of shape, histogram, texture, and granulometric features. Range query with radius R = 0.

Fig 16.

Example of CBIR using the combination of shape, histogram, moment-based, Radon-domain, and granulometric features. Range query with radius R = 0.

An important characteristic of the methodology implemented in this work is the use of an a priori breast density composition classification made by radiologists as an initial stage for image similarity query training. In an a posteriori stage, the system could be improved using the relevance feedback technique based on visual inspection by radiologists to determine the degree of similarity between the query and retrieved images. A supervised artificial neural network could be trained to match the similarity perception of radiologists; this could lead to improved performance, as suggested by Muramatsu et al.¹²

CONCLUSION

Regardless of the fact that the key features that need to be assessed in diagnosing breast pathology are microcalcifications and masses, the evaluation of breast density (high-density fibroglandular tissue) and asymmetry plays an important role in the diagnostic process. In fact, the evaluation of bilateral breast asymmetry based on density, shape, and size is usually the first stage in the mammographic evaluation process. Radiologists look for calcifications, masses, asymmetry, and architectural distortion in mammograms: a CBIR system for mammography should include the possibility of query by similarity based on all of these features. Basically, a hierarchical structure should be implemented for the characterization of breast images beginning with general structural features, such as size, shape, and density, and continuing with more specific features associated with radiological findings such as contours of masses and the number as well as spatial distribution of microcalcifications in a cluster. Thus, a query for CBIR may be performed based on the similarity between general structural features of the breast, similarity between features associated with a specific radiological finding, or similarity between ROIs in mammograms. The concept of similarity is notably important because no two mammograms or ROIs may be expected to be identical, even when belonging to the same diagnostic category, and a perfect or exact match to a query is improbable. The use of vectors of quantitative parameters to index image features facilitates the use of simple distance measures (such as the Euclidean distance) to select the cases that are most similar to the query sample. In this context, a study of several types of quantitative features focused on breast density, size, and shape for application in CBIR of mammograms was presented in this paper. The evaluation of the performance of the proposed procedures for CBIR was based upon the precision versus recall curve. The results indicate that, while the statistics of the gray-level histograms of subregions of the breast in mammograms can provide high levels of precision for mammographic image retrieval based on structural features, results can be improved further by the inclusion of shape, Radon-domain, moment-based, texture, and granulometric features. Regardless, it should be possible to improve the performance of a CBIR system by using relevance feedback (ratings of radiological similarity and clinical usefulness) provided by several radiologists in training a supervised artificial neural network. We have initiated studies to further explore the possibilities discussed above.