Dynamic thermal time model of cold hardiness for dormant grapevine buds

Abstract

Background and Aims

Grapevine (Vitis spp.) cold hardiness varies dynamically throughout the dormant season, primarily in response to changes in temperature. The development and possible uses of a discrete-dynamic model of bud cold hardiness for three Vitis genotypes are described.

Methods

Iterative methods were used to optimize and evaluate model parameters by minimizing the root mean square error between observed and predicted bud hardiness, using up to 22 years of low-temperature exotherm data. Three grape cultivars were studied: Cabernet Sauvignon, Chardonnay (both V. vinifera) and Concord (V. labruscana). The model uses time steps of 1 d along with the measured daily mean air temperature to calculate the change in bud hardiness, which is then added to the hardiness from the previous day. Cultivar-dependent thermal time thresholds determine whether buds acclimate (gain hardiness) or deacclimate (lose hardiness).

Key Results

The parameterized model predicted bud hardiness for Cabernet Sauvignon and Chardonnay with an r² = 0·89 and for Concord with an r² = 0·82. Thermal time thresholds and (de-)acclimation rates changed between the early and late dormant season and were cultivar dependent but independent of each other. The timing of these changes was also unique for each cultivar. Concord achieved the greatest mid-winter hardiness but had the highest deacclimation rate, which resulted in rapid loss of hardiness in spring. Cabernet Sauvignon was least hardy, yet maintained its hardiness latest as a result of late transition to eco-dormancy, a high threshold temperature required to induce deacclimation and a low deacclimation rate.

Conclusions

A robust model of grapevine bud cold hardiness was developed that will aid in the anticipation of and response to potential injury from fluctuations in winter temperature and from extreme cold events. The model parameters that produce the best fit also permit insight into dynamic differences in hardiness among genotypes.

INTRODUCTION

Cold hardiness (H_c) in perennial plants during dormancy varies by species, cultivar and antecedent weather, among other causative factors (Schnabel and Wample, 1987; Wolf and Cook, 1992; Leinonen et al., 1995; Kanneganti et al., 1998; Ebel et al., 2005). Hardiness follows a general sequence of acclimation and deacclimation. During acclimation plants gain H_c as the temperature decreases, which coincides temporally with satisfying the chilling requirement often discussed in the dormancy literature (Richardson et al., 1974). During the subsequent deacclimation, plants are said to be eco-dormant (Lang et al., 1987), and changes in H_c respond to higher temperatures, finally leading up to budbreak in spring (Kalberer et al., 2006; Keller, 2010). Hardiness often remains quite stable in mid-winter as long as temperatures remain relatively low and stable; this has led some authors (Proebsting et al., 1980; Jiang and Howell, 2002) but not all (Wolf and Cook, 1992; Kwon et al., 2008) to treat this mid-winter period as physiologically unique.

Rates of acclimation and deacclimation vary dynamically and are reversible (Damborska, 1978; Wolf and Cook, 1992; Gu et al., 2002), but as budbreak approaches the loss of H_c ceases to be reversible (Fennell, 2004; Kalberer et al., 2006). In addition, H_c responds to fluctuations in ambient temperature (Proebsting et al., 1980; Wolf and Cook, 1992; Hubackova, 1996; Keller, 2010). In grapevines (Vitis spp.), the role of photoperiod is not as obvious as that of temperature. A short photoperiod induces bud dormancy, but low temperature seems to be required for full cold acclimation (Schnabel and Wample, 1987; Fennell and Hoover, 1991). Cultivars differ in rates of acclimation and deacclimation, maximum level of H_c and response to temperature fluctuations (Mills et al., 2006); thus, predictive models potentially can provide information on site suitability for grape production and for cultivar selection. Predictive models are also useful to growers who can respond with frost protection measures in advance of injury-inducing low temperatures or with adjustments to pruning in the aftermath of these low temperatures (Keller and Mills, 2007). Finally, such models may be used to estimate potential impacts of climate change scenarios.

Empirical estimates of H_c in woody perennials can be derived by several techniques, the most common of which is referred to as differential thermal analysis (DTA) or low temperature exotherm (LTE) analysis (Andrews et al., 1983; Tinus et al., 1985; Wolf and Pool, 1987; Burr et al., 1990; Wisniewski et al., 1990; Mills et al., 2006). This method measures the release of latent heat, termed LTE, when symplastic water freezes; LTE₅₀ denotes the temperature at which 50 % of the organ or tissue samples are injured. Estimates of H_c are of particular interest for dormant buds that contain vegetative and reproductive primordia that represent the yield potential for the subsequent growing season. Empirical estimates of H_c can be used to develop dynamic models which, along with weather forecasts, may predict H_c in advance of critically low temperatures.

Modelling acclimation and deacclimation in perennial plants has been approached using varying degrees of detail [e.g. Kobayashi et al., 1983 (Cornus spp.); Rowland et al., 2005 (Vaccinium spp.); Ebel et al., 2005 (Citrus unshiu)]. To accommodate changes in acclimation, an empirical model of H_c in Lolium spp. fitted a logistic function that was derived from data obtained in a temperature gradient tunnel (Gay and Eagles, 1991). First-order discrete dynamic models were developed for overwintering cereals and alfalfa (Medicago sativa), where acclimation and deacclimation were defined as rate variables, and both time and photoperiod as driving variables (Kanneganti et al., 1998; Fowler et al., 1999). Cold hardiness was estimated by adding the change in H_c (ΔH_c) on the current day to H_c from the previous day. The aforementioned work was conducted under controlled conditions and thus does not incorporate meteorological data or reflect natural fluctuations in ambient temperature. For Douglas fir (Pseudotsuga menziesii) there is a second-order dynamic model with a logistic component that includes a temperature-dependent maximum H_c (Leinonen et al., 1995). Andrews et al. (1987) published a dynamic conceptual model of cherry (Prunus avium) bud hardiness that calculated ΔH_c on an hourly basis from hourly air temperatures. This model was specific to the mid-winter period defined as after autumn acclimation and before spring deacclimation.

Although there are several published models for determining grapevine chilling requirements and/or budbreak (McIntyre et al., 1987; Moncur et al., 1989; Dokoozlian, 1999; Kwon et al., 2008; Andreini et al., 2009; García de Cortázar-Atauri et al., 2009), there is no dynamic predictive model available for grapevine H_c. Current models are rudimentary and largely rely on post-hoc statistical analyses correlating H_c with ambient air temperature at or before the time of sampling. Proebsting et al. (1980) found a correlation between the average temperature of the preceding 2 d and grape bud hardiness. Wolf and Cook (1992) estimated correlations between current LTE₅₀ and average air temperature for the previous 1, 3, 5 or 7 d. Jiang and Howell (2002) incorporated temperatures for the preceding 1–7 d in regression equations to predict H_c. The correlation approach does not apply a biological basis for model parameterization and, contrary to experience, it implies that H_c is independent of earlier weather conditions. Regression equations cannot provide insight into the H_c phenomenon beyond confirming the obvious importance of temperature.

To overcome these weaknesses, the present work took advantage of a 22-year database of LTE₅₀, the most commonly used quantitative indicator of H_c, to develop and evaluate a discrete dynamic model to predict H_c of dormant grapevine buds. Instead of using a post-hoc correlation approach, the database, in combination with the integration of acknowledged concepts of bud dormancy, allowed us to apply a biological basis for model parameterization. This included identification of upper and lower temperature limits for H_c, temperature thresholds for acclimation and deacclimation, acclimation and deacclimation rates, and changes of these thresholds and rates as the buds transition from endo- to eco-dormancy. We assumed temperature, expressed as thermal time, to be the primary environmental determinant of H_c, as well as of its rate of change, while recognizing that these relationships are subject to seasonal variation. Model variants were parameterized for three distinct grape genotypes and permit biological insight beyond simple model equations.

MATERIALS AND METHODS

A database (1988–2010) of grapevine H_c maintained by Washington State University provided input data for model development and testing. The database comprises LTE₅₀ values for dormant buds from genetically diverse cultivars of field-grown grapevines. The LTE₅₀ values were determined by DTA (Andrews et al., 1983; Wample et al., 1990; Mills et al., 2006) conducted at varying intervals (2 d to 2 weeks), as time permitted, from leaf fall in autumn (normally at the time of the first frost) to budswell in spring. These two phenological events correspond to modified E-L stages 47 and 2, respectively (Coombe, 1995), and typically occurred in October and in April, respectively. Dormant buds were collected using the protocol described in Mills et al. (2006) from vines located at or within 1 km of the Irrigated Agriculture Research and Extension Center in Prosser, WA, USA (46·30 °N latitude, 119·75 °W longitude). Meteorological data for the on-site weather station were provided by the Washington State University Agricultural Weather Network (AgWeatherNet, http://weather.wsu.edu). We focused on two commercially important V. vinifera cultivars (Chardonnay and Cabernet Sauvignon) and one V. labruscana cultivar (Concord). The empirical data sets comprised 22 years for Cabernet Sauvignon, 14 years for Chardonnay and 15 years for Concord. Approximately half of the available dormant seasons (10 years for Cabernet Sauvignon, 6 years for Chardonnay and 7 years for Concord) were selected randomly to be used for model optimization; the remainder were reserved for model evaluation.

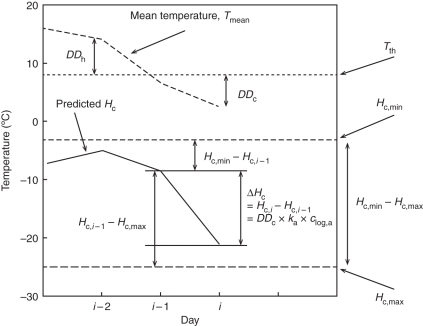
Abbreviations and units of measurement used in model parameterization and evaluation are listed in Table 1. Using a discrete dynamic approach (Fig. 1) with 1 d time steps from leaf fall to budswell, H_c, expressed as the predicted LTE₅₀ of dormant buds, was estimated in finite difference form at the current time (i) from the previous day's value (H_c,_i–1) and the change in hardiness (ΔH_c):

(1)

Table 1.

Symbols, abbreviations and units of measurement used in text and model mathematics

Abbreviation	Definition	Unit
B	Bias or mean error	°C
clog,a	Logistic component during acclimation	Dimensionless
clog,d	Logistic component during deacclimation	Dimensionless
DDc	Chilling degree-days	°C
DDh	Heating degree-days	°C
DTA	Differential thermal analysis
EDB	Eco-dormancy boundary, DDc accumulation required to start eco-dormancy	°C
Hc	Cold hardiness	°C
Hc,i	Cold hardiness for day i	°C
Hc,i–1	Cold hardiness for day i–1	°C
Hc,initial	Initial cold hardiness, genotype-specific constant	°C
Hc,max	Maximum hardiness (most hardy condition), genotype-specific constant	°C
Hc,min	Minimum hardiness (least hardy condition), constant	°C
ΔHc	Change in cold hardiness	°C
ka,eco	Acclimation rate during eco-dormancy	°C °C−1
ka,endo	Acclimation rate during endo-dormancy	°C °C−1
kd,eco	Deacclimation rate during eco-dormancy	°C °C−1
kd,endo	Deacclimation rate during endo-dormancy	°C °C−1
LTE50	Low-temperature exotherm, temperature lethal to 50 % of the population	°C
RMSE	Root mean square error	°C
Tmax	Maximum daily temperature	°C
Tmean	Mean daily temperature	°C
Tmin	Minimum daily temperature	°C
Tth,eco	Threshold temperature for calculating degree-days during eco-dormancy	°C
Tth,endo	Threshold temperature for calculating degree-days during endo-dormancy	°C

Fig. 1.

Discrete dynamic approach to modelling cold hardiness (H_c), where H_c on the current day is equal to the change in H_c (ΔH_c) added to the H_c from the previous day (H_c,i = ΔH_c + H_c,i–1). Chilling degree-days (DD_c) below a threshold temperature (T_th) lead to acclimation, whereas heating degree-days (DD_h) above T_th lead to deacclimation.

The ΔH_c is dependent on thermal time, which in turn is calculated from the mean daily air temperature, the driving force for changes in acclimation or deacclimation:

(2)

(3)

(4)

where DD_c is the thermal time below a threshold temperature (T_th), expressed as chilling degree-days; DD_h is the thermal time above a T_th, expressed as heating degree-days. These variables are conceptually familiar to scientists and growers who refer to growing degree-days to normalize rates of plant development across growing seasons. The T_th, as well as the acclimation rate constant (k_a) and the deacclimation rate constant (k_d), are unique by genotype and change during the dormant season (Table 2; cf. Kalberer et al., 2006). Using separate rates for acclimation and deacclimation accounts for hysteresis that is not captured if regression analysis is used to model H_c as a function of temperature (e.g. Hubackova, 1996; Jiang and Howell, 2002). The basis for the changes in T_th, k_a and k_d is illustrated in Fig. 2, which shows that the LTE₅₀ curves of the three cultivars are nearly parallel during acclimation in autumn but diverge during deacclimation in spring. This phenomenon was modelled by dividing the dormant season into two periods, allowing T_th, k_a and k_d to be reset after a particular cultivar has accumulated a certain number of DD_c. This division is conceptually similar to fulfilling a chilling requirement or to the boundary between endo-dormancy and eco-dormancy (EDB; Lang et al., 1987; Wolf and Cook, 1992; Kwon et al., 2008), and divides the winter into an endo-dormancy period dominated by acclimation and an eco-dormancy period dominated by deacclimation. Thus, T_th, k_a and k_d were optimized sequentially for these two periods, as indicated by subscripts endo and eco in the subsequent text.

Table 2.

Model parameters used to simulate cold hardiness (H_c) of three grape cultivars

Parameter	Concord	Chardonnay	Cabernet Sauvignon
Hc,initial (°C)	–11·94	–10·55	–9·99
Hc,max (°C)	–29·73	–25·24	–24·63
Hc,min (°C)	–3·00	–3·00	–3·00
Tth,endo (°C)	12·50	11·75	11·75
ka,endo (°C)	0·13	0·14	0·14
kd,endo (°C)	0·01	0·01	0·01
EDB (°C)*	–700	–750	–850
Tth,eco (°C)	4·25	3·75	5·75
ka,eco (°C °C−1)	0·01	0·07	0·01
kd,eco (°C °C−1)	0·16	0·13	0·12
RMSE (°C)	2·05	1·40	1·47

Using the optimization data set, parameters were estimated by iteration to minimize the root mean square error (RMSE) between observed and predicted H_c.

* DD_c values are negative.

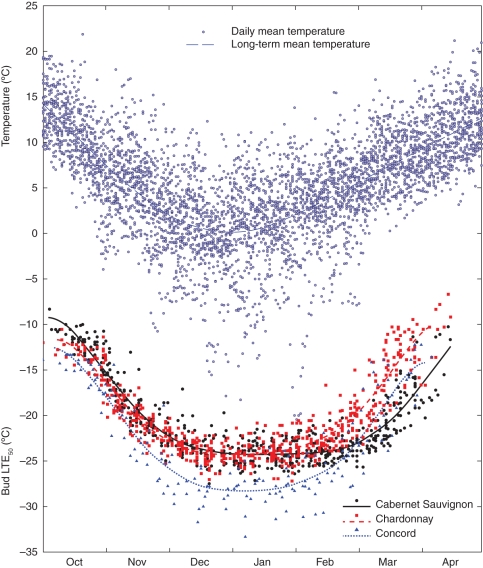
Fig. 2.

Daily mean air temperature and measured bud cold hardiness (H_c), expressed as low-temperature exotherms (LTE₅₀), of three grape cultivars over the dormant season for the period 1988–2010. Note that H_c measurements usually started in early–mid October and ended in early–mid April. Symbols represent daily or measured values; lines represent long-term (n ≥14 years) averages.

We applied asymptotic bounds on the absolute lowest and highest possible values of H_c to ΔH_c with logistic functions (Mooney and Swift, 1999):

(5)

(6)

where c_log (dimensionless) varies from 0 to 1, and the subscripts a and d refer to acclimation and deacclimation, respectively. The physiological maximum bud hardiness (H_c,max) was computed as the mean lowest measured LTE₅₀ by cultivar. The physiological minimum bud hardiness (H_c,min) corresponds to the highest LTE₅₀ (i.e. least hardy) and was set to –3 °C, which is roughly the hardiness of green tissues (Fennell, 2004).

Initial conditions (H_c,initial) were computed by cultivar as the mean of the earliest measured LTE₅₀ near leaf fall. Thus, model inputs were the cultivar-specific constants and T_min and T_max (2 m above ground) for the current day. Model output was a dynamic value of H_c (i.e. predicted LTE₅₀) for dormant buds at the location represented by the input data. The model was coded and statistical analyses were conducted using SAS (version 9·1, SAS Institute, Cary, NC, USA). Model parameters were optimized by stepwise selection (Cesaraccio et al., 2004) and correlation (SAS, Proc. Reg.) of predicted against observed H_c, until the root mean square error (RMSE) from the 1:1 line was minimized (Willmott, 1982). In addition, the mean error or bias (B) of predicted against observed H_c was calculated to test model accuracy. Sensitivity analysis of the numerical model was performed by varying the parameters for each cultivar. At least 60 000 simulations were run, with each temperature parameter changing by 0·25 °C, each thermal time parameter changing by 50 DD and each rate parameter changing by 0·01 °C °C⁻¹ while keeping other parameters constant. The model was evaluated using optimized parameters by correlation analysis (SAS, Proc. Reg.), using the data set aside for evaluation.

RESULTS

The optimized, cultivar-specific model parameters are presented in Table 2. Concord clearly was the hardiest of the three cultivars studied, with the lowest H_c,initial and H_c,max. The H_c,initial and H_c,max of the two V. vinifera cultivars (Chardonnay and Cabernet Sauvignon) both differ by <1 °C, as might have been expected from the measured LTE₅₀ data (Fig. 2). However, bud H_c changes dynamically during the dormant season (Fig. 2), and the deacclimation rate during eco-dormancy (k_d,eco) turned out to be very important in understanding cultivar-specific H_c patterns. Because of its high k_d,eco, Concord lost hardiness quickly in the spring. Chardonnay ended the dormant season the least hardy due to its low T_th,eco, which corresponds to its vulnerability to late frosts. Cabernet Sauvignon, whose budbreak at this site occurs on average 10 d after that of Chardonnay and Concord, had the highest H_c,initial and H_c,max, required the most DD_c to enter into eco-dormancy and had the highest threshold temperature during eco-dormancy (T_th,eco). In contrast, k_a,endo and k_d,endo were similar for all three cultivars, while T_th,endo and k_d,eco were similar for Chardonnay and Cabernet Sauvignon but higher for Concord (Table 2).

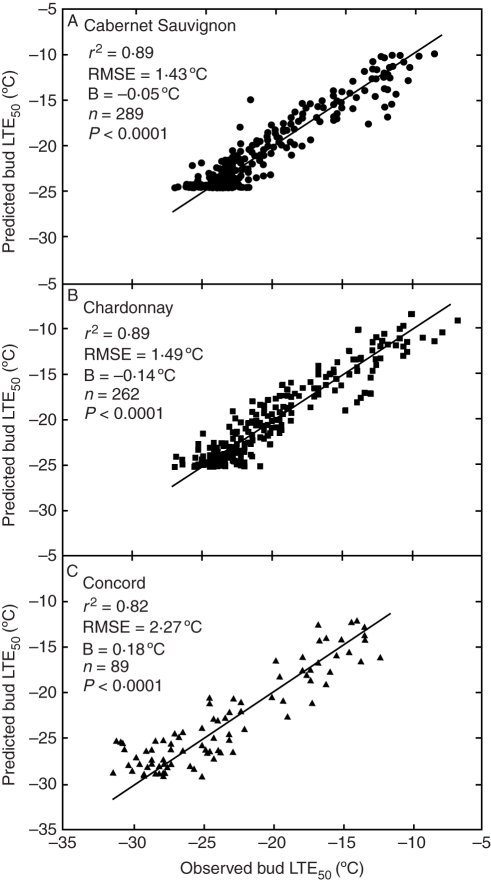
The numerical model derived from the optimization data set was fitted to the empirical data from the evaluation data set and generally showed good agreement. Correlation analysis demonstrated that the variation in observed bud H_c explained 89 % of the variation in predicted H_c for both Cabernet Sauvignon (Fig. 3A) and Chardonnay (Fig. 3B). The Concord version of the model is somewhat less accurate (Fig. 3C), most probably because of fewer years with less frequent measurements available (cf. Fig. 2). Nonetheless, even for Concord, the model showed both high precision (RMSE = 2·27 °C) and high accuracy (B = 0·18 °C). The lower bound or clipped feature on predicted H_c for all three cultivars (Fig. 3) resulted from using a fixed H_c,max (Table 2) across all years.

Fig. 3.

Comparison between model predictions and measurements of bud cold hardiness (expressed as low-temperature exotherms, LTE₅₀) for Cabernet Sauvignon (A; 12 years), Chardonnay (B; 8 years) and Concord (C; 8 years) grapevines. Root mean square error (RMSE) calculated from 1:1 line, using the evaluation data set.

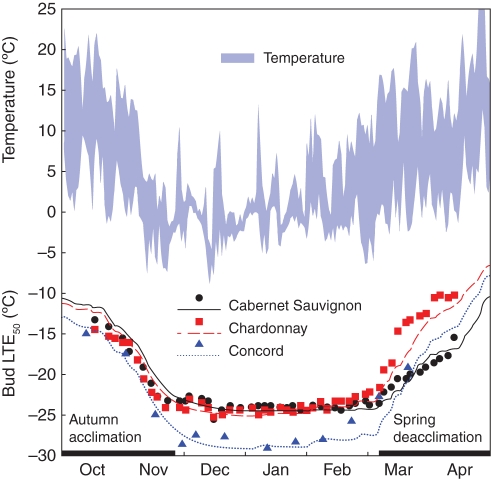
Model output for a single dormant season (Fig. 4) demonstrates the useful aspects of the discrete dynamic approach, as well as its limitations. By changing only the cultivar-specific parameters (Table 2), the model correctly predicted the genetically determined differences among cultivars in bud H_c (Fig. 4). The similarity in seasonal trends between the long-term LTE₅₀ values shown in Fig. 2 and the single-year model output shown in Fig. 4 is evident. For instance, although Concord reached the lowest maximum H_c in mid-winter, its predicted hardiness curve crossed that of Cabernet Sauvignon, but not that of Chardonnay, in the period leading up to budbreak in spring. The predicted values were generally within 2 °C (90^th percentile) of the observed LTE₅₀ values, even when the model over-predicted H_c for Cabernet Sauvignon and Chardonnay during autumn acclimation and under-predicted H_c for Chardonnay and Concord during spring deacclimation (Fig. 4). However, while seasonal trends and cultivar differences were especially well predicted by the model, predictions of short-term changes driven by fluctuations in temperature were somewhat less accurate (Fig. 4).

Fig. 4.

Daily minimum and maximum temperatures, and measured bud cold hardiness (expressed as low-temperature exotherms, LTE₅₀; symbols) and LTE₅₀ predicted by a dynamic thermal time model (lines) for three grape cultivars during one dormant season (2000–2001).

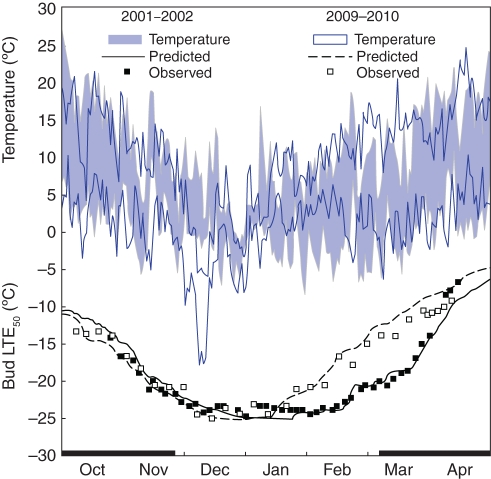
The model also simulated the response of grapevines to disparate temperature patterns (Fig. 5). The accuracy of prediction of H_c for Chardonnay buds was similar in 2001–2002 and in 2009–2010, although the former period was taken from the evaluation data set and the latter from the optimization data set. Both measured and predicted H_c followed the typical seasonal pattern of acclimation after leaf fall, prolonged H_c.max in mid-winter and subsequent deacclimation in spring. However, the cold event in early December 2009 that was associated with a 4·1 °C gain in measured LTE₅₀ was absent in 2001. In addition, during the 2 months from mid January through mid March, 2010 had 46 d with T_min >0 °C and 36 d with T_max >10 °C. This contrasts with only 11 d with T_min >0 °C and 27 d with T_max >10 °C in 2002 (Fig. 5). Thus, the two dormant seasons also contrasted in the temperatures during the eco-dormancy period, during which 2010 was on average 2·8 °C warmer than 2002. The model accurately predicted the resulting early deacclimation and associated loss of H_c that occurred in 2010. However, during the period preceding budbreak the model underestimated H_c by 2·7 °C in 2001 and overestimated it by 2·1 °C in 2010.

Fig. 5.

Daily minimum and maximum temperatures, and predicted and observed bud cold hardiness (expressed as low-temperature exotherms, LTE₅₀) of Chardonnay grapevines in two dormant seasons with disparate temperature patterns (2001–2002 drawn from the evaluation data set; 2009–2010 drawn from the optimization data set).

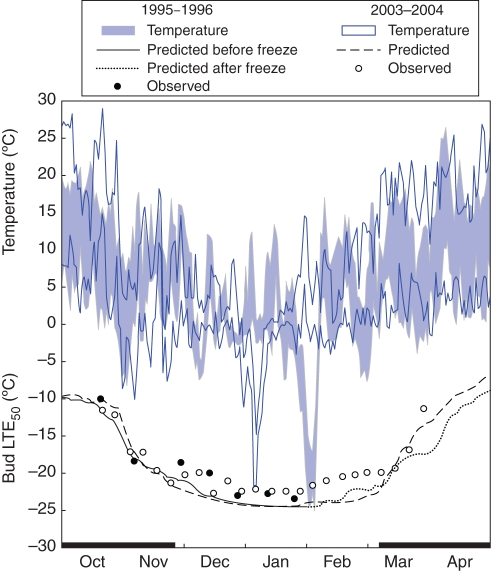
Taking Cabernet Sauvignon as an example, both DTA analysis and model simulation correctly predicted the lethal bud damage caused by the extreme freeze event (–25·3 °C) in late January 1996 (Fig. 6). Although LTE data were not collected for Chardonnay and Concord that winter, model simulations indicated that Chardonnay would sustain close to 50 % bud injury, whereas Concord would be hardy enough to escape serious injury (data not shown). These predictions were confirmed by sampling and dissection of compound buds (each with a primary, secondary and tertiary bud) following the freeze event: 63 % of primary buds, 15 % of secondary buds and 11 % of tertiary buds were killed in Cabernet Sauvignon (n = 289), Concord sustained 18 % lethal primary bud damage, 10 % secondary bud damage and 3 % tertiary bud damage (n = 442), but insufficient numbers of Chardonnay buds were sampled to permit any firm conclusions. Measurements of H_c for Cabernet Sauvignon were terminated after that event, because the condition of the available bud population was too erratic for DTA analysis. Nevertheless, the model was used to continue simulating the deacclimation phase of potentially surviving buds in late winter and spring (see dotted line in Fig. 6). A similar, but less severe, cold event (–21·7 °C) occurred in January 2004, and both the DTA analysis (LTE₁₀ = –21·9 °C) and the model correctly indicated that Cabernet Sauvignon would sustain little if any bud damage at that temperature (Fig. 6). This was despite the model simulation not being as accurate in mid-winter of the 2003–2004 season, underestimating H_c by up to 3·2 °C. Chardonnay and Concord also did not sustain any bud injury that year, and both DTA analysis and model simulations showed these cultivars to have lower H_c at the time of the freeze event than did Cabernet Sauvignon (data not shown).

Fig. 6.

Daily minimum and maximum temperatures, and predicted and observed bud cold hardiness (expressed as low-temperature exotherms, LTE₅₀) of Cabernet Sauvignon grapevines in two dormant seasons (1995–1996 and 2003–2004), with a lethal freeze event at the end of January 1996. Note that measurements ceased after the cold event due to unavailability of live buds.

DISCUSSION

We formulated and evaluated a numerical model, using a dynamic thermal time approach, which successfully simulates the changes in bud H_c of three distinct Vitis spp. genotypes throughout the dormant season and in multiple years. We are not aware of any published dynamic models of grapevine H_c, but the RMSEs in the present model compare favourably with those reported for Douglas fir by Leinonen et al. (1995). Fowler et al. (1999) reported r² = 0·964 for their model of winter cereal hardiness. However, Leinonen et al. (1995) modelled only the acclimation period, relying on a single year of data, and Fowler et al. (1999) presented data for 2 years compared with our 6–10 years (depending on genotype) of grape bud LTE₅₀ values used for model parameterization and optimization, and 8–12 years of LTE₅₀ values used for model evaluation.

The optimized model parameters were especially effective at simulating seasonal trends of acclimation after leaf fall, prolonged mid-winter hardiness and deacclimation in spring. Another key strength was the model's ability to simulate H_c in response to disparate seasonal temperature patterns and unusual cold or warm spells. However, this seemed to be at the expense of capturing some of the short-term dynamics in H_c due to fluctuating temperatures. To improve the model's ability to extrapolate beyond measured H_c values, it could be re-optimized to enhance short-term accuracy on the temporal scale of weather forecasts, as opposed to season-long accuracy. However, some uncertainty is inherent in the use of ambient temperature in model parameterization and evaluation, because DTA analysis is conducted at bud temperature, and air and bud temperatures are often decoupled (Grace, 2006). Despite these limitations, the current model iteration accurately predicted not only the destructive freeze event of 1996, but also the low level of bud damage resulting from the less severe freeze event of 2004.

The model parameters computed here and the simulations run during the sensitivity analysis permit generalizations about how cold acclimation, mid-winter hardiness and deacclimation are influenced by grape genotype, dormancy status and temperature. The cultivars tested here had similar H_c,min, k_a and k_d during the autumn acclimation period, but differed in terms of H_c,initial, H_c,max, EDB, T_th, k_a and k_d during the deacclimation period following mid-winter. The present results confirm research comparing Vitis cultivars subjected to controlled temperature regimes (Damborska, 1978; Schnabel and Wample, 1987; Wolf and Cook, 1992; Gu et al., 2002). However, our results do not support the notion that, across plant species, acclimation occurs more slowly than deacclimation (Kalberer et al., 2006). Thus, the reversible nature of our model with independent acclimation and deacclimation may be of particular interest for improving dormancy and phenology models.

The present model is based on a number of simplifications: LTE₅₀ data were determined for only one location; thermal time was calculated from mean daily temperature; a fixed H_c,max was used; and an abrupt transition from endo- to eco-dormancy was applied. Extending the model to substantially different meso- or macroclimates may require full integration of thermal time over each day. Furthermore, one might argue that the EDB is only a convenient appropriation from the dormancy literature (Lang et al., 1987; Cesaraccio et al., 2004; Kwon et al., 2008). The chilling time required to reach this boundary found here places the EDB in mid-winter, in contrast to some authors (e.g. Pouget, 1972; Dokoozlian, 1999) who place dormancy release for grapes much earlier. However, Dokoozlian (1999) also reported that a chilling duration of 800 h at 0 °C, the longest and coldest treatment combination he tested, resulted in the most rapid and most uniform budbreak. These simplifications notwithstanding, the ability of our model to simulate H_c in distinct Vitis genotypes and over diverse dormant seasons suggests that it may be successfully applied to other climates and to questions regarding climate change effects.

Cold injury remains an environmental challenge in many fruit-producing regions. Implementing protective measures (e.g. wind machines) unnecessarily is expensive, whereas not implementing such measures when they would be needed and effective can lead to substantial economic loss across a region in a single cold event. Despite a general winter warming trend and a projected decrease in extreme cold events (Diffenbaugh et al., 2005), it is not clear whether the frequency and severity of cold injury will decrease in the future. Warmer autumn temperatures may be associated with slower cold acclimation (Keller et al., 2008), and the present data show that unseasonable warm spells are associated with a loss of H_c (cf. Kalberer et al., 2006). This can predispose plants for subsequent cold injury, especially if such episodes are followed by extreme cold. Therefore, future effects of overall warmer winters associated with global climate change are uncertain.