Lossless Compression of Volumetric Medical Images with Improved Three-Dimensional SPIHT Algorithm

Abstract

This article presents a lossless compression of volumetric medical images with the improved three-dimensional (3-D) set partitioning in hierarchical tree (SPIHT) algorithm that searches on asymmetric trees. The tree structure links wavelet coefficients produced by 3-D reversible integer wavelet transforms. Experiments show that the lossless compression with the improved 3-D SPIHT gives improvement about 42% on average over two-dimensional techniques and is superior to those of prior results of 3-D techniques. In addition, we can easily apply different numbers of decomposition between the transaxial and axial dimensions, which is a desirable function when the coding unit of a group of slices is limited in size.

Digital technology has given a great advantage to the medical imaging area. Medical images, however, require huge amounts of memory, especially volumetric medical images, such as computed tomography (CT) and magnetic resonance (MR) images. Because of the limitations of storage and transmission bandwidth of the images, the main problem of the technology lies in how to compress a huge amount of visual data into a low-bit-rate stream, because the amount of medical image data would overwhelm the storage device without an efficient compression scheme.

Compression schemes can be generally classified into two types: lossless and lossy compression. Lossy compression usually provides much higher compression than lossless compression, because the reconstructed image is not exactly the same as the original image. Although lossy compression is generally acceptable for image browsing, lossless compression of medical image data has been required by doctors for accurate diagnosis and legal protection because it allows exact recovery of the original image.

Volumetric medical images are a three-dimensional (3-D) image data set and can be considered as a sequence of two-dimensional (2-D) images or slices. A simple way is to directly apply a 2-D compression algorithm to each slice independently. However, the slices are generally highly correlated with one another, so a transform is used to decorrelate the data and to improve performance of compression. Therefore, the 3-D-based approaches could provide better compression results. In a 3-D approach, contiguous groups of slices (GOS) are coded, and the small GOS sizes are desirable for random access to certain segments of slices.

The embedded zero-tree wavelet (EZW)¹ coding algorithm was introduced by Shapiro with excellent compression results. Later, Said and Pearlman proposed a more efficient coding algorithm using set partitioning in hierarchical tree (SPIHT) and applied it to both lossy² and lossless³ compression of images. Kim and Pearlman⁴ extended 2-D to 3-D for video, and Kim and Pearlman⁵ utilized it for volume image compression.

In this article we use Kim and Pearlman’s⁵ lossless 3-D SPIHT with asymmetric tree structure. Our experiments demonstrate that the lossless compression of the asymmetric tree 3-D SPIHT (AT-SPIHT) algorithm outperforms the symmetric tree 3-D SPIHT algorithm. In addition, we show that the AT-SPIHT gives flexibility of choosing the GOS size and decomposition levels and gives excellent results for small GOS sizes.

MATERIALS AND METHODS

Asymmetric Tree Structure of 3-D SPIHT

In previous work, Kim and Pearlman⁵ used the 3-D SPIHT compression kernel with the tree structure introduced in Kim et al.⁶ This tree structure is just a simple extension of the symmetric 2-D SPIHT tree structure. Other researchers have proposed a more efficient tree structure.^{7, 8} The 3-D SPIHT algorithm is one of the tree-based coders. Tree-based coders tend to give better performance when tree depth is long and the statistical distribution of magnitudes of wavelet coefficients is uneven between the intraslice and interslice directions. Therefore, the main idea of this tree structure is to make the trees longer, since that increases the probability of a coefficient value being zero as we move from root to leaves. To make that kind of tree, we can simply decompose into more levels and change the linkage of coefficients. We can not always decompose to more levels since there is a limitation according to the image size and GOS size. On the other hand, the asymmetric tree structure always gives a longer tree than that of the normal 3-D SPIHT.

Figure 1 portrays the tree structures among the original 2-D tree structure after two-level spatial decompositions, the original 3-D tree structure after two-level wavelet packet decompositions, and the 3-D asymmetric tree structure after two-level wavelet packet decompositions. To form trees of 2-D SPIHT as shown in Figure 1a, groups of 2 × 2 coordinates were kept together in the lists. On the 3-D sub-band structure in Figure 1b, there are 3-D transaxial and axial trees and their parent–offspring relationships. To apply wavelet packet decomposition, the full axial decomposition precedes the transaxial decompositions, where the node divides in the additionally split sub-bands. The symmetric tree structure of 3-D SPIHT is a straightforward extension from the 2-D case to form a node in 3-D SPIHT as a block of eight adjacent pixels with two extending to each of the three dimensions, hence forming a node of 2 × 2 × 2 pixels. The asymmetric tree structure shown in Figure 1c in each coefficient frame is exactly the same as the 2-D SPIHT tree structure except that the top-left coefficient of each 2 × 2 group in the lowest transaxial sub-band of the LL_t and LH_t bands links to a group in another axial sub-band at the same transaxial subband location.

Figure 1.

Comparison of tree structures: (a) 2-D original tree structure after two-level spatial decomposition, (b) 3-D original tree structure after two-level wavelet packet decomposition, (c) 3-D asymmetric tree structure after two-level wavelet packet decomposition.

Figure 2 shows another view of the asymmetric tree structure. In this figure, there are eight frames which are transformed in both the transaxial and axial domains in two levels. The new tree structure has 2 × 2 wavelet coefficients element in the axial root sub-band (LL_t) rather than 2 × 2 × 2 wavelet coefficients element.

Figure 2.

Asymmetric tree structure.

In 2-D SPIHT, the top-left coefficient of each 2 × 2 group in the lowest sub-band is not part of any tree. On the other hand, the top-left coefficient of each 2 × 2 group in the lowest transaxial sub-band in the asymmetric tree structure is linked with the 2 × 2 offspring group in the same transaxial location of the following axial sub-band except the highest axial sub-band. This means that the three coefficients of the 2 × 2 group are linked with the 2 × 2 offspring group in the same coefficient frame, and one is linked in another frame. As we can see in Figure 2, the top-left coefficient of each 2 × 2 group in the lowest transaxial sub-band of the axial LL_t band has one 2 × 2 offspring group in the axial LH_t band, and the top-left coefficient of each 2 × 2 offspring group in the lowest transaxial sub-band of the axial LH_t band has two 2 × 2 offspring groups in the axial H_t band. This means that the top-left coefficients in the LL_t and the LH_t band are linked with the coefficients which represent the same transaxial location in the following axial sub-band. Therefore, the top-left coefficient of each 2 × 2 offspring group in the lowest transaxial sub-band of the axial H_t band does not have any offspring because there are no more axial sub-bands. In this manner, the first stage of the tree is constructed, as shown by the arrows in Figure 2. To grow the tree further, each coefficient group is linked with each transaxial sub-band, the same as with original 2-D SPIHT. Therefore, each 2 × 2 coefficient group in the lowest transaxial sub-band of the axial LL_t band has three 2 × 2 offspring groups in the axial LL_t band and one 2 × 2 offspring group in the LH_t band, and each 2 × 2 offspring group in the lowest transaxial sub-band of the axial LH_t band has three 2 × 2 offspring groups in the axial LH_t band and two in the H_t band. Each 2 × 2 offspring group in the lowest transaxial sub-band of the axial H_t band has three 2 × 2 offspring groups in the same axial H_t band because it is the highest-frequency sub-band.

One potential advantage over the original symmetric tree structure is that it can be applied more easily to a different number of decompositions between the transaxial and axial dimensions because this tree structure is naturally unbalanced. This function is very useful when the frame size is big and axial decomposition levels are limited. In that case, we can decompose to more levels in the transaxial domain than in the axial domain. More transaxial decompositions usually produce noticeable coding gain. The tree structure of this different number of decompositions can be extended easily. For a higher number of axial decompositions, the tree structure can be also extended. Kim et al.⁶ also used an unbalanced tree structure, but it was more difficult to apply.

Filter Implementation

We use the same set of filters as used in Kim and Pearlman’s work.⁵ In this work, S + P, I(2,2), and I(4,2) filters are used for constructing wavelet transforms to map integers to integers. In the following, we provide the equations of the filter sets: I(2,2) filter:

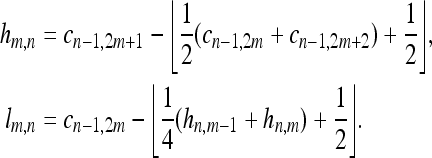1

I(4,2) filter:

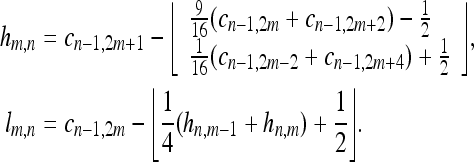2

S + P filter:

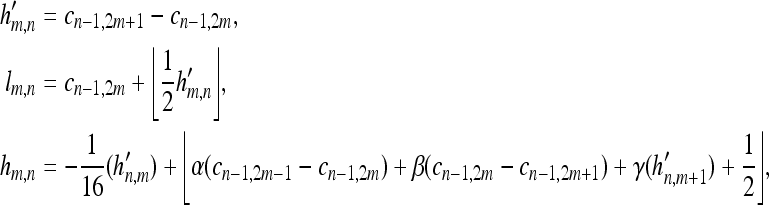3

where ⌊·⌋ denotes downward truncation. In Kim and Pearlman’s work,⁵ the predictor parameters of the S + P filter, α = 3/16, β = 8/16, and γ = 6/16, were selected to get better performance for medical images.

RESULTS

We test the symmetric tree 3-D SPIHT and the asymmetric tree 3-D SPIHT (AT-SPIHT) algorithms on the 8-bit CT and MR volumetric medical images used in the work of Bilgin et al.⁹ Table 1 shows the description of these images. The first slices of each data set are shown in Figure 3.

Table 1.

Description of the Volumetric Medical Images

	History	Age	Sex	File Name	Voxel Size (mm)	Volume Size
CT	Tripod fracture	16	M	Skull	070 × 0.70 × 2	256 × 256 × 192
	Healing scaphoid fracture	20	M	Wrist	017 × 0.17 × 2	256 × 256 × 176
	Internal carotid dissection	41	F	Carotid	025 × 0.25 × 1	256 × 256 × 64
	Apert’s syndrome	2	M	Aperts	035 × 0.35 × 2	256 × 256 × 96
MR	Normal	38	F	Liver_t1	145 × 1.45 × 5	256 × 256 × 48
	Normal	38	F	Liver_t2e1	137 × 1.37 × 5	256 × 256 × 48
	Left exopthalmos	42	M	Sag_head	098 × 0.98 × 3	256 × 256 × 48
	Congenital heart disease	1	M	Ped_chest	078 × 0.78 × 5	256 × 256 × 64

Figure 3.

Description of volumetric medical images: first slice of each data set. (a) Skull, (b) Wrist, (c) Carotid, (d) Aperts, (e) Liver_t1, (f) Liver_t2e1, (g) Sag_head, (h) Ped_chest.

We first compare the performance of lossless compression with GOS = 16 and 8 for three and two levels of decompositions, respectively, in both the axial and transaxial domains. Table 2 gives average lossless compression results in bits per pixel (bpp) using the symmetric tree 3-D SPIHT and the AT-SPIHT with different filters [S + P, I(2,2), I(4,2)]. To get the compression ratio in 8-bpp images, we can divide 8 by the compression rate (in bpp). For the I(4,2) filter, we apply the filter only to the transaxial domain and use a shorter filter [eg, I(2,2)] in the axial domain. AT-SPIHT gives a better performance than that of symmetric tree 3-D SPIHT except Carotid and Skull images when GOS = 16. We also provide the bit-rates of AT-SPIHT with larger GOS. To keep the three-level decompositions, the symmetric tree structure 3-D SPIHT needs an even number of coefficient frames in the lowest axial sub-band to keep the 2 × 2 × 2 wavelet coefficients element in the band. However, the AT-SPIHT does not have this limitation because the tree structure uses a 2 × 2 wavelet coefficient element. This gives us flexibility in choosing the size of the GOS. For example, Aperts, Liver_t1, and Liver_t2 images have 48 slices. The symmetric tree structure 3-D SPIHT needs either 16 GOS or 48 GOS to have three-level decompositions in the axial domain. However, AT-SPIHT can use 16, 24, or 48 GOS with three-level axial decompositions, so that we can flexibly choose the GOS according to the system memory.

Table 2.

Bit Rates after Lossless Compression

Image		3-D SPIHT		AT-SPIHT
(GOS Sizes)	GOS	8	16	8	16	24/32/88	48/64/176
Aperts	S+P	1.1197	1.0543	1.1020	1.0397	1.0345	1.0238
(8,16,24,48)	I(2,2)	1.0428	0.9738	1.0188	0.9522	0.9455	0.9285
	I(4,2)	1.0250	0.9558	1.0028	0.9375	0.9300	0.9147
Carotid	S+P	1.5995	1.4977	1.5856	1.4973	1.4608	1.4500
(8,16,32,64)	I(2,2)	1.6066	1.5272	1.5942	1.5340	1.5075	1.4930
	I(4,2)	1.5901	1.5115	1.5791	1.5192	1.4935	1.4790
Liver_t1	S+P	2.5428	2.3997	2.5045	2.3690	2.3355	2.3103
(8,16,24,48)	I(2,2)	2.4913	2.3573	2.4368	2.3120	2.2605	2.2300
	I(4,2)	2.4580	2.3270	2.4058	2.2857	2.2365	2.2075
Liver_t2	S+P	1.8923	1.7483	1.8817	1.7440	1.7085	1.6850
(8,16,24,48)	I(2,2)	1.9035	1.7823	1.8632	1.7463	1.6940	1.6730
	I(4,2)	1.8667	1.7500	1.8295	1.7170	1.6665	1.6461
Ped chest	S+P	2.2000	2.1045	2.1576	2.0540	2.0310	2.0080
(8,16,32,64)	I(2,2)	1.9988	1.8105	1.9244	1.7650	1.6920	1.6570
	I(4,2)	1.9134	1.7835	1.9104	1.7550	1.6835	1.6490
Sag_head	S+P	2.3468	2.2400	2.3108	2.2023	2.1795	2.1308
(8,16,24,48)	I(2,2)	2.1468	2.0563	2.1010	2.0060	1.9565	1.9300
	I(4,2)	2.1422	2.0517	2.0965	2.0017	1.9530	1.9264
Skull	S+P	2.3210	2.1134	2.4483	2.1661	2.1108	2.0790
(8,16,32,64)	I(2,2)	2.3318	2.1081	2.3159	2.0399	1.9852	1.9583
	I(4,2)	2.2980	2.0464	2.2976	2.0250	1.9708	1.9443
Wrist	S+P	1.4695	1.3689	1.4503	1.3550	1.3140	1.3090
(8,16,88,176)	I(2,2)	1.3758	1.2459	1.3430	1.2173	1.1445	1.1320
	I(4,2)	1.3475	1.2231	1.3170	1.1976	1.1270	1.1150

In addition to the flexibility of choosing GOS, we can also choose many different levels of decompositions in the transaxial domain. As mentioned in the previous section, we can easily apply different numbers of decompositions between the transaxial and axial domains to the AT-SPIHT. This feature is highly desirable when GOS size is limited. To show the performance of different numbers of decompositions, we kept the same number of axial decompositions (two levels for GOS = 8) and used more levels of transaxial decompositions. Table 3 shows the average bit-rates with different numbers of decompositions when GOS = 8. We can see that the coding performance is improved with more levels of decomposition in the transaxial domain, and beyond three or four levels of decomposition the improvement is very small. In the case of the Aperts image, for example, the AT-SPIHT with GOS = 8 is better than symmetric tree 3-D SPIHT with GOS = 16 for more than three levels of decomposition in the transaxial domain. For the other images, the bit rates of AT-SPIHT with GOS = 8 and higher levels of decomposition in the transaxial domain are comparable to those of the symmetric tree 3-D SPIHT with GOS = 16. This is an important feature of AT-SPIHT since the efficient compression of small GOS allows easier and finer random access to a small number of slices.

Table 3.

Average Bit Rates of Different Numbers of Decomposition in Transaxial Direction when GOS = 8

Image	Levels	2	3	4	5	6
Aperts	S+P	1.1120	1.0551	1.0452	1.0435	1.0427
	I(2,2)	1.0188	0.9740	0.9661	0.9653	0.9650
	I(4,2)	1.0028	0.9592	0.9519	0.9514	0.9512
Carotid	S+P	1.5856	1.5516	1.5446	1.5419	1.5412
	I(2,2)	1.5942	1.5653	1.5621	1.5613	1.5610
	I(4,2)	1.5791	1.5571	1.5490	1.5483	1.5480
Liver_t1	S+P	2.5045	2.4538	2.4408	2.4373	2.4363
	I(2,2)	2.4368	2.3962	2.3893	2.3878	2.3877
	I(4,2)	2.4058	2.3643	2.3573	2.3563	2.3557
Liver_t2	S+P	1.8817	1.8380	1.8288	1.8278	1.8270
	I(2,2)	1.8632	1.8237	1.8160	1.8150	1.8145
	I(4,2)	1.8295	1.7910	1.7840	1.7833	1.7828
Ped_chest	S+P	2.1576	2.1218	2.1099	2.1056	2.1041
	I(2,2)	1.9244	1.8992	1.8932	1.8919	1.8909
	I(4,2)	1.9104	1.8855	1.8795	1.8782	1.8772
Sag_head	S+P	2.3108	2.2670	2.2572	2.2552	2.2543
	I(2,2)	2.1010	2.0592	2.0517	2.0498	2.0497
	I(4,2)	2.0965	2.0553	2.0483	2.0470	2.0465
Skull	S+P	2.4483	2.4286	2.4235	2.4221	2.4214
	I(2,2)	2.3159	2.3008	2.2993	2.2986	2.2981
	I(4,2)	2.2976	2.2832	2.2819	2.2812	2.2806
Wrist	S+P	1.4503	1.3994	1.3855	1.3820	1.3812
	I(2,2)	1.3430	1.2977	1.2864	1.2829	1.2815
	I(4,2)	1.3170	1.2715	1.2618	1.2585	1.2570

Table 4 shows the comparisons of lossless compression performance with other compression algorithms. In this table, all 3-D compression techniques use three-level decompositions on the entire image volume. The reason for using the whole image volume as a GOS is to compare it with other results.^{9, 10} We chose the I(4,2) filter for AT-SPIHT and 3-D SPIHT because this filter gives the best result among the three filters [S + P, I(2,2), I(4,2)]. The other 3-D compression techniques, such as 3-D EZW, 3-D CB-EZW, and Xiong’s method, use the I(2 + 2,2) integer filter because this filter usually gives the best result with these compression algorithms. AT-SPIHT performs better than 3-D SPIHT, with the single exception of the Carotid image. When we compare it with other 3-D compression methods, AT-SPIHT still outperforms the other methods, except for the Carotid and Aperts images with 3-D CB-EZW.

Table 4.

Comparison of Different Image Compression Methods on the CT Data after Three-Level Decompositions of the Whole Data Set

Method	Skull	Wrist	Carotid	Aperts
AT-SPIHT	1.9180	1.1150	1.4790	0.9090
3-D SPIHT	1.9550	1.1390	1.4680	0.9340
3-D EZW	2.2251	1.2828	1.5069	1.0024
3-D CB-EZW	2.0095	1.1393	1.3930	0.8923
Xiong	1.9950
JPEG-LS	2.8460	1.6531	1.7388	1.0637
JPEG2000	3.0877	1.7902	1.9896	1.2822
2-D SPIHT	2.6921	1.8378	1.9823	1.2330
CALIC	2.7250	1.6912	1.6547	1.0470
Gzip	3.8576	2.7751	2.8551	1.8243
UNIX Compress	4.1357	2.7204	2.7822	1.7399

DISCUSSION

We showed a lossless compression of volumetric medical images with the asymmetric tree 3-D SPIHT (AT-SPIHT) algorithm. We presented our results by an approach that leads to wavelet transforms that map integers to integers, which can be used for lossless and lossy coding. Because the SPIHT algorithm with integer filters is fully embedded, the decoder can stop the decoding process at any point of the bitstream and reconstruct the best-quality image at that bit rate. Furthermore, the AT-SPIHT can be applied more easily to a different number of decompositions between the transaxial and axial dimensions using the naturally unbalanced characteristic of the tree structure.

For the different number of decompositions between the transaxial and axial dimensions, we can expect coding gain as we decompose to more levels. When we compare between two-level and six-level decompositions in transaxial dimension of I(4,2) filter with GOS = 8, there is about 2.4% improvement with six-level decompositions.

For the effect of size of GOS on the performance of AT-SPIHT, a larger-size GOS gives better compression performance. When we compare GOS = 8 with the entire image volume, we can expect about an 11% improvement. With GOS >16, we get a 4.4% improvement, and with GOS >24, expect only a 1.6% improvement in the case of the I(4,2) filter. However, as the GOS becomes larger, a larger size of memory is required and random access to segments of slices in the bit stream becomes coarser.

We saw that the AT-SPIHT performs much better than the methods that use independent lossless coding of slices, because independent coding of slices does not exploit the inter slice dependencies. Numerical results show that the compressed bit rates for the AT-SPIHT yield improved results about 42% on average compared with 2-D techniques. The best results among the 2-D techniques were obtained with JPEG-LS, which is still 28% less efficient than AT-SPIHT on average. JPEG-LS is an international standard for lossless and near-lossless compression with a nonembedded code stream. These results suggest that the 3-D approach to compress the volumetric medical images should be used to exploit their interslice dependences.

CONCLUSION

In this article, we have implemented the asymmetric tree structure to the 3-D SPIHT algorithm for lossless compression of volumetric medical data. In addition to the improvement over the symmetric tree 3-D SPIHT in terms of bit rates, one of the nice benefits of using asymmetric tree structure is the flexibility of choosing the size of GOS and the number of decomposition levels because the number of decomposition levels in the transaxial domain is totally independent of the number of decomposition levels in the axial domain. Therefore, AT-SPIHT can be used when there are as few as two slices in a GOS. Our experiments showed that 3-D compression methods provide significantly higher compression compared with 2-D methods.