A mathematical model of the urine concentrating mechanism in the rat renal medulla. II. Functional implications of three-dimensional architecture

Abstract

In a companion study [Layton AT. A mathematical model of the urine concentrating mechanism in the rat renal medulla. I. Formulation and base-case results. Am J Physiol Renal Physiol. (First published November 10, 2010). 10.1152/ajprenal.00203.2010] a region-based mathematical model was formulated for the urine concentrating mechanism in the renal medulla of the rat kidney. In the present study, we investigated model sensitivity to some of the fundamental structural assumptions. An unexpected finding is that the concentrating capability of this region-based model falls short of the capability of models that have radially homogeneous interstitial fluid at each level of only the inner medulla (IM) or of both the outer medulla and IM, but are otherwise analogous to the region-based model. Nonetheless, model results reveal the functional significance of several aspects of tubular segmentation and heterogeneity: 1) the exclusion of ascending thin limbs that reach into the deep IM from the collecting duct clusters in the upper IM promotes urea cycling within the IM; 2) the high urea permeability of the lower IM thin limb segments allows their tubular fluid urea content to equilibrate with the surrounding interstitium; 3) the aquaporin-1-null terminal descending limb segments prevent water entry and maintain the transepithelial NaCl concentration gradient; 4) a higher thick ascending limb Na⁺ active transport rate in the inner stripe augments concentrating capability without a corresponding increase in energy expenditure for transport; 5) active Na⁺ reabsorption from the collecting duct elevates its tubular fluid urea concentration. Model calculations predict that these aspects of tubular segmentation and heterogeneity promote effective urine concentrating functions.

in a companion paper (19), which we refer to as study 1, we formulated a region-based mathematical model of the urine concentrating mechanism in the renal medulla of the rat kidney. The general aim of study 1, and of this study, which we call study 2, is to investigate the effects of structural heterogeneity in the urine concentrating mechanism of the renal medulla.

As noted in our recent reviews (22, 34), we believe that the urine concentrating mechanism should be considered in light of the radial and axial inhomogeneity revealed in anatomic studies. Kriz and colleagues (13, 14, 16, 18) have reported that the organization of tubules and vessels is highly structured in the outer medulla (OM) of a number of mammalian species, including rats and mice. Tubules are organized around tightly packed vascular bundles, with the collecting ducts (CDs) and thick ascending limbs (TALs) found distant from vascular bundles and descending limbs positioned nearer the bundles. Cluster of CDs form the dominant organizing structural elements for the arrangement of the tubules and vessels in the inner medulla (IM) (30, 32). In the upper IM, the descending thin limbs of Henle's loops and descending vasa recta (DVR) are nearly always located outside and surrounding the CD clusters (31, 32). In contrast, the ascending thin limbs and ascending vasa recta (AVR) are arranged nearly uniformly across the IM, both inside and outside the CD clusters (31, 32). The structural organization, in the OM and IM, is believed to result in preferential interactions among tubules and vasa recta; these interactions may contribute to more efficient countercurrent exchange or multiplication, to urea cycling and IM urea accumulation, and to sequestration of urea or NaCl in particular tubular or vascular segments (2, 3, 11, 15, 17, 20, 24, 28, 40, 45).

In this study 2, we investigate, in the context of the urine concentrating mechanism, several instances of tubular segmentation or heterogeneity found (or hypothesized) in the rat medulla. We begin by assessing the effects of two segments of the long loops of Henle. First is the IM segment of the thin limbs that turns within the first millimeter of the IM. Second is a terminal segment of the descending thin limbs of the loops of Henle that reach beyond the first millimeter of the IM; that segment spans the lower 60% of the IM portion of those descending limbs and appears to be impermeable to water but highly permeable to urea. We also assess the effects of differing Na⁺ active transport rates along the outer and inner stripe segments of the TALs (9), and along the CD, and the effects of eliminating chloride and urea transporters along segments of the nephron.

For base-case model parameters and model results, see study 1.

MATHEMATICAL MODEL

In the model presented in study 1, the complex structural organization of the OM (15, 18) and of the IM (30–32) was represented by means of concentric regions, centered about a vascular bundle in the OM and about a CD cluster in the IM. The radial positions of structures were incorporated by assigning appropriate tubules and vasa recta (or fractions thereof) to each concentric region. In the OM, four concentric regions are centered on a vascular bundle: an innermost region containing the central vascular bundle (R1); a peripheral region of the vascular bundle (R2); a region neighboring the vascular bundle (R3); and the region most distant from the vascular bundle (R4). The radial organization of the IM is represented by means of two concentric regions centered on a CD cluster: an intercluster region (R5) and an intracluster region (R6) (see Fig. 1 in study 1) (19).

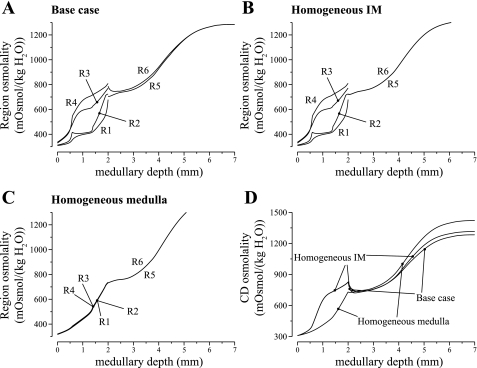
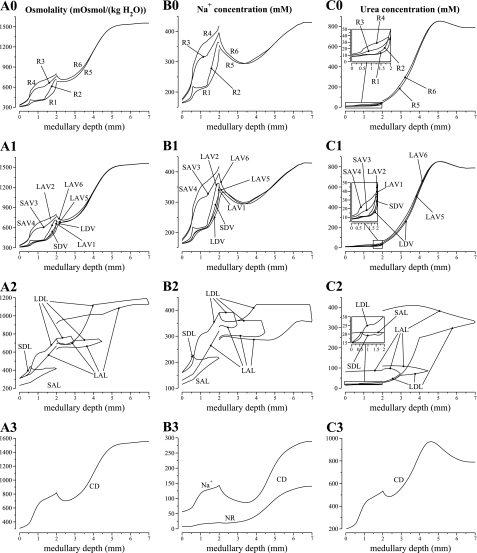
Fig. 1.

Region and collecting duct (CD) osmolality profiles, as a function of medullary depth, for varying degrees of regionalization, obtained by increasing region boundary Na⁺ and urea permeabilities in selected portions of the medulla. A: base case. B: homogeneous inner medulla (IM) case. C: homogeneous medulla case. D: CD osmolality profiles for 3 cases.

The model equations represent solute and water conservation in the tubules, vasa recta, and interstitial spaces. Transmural transport is represented by single-barrier expressions for osmotic water fluxes, solute diffusion, and active solute transport. Solutions of the model equations predict steady-state solute concentrations and fluid flow rates in tubules, in vasa recta, and in the interstitia of concentric regions. Model results, which were obtained using parameters based on experimental measurements and which showed a generally increasing osmolality gradient along the corticomedullary axis, are consistent with fundamental experimental findings (19).

RESULTS

Radial Organization of Tubules and Vessels

To assess the impact of regionalization on model results, we conducted two simulations in which the radial organization of tubules and vessels was eliminated in all or part of the model medulla. In the first case, we eliminated the radial organization in the IM only. That was achieved by setting the solute permeabilities between the IM regions R5 and R6 to 100 × 10⁻⁵ cm/s throughout the IM. The interregion solute permeabilities were unchanged in the OM. We refer to this case as the “homogeneous IM case.” In another case, which we refer to as the “homogeneous medulla case,” we eliminated radial organization throughout the medulla by setting all interregion solute permeabilities to 100 × 10⁻⁵ cm/s.

Fluid osmolality profiles for the concentric regions and for the CD, for the base case and for the two alternative cases, are exhibited in Fig. 1. In both alternative cases, the model predicted that when regionalization was eliminated, the concentrating capability of the model increased. A more concentrated urine was produced, with an osmolality of 1,314 and 1,332 (in units of mosmol/kgH₂O), in the homogeneous IM case and in the homogeneous medulla case, respectively, compared with the base-case value of 1,283. It is noteworthy that the homogeneous medulla case predicted that, if radial organization were eliminated in the OM, the concentrating capability of the model OM would decrease, in the sense that the CD fluid osmolality at the OM-IM boundary decreased from the base-case value of 820 to 722 mosmol/kgH₂O. However, that decrease in OMCD fluid osmolality was accompanied by an elevation of DVR fluid osmolality (see the increase in R1 osmolality, relative to the base case, in Fig. 1). A more concentrated DVR fluid has less of a diluting effect on the IM concentrating mechanism, resulting in the eventual production of a urine with an osmolality that is higher than the base case, and similar to the homogeneous IM case.

These results are consistent with those obtained in a previous modeling study (25). Both studies suggest that the concentrating capability of the IM would be significantly improved if the tubules and vessels were randomly distributed and surrounded by a common interstitial fluid at each medullary level, rather than being organized around CD clusters in the initial IM. That is, concentrating capability would be improved, if at each medullary level, all tubules and vessels interacted through a well-stirred bath. Given these results, we therefore hypothesize that the functional implications of the radial organization of the renal medulla may lie not directly in the urine concentrating mechanism, but, perhaps, in the preservation of oxygen to the deep medulla (see discussion), in potassium and acid-base metabolism, or in the embryological cost for development, etc.

Given these considerations, particularly the assumption that in the upper IM DVR should be isolated from most, but perhaps not all, other tubules, one might ask this question: where should other structures be located to augment the concentrating effect? Below, we consider the impacts of the extracluster positions of the thin ascending limbs in the upper IM.

Upper IM Position of Ascending Thin Limbs

The long ascending limb (LAL) of a loop that reaches into the final 2 mm of the model medulla is denoted LAL_L and was assumed to occupy a position external to the CD cluster in the upper IM. (In contrast, the LAL of a loop having its bend within the upper IM ascends neighboring within the CD cluster.) In the deep IM, the high urea permeability of the aquaporin-1 (AQP1)-null segments of the long descending limbs (LDLs) facilitates urea entry into the loop lumen. If that urea isn't reabsorbed from the LALs before their return to the OM, it would impose a diluting effect on the IM concentrating mechanism. Thus, in study 1, we have proposed that, by occupying an extracluster position in the upper IM, the LALs, together with the DVR, act as countercurrent exchangers to promote urea cycling within the IM. To investigate that hypothesis, we conducted a simulation in which the LAL_L occupied an intracluster position throughout the IM.

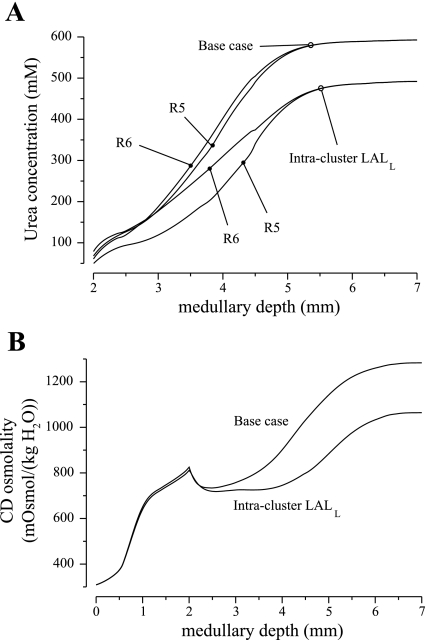
Figure 2 shows model IM interstitial fluid urea concentration and CD tubular fluid osmolality profiles obtained for this case; the corresponding base-case profiles are included for comparison. These results show that if the LAL_Ls occupied an intracluster position throughout the IM, then the difference in urea concentration between the two IM regions would be augmented. That is because the tubular fluid urea concentration in the upper IM segment of LAL_L is higher than that of the intercluster interstitial fluid, and thus serves as a urea source. When the LAL_L stayed within the CD cluster, it carried out a fluid that had a higher urea concentration and thus osmolality, relative to the base case, which produced a diluting effect. The cycling of urea within the IM, through the LAL_L to the DVR, was also disrupted. As a result, the interstitial fluid urea concentration was lowered, relative to the base case, in both regions throughout the IM; the concentrating effect of the model IM was reduced; and the urine osmolality was predicted to be 1,064 mosmol/kgH₂O, 17.1% lower than the base case. Thus these results suggest the role of the LAL_L in urea cycling and effective urine concentrating functions.

Fig. 2.

IM region urea concentration and CD osmolality obtained by assigning an intracluster position to the long ascending limbs (LALs) associated with loops that reach into the deep IM (denoted LAL_L). Base-case profiles are included for comparison. The “intracluster LAL_L” case yielded lower interstitial urea concentrations and an impaired concentrating effect.

Anatomic findings distinguish three subpopulations of Henle's loops in the IM (22). Subpopulation 1 corresponds to loops of Henle that reach no more than ∼1 mm into the IM and that do not label for AQP1 in their IM segments. Subpopulation 2 corresponds to loops that reach >1 mm, and no more than about 3–3.5 mm, into the IM, and that label for AQP1 in the upper ∼40% of the IM portions of their descending limbs. Below this point, they fail to express AQP1 for the remaining 60% of their IM lengths. Subpopulation 3 corresponds to loops that reach into the final 1–2 mm of the IM and that also label for AQP1 in the upper ∼40% of the IM portion of their descending limbs. Half of these loops, instead of having narrow hairpin bends with only a small transverse segment, have a broad transverse segment that includes part of the ClC-K1-positive prebend region of the descending thin limb and part of the ascending thin limbs (33). These broad bends tend to be close to, and curved laterally around, the very large terminal CDs in this region. Because many of these loop segments were discovered recently, their transport properties have not been well characterized. Thus we investigate below the effects of axial inhomogeneity of loop of Henle transport properties.

Water Permeability of Papillary LDL Segment

Based on perfused tubule studies in rats (10) and other mammals (35), the rat descending thin limb has usually been assumed to be highly water permeable up to the loop bend, or until the beginning of the prebend segment (27, 38, 41) (an exception is in Ref. 39). Indeed, descending limb water permeability was considered as an essential element of the passive mechanism (12, 37): water absorption from the descending thin limb was hypothesized to raise the NaCl concentration of tubular fluid entering the ascending thin limb and thus promote a larger transepithelial gradient favoring NaCl absorption from the ascending thin limb. However, recent experiments by Pannabecker and coworkers (6, 30) have revealed a substantial terminal segment along the IM descending thin limbs that do not express AQP1 and that appear to be water impermeable. That segment is represented in the model as the LDL3 segment and assumed to have zero water permeability.

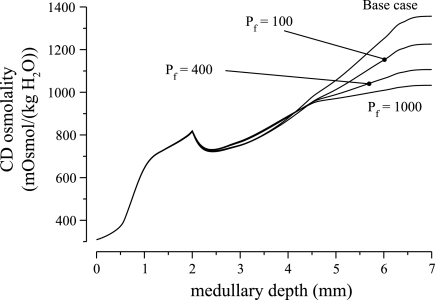
We investigated the impact of LDL3 osmotic water permeability by varying it from 0 to 1,000 μm/s; model results are summarized in Fig. 3. As LDL3 osmotic water permeability increased from 0 to 1,000 μm/s, urine osmolality decreased to 963.1 mosmol/kgH₂O, a 25.0% relative decrease. The model predicted that tubular fluid osmolality in LDL3 is hyperosmotic to local interstitial fluid. Thus, as LDL3 water permeability increased, water entered LDL3, diluting its tubular fluid and reducing Na⁺ absorption near the loop bend. Consequently, urine osmolality decreased, whereas urine flow rate increased.

Fig. 3.

Parameter studies for water permeability of LDL3. Shown is CD fluid osmolality as a function of medullary depth. Results indicate that higher LDL3 water permeability reduces concentrating effect.

Urea Permeabilities of Thin Limbs of Henle

Considerable uncertainty remains in the specification of urea permeabilities of the thin limbs of Henle in the IM. Microperfusion studies by Imai (10) have shown a substantial scatter in permeabilities in ascending thin limbs: in hamsters, values ranges from ∼3 to 40 × 10⁻⁵ cm/s; in rats, from ∼12 to 40 × 10⁻⁵ cm/s. Liu et al. (29) reported significant urea permeability value (∼25 × 10⁻⁵ cm/s) along thin ascending limbs in the lower two-thirds of the IM. These measurements suggest that urea permeability in thin limbs may be spatially heterogeneous. In chinchillas, Chou and Knepper (5) reported ascending thin limb urea permeability of ∼170 × 10⁻⁵ cm/s. In our model, we assumed that the urea permeability of the upper 40% of the IM portion of LDL of the long loops of Henle that reach into the deep IM is 13 × 10⁻⁵ cm/s, the lower 60% of those LDL is 180 × 10⁻⁵ cm/s, and the IM portion of the associated LAL is 190 × 10⁻⁵ cm/s. In the following set of parameter studies, we assess the effects of different urea permeabilities in the thin limbs of Henle.

We consider the following cases, in which we varied the urea permeabilities of the lower 60% of the IM portion of the LDL (which we refer to as the LDL3 segment) and/or the entire IM portion of the LAL associated with loop of Henle that reaches beyond the first millimeter of the IM. The urea permeabilities of the upper 40% of the LDL IM segment and of the OM portions of the loops were kept at base-case values. In two cases, which we refer to as the “low LDL case” and “low LAL case,” we assumed that the LDL3 segment or the LAL (but not both) has a low urea permeability of 1 × 10⁻⁵ cm/s. In two other cases, which we refer to as the “moderate LDL case” and the “moderate LAL case, ”we assumed that the LDL3 segment or the LAL only has a moderate urea permeability of 20 × 10⁻⁵ cm/s. In another case, the “moderate LDL-LAL case,” we assumed that both the LAL and LDL3 segment have a moderate urea permeability. These urea permeabilities are summarized in Table 1.

Table 1.

Effects of thin limb urea permeabilities

	Base Case	Low LDL	Low LAL	Moderate LDL	Moderate LAL	Moderate LDL-LAL	Pipe Mode
	Purea,×10−5 cm/s
LDL3	180	1	180	20	180	20	1
LDLS	200	200	200	200	200	200	1
LAL	190	190	1	190	20	20	1
LALS	200	200	200	200	200	200	1
	Urine composition
Osmolality,	1,283	799	724	953	986	902	1,554
mosmol/kgH2O
Na+ concentration, mM	266	238	140	241	203	215	288
Urea concentration, mM	593	159	358	305	449	327	790
NR concentration, mM	119	112	65	116	96	103	140
Flow rate, nl•min−1•nephron−1	0.0627	0.0665	0.114	0.0645	0.0774	0.0727	0.0531

P_urea, urea permeability; LDL2, upper 40% of inner medullary (IM) portion of LDL; LDL3, lower 60%; LDL_S and LAL_S, descending and ascending thin limbs of long loops that turn within the first millimeter of the IM.

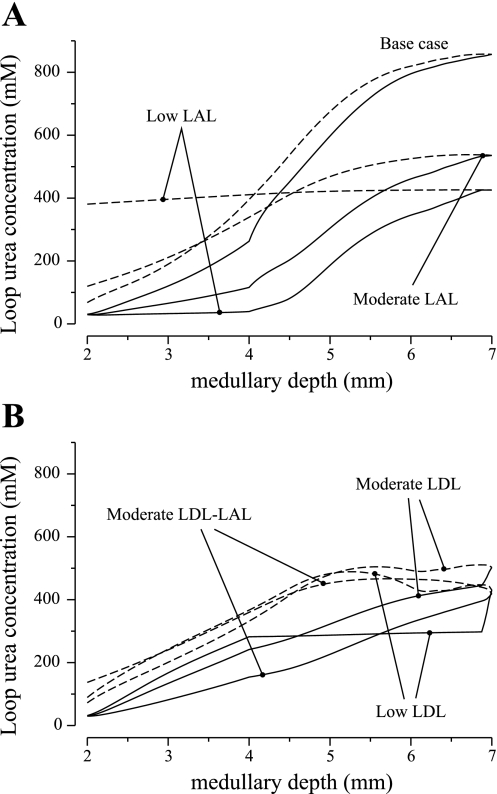
Tubular fluid urea concentration profiles along the IM portion of the longest loop of Henle are exhibited in Fig. 4. Urine composition and flow rate are exhibited in Table 1. In all cases, in which the urea permeability of one or more segments of the thin limbs of Henle was lowered, the model's concentrating capability was negatively impacted to a substantial degree. In the low LAL case and the moderate LAL case, urea entered the LDL, raising the tubular fluid osmolality (see Fig. 4A). Because the LAL urea permeability was not sufficiently high, the tubular fluid urea concentration of the LAL failed to nearly equilibrate with the surrounding interstitial fluid, and the LALs carried a fluid into the OM that was more concentrated than the corresponding LDL fluid, in large part because of its elevated urea content. The resulting diluting effect yielded low urine osmolalities of 724 and 986 mosmol/kgH₂O for the low LAL case and moderate LAL case, respectively.

Fig. 4.

Parameter studies for urea permeabilities of LDL3 and thin ascending limb. Shown are loop urea concentration profiles, obtained for the 5 alternative cases and for the base case, as a function of IM depth. Solid lines, descending limb; dashed lines, ascending limb. Model's urine concentrating capability was substantially impaired in all alternative cases (see Table 1).

In the low LDL case, the osmolality along the LDL3 segment changed little (see Fig. 4B), because that segment was assumed to be impermeable to water and had low permeabilities to both Na⁺ and urea. Along the lower half of the IM, urea entered the highly urea-permeable LAL, raising the tubular fluid urea concentration, and therefore osmolality, along the flow direction. Because urea was carried away from the deep IM by the LALs, the papillary interstitial fluid urea concentration was lowered, which increased urea reabsorption from the IMCD. The resulting decrease in urea concentration led to a drop in fluid osmolality along the deep IMCD, and, consequently, a urine with a low osmolality of 799 mosmol/kgH₂O was produced. Indeed, that urine osmolality was lower than the osmolality of the CD tubular fluid at the OM-IM boundary (811 mosmol/kgH₂O). A similar argument applies to the moderate LDL case, albeit to a lesser degree owing to the higher LDL3 urea permeability.

In the “moderate LDL-LAL case,” urea entered the LDL, raising its fluid osmolality (see Fig. 4B). However, with only a moderate urea permeability, the LDL fluid urea concentration did not nearly equilibrate with the surrounding interstitial fluid. As a result, around the loop bend, urea continued to enter for a substantial segment (∼1 mm for the longest loop) along the LAL. That urea entry, when taken in isolation, produced a diluting effect on the system. Along the remainder of the IM LAL, urea was reabsorbed from the LAL. However, because the LAL only had a moderate urea permeability, its tubular fluid urea concentration remained significantly higher than the local interstitial fluid. At the OM-IM boundary, the fluid osmolality of the longest LAL was predicted to be 640 mosmol/kgH₂O, which is higher than the base case (628 mosmol/kgH₂O). A urine with an osmolality of 844 mosmol/kgH₂O was produced.

Taken together, these results suggest that if the loops of Henle are to have significant urea permeabilities, those permeabilities must be sufficiently high, in both limbs, for tubular fluid urea to nearly equilibrate with the interstitium, to facilitate an effective IM concentrating mechanism.

We also considered the low urea permeability limit of the loop of Henle: the LDL3 segment as well as the LAL were assumed to have nearly zero urea permeability. The urea permeabilities assumed in this case correspond to the “pipe mode” that we considered in a previous study (23) (see Table 1); thus we will refer to this case as the pipe mode. Key model results are summarized in Table 1 and displayed in Figs. 5 and 6. Figure 5 shows axial osmolality, Na⁺ concentration, and urea concentration profiles in the concentric regions and in each class of tubule and vessel (and NR concentration in the CD); Fig. 6 shows water flow rates.

Fig. 5.

Osmolalities and concentration profiles of concentric regions, tubules, and vasa recta, obtained for the “pipe mode,” which assumes low loop urea permeabilities. The ordinate is identified at the top of each column: column A, osmolality; column B, Na⁺ or NR concentration; column C, urea concentration. The topmost row, indicated by 0, contains profiles for the interstitia of the regions. Row 1 contains profiles for the vasa recta; row 2, loops of Henle; and row 3, CD. Note variation, among panels, in ordinate scalings. Compared with the base-case model (Fig. 2 in Ref. 19), the pipe mode predicts a low fluid osmolality along the LDL3 segment, but a substantially higher urine osmolality.

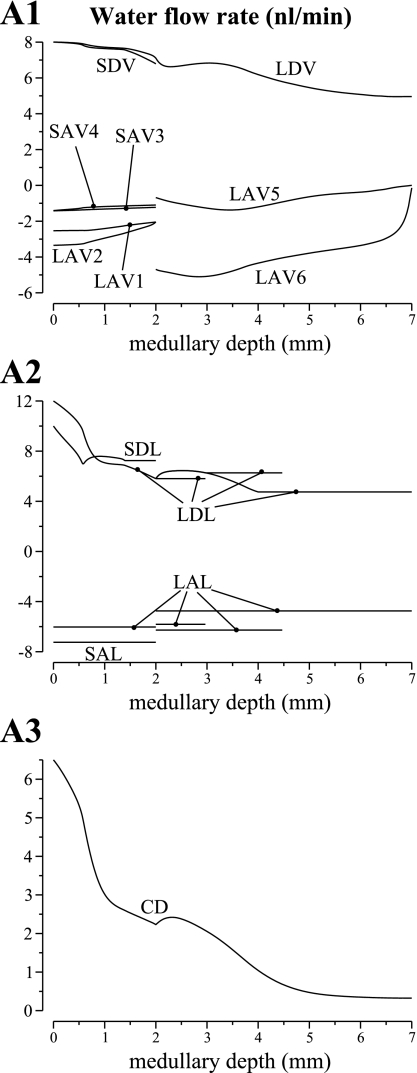
Fig. 6.

Water flows in tubules and vasa recta, given per individual tubule or vessel. Results were obtained for the pipe mode. Notation is analogous to that used in Fig. 5. Negative flows in ascending limbs and ascending vasa recta are directed toward the cortex; flows in descending structures are directed toward the papillary tip. No axial flow is assumed in the regions.

The pipe mode predicted a urine osmolality of 1,554 mosmol/kgH₂O and a urine flow rate of 0.0531 nl·min⁻¹·nephron⁻¹. Model urine Na⁺, urea, and NR concentrations are 288, 790, and 140 mM, respectively. The concentrating processes in the OM are similar to the base case and thus are not discussed. Below, we summarize the IM urine concentrating mechanism corresponding to the pipe mode, which is similar to the processes described in Refs. 23 and 24. Because LDL3 permeabilities to NaCl and urea were low, their transepithelial fluxes were small, and therefore the LDL3 segment functions much like a conduit or a “pipe” with respect to NaCl and urea. At the prebend segment, the LDL permeability to NaCl increased greatly, and that high permeability was sustained along the LAL. Because of urea absorbed from the IMCD (and especially urea absorbed from the innermost IMCD), the interstitial urea concentration was high and the concentrations of electrolytes were low. Thus a large transepithelial gradient favored NaCl absorption around the loop bend, particularly for those loops that reach deep into the papilla. Along the LAL, NaCl continued to be absorbed; indeed the LAL served as a near equilibrating segment for NaCl. However, as fluid ascended the LAL, the gradient favoring its absorption diminished, owing to the NaCl that was absorbed from loop bends that turn nearer the OM-IM boundary. Taken together, this mode concentrates principally by the vigorous net absorption of solute, viz., NaCl, from loop bends, which is unaccompanied by water absorption from loop bends.

The pipe mode attains a substantially higher urine osmolality because the nearly zero urea permeabilities of the lower LDL and of the LAL allow only small transepithelial urea fluxes and facilitate urea accumulations in the interstitium, especially in the deep IM. The higher interstitial urea concentration reduces urea reabsorption from the IMCD, which raises the urea concentration and osmolality of the IMCD tubular fluid, and, eventually, of the urine. Although the pipe mode predicted a urine urea concentration that may be unphysiologically high, we have shown, in previous studies (23, 24), that it can produce a urine with composition more consistent with experimental measurements, provided that the IMCD transport properties are adjusted appropriately.

Even though the pipe mode produced a higher concentrating effect, the assumed thin limb urea permeability appears to be inconsistent with the significant urea permeabilities revealed in isolated perfused thin limb experiments in a number of species (5, 10, 29) and by preliminary measurements by others (Dantzler WH, Evans KK, and Pannabecker TL, unpublished observations) in defined regions of rat IM thin limbs. One potential benefit of the base-case configuration over the pipe mode may be that, by allowing urea entry into the loops of Henle, the base-case configuration facilitates urea cycling: from the IMCD into the LAL, via the distal tubules, and eventually back to the CD. To assess the validity of this hypothesis, we compare the urea flow rates of the TALs associated with the short- and long-loop nephrons and of the CD at the corticomedullary boundary. The base-case urea flow rates (given in pmoles per minute per nephron) are 112, 139, and 201, respectively, whereas the pipe mode predicted the corresponding urea flow rates to be 103, 162, and 212, respectively. No substantial differences were found between the corresponding urea flow rates. Thus model results suggest that urea cycling in the pipe mode is comparable to that of the base-case configuration.

Transport Properties of Long-Loop Subpopulation 1

Immunohistochemical localization studies indicate that the IM portions of the loops of Henle that have their bends within the first millimeter below the OM-IM border do not express AQP1. However, their transport properties, with regard to water and other solutes, have not been measured. Our model assumes that these loops are water impermeable but highly urea permeable, consistent with the AQP1-null segments of the longer loops of Henle.

To investigate the sensitivity of model results to the zero water permeability assumed for the IM segments of the LDLs of the long loops of Henle subpopulation 1, we conducted a simulation in which those segments were assigned a high water permeability of 2,200 μm/s, similar to the AQP1-positive IM segment of the LDLs subpopulations 2 and 3. When the descending thin limbs of those loops were made water permeable, water entered because the LDL fluid osmolality was higher than the intercluster interstitial fluid. That lowered the luminal fluid Na⁺ concentration and reduced Na⁺ reabsorption along the loop bend. As a result, the Na⁺ concentration and osmolality of the local interstitial fluid were lowered, which in turn had the effect of reducing water reabsorption from the IMCD. This effect is more pronounced in the longer loops among the subpopulation. For the shorter loops, which constitute a large fraction of the loop population owing to the model assumption that the IM loop population approximates an exponential-like function (see Eq. 1 in study 1), there was less water secretion along their (shorter) LDL. Thus their Na⁺ reabsorption was lowered to a lesser degree. Overall, the reduction of the model's concentrating effect is small: the model predicted a urine osmolality of 1,277 mosmol/kgH₂O, 0.47% below the base case.

In the base case, the urea permeabilities of both limbs of these loops were assumed to be high: 200 × 10⁻⁵ cm/s. To assess the effects on model results of variations in urea permeabilities of the thin limbs of the long-loop subpopulation 1, we considered five cases: “case 1,” low descending limb permeability (1 × 10⁻⁵ cm/s) and high ascending limb permeability (200 × 10⁻⁵ cm/s); “case 2,” moderate descending limb permeability (20 × 10⁻⁵ cm/s) and high ascending limb permeability (200 × 10⁻⁵ cm/s); “case 3,” high descending limb permeability (200 × 10⁻⁵ cm/s) and low ascending limb permeability (1 × 10⁻⁵ cm/s); “case 4,” high descending limb permeability (200 × 10⁻⁵ cm/s) and moderate ascending limb permeability (20 × 10⁻⁵ cm/s); and “case 5,” moderate descending and ascending limb permeabilities (20 × 10⁻⁵ cm/s). In all cases, the model predicted a urea osmolality that is slightly lower than base case; but that difference is small, at most 3.0% (case 1).

Taken together, these results suggest that model results are nearly insensitive to the water and urea permeabilities of the loops of Henle subpopulation 1.

Our model assumes that the active Na⁺ transport rate of ascending thin limbs decreases in a steep exponential function in a narrow stripe immediately below the OM-IM border (see Eq. 5 in study 1); beyond the first millimeter below that border, the ascending thin limbs have practically no active transport. To assess the roles, in the context of the overall concentrating effect, of a small amount of active Na⁺ transport that is restricted near the IM base, we conducted a simulation in which the ascending thin limbs were assumed to have no active Na⁺ transport throughout the entire IM. The elimination of active transport along all ascending thin limbs lowered the Na⁺ reabsorption from the loops of Henle and water reabsorption from the initial portion of the IMCD. As a result, a lower urine osmolality of 1,224 mosmol/kgH₂O, 4.6% lower than the base case, was predicted. These results suggest that a small amount of active transport near the IM base has a significant impact on the overall concentrating effect. Nonetheless, that active transport is not critical to the model's concentrating mechanism; even when it was eliminated, the model produced a moderately concentrated urine.

TAL Maximum Na⁺ Transport Rate

The base-case TAL Na⁺ active transport rate (V_max) is 10.5 nmol·cm⁻²·s⁻¹ in the outer stripe and 25.9 nmol·cm⁻²·s⁻¹ in the inner stripe, based on Na⁺-K⁺-ATPase activities reported by Garg et al. (9). The effect of inhomogeneous TAL Na⁺ active transport was investigated by comparing base-case results to three alternative cases, each of which had uniform V_max all along the TAL (and the prebend also, for one of the model short loops). For the three cases, the active transport rate (in nmol·cm⁻²·s⁻¹) was set to 10.5 (“low”), 25.9 (“high”), and 19.95 (“average”). The average rate was computed so that its V_max value, weighted by the TAL radius, equaled the (inhomogeneous) base-case values of V_max, weighted by the TAL radius (the weighting was accomplished by means of appropriate definite integrals).

For the base case and three alternative cases, Fig. 7 exhibits the CD fluid osmolality profiles. The average case yielded an OM-IM boundary CD fluid osmolality that was 14.2% lower than the base-case value, even though the two cases should have similar energy cost. The lower OM concentrating capability in turns yielded a urine osmolality of 1,177 mosmol/kgH₂O, which is 8.26% lower than the base case. The high case produced an OM-IM boundary CD fluid osmolality that exceeded the base-case value by 8.27%. However, the higher OM concentrating effect was not significantly augmented in the IM; the high case produced a urine osmolality of 1,360 mosmol/kgH₂O, which is only 6.0% above the base case. In the low case, fluid osmolality was increased along the OMCD by a factor of 1.56 only, relative to blood plasma osmolality, compared with 2.5 in the base case; OM-IM boundary CD fluid flow was increased by 69.1% relative to the base case. Thus the low case, with a more dilute fluid entering the IM via the CD at a higher rate (relative to the base case), imposed a substantially increased load on the IM concentrating mechanism. As a result, the low case produced a urine with an osmolality of only 748 mosmol/kgH₂O, which is 50.0% below base case.

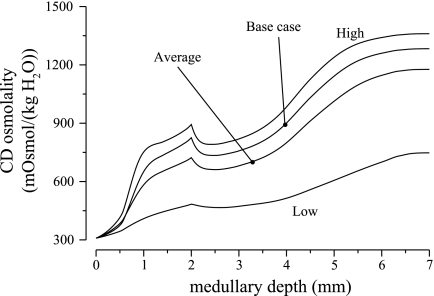
Fig. 7.

CD tubular fluid osmolalities for differing thick ascending limb (TAL) Na⁺ active transport rates. “High,” “Average,” and “Low” cases correspond to uniform TAL Na⁺ transport rates of 25.9, 19.95, and 10.5 nmol·cm⁻²·s⁻¹, respectively. High transport rate generates the highest CD fluid osmolality, but at a high energy cost. Both average and low transport rates decrease CD fluid osmolality substantially.

CD Maximum Na⁺ Active Transport Rate

Active Na⁺ absorption from the model CD, especially along the upper IM segment, facilitates the IM concentrating mechanism by raising the urea concentration in CD tubular fluid and by reducing the load presented to the concentrating mechanism in the deep portion of the model IM. Because a wide range of values has been reported for Na⁺ active transport rates in CD (42), we determined the sensitivity of model results to this parameter by considering alternative CD active Na⁺ transport rates. In the “no OM transport case,” active Na⁺ transport rates along the OMCD, which in the base case were set to 3 and 5 nmol·cm⁻²·s⁻¹ in the outer stripe and inner stripe, respectively, were eliminated. IMCD transport rates were kept at base-case value. In the average case, the maximums active Na⁺ transport rate was set to 4.4 nmol·cm⁻²·s⁻¹, the spatial average of the base-case maximum transport rate, along the entire IMCD. In the low case and in high case, the IMCD maximum active Na⁺ transport rate was set to half and 1.5 times of its base-case value, respectively. Except for the no OM transport case, OMCD active Na⁺ transport rates were set to base-case values.

Profiles of CD tubular fluid osmolality, fluid solute concentrations, and fluid flow rates are shown in Fig. 8, for the base case and for four alternative cases. All four alternative cases produced a urine that is less concentrated than the base case. The no OM transport case predicted that the OMCD active Na⁺ transport had only a minimal effect on the OM concentrating mechanism. The CD tubular fluid osmolality was predicted to be 800 mosmol/kgH₂O, only 3.1% below the base case. However, the composition of that CD fluid is substantially different from the base case: in the no OM transport case, the Na⁺, urea, and NR concentrations of the CD fluid were predicted to be 237, 344, and 165 mM, respectively, at the OM-IM boundary, whereas in the base case, those solute concentrations were 155, 518, and 209 mM. Note that by not facilitating Na⁺ reabsorption via active transport, the CD failed to deliver to the IM a fluid that is highly concentrated in urea. Additionally, the active Na⁺ transport along the OM also increases water reabsorption. The CD fluid flow water was 2.18 nl/min at the OM-IM boundary in the base case, but 2.76 nl/min in the no OM transport case. A larger load thus presented to the IM concentrating mechanism reduced its effectiveness. As a result, the urine osmolality was predicted to be only 941 mosmol/kgH₂O in the no OM transport case, which is 26.7% below the base case.

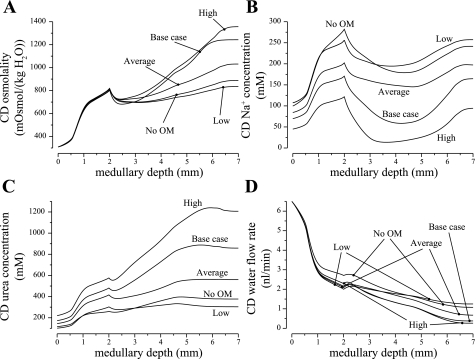
Fig. 8.

Parameter studies for differing CD Na⁺ active transport rates. “High” and “Low” cases correspond to IMCD Na⁺ transport rates 1.5 and 0.5 times of base-case value; “Average” case corresponds to uniform IMCD Na⁺ transport rate of 5.525 nmol·cm⁻²·s⁻¹; “No OM” case corresponds to zero OMCD Na⁺ transport rate. High transport rate generates the highest CD fluid osmolality, but at a low urine flow rate. Both average and low transport rates decrease CD fluid osmolality substantially.

The average case and low case produced urine osmolalities of 1,110 and 965 mosmol/kgH₂O, respectively, which are substantially below the base-case value (1,283 mosmol/kgH₂O), even though the CD fluid osmolalities at the OM-IM boundary are similar in three cases. That impairment in the IM concentrating mechanism can be attributed, in part, to the increases in the load presented by the CD, in the two alternative cases, to the concentrating mechanism in the deep IM. By the vigorous active reabsorption of Na⁺ (with a V_max, Na of 8 nmol·cm⁻²·s⁻¹), the base-case IMCD lost 64.7% of its Na⁺ and 44.5% of its fluid in the first 2 mm of the IM. With that V_max,\Na substantially lowered, the IMCD in the average case lost only 28.0% of its Na⁺ and 24.5% of its water, and in the low case lost 21.7% of its Na⁺ and 16.4% of its water along the first 2 mm of the IM. Even though average case V_max, Na was higher in the deep IM, the vigorous Na⁺ reabsorption there did not sufficiently reduce the CD fluid flow to attain a steep axial osmolality gradient. The higher load presented by the IMCD to the concentrating mechanism in the deep IM lowered the concentrating effect, in large part by reducing urea reabsorption from the IMCD. Indeed, although the urine urea concentrations in the average case and low case were lower than in the base case (494 and 381 mM, compared with the base-case values of 593 mM), the urine urea flow rates were actually higher in those two alternative cases (0.0979 and 0.170, compared with 0.0627 pmol/min in the base case), owing to the much higher urine flow rates. Because more urea was excreted, less urea was returned to the cortex via the ascending limbs, and less urea reentered the medulla via the CD. At the corticomedullary boundary, CD fluid urea concentrations were 177 and 165 mM in the average and low cases, which are 5.85 and 12.2% lower than the base case (188 mM). Without a sufficient amount of urea delivered to the IM, the IM concentrating mechanism failed to function effectively.

When IMCD V_max, Na was set to 50% higher than the base case, with OM V_max, Na kept at base-case value, the model predicted that a urine with osmolality of 1,497 mosmol/kgH₂O, 16.7% higher than the base case, and a urine flow rate of 0.0300 nl/min, 52.2% lower than the base case. The higher IMCD V_max, Na rapidly reduced CD tubular flow rate by 59.6% along the first 2 mm of the IM (compared with 44.5% in the base case). As a result, CD tubular urea concentration increased 64.7%, from 562 mM at the OM-IM boundary to 926 mM 2 mm below the IM base. However, the rapid urea efflux in the deep IM, which followed the high CD urea permeability, gave rise to a rapid decrease in CD fluid urea concentration. Thus, in the final millimeter of the IM, both the interstitial and CD fluid osmolalities stopped their ascent.

CD Urea Permeability

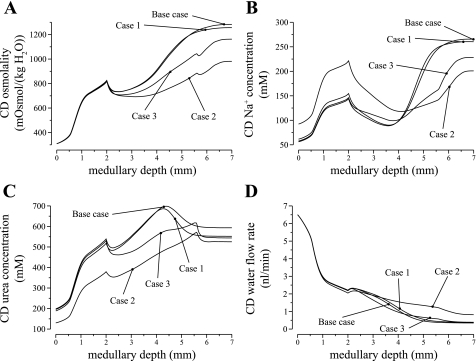
To preserve urea delivery to the deep IM, the model assumed that CD urea permeability was low throughout the OM and the initial 1/5 of the IM (3 × 10⁻⁶ cm/s), which is not inconsistent with low urea permeability values reported in microperfusion studies (36) or those used in mathematical models of the CD (43, 44), although our values may correspond to the lower limit. To study the impact of a slightly higher, but still low, OM and early IMCD urea permeability, we conducted a simulation in which CD urea permeability was set to 1 × 10⁻⁵ cm/s in the OM and in the initial one-fifth of the IM. In the remaining half of the IM, CD urea permeability increases exponentially to 110 × 10⁻⁵ cm/s as in the base case.

Our simulation results indicate that, with an 3.3-fold increase in early CD urea permeability, the concentrating capability of the model medulla was reduced, but a moderately concentrated urine was produced. We exhibit in Fig. 9 the osmolality, Na⁺ concentration, urea concentration, and water flow rate profiles of the CD, for this case (labeled case 1) and for the base case. A higher urea permeability increased urea reabsorption from along the CD and yielded a lower CD tubular urea concentration. However, except in the terminal millimeter of the IM, CD tubular fluid osmolalities are similar in both cases, owing to the moderate CD water permeability that allowed the CD fluid to approximately equilibrate with the local interstitium. Owing to the increased urea reabsorption along the early CD, the CD urea flow into the deep IM was sufficiently low that, when CD urea permeability was increased in the deep IM, urea reabsorption from the IMCD far exceeded water reabsorption, leading to a substantial decrease in CD urea concentration. As a result, the model produced a less concentrated urine than the base case (1,256 compared with 1,283 mosmol/kgH₂O) and at a lower urine flow rate.

Fig. 9.

Parameter studies for differing CD urea permeability profiles. Case 1, higher urea permeability (1 × 10⁻⁵ cm/s) in OMCD and initial IMCD; case 2, IMCD urea permeability increases abruptly at x = L_OM + 0.7L_IM; case 3, same as case 2 but with initial IMCD urea permeability increased by 10-fold from base case. A: CD tubular fluid osmolality. B and C: CD Na⁺ and urea concentrations. D: CD water flow rate. The alternative CD urea permeability profiles yielded lower urine osmolalities.

We conducted additional simulations, in which CD urea permeability was assumed to increase abruptly, rather than exponentially, such that P_CD, urea(x) = P₀ for x ≤ x_CD and P_CD, urea(x) = P₁ for the remainder of the IM. We obtained model results for three different positions of the step change: x_CD = L_OM + aL_IM, for a = 0.6, 0.7, and 0.8, where L_OM and L_IM denote the lengths of the model OM and IM, respectively (L_OM = 2 mm and L_IM = 5 mm). All three cases produced urine that was less concentrated than the base case (1,178, 981, and 878, respectively, compared with 1,283 mosmol/kgH₂O). Figure 9 shows the osmolality, Na⁺ concentration, urea concentration, and water flow rate profiles of the CD, for the a = 0.7 case (labeled case 2). The concentrating ability of the system was lowered using the three alternative CD urea permeability profiles because, in all three cases, CD urea permeability remained low for a larger portion of the IM (recall that in the base case, CD urea permeability begins to increase after the initial one-fifth of the IM).

The lower urea reabsorption in turn reduces water reabsorption from the initial IMCD; thus CD tubular fluid enters the terminal IM at a rate substantially higher in the alternative cases compared with the base case. For the a = 0.7 case, e.g., CD tubular fluid flow rate at the mid-IM was 77.2% higher than the base case. This load imbalance negatively impacts the effective operation of the IM concentrating mechanism.

We also considered a second case in which CD urea permeability increases abruptly at x_CD = L_OM + 0.7L_IM. To increase urea reabsorption, the urea permeability of the initial IMCD was increased to 3 × 10⁻⁵ cm/s; OMCD urea permeability was kept at the base-case value. The osmolality, Na⁺ concentration, urea concentration, and water flow rate profiles of the CD are shown in Fig. 9 (labeled case 3). With these CD urea permeability profiles, the model predicted a urine osmolality of 1,162 mosmol/kgH₂O, 9.43% less than the base case, at a comparable urine flow rate. With the higher urea permeability along the initial IMCD, much urea was absorbed: IMCD urea flow decreased by 54% along the first 2 mm of the IM (compared with 28% in the base case). Thus, with the lower urea delivery to the deep IM, the concentrating effect of the system was lowered.

Simulations of Knockout Experiments

Studies in transgenic mice have shown that the elimination of transporter proteins that are thought to play a key role in the IM concentrating mechanism results in impaired urine concentrating capability. In particular, mice lacking Clc-k1, the chloride transporter found in long-loop prebends and in the thin ascending limbs, have greatly reduced concentrating capability, as do mice lacking UT-A1 and UT-A3, the urea transporters found in the IMCD (1, 7, 8).

We conducted simulation experiments using model parameters that might be appropriate for Clc-k1-null and UT-A1/A3-null rats. In the Clc-k1-null case, we reduced thin ascending limb and prebend segment Na⁺ permeability from its base-case value of 80 × 10⁻⁵ to 10⁻⁵ cm/s. In the UT-A1/A3-null case, we reduced IMCD urea permeability from normally high physiological values, represented by an increasing permeability along the middle and terminal IMCD, attaining maximum of 110 × 10⁻⁵ cm/s; the maximum IMCD urea permeability was lowered to 2 × 10⁻⁵ cm/s.

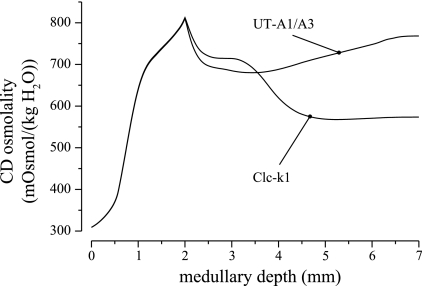
In both cases, the model's concentrating capability is substantially impaired, particularly in the IM. CD tubular fluid osmolality profiles are displayed in Fig. 10. In the Clc-k1-null case, the low prebend and thin ascending limb Na⁺ permeabilities limited Na⁺ reabsorption from the loops. Consequently, an axial osmolality gradient failed to be established along the IM interstitium, and less than half of the IMCD tubular fluid was reabsorbed. A urine with a relatively low osmolality of 574 mosmol/kgH₂O was produced. Indeed, the urine osmolality was lower than the CD tubular fluid osmolality at the OM-IM boundary, because the active reabsorption of Na⁺ and passive reabsorption of urea from the IMCD outpaced that of water. In the UT-A1/A3 case, only 19.1% of the urea flow was reabsorbed along the IMCD owing to the reduced urea permeability, compared with 79.9% in the base case. As a result, only 33.0% of the IMCD fluid flow was reabsorbed, and a urine of a relatively low osmolality of 768 mosmol/kgH₂O was predicted. These results are in general agreement with experimental findings in transgenic mice (1, 7, 8). It is noteworthy that in both case, the OM concentrating capability was minimally affected.

Fig. 10.

CD tubular fluid osmolality obtained for simulations of Clc-k1-null and urea transporter UT-A1/A3-null rats. Both cases show substantial impairment in urine concentrating capability.

DISCUSSION

We have conducted a number of parameter studies to determine the impact of assumptions that were needed for model formulation, but for which experimental data are lacking. In addition, we used the model to study, in the context of the urine concentrating mechanism, the functional implications of the radial organization of the tubules and vessels. And we assessed several aspects of tubular heterogeneity and segmentation, with respect to transmural transport. Our results indicate or predict the following.

• 1) The radial organization of the OM, with respect to vascular bundles, promotes urea cycling within the IM by facilitating, in the OM, the direct transfer of urea from AVR to DVR; in contrast, the radial organization of the IM, with respect to the CD clusters, does not appear to substantially promote solute sequestration, nor does it improve the concentrating capability of the model IM.

• 2) The extracluster position occupied by the long ascending thin limbs in the upper IM promotes urea cycling within the IM by facilitating the direct transfer of urea from those ascending thin limbs to the DVR.

• 3) To avoid dissipating the urea gradient in the deep IM, the lower IM portion of the thin limbs of Henle should be highly urea permeable, so that their tubular fluid urea content equilibrates with the surrounding interstitium, or both be nearly urea impermeable, to prohibit urea entry.

• 4) The AQP1-null LDL segment plays an important role, inasmuch as its nearly zero water permeability is indispensable for an effective IM concentrating mechanism.

• 5) A higher TAL Na⁺ active transport rate in the inner stripe, relative to the outer stripe, significantly augments concentrating capability without a corresponding increase in energy expenditure for transport, relative to the case with homogeneous transport rate is scaled to give approximately equivalent total transport along the TAL.

• 6) Active Na⁺ reabsorption from the CD facilitates the IM concentrating mechanism by elevating the CD tubular fluid urea concentration and by reducing the load presented to the concentrating mechanism in the deep IM.

• 7) The deletion of Clc-k1 or UT-A1/A3 transporters leads to substantial impairment of the IM urine concentrating capability, consistent with experimental findings. In contrast, the OM concentrating capability is minimally affected.

A somewhat surprising result of this study is that the marked radial organization of the upper IM, which is centered on the CD clusters, appears to have minimal impact on the interstitial solute concentrations that surround tubules and vessels. In particular, the model failed to predict the sequestration of urea in the CD clusters previously hypothesized by us (22, 24). Because the IM radial organization has little impact on interstitial solute concentrations, its role in the IM concentrating mechanism is unclear. Indeed, our parameter study suggests that when the radial organization in the IM was eliminated, the concentrating capability of the model improved, although not drastically.

To understand the functional implications of the IM structural organization, we first note that the organization of tubules and vessels around CD clusters in the upper IM, with the DVR located outside the CD clusters, is similar to the OM radial organization around vascular bundles, in the sense that, in both OM and upper IM, the DVR and CDs are isolated from each other. Since it is physically impossible for the OM radial organization to dissipate immediately once the tubules and vessels reach the IM, it may be that the radial organization in the upper IM is a necessary continuation of the OM structures.

Furthermore, the radial organization in the OM not only has a significant impact on urea sequestration and fluid concentration in the OMCD, as demonstrated in a previous modeling study (21), but that radial organization also preserves oxygen supply to the IM, as shown in a modeling study of oxygen transport in the rat OM (4). The supply of oxygen to the renal medulla barely exceeds its oxygen requirements; thus, indeed, the mammalian kidney is particularly vulnerable to hypoperfusion. In a modeling study (4), we predicted that the segregation of DVR, the main supply of oxygen, at the center and periphery of the vascular bundles gives rise to large radial differences in oxygen tension between regions, limits oxygen reabsorption from DVR that reach into the IM (i.e., long DVR), and helps preserve oxygen supply to the IM. That model predicted that 92.4% of the oxygen supplied by the long DVR at the corticomedullary boundary reached the IM, but if the radial organization in the OM was eliminated, only 53.0% of that oxygen reached the IM. Thus we propose that the radial organization in the upper IM may serve a similar purpose: to preserve the oxygen supply to the deep portion of the IM. We further hypothesize that a substantial oxygen tension (Po₂) gradient may be found between the intra- and intercluster regions, because of the oxygen-rich DVR are segregated within the intercluster region, and because the active Na⁺ transport along the IMCD may pose a high oxygen demand and lower the Po₂ in the intracluster region. The validity of these hypotheses may be assessed if the Po₂ can be measured for the inter- and intracluster interstitial fluids.

However, it may be premature to jump to the conclusion that the radial positions of tubules and vessels in the upper IM is entirely meaningless, in the context of the urine concentrating mechanism. Some important features of the three-dimensional architecture of the rat IM, or of the urine concentrating mechanism, may not have been discovered or may not be well represented in the model. One example is that the model does not represent the interstitial nodal compartments, revealed in the upper IM, that are bounded by CDs, ascending thin limbs, and AVR and which appear to promote preferential interactions among these three structures (32). Another point of view is to consider the upper IM radial organization as a constrained optimization problem: given that the DVR are to be isolated from the IMCD, where should the thin limbs of loops of Henle be located, to maximize the IM concentrating effect? Our model suggests that the thin ascending limbs associated with loops of Henle that reach into the deep IM should occupy an intercluster position. A position neighboring the DVR allows the transfer of urea from the ascending thin limbs to the DVR, which facilitates the cycling of urea within the IM and improves the IM concentrating effect.

Pipe Mode vs. Solute-Secretion Mode

The transport properties for loops of Henle in the present model are similar to the “solute-secretion” hypothesis proposed in Ref. 23. In that study, we also considered the low loop of Henle urea permeability limit in an alternative configuration that we called the pipe mode. In the pipe mode, the AQP1-null portions of the loops of Henle are assumed to have a nearly zero urea permeability. The pipe mode concentrates by vigorous absorption of NaCl from loop bends that is unaccompanied by water absorption from loop bends and that is not matched by significant solute (e.g., urea) secretion.

Model results in the present study suggest that, compared with the solute-secretion mode (i.e., the base case), the pipe mode is more effective in sustaining a high interstitial fluid urea concentration in the deep IM, is more effective in cycling urea within the medulla, and can produce a substantially more concentrated urine, albeit at a lower urine flow rate. (It is noteworthy that the loop transport properties in the IM urine concentrating model in Ref. 24 were based on the pipe mode, and that model produced a urine at an osmolality and at a flow rate that are both higher than the present base case.) However, the low loop urea permeability assumption in the pipe mode appears to be inconsistent with the significant urea permeabilities revealed in isolated perfused thin limb experiments in a number of species (5, 10, 29). Thus it appears that the rat kidney may have developed a urine concentrating mechanism that is more similar to the solute-secretion mode, rather than the pipe mode, even though our model results suggest that the latter may constitute a more effective concentrating mechanism. It is also noteworthy that our previous study (23) suggests that the concentrating capability of the pipe mode improves when the water permeability of the AQP1-null LDL segment increases, but microperfusion measurements indicate a nearly zero water permeability along that segment (6), which is more consistent with the high urea permeability limit.

Inhomogeneous TAL and CD Active Na⁺ Transport

A comparison of our base-case results to a simulation having a total rate of energy expenditure for active Na⁺ transport that is approximately equal to the base case, but uniform maximum active Na⁺ transport rate all along the TAL indicates that concentrating efficiency, in both the OM and IM, is increased by transport rate inhomogeneity along the TAL: consistent with theoretical predictions (26), for a fixed energy cost, the concentrating effect, assessed by CD fluid osmolality at the OM-IM boundary and by urine osmolality, can be increased by a higher transport rate deeper in the OM.

To ensure that the urea concentration in the CD remains sufficiently high, relative to NaCl concentration, along the course of the CD, we have assumed active Na⁺ absorption along the CD, and that active absorption is especially vigorous near the IM base. This absorption also promotes osmotic water absorption from the CD, and thus it helps regulate the load that CD contents present to the papilla. Active Na⁺ absorption from the IMCD has been represented in some previous model studies (e.g., Refs. 27, 39, and 41). However, our maximum transport rate V_max, Na (8 nmol·cm⁻²·s⁻¹ near the IM base) is higher than rates previously used in models of the urine concentrating mechanism, although it is compatible with experimental studies (42). We acknowledge, however, that the spatially inhomogeneous Na⁺ transport used in our model is not based on experimental findings but is formulated to regulate CD flow and urea content along the model papilla. Given the axial inhomogeneity and tubular segmentation revealed in the loops of Henle and along the CD, it is not unlikely that the maximum active Na⁺ transport rate is axially inhomogeneous along the CD.

Taken together, the results of this study indicate the importance of measuring the transport properties of the long loops of Henle and of the CD, taking into account the likelihood of axial inhomogeneity in these properties.

GRANTS

This research was supported by National Institute of Diabetes and Digestive and Kidney Diseases Grant DK089166 and National Science Foundation Grant DMS-0701412.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.