Nephron blood flow dynamics measured by laser speckle contrast imaging

Abstract

Tubuloglomerular feedback (TGF) has an important role in autoregulation of renal blood flow and glomerular filtration rate (GFR). Because of the characteristics of signal transmission in the feedback loop, the TGF undergoes self-sustained oscillations in single-nephron blood flow, GFR, and tubular pressure and flow. Nephrons interact by exchanging electrical signals conducted electrotonically through cells of the vascular wall, leading to synchronization of the TGF-mediated oscillations. Experimental studies of these interactions have been limited to observations on two or at most three nephrons simultaneously. The interacting nephron fields are likely to be more extensive. We have turned to laser speckle contrast imaging to measure the blood flow dynamics of 50–100 nephrons simultaneously on the renal surface of anesthetized rats. We report the application of this method and describe analytic techniques for extracting the desired data and for examining them for evidence of nephron synchronization. Synchronized TGF oscillations were detected in pairs or triplets of nephrons. The amplitude and the frequency of the oscillations changed with time, as did the patterns of synchronization. Synchronization may take place among nephrons not immediately adjacent on the surface of the kidney.

tubuloglomerular feedback (TGF) has an important role in autoregulation of renal blood flow and glomerular filtration rate (GFR). The anatomic basis for TGF is the juxtaglomerular apparatus, located where the thick ascending limb of the loop of Henle passes in close proximity to the glomerulus and arterioles of the same nephron. Each nephron has its own juxtaglomerular apparatus and TGF mechanism, and each engages in interactions with other nephrons whose afferent arterioles branch from a single arterial trunk (16, 20). Activation of the TGF response by microperfusion of one member of such a pair reduces blood flow and single-nephron GFR in both (20). Because of the high gain and the delay in signal transmission in the feedback loop, the TGF mechanism gives rise to self-sustained oscillations in tubular pressure and flow and in single-nephron blood flow (19). The interaction between TGF mechanisms enables the oscillations in coupled nephrons to synchronize (16, 23, 24, 32, 40). Activation of TGF in one nephron induces membrane depolarization in its afferent arteriole. The depolarization propagates electronically to nearby afferent arterioles and leads to nephron-nephron interaction. Synchronization of the oscillations most likely results from the exchange of electrical signals propagated along the wall of arterioles that connect them (24).

Experimental studies of synchronization have been limited to measurements made on two or three nephrons (16, 32, 40). The results suggest that more than two nephrons may become synchronized, but thus far technical limitations of existing methodologies have prevented a determination of the extent and the dynamics of synchronization. Estimating the number of nephrons that form synchronized clusters at any given time and assessing the factors that modify cluster size require a method for measuring dynamical phenomena in many nephrons simultaneously, and for longer time periods than have been possible until now. To solve these technical problems we have used laser speckle contrast imaging to measure relative blood flow changes with time in many nephrons on the kidney surface of anesthetized rats.

Laser speckle contrast imaging provides measurements of surface blood flow in tissues or organs with high spatial and temporal resolution. Laser speckle is an interference pattern produced when coherent light is reflected or scattered from different parts of an illuminated surface. If the surface is rough, with surface height variations larger than the wavelength of the light used, light from different parts of the surface will have traveled different distances when reaching an observation point. The resulting intensity at such a point, recorded by a photodetector such as a charge-coupled device (CCD) camera focused on the illuminated area, is determined by the algebraic addition of all the wave amplitudes arriving at that point. The light intensity at that point will be at a minimum if all the individual waves cancel out and at a maximum if all the waves arrive at the point in phase. Motion on the surface, as when blood moves through blood vessels, causes fluctuations in the interference pattern and therefore a blurring of the speckle pattern and a reduction in the local speckle contrast (3). This blurring can be used to provide quantitative information about the movement by coding velocity distributions as variations in speckle contrast (3, 5, 29, 39). The technique has successfully assessed perfusion in a variety of tissues including skin (14, 35), burns (34), and retina (6, 37) and endoscopically in joints (4). In addition to these applications in which blood flow is low and time-dependent variations were not sought, the method detects activity-related temporal and spatial heterogeneity of cerebral blood flow (9, 12, 26, 36, 39). Formal evaluations provide strong underpinnings to the use of laser speckle perfusion imaging (3, 5, 29, 31).

METHODS

Animals.

Experiments were performed on male Sprague-Dawley rats, body weight 275–325 g, purchased from Taconic (Lille Skensved, Denmark). All experimental protocols were approved by the Danish National Animal Experiments Inspectorate and were conducted in accordance with guidelines of the American Physiological Society. The animals were fed standard rat chow and allowed access to tap water ad libitum.

Anesthesia was induced by placing the rats in a chamber containing 8% sevoflurane (Sevorane, Abbott Scandinavia, Solna, Sweden) delivered in 65% nitrogen-35% oxygen. A tracheotomy was performed, and the rat was placed on a servo-controlled heating table to maintain a constant body temperature of 37°C. The rat was connected to a mechanical animal ventilator (tidal volume 0.8 ml/100 g body wt) at a frequency of 60 breaths/min. The final sevoflurane concentration needed to maintain sufficient anesthesia was 2–2.5%.

For arterial pressure measurements, a polyethylene (PE-50) catheter was placed in the left carotid artery. Mean arterial pressure (MAP) was measured with a Statham P23-dB pressure transducer (Gould, Oxnard, CA). Two PE-10 catheters in the right jugular vein allowed for continuous intravenous infusions. Isotonic saline was given continuously at a rate of 20 μl/min. The muscle relaxant cisatracurium (Nimbex, 0.85 mg/ml; GlaxoSmithKline, Brøndby, Denmark) was administered as a 0.5 ml bolus, followed by continuous infusion (20 μl/min, giving 17 μg/min). The abdominal aorta and left kidney were exposed through a midline and subcostal incision.

In the validation experiments a tapered and curved PE-10 catheter was introduced through the left iliac artery and advanced through the abdominal aorta and ∼1 mm into the left renal artery. Test agents were administered through this catheter directly into the renal artery to minimize systemic effects. The catheter did not interfere with renal blood flow measurements. A noncannulating precalibrated ultrasonic flow probe (1PRB; Transonic T 420) was placed around the left renal artery to measure renal blood flow. The left ureter was catheterized (PE-10 connected to PE-50) to ensure free urine flow. The rat was allowed to recover for 30 min after the surgical procedures were completed before the experimental protocol was begun.

Laser speckle imaging.

We used the Moor FLPI laser speckle camera from Moor Instruments (Millwey, Axminster, UK). The camera is a rectangular box, 22 cm wide, 23 cm high, and 7 cm thick, mounted on a stand clamped to the tabletop. Coherent infrared light is delivered to the object, in this case the renal surface, from a 5-cm × 8-cm plate and collected through a lens just adjacent to the excitation source. The box contains the optics, the laser source, the sensor, digital circuit boards, and a power supply. The camera circuits deliver output via USB and FireWire (IEEE-1394) connections to a computer running under Microsoft Windows XP. Proprietary software from the manufacturer is used to view the output, to make adjustments to the camera, and then to write output files to a computer disk.

The camera's vertical and angular positions are crudely adjustable. the positions are not calibrated. and no measurement scales are provided. The camera has a single lens with a polarizing filter. The camera box has zoom and focus controls, but the positions of these controls are not calibrated, so we designed a spatial calibration scheme as described below. We positioned the camera ∼18 cm above the renal surface to image it. No adjustments to the kidney were needed to acquire the laser speckle image. Lights in the room were dimmed when the laser speckle camera was recording image data, and all light sources used for animal surgery were turned off.

The proprietary software displays the speckle image and provides for adjustments of the system's sensitivity to prevent extremes of saturation. The exposure time of the camera is 4 ms, and the sampling rate is 25 frames/s. The flow imager can operate to provide either high temporal or high spatial resolution. In high-temporal-resolution mode speckle contrast is calculated in the spatial domain in every frame as the ratio of the standard deviation to the mean of the intensities in a small region of the image (5, 9). As a result, a flow image (115 × 153 pixels) can be acquired at the frame rate of the camera (25 frames/s) but at relatively low spatial resolution, a single pixel corresponding to ∼100 μm² on the renal surface. To obtain maximal spatial resolution we used the high-spatial-resolution mode, in which speckle contrast is calculated in the time domain as the ratio of the standard deviation to the mean of the intensities of a given pixel in a small time interval (5, 9). This mode allows us to resolve single arterioles on the renal surface, to provide precise alignment of the light and speckle images, and therefore to identify the precise locations of the “star” vessels, as described below. In this study we used a time interval of 1 s, so that the standard deviation and the means were based on 25 samples from each pixel every second. As a result a flow image, 576 × 768 pixels, ∼4 μm²/pixel on the renal surface, is obtained where the intensity at each pixel location is the average value over the 1-s sampling interval.

With the proprietary software, five regions of interest can be placed at arbitrary locations in the image field; each region generates a separate time series. The area covered by each of these regions of interest can be adjusted, but the sizing is done relative to the image and not to the size of the object being observed. We therefore designed our own sampling routine for image analysis and used output from the regions of interest only as a means of observing the progress of the experiment. The observations we report were made over periods of 30–40 min, during which the measured variables appeared stable. Observations of this duration generate binary data files in excess of 5 GB.

We estimated single-nephron blood flow velocity in efferent arterioles and their first-order branches on the surface of a kidney (the star vessels), structures that cannot be identified in laser speckle images. To identify these blood vessels we therefore made separate digital images of the renal surface, using intravenous infusion of lissamine green to outline the vascular structures. In each experiment, after the laser speckle imaging was completed, a digital camera (Nikon D70) was mounted on a stereomicroscope positioned over the renal surface. For this process an incandescent light transmitted with fiber-optic bundles illuminated the kidney. A 0.1-ml bolus of lissamine green 5% was injected intravenously, and images of the surface were recorded at 1-s intervals. The analytic process requires the digital image to be aligned with and scaled to the laser speckle image. To facilitate this image registration we placed two hairs from the animal on the renal surface, crossing each other. For the last image recorded with the digital camera we placed a piece of paper, cut to 5 mm, on the renal surface for spatial calibration.

Image analysis.

We used a three-step procedure to measure changes in blood flow in single star vessels with time. The individual speckle images lack the necessary detail and are too noisy for alignment with digital images recorded after lissamine green administration. To resolve features such as the crossed hairs and major vessels that are useful for aligning the flow images with the digital image, we generated a single image showing the average pixel intensity over the entire recording period, using software written in MatLab (R2009a, MathWorks, Natick, MA). The program extracts the individual flow images from the binary data file and averages the intensity information at each pixel location over the duration of the experiment. The output of this program is a single black-and-white (8-bit grayscale) image in portable internet graphics (.png) format showing the average intensity (flow) of each of the 442K pixels. The image is scaled to maximize contrast and opened in Adobe Photoshop (version 11, Adobe Systems, San Jose, CA).

A digital color image is selected in which efferent arterioles, their first-order branches, or both, are visible. The image selected for this purpose is one of those in which the dye first appears, before it reaches the tubules surrounding the vascular structures. The digital image is also opened in Adobe Photoshop. The blue and green channels are removed from the digital image, leaving a black-and-white image representing only the red channel. This procedure increases the contrast between the green dye in the vessels and the surrounding tissues. The digital image is then copied to a new layer in Photoshop and rotated and scaled to the laser speckle image by aligning the crossed hairs in the two images. Black circles, 10 pixels in diameter, are placed over each of the identifiable efferent arterioles or their first-order branches (the star vessels). Once this identification and marking process is completed the layer with the digital image is deleted, leaving the speckle image with the identification markers superimposed. We save this composite image in .png format.

We open the composite .png image in a MatLab window with a mouse-controlled cursor and identify the positions of the star vessels by recording the x- and y-coordinates of each identification marker with the cursor. The coordinate data are stored in an ASCII file.

We next open the original binary file containing the flow images and the file containing the coordinate values. At each of these locations the program samples a centered 15 × 15-pixel array, averages the 225 pixel values at each sampled time in the experiment, and writes the value to an output file as a single value in a time series. The program takes its input from a single location and completes the analysis over the duration of the experiment. The program then restarts the process at the next location. With this set of procedures we can routinely identify 50–60 vascular structures on the renal surface for analysis. The output is a collection of time series with relative blood flow change as a function of time for each of the identified star vessels.

Method validation.

Whole kidney blood flow was measured with an ultrasonic flow probe (1PRB; Transonic T 420) placed around the left renal artery. An arterial catheter was inserted into the left femoral artery and guided into the left renal artery. Bolus injections of angiotensin II were made into the renal artery at four different doses (0.5, 1.0, 2.0, and 4.0 ng) while recording whole kidney blood flow and single-nephron blood flow change with laser speckle microscopy. A constant infusion of acetylcholine (1.5 nmol/min) was next administered through the same arterial catheter.

Analysis of single-nephron blood flow dynamics.

Our primary long-term goals in applying laser speckle contrast imaging to the kidney are to determine whether the TGF-mediated oscillations in single-nephron blood flow can be detected in many nephrons simultaneously, to determine whether the oscillations of different nephrons synchronize, and to study the factors that affect the oscillations and the patterns of synchronization. Oscillations could be detected in most or all nephrons, but the oscillations and the synchronization patterns had time-dependent properties. Analysis therefore required a method that could determine frequency as a function of time. We used wavelet transforms to satisfy this need, transforming the original time series from individual nephrons into a time series consisting of the instantaneous frequency of the TGF-mediated oscillation as a function of time.

The wavelet transform of a signal x(t) can be written as:

$$W_x(a,b)=\frac{1}{\sqrt{a}}{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}x(t){\psi }_{a,b}^{*}(t)\mathrm{d}t}$$ (1)

where ψ(τ) is referred to as the “mother” function; ψ_a,b = ψ([t − b]/a) is a translated and scaled function with a and b characterizing the timescale and temporal localization, respectively; the asterisk refers to the complex conjugate; and x(t) is the time series. To investigate the presence of various rhythmic components, the Morlet wavelet has often been used. The simplified expression of this wavelet has the form:

$$\psi (\tau )={\pi }^{-1/2}\exp (j2\pi f_0\tau )\exp \left[-\frac{{\tau }^2}{2}\right]$$ (2)

The Morlet wavelet is a harmonic function modulated by a Gaussian function. The parameter f₀ localizes the wavelet in the time and frequency domains by defining an observation window and the number of oscillations of the wavelet within it. For the relatively slow physiological processes considered in this work we can use f₀ = 1. Increasing f₀ improves frequency resolution but reduces temporal resolution. The relation between the scale a and the central frequency f for the scaled function is f = 1/a. The mean value of each time series was subtracted from each term before application of the wavelet transform.

From the wavelet transform coefficients W_x(a,b) [or W_x(f,b)], the time-dependent power spectral density E_x(f,b)∼|W_x(f,b)|² can be estimated. The result is a surface in three-dimensional space E_x(f,b) whose sections at fixed time moments b = t₀ correspond to the local power spectrum. At each time point b = t_i we determined the local maxima of E_x(f,b) in the frequency range of the TGF oscillation (0.01–0.04 Hz) and the corresponding frequency, f(t_i)_{loc max}, where the maximum value is attained. The time series consisting of the individual f(t_i)_{loc max} were then used for further analysis.

When estimating speckle contrast over 1-s intervals the camera software uses a moving average algorithm (5, 9) to provide single pixel values. The moving average technique provides some low-pass filtering, but higher-frequency signals can still be aliased into the time series. We sample the flow velocity in arterioles, and heart rate oscillations may therefore be a source of aliased power. To test this possibility, we performed one experiment with the camera in the high-temporal-resolution mode using an image sampling rate of 25 Hz, making it possible to resolve oscillations in flow at the heart rate of a rat. Applying standard fast Fourier transform (FFT) techniques, we detected an oscillation at 5.8 Hz, which lies within the usual frequency bandwidth of the rat heart rate. In the time series obtained with the high sampling rate the spectral power of the TGF oscillation was 18.5 times greater than that of the heart rate signal. Spectral power of the heart rate signal is thus a small fraction of TGF power, even in the absence of a low-pass filter. The fraction of power aliased into the TGF bandwidth would therefore be negligible. In the high-spatial-resolution mode, that fraction would be reduced further because of the signal filtering provided by the moving average algorithm. We conclude that aliasing from the heartbeat can be ignored.

Synchronization is typically defined to occur when two or more limit cycle oscillators have the same frequency. The frequency information from the experiments is contained within the time series of frequencies calculated from the wavelet transform for each efferent arteriole. As a measure of the similarity of the instantaneous frequency, and thus the degree of synchronization, of the TGF oscillations in two nephrons, we calculated the difference, D_a,b, between the time series recorded from the ath and bth nephrons, i.e.,

$$D_{a,b}=\sqrt{{\displaystyle \sum _i{\left[f{(i)}_a-f{(i)}_b\right]}^2}}$$ (3)

where f(i)_n is the frequency at the ith time step in wavelet records from the nth nephron. If the TGF-mediated oscillations in the two nephrons have exactly the same frequency at all time points i, D_a,b will be zero; otherwise, D_a,b > 0 and its magnitude will be proportional to the difference in the instantaneous frequencies weighted over the entire recording period.

We applied hierarchical cluster analysis to investigate possible global patterns of synchronization on the surface of the kidney and to detect groups of synchronized nephrons. Cluster analysis is based on a comparison of similarities between an ensemble of elements using a proximity measure and was used in these studies as a surrogate for synchronization. We performed hierarchical clustering with the algorithm for agglomerative single-link clustering in MatLab, using D_a,b as a proximity measure. The clustering algorithm sorts all pairs according to the proximity measure. The pairs with the most similar time frequency records are considered as belonging to the same cluster. The result of the algorithm is displayed as a dendrogram, where the link between the elements represents the value of the proximity measure for the elements connected by the corresponding graph. The longer the path between two nephrons in the dendrogram, the less similar the time-frequency behavior of their TGF-mediated oscillations.

RESULTS

Figure 1 illustrates the stages in the analysis of laser speckle images. Figure 1A is an image of the ventral surface of the left kidney of a rat made with a laser speckle contrast camera. The camera output was sampled at 1 Hz for 40 min, and the light intensity at each of 442K pixels was averaged over the course of the experiment. The crossed hairs placed on the renal surface are black in the laser speckle image because they are stationary. Lighter areas are distributed over the surface. Very often, but not always, these spots are aligned with efferent arterioles identified from digital imaging. Figure 1B shows the image captured with an ordinary digital camera overlaid on and aligned with the laser speckle image. The digital image was taken in color after intravenous lissamine green injection and converted to black-and-white by removing the blue and green channels. Dark spots in this image mark the first appearance of the dye bolus as it appears on the renal surface. The crossed hairs are white. Figure 1C shows the black circles used to mark the locations of efferent arterioles from the combined image shown in Fig. 1B. The digital image will be deleted, and the resulting image will be used to record the coordinates of the efferent arterioles.

Fig. 1.

A: averaged laser speckle image of the left kidney of a rat. The image was sampled and stored at 1 Hz for 40 min. The average over the 40-min sampling period was calculated at each of 442K pixels. The crossed hairs in the middle of the image field were placed on the kidney to permit alignment of the images from laser speckle and digital microscopy. Bar, 2 mm. B: microscopic image aligned with the laser speckle image from A. The microscopic image was taken during intravenous injection of lissamine green to outline blood vessels on the renal surface. The microscopic image selected was taken from the first 1–2 s after the appearance of the dye front on the kidney surface. C: composite laser speckle-microscopic image from B with efferent arteriole locations shown as black circles. The locations were marked on the microscopic image, which was removed after the identification process was complete.

Figure 2, top, shows typical recordings obtained from two different star vessels on the surface of a kidney. To aid visualization only the first 1,000 s of an experiment that lasted 2,500 s are shown in the figure. A low-pass Kaiser Bessel filter using a cutoff frequency of 0.55 Hz and attenuation of 100 dB was applied to each of these time series to better illustrate the TGF-mediated oscillations, seen in Fig. 2, bottom.

Fig. 2.

Top: original recordings from 2 efferent arterioles. Bottom: original recordings, low-pass filtered, to emphasize tubuloglomerular feedback (TGF)-mediated oscillations.

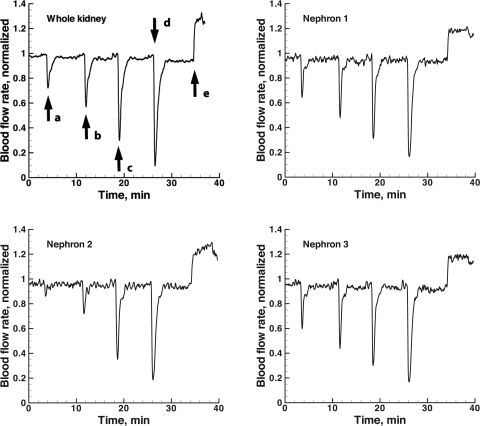
Figure 3 shows representative nephron time series from a rat receiving bolus injections of angiotensin II at four different concentrations into the renal artery. The end of the time series shows the response of the same nephron to an acetylcholine infusion. Whole kidney blood flow measurements from the same experiment are also shown. Bolus injections of angiotensin II induce reductions of blood flow in both the single-nephron and whole kidney measurements. The time course of the response to each dose is similar in the two sets of observations. The response of each increases with increasing doses of the vasoconstrictor, and both show increased blood flow when acetylcholine was infused at a constant rate into the renal artery.

Fig. 3.

Whole kidney blood flow (top left) together with recordings from 3 different efferent arterioles during infusions of 4 different levels of angiotensin II and acetylcholine. Infusions were made into the left renal artery. Each time series was normalized to the maximum value over the first 32 min of the experiment, before acetylcholine was infused. The doses of angiotensin II were 0.5 (a), 1.0 (b), 2 (c), and 4 (d) ng. The dose of acetylcholine was 1.5 nmol/min (e). The time series were from the experiment whose images are shown in Fig. 1.

Table 1 contains a comparison of the changes in whole kidney blood flow with blood flow in single nephrons measured with laser speckle imaging, in response to the four doses of angiotensin II and to acetylcholine. Whole kidney blood flow measurements provide absolute values of flow, but no absolute calibration is possible with the laser speckle method. Fractional changes in whole kidney blood flow were therefore calculated for comparison with single-nephron responses. Twelve nephrons were selected for analysis in kidneys from each of six rats. The mean whole kidney blood flow in the six rats was 5.4 ± 0.48 (SE) ml/min. The responses of all nephrons in a single kidney to each dose were averaged and compared with the whole kidney blood flow response. The average ratio of single-nephron blood flow change to whole kidney blood flow change is shown in Table 1. Whole kidney blood flow and single-arteriole blood flow both declined with angiotensin II. The fractional decline increased with dose in both flows. Both sets of flows increased with acetylcholine. The fractional single-nephron blood flow changes were smaller than those in whole kidney blood flow.

Table 1.

Comparison of whole kidney and single-nephron blood flow rate responses to angiotensin II and acetylcholine

	ΔRBF	ΔSNBF	ΔSNBF/ΔRBF
Angiotensin II
0.5 ng	−0.24 ± 0.03	−0.18 ± 0.06	0.69 ± 0.29
1.0 ng	−0.43 ± 0.02	−0.32 ± 0.10	0.68 ± 0.26
2.0 ng	−0.62 ± 0.04	−0.41 ± 0.12	0.68 ± 0.16
4.0 ng	−0.83 ± 0.05	−0.72 ± 0.06	0.90 ± 0.04
Acetylcholine
1.5 nmol/min	0.35 ± 0.03	0.30 ± 0.03	0.94 ± 0.05

Whole kidney blood flow rate (RBF) and single-nephron blood flow rate (SNBF) responses to angiotensin II and acetylcholine. Responses are shown as fractional change (Δ) in blood flow rate, with the preinjection value as the reference point. Results are shown as average ± SE fractional change. Nephron blood flow measurements are from 12 efferent arterioles in each of 6 rats.

Figure 4 shows the average ± SE instantaneous TGF frequency of 66 efferent arterioles in a single rat kidney and a color-coded plot of the instantaneous TGF frequency in each of the 66 arterioles. Constant frequency for the individual arterioles would be displayed as a constant color over the duration of the experiment. Figure 4 reveals variation in TGF frequency in all arterioles. The frequency changes occur at the same time in selected arterioles, but not in all. The frequency variations are not periodic, as shown in a later figure (see Fig. 8). The average frequency of all arterioles varies also, but the variation as shown by the SE envelope is large, consistent with the observation that the frequency changes among arterioles are often not correlated.

Fig. 4.

Top: mean frequency of TGF oscillation from 66 nephrons (red line) + 1 SE as a function of time (blue lines). Bottom: frequency of TGF oscillation as a function of time for each of the 66 sampled nephrons. Frequency of each nephron is coded by color, according to the color bar at right.

Fig. 8.

Recordings from 3 pairs of efferent arterioles, showing relative blood flow as a function of time on left and frequency as a function of time on right. The 3 pairs are those with the lowest proximity measure in Fig. 6.

This lack of correlation is further illustrated in Fig. 5, which is a plot of the relation between the proximity measure D_a,b, defined in Eq. 3, and the distance between the arterioles on the surface of the kidney. If the instantaneous frequencies in the TGF range are identical and vary in parallel in two nephrons, the proximity measure will be 0. The greater the difference between the two nephrons the larger the value of D_a,b. There is only a weak correlation between the proximity measure and the distance between the arterioles, with a correlation coefficient of 0.11 (P < 0.01). Even if two arterioles are quite close to each other on the renal surface, they may display very different dynamics in the frequency range of the TGF-mediated oscillation. On the other hand, it is also clear from Fig. 5 that there is a subset of nephrons (Fig. 5, bottom left) where the proximity measure is close to zero, indicating highly synchronized dynamics. This pattern was the same in nine recordings of the surface flow, with an average correlation coefficient between interarteriolar distance and D_a,b of 0.11 ± 0.05 (n = 9).

Fig. 5.

Scatter plot of the relation between the distance between 2 “star” vessels on the surface of the kidney and the value of the proximity measure (see text) for the 2 recordings. A total of 56 recordings yielding 1,953 different comparisons were analyzed. The correlation coefficient was 0.11 (P < 0.01).

To better visualize possible patterns of synchronization on the surface of the kidney, we applied hierarchical cluster analysis. A typical result, plotted as a dendrogram, is shown in Fig. 6, left. The clustering was performed by using the proximity measure D_a,b defined in Eq. 3. The dendrogram consists of many vertical lines connecting the objects in the hierarchical tree. The location of each vertical line on the horizontal axis represents the value of the proximity measure D_a,b between the two objects being connected, and each leaf—the horizontal lines to the extreme right in Fig. 6—in the dendrogram corresponds to one time series of instantaneous frequencies from one efferent arteriole. It should be noted that just because two leaves (each representing a time series of instantaneous frequencies of TGF) are placed next to each other they need not be similar (i.e., have a low proximity score).

Fig. 6.

Results of time-frequency analysis of time series taken from each of 56 locations on the surface of the kidney of yet another rat. Left: cluster analysis. Right: TGF frequency as a function of time for each of the 56 efferent arterioles. Frequency is coded by color, using the same calibration bar as shown in Fig. 4. Each row corresponds to a single efferent arteriole the location of which is shown in Fig. 7. Numbers on right are arteriolar identifiers.

We used the arteriolar distribution pattern generated by the clustering algorithm to align the arteriolar time series of instantaneous frequencies in Fig. 6, right. This panel permits a comparison of instantaneous TGF frequencies among the nephrons. It is clear in this experiment also that TGF frequency varies with time, that there are many nephrons that operate at a common frequency at any given time, and that nephrons with a common frequency during some fraction of the observation time may not be synchronized with each other at other times. Four or five nephron clusters, each with very similar TGF dynamics, were present in the data sets from all nine experiments we analyzed. Each cluster typically consists of two or three nephrons. In Fig. 6, the three clusters with the lowest score of the proximity measure consist of nephrons 3 and 4, nephrons 10 and 32, and nephrons 21, 22, and 24. As can be seen from Fig. 7, where the nephrons belonging to the same cluster are connected by blue lines, the nephrons in a given cluster are near each other on the surface of the nephron but not necessarily closest neighbors.

Fig. 7.

Locations of 56 efferent arterioles on the surface of a single rat kidney. The efferent arterioles correspond to those shown in Fig. 6. Each location is designated by a unique identifying number (1–56) and located on the map according to its x,y-coordinates. Blue lines connect 2 or more arterioles shown to have a low proximity score, which implies strong clustering. Red line encircles a group of nephrons that have somewhat higher scores, but all of whose members have lower frequency TGF oscillations than the other nephrons.

Cluster analysis also identified a group of nephrons with TGF dynamics very different from those of the majority of nephrons. The seven nephrons at the top of the dendrogram in Fig. 6 have a higher frequency than the other nephrons for most of the duration of the experiment. As can be seen from Fig. 7, these seven nephrons are all localized close together on the surface of the kidney in the area enclosed by the red line.

While a low score on the proximity measure indicates a similarity in TGF dynamics between nephrons, it is not possible to give an exact value below which nephrons are synchronized and above which they are not. The three clusters identified in Fig. 6 do, however, identify synchronized nephrons as illustrated in Fig. 8. Figure 8, left, displays time series recorded simultaneously from the three different arteriolar pairs, one pair from each of the three clusters shown in Fig. 7. Figure 8, right, shows the time-frequency results from the nephron pairs in Fig. 8, left. A Kaiser Bessel filter using a cutoff frequency of 0.55 Hz and attenuation of 100 dB was applied to each time series as a low-pass filter to improve visualization; the wavelet transforms were applied to unfiltered raw data. Only the first 1,500 s of an experiment that lasted 2,500 s are shown in Fig. 8, again to aid visualization. TGF oscillations can be seen in each of the time series. The oscillations in each of the pairs are interrupted intermittently, usually at the same time for the paired nephrons of a single cluster, but not necessarily for the nephrons of the other clusters. Experimental conditions were not changed when these interruptions occurred, nor were there detectable changes in blood pressure. The similarity of the time series within each cluster supports the result of the analysis suggesting the presence of an interaction and therefore of synchronization between these paired nephrons.

DISCUSSION

We describe a method, laser speckle contrast imaging, that provides excellent spatial resolution and, for the dynamics of renal blood flow regulation, excellent temporal resolution. The method was first introduced into clinical medicine to measure blood flow in the human retina (6, 37) and skin (14, 15, 33, 35). More recently, it has been applied to other clinical problems (4, 34, 43) and used to measure changes in local brain blood flow in experimental animals (3, 26, 36, 39, 44). The apparatus applies coherent infrared illumination to a surface, records changes in laser speckle contrast, and provides a signal for each pixel location imaged by the detector, a CCD. Localized motion on the surface reduces speckle contrast, which is recorded as a decrease in signal intensity with pixel-by-pixel resolution. A change in pixel intensity therefore corresponds to a change in local surface motion. Further analysis is based on the assumption that flow of blood cells is the only significant source of motion. The change signals recorded with laser speckle contrast imaging are proportional to the changes in speed of the motion. The theory of laser speckle contrast imaging has been developed in detail elsewhere (3, 5, 29, 31).

We developed analytical methods to obtain time-dependent signals from the efferent blood vessels of individual nephrons, and we used these techniques to validate the imaging method with bolus injections of angiotensin II into the renal artery while recording laser speckle images of the exposed kidney surface and of whole kidney blood flow. Blood flow decreased with both measurement techniques, and the time-dependent pattern of blood flow change was similar for the two, as seen in Fig. 3. The fractional blood flow change is smaller with laser speckle measurements of surface cortical nephrons than with whole kidney blood flow measured with ultrasound (Table 1). An infusion of acetylcholine into the renal artery increased blood flow as detected by both methods, the time-dependent pattern was similar in the two, and the fractional change was also less with the laser speckle recordings. The laser speckle camera obtains signals only from cortical nephrons and only from the surface nephrons of that group. Whole kidney measurements also reflect responses to vascular challenges of longer juxtamedullary nephrons known to have robust TGF mechanisms. We presume that the relatively minor differences are due to the differences in nephron populations sampled by the two methods.

Laser speckle contrast imaging provides an opportunity for measuring blood flow at many sites simultaneously on the surface of an organ at relatively high sampling rates. For regulatory processes in the renal circulation the two fastest macroscopic processes are TGF and the myogenic mechanism, with oscillations at 0.02–0.04 Hz and 0.1–0.2 Hz, respectively. Sampling either oscillation at 1 Hz is sufficient to provide accurate estimates of both frequency and amplitude.

Laser speckle contrast imaging has the additional advantage that, apart from exposing the kidney and placing it in a plastic cup, the measurement process requires no separate measurement tools, such as flow probes placed on the renal artery or micropipettes in renal tubules. A laser Doppler method adapted for use in renal efferent tubules also requires no direct manipulation of the kidney, but it measures relative blood flow rate in only a single arteriole (30, 41).

One of our interests in applying laser speckle contrast imaging is to detect synchronization in single-nephron blood flow (16, 32, 40), to investigate possible global patterns of synchronization on the surface of the kidney, and to identify and evaluate the importance of factors that affect the synchronization and the patterns of synchronization between nephrons. Synchronization is possible only in the presence of an interaction between two or more nonlinear systems with oscillatory or chaotic motion (1, 27). TGF is a nonlinear feedback mechanism that generates autonomous oscillations because of the high feedback gain and the delay between the first appearance of a change in tubular flow rate at the glomerulus and the arrival of this change at the macula densa, the TGF-sensing site. The TGF mechanism in each nephron therefore generates the oscillation that is the basis for synchronization among nephrons. Activation of TGF in one nephron affects vascular resistance in another nephron with a close arteriolar connection, demonstrating the functional effect of interactions between nephrons (20). Electrical signals caused by TGF activation in one nephron are conducted electronically along the wall of that nephron's afferent arteriole to other afferent arterioles, showing the pathway for the interaction (24). The measured length constant for electronic conduction is sufficient to allow electrotonic signal conduction among several nephrons (24, 38). Synchronized nephron oscillations should give rise to oscillations of flow in the arterial trunk supplying the oscillating afferent arterioles, an effect that will reinforce synchronization by electrical signaling (23).

Synchronization of elements (nephrons) in a network like the renal vasculature can lead to aggregation and the formation of a coherent functional structure. New properties often emerge from the formation of such aggregates. In the kidney the organization of nephrons into synchronized clusters is likely to have functional consequences. As an example, nephron synchronization is reduced in rats with a genetic form of hypertension (spontaneously hypertensive rats) (32), a change that will likely lead to smaller-sized and shorter-lived nephron clusters. In these rats and also in those with renovascular hypertension, the oscillation induced by TGF undergoes a change to chaotic dynamics (18, 42). Both TGF gain (11, 17, 22) and arteriolar electrical conductance (8, 38) are increased over normal values in hypertension, and either change, or both, can cause the change to chaos (21, 23). The sequence of events in the change to chaos and the loss of synchronization have not yet been determined, nor is it known whether these changes have a causal role in the development of chronic hypertension or are consequences of it.

Theoretical work on the phenomenon of synchronization has been performed largely on simple systems consisting of two nonlinear mechanisms, each capable of a self-sustained oscillation, with the interaction the only variable subject to change (1, 27). An arterial trunk from which 20 or more afferent arterioles branch hardly conforms to this description (7, 25), and it seems fair to state that there is no rigorous theoretical basis for the analysis of anything as complex as a large number of interacting nephrons.

The test for synchronization is usually the detection of frequency or phase locking between two or more oscillators as a result of an interaction between them. Application of these measures in each of 1,500 or more pairs of nephrons as in the present recordings is a daunting task. We therefore decided to compare the time-frequency estimates of the TGF oscillation as derived from wavelet transforms and to apply a clustering algorithm to detect possible clusters of nephrons having synchronized oscillations in efferent blood flow. The comparison was made by calculating a proximity measure. The proximity measure is the euclidean distance between paired time series of the instantaneous frequency of the TGF-mediated oscillation, as defined in Eq. 3 in methods. This is a comparison of the frequency of the TGF-mediated oscillation at 1-s intervals for the duration of the experiment. The comparison generates a score for each pair, and the clustering algorithm sorts the scores into the cluster dendrogram shown in Fig. 6. The clustering is intended to serve as a surrogate for more rigorous synchronization criteria, but it provides no absolute basis for deciding which pairs are synchronized and which are not; any further sorting will require additional analysis. For the time being we have limited our classification of coupled nephrons into those with the lowest scores.

In agreement with previous work (16, 40) it was possible to identify pairs or triplets of synchronized nephrons with the present technique, as shown in Fig. 8. These were the clusters with the lowest score of the proximity measure, providing justification for the present analytical approach. It is noteworthy that the synchronized nephrons were not necessarily nearest neighbors, but could be some distance from each other on the surface of the kidney. This finding is in agreement with the results of Chen et al. (8), who performed stop-flow microperfusion in two nephrons simultaneously, measured the response in one nephron of increasing loop of Henle perfusion rate in the other, and then measured the arterial-arteriolar distance between them on vascular casts. They detected interactions at distances along the vascular tree >1.5 mm. It is therefore not surprising that nephrons separated by some distance can become synchronized.

Experimental evidence supports the suggestion that nephron interactions are mediated by electrotonic signal conduction along the afferent arteriolar and arterial wall. For nephrons to become synchronized it is therefore necessary that they derive their afferent arterioles from a common arterial trunk. This requirement probably explains why nephrons that are close together on the renal surface may not necessarily be synchronized. As can be seen in Fig. 5, efferent arterioles that are close together in most cases have TGF dynamics that differ from each other, suggesting that the interaction between the corresponding nephrons is weak. We hypothesize that this reflects the underlying vascular structure, and that the nonsynchronized neighboring nephrons derive their afferent arterioles from different arterial trunks. This is clearly an exciting issue for future studies.

The view that simple electrotonic signal conduction is the only process supporting synchronization arises from the design of experiments designed to measure signal propagation (8, 24, 38), and is probably oversimplified. Nephrons are active elements in a network. To the extent that signals reach afferent arterioles and cause them to become synchronized, each nephron acts as a repeating amplifier serving to maintain the signal amplitude over a distance greater than might be expected from an electrotonic space constant. Whether this form of signal amplification actually occurs in the kidney and how large an ensemble it synchronizes is unknown and is a subject this new imaging method may help to clarify. The observation that nephrons at a distance from each other may synchronize has an implication for vascular structure. The conventional view is that the kidney can be divided into lobules defined by the vascular supply. An alternative view, supported by a detailed set of measurements based on computed tomography by Nordsletten et al. (25), is that the vascular structure is that of a tree, with a fractal structure and without named branches. If that alternative is more nearly correct, the branch points would be expected to vary, and certain combinations of branchings would be more likely than others to support signal propagation over a distance.

The time-varying nature of the TGF frequencies and of the patterns of synchronization that result is another new result arising from the application of the new method. Earlier studies using whole kidney blood flow measurements showed time-varying behavior but obviously could not resolve either the behavior of individual nephrons or interactions among them (10, 13, 28, 45, 46). Because making observations with this camera requires no additional instruments, and specifically no micropipettes in tubules, much longer experiments are possible, permitting us to capture the appearance of these new dynamics. Nothing in the experimental design could be correlated with these changes in dynamics, and one can only speculate about its causes. It will be important to understand the origins of this phenomenon.

One possible cause of these dynamics is the set of extrarenal agents, blood pressure, and neural inputs known to affect kidney blood flow. We did no experiments to rule out this possibility, but the arrival of such signals would be expected to affect all nephrons simultaneously, as shown by the validation experiments in Fig. 2. The variations we observed did not affect all arterioles simultaneously. An alternate possibility, not tested in these experiments, is that the complex nature of the renal vascular network, with active nonlinear elements (nephrons) widely distributed, gives rise to high-order interactions without the benefit of extrarenal signals (2).

In summary, we have applied laser speckle contrast imaging to the surface of kidneys in anesthetized rats for periods of 30 min or longer. We developed software to extract time series from each of 442K pixels, determined the location of efferent arterioles on the renal surface, and made time series specifically for those locations. We validated the method by comparing results from bolus injections of angiotensin II and from acetylcholine infusion on whole kidney blood flow and efferent arteriolar blood flow rate. The responses had small differences but were similar. The new method detected oscillations in 50 or more nephrons on the renal surface. We developed an analytical method for detecting and measuring nephron synchronization, which we found. With this method we also detected significant time variation in the oscillation frequencies and in the patterns of nephron synchronization.

GRANTS

The work was supported by National Institutes of Health Grant EB-003508 and by a grant from the Lundbeck Foundation of Denmark to D. J. Marsh, by grants from the Danish Medical Research Council, the Novo Nordisk Foundation, and the Danish Heart Association to N.-H. Holstein-Rathlou, and by a grant from the “Scientific and scientific-pedagogic staff of innovative Russia” program of the Russian government to A. N. Pavlov.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).