Abstract
It has been observed that vasoactivity of explanted descending vasa recta (DVR) is modulated by intrinsic nitric oxide (NO) and superoxide (O2−) production (Cao C, Edwards A, Sendeski M, Lee-Kwon W, Cui L, Cai CY, Patzak A, Pallone TL. Am J Physiol Renal Physiol 299: F1056–F1064, 2010). To elucidate the cellular mechanisms by which NO, O2− and hydrogen peroxide (H2O2) modulate DVR pericyte cytosolic Ca2+ concentration ([Ca]cyt) and vasoactivity, we expanded our mathematical model of Ca2+ signaling in pericytes. We incorporated simulations of the pathways that translate an increase in [Ca]cyt to the activation of myosin light chain (MLC) kinase and cell contraction, as well as the kinetics of NO and reactive oxygen species formation and their effects on [Ca]cyt and MLC phosphorylation. The model reproduced experimentally observed trends of DVR vasoactivity that accompany exposure to Nω-nitro-l-arginine methyl ester, 8-Br-cGMP, Tempol, and H2O2. Our results suggest that under resting conditions, NO-induced activation of cGMP maintains low levels of [Ca]cyt and MLC phosphorylation to minimize basal tone. This results from stimulation of Ca2+ uptake from the cytosol into the SR via SERCA pumps, Ca2+ efflux into the extracellular space via plasma membrane Ca2+ pumps, and MLC phosphatase (MLCP) activity. We predict that basal concentrations of O2− and H2O2 have negligible effects on Ca2+ signaling and MLC phosphorylation. At concentrations above 1 nM, O2− is predicted to modulate [Cacyt] and MCLP activity mostly by reducing NO bioavailability. The DVR vasoconstriction that is induced by high concentrations of H2O2 can be explained by H2O2-mediated downregulation of MLCP and SERCA activity. We conclude that intrinsic generation of NO by the DVR wall may be sufficient to inhibit vasoconstriction by maintaining suppression of MLC phosphorylation.
Keywords: calcium signaling, hydrogen peroxide, superoxide, vascular smooth muscle
nitric oxide (NO) acts as a local vasodilator in the renal medulla and plays an important role in the maintenance of medullary perfusion, medullary oxygenation, and blood pressure. Chronic inhibition of nitric oxide synthase (NOS) reduces medullary blood flow (MBF) and is associated with sodium retention and the development of hypertension (8, 41). Whereas NO increases MBF by promoting the vasodilation of descending vasa recta (DVR) or juxtamedullary arterioles, superoxide (O2−) and hydrogen peroxide (H2O2) act to reduce MBF by mechanisms that remain to be fully elucidated (17, 37). In addition, NO inhibits, whereas O2− enhances, thick ascending limb sodium reabsorption (23). Hence, interactions between NO and O2− likely contribute to the long-term control of blood pressure; when the balance between these two radicals is shifted in favor of O2− (such as in diabetes and atherosclerosis, conditions that promote oxidative stress), renal vasoconstriction and tubular reabsorption increase, favoring hypertension (17).
In a recent microperfusion study of DVR (4), we showed that intrinsic production of NO and reactive oxygen species (ROS) affects DVR vasoactivity. To elucidate the cellular pathways by which NO, O2−, and H2O2 modulate DVR contraction, in the present study we expanded our mathematical model of Ca2+ signaling in DVR pericytes to account for the effects of NO and ROS and to predict the degree of vessel contraction.
Smooth muscle contraction is initiated by an increase in cytosolic Ca2+ concentration ([Ca]cyt). Increased binding of Ca2+ to calmodulin (CaM) activates myosin light chain kinase (MLCK), which then phosphorylates myosin light chains (MLC) in the presence of ATP, thereby increasing the cycling rate of actin-myosin cross-bridge formation and generating the active force needed for muscle contraction. Most of the vasodilatory effects of NO on smooth muscle cells appear to be mediated by cGMP. Activity of the NO/cGMP pathway favors reduction in the fraction of phosphorylated myosin, via two different mechanisms: 1) an increase in the activity of myosin light chain phosphatase (MLCP), and 2) modulation of Ca2+ transport that lowers [Ca]cyt, decreases Ca2+ binding to CaM, and thereby reduces MLCK activity.
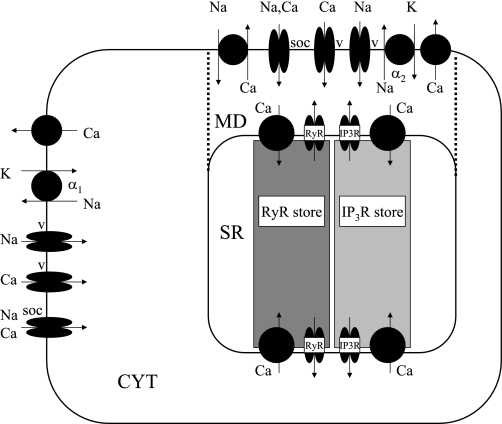
We incorporated these and other signaling pathways in our mathematical model of DVR pericytes as described in model description. The data on which this and prior versions of the model are based have been largely derived from studies of DVR pericyte channel architecture, as well as measurements of [Ca]cyt signaling, ROS generation, and vasoactivity in explanted, microperfused DVR. As such, we delineate mechanistic interactions that exist within the DVR wall but cannot readily extrapolate them to predict the balance of their effects on MBF, in vivo. As illustrated in Fig. 1, the model accounts for plasma membrane (PM) and sarcoplasmic reticulum (SR) pumps, exchangers and ion channels, cytosolic and store Ca2+ buffering, and the existence of subplasmalemmal microdomain spaces in which Na+/Ca2+ exchangers and the α2 isoform of the Na+-K+-ATPase are exclusively expressed (30, 39). We recently examined two configurations for ryanodine receptors (RyR) and IP3 receptors (IP3R), and concluded that oscillatory behavior is most consistently reproduced if they reside on separate SR stores in DVR pericytes (13), hence our assumption of separate RyR and IP3R store compartments here.
Fig. 1.
Schematic representation of the descending vasa recta (DVR) pericyte cell, with its 3 compartments: bulk cytosol (CYT), microdomains (MD), and sarcoplasmic reticulum (SR). We assume that ryanodine receptors (RyR) and IP3 receptors (IP3R) reside on separate SR stores. Not shown are KCa, Kir, KATP, and Kv channels.
MODEL DESCRIPTION
In this section, we successively develop the equations that describe 1) MLCK activation and MLC phosphorylation; 2) temporal variations in the intracellular concentrations of NO, O2−, and H2O2; 3) soluble guanylate cyclase (sGC) activation by NO and the subsequent effects on cGMP formation; 4) cGMP-dependent and -independent pathways affecting MLC phosphorylation; and 5) ROS effects on those pathways. The other equations of the model, those that yield the K+, Na+, Cl−, and Ca2+ currents, as well as transmembrane electrical potential differences, were described in detail in our previous work and are summarized in the appendix of reference (13).
MLCK Activation and MLC Phosphorylation
CaM activation of MLCK.
CaM has four Ca2+ binding sites, two at the N terminus (low affinity) and two at the C terminus (high affinity). Binding of Ca2+ to those sites yields the CaM·Ca4 complex. In turn, binding of CaM·Ca4 to MLCK to form MLCK·CaM·Ca4 increases its kinase activity. We use the kinetic scheme proposed by Fajmut et al. (19) to determine the kinetics of formation of MLCK·CaM·Ca4, i.e., the active form of MLCK. This scheme, illustrated in Fig. 1 in Ref. 19, includes 6 different CaM species and 14 rate constants and is a simplified representation of the full model which requires specification of 24 rate constants for 8 species. As depicted in the figure, the subscripts N and C represent two binding sites each for Ca2+ at the N and C termini of CaM, respectively, whereas the subscript M represents the CaM binding site occupied by MLCK. An underscore (_) denotes an unoccupied state for each of these binding sites. With this notation, CaMNCM designates MLCK·CaM·Ca4. The corresponding kinetic equations can be expressed as
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where the on- and off-rate constants are denoted by kiCaM and k−iCaM, respectively, and [MLCK]free represents the concentration of free (unbound) MLCK. For simplicity, we omit in these kinetic equations the subscript “cyt” that denotes the cytosolic compartment. In addition, conservation of total calmodulin ([CaM]tot) and total MCLK ([MLCK]tot) yields
| (6) |
| (7) |
The total concentration of CaM and MLCK is taken as 10 and 2 μM, respectively (19). Equations 1–7 are sufficient to determine the concentration of the six CaM species and the unbound MLCK.
MLCK-dependent phosphorylation of myosin.
The fraction of myosin cross bridges that are phosphorylated quantifies the contractile force. Following the approach of Yang et al. (54), we assume that MLCK·CaM·Ca4-dependent activation of MLC is the only mechanism regulating contractile strength in smooth muscle, and we use the four-state kinetic model illustrated in Fig. 6 in Ref. 54 to describe myosin phosphorylation. Four species are considered: free cross bridges (Myo), phosphorylated cross bridges (MyoP), attached phosphorylated, cycling cross bridges (AMyoP), and attached dephosphorylated, noncycling cross bridges (AMyo). The concentration of these MLC species is determined by solving the following set of equations
| (8) |
| (9) |
| (10) |
| (11) |
The total concentration of myosin species ([Myo]tot) is taken as 30 μM (18). The rate constants k1Myo and k6Myo represent the activity of MLCK, and are taken to be proportional to the concentration of the fully activated form of the enzyme
| (12) |
where kMLCKMyo has a fixed value. The rate constants k2Myo and k5Myo represent the activity of MLCP and are calculated as described below. The rate constants k3Myo, k4Myo, and k7Myo are fixed. The values of the parameters related to CaM activation of MLCK and MLCK-dependent phosphorylation of MLC are respectively given in Tables 1 and 2.
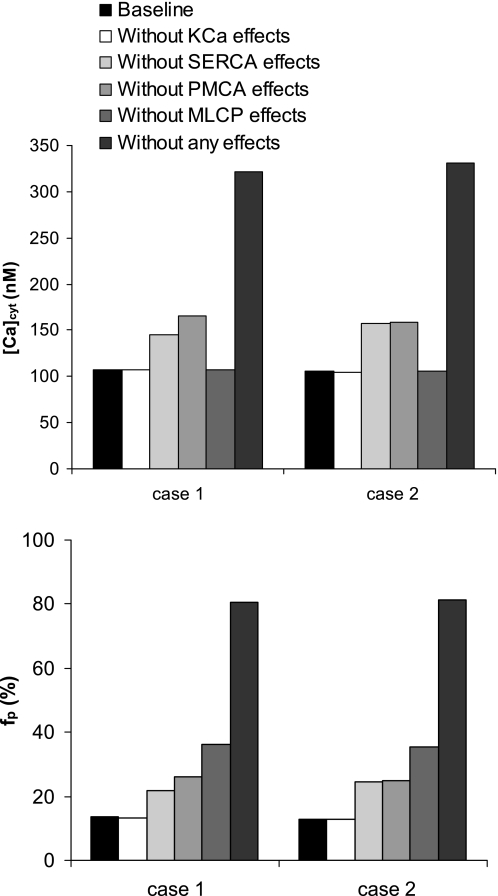
Fig. 6.
Contribution of each NO- and cGMP-mediated pathway to resting values of [Ca2+]cyt (top) and fraction of phosphorylated myosin (bottom). Results are shown for cases 1 and 2.
Table 1.
| Reaction j | kCaMj, μM−2·s−1 | kCaM−j, s−1 |
|---|---|---|
| 1 | 2.8 | 6.0 |
| 2 | 100 | 800 |
| 3 | 2.8 | 6.0 |
| 4 | 100 | 800 |
| 5 | 1,000 | 20 |
| 6 | 12.5 | 5.0 |
| 7 | 1,000 | 1.0 |
Table 2.
| Parameter | Value |
|---|---|
| kMLCKMyo | 4.0 × 106 M−1·s−1 |
| kMLCPMyo | 0.4 s−1 |
| k3Myo | 1.8 s−1 |
| k4Myo | 0.1 s−1 |
| k7Myo | 0.045 s−1 |
Correlation between MLC phosphorylation and contractile force.
The fraction of phosphorylated myosin (fP) is given by
| (13) |
As shown by Lee et al. (34), there is a good correlation between this fraction and the contractile force in arterial smooth muscle. Interpolation of the data shown in their Fig. 3C, measured in smooth muscle strips using a force transducer, yields the following correlation between fP and the contractile force (Fcontract), expressed relative to the maximum recorded force
| (14) |
Fig. 3.
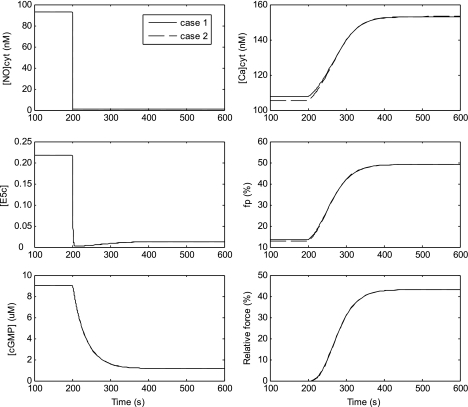
Simulated effects of Nω-nitro-l-arginine methyl ester (l-NAME) on DVR pericyte Ca2+ signaling. Initially, the system is at rest. At t = 200 s, NO influx is reduced 100-fold; that is, JNOendo is multiplied by 0.01 (Eq. 15), while all other parameters are left unchanged. Consequently, [NO]cyt drops sharply (top left), followed by the fraction of sGC that is fully activated (E5c; middle left). The subsequent reduction in cGMP levels (bottom left) in turn raises cytosolic Ca2+ concentration ([Ca]cyt; top right), increases MLCK activity and fp (middle right), and raises the relative contractile force (Fcontract; bottom right). Case 1 assumes that the microdomain concentration of NO, reactive oxygen species (ROS), and cGMP is the same as that in the bulk cytosol, whereas case 2 assumes that it is zero.
Kinetics of Formation of NO, O2−, and H2O2
NO.
In explanted DVR, we assume that the only source of NO is the vascular endothelium. Once generated, endothelial NO diffuses into pericytes where it partially reacts with other species or diffuses across the abluminal pericyte cell surface into the bath. In endothelial and smooth muscle cells, NO is consumed by several scavengers, such as O2−, oxygen, and thiols. NO reacts with O2− to form peroxynitrite (ONOO−), according to the following equation
where the rate constant kNO, O2− has been estimated as 1.9 × 1010 M−1·s−1 (32). As in the study of Yang et al. (53), we assume that the consumption rate of NO by all scavengers other than O2− can be expressed as a first-order process, with a lumped NO consumption rate constant denoted by kNO, cons (taken as 0.01 s−1). Changes in the cytosolic concentration of NO are thus given by
| (15) |
where Vcyt is the cytosol volume and A is the total membrane surface area, estimated as 0.5 pl and 1.21 × 10−5 cm2, respectively (14). JNOendo denotes the NO flux from the endothelium, and PNO the membrane permeability to NO. The concentration of NO in the bath is taken to be negligible. We also assume that half the cell membrane abuts the endothelium, while the other half is exposed to the bath.
O2−.
We consider two sinks for O2− in DVR pericytes: the reaction with NO to form ONOO− and the reaction catalyzed by superoxide dismutase (SOD) to form H2O2
Following the approach of Buerk et al. (2), the rate for this reaction (which occurs in 2 steps) is expressed as the product kSOD, O2− [SOD] [O2−]cyt, where [SOD] is taken as a constant (1 μM) and kSOD, O2− is taken as 1.6 × 109 M−1·s−1. Changes in the cytosolic concentration of O2− are then expressed as
| (16) |
The first term represents the net generation rate of O2− within the pericyte, the second one corresponds to electrodiffusion of O2− into the external medium (where its concentration is taken to be negligible), and the last two represent cytosolic O2− consumption. GO2− denotes the volumetric generation rate of O2−, PO2− is the pericyte permeability to O2−, and ζ = −FVmcyt/RT is the normalized electrical potential difference. We recognize that many enzymes can generate O2− and that it is synthesized by vascular walls and salt-transporting epithelia within the kidney (23). Vascular O2− generation is thought to be predominantly mediated by NADPH oxidases (1, 35), and we previously observed that dihydroethidium oxidation to ethidium occurs primarily within pericytes rather than endothelia (59). Accordingly, we assume that the source of O2− generation (GO2−) in explanted DVR is predominantly pericyte NADPH oxidase.
H2O2.
We assume that the principal sink for H2O2 is its degradation by catalase (CAT). The two-step process can be summarized as
The corresponding reaction rate is expressed as the product kcat[CAT][H2O2]cyt, where kcat is taken as 3.4 × 107 M−1·s−1 (40). Conservation of cytosolic H2O2 can be expressed as
| (17) |
where| JH2O2endo denotes the influx of H2O2 from endothelial cells, and PH2O2 is the permeability of the pericyte membrane to H2O2. The external concentration of H2O2 is taken to be zero.
Parameter values.
The pericyte permeability to NO is taken as 0.03 cm/s, based upon our previous estimates for membranes that do not express aquaporin-1 water channels (12, 57). The value of JNOendo is chosen as 4.0 × 10−13 mol·cm−2·s−1 to yield a resting [NO]cyt on the order of 100 nM in pericytes. Thus total NO influx into the cytosol is predicted as 2.4 × 10−18 mol/s. This value is consistent with our estimate of the total amount of NO generated within the endothelial cell, that is ∼5 × 10−18 mol/s, based on a volumetric NO generation rate of ∼50 μM/s (2, 12) and an endothelial cell volume on the order of 0.1 pl (or 100 μm3).
The diffusivity of O2− and H2O2 in dilute solution is on the order of 2,800 μm2/s (6). Assuming that membrane hindrance effects lower solute diffusivity by a factor of 5 (9), and that the pericyte and adjacent basement membrane thickness is ∼1 μM, a rough estimate of the overall permeability to O2− and H2O2 is 600 μm/s, or 0.06 cm/s. If GO2− is taken as 3.0 μM·s−1, the resting [O2−]cyt is 0.8 nM, in accordance with literature estimates suggesting that the intracellular concentration of O2− is subnanomolar (20).
We did not find any measurements of H2O2 resting concentrations in vascular smooth muscle cells. Estimates of [H2O2]cyt in other cells vary over a wide range, between 1 and 700 nM for routine signaling (47). Measured H2O2 concentrations in the renal medullary interstitium range from 50 to 300 nM (51). In this model, the value of JH2O2endo is taken as 3.0 × 10−12 mol·cm−2·s−1, and the intracellular concentration of catalase as 20 μM (5), so as to yield a resting [H2O2]cyt of 50 nM. Table 3 summarizes the kinetic parameters of NO, O2−, and H2O2 formation.
Table 3.
Parameters related to NO, O2−, and H2O2 kinetics
| Parameter | Description | Value | Reference |
|---|---|---|---|
| kNO, O2− | NO-O2− reaction rate constant | 1.9 × 1010 M−1·s−1 | 32 |
| kNO, cons | Lumped NO consumption rate constant | 0.01 s−1 | 53 |
| kSOD, O2− | O2−-SOD reaction rate constant | 1.6 × 109 M−1·s−1 | 2 |
| kcat | H2O2-catalase reaction rate constant | 3.4 × 107 M−1·s−1 | 40 |
| [SOD] | SOD concentration | 1 μM | 2 |
| [CAT] | Catalase concentration | 20 μM | 5 |
| JNO | Influx of NO from endothelium | 4.0 × 10−13 mol·cm−2·s−1 | Est. |
| GO2− | Volumetric rate of O2− generation | 3.0 μM·s−1 | Est. |
| JH2O2 | Influx of H2O2 from endothelium | 3.0 × 10−12 mol·cm−2·s−1 | Est. |
| PNO | Membrane permeability to NO | 0.03 cm/s | 12, 57 |
| PO2− | Membrane permeability to O2− | 0.06 cm/s | Est. |
| PH2O2 | Membrane permeability to H2O2 | 0.06 cm/s | Est. |
NO, O2−, and H2O2: nitric oxide, superoxide, and hydrogen peroxide, respectively.
Activation of sGC and cGMP Generation
sGC activation by NO.
The activation of sGC by NO is modeled as a two-step process, following the approach of Yang et al. (53). NO first binds to basal sGC (denoted by Eb) to form an intermediate six-coordinate ferrous nitrosyl heme complex (denoted by E6c), which is then converted to a fully activated five-coordinate complex (denoted by E5c). The first step in this NO binding process is expressed as a reversible reaction. The subsequent transition from E6c to E5c is thought to occur via two parallel pathways (one NO dependent and the other NO independent), both of which are represented as a single-step irreversible process. Finally, the dissociation of NO from E5c, or deactivation of E5c, is modeled as a first-order, irreversible reaction (53). The corresponding kinetic equations are written as
| (18) |
| (19) |
| (20) |
where [Ei] represents the fractional concentration of Ei (i = b, 6c, 5c) relative to the total sGC concentration, which is taken to remain constant. As in the study of Yang et al. (53), sGC desensitization to NO is modeled by means of a negative feedback loop: the dissociation of NO from sGC and the conversion of E5c to Eb are assumed to be mediated by cGMP (which may not be the direct inhibitor, but a second messenger). Thus the rate constant k4sGC is expressed as
| (21) |
where K4sGC has a fixed value of 98 × 103 M−1·s−1.
cGMP production and degradation.
We assume that the production of cGMP from GTP depends principally on E5c levels, and that the hydrolysis of cGMP into GMP by various isoforms of cyclic nucleotide phosphodiesterases (PDEs) is the main cGMP degradation pathway (53). The net rate of cGMP formation is expressed as
| (22) |
where Vmax, sGC represents the maximal rate of cGMP production when [E5c] = 1. To model the activation of PDEs by cGMP, the maximal rate of cGMP hydrolysis by PDEs is taken to be proportional to cGMP concentration (53), that is Vmax, PDE = kPDE[cGMP]. Hence Eq. 22 may be rewritten as
| (23) |
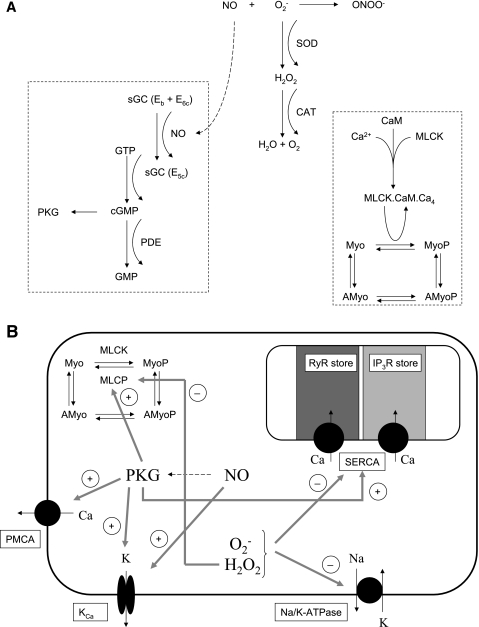
Parameters related to the kinetics of sGC and cGMP formation are given in Table 4. The signaling cascades described above, from the influx of NO into the cytosol to the formation of cGMP and PKG, are summarized in Fig. 2A.
Table 4.
| Parameter | Definition | Value |
|---|---|---|
| k1sGC | Eb-NO forward rate | 2.0 × 109 M−1·s−1 |
| k−1sGC | Eb-NO backward rate | 100 s−1 |
| k2sGC | E6c forward rate | 0.1 s−1 |
| k3sGC | E6c-NO forward rate | 3 × 106 M−1·s−1 |
| K4sGC | E5c forward rate | 9.8 × 104 M−1·s−1 |
| Vmax, sGC | cGMP maximal production rate | 1.09 μM·s−1 |
| kPDE | cGMP hydrolysis rate constant | 0.032 s−1 |
| KM, PDE | cGMP hydrolysis constant | 2.0 μM |
Eb is the basal form of sGC, E6c is an intermediate complex, and E5c is the fully activated form of sGC. Values are taken from Ref. 53.
Fig. 2.
A: schematic representation of the signaling cascades incorporated into the model. Nitric oxide (NO) diffuses from endothelial cells into DVR pericytes and reacts with superoxide (O2−) to form peroxynitrite (ONOO−). O2− also reacts with superoxide dismutase (SOD) to form H2O2. The latter is then converted by catalase (CAT) to yield H2O and O2. NO converts the basal and intermediate forms of sGC into its fully activated form, E5c, which in turn stimulates the production of cGMP. The latter then activates the formation of cGMP-dependent protein kinase (PKG). Also shown is the formation of the fully activated form of MLCK, that is, MLCK·CaM·Ca4, and the subsequent stimulation of myosin light chain phosphorylation. B: effect of signaling molecules on Ca2+ dynamics. The model accounts for NO- and cGMP-mediated stimulation of Ca2+ extrusion by the plasma membrane ATPase (PMCA), of Ca2+ uptake by the SR ATPase (SERCA), of K+ efflux via Ca2+-dependent K+ channels (KCa), and of MLCP activity. It also considers the inhibitory effects of O2− and H2O2 on SERCA and Na+-K+-ATPase, as well as the inhibition of MLCP activity by H2O2.
Effects of cGMP on Ca2+ Signaling and Vasocontractility
Instead of representing explicitly the poorly understood cascade of events through which cGMP exerts its effects, we assume that the effects of cGMP on Ca2+ ionic currents and MLCP activity can be expressed using a regulatory function R([cGMP]), such that R is zero when [cGMP] is zero, and R tends toward unity when [cGMP] approaches its saturation level (53). A Hill equation is chosen for this regulatory function
| (24) |
The parameters KM and n depend on the mechanism that is modulated by cGMP. Implicit in the use of Eq. 24 is the assumption that the cGMP-induced cascade of events is nearly instantaneous, that is, that cGMP exerts its effects without any delays.
Effects of cGMP on MLCP activity.
The study of Lee et al. (34) suggests that cGMP indirectly activates MLCP and that this mechanism underlies cGMP-induced Ca2+ desensitization in vasodilation. The investigators found that the effect of 10 μM 8-Br-cGMP on MLC phosphorylation could be simulated with a 3.8-fold increase in MLCP activity. Based upon these data, we assume that the rate constants that characterize the activity of MLCP are given by
| (25) |
where KM, cGMPMLCP is taken as 5.5 μM (53).
Effects of cGMP on KCa channels.
NO-induced activation of calcium-activated K+ (KCa) channels appears to involve both cGMP-dependent and cGMP-independent pathways (42). Yang et al. (53) simulated these effects assuming that NO and cGMP separately shift the voltage dependence of the single-channel open probability (PoKCa) toward more negative potentials, such that
| (26) |
| (27) |
Effects of cGMP on SR Ca2+-ATPase (SERCA).
Eggermont et al. (15) reported that 72–81% of SERCA mRNA encodes the nonmuscle isoform SERCA2b in smooth muscle. SERCA2 isoforms are regulated by phospholamban (PLB), which in its unphosphorylated form inhibits SERCA activity by decreasing its affinity for Ca2+ through direct interaction (27). Cornwell et al. (7) showed that cGMP (≥100 nM) activates SERCA via phosphorylation of PLB. In pig cardiac SR, PKA or PKG stimulation of the rate of SR Ca2+ uptake decreased the Ca2+ concentration for half-maximal activation (Kmf) from 0.40 to 0.18 μM without affecting the maximum rate of transport (44). Conversely, in pig stomach cells, Kmf almost doubled in the presence of unphosphorylated PLB, from 0.34 to 0.61 μM for SERCA2a and from 0.17 to 0.31 μM for SERCA2b (52). To account for these effects, the SERCA uptake current from compartment j (j = cyt or md) into the SR Ca2+ stores is calculated as
| (28) |
where
| (29) |
The data of Cornwell et al. (7) suggest that cGMP concentration must be at least in the 100 nM range to noticeably phosphorylate PLB; hence we assume that KSERCAM, cGMP equals 500 nM. The affinity of SERCA for Ca2+ in the absence of cGMP (Kmf*) is taken as 0.59 μM so that the affinity (Kmf) equals 0.31 μM under resting conditions (21). The parameters Kmr and H are respectively taken as 1.7 mM and 2 (13).
Note that Eq. 28 allows for backflux through the pump. As observed in SR membrane vesicles, the SR Ca2+ pump is a reversible enzyme capable of transporting Ca2+ in both directions (38, 50). Reversal of the pump is accompanied by ATP synthesis (29, 38). However, the extent to which backflux occurs to slow uptake under physiological conditions remains unclear; it is thought that the net transport rate across the pump never reverses physiologically (45).
Effects of cGMP on plasmalemmal Ca2+-ATPase.
Yoshida et al. (56) found that cGMP-dependent PKG stimulates the plasma membrane Ca2+-ATPase (PMCA). In the presence of 10 μg/l PKG and 1 μM cGMP, the maximum rate of transport was increased by 180%, but the affinity for Ca2+ was not significantly altered. The Ca2+ current across the plasma membrane Ca2+-ATPase in compartment j (j = cyt or md) is thus estimated as
| (30) |
where
| (31) |
The value of KPMCAM, cGMP is taken as 1 μM, and the maximum current in the absence of cGMP (IPMCA, max*) is taken as 2.9 pA so that the maximum current (IPMCA, max) equals 12 pA under resting conditions (13).
Effects of ROS on Ca2+ Signaling and Vasocontractility
The multiple interactions of ROS with ion transport mechanisms were reviewed in great detail by Kourie (33). Demonstrated effects of ROS in smooth muscle cells include inhibition of SR Ca2+-ATPase and Na+-K+-ATPase pumps (see Tables 7 and 8 in Ref. 33).
Table 7.
Predicted baseline solute concentrations
| Cytosolic Concentrations |
Microdomain Concentrations |
|||
|---|---|---|---|---|
| Case 1 | Case 2 | Case 1 | Case 2 | |
| [NO] | 93 nM | 93 nM | 93 nM | ∼0 |
| [cGMP] | 9.0 μM | 9.0 μM | 9.0 μM | ∼0 |
| [O2−] | 0.83 nM | 0.83 nM | 0.83 nM | ∼0 |
| [H2O2] | 50 nM | 50 nM | 50 nM | ∼0 |
| [Ca] | 108 nM | 105 nM | 154 nM | 372 nM |
| [Na] | 8.8 mM | 9.2 mM | 16.2 mM | 20.7 mM |
| [K] | 144 mM | 141 mM | 143 mM | 131 mM |
| [Cl] | 26 mM | 23 mM | 23 mM | 17 mM |
Case 1 assumes that the concentration of NO and reactive oxygen species (ROS) in subplasmalemmal microdomains is equal to that in the cytosol, whereas case 2 assumes that NO and ROS microdomain concentrations are negligible.
Effects of ROS on SERCA.
Susuki et al. (48) observed that exogenous hypoxanthine (HX; 0.1–100 μM) plus xanthine oxidase (XO; 10 mU/ml) produced an HX concentration-dependent inhibition of SERCA. This inhibition was completely blocked by SOD but not by mannitol or desferrioxamine, suggesting that O2− is the direct inhibitor. We fitted their data to correlate the degree of SERCA inhibition (0 ≤ θSERCAHX ≤ 1), with HX concentration using a Hill equation with a coefficient of 0.5
| (32) |
If KM, HXSERCA is taken as 10 μM, Eq. 32 predicts that 1, 10, and 100 μM HX inhibit the activity of SERCA by 24, 50, and 76%, respectively, in good agreement with the measured data (48). Since our model does not explicitly account for the kinetics of HX-induced O2− formation, we use a simplified approach to relate the concentrations of HX and XO to that of O2−. The HX/XO system generates two molecules of O2− for every molecule of HX used (36); however, O2− is likely to be scavenged by other reactants. In the absence of specific data, it is not possible to precisely determine the rate of O2− scavenging in these experiments. As a rough approximation, we assume that the equilibrium concentration of O2− is equal to twice the initial concentration of HX if the latter is the rate-limiting reactant; that is, we neglect any O2− scavenging. The inhibitory effect of O2− on SERCA activity is then approximated as
| (33) |
where KM, O2−SERCA = 2·KM, HXSERCA.
Although the study of Susuki et al. (48) suggested that H2O2 doesn't affect SERCA Ca2+ uptake, Grover et al. (24) found that H2O2 inhibits SERCA2b activity in microsomes with a half-maximal inhibitory concentration of 66 μM. The inhibitory effect of H2O2 on SERCA is thus determined as
| (34) |
where KM, H2O2SERCA equals 66 μM. The maximum current through SERCA is then expressed as
| (35) |
where ISERCA, max* is a constant, taken as 100 pA (13).
Effects of ROS on Na+-K+-ATPase.
Elmoselhi et al. (16) observed that ouabain-sensitive Rb+ uptake by denuded coronary artery rings was inhibited by exposure to either to H2O2 (with a half-maximal inhibitory concentration of 0.56 mM) or to O2− generated by 0.3 mM xanthine and XO (with a half-maximal inhibitory concentration of 0.08 mU/ml). The effect of H2O2 was not overcome by SOD and that of O2− was not prevented by catalase. We therefore assume that H2O2 and O2− each reduces the maximum current through both isoforms (α1 and α2) of the Na+-K+-ATPase pump, such that:
| (36) |
In these experiments, measurements were performed at t = 10 min; thus we assume that 0.08 mU/ml XO (i.e., the rate-limiting reactant) resulted in the formation of 2·10·(0.08 nmol/ml) = 1.6 μM O2−, and the constant KM, O2−NaK is taken as 1.6 μM.
Other effects.
As reviewed by Ardanaz and Pagano (1), H2O2 may modulate the transduction pathways of smooth muscle contraction in several other ways, including Ca2+ activation of Ca2+ release by RyR and IP3R, stimulation of extracellular Ca2+ influx, and inhibition of MLCP. However, the underlying mechanisms remain unclear or controversial. We include in our study the potential effect of H2O2 on MLCP using a regulatory function as described above (Eq. 24). That is, MLCP inhibition is modeled by dividing k2Myo and k5Myo by R(H2O2, MLCP)
| (37) |
The Michaelis-Menten constant KM, H2O2MLCP is fixed at 1 μM, and the enhancement factor αMLCP is chosen as 4.0 so as to fit experimental data (see below). The NO- and ROS-mediated effects on Ca2+ signaling are summarized in Fig. 2B, and related parameters are given in Table 5.
Table 5.
Parameters related to NO- and ROS-mediated effects on Ca2+ signaling
| Parameter | Definition | Value | Reference |
|---|---|---|---|
| KM, cGMPMLCP | cGMP concentration at half-maximal activation of MLCP (Eq. 25) | 5.5 μM | 53 |
| KM, cGMPSERCA | cGMP concentration at half-maximal activation of SERCA (Eq. 29) | 500 nM | Est. |
| KM, cGMPPMCA | cGMP concentration at half-maximal activation of PMCA (Eq. 31) | 1 μM | Est. |
| KM, cGMPKCa | cGMP concentration at half-maximal activation of KCa channels (Eq. 27) | 0.55 μM | (53) |
| VM, cGMPKCa | Constant for activation of KCa channels by cGMP (Eq. 27) | 66.9 mV | (53) |
| KM, NOKCa | NO concentration at half-maximal activation of KCa channels (Eq. 27) | 200 nM | (53) |
| VM, NOKCa | Constant for activation of KCa channels by NO (Eq. 27) | 100 mV | (53) |
| VCa | Constant for voltage-dependence of KCa channel open probability (Eqs. 26 and 27) | −53.7 mV | (53) |
| VB | Constant for voltage-dependence of KCa channel open probability (Eqs. 26 and 27) | 283.7 mV | (53) |
| kKCa | Constant for voltage-dependence of KCa channel open probability (Eq. 26) | 30.8 mV | (53) |
| KM, O2−SERCA | O2− concentration at half-maximal inhibition of SERCA (Eq. 33) | 20 μM | Est. |
| KM, H2O2SERCA | H2O2 concentration at half-maximal inhibition of SERCA (Eq. 34) | 66 μM | (24) |
| KM, O2−NAK | O2− concentration at half-maximal inhibition of Na+-K+-ATPase (Eq. 36) | 1.6 μM | Est. |
| KM, H2O2NAK | H2O2 concentration at half-maximal inhibition of Na+-K+-ATPase (Eq. 36) | 0.56 mM | (16) |
| KM, H2O2MLCP | H2O2 concentration at half-maximal inhibition of MLCP (Eq. 37) | 1 μM | Est. |
| αMLCP | Constant for H2O2-mediated inhibition of MLCP (Eq. 37) | 4.0 | See text |
SERCA, SR Ca2+-ATPase; MLCP, myosin light chain phosphatase; PMCA, plasma membrane Ca2+-ATPase.
Numerical Methods
The present model yields the intracellular concentrations of K+, Na+, Cl−, Ca2+, NO, O2−, H2O2, cGMP, and other related species as a function of time. To obtain these profiles, we first specify an initial state. We then use the concentrations at a given time step to determine the concentration of fully activated MLCK, the fraction of MLC that are phosphorylated and the relative contractile force (Eq. 14), as well as the magnitude of NO- or ROS-mediated effects on Ca2+ currents (Eqs. 25–37). The Ca2+ currents into and out of the SR can then be calculated. We also determine Ca2+ currents across the plasma membrane, and in between the cytosol and microdomains, as described in the appendix of Ref. 13. The fluxes and reaction terms for all other species considered in the model are subsequently determined (see Eqs. 15–23 above for NO, ROS, and related species, and the aforementioned appendix for the other solutes). Given the currents and fluxes, the time derivatives of solute concentrations and transmembrane potentials are calculated as previously described (13). The resulting differential equations are then integrated to yield concentrations and potentials at the next time step.
Parameter values for the new additions to the model (i.e., the equations given above) are listed in Tables 1–5. All other parameters can be found in Table 1 of Ref. 13.
The resting state is obtained by specifying arbitrary initial conditions and solving the dynamic equations until equilibrium is reached. Table 6 displays the resting values of all model variables. These were obtained assuming that the microdomain concentrations of NO, cGMP, and ROS are equal to those in the cytosol (see case 1 below).
Table 6.
Equilibrium values of model variables (case 1)
| Cytosol | Microdomain | |
|---|---|---|
| Transmembrane potential, Vm | −79.9 mV | −79.9 mV |
| Potassium concentration, [K+] | 143.5 mM | 142.5 mM |
| Sodium concentration, [Na+] | 8.8 mM | 16.2 mM |
| Chloride concentration, [Cl−] | 25.9 mM | 23.3 mM |
| Calcium concentration, [Ca2+] | 107.8 nM | 154.4 nM |
| IP3 concentration, [IP3] | 242 nM | 249 nM |
| NO concentration, [NO] | 92.8 nM | 92.8 nM |
| O2−concentration, [O2−] | 0.83 nM | 0.83 nM |
| H2O2 concentration, [H2O2] | 50.0 nM | 50.0 nM |
| Fraction of basal sGC, [Eb] | 0.275 | |
| Fraction of activated sGC, [E5c] | 0.217 | |
| cGMP concentration, [cGMP] | 9.04 μM | |
| Concentration of Ca2+ buffers other than calmodulin, [Bf] | 13.9 μM | 19.6 μM |
| Concentration of CaM species [CaM___] | 0.012 μM | 0.024 μM |
| Concentration of CaM species [CaM-c-] | 0.043 μM | 0.088 μM |
| Concentration of CaM species [CaMNC-] | 7.94 μM | 7.89 μM |
| Concentration of CaM species [CaM-CM] | 1.94 μM | 1.89 μM |
| Concentration of MLCK·CaM·Ca4 | 0.056 μM | 0.112 μM |
| Concentration of free myosin cross bridges, [Myo] | 7.76 μM | |
| Concentration of phosphorylated cross bridges, [MyoP] | 0.644 μM | |
| Concentration of attached dephosphorylated, noncycling cross bridges, [AMyo] | 18.20 μM | |
| RyR Ca2+ release current parameter ω | 0.665 | 0.891 |
| IP3R Ca2+ release current parameter x000 | 0.114 | 0.082 |
| IP3R Ca2+ release current parameter x001 | 0.085 | 0.087 |
| IP3R Ca2+ release current parameter x010 | 0.149 | 0.153 |
| Voltage-dependent Ca2+ current (ICa, L): activation variable dL | 3.33 × 10−5 | 3.36 × 10−5 |
| Voltage-dependent Ca2+ current (ICa, L): inactivation variable fF | 0.999 | 0.999 |
| Voltage-dependent Na+ current (IVONa): activation variable mVONa | 8.51 × 10−6 | 8.64 × 10−6 |
| Voltage-dependent Na+ current (IVONa): inactivation variable hVONa | 0.894 | 0.893 |
| Delayed rectifier K+ current (IK, v): probability P1 | 4.57 × 10−3 | 4.59 × 10−3 |
| Delayed rectifier K+ current (IK, v): probability P2 | 4.57 × 10−3 | 4.59 × 10−3 |
| Ca2+-activated K+ current (IK, Ca): fast activation component PF | 0.947 | 0.960 |
| Ca2+-activated K+ current (IK, Ca): slow activation component PS | 0.947 | 0.960 |
| Ca2+-dependent Cl− current (ICl, Ca): fraction of channel in state C1 | 6.39 × 10−3 | 9.10 × 10−3 |
| Ca2+-dependent Cl− current (ICl, Ca): fraction of channel in state C2 | 4.13 × 10−5 | 8.43 × 10−5 |
| Ca2+-dependent Cl− current (ICl, Ca): fraction of channel in state C3 | 2.67 × 10−7 | 7.81 × 10−7 |
| Ca2+-dependent Cl− current (ICl, Ca): fraction of channel in state O1 | 5.73 × 10−3 | 8.17 × 10−3 |
| Ca2+-dependent Cl− current (ICl, Ca): fraction of channel in state O2 | 1.11 × 10−4 | 2.27 × 10−4 |
| Ca2+-dependent Cl− current (ICl, Ca): fraction of channel in state O3 | 7.19 × 10−6 | 2.10 × 10−5 |
The Ca2+ concentration in the sarcoplasmic reticulum (SR) is predicted as 560 and 528 μM, respectively, in the ryanodine receptor (RyR) and IP3 receptor (IP3R) stores. The concentration of calsequestrin in the SR is predicted as 57.6 and 55.6 μM, respectively, in the RyR and IP3R stores.
Model equations are programmed using Matlab, and calculations are performed on a computer equipped with an Intel Core2 Duo 2.4-GHz processor with 2 GB of RAM.
RESULTS
Model Validation
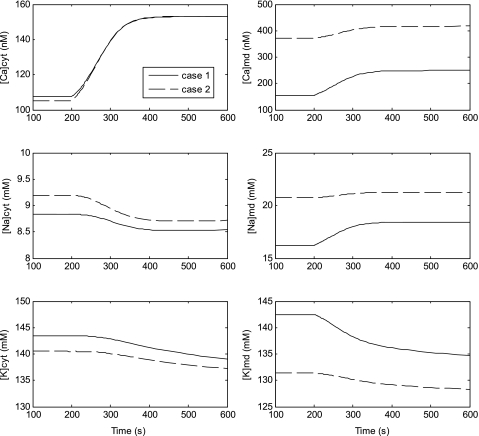
As illustrated in Fig. 1, our model takes into account the presence of subplasmalemmal microdomains. As described in our previous work (14), the concentration of Ca2+ and Na+ in particular is predicted to be significantly greater in these isolated microdomains than in the bulk cytosol. Since it remains unclear whether NO, O2−, and H2O2 are either generated or present in significant amounts in the microdomains, we considered two limiting cases in this study: the microdomain concentrations of NO, cGMP, and ROS were assumed to be either equal to those in the cytosol (case 1) or negligible (case 2). In case 2, NO and ROS modulate only the fluxes into/from the bulk cytosol, not those into/from the microdomains. Shown in Table 7 are the resting concentrations of NO, O2−, H2O2 and other ions predicted by the model. The principal difference between the two cases is the microdomain Ca2+ concentration ([Ca]md). In case 2, there is no cGMP-induced activation of the two microdomain Ca2+-ATPases (SERCA and PMCA), and the lower Ca2+ efflux from this compartment results in a significantly higher [Ca]md: the predicted value of [Ca]md assuming a negligible microdomain NO concentration is more than twice that obtained assuming homogenous NO concentrations throughout the cell (372 vs. 154 nM). The higher [Ca]md also raises the microdomain concentration of Na+ ([Na]md) via the Na+/Ca2+ exchanger (NCX), which is expressed only above the microdomains (30, 39); microdomain-to-cytosol Na+ electrodiffusion subsequently increases [Na]cyt slightly.
The fraction of phosphorylated MLC (fP) at rest is predicted as 13.5 and 13.0% in cases 1 and 2, respectively. These values are in good agreement with experimental data: in canine tracheal smooth muscle, fp was found to range between 15 and 20% (31, 46), and in smooth muscle strips from rabbit femoral arteries fp values were on the order of 10% (34).
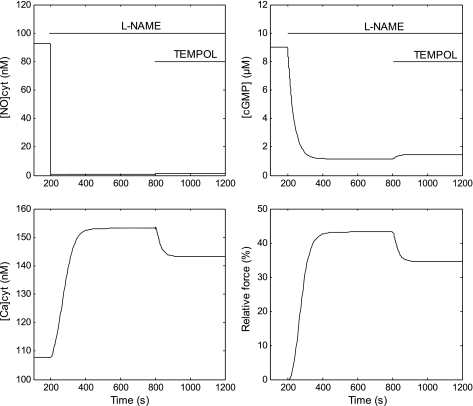
We first validated our model of NO signaling in DVR pericytes by comparing the predicted and measured effects of the NOS inhibitor Nω-nitro-l-arginine methyl ester (l-NAME) on DVR contractility. l-NAME (10−4 M) has been found to be a potent vasoconstrictor of explanted DVR (4). Here, l-NAME-induced inhibition of NOS was simulated by reducing the net influx of NO into the cytosol by 99%. As described in model description, the subsequent reduction in cGMP levels reduces MLCP activity and increases the fraction of phosphorylated MLC, thereby raising the relative contractile force. The model predicts that 99% inhibition of NOS raises [Ca]cyt to ∼150 nM, and the fraction of phosphorylated myosin to ∼50%, as illustrated in Fig. 3. The relative contractile force (Fcontract) is predicted to be 43%. That value is consistent with the observation that l-NAME reduces luminal diameter of microperfused DVR by 49% (at the end of the 10 min treatment, see Fig. 1B in Ref. 4).
Figure 3 also illustrates the kinetics of NOS inhibition. We assume that the 99% decrease in the NO influx occurs instantaneously at t = 200 s. Following the precipitous drop in [NO]cyt, the concentration of the activated form of sGC (E5c) drops within 15 s; indeed, the slowest sGC reaction rates are ∼0.1 s−1 (Table 4). It then takes ∼200 s for the concentration of cGMP to reach its equilibrium value, because some of the cGMP rate constants are very small, on the order of 0.03 s−1 (Table 4). Given our implicit assumption that cGMP-mediated effects on Ca2+ currents and MLCP activity are immediate, the model predicts that [Ca]cyt adjusts on a similar time scale to [cGMP]cyt.
We previously observed that l-NAME-induced DVR vasoconstriction is reversed by the addition of 8-Br-cGMP (10−4 M) to the bath (4), which favors the interpretation that NOS inhibition leads to reduction of cGMP-mediated signaling and that cGMP remains effective in the presence of l-NAME. To further validate our model, we simulated the same scenario: the concentration of cGMP was raised to 100 μM, 400 s after the first exposure to l-NAME. The model predicts that the addition of cGMP entirely reverses l-NAME-induced vasoconstriction (results not shown).
Concentration Profiles with NOS Inhibition
The effects of NOS inhibition on pericyte [Ca]cyt have not been measured directly. We thus used our model to determine how l-NAME modulates [Ca]cyt and [Ca]md, as well as the concentrations of Na+ and K+ (Fig. 4). In case 1, where the cytosolic and microdomain NO concentrations are equal, NOS inhibition raises both [Ca]cyt and [Ca]md through inhibition of cGMP pathways. In case 2, where the microdomain concentration of NO is zero, inhibition of NOS first raises [Ca]cyt, thereby stimulating Ca2+ uptake from the cytosol into the SR; this in turn augments the release rate of Ca2+ into the microdomains via RyR and IP3R. The resulting increase in [Ca]md is nevertheless smaller than in case 1. In both cases, the [Ca]md increase stimulates NCX, which then raises [Na]md. As noted above, NCX is not expressed above the cytosol; thus, [Na]cyt is predicted to decrease because the filling of SR Ca2+ stores reduces Na+ (and Ca2+) fluxes through store-operated, nonselective cation channels (SOC). In parallel, membrane depolarization (1–2 mV) slightly lowers [K]cyt and [K]md.
Fig. 4.
Simulated effects of l-NAME on Ca2+, Na+, and K+ concentrations in the bulk cytosol (left) and the microdomains (right). Results are shown for cases 1 and 2.
Contribution of cGMP Pathways to Resting [Ca]cyt
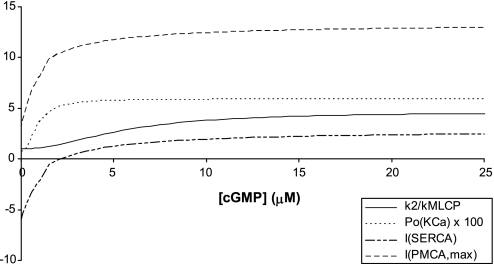
We then sought to assess the contribution of each of the pathways through which NO modulates Ca2+ signaling in pericytes. As a first step, we examined the dependence of model variables on cGMP levels. As described above, four variables are taken to vary directly in proportion to [cGMP]: the MCLP rate constant (k2Myo, Eq. 25), the open probability of KCa channels (PoKCa, Eqs. 26 and 27), the Ca2+ uptake current into the SR (ISERCA, Eqs. 28 and 29), and the maximum Ca2+ current across PMCA (IPMCA, max, Eq. 31). As shown in Fig. 5, the relative MLCP rate constant increases from 1 to 4.6 as [cGMP] increases from 0 to 45 μM (all else being equal), and then reaches a plateau. Given that the resting value of [cGMP] is predicted as 9.0 μM (Table 7), k2Myo is expected to be quite sensitive to physiological [cGMP] variations. In contrast, the open probability of KCa channels attains its equilibrium value of 0.059 much faster, as soon as [cGMP] reaches 9 μM. However, since PoKCa is so low, cGMP-induced (or NO-induced) variations in KCa currents should remain small.
Fig. 5.
Sensitivity of cGMP-dependent variables to cGMP levels. Displayed are the relative MCLP rate constant (k2Myo/kMLCPMyo, Eq. 25), the open probability of KCa channels (PoKCa, Eqs. 26 and 27) expressed as a percentage, the Ca2+ uptake current into the SR (ISERCA; Eqs. 28 and 29) in pA, and the maximum Ca2+ current across PMCA (IPMCA, max; Eq. 31) in pA, as a function of cytosolic cGMP concentration.
The maximum PMCA current rises rapidly from 2.9 to 12.4 pA as [cGMP] increases from 0 to 10 μM and reaches a plateau soon thereafter. Similarly, the SERCA current rises steeply from −6.0 to +2.0 pA as [cGMP] increases from 0 to 10 μM, then rises more slowly toward an equilibrium value of 2.7 pA. The predicted negative current values at very low cGMP levels stem from the fact that the affinity of SERCA pumps for cytosolic Ca2+ is then very low (i.e., Kmf is very high). As described above, ex vivo the pump may indeed function in backward mode. Under physiological conditions, however, the net rate of Ca2+ transport through SERCA does not reverse (45). In the calculations displayed in Fig. 5, all variables except for [cGMP] were kept fixed, so that a negative current was possible. Physiologically, Ca2+ uptake and release fluxes across the SR membrane vary jointly and the overall SERCA current remains positive. Overall, Fig. 5 suggests that both ISERCA and IPMCA, max vary significantly over the physiological range of [cGMP].
We then examined the effects of inhibiting each of the NO- and cGMP-mediated pathways in turn, while keeping the baseline concentrations of NO and ROS constant. The experimental data reviewed above (model description) suggest that O2− and H2O2 modulate Ca2+ signaling and the extent of MLC phosphorylation directly (i.e., independently of their effect on NO) only when their concentration is in the micro- to millimolar range. Thus, under resting conditions, their direct impact on [Ca]cyt and fp is negligible (results not shown).
As expected, under baseline conditions, NO- and cGMP-mediated effects on KCa channels are also calculated to be negligible (Fig. 6). In contrast, the basal activation of PMCA or SERCA by cGMP is predicted to mediate tonic repression of [Ca]cyt and fP. More specifically, our simulations indicate that [Ca]cyt would rise from 108 to 165 nM (case 1) or 159 nM (case 2) without cGMP-induced activation of PMCA, and fP would increase correspondingly to 26.0 or 24.7%. Similarly, without tonic activation of SERCA by cGMP, [Ca]cyt would rise from 108 to 146 (case 1) or 158 nM (case 2), and fP would increase to 21.7 or 24.5%.
Our model also suggests that cGMP-mediated activation of MLCP (Eq. 25) imposes tonic reduction of MLC phosphorylation; if cGMP did not stimulate MLCP, fP would be 36.3 (case 1) or 35.2% (case 2). Finally, our results indicate that the net effect of cGMP and NO on DVR contractile tone is greater than the sum of their individual effects: as displayed in Fig. 6, in the absence of any NO- and cGMP-mediated effects, [Ca]cyt would be ∼330 nM and fp ∼80%, which corresponds to a relative contractile force of 93%.
The reason the joint response is greater than the sum of the individual responses has to do with the properties of RyR Ca2+ release currents. The open probability of ryanodine receptors (PoRyR) and the RyR current increase rapidly as [Ca] rises above a ∼200 nM threshold, as we previously described (13). Separately abolishing the cGMP-mediated activation of SERCA or that of PMCA is not sufficient to increase [Ca]cyt beyond this limiting value. However, when both activating effects are eliminated, [Ca]cyt rises above the threshold; the [Ca]cyt increase is then amplified by the ensuing increase in RyR Ca2+ release from the SR; hence the nonlinear response.
Mechanisms Underlying O2−-Induced Vasoconstriction
In explanted microperfused DVR, application of the SOD mimetic Tempol or the NADPH oxidase inhibitor apocynin per se does not affect DVR diameter (4), which strongly suggests that basal levels of O2− are too low to affect vascular tone. However, both Tempol (10−3 M) and apocynin (10−4- 10−3 M) partly reverse DVR vasoconstriction induced by l-NAME (4). We simulated these experimental conditions to determine whether, in the presence of l-NAME, O2− is present at sufficiently high concentrations to exert a direct (i.e., NO-independent) effect on DVR tone.
In agreement with experimental observations, the model predicts that raising the concentration of SOD (or Tempol) to 10−3 M reduces the relative contractile force. Our results suggest that the SOD-induced [O2−]cyt reduction raises [NO]cyt in preconstricted pericytes from 0.7 to 1.3 nM, which in turn raises the concentration of cGMP by 0.3 μM, resulting in a lower fraction of phosphorylated MLC and leading to vasorelaxation, as shown in Fig. 7. The predicted reduction (∼10%) is somewhat smaller than what has been observed experimentally and depends very little on the presumed level of NOS inhibition (results not shown). There are several possible reasons for this discrepancy. First, our assumption that the bath concentration of NO is zero may result in an overestimation of the NO diffusive efflux, to the detriment of the NO-O2− reaction term; the pericyte membrane permeability to NO is also very uncertain. In addition, we did not account for the likely (but difficult to quantify) increase in NO influx into the pericyte following Tempol-induced elevations in endothelial NO levels.
Fig. 7.
Predicted effects of Tempol (10−3 M) on DVR perycites preconstricted by l-NAME. At t = 200 s, JNOendo is multiplied by 0.01 (Eq. 15) to simulate l-NAME administration. Then, at t = 800 s, the SOD concentration is multiplied by 1,000 (Eq. 16) to simulate the addition of Tempol. The cytosolic concentrations of NO, cGMP, and Ca2+, as well as the relative contractile force, are shown as a function of time. Results are shown for case 1; those for case 2 are nearly indistinguishable.
Our model also predicts that if NO formation were entirely inhibited by l-NAME, that is, if [NO]cyt were zero (instead of 0.7 nM) following exposure to l-NAME, further addition of SOD or Tempol would have no effect on vasoconstriction (results not shown). This suggests that the vasodilatory effects of Tempol on preconstricted DVR are entirely mediated by NO. In order words, at physiological concentrations, O2− affects Ca2+ signaling indirectly, via its scavenging of NO.
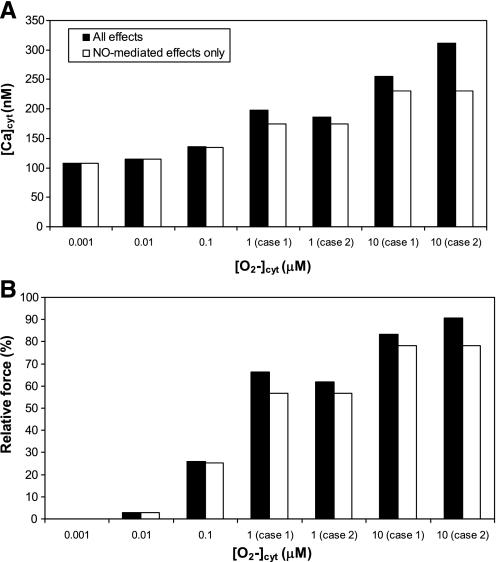
Oxidative stress is characterized by high levels of O2−. To investigate the different ways in which O2− modulates Ca2+ signaling when its concentration is elevated, we simulated increases in [O2−]cyt either with or without accounting for O2−-mediated inhibition of SERCA (Eq. 34) and Na+-K+-ATPase pumps (Eq. 36). Elevations in [O2−]cyt should also enhance [H2O2]cyt, but in this set of simulations we did not consider the additional effects of H2O2 on DVR tone (which are examined below). As displayed in Fig. 8, O2− induces significant, concentration-dependent vasoconstriction. At a concentration of 0.1, 1.0, and 10 μM, O2− is predicted to generate a relative contractile force of ∼25, 60, and 85%, respectively. Moreover, under 1 μM, O2− regulates [Ca]cyt and vessel contractility predominantly via its scavenging effect on NO; that is, O2−-mediated inhibition of SERCA and Na+-K+-ATPase pumps is negligible, as expected given that the corresponding Michalis-Menten constants are on the order of 1−10 μM.
Fig. 8.
Predicted cytosolic Ca2+ concentration (top) and relative contractile force (bottom) at steady state as a function of O2− concentration. The O2− concentration was fixed at a given value by adjusting the O2− volumetric generation rate (GO2− in Eq. 16). Below 1 μM O2−, results for cases 1 and 2 are nearly indistinguishable.
At or above 1 μM, O2− significantly reduces Na+-K+-ATPase and SERCA activity. By itself, the O2−-mediated inhibition of Na+-K+-ATPase raises the cytosolic and microdomain concentrations of Na+, thereby stimulating NCX and enhancing Ca2+ influx into the cell. The resulting [Ca]cyt increase is more pronounced in case 1, since O2− inhibits the sodium pumps in both compartments under these conditions.
Similarly, by itself, the O2−-mediated inhibition of SERCA reduces SR Ca2+ uptake and raises the cytosolic and microdomain concentrations of Ca2+. However, here the [Ca]cyt increase is more pronounced in case 2: in this latter case, O2− inhibits only the SERCA that are located at the SR-cytosol interface (i.e., not those at the SR-microdomain interface), thereby maintaining higher Ca2+ levels in the SR, and thus greater receptor-mediated Ca2+ release into the cytosol, than in case 1.
Thus the inhibition of Na+-K+-ATPase and that of SERCA both act to enhance [Ca]cyt, but in different ways: the former, through secondary effects on NCX, augments Ca2+ influx into the cell, whereas the latter alters the distribution of Ca2+ among the different intracellular compartments. Since O2− induces half-maximal inhibition of Na+-K+-ATPase at a concentration of 1.6 μM, vs. 20 μM for that of SERCA (Table 5), the effects of Na+-K+-ATPase inhibition predominate at 1 μM O2−. Thus, at that concentration, [Ca]cyt increases more in case 1 than in case 2 (Fig. 8). Conversely, at 10 μM O2−, [Ca]cyt rises higher in case 2 than in case 1, suggesting that the effects of SERCA inhibition are then preponderant.
Mechanisms Underlying H2O2-Induced Vasoconstriction
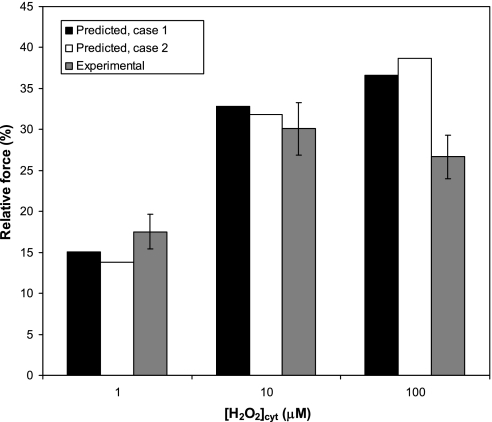
In explanted DVR, H2O2 induces concentration-dependent vasoconstriction at concentrations ranging from 1 to 100 μM (4). To examine the underlying mechanisms, we simulated the effects of raising the intracellular concentration of H2O2 to 1, 10, and 100 μM. As described above, the model accounts for the inhibitory effects of H2O2 on Na+-K+-ATPase, SERCA, and MLCP but neglects other possible H2O2-mediated pathways. The agreement between our predictions and experimental trends is nevertheless good. As summarized in Fig. 9, H2O2 is predicted to induce a relative contractile force of ∼15, 30, and 35% at 10−6, 10−5, and 10−4 M, respectively. Observed reductions of luminal diameter were 18, 30, and 27% at those concentrations, respectively (4).
Fig. 9.
Predicted relative contractile force and experimental change in luminal diameter of microperfused DVR as a function of H2O2 concentration at steady state. The H2O2 concentration was fixed at a given value by adjusting the H2O2 influx ( JH2O2endo in Eq. 17). At 100 μM H2O2, the relative contractile force is predicted to oscillate slightly in case 1; shown here is its average value.
As expected from the Michaelis-Menten constants describing the effect of H2O2 on SERCA (66 μM) and Na+-K+-ATPase pumps (560 μM), the model predicts that at or below 10 μM, H2O2 regulates vessel contractility predominantly by inhibiting MLCP activity. That is, there is no significant difference in [Ca]cyt and Fcontract regardless of whether H2O2-mediated SERCA and Na+-K+-ATPase inhibition is taken into consideration (results not shown).
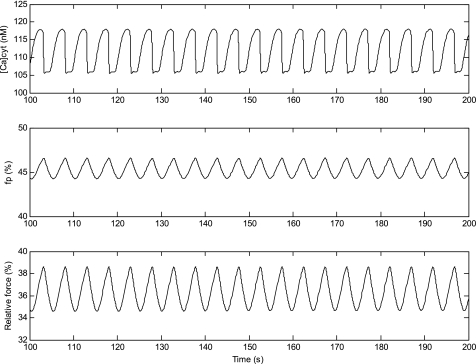
At 100 μM, however, the inhibitory effects of H2O2 on SERCA become more important. In fact, in case 1, those effects generate small [Ca]cyt oscillations (of a magnitude of 12 nM and a periodicity of 5 s) as shown in Fig. 10. Case 1 assumes that the concentration of NO and ROS is identical in the bulk cytosol and the microdomains. Thus the H2O2-mediated inhibition of SERCA modulates Ca2+ uptake into the SR from both compartments; a small reduction in the rate of Ca2+ uptake from the microdomains into the SR allows [Ca]md to rise above the calcium-induced calcium-release (CICR) threshold, thereby generating oscillations (see Ref. 13 for a full explanation of the mechanisms predicted to underlie [Ca]cyt oscillations in DVR pericytes). The [Ca]cyt oscillations in turn generate oscillations in the fraction of phosphorylated myosin and in the relative contractile force (which varies between 34.6 and 38.6%; Fig. 10). Without H2O2-mediated inhibition of SERCA, the predicted contractile force would remain constant at 33.3%.
Fig. 10.
At a concentration of 100 μM, H2O2 is predicted to induce small oscillations in [Ca]cyt (top), the fraction of myosin species that is phosphorylated (middle), and the relative contractile force (bottom) in case 1.
In case 2, which assumes that NO and ROS concentrations are zero in the microdomains, H2O2 does not modulate Ca2+ uptake from the latter compartment and therefore does not generate [Ca]cyt oscillations. Nevertheless, even in that case, the inhibitory effects of 100 μM H2O2 on SERCA alter Ca2+ uptake from the bulk cytosol and vessel contractility: [Ca]cyt would be 10 nM lower (105 vs. 115 nM), and Fcontract would be 7% lower (31.4% vs. 38.7%) without those effects.
DISCUSSION
The main objective of this study was to elucidate the cellular mechanisms by which NO, O2−, and H2O2 modulate [Ca]cyt and cell contraction in DVR pericytes. For this purpose, we expanded our mathematical model of Ca2+ signaling in pericytes (13) to incorporate 1) the pathways leading from an increase in [Ca]cyt to the activation of MLCK and cell contraction as well as 2) the kinetics of NO and ROS formation and their effects on [Ca]cyt and MLC phosphorylation. Our approach for the latter is conceptually similar to that of Yang et al. (53), but their study did not include ROS, nor the effects of NO on SERCA and PMCA.
We first validated our model by comparing its predictions with our recent experimental findings (4). The model adequately reproduced the modulation of DVR contraction following administration of l-NAME, 8-Br-cGMP, Tempol, and H2O2, although neglecting the effects of Tempol to modulate endothelial NO release probably underestimated its propensity to induce vasodilation (Figs. 3, 7, and 9). Our results suggest that under resting conditions, NO-induced activation of cGMP significantly lowers [Ca]cyt and the fraction of phosphorylated MLC by stimulating Ca2+ uptake from the cytosol into the SR via SERCA, increasing Ca2+ efflux into the extracellular space via PMCA, and activating MLCP. The effects of basal levels of NO and cGMP on KCa channels is predicted to be insignificant (Fig. 6).
We also found that basal levels of O2− and H2O2 have negligible direct effects on Ca2+ signaling and MLC phosphorylation. In particular, our model predicts that l-NAME and Tempol modulate the contraction of explanted DVR not because they affect O2− levels per se, but as a result of variations in NO concentration. Several experimental observations support these findings: the addition of Tempol alone has no effect on DVR tone (4), and l-NAME does not increase O2− levels very significantly (60); indeed, the predominant O2− scavenger is SOD.
Even at supraphysiological concentrations, O2− is predicted to modulate [Ca]cyt and MCLP activity mostly in indirect ways, that is, by reducing NO bioavailability (Fig. 8). Whether such effects on NO bioavailability are as significant in vivo, where NO can diffuse from the cell to be scavenged by hemoglobin, is uncertain. Notably, the reaction of NO with hemoglobin is orders of magnitude faster than its consumption by O2−. Moreover, endothelial shear-mediated increases in the basal rate of NO production could be a significant variable (58).
The reported effects of H2O2 on vasoactivity vary depending upon species, vessel type, concentration, and experimental conditions (3, 22, 55). In DVR, H2O2 causes vasoconstriction at concentrations ranging from 1 to 100 μM, and vasodilation at 1 mM (4). As reviewed by Ardanaz and Pagano (1), H2O2 is thought to modulate Ca2+ signaling and MLC phosphorylation via many different mechanisms, few of which have been well characterized. It has been shown that H2O2 modifies both Ca2+ transport and Ca2+ sensitization. The former includes modulation of voltage-gated channel activity as well as secondary effects on NCX and ER/SR Ca2+ release and uptake. Changes in Ca2+ sensitization may be mediated through activation of Rho kinase and MAP kinases with attendant inhibition of MLCP to favor myosin phosphorylation (1). Given the many uncertainties, in the current study, we focused on three likely mechanisms by which H2O2 may affect vessel contractility: namely, its inhibition of SERCA, Na+-K+-ATPase, and MCLP activity. This was sufficient to yield good agreement between measured and predicted H2O2-induced pericyte contraction, as illustrated in Fig. 9.
Several studies suggest that H2O2 activates, whereas NO inhibits, voltage-operated Ca2+ channels in vascular smooth muscle cells (26, 49, 55). Since the underlying mechanisms remain elusive, we examined the effects of varying the maximum conductance of L-type channels in DVR pericytes. The model predicts that neither a 10-fold conductance increase nor complete channel inhibition significantly affects Ca2+ signaling and vessel contraction (results not shown). However, it is possible that NO and/or H2O2 modify the voltage-dependence of L-type channels or activation/inactivation time constants. More detailed simulations of signaling by H2O2 would require further experimental studies of its specific role in DVR pericytes and endothelia.
In the absence of data to guide a choice, we examined two limiting cases. Case 1 assumes that the concentration of NO, O2−, and H2O2 in the subplasmalemmal microdomains is the same as that in the bulk cytosol, whereas case 2 assumes that it is zero. Although these two hypotheses yield different predictions in regards to [Ca]md, the value of which cannot be readily measured, they produce similar effects on “measurable” variables, making it difficult to conclude as to which best simulates reality. One notable exception concerns the effects of 100 μM H2O2, which is predicted to generate small [Ca]cyt oscillations in case 1 only (Fig. 10), due to cyclic Ca2+ uptake and release from the SR. Such H2O2-induced [Ca]cyt oscillations have been reported in some endothelial cells (28), where they were also found to result from internal Ca2+ release from the endoplasmic reticulum.
With respect to intracellular distribution of ROS, more complex scenarios than those considered in the current model seem possible. For example, the diffusion barrier between cytosol and microdomain might differentially modulate transport of NO, O2−, and H2O2 between compartments. Intracellular channels, such as aquaporins, might afford differential permeability to some species. Moreover, spatial variation of expression of SOD, catalase, or other antioxidants in the cytosol, microdomains, or mitochondria might affect local ROS concentrations within cells, providing a means for fine regulation of smooth muscle contraction.
These simulations largely reflect putative intrinsic production and signaling of NO and O2− within the DVR wall. Cao and colleagues (4) observed that blockade of NO generation led to substantial vasoconstriction that was partly reversed by scavenging O2− or inhibiting O2− generation. Those experiments were performed under conditions of luminal shear stimulation, i.e., during isolated vessel microperfusion, which markedly enhances endothelial NO generation (58). Other studies in explanted tissue preparations, in which DVR were not perfused, have elegantly shown that NO and O2− from adjacent epithelia can reach DVR pericytes to modify pericyte cytoplasmic Ca2+ levels (10). In both studies, the explanted preparations favored limiting conditions that maximized NO and O2− generation by either vascular or epithelial structures. These studies served to demonstrate events that can occur ex vivo while the actual interplay of events in vivo is likely to be more varied and complex.
The renal outer medulla is sharply divided into vascular bundles wherein DVR and ascending vasa recta reside, and the interbundle region where transporting epithelia reabsorb salt and water (43). Focusing on NO in the outer medulla, its consumption by hemoglobin within vascular bundles suggests that a standing concentration gradient of NO might be established, falling from the interbundle region, wherein thick ascending limbs and collecting ducts reside, toward the vascular bundle centers. However, NO generation within the DVR wall should modify that gradient, generally raising the mean levels of NO within vascular bundles as well as the outer medullary interbundle region, as we recently predicted (11). The possibility that both vasoactivity and Na+ reabsorption could be influenced, i.e., as a mechanism of vascular-tubular cross talk that mediates pressure natriuresis, can be entertained. Moreover, other signaling molecules are likely to participate in tubular-vascular and vascular-tubular cross talk. Both prostaglandins and adenosine are generated by many cell types and each can influence both vasoactivity and epithelial Na+ reabsorption (25, 61). The renal outer medulla is largely inaccessible in vivo, so that mathematical simulations that account for the generation and consumption of signaling molecules as well as their effects on intracellular targets may be needed to gain further insight into these possibilities.
GRANTS
This work was supported by National Institutes of Health Grants R01 DK053775 (to A. Edwards), R37 DK042495 and R01 DK067621 (to T. L. Pallone), and American Heart Association Grant 09SDG2130035 (to C. Cao).
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
REFERENCES
- 1. Ardanaz N, Pagano PJ. Hydrogen peroxide as a paracrine vascular mediator: regulation and signaling leading to dysfunction. Exp Biol Med 231: 237–251, 2006 [DOI] [PubMed] [Google Scholar]
- 2. Buerk D, Lamkin-Kennard K, Jaron D. Modeling the influence of superoxide dismutase on superoxide and nitric oxide interactions, including reversible inhibition of oxygen consumption. Free Radic Biol Med 34: 1488–1503, 2003 [DOI] [PubMed] [Google Scholar]
- 3. Burke-Wolin T, Abate CJ, Wolin MS, Gurtner GH. Hydrogen peroxide-induced pulmonary vasodilation: role of guanosine 3′,5′-cyclic monophosphate. Am J Physiol Lung Cell Mol Physiol 261: L393–L398, 1991 [DOI] [PubMed] [Google Scholar]
- 4. Cao C, Edwards A, Sendeski M, Lee-Kwon W, Cui L, Cai CY, Patzak A, Pallone TL. Intrinsic nitric oxide and superoxide production regulates descending vasa recta contraction. Am J Physiol Renal Physiol 299: F1056–F1064, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Chance B, Sies H, Boveris A. Hydroperoxide metabolism in mammalian organs. Physiol Rev 59: 527–605, 1979 [DOI] [PubMed] [Google Scholar]
- 6. Chen B, Deen WM. Analysis of the effects of cell spacing and liquid depth on nitric oxide and its oxidation products in cell cultures. Chem Res Toxicol 14: 135–147, 2001 [DOI] [PubMed] [Google Scholar]
- 7. Cornell TL, Pryzwansky KB, Wyatt TA, Lincoln TM. Regulation of sarcoplasmic reticulum protein phosphorylation by localized cyclic GMP-dependent protein kinase in vascular smooth muscle cells. Mol Pharmacol 40: 923–931, 1991 [PubMed] [Google Scholar]
- 8. Cowley AW, Jr, Mori T, Mattson D, Zou AP. Role of renal NO production in the regulation of medullary blood flow. Am J Physiol Regul Integr Comp Physiol 284: R1355–R1369, 2003 [DOI] [PubMed] [Google Scholar]
- 9. Denicola A, Souza JM, Radi R, Lissi E. Nitric oxide diffusion in membranes determined by fluorescence quenching. Arch Biochem Biophys 328: 208–212, 1996 [DOI] [PubMed] [Google Scholar]
- 10. Dickhout JG, Mori T, Cowley AW., Jr Tubulovascular nitric oxide crosstalk: buffering of angiotensin II-induced medullary vasoconstriction. Circ Res 91: 487–493, 2002 [DOI] [PubMed] [Google Scholar]
- 11. Edwards A, Layton AT. Nitric oxide and superoxide transport in a cross-section of the rat outer medulla. II. Reciprocal interactions and tubulo-vascular cross-talk. Am J Physiol Renal Physiol 299: F634–F637, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Edwards A, Layton AT. Nitric oxide and superoxide transport in a cross section of the rat outer medulla. I. Effects of low medullary oxygen tension. Am J Physiol Renal Physiol 299: F616–F633, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Edwards A, Pallone TL. Mechanisms underlying angiotensin II-induced calcium oscillations. Am J Physiol Renal Physiol 295: F568–F584, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Edwards A, Pallone TL. Modification of cytosolic calcium signaling by subplasmalemmal microdomains. Am J Physiol Renal Physiol 292: F1827–F1845, 2007 [DOI] [PubMed] [Google Scholar]
- 15. Eggermont JA, Wuytack F, Verbist J, Casteels R. Expression of endoplasmic-reticulum Ca2+-pump isoforms and of phospholamban in pig smooth-muscle tissues. Biochem J 271: 649–653, 1990 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Elmoselhi AB, Butcher A, Samson SE, Grover AK. Free radicals uncouple the sodium pump in pig coronary artery. Am J Physiol Cell Physiol 266: C720–C728, 1994 [DOI] [PubMed] [Google Scholar]
- 17. Evans R, Fitzgerald S. Nitric oxide and superoxide in the renal medulla: a delicate balancing act. Curr Opin Nephrol Hypertens 14: 9–15, 2005 [DOI] [PubMed] [Google Scholar]
- 18. Fajmut A, Dobovisek A, Brumen M. Mathematical modeling of the relation between myosin phosphorylation and stress development in smooth muscles. J Chem Inf Model 45: 1610–1615, 2005 [DOI] [PubMed] [Google Scholar]
- 19. Fajmut A, Jagodic M, Brumen M. Mathematical modeling of the myosin light chain kinase activation. J Chem Inf Model 45: 1605–1609, 2005 [DOI] [PubMed] [Google Scholar]
- 20. Ferrer-Sueta G, Radi R. Chemical biology of peroxynitrite: kinetics, diffusion, and radicals. ACS Chem Biol 4: 161–177, 2009 [DOI] [PubMed] [Google Scholar]
- 21. Flynn ER, Bradley KN, Muir TC, McCarron JG. Functionally separate intracellular Ca2+ stores in smooth muscle. J Biol Chem 276: 36411–36418, 2001 [DOI] [PubMed] [Google Scholar]
- 22. Fujimoto S, Asano T, Sakai M, Sakurai K, Takagi D, Yoshimoto N, Itoh T. Mechanisms of hydrogen peroxide-induced relaxation in rabbit mesenteric small artery. Eur J Pharmacol 412: 291–300, 2001 [DOI] [PubMed] [Google Scholar]
- 23. Garvin J, Ortiz P. The role of reactive oxygen species in the regulation of tubular function. Acta Physiol Scand 179: 225–232, 2003 [DOI] [PubMed] [Google Scholar]
- 24. Grover AK, Samson SE, Misquitta CM. Sarco(endo)plasmic reticulum Ca2+ pump isoform SERCA3 is more resistant than SERCA2b to peroxide. Am J Physiol Cell Physiol 273: C420–C425, 1997 [DOI] [PubMed] [Google Scholar]
- 25. Hebert SC, Andreoli TE. Control of NaCl transport in the thick ascending limb. Am J Physiol Renal Fluid Electrolyte Physiol 246: F745–F756, 1984 [DOI] [PubMed] [Google Scholar]
- 26. Hool LC. Evidence for the regulation of L-type Ca2+ channels in the heart by reactive oxygen species: mechanism for mediating pathology. Clin Exp Pharmacol Physiol 35: 229–234, 2008 [DOI] [PubMed] [Google Scholar]
- 27. Horowitz A, Menice CB, Laporte R, Morgan KG. Mechanisms of smooth muscle contraction. Physiol Rev 76: 967–1003, 1996 [DOI] [PubMed] [Google Scholar]
- 28. Hu Q, Corda S, Zweier JL, Capogrossi MC, Ziegelstein RC. Hydrogen peroxide induces intracellular calcium oscillations in human aortic endothelial cells. Circulation 97: 268–275, 1998 [DOI] [PubMed] [Google Scholar]
- 29. Inesi G, Zhang Z, Lewis D. Cooperative setting for long-range linkage of Ca2+ binding and ATP synthesis in the Ca2+ ATPase. Biophys J 83: 2327–2332, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Juhaszova M, Ambesi A, Lindenmayer GE, Bloch RJ, Blaustein MP. Na+-Ca2+ exchanger in arteries: identification by immunoblotting and immunofluorescence microscopy. Am J Physiol Cell Physiol 266: C234–C242, 1994 [DOI] [PubMed] [Google Scholar]
- 31. Kai T, Yoshimura H, Jones KA, Warner DO. Relationship between force and regulatory myosin light chain phosphorylation in airway smooth muscle. Am J Physiol Lung Cell Mol Physiol 279: L52–L58, 2000 [DOI] [PubMed] [Google Scholar]
- 32. Kissner R, Nauser T, Bugnon P, Lye PG, Koppenol WH. Formation and properties of peroxynitrite as studied by laser flash photolysis, high-pressure stopped-flow technique, and pulse radiolysis. Chem Res Toxicol 10: 1285–1292, 1997 [DOI] [PubMed] [Google Scholar]
- 33. Kourie JI. Interaction of reactive oxygen species with ion transport mechanisms. Am J Physiol Cell Physiol 275: C1–C24, 1998 [DOI] [PubMed] [Google Scholar]
- 34. Lee MR, Li L, Kitazawa T. Cyclic GMP causes Ca2+ desensitization in vascular smooth muscle by activating the myosin light chain phosphatase. J Biol Chem 272: 5063–5068, 1997 [DOI] [PubMed] [Google Scholar]
- 35. Lyle AN, Griendling KK. Modulation of vascular smooth muscle signaling by reactive oxygen species. Physiology 21: 269–280, 2006 [DOI] [PubMed] [Google Scholar]
- 36. Macarthur H, Westfall TC, Riley DP, Misko TP, Salvemini D. Inactivation of catecholamines by superoxide gives new insights on the pathogenesis of septic shock. Proc Natl Acad Sci USA 97: 9753–9758, 2000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Makino A, Skelton MM, Zou AP, Cowley AW., Jr Increased renal medullary H2O2 leads to hypertension. Hypertension 42: 25–30, 2003 [DOI] [PubMed] [Google Scholar]
- 38. Makinose M, Hasselbach W. ATP synthesis by the reverse of the sarcoplasmic calcium pump. FEBS Lett 12: 271–272, 1971 [DOI] [PubMed] [Google Scholar]
- 39. Moore EDW, Etter EF, Philipson KD, Carrington W, Fogarty KE, Lifshitz LM, Fay FS. Coupling of the Na+/Ca2+exchanger, Na+/K+ pump and sarcoplasmic reticulum in smooth muscle. Nature 365: 657–660, 1993 [DOI] [PubMed] [Google Scholar]
- 40. Mueller S, Riedel HD, Stremmel W. Determination of catalase activity at physiological hydrogen peroxide concentrations. Anal Biochem 245: 55–60, 1997 [DOI] [PubMed] [Google Scholar]
- 41. Nakanishi K, Mattson DL, Cowley AW., Jr Role of renal medullary blood flow in the development of l-NAME hypertension in rats. Am J Physiol Regul Integr Comp Physiol 268: R317–R323, 1995 [DOI] [PubMed] [Google Scholar]
- 42. Onoue H, Katusic ZS. The effect of 1H-[1,2,4]oxadiazolo[4,3-a]quinoxalin-1-one (ODQ) and charybdotoxin (CTX) on relaxations of isolated cerebral arteries to nitric oxide. Brain Res 785: 107–113, 1998 [DOI] [PubMed] [Google Scholar]
- 43. Pallone TL, Turner MR, Edwards A, Jamison RL. Countercurrent exchange in the renal medulla. Am J Physiol Regul Integr Comp Physiol 284: R1153–R1175, 2003 [DOI] [PubMed] [Google Scholar]
- 44. Raeymaekers L, Hofmann F, Casteels R. Cyclic GMP-dependent protein kinase phosphorylates phospholamban in isolated sarcoplasmic reticulum from cardiac and smooth muscle. Biochem J 252: 269–273, 1998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Shannon TR, Wang F, Puglisi J, Weber C, Bers DM. A mathematical treatment of integrated Ca dynamics within the ventricular myocyte. Biophys J 87: 3351–3371, 2004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Sieck GC, Han YS, Prakash YS, Jones KA. Cross-bridge cycling kinetics, actomyosin ATPase activity and myosin heavy chain isoforms in skeletal and smooth respiratory muscles. Comp Biochem Physiol Part B 119: 435–450, 1998 [DOI] [PubMed] [Google Scholar]
- 47. Stone JR. An assessment of proposed mechanisms for sensing hydrogen peroxide in mammalian systems. Arch Biochem Biophys 422: 119–124, 2004 [DOI] [PubMed] [Google Scholar]
- 48. Suzuki YJ, Ford GD. Inhibition of Ca2+-ATPase of vascular smooth muscle sarcoplasmic reticulum by reactive oxygen intermediates. Am J Physiol Heart Circ Physiol 261: H568–H574, 1991 [DOI] [PubMed] [Google Scholar]
- 49. Tabet F, Savoia C, Schiffrin EL, Touyz RM. Differential calcium regulation by hydrogen peroxide and superoxide in vascular smooth muscle cells from spontaneously hypertensive rats. J Cardiovasc Pharmacol 44: 200–208, 2004 [DOI] [PubMed] [Google Scholar]
- 50. Takenaka H, Adler P, Katz A. Calcium fluxes across the membrane of sarcoplasmic reticulum vesicles. J Biol Chem 257: 12649–12656, 1982 [PubMed] [Google Scholar]
- 51. Taylor NE, Cowley AW., Jr Effect of renal medullary H2O2 on salt-induced hypertension and renal injury. Am J Physiol Regul Integr Comp Physiol 289: R1573–R1579, 2005 [DOI] [PubMed] [Google Scholar]
- 52. Verboomen H, Wuytack F, De Smedt H, Himpens B, Casteels R. Functional difference between SERCA2a and SERCA2b Ca2+ pumps and their modulation by phospholamban. Biochem J 286: 591–596, 1992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Yang J, Clark JW, Bryan RM, Robertson CS. Mathematical modeling of the nitric oxide/cGMP pathway in the vascular smooth muscle cell. Am J Physiol Heart Circ Physiol 289: H886–H897, 2005 [DOI] [PubMed] [Google Scholar]
- 54. Yang J, Clark JW, Jr, Bryan RM, Robertson C. The myogenic response in isolated rat cerebrovascular arteries: smooth muscle cell model. Med Eng Phys 25: 691–709, 2003 [DOI] [PubMed] [Google Scholar]
- 55. Yang ZW, Zheng T, Zhang A, Altura BT, Burton MA. Mechanisms of hydrogen peroxide-induced contraction of rat aorta. Eur J Pharmacol 344: 169–181, 1998 [DOI] [PubMed] [Google Scholar]
- 56. Yoshida Y, Su HT, Cai JQ, Imai S. Cyclic GMP-dependent protein kinase stimulates the plasma membrane Ca2+ pump ATPase of vascular smooth muscle via phosphorylation of a 240-kDa protein. J Biol Chem 266: 19819–19825, 1991 [PubMed] [Google Scholar]
- 57. Zhang W, Pibulsonggram T, Edwards A. Determinants of basal nitric oxide concentration in the renal medullary microcirculation. Am J Physiol Renal Physiol 287: F1189–F1203, 2004 [DOI] [PubMed] [Google Scholar]
- 58. Zhang Z, Pallone TL. Response of descending vasa recta to luminal pressure. Am J Physiol Renal Physiol 287: F535–F542, 2004 [DOI] [PubMed] [Google Scholar]
- 59. Zhang Z, Rhinehart K, Kwon W, Weinman E, Pallone TL. ANG II signaling in vasa recta pericytes by PKC and reactive oxygen species. Am J Physiol Heart Circ Physiol 287: H773–H781, 2004 [DOI] [PubMed] [Google Scholar]
- 60. Zhang Z, Rhinehart K, Solis G, Pittner J, Lee-Kwon W, Welch WJ, Wilcox CS, Pallone TL. Chronic ANG II infusion increases NO generation by rat descending vasa recta. Am J Physiol Heart Circ Physiol 288: H29–H36, 2005 [DOI] [PubMed] [Google Scholar]
- 61. Zou AP, Nithipatikom K, Li PL, Cowley AW., Jr Role of renal medullary adenosine in the control of blood flow and sodium excretion. Am J Physiol Regul Integr Comp Physiol 276: R790–R798, 1999 [DOI] [PubMed] [Google Scholar]