Multivariate Statistical Model for 3D Image Segmentation with Application to Medical Images

Abstract

In this article we describe a statistical model that was developed to segment brain magnetic resonance images. The statistical segmentation algorithm was applied after a pre-processing stage involving the use of a 3D anisotropic filter along with histogram equalization techniques. The segmentation algorithm makes use of prior knowledge and a probability-based multivariate model designed to semi-automate the process of segmentation. The algorithm was applied to images obtained from the Center for Morphometric Analysis at Massachusetts General Hospital as part of the Internet Brain Segmentation Repository (IBSR). The developed algorithm showed improved accuracy over the k-means, adaptive Maximum Apriori Probability (MAP), biased MAP, and other algorithms. Experimental results showing the segmentation and the results of comparisons with other algorithms are provided. Results are based on an overlap criterion against expertly segmented images from the IBSR. The algorithm produced average results of approximately 80% overlap with the expertly segmented images (compared with 85% for manual segmentation and 55% for other algorithms).

Magnetic resonance imaging (MRI) has become one of the most important non-invasive diagnostic tools introduced in the field of medicine in recent years. At present, most interpretation of MR images is accomplished from a large number of images representing “slices” through the object, which must be studied in order to formulate a diagnosis. This may suffice for the detection of abnormalities, but it does not serve other tasks such as surgical or radiation therapy planning.^1,2 These tasks require mental visualization of the areas of abnormalities, which has been shown to be difficult, and dependent on the observer’s experience and imagination. It is desirable to have a more realistic view of the images acquired in the scans, and thus three-dimensional (3D) visualization is wanted. The 3D surfaces of the anatomy help the physician understand the complex nature of the features presented in the 2D slices.³ The use of 3D medical images has been reported in a number of areas, including the visualization of fractures,⁴ craniofacial abnormalities,^5,6 intercranial structures,⁷ and the arterial circulation.^8,9 They are also used in radiation therapy^10,11 and surgical planning.^1,2,12

To fully realize the usefulness of 3D visualization, it is desirable to segment the 2D slices prior to 3D reconstruction. Prior segmentation can be done at a purely 2D level, in which each image is considered independent of adjoining images. The major drawback of such approaches is that, in considering each image independently, they ignore the spatial relationship of the image as a part of a 3D object. Conversely, 3D segmentation after the creation of the 3D volume incorporates the spatial relationship of the 2D slices, but it can be contaminated by data introduced in the interpolation of the 3D volume. Thus a sort of hybrid approach is necessary to benefit from both areas.

In the hybrid approach, although 2D segmentation is done, the spatial relationship of the slices is used as a part of the model. This additional information leads to more accurate segmentations as all information is now being considered rather than just a subset. One of the drawbacks of these approaches is the increased number of variables and thus the computational complexity of the model. Such a system should also be able to handle sequences in which the interslice and interpixel distances are not necessarily equal.

RELATED REPORTS

Segmentation of MRI images can be achieved in different ways,¹³ one of the most popular of which is identifying the tissue based on its multi-spectral values (T1, T2, PD). One example is provided by neural networks trained on the tissue-specific multispectral values. Ozkan et al¹⁴ present preliminary results of a computer system for automatic multispectral MRI analysis. Amarkur et al¹⁵ present another neural net approach to solving the problem, based on the Hopfield network. MARA (Multi-layer Adaptive Resonance Architecture),¹⁶ which uses a stable and plastic self-organizing neural network, is capable of recognizing, reconstructing, and segmenting the traces of previously learned binary patterns. The recognition and reconstruction properties of the network are invariant with respect to distortion, noise, translation, scaling, and partial rotation of the original training patterns. Katz et al¹⁷ have reported segmentation of the aorta from MRI with a translation invariant method (i.e., the method is invariant to the orientation of the images), where they used a backpropagation neural network. Chen et al¹⁸ have proposed a general purpose medical image segmentation technique that uses constraint satisfaction neural networks (CSNN), Li et al¹⁹ used a Boolean Neural Network (BNN) to both segment and label MR brain images.

In 1989, Beaulieu and Goldberg²⁰ used a hierarchical stepwise approach to segmentation to produce an image that is segmented and arranged such that the largest (and supposedly most important) sections of the image were placed at the top of the structure and the smaller ones at the bottom. The disadvantage of using this method with the MR images is that in medical images, there is no guarantee that the anomalies of interest will be of a certain size, either large or small. Perez and Gonzalez²¹ used an adaptive threshold algorithm for segmentation that was based on the reflectance of the image. Later, Gutfinger and Sklansky²² introduced the idea of mixed adaptation for classification of tissues in MR images. This technique combines unsupervised clustering with supervised classification and uses the tissue parameters to classify different tissue types. The individual processes of clustering and classification are based on standard pattern-recognition techniques. The drawbacks of this method are the need for user interaction in the clustering stage, and the fact that the algorithm was not developed directly for MR images. The advantages are the ability to integrate other imaging modalities for a more robust classification. In another pattern-recognition approach²³, three MR images are acquired for a region of interest using spin-echo pulse sequence in a manner that allows the calculation of MR-related physical parameters from the image intensity data. After preprocessing, the three MR-related parameters are calculated for each location. Then, in a supervised training environment, this calculated data set is used with the acquired image data set in a minimum-distance classifier to assign a class-specific color or gray level to each location in the image.

Unser and Murray²⁴ used a feature-extraction method for segmentation of the image based on the different textures of the various parts of the image. This approach requires that there be some textural difference between the regions of the image, and in medical images there may not always be appropriate texture separation. Saeed et al²⁵ used a combination of knowledge-base and texture definition of the intensity to segment the brain from the surrounding tissue. A thresholding and contour extraction process was used to isolate the brain. The result was then passed through a knowledge algorithm that incorporated information such as approximate brain position and size, along with a generic shape definition of the brain. This work deals only with isolating the contour of the brain as a whole rather than the regions within the brain. Thus it allows for the reconstruction of the brain but does not handle the internal features. In addition it is not a 3D system. In another study, Poon and Braun²⁶ present a contour model that incorporates region analysis for segmentation. Their deformable model uses an iterative method to minimize an energy function for N contours corresponding to N + 1 regions.

As can be seen from the cross-section of work presented above, numerous methods have been proposed for dealing with segmentation and classification of images. These methods do not all guarantee the classification with the least possible number of errors, which is an important issue in diagnosis. One reason for this difficulty in classification is the complex nature of the images. What we present in this article is an algorithm that guarantees the minimization of possible errors and so provides the most accurate classification based on the quality of the input signal, which is the real added value of this research.

GENERAL MODEL DESCRIPTION

The proposed solution to minimize possible errors uses the 3D relative distribution of the pixel-intensities to form a probabilistic model, which is built using the properties of the co-occurrence matrices in all directions of neighborhood for each pixel. This allows the construction of probabilities for the occurrence of a particular configuration of neighborhoods for each class of slice orientation. A general block diagram showing how the segmentation fits into a system is shown in Figure 1.

Figure 1.

A general block diagram showing how the developed segmentation (shaded) fits into an overall system.

Before segmentation, it is necessary to remove any artifacts produced from noise. The filter must be able to take into account the inherent 3D nature of the images and it must operate in a way that enhances discontinuities while smoothing similarities, thus sharpening the borders and reducing the noise within the various regions. (A 3D anisotropic diffusion filter is the best choice).²⁷

A 3D statistical model was developed to analyze the images, to extract region-based statistics, and to act as the basis for the segmentation model. This also makes use of the 3D nature of the images. It takes into account the fact that in MR studies, the adjoining images should be included in the determination of regional classification of pixels. The algorithm, though, makes allowances for the situation in which the interslice distance is vastly greater than the interpixel distance. The model does not specifically address a particular anatomy, but is general enough to be used in other applications and thus can be used for other types of 3D image sets.

In MR images, a large region of low-valued pixels corresponding to the background region within the image gives the histogram a bi-modal structure. This region is removed during the segmentation in order to enhance performance. Although the model can handle inclusion of the background, the saving in performance (gained from not having to test each background voxel against every segment), is significant because at least half of the voxels do not have to undergo the full test.

At the same time, the regions of useful data within the image (the data representing the tissues) is confined to a relatively small range of intensities and so, if segmentation is attempted on this small range, the results will be affected by the small separation and the possible overlap of regions. Small separation results in higher probability of misclassification (classification errors) of pixels and the possible inclusion of small regions into larger ones, which can be corrected by stretching the range of useful data that enhance region separation and prevent small regions from being lost. The stretching process is done globally on the sequence to avoid affecting the relative statistics of the regions. The next step is the selection of the statistical analysis space (SAS) for use within the segmentation model. Various SASs have been used, the image itself,^22,15 gray-level histograms,^21,28,29 co-occurrence maps,^30,31 and multi- spectral images.^14,32

Because both region and boundary information are required for proper segmentation, a method that combines these two features is desirable. Separate processing of regions and boundaries using different models is possible, but then it leaves the task of combining the results of the models in a meaningful manner. Thus a SAS providing both region and boundary information in the same analysis space for the model is ideal. With this in mind, the co-occurrence matrices are chosen as the SAS, and a probabilistic model is selected as the segmentation methodology.

MULTIVARIATE STATISTICAL MODEL

The statistical model is called the “Multivariate Minimum Total Probability of Misclassification Model,” and for short we refer to it as the MMTPM model. The classification of images is carried out through the use of a statistical model, based on the knowledge of neighborhood orientations determined from the co-occurrence matrices. This model is used to classify the current pixel as a function of its neighbors. The classification uses a multivariate probability structure to determine the best classification for the current pixel, which then gets assigned to that pixel. Removal of the background is done with a thresholding algorithm because the histogram displays bi-modal tendency, and thresholding is required to remove the relatively large region formed by the background (otherwise it will disrupt the probabilities).

Statistical Analysis Space

Consider a sequence of images for an MRI acquisition series of n images. Images are numbered in consecutive order, 1, 2, 3, ..., i−1, i, i+l,...n. Let I_i, represent the ith image of the sequence, and I_i(x,y) be the pixel at location (x,y) of the ith image of the sequence, then the 8-neighbors of pixel (x,y) are given by the set

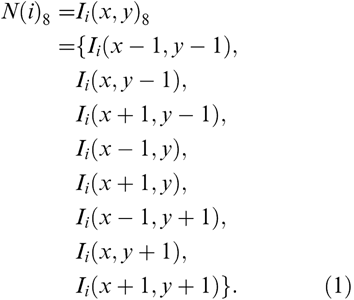For the images on either side of this image, i.e., I_i−1 and I_i+1, the 8-neighbors of the corresponding pixels, I_i−1(x,y) and I_i+1(x,y), are given by N(i−1)₈ and N(i+1)₈. Thus the adjacent 8-neighbors are given by

and the total 3D 8-neighbors are given by

This results in a total of 26 adjacent pixels.

Let any pixel (x,y) be represented by p, and a pixel that is a Δ-neighbor of p be denoted as p + Δ and the gray-level intensity of a pixel p for image i is given by g_i(p), where G ≥ g ≥ 0. Then the gray level histogram for the entire image set is given by

where δ (g ; g_i(p)) is the Kronecker delta function. The gray-level histogram for a single image is obtained by restricting the summation to a single image. The gray-level co-occurrence matrix is defined as the frequency of occurrence of two pixels with certain intensity levels. This measures how often a pixel of intensity g lies next to a pixel of intensity h. And for the entire image set for a particular n-pair the co-occurrence matrix is defined as³¹

Thus for the δ-pairs for the set N(i)_3D there are 26 matrices defining the frequency of occurrence of two pixels of given intensity, one for each direction. The co-occurrence matrices can be shown to be composed of on-diagonal and off-diagonal elliptically shaped peaks (see reference 31 for a full proof). The on-diagonal peaks are directly related to the different regions within the image, while the off-diagonal peaks are related to the length of the boundaries. The on-diagonal peaks, are centered along the diagonal of the co-occurrence matrix with major and minor axes parallel and perpendicular to the diagonal, respectively. The axis perpendicular to the diagonal is related to the noise present in the image and can be estimated by the variance of the background noise. The axis parallel to the diagonal is related to the variance of the region itself. Thus the variance of the region may be determined from the length of the axis parallel to the diagonal. Thus an analysis of the histogram formed from the diagonal provides the statistical information needed for the regions of the image. These matrices make up the definition of the analysis space used by the statistical algorithm. Assuming that the directions of co-occurrence are the variables, a multivariate distribution is needed to determine the best classification. This is accomplished by determining the estimated minimum total probability of misclassification (TPM) for each pixel, which in turn is based on the minimum Expected Cost of classification Methodology (ECM) that attempts to separate values into different populations based on a statistical and probabilistic analysis of the populations.³³ A misclassification is defined by placing a pixel in the wrong population, and a good classification procedure should attempt to minimize the probability of misclassifications. In addition, an optimal classification rule should take into account not only the statistics of the populations but also the prior probabilities of occurrence.

Multi-Population Analysis

Let the population densities be f_i(x) for populations π_i for i = 1, 2, 3, ..., g. Also let the prior probability of population π_i be p_i, and the cost of allocating to π_k when it belongs to π_i be c(k|i) for k,i = 1, ..., g. Then for i = k, c(k|i) = 0. Let R_k be the region k. The probability of classifying a value as π_k when it belongs to π_i is

Then the expected cost of misclassifying a value x belonging to π₁ as belonging to π₂ or π₃,B,π_g is

The values for ECM(2),...,ECM(g) can be obtained in a similar manner.

The total cost ECM is derived by multiplying each ECM by the prior probability of that population; thus;

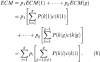Thus an optimal allocation of values occurs when the total ECM is minimized. This occurs when

is minimum.

Now if the cost of misclassification is equal for all regions (equate to 1 for simplicity), then the ECM is simply the TPM, and the assignment is to the population π_k, for which

is minimum. This occurs when the term p_k f_k (x) is maximum. Thus the assignment simply becomes this: Assign value x₀ to R_k for which p_k f_k (x₀) is greatest.

Now, using this assignment and assuming that the populations are normal such that

P_if_i(x) becomes

Taking the log of this will not affect the order of the values, thus:

Because the term with pi is constant, it can be eliminated without affecting the order; thus the assignment simply becomes this:

Assign value x₀ to R_k if:

is greatest.

Once again the values of µ_i and Σ_i may be estimated from the sample means and sample covariances, thus:

and the discriminant becomes

This measure includes the squared statistical distance of the value from the mean, the prior probability, and the determinant of the covariance.³³ The value x₀ represents the intensity of the pixel under consideration.

SEGMENTATION USING THE MMTPM

The general definition of a segment in an image I is a region having homogeneous properties defined by a homogeneity predicate Q, which depends on the context of the problem. The definition of the segmentation problem then follows to be dividing the image I into a set of n regions R_i, where

the homogeneity predicate Q(.) defines the conformity of all points in the region R_i to the region model. The homogeneity predicate and partitioning of the image have the properties that any region satisfies the predicate, and the union of any two regions fails the predicate

The MMTPM algorithm selects the best segment for a voxel based on neighborhood of that voxel. All the components considered by the MMTPM are intensity means, their variances, and prior probabilities. The neighborhood used in taking the decision of classification of that voxel can be defined by a set of vectors, which if added to the coordinates of the central voxel will result in the coordinates of the voxels used in the classification

where Φ is the region around voxel x_i, y_i, z_i that is being used for taking the decision. A constraint that is imposed during the decision is weighing that decision by the distance of every neighbor from the voxel under consideration. This is obvious, because deciding on a voxel class using another far voxel is less likely to be true than that made using a nearby neighboring voxel. The Euclidean distance is considered through the following:

For every voxel v a decision function must be evaluated:

where C is the class being tested and p is the prior probability of that class C. After evaluating equation (24) for every possible class, the voxel is assigned to the class resulting in the largest Total Distance Function (TDF).

Autonomous Operation: Segments Detection Using the Zero Crossing of the Co-occurrence Diagonal

The algorithms that are stated here have been developed by us and tested on the MMTPM algorithm. The co-occurrence matrices count the frequency of repetitions of gray level intensities for a predefined neighborhood. Within a segment S, it is more likely to find voxels of equal intensities than across the borders of two segments. Consequently, for peaks along the diagonal of the co-occurrence matrix, it is highly possible to find a segment whose mean intensity is very near those peaks. Because the co-occurrence matrix does not show the spatial relationship between the pairs of voxels contributing to a certain entry CM(i, j), we cannot say for sure if that peak belongs to a segment. By considering more than one co-occurrence matrix each for each different neighborhood, the decision made about the means of those segments becomes more accurate. To combine the co-occurrences, they are multiplied so that ultimately we will have the regions that all the co-occurrences showed may be segments. Because we are interested in the cases where both voxels are equal, then the co-occurrence diagonal is the only component of the co-occurrence matrix to be considered. Assume the following:

1. xa, ya, za Additives to the x, y, z coordinates that define the neighborhood for which the co-occurrence will be calculated

2. CM_xa,ya,za The co-occurrence matrix for the neighborhood xa, ya, za

3. CMS_xa,ya,za The smoothed co-occurrence matrix for the neighborhood xa, ya, za

4. I_Max Maximum gray-level intensity

The sequence is as follows:

1. Smooth the co-occurrence matrix using an averaging filter repeatedly. The number of times used in the experiments was I_Max/10.

   

   
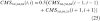
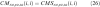
2. Multiply the smoothed co-occurrences together; the result should look like Figure 2.

   
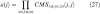
3. Approximate the derivative to be

   

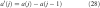
4. For each zero crossing at intensity v, set the mean of the current segment MS = v.

5. Train the algorithm using the voxels equal to the means as an initial portion of the segments.

6. Take the ratio of those voxels as an initial estimate of the prior probabilities.

Figure 2.

Values of alpha obtained from the sequence 1_24 (log scale).

Iteration after Parameter Initialization

The classical Iterated Conditional Modes (ICM) algorithm searches for the peak over a surface of a 2D function in two parameters through successively maximizing/minimizing each of the variables.

1. Start by any two arbitrary modes θⁱ₁θⁱ₂.

2. Find θⁱ⁺¹₁ by solving

   
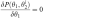
3. Find θⁱ⁺¹₂ by solving

   

4. Repeat until no better solution is found

The algorithm is a local minimization algorithm that will converge to the peak nearest the initialization point. In our case, the two sets of variables through which we will iterate are the set of classifier parameters □ and the sets of voxels defining the segments S_i, i = 1 ... K.

The ICM algorithm has been widely used for parameter estimation. Given the classifier parameters □, the voxels having the highest likelihoods in each segment S₁, S₂, ..., S_k are identified. The second step is updating the classifier parameters □ such that the likelihoods of those sets of voxels are maximized. During each of the iterations, the function describing the system is conditioned by the mode of one of the sets of variables. Because it is a local maximization/minimization algorithm, the ICM must iterate in a system initialized near the global minimum so that it converges correctly. Because the co-occurrence matrices provide an interpretation of the image, showing where the centers of the segments reside, the initialization has been carried out near the global maximum/minimum.

When the ICM algorithm is applied in a pure manner, the system will get stuck in local minima. To avoid this, and by further experimentation, we found that slow update of parameters toward the peak direction leads to convergence, as demonstrated by the results in Table 1. We also found that as we approached the peak, smaller update steps were feasible, and led to tuning the convergence. As a result, an update metric was used, which is inversely proportional to the difference in overlap between the last two iterations.

Table 1.

Experimental results showing overlap ratio with “ground truth” segmentations

Overlap with Ground Truth Images
Sequence Number	White Matter	Gray Matter
1_24	0.813946	0.849438
100_23	0.854365	0.893464
11_3	0.830839	0.869399
110_3	0.803721	0.848077
111_2	0.842378	0.870864
112_2	0.832793	0.882588
12_3	0.825778	0.853163
191_3	0.844526	0.883364
13_3	0.857874	0.892634
202_3	0.822301	0.854037
205_3	0.745637	0.725109
7_8	0.761533	0.78255
8_4	0.811621	0.842932
17_3	0.666087	0.567334
4_8	0.695134	0.701771
15_3	0.73838	0.763548
5_8	0.71868	0.715469
16_3	0.753587	0.798595
2_4	0.653763	0.546622
6_10	0.745025	0.732425
Average	0.780898	0.793669

The parameter update took the following form:

where a^[+] is the updated parameter value, a is the old parameter value, a* is the value found when using the ICM algorithm, and β is the update ratio. The update ratio was estimated using

where O is the overlap between the last two iterations and, initialized by O, a and b are constants that were set to 0.4 and 0.5 during the experiments. The overlap O is defined as the number of common voxels in all segments divided by the total number of voxels.

In Figure 3, the prior probability of each segment is demonstrated across iterations for sequence 1_24. It is very clear that in both cases the system settles on two main segments and a set of small ones. The difference between the two cases is that when successive peak suppression is used, many segments that sometimes number 50 are detected. As demonstrated in Figure 4, and for sequence 1_24, 26 segments were detected, from which two were the main ones at the very end.

Figure 3.

Prior probability variation across iterations using “zero-crossing” detection.

Figure 4.

Overlap coefficient versus iterations for different sequences.

The iterations stop once no better segments are found, or after the maximum number of iterations. In our experiments, 20 iterations were sufficient for the overlap value to exceed 99%.

Experimental Steps

1. Initialize the MMTPM for zero crossing segment detection

2. While the number of iterations < MaxIterations

   1. segment the image
   2. update the parameters from the segmented image

3. Repeat through step 2

4. Label after segmentation

After the correct segments have been estimated, the tissue in each segment should be labeled. Labeling was carried out by finding the nearest neighbor to the central intensity of the segment. The centers of each of the white and gray segments were estimated using image 1_24, and after the segmentation was completed, the central intensity of each segment was found by calculating the mean of all voxel intensities inside that segment.

Experimental Steps

1. Find the mean intensity of each segment

2. For each known tissue class, calculate the distance ||Segment Intensity-Tissue intensity| known from a training set.

3. Label the segment with the nearest tissue

EXPERIMENTAL RESULTS

Experiments were carried out using 20 normal MR brain data sets and their manual segmentations provided by the Center for Morphometric Analysis at Massachusetts General Hospital as part of the Internet Brain Segmentation Repository (IBSR). The data sets are available at http://neuro-www.mgh.harvard.edu/cma/ibsr . The IBSR project mission “is to encourage the development and evaluation of segmentation methods by providing raw test and image data, human expert segmentation results, and methods for comparing segmentation results.” The ISBR provides 20 Tl-weighted 3D coronal MR image sequences from normal patients after positional normalization, along with the expert segmentation for each image. The imaging parameters for the sequences used are also found on the IBSR Web site. The expert manual segmentations provide the basis for a “ground-truth” set to be used for comparative study. Comparison is acheived through the use of an overlap measure between the experimental segmentation under consideration and the ground-truth expertly segmented images. The overlap ratio is defined as the ratio of the sum of the voxels with the same label in both the segmented image and the ground-truth image to the total number of voxels with the same label in either image. Because there is no definition for what constitutes a perfect segmentation, cross comparison between two segmentations is conducted using the previously defined overlap metric. The overlap metric is used as a measure of similarity between manually segmented images and those segmented using different algorithms in order to assess the segmentation accuracy.

Prior to segmentation, noise removal is achieved by the use of a non-linear anisotropic filter, which is basically a diffusion filter based on the filter presented in Gerig et al.³⁴ and expanded to handle three dimensions. It allows the smoothing of regions within the images while enhancing the discontinuities present between tissue types. The filter looks at the pixels in the neighborhood of the pixel under consideration and outputs a modification in the value of the current pixel to better fit its neighbors. The process is carried out slowly and slows down as the number of iterations in re-applying the filter increases, to the limit, where the changes in pixel intensities will eventually become negligible. At this point in the process, the noise in the images has been reduced, and they are ready for classification.

Because the final algorithm is used for segmentation, and because intensities are used in labeling, using the gray-level intensities of voxels, those processes are very sensitive to intensity level variations. Intensity variations from different sequences can cause mislabeling of the segments. A global intensity correction was used to maximize the histogram intersection between the sequences under consideration and a single sequence used as a “training set.” To achieve this correction, and to smooth out differences between the number of voxels in each image, we use the normalized histograms. The histograms, being the frequency of repetition of the present intensities, are normalized against the total number of non-background voxels present in the cerebrum in each image.

In addition, the data supplied by the center for Morphometric analysis poses a number of difficulties during brain segmentation, and those cases clearly were carefully chosen by the center. Among those difficulties are the sudden intensity variations that appear in some cases. To determine the correct direction of the solution, investigations of normal, intensity as well as cases with sudden variations in intensity were carried out. A useful test involved calculating the normalized histogram intersection between each of two consecutive slices. The result should be high, for one obvious reason: the number of voxels per tissue that change between slices are few, and usually the percentages of tissue voxels between every two consecutive slices are very near to each other. This means that the distributions of voxel intensities between each two consecutive slices are nearly the same. We applied a correction algorithm that was able to nearly match the mean and variance across slices, thus correcting for any sudden intensity variation.

Before the data were segmented, the images were corrected by the intensity correction mechanism (for both sudden intensity variations in a single image and a global intensity for the sequence), and filtered using a 3D anisotropic filter with kappa = 5 for 10 iterations (the value was chosen from experimental analysis). The images were segmented using the autonomous segmentation, where the MMTPM classifier parameters were initialized from the image to be segmented. Initialization was carried out once using the “zero-crossing” algorithm.

Some sample original and segmented images for sequence 100_23 are shown in Figure 5. The segmented results were then compared with the ground-truth segmentations provided by IBSR. The comparison criteria used were the overlap ratios comparing the results for the gray and white matter brain segments (Table 1). Because sequence 1_24 was used in training (for the intensity correction algorithm), it was not used again in testing, and was not used during the averaging process in the last row of Table 1.

Figure 5.

Sample image segmentations (sequence 100_23).

Table 2 shows the same overlap calculations using various segmentation algorithms provided by IBSR for comparison with the results from the MMTPM algorithm. The overlap ratio is defined as the ratio of the sum of the voxels with the same label in both the segmented image and the ground-truth image to the total number of voxels with the same label in either image.

Table 2.

Comparisons with Results Provided by the Internet Brain segmentation repository (IBSR)

Segmentation Technique	Gray Matter	White Matter
Adaptive MAP	0.564	0.567
Biased MAP	0.558	0.562
Fuzzy c-means	0.473	0.567
Maximum aposteriori probability (MAP)	0.550	0.554
Maximum-likelihood	0.535	0.551
Tree-structure k-means	0.477	0.571
Manual (4 brains averaged over 2 experts)	0.876	0.832
MMTPM	0.794	0.781

MAP: Maximum Aposteriori Probability; MMTPM: Multivariate Minimum Total Probability of Misclassification Model.

As can be seen from Table 2, the MMTPM algorithm attained a 79.4% overlap on the gray matter and a 78.1% overlap on the white matter. This is a much better result than those obtained with other techniques. It is also just short of the 87.6% and 83.2% for gray and white matter, respectively obtained from averaging over two human experts.

CONCLUSIONS

In this article we describe a multivariate multi-population statistical model that built and applied to the problem of 3D segmentation. The test results showed that the whole system was able to attain accuracies higher than standard techniques when applied to a common set of sequences. Analytically, we proved that the current multivariate model will reach the lowest possible probability of misclassification for pixels, and so achieve the highest possible accuracy.

The results were obtained using images and segmentations provided by IBSR for use in comparison of segmentation techniques for MR brain images. The accuracy attained was shown to be better than many standard algorithms, but it still falls short of that attained by trained human experts.

Although the real value is the very high accuracy, there is a cost in terms of performance. Additional research to achieve improved accuracy, performance increases, and information sharing between the statistical system and other systems built in our research labs is ongoing.