Number without a language model

Abstract

Cross-cultural studies suggest that access to a conventional language containing words that can be used for counting is essential to develop representations of large exact numbers. However, cultures that lack a conventional counting system typically differ from cultures that have such systems, not only in language but also in many other ways. As a result, it is difficult to isolate the effects of language on the development of number representations. Here we examine the numerical abilities of individuals who lack conventional language for number (deaf individuals who do not have access to a usable model for language, spoken or signed) but who live in a numerate culture (Nicaragua) and thus have access to other aspects of culture that might foster the development of number. These deaf individuals develop their own gestures, called homesigns, to communicate. We show that homesigners use gestures to communicate about number. However, they do not consistently extend the correct number of fingers when communicating about sets greater than three, nor do they always correctly match the number of items in one set to a target set when that target set is greater than three. Thus, even when integrated into a numerate society, individuals who lack input from a conventional language do not spontaneously develop representations of large exact numerosities.

Does learning language change the way we think about number? The exact quantities to which words like “seven,” “eight,” and “nine” refer seem so basic it is hard to imagine that we might need the word “seven” to have the concept seven. But evidence from groups who have not been exposed to conventional numerical systems suggests that language, particularly the numeral list in a count routine, may be importantly involved in the ability to represent the exact cardinal values of large sets.

The Mundurukú (1) and Pirahã (2) are Amazonian people in rural Brazil whose languages do not contain words for exact numbers larger than five (the Mundurukú) or any exact number words at all (the Pirahã).* Adults in these cultures have not been reported to invent ways to communicate about the large numbers for which they do not have words. In addition, these groups do not display a robust ability to match sets exactly with respect to number, except when a one-to-one correspondence strategy is readily available (e.g., pairing each object in one visible row with a corresponding object in a second visible row) (3). The absence of a linguistic model for representing exact number (in this case, a count list) could explain the difficulties Pirahã and Mundurukú adults have representing large exact numbers (2, 4–6). However, their difficulties could just as easily be explained by the absence of culturally supported contexts in which exact number must be encoded (7, 8). To disentangle these possibilities, we investigated the numerical abilities of individuals who lack a linguistic model for number but who live in the numerate culture of Nicaragua: “homesigners.”

Homesigners are profoundly deaf individuals whose hearing losses prevent them from acquiring the spoken language that surrounds them, and who have not had the opportunity to learn a conventional sign language (10–14). They use homemade gestures to communicate with the hearing individuals around them. However, homesigners living in western cultures participate in worlds that are fully numerate and deal in exact (and not just approximate) large numbers. In other words, homesigners are surrounded by a culture in which exact number is valued, and they have at least partly mastered the monetary system of their culture (as detailed later). If living in a numerate culture is sufficient to foster complete representations of exact number concepts in the absence of input from a conventional language, homesigners might be expected to succeed on communicative and noncommunicative tasks requiring representations of large exact numerical quantities outside of the domain of money, tasks on which the Mundurukú and Pirahã fail.

Participants were four adult homesigners in Nicaragua, ages 20–29 y (three men), who did not know one another. Their hearing losses prevent them from acquiring Spanish and they do not have access to Nicaraguan Sign Language. They use homesign exclusively to communicate with the hearing individuals around them. The four homesigners show no congenital cognitive deficits and performed as well as hearing siblings and friends on tasks testing mental rotation skills (SI Materials and Methods). They hold jobs, make money, and interact socially with hearing friends and family. None had attended school regularly. To separate effects of illiteracy and lack of schooling from lack of a conventional count list, we tested four unschooled, hearing Nicaraguans (ages 16–36 y, all female) who are fluent Spanish speakers. To rule out deafness and communicating in the manual modality as a cause of any deficits we might observe, we tested two fluent deaf users of American Sign Language (ASL): one man, age 69 y, and one woman, age 66 y.

Because homesigners do not share a language with the experimenters, any failures on our tasks might have been a result of our inability to communicate the goal of the task successfully, rather than the homesigners’ lack of conceptual knowledge. To address this concern, the first author, who knows no sign language, tested the deaf ASL signers using the same gestures and techniques she used to convey the task goals to the homesigners.

Results

We first asked whether homesigners were familiar enough with their society's moneyed economy to make correct judgments about monetary values. We designed a series of tasks to assess their recognition of currency (shown, for example, by gesturing a five and two zeroes for a 500-unit bill); their ability to compare the relative value of the currency (shown, for example, by determining whether a 10-unit or a 20-unit bill has more value); and their ability to compare coins and bills of different currency type (shown, for example, by determining whether a set of nine 10-unit coins has more or less value than a 100-unit bill). All four homesigners identified money correctly and could assess its relative value, and three of the four homesigners performed with greater than chance accuracy on all monetary tasks (SI Materials and Methods and Fig. S1 provides more information).

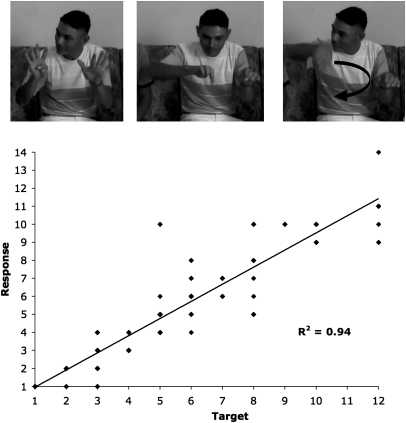
Next, we asked whether homesigners used their gestures to express number in spontaneous communication outside of a monetary context. We presented 10 short animated stories in which number was critical to the plot, asking them to retell the stories to a relative or friend who had not watched the vignette but who was familiar with the storyteller's homesign. All four homesigners extended their fingers to indicate the number of objects in the vignettes (Fig. 1 Upper).

Fig. 1.

Spontaneous communication about number. Upper: A homesigner describing a vignette in which 10 sheep (Left) stand in (Center) a pen (Right). Note that the homesigner incorrectly extended nine fingers to describe the number of sheep. Lower: The number of fingers the homesigners extended (y axis) as a function of the number of objects actually shown in the vignette (x axis). Because not all participants produced an equal number of gestures in the stories, the weighted average correlation coefficient is shown.

We then asked whether these gestures encoded exact cardinal values. As the number of objects grew, so did the average number of fingers the homesigners extended, but the number of fingers was only sometimes exactly correct (Fig. 1 Lower). Homesigners thus used gesture to track the approximate values of sets rather than the exact values, at least in their narratives.

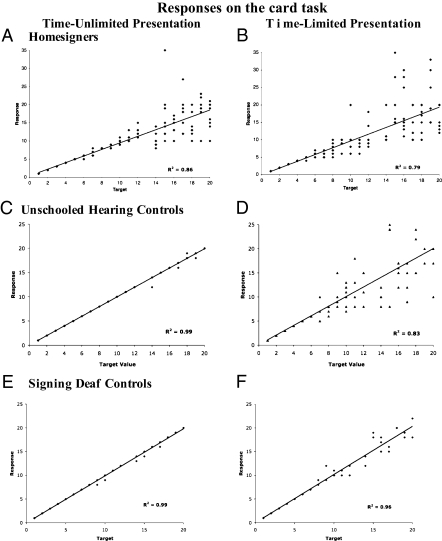
To determine whether homesigners used gesture accurately in tasks designed to elicit exact number, we showed them cards depicting different numbers of items and asked them to report how many items were on each card, without (Fig. 2A) and with (Fig. 2B) time pressure (15, 16). On the time-unlimited version (presented first), if the participants held up the wrong number of fingers on an item, the experimenter indicated that their response was incorrect and repeated the trial, often helping them get to the correct answer by grouping the objects, by covering sets of objects, or by pointing to individual objects. This procedure was used to ensure that the homesigners understood that we wanted the exact number of items, not an approximation. We report the first response to each target item, before the participant received help from the experimenter on that item. On the time-limited version, only approximations were possible.

Fig. 2.

Elicited communication about sets containing different numbers of items. Responses given by the three test groups when asked to describe cards containing different numbers of items under two conditions: (A, C, and E) time-unlimited presentation (which could be solved by counting) and (B, D, and F) time-limited presentation (which had to be solved by estimating). The average correlation coefficient is shown for each condition.

Homesigners were 100% accurate on target sets of one, two, and three for both time-unlimited (Fig. 2A) and time-limited (Fig. 2B) versions of the task.^† However, they performed significantly less well on target sets greater than three on both versions, coming close to the value of the target number but achieving the exactly correct value on fewer than half the trials. They produced exactly correct gestures on only 44% [standard error (SE), 8%] of the time-unlimited trials and 31% (SE, 4%) of the time-limited trials involving sets greater than three. These performance levels on large sets were significantly lower than those on small sets for the time-unlimited and time-limited trials [t(3) = 6.852 (P = 0.006) and t(3) = 16.653 (P = 0.0003), respectively, two-tailed paired-samples t tests]. The homesigners’ performance on large sets (>3) in the time-limited condition was marginally worse than their performance in the time-unlimited condition [31% vs. 44%, two-tailed paired-samples t test, t(3) = 2.093, P = 0.12].^‡

The unschooled hearing control subjects and the signing deaf control subjects also performed perfectly on small target sets for both time-unlimited (Fig. 2 C and E) and time-limited (Fig. 2 D and F) trials. However, unlike the homesigners, they also performed well on sets greater than three on the time-unlimited trials when they had as much time as they wanted and could count. A mixed models logistic regression revealed a main effect of participant type: homesigners were significantly less accurate on sets greater than three than both the unschooled hearing control subjects and the signing deaf control subjects (both P < 0.001); the two control groups did not differ from each other (P = 0.174).

On the time-limited trials, on which everyone was forced to estimate, overall performance across groups dropped on sets greater than three: 31% correct for homesigners, 34% for hearing controls, and 50% for signing deaf controls. A mixed-models logistic regression revealed no significant difference in accuracy between homesigners and the hearing controls (P = 0.586), or between the two control groups (P = 0.159). We did find a significant difference in accuracy between homesigners and the signing deaf controls (P < 0.05); one of the two signers was a particularly good estimator and estimated perfectly on sets as large as 11.

Moreover, although all three groups were more accurate on the time-unlimited task than the time-limited task for sets greater than three, the mixed-models logistic regression showed an interaction between task condition and participant type: homesigners’ improvement was significantly less than the unschooled hearing control subjects’ (P < 0.001) and less than the signing deaf control subjects’ (P = 0.037). The signers’ improvement was also significantly less than the hearing control subjects’ (P = 0.041) because the signers did so well on the time-limited task that there was little room left for improvement when time was unlimited.

The homesigners’ inability to provide exactly correct values might mean that they do not know that each set has a unique exact value, and that finger gestures can represent this value. Alternatively, they might know that each set has an exact value, but lack an effective technique for determining or representing that value, particularly for large sets. That homesigners did better on time-unlimited than time-limited trials for large sets is consistent with the possibility that they understood they were to represent exact number, but just had noisy strategies for doing so.

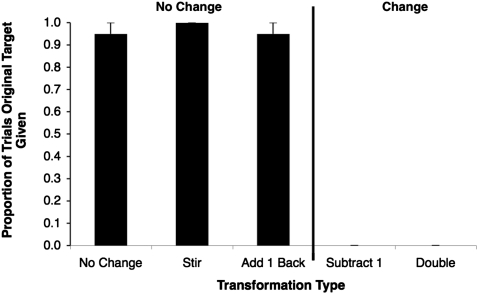
To distinguish these possibilities, the experimenter put a number of objects (n = 3–20) in an opaque box, extended fingers to indicate the number of objects, transformed the array, changing the number of objects or not, and then asked the homesigner to report the number of objects currently in the box (17). All four homesigners performed well on this task (Fig. 3). After transformations that did not change the number of objects, homesigners produced the number gesture they originally saw on 97% (SE, 3.3%) of trials. After transformations that did change number, homesigners never produced the original number gesture [two-tailed paired-samples t test comparing trials that did and did not change number, t(3) = 29.08; P < 0.00008]. They understood that these transformations changed number, and that the gesture used to describe the quantity had to change as well. Furthermore, they adjusted their gestures in the right direction on 92.5% of trials.

Fig. 3.

Elicited communication about sets that do and do not change in number. Graph displays how often homesigners gave back the number gesture they were shown originally after transformations that did change number (two bars on right: removing one object, doubling the number of objects) and transformations that did not change number (three bars on left: adding back the one object that was taken away, leaving the objects alone, stirring the objects). Error bars indicate SE.

Homesigners thus understand that each set has an exact numerical value, and that the gesture representing it must represent a smaller set if items are removed, and a larger set if items are added. However, they do not have an errorless way of arriving at a gestural representation for that new value, at least when dealing with large sets.

However, what if a gesture response is not required? Homesigners might, under these circumstances, not only display an understanding of the concept of exact cardinal value but also demonstrate an ability to arrive at exact numerical values. The next study explores this possibility.

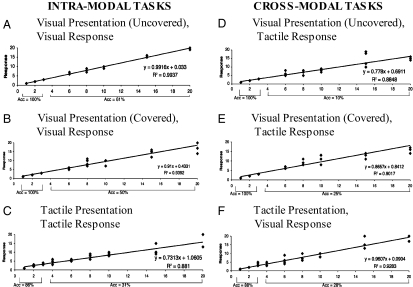
We administered six match-to-sample tasks comparable to tasks used to assess the Pirahã’s grasp of number concepts (2, 3): three intramodal tasks (two visually presented tasks, one tactilely presented) and three cross-modal tasks (requiring a response in a different modality from the target). Homesigners’ performance resembled the performance of the Pirahã: high accuracy (93% ± 3.8%) on small sets of one, two, and three; lower accuracy (33% ± 5.1%) on sets greater than three [two-tailed paired-samples t test, t(3) = 10.958, P = 0.002]. The unschooled hearing control subjects and the signing deaf control subjects also performed well on small sets of one, two, and three (100% accuracy). However, unlike the homesigners, they excelled on sets larger than three (91% and 94%, respectively) in which they could (and did) count. A mixed-models logistic regression revealed a main effect of participant type: homesigners were less accurate on sets greater than three than the hearing and deaf control subjects (both P < 0.001), and the two control groups did not differ (P = 0.474). Importantly, the homesigners’ average responses to each target centered on the target value and thus were approximately, but not exactly, correct (Fig. 4; Figs. S2 and S3 show the control groups’ performance).

Fig. 4.

Number in noncommunicative tasks. The graphs display the homesigners’ responses on the six match-to-sample tasks: intramodal tasks (presentation and response in the same modality; A–C) and cross-modal tasks (presentation and response in different modalities; D–F). The function expressing the best linear fit is shown for each task.

A closer look at the R² values in Fig. 4 indicates that homesigners’ incorrect responses came closer to the correct target value in some conditions than in others. In fact, in Fig. 4A, the visible object matching condition, although they were correct on only 61% of trials for sets larger than, their R² value was 0.994, which means that their incorrect responses were only one or two off from the target, even at the largest target sets. The homesigners could have arrived at the exactly correct value by lining up the response objects next to the target objects. Instead, they used their fingers to establish one-to-one correspondence with the objects in the target set, and then used those fingers to decide how many objects should be in the response set. This strategy ought to help in the condition in which the objects were hidden (Fig. 4B) and, indeed, the homesigners’ R² value on this condition was also quite high, at 0.939 (although not as high as when the objects were visible, presumably because the homesigners could not go back and check their work when the objects were hidden).

Note that making the number of items in a response set exactly equal to the number in a target set is particularly difficult when the items are presented sequentially, as sequential targets do not persist in time or space (Fig. 4 C and F). The unschooled hearing and signing deaf control subjects always counted on these trials. If homesigners are using gesture as a general count routine, we might expect them to resort to fingers on these particularly difficult match-to-sample tasks. Contrary to expectations, however, no homesigner spontaneously used fingers for the sequentially presented tactile items. Using fingers to index objects appears to be a strategy that the homesigners have developed to deal with visible arrays of objects (indeed, this strategy may account for their near-perfect performance through 10 on the time-unlimited condition of the card task; Fig. 2). However, the insight that fingers can be aligned in one-to-one correspondence with visible sets did not bring with it the insight that one-to-one correspondence guarantees numerical equivalence. The homesigners did not deploy the finger strategy when it would have been most useful (matching sequential sets), nor did they use one-to-one correspondence in its simplest form (pairing the items in the response set with the items in the visible target set).

Discussion

We have found that homesigners, who are not exposed to a conventional numerical system but who live in and are adept at navigating an otherwise numerate culture, use gesture to communicate about number. They also appreciate that a set of objects has an exact cardinal value, and that a unique gesture communicates that value. Thus, unlike the Pirahã and Mundurukú, who do not use their fingers to communicate or reason about number, the homesigners’ cultural environment seems to support communication about number (even exact number), recognition of exact numerosity, and quite accurate reasoning within the domain of money.

However, despite the fact that homesigners use their fingers to communicate about number, they do not consistently produce gestures that accurately represent the cardinal values of sets containing more than three items. Moreover, they cannot reliably make the number of items in a second set match the number in a target set if the sets contain more than three items. Under certain circumstances, they can use their fingers to establish one-to-one correspondence and thus achieve greater accuracy than they would have with pure approximation, but they do not make general use of this strategy (in, for example, sequential sets).

Our results raise two important questions regarding (i) what aspects of number representations homesigners lack and (ii) why homesigners have these deficits. Homesigners may lack stable summary symbols for each integer—symbols that stand for the cardinal value of the entire set, not just individuals within a set (fingers are easily, perhaps too easily, mapped onto individuals). They may also lack the principle of the successor function—that each natural number n has a successor that is exactly n + 1. That is, homesigners’ number gestures are not embedded in a count routine. In addition, homesigners may fail to appreciate that one-to-one correspondence guarantees numerical equivalence. That is, homesigners’ number gestures are not used as a tally system. With respect to why, several possibilities remain open. Exposure to a linguistic system that contains a count routine may be essential to develop representations of exact number (4, 6). But other aspects of language could also play a role (e.g., by providing rules for combining expressions recursively; providing evidence that numerals are quantifiers; providing stable symbols to overcome working memory limitations). Moreover, nonlinguistic representational and computational resources (e.g., tally systems, Arabic numerals, abacus) have the potential to lead to flexible, domain-general representations of large exact numbers.

In sum, we have found that adults who do not have conventional language but are otherwise integrated into a numerate social and cultural world have difficulty generating exact values for sets larger than three. A cultural context in which exact number representations are valued, and a social context in which one's communicative partners share a counting routine and an associated system of exact number concepts, are not enough to scaffold the creation of a count routine or representations of exact number that are flexible and generalize across domains.

Materials and Methods

Number Narrative.

The vignettes, piloted with American hearing children to ensure that they elicited talk about number, were organized into two sets of 10 that were identical except for the numbers of objects or actions (Table S1 and SI Materials and Methods).

The experimenter played each vignette to the homesigner once in the presence of a relative or friend (the recipient), who was able to communicate with the homesigner and could not see the computer screen. The experimenter then encouraged the homesigner to relay the vignette events to the recipient. The homesigner could rewatch the vignette at any time. If the homesigner did not mention the number of objects or actions in the story, the experimenter encouraged the recipient to ask about them. All homesigners required this for the first story, and very rarely thereafter; recipients also spontaneously started asking for numerical clarification if it was not provided in the first retelling of the story by the homesigner.

Homesigners were given one set of vignettes at the beginning of testing and the second set near the end of all testing (≥24 h later). The order of presentation was counter-balanced. The current data are from the first set and reflect the numerical gestures used before homesigners’ intensive work on the other numerical tasks.

Card Task.

Time-unlimited condition.

Participants saw four sets of eight cards, each of which depicted between one and 30 items. Each set showed a different kind of object; the card depicting one item in each set was presented first. We limited our analysis to the targets from one to 20 (24 of 32 trials). In the time-unlimited condition, the participant had as much time as he or she required to assess the number of objects. The experimenter presented cards with items of the same type on a page and asked what was on the card by shrugging with a questioning facial expression. Most participants labeled the item (e.g., if the card showed one ball, the homesigners produced their gesture for “ball,” the hearing controls said the Spanish word, and the signers used the ASL sign). For the homesigners and the signers, the experimenter then nodded and gestured “one” (holding up one index finger, the gesture all homesigners used spontaneously for “one” in the vignette task). For the hearing controls, the experimenter nodded and said “una pelota.” Participants often imitated the experimenter's gesture or word. The experimenter then presented the remaining cards in a fixed random order. All participants readily understood the task and responded with numerical gestures or words. If participants’ first responses were incorrect, they often received a second or third chance with help from the experimenter, who pointed to each object or covered some items to break the larger sets into more manageable units. This procedure also ensured that the participants, particularly the homesigners, understood that the experimenter expected an exact enumeration of the objects, not an estimate. The current data represent the homesigners’ first response to each card, and do not include any responses produced after participants received this kind of support on the item.

Time-limited condition.

The experimenter showed the card for 1–2 s, turned it over, and then asked the participant to respond. Participants thus had to estimate the number of objects. If participants asked to see the card again, the experimenter showed it a second time for 1–2 s. All participants readily produced number hand shapes or verbal number responses. All participants received the time-unlimited version first to orient them to the task and to ensure that the time-limited version, which required estimation, did not suggest that estimation was being elicited in the time-unlimited version.

Assessment of Exact Numerosity.

In the assessment of exact numerosity (17), the experimenter placed in a box a number of items ranging from three to 20. Participants saw five transformations for each quantity: two that changed the number of objects in the box (removing one object; doubling the number of objects), and three that did not change the original number (adding back the one object that was taken away; leaving the objects alone; stirring the objects). Transformations were presented in random order, with the exception that subtract-one and add-one-back always occurred in immediate succession. The double transformation was presented too rapidly for exact enumeration, but the experimenter showed the participant that one object was being removed or added in the subtract-one and add-one-back transformations.

Two training trials were given with the starting number of two in the no-change and double transformations. All participants answered correctly. Test trials used three, six, seven, nine, and 20 as the starting numbers, presented in a random order. All transformations were performed on each starting number. Responses reproducing the original number gesture were coded as correct on the no-change, stir, and add-one-back transformations, and as incorrect on the subtract-one and double transformations.

Numerical Matching.

There were six matching tasks. The three intramodal tasks were (i) one visual task with disks that were visible during the entire trial; (ii) one visual task with disks that were covered when participants began building their response set; and (iii) one tactile task in which participants had to match the number of times the experimenter knocked on their fists with their own knocks on her fist. In the three intermodal tasks, participants: (iv) produced knocks in response to visible disks; (v) produced knocks in response to hidden disks; and (vi) gave a set of disks equal to the number of knocks on their fist. The order of presentation of tasks varied across participants, although each received the uncovered visual match task first.

Visual matching (uncovered).

In uncovered visual matching tasks, the experimenter and the participant each had a large number of white poker chips. Participants received two training trials in which the experimenter created target sets of one and then two chips. Leaving the array in view, the experimenter encouraged participants to create an identical array with their disks. Every participant readily understood the task; no training trial was repeated.

Test trials were conducted in the same manner. Target arrays were one, two, three, six, eight, 10, 15, and 20, presented in a fixed, random order. For larger sets (15 and 20), target sets were placed in two rows, usually of seven and eight for 15, and 10 and 10 for 20. Nonnumerical factors were confounded with number: larger sets had longer line length and more total surface area.

Visual matching (covered).

The uncovered visual matching condition was identical to the uncovered visual match condition, except that the experimenter covered her target array as soon as participants began building their own array. Participants were given as much time as they required to assess the quantity of the target array. Targets used the same values as the uncovered visual matches, but were presented in a different random order.

Tactile matching.

In the tactile matching task, the experimenter knocked participants’ fists a number of times and instructed them to do the same to her fist. Because of the added task demands of tracking sequential events, training trials were given as for the uncovered visual matching task. Participants who failed the two-knock training trial received feedback that their response was incorrect and the trial was repeated. All such participants passed the second trial. Target sets were one, two, three, four, six, eight, 10, 15, and sometimes 20, presented in a fixed, random order. Continuous quantities were again confounded with number; the larger the set, the longer the duration of the experimenter's knocking. With two of the more capable participants, we also attempted this task using toe taps instead of fist knocks to free the homesigners’ hands; neither participant used his hands, and neither was more accurate with toe taps than with fist knocks.

Cross-modal conditions.

The three cross-modal conditions were cross-modal visual to tactile match (target left uncovered), cross-modal visual to tactile match (target covered), and cross-modal tactile to visual match. Target sets were the same as in the other tasks, and were presented in novel fixed, random orders.

Coding.

All data were coded by the first author and reliability was coded by a blind coder. In all cases, reliability was very high. For the homesigners, agreement between coders was 99% on the money task (SI Materials and Methods), 96% in the narrative task, 98.5% in both conditions of the card task, 100% in the exact numerosity task, and 97% on the numerical matching task. For the unschooled hearing control subjects, agreement between coders was 100% (money), 98.4% (cards), and 98.9% (numerical matching). For the signing deaf control subjects, agreement between coders was 99.0% (cards) and 100% (numerical matching). Disagreements were easily resolved by rewatching the trial; all cases were notation errors.