Unlocking the time resolved nature of electron microscopy

During the past few years, Zewail (1) and others (2, 3) have reported a remarkable series of advances that unlock the inherent time resolution in EM by introducing a laser-excited photocathode to produce timed pulses of electrons in the microscope in synchronism with a pump laser that interacts with the specimen. These experiments use variable pump-probe delays to measure the temporal evolution of the specimen after the pump excitation. If the electron-probe pulses are short and limited in intensity, then they will each contain essentially one electron, producing a well-defined single-electron wave packet scattering in the specimen. This single-electron picture provides the foundation for interpretation of high-resolution spatial information in lateral x–y directions averaged over the specimen thickness (4). In this experiment, temporal resolution depends on the length of the wave packet in the z direction and its velocity.

Since its invention in the late 1930s, EM has served as a workhorse tool for structural characterization in materials physics. Therefore, it would seem that the technology that makes it possible, and the associated physical science that it reveals, should be well-explored by now. Despite this, it has only been within the last 10 y that control of aberrations has allowed the routine preparation of sub–Angstrom-sized probes for use in EM (5). As a result, we are now experiencing a swift development of new microscopy techniques based on our improved capability to control the lateral properties of kilovolt electron beams, even to the Angstrom level, allowing us to locate, identify, and discover the function of atoms, singly and in small groups, imbedded within bulk materials (6).

A few moments of thought about the longitudinal size of the electron wave packet produces an expectation for the temporal accuracy of scattering in the electron microscope. Electron emission in the EM typically produces electrons having an energy spread of about 1 eV, corresponding to a longitudinal size of about 1 μm. During acceleration to half the speed of light, and propagation to the sample, the electron wavepacket spreads to as much as 100 μm. Therefore, the transit time of the wavepacket through the thin sample is about 500 fs, defining a measurement uncertainty for the timing of a specimen interaction. Thus, EM, equipped as described above with a method for timed creation of single electron wave packets, provides an ideal platform for measuring the temporal evolution of excitations in materials on the picosecond time scales.

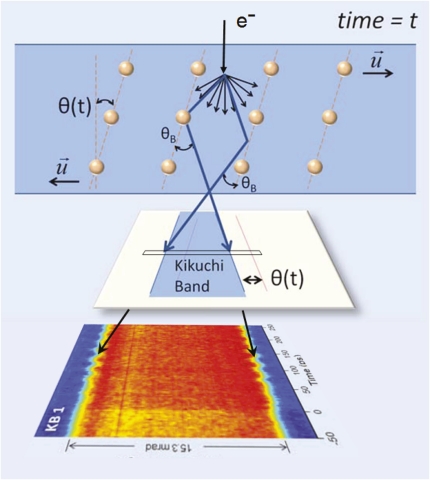
In an experiment reported in PNAS, Yurtsever and Zewail (7) use Kikuchi bands as sensitive measures of the tilt of crystallographic planes in single crystal silicon. As illustrated in Fig. 1 (adapted from their discussion), these bands arise when a primary electron scatters in the specimen, producing a broad scattering distribution around its initial direction. Some of these electron paths satisfy Bragg scattering conditions for particular sets of planes, producing bands of intensity in the far field (8). Kikuchi bands are rigidly tied to the orientation of the planes themselves, whereas diffraction spots have positions defined relative to the unscattered electron beam. Thus, diffraction spot positions are only weakly dependent on crystal tilt, while Kikuchi bands shift strongly in concert with the tilted planes, as depicted in Fig. 1. These bands also appear in electron and ion channeling maps and Annular Dark Field rocking beam maps obtained in the Scanning Transmission Electron Microscope.

Fig. 1.

Scattering diagram for Kikuchi bands. Subsequent to a diffuse scattering event, some scattered electrons satisfy the Bragg condition (θ_B) for a local crystal plane. Multiple Bragg scattering then produces a band of intensity, and its position accurately tracks the local tilt of the crystal plane. Intensity falling within a narrow section of the Kikuchi band can be assembled in a map of intensity as a function of scattering angle vs. time, as depicted here, below an imaginary slit that crosses the Kikuchi band intensity (modified from ref. 7).

In the work, a small amount of heat is injected into an electron transparent specimen using a femtosecond laser pump pulse focused into a micrometer-sized area. At a position that is some microns away, the microscope is set up to produce a convergent beam electron diffraction pattern using a 100-nm-sized electron probe. This convergent beam pattern naturally contains Kikuchi bands and diffraction information, as described above in Fig. 1. The interesting behavior is revealed when the microscope beam current is triggered by the probe photons at some delay time relative to the pumping heat pulse. Using a short pulse with a limited intensity, a single-electron time-resolved convergent beam pattern is then obtained for the delay time (t). Statistical accuracy is built by averaging the scattered intensity for many pump-probe pulses. A time-dependent analysis can be assembled stroboscopically by varying the delay time, as depicted at the bottom in Fig. 1, where scattered intensity in a line across one Kikuchi band in the convergent beam map is displayed as a function of the delay time. In Fig. 1, we have imagined how a physical slit, placed across the Kikuchi band, might allow the Kikuchi scattering to be obtained as a function of time. In the reported experiment, the Kikuchi data were assembled from 2D diffraction datasets subsequent to the experiment.

The results, summarized in the color map in Fig. 1, show a sharp shift of the

Experiments like these promise to illuminate mechanisms of energy transfer through phonon propagation in nanoscale-sized objects.

Kikuchi bands, corresponding to a tilt of the chosen lattice planes, commencing at some time after the pump pulse (designated t = 0 here), and continuing with a damped oscillatory structure for several tens of picoseconds. This technique seems to capture, in a very precise manner, the temporal and structural behavior of a well-defined shear wave, initiated by the remote heat pulse, and which propagates in a particular direction with a measurable group velocity. Using Kikuchi bands generated by lattice planes oriented in other directions, a complete description of the total propagating lattice distortion at the probe position can be obtained. In this particular case, the confinement of the heat pulse within the sample boundaries constrains the mechanical response of the sample to the heat pulse.

Thus, experiments like these promise to illuminate mechanisms of energy transfer through phonon propagation in nanoscale-sized objects. In the above experiment, for instance, Kikuchi information mapped to different specimen positions would describe the 2D flow of thermal energy in a thin nanoscale object. In a nanoparticle, we would expect to find standing waves of motion, confined within lateral boundaries, suggesting ways to maximize practical use of such an object—perhaps for concentrating a diffuse thermal source into particular places for efficient energy harvesting. In the future, tilt tomographic techniques may allow the 3D behavior of the particle to be obtained.

The work also highlights that the electron microscope is a highly versatile experimental platform capable of precise preparation of electron wave packets, placing them on interesting features of a nanoscale object and accurately measuring properties of the resulting scattering. The temporal as well as the spatial domain is accessible, allowing complex specimen excitations to be analyzed in position, phase, and time. This information will prove invaluable in the future design of nanoscale materials for practical use.