Spectrally and spatially configurable superlenses for optoplasmonic nanocircuits

Abstract

Energy transfer between photons and molecules and between neighboring molecules is ubiquitous in living nature, most prominently in photosynthesis. While energy transfer is efficiently utilized by living systems, its adoption to connect individual components in man-made plasmonic nanocircuits has been challenged by low transfer efficiencies that motivate the development of entirely new concepts for energy transfer. We introduce herein optoplasmonic superlenses that combine the capability of optical microcavities to insulate molecule-photon systems from decohering environmental effects with the superior light nanoconcentration properties of nanoantennas. The proposed structures provide significant enhancement of the emitter radiative rate and efficient long-range transfer of emitted photons followed by subsequent refocusing into nanoscale volumes accessible to near- and far-field detection. Optoplasmonic superlenses are versatile building blocks for optoplasmonic nanocircuits and can be used to construct “dark” single-molecule sensors, resonant amplifiers, nanoconcentrators, frequency multiplexers, demultiplexers, energy converters, and dynamical switches.

Nonradiative energy transfer between nanoobjects is limited to distances of only a few nanometers, making photons the most attractive long-distance signal carriers. However, once the photon is emitted by a donor quantum emitter, the probability of acceptor absorbing its energy becomes negligibly small. Therefore, realizing efficient and controllable on-chip interactions between single photons and single quantum emitters, which are crucial for single-molecule optical sensing and quantum information technology, remains challenging. This problem is mitigated by optical microcavities (OMs), which can significantly boost the probability of a photon reabsorption through acceptor molecules (1) via efficient trapping and recirculating of photons (2). OMs also strongly modify radiative rate of emitters at select frequencies corresponding to cavity modes, which can provide local density of optical states (LDOS) exceeding that of the free space by orders of magnitude (2–5). In turn, noble-metal nanostructures can enhance emission of free-space photons by excited molecules (effectively acting as nano-analogs of radio antennas) (6–12) or facilitate relaxation by coupling to surface plasmons (SPs) (13–15). Consequently, both plasmonic nanostructures and OMs can modify the LDOS (16, 17), but the OM approach suffers from limited accessibility of the intracavity volume by target molecules [which should either be incorporated into the cavity material (3, 4) or interact with photonic modes via their weak evanescent tails (5, 18–20)], while high dissipative losses in metals create fundamental limitations for long-distance energy and information transfer through surface plasmons (21).

Results and Discussion

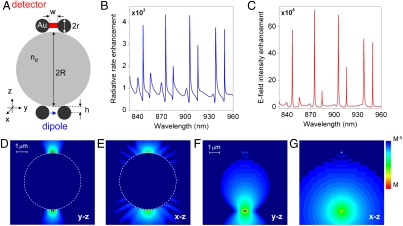
In this paper, we develop a previously undescribed approach for photon generation and energy transfer in optoplasmonic circuits that combines subwavelength confinement of electromagnetic fields near plasmonic nanoantennas with long photon dwelling times provided by high-Q OMs and thus achieves cascaded photon-emitter interactions over long (up to hundreds of microns) length scales. To demonstrate a general physical concept rather than optimized engineering solutions, we consider model structures composed of spherical micro- and nanoparticles and analyze them within the framework of the generalized Mie theory (GMT) (detailed in Methods) (22–24). One possible realization of an optoplasmonic superlens is shown in Fig. 1A and consists of two Au nanodimer antennas (10, 11) coupled to OM via nanoscale-size gaps. The structure is excited by the electric field E(r)e^iωt of a donor dipole source with the transition moment p, which is centered in the gap of one of the nanodimers and serves as a model of a quantum emitter [e.g., atom, molecule or quantum dot (QD)]. The donor dipole can lose its energy either radiatively by emitting a free-space photon or nonradiatively through dissipation in metal, and, within the validity of the Fermi’s golden rule, its total decay rate can be expressed as a weighted sum of possible decay channels. The changes in the LDOS at the dipole position induced by the optoplasmonic superlens are used to redistribute the “weights” of available channels. The resulting modification of the dipole radiative γ_r and nonradiative γ_nr rates can be obtained via classical calculations of the electromagnetic fields (7, 15, 25) (see Methods).

Fig. 1.

Resonant amplifying superlens. (A) A schematic of the optoplasmonic superlens composed of a polystyrene microsphere and two Au nanodimer antennas (R = 2.8 μm, n_d = 1.59, r = 75 nm, w = 25 nm, h = 80 nm). The structure is excited by an electric dipole shown as the blue arrow. (B) Radiative rate enhancement of the dipole (over the free-space value, 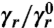) as a function of wavelength. (C) Electric field intensity enhancement in the gap of the acceptor antenna (over the value generated at the same position by a free-space dipole, |E|²/|E₀|²). (D and E) Electric field intensity distribution in the y-z (D) and x-z (E) planes (log scale) at one of the resonant peaks in B and C (λ = 905.4 nm). (F and G) Electric field intensity distribution at the same wavelength in the y-z (F) and x-z (G) planes (log scale) in the absence of the microsphere.

The dipole radiative rate enhancement is calculated by integrating the power flux through the closed surface encompassing the emitter and the superlens γ_r = 1/2 Re ∮_S(E(r) × H^∗(r))·ndr (n is a unit vector normal to the surface) and normalizing to the power 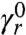radiated by the same source in vacuum. The polarization of the donor dipole is chosen to be oriented along the dimer axis as this orientation yields the dominant contribution to the radiative rate enhancement (Fig. 1A). Fig. 1B shows that the presence of the superlens yields two-orders-of-magnitude resonant enhancement of the dipole radiative rate. The resonant peaks in Fig. 1B are a manifestation of the excitation of the high-Q whispering-gallery (WG) modes in the OM (see Figs. S1 and S2), when photons are temporarily trapped inside the microcavity by total internal reflection. The “acceptor” nanoantenna coupled to the opposite side of the microcavity provides a well-defined output channel, which dominates all other channels of light out-coupling via evanescent leakage through the cavity walls. The localized plasmon oscillations induced in the acceptor antenna provide both dramatic field enhancement and light localization (Fig. 1 C–E). The electric field intensity distributions around the superlens demonstrate that the majority of the light emitted by the dipole is captured by the superlens and relocalized in the acceptor nanoantenna (Fig. 1 D and E). In the absence of the OM the electric field intensity induced on the acceptor antenna drops four orders of magnitude, ruling out the possibility that it is directly absorbing the far-field radiation (see Fig. 1 F and G and Fig. S3). Furthermore, plasmonic nanoantennas enable the detection of Raman radiation scattered by single molecules owing to the extreme concentration of the intensity of both the incident light and the Raman radiation in the form of localized surface plasmons (26–29). Optoplasmonic superlenses can be configured to further amplify the pump and Raman intensity, to capture the Raman-scattered light in the form of OM-trapped photons, and to subsequently refocus into another plasmonic nanoantenna.

In the configuration shown in Fig. 1A, the SP oscillations localized on the acceptor nanoantenna are converted into free photons that can be collected by conventional far-field optics. Other detection modalities are, however, available as well. For example, locally addressable on-chip electrical detection of surface plasmons has already been successfully demonstrated by using germanium wires (30), gallium arsenide structures (31), organic photodiodes (32), and superconducting single-photon detectors (33). Finally, light trapped in the optical microcavity can be evanescently out-coupled into an optical fiber (34), a planar optical waveguide (35, 36), or into another microcavity resonator (24, 37). The combination of dramatic field nanoconcentration and cascaded signal enhancement in optoplasmonic superlenses with the possibility of the on-chip routing and detection of the amplified signal paves the way for the realization of sensitive “dark” optoplasmonic platforms for single-molecule detection.

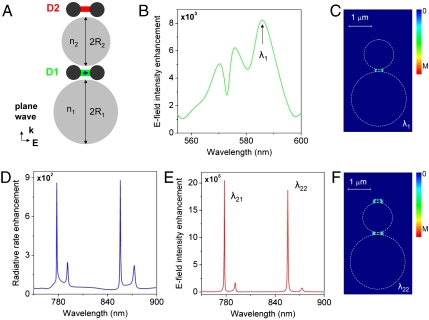
While an individual optoplasmonic superlens can serve as a superresolution magnifying glass for the investigation of nanoscale objects, additional functionality can be obtained by integrating the superlenses into discrete networks. One example of a simple optoplasmonic circuit, which combines the functions of light localization, frequency conversion, and wavelength multiplexing, is schematically shown in Fig. 2A. It consists of two OMs (M1 and M2) with nonoverlapping WG mode peaks (which can be tuned by OM morphology and material; see Fig. S1) and two plasmonic nanoantennas (D1 and D2) with a nanoantenna-coupled dipole sandwiched between the OMs. M1 is illuminated by a plane wave propagating along the z-axis. The incident light transverses M1 and is focused into the gap of the adjacent nanoantenna D1 where it generates a strong resonant and localized intensity enhancement at wavelength λ₁ (Fig. 2 B and C). Nanoantenna D2 remains dark due to the efficient shielding through M2, which is in the off-resonance state at λ₁. The hot spot at D1 can also be formed by refocusing the field radiated by another dipole source with emission wavelength λ₁ (similar to the case shown in Fig. 1A).

Fig. 2.

Light in-coupling, frequency conversion, and multiplexing in optoplasmonic circuits. (A) A schematic of the optoplasmonic multiplexer (R₁ = 1.2 μm, n₁ = 1.45, R₂ = 0.65 μm, n₂ = 2.4, r = 55 nm, w = 20 nm, h = 60 nm). (B) Enhancement (over the free-space value) of the electric field intensity detected at D1 under the plane wave excitation. (C) Electric field intensity distribution (linear scale) in the multiplexer at λ₁ = 585 nm under the plane wave illumination. (D) Radiative rate enhancement of the dipole at D1 as a function of wavelength. (E) Electric field intensity enhancement detected at D2 under the excitation by the emitting dipole at D1 as a function of wavelength. (F) Electric field intensity distribution (linear scale) in the multiplexer at λ₂₂ = 855.5 nm under the illumination by the emitting dipole at D1.

Acceptor molecules or QDs located in the gap of antenna D1 can be excited through the strongly enhanced localized field, provided that their absorption bands overlap with the hot spot wavelength λ₁. The excited acceptors eventually relax through emission of a photon. Due to the lack of coherence between the excitation and emission, the two processes can be treated independently (see Methods) (7). The enhancement of the radiative rate for a dipole located in the gap of D1 is plotted as function of the wavelength in Fig. 2D. The radiative rate is dramatically enhanced at defined wavelengths (λ₂₁ and λ₂₂) owing to the strong LDOS modification at D1 caused by the presence of M2 (M1 is off-resonance in this frequency range). The photons emitted in the gap of D1 can excite multiple WG modes in M2; and their resonant refocusing in the nanoantenna D2 results in the formation of a multicolor nanoscale hot spot in D2 (Fig. 2 E and F). The outlined optoplasmonic circuit could be implemented using a broadband emitter with a spectrum overlapping several WG modes (38, 39) or a cluster of narrow-band emitters such as size-selected QDs that allow dense packing without compromising their optical properties (40).

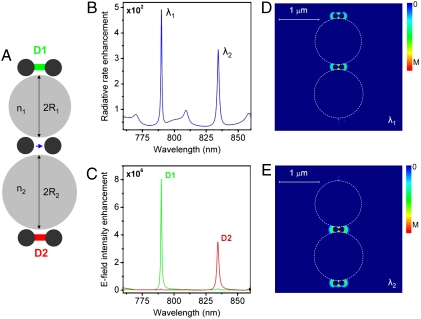
The underlying physical mechanisms behind the optoplasmonic wavelength multiplexing detailed in Fig. 2, where a localized single-color hot spot can create a multicolor hot spot in a distant nanoantenna, can be naturally extended to design optoplasmonic demultiplexers. A schematic of a simple circuit element that performs wavelength-selective demultiplexing of emitted photons is shown in Fig. 3A. In this case, the strong resonant LDOS modification at the dipole position located between the OMs generates a double-peak radiative rate enhancement spectrum within a chosen frequency band (Fig. 3B). If the OMs are selected to provide spectrally offset WG mode resonances, photons of different colors (λ₁ and λ₂) can be refocused into two spatially separated hot spots located at D1 (λ₁) and D2 (λ₂), respectively (Fig. 3 C–E).

Fig. 3.

Optoplasmonic frequency demultiplexer. (A) A schematic of the optoplasmonic demultiplexer: A field generated by the emitting dipole (shown as a blue arrow) is monitored in the gaps of two nanoantennas (R₁ = 0.57 μm, n₁ = 2.4, R₂ = 0.6 μm, n₂ = 2.4, r = 65 nm, w = 25 nm, h = 70 nm). (B) Dipole radiative rate enhancement as a function of wavelength. (C) The frequency spectra of the electric field intensity enhancement detected at D1 (green) and D2 (red). (D and E) Electric field intensity distributions (linear scale) in the demultiplexer at λ₁ = 790 nm (D) and λ₂ = 834 nm (E).

Integration of high-Q photonic elements into optoplasmonic circuits not only enables wavelength selectivity and efficient transfer of electromagnetic energy over longer distances but also offers the opportunity of cascaded signal amplification via efficient interaction of trapped photons with the gain medium inside the microcavity. This is at stark difference with conventional lossy nanoplasmonic components based on nanowires (13, 41) and channel plasmon polaritons (42) or SP loss compensation in planar device configurations (43, 44). The proposed optoplasmonic components also provide opportunities for realizing active nanoplasmonic circuit elements for field modulation and frequency switching, because the photon recycling in microcavities greatly enhances the sensitivity of light to small changes in refractive index (45). These properties are still missing in conventional nanoplasmonic circuitry due to the inherent weakness of the available material (e.g., thermo-, electro-, or magneto-optical) effects and the small propagating distance of SPs in metals (21).

While this work introduces the theoretical concepts of optoplasmonic superlenses, recent advances in nanofabrication technologies put the fabrication of these structures within reach. Our simulations predict significant radiative rate and light intensity enhancement with nanoantenna gaps sizes and position tolerances achievable by standard lithography (Fig. S4). Promising approaches to fabricate optoplasmonic networks include two-step electron-beam (46) and soft (47) lithography, template-assisted self-assembly (48), nanoassembly (16), and optical tweezers (49, 50) (see Fig. S5 for examples of possible realizations of optoplasmonic elements). It should be noted that OM shape and surface imperfections could have a detrimental impact on the spectral and energy transfer characteristics of optoplasmonic superlenses due to WG modes splitting and multimode coupling. Both of these effects, which become more pronounced with the increase of the OM size (51), can, however, be alleviated by a proper engineering of the OM shape. Carefully designed OM shapes can be used to suppress some of the WG modes and thus to rarefy the OM spectrum (e.g., higher-radial-order WG modes are suppressed in microring resonators) (35, 36).

Successful realization of the proposed elements offers new opportunities for giant, highly frequency-sensitive and dynamically controlled enhancement, transfer and routing of light on the nanoscale, and could form a basis for new platforms for single-molecule imaging, bio(chemical) sensing, and quantum information processing that interface photonic, plasmonic, and electrical functionalities. Because electromagnetic signals in the proposed optoplasmonic networks may not only be detected but also launched and switched electrically, they could enable “dark” on-chip integrated circuits with all the coupling occurring in the near-field.

Methods

We calculate the radiative decay rate γ_r of the dipole p at the emission wavelength λ_em as the power fraction radiated into the far-field by integrating the energy flux through the closed surface surrounding both the dipole and the optoplasmonic superlens. The nonradiative rate γ_nr is found by integrating the energy flux through the closed surfaces enclosing individual lossy metal particles. The total decay rate γ = γ_r + γ_nr can also be calculated from the total work per unit time that the electric field radiated by the dipole does on the dipole current: γ ∝ Im{E(r₀,λ_em)·p}. The external quantum efficiency of optoplasmonic structures is defined as the ratio of the radiative and total decay rates: q = γ_r/γ. In turn, the excitation rate of an emitter with a transition dipole p is governed by the local field E_exc at the excitation wavelength λ_exc: γ_exc ∝ |E_exc(r₀,λ_exc)·p|² (7).

Generalized multiparticle Mie theory is used for all the calculations, which provides an exact analytical solution of Maxwell’s equations for an arbitrary cluster of L spheres (22). The total electromagnetic field scattered by the cluster is constructed as a superposition of partial fields scattered by each sphere. The incident, partial scattered, and internal fields are expanded in the orthogonal basis of vector spherical harmonics represented in local coordinate systems associated with individual particles: 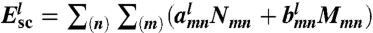, l = 1,…L. A matrix equation for the Lorenz–Mie multipole scattering coefficients (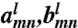) is obtained by imposing the continuity conditions for the tangential components of the electric and magnetic fields on the particles surfaces, using the translation theorem for vector spherical harmonics and truncating the infinite series expansions to a maximum multipolar order N. Experimentally obtained Au refractive index values from Johnson and Christy (52) are used in the simulations.