Incomplete lineage sorting patterns among human, chimpanzee, and orangutan suggest recent orangutan speciation and widespread selection

Abstract

We search the complete orangutan genome for regions where humans are more closely related to orangutans than to chimpanzees due to incomplete lineage sorting (ILS) in the ancestor of human and chimpanzees. The search uses our recently developed coalescent hidden Markov model (HMM) framework. We find ILS present in ∼1% of the genome, and that the ancestral species of human and chimpanzees never experienced a severe population bottleneck. The existence of ILS is validated with simulations, site pattern analysis, and analysis of rare genomic events. The existence of ILS allows us to disentangle the time of isolation of humans and orangutans (the speciation time) from the genetic divergence time, and we find speciation to be as recent as 9–13 million years ago (Mya; contingent on the calibration point). The analyses provide further support for a recent speciation of human and chimpanzee at ∼4 Mya and a diverse ancestor of human and chimpanzee with an effective population size of about 50,000 individuals. Posterior decoding infers ILS for each nucleotide in the genome, and we use this to deduce patterns of selection in the ancestral species. We demonstrate the effect of background selection in the common ancestor of humans and chimpanzees. In agreement with predictions from population genetics, ILS was found to be reduced in exons and gene-dense regions when we control for confounding factors such as GC content and recombination rate. Finally, we find the broad-scale recombination rate to be conserved through the complete ape phylogeny.

A prime objective of studying DNA sequences from primate species is to understand the speciation processes and the genomic and phenotypic divergence of the species. The role of natural selection in these processes is particularly interesting to understand. Recently, Locke et al. (2011) added the orangutan to the list of fully sequenced primates, and this opens the investigation of a new time epoch in primate evolution. Whole-genome analysis of the five-way alignment of the three great apes—human, chimpanzee, and orangutan—using macaque and marmoset as outgroups, allows us to gain insight into evolution on the primate branch leading to human, including knowledge on the speciation processes and speciation times for human, chimpanzee, and orangutan. The variation in divergence times between sequences from different species contains information about the effective population sizes of the ancestral species, and by estimating the effective population sizes, we can disentangle the times of divergence of genomes from the times of divergence of species. Furthermore, the imprint of natural selection shows as variations in the effective population size estimated locally in the genome, and this signature is therefore an important tool for analyzing the effects of selection and their interaction with the effects of recombination and migration.

The power to infer the ancestral effective population sizes, the times when species split, and recombination rates is particularly high when gene genealogies vary along the genome. In particular, a gene genealogy may be different from the species phylogeny. This phenomenon is called incomplete lineage sorting (ILS). ILS occurs when the effective population size suggests coalescence times, which are of the order of the time span between speciation events or smaller (see Fig. 1A,B). ILS shows in the alignment of the genomes for human, chimpanzee, and gorilla, where it leads to gene genealogies different from the species phylogeny for >25% of the genome (Chen and Li 2001; Yang 2002; Wall 2003; Patterson et al. 2006; Hobolth et al. 2007). The interval between the human–chimpanzee and orangutan speciation event is much longer. Nevertheless, if we use 10.4 million years (Myr) as the time between speciation events, 64,000 as the effective population size of the human–chimpanzee ancestor, and 20 yr as the generation time (estimates of Burgess and Yang 2008), we expect 0.9% ILS. With whole-genome alignments of human, chimpanzee, and orangutan, we are in a position to investigate whether population parameters are, indeed, within a range that generates ILS.

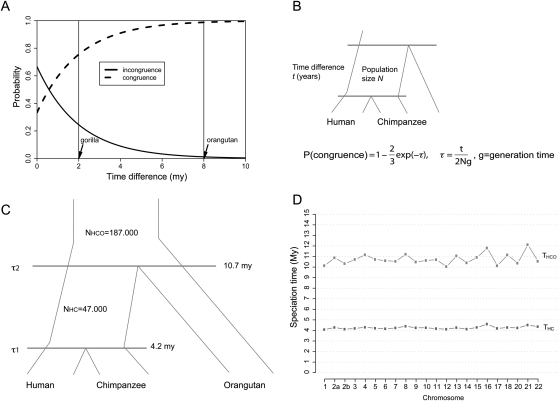
Figure 1.

(A) Probability of (in)congruence as a function of difference in speciation time τ. Consider the human–chimpanzee–gorilla triplet. With a speciation time difference of 2 million years (Myr), a generation time of 20 yr, and an effective human–chimpanzee population size of 50,000, we obtain an incongruence probability of 25%. Assuming a speciation time difference of 8 Myr for the human–chimpanzee–orangutan triplet, we obtain a congruence probability of 98.8%. Thus, the coalescent process predicts 1.2% lineage sorting between human, chimpanzee, and orangutan. (B) If the number of generations r between the speciation time of the three species and the speciation time of human and chimpanzee is small compared to the ancestral (effective) population size N of the human–chimpanzee common ancestor, then a gene from human and chimpanzee does not necessarily find common ancestry within the human–chimpanzee common ancestors. Here τ = t/(2Ng), where g is the generation time in years. (C) Average parameter estimates for the global analysis. (D) The mean time estimates for speciation for 21 autosomal chromosomes.

Detailed genomic analyses of ILS patterns are used to infer population processes in the ancestral species, including those of natural selection. Due to linkage between positions in the genome, neutrally evolving regions are affected by selection on nearby regions. A region under purifying selection can cause significant reduction in polymorphism in a linked neutral region. This effect is termed background selection (Charlesworth et al. 1993), and it results in a smaller effective population size and a smaller amount of ILS. The effect is less pronounced in regions with a high recombination rate. Positive directional selection on a gene has a similar but broader effect, and it can therefore lead to an extended region without any ILS. Balancing selection, on the other hand, is expected to generate a higher amount of ILS.

We use a hidden Markov model that directly infers the local genealogy of the human, chimpanzee, and orangutan species to show that ILS occurs within ∼1% of the genome. We use the patterns of ILS to disentangle human–orangutan speciation from human–orangutan divergence. This allows us to estimate the population sizes of the ancestral species (e.g., Chen and Li 2001; Hobolth et al. 2007; Dutheil et al. 2009) as well as the variations in the effective population sizes for different parts of the genome (e.g., McVicker et al. 2009). More than 100,000 very short segments of the genome support gene genealogies different from the species tree. In addition, we find long regions (larger than 2 kb) with ILS scattered throughout the genome. The proportion of base pairs with ILS correlates positively with the human broad-scale recombination rate, as estimated by the deCODE recombination map data (Kong et al. 2002) and equilibrium CG content. The correlation is very strong and suggests widespread selection throughout the genome, as well as a striking conservation of broad-scale recombination rate over >12 Myr. Also, the amount of ILS in exons is significantly less than in introns, consistent with weaker selective forces operating on introns.

Results

Evidence for incomplete lineage sorting

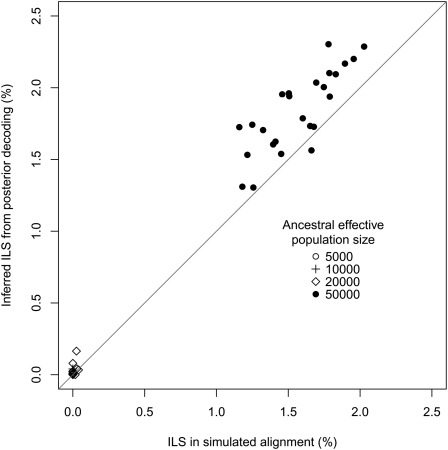
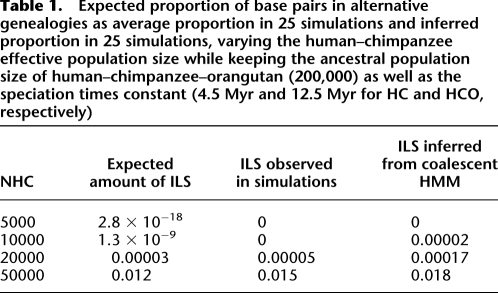
The coalescent hidden Markov model (HMM) is formulated assuming that ILS occurs. To verify this assumption, we simulated alignment data using the CoaSim program (Mailund et al. 2005) with parameters chosen to mimic the human, chimpanzee, orangutan, macaque/marmoset phylogeny, i.e., speciation times of 4.5 Myr for human and chimpanzee and 12.5 Myr for human, chimpanzee, and orangutan, a generation time of 20 yr, a recombination rate of 1.5 cM/Mbp, population numbers of N = 10,000 for the human lineage and N = 30,000 for the chimpanzee lineage, and a variable human–chimpanzee ancestral effective population size to produce different levels of ILS. Twenty-five replicate simulations of 1 Mbp of sequence were performed, and for each we used posterior decoding of the coalescent HMM to infer ILS. The result is that the model accurately infers ILS when the expected frequency is above 0.2%, and finds no evidence of ILS when it is low (Fig. 2; Table 1).

Figure 2.

Inferred (from posterior decoding) versus expected (from simulations) amounts of ILS as a function of the human–chimp ancestral population size.

Table 1.

Expected proportion of base pairs in alternative genealogies as average proportion in 25 simulations and inferred proportion in 25 simulations, varying the human–chimpanzee effective population size while keeping the ancestral population size of human–chimpanzee–orangutan (200,000) as well as the speciation times constant (4.5 Myr and 12.5 Myr for HC and HCO, respectively)

Application of the coalescent HMM on 1-Mbp alignments (chunks) of real data show convergence for 2017 chunks that were subsequently analyzed in detail. The remaining fragments may be cases in which ILS is absent or represented by pieces below the detection limit. We further removed chromosome X (58 chunks) because we suspect a high rate of sequencing errors (see Supplemental Material Section 1; Supplemental Fig. S1), and we removed chromosome 19 (12 chunks) because of a very poor alignment quality. The converged fragments all provide evidence for ILS. The average frequency of ILS was 1.4% of the bases in the converged fragments as estimated from posterior decoding (see Supplemental Material; Supplemental Fig. S1). We therefore conclude that human is closer to orangutan than to chimpanzee in 0.8% of the genome, and chimpanzee is closest to orangutan in 0.6% of the genome.

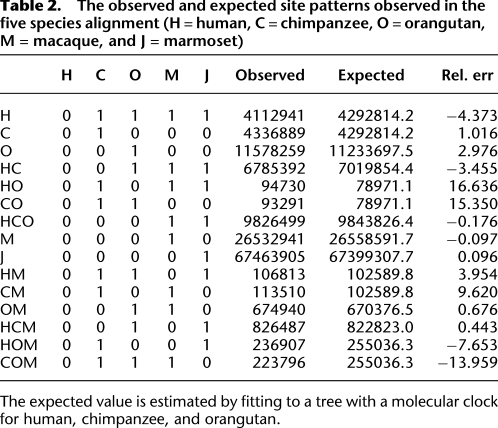
Since the coalescent HMM predictions may be affected by model misspecification (such as substitution model inadequacy or alignment artifacts), we investigated evidence for ILS applying simpler approaches based on segregating sites and shared indels (see Supplemental Material Sections 2, 3). When fitting the pattern of each segregating site to a single phylogenetic tree by maximum likelihood, we observe a 20% excess of sites grouping HO and CO (Table 2). This is as expected when ILS is present. Allowing for ILS by adding a single parameter that describes the effect of incomplete lineage sorting (Supplemental Fig. S2B) results in a much-improved fit (see Supplemental Table S2).

Table 2.

The observed and expected site patterns observed in the five species alignment (H = human, C = chimpanzee, O = orangutan, M = macaque, and J = marmoset)

The expected value is estimated by fitting to a tree with a molecular clock for human, chimpanzee, and orangutan.

We then examined indels to find evidence of ILS. We do not expect indels of size >5 bp in well-aligned regions to be alignment or assembly artifacts. Rather, we see them as rare genomic events unlikely to have occurred more than once (Supplemental Figs. S3, S4). Indels shared among the species human, chimpanzee, orangutan, and macaque should therefore be homologous and informative of the local genealogy. In fact, we find an excess of sites supporting the genealogy of the indel among informative sites close to the indel (Supplemental Figs. S5, S6), and ∼2% of the indels support alternative genealogies (either human/orangutan or chimpanzee/orangutan) after removal of tandem repeats.

Speciation times and ancestral population sizes

In the presence of ILS, the divergence times can be separated from the speciation times. Assuming a substitution rate of 1.0 × 10⁻⁹ per year and a generation time of 20 yr, we find very recent speciation times for human and chimpanzee and for these and the orangutan (see Fig. 1C). The human–chimpanzee speciation is estimated to be 4.22 Mya (standard error interval [4.20, 4.24]) and the human orangutan speciation to be 10.70 Mya [10.62, 10.78]. The average sequence divergence time of the latter is 18.17 Mya [18.08, 18.28]—a reflection of the large effective population size of 187,000 [185, 189] of the human–chimpanzee–orangutan ancestral species. The human–chimpanzee ancestral population size is 47,000 [46.5, 47.5]. The inferred speciation times are similar across the 21 autosomes analyzed (Fig. 1D).

The standard errors are very small due to the large amount of data, but the divergence and speciation times are estimated conditioned on the substitution rate, so the real uncertainty is dominated by uncertainty in that rate. Should rates of 0.8 × 10⁻⁹ and 1.2 × 10⁻⁹ be reasonable, a human–chimpanzee speciation time between 3.4 and 5.0 Mya and a human–orangutan speciation between 8.6 and 12.9 Mya would also be reasonable.

Genomic patterns of ILS

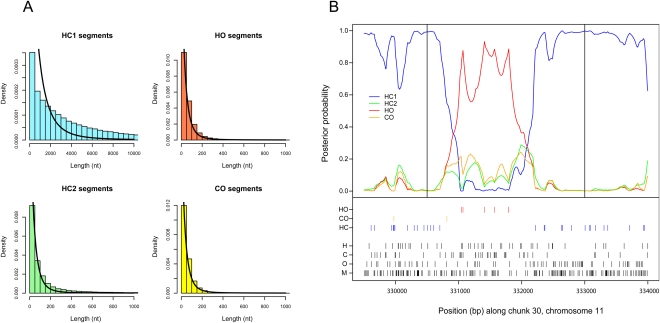
The genomic fragments with alternative genealogies are expected to be very small. The estimated mean length of a region under ILS with the estimated parameters is just below 100 bp when calculated using the method of Mailund et al. (2011), and they are therefore expected to be difficult to identify. From the posterior decoding, we estimated a mean length of fragments with alternative genealogies as 93 bp for the HO state and 73 bp for CO, with 75% of observations between 17 and 93 bp assuming equal expected length of fragments in the two states. The average length of fragments supporting HC1 is 6.3 kbp, with 75% of observations between 0.9 kb and 7.8 kb. The distribution of lengths of regions supporting each state is shown in Figure 3A. The shape of each distribution resembles a geometric distribution (black fitted line in Fig. 3A) but with a heavier tail. The model will have an increased likelihood of confusing the species phylogeny (HC1) and the HC2, pinpointing coalescent events in the human–chimpanzee–orangutan ancestor. This may explain the surplus of short fragments in HCl and the excess of long fragments in HC2 (when compared to HO and CO).

Figure 3.

(A) The distribution of fragment lengths supporting each of the four states. A geometric distribution (full line) is fitted to the observed distribution. (B) Examples of an alignment supporting the alternative [(H,O),C] genealogy. The top of the figure shows the posterior probability of being in the basic state (HC1) or in each of the three alternative states (HC2, HO, or CO). The bottom of the figure indicates informative sites and singletons.

We focused on the identification of the most extreme cases of ILS covering >2000 bp with high posterior probability. An example of a long region with high posterior probability of the HO genealogy is shown in Figure 3B, and the Supplemental Material lists such regions. The candidate region of the example in Figure 3B shows an excess of HO sites as well as a number of chimpanzee singleton sites larger than the number of human and orangutan singleton sites in accordance with human and orangutan being the most closely related species in this region. Such long regions of ILS appear uniformly distributed over the genome (see Supplemental Fig. S7).

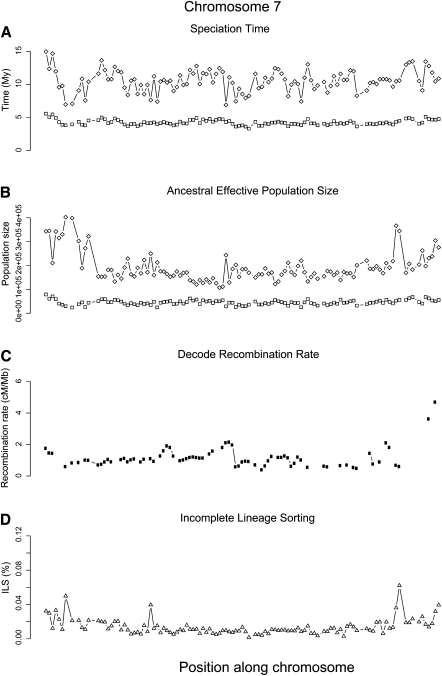
The analysis of 1-Mbp fragments allows broad chromosomal patterns of ILS and estimated effective population sizes to be studied. Figure 4 shows the results for chromosome 7, and those for the remaining chromosomes are presented as a separate file in the Supplemental Material. The estimated speciation times are relatively constant along the chromosome. For ILS and effective population sizes, values become higher closer to the telomeres, and this correlates well (Kendall's τ = 0.11, P-value = 2.9 × 10⁻¹⁰) with the pattern of recombination estimated from the deCODE map (Fig. 4; Kong et al. 2002). ILS correlates even more strongly (Kendall's τ = 0.25, P-value < 2.2 × 10⁻¹⁶) with the equilibrium GC content, which is known to be a good predictor of the long-term recombination rate (Duret and Arndt 2008). The CoalHMM method accounts for variation in GC content through the substitution model, which is estimated separately for every 1-Mbp alignment, and we do not expect the amount of ILS to be directly influenced by the GC content.

Figure 4.

Example estimates along chromosome 7, divided into 131 chunks of 1 Mb of alignment. (A) Estimated speciation times for human–chimpanzee (squares) and human–orangutan (diamonds). (B) Estimated effective sizes of the human–chimpanzee ancestral species (squares) and the human–chimpanzee–orangutan ancestral species. (C) Average recombination rate for each chunk based on the deCODE map. (D) The percentage of incomplete lineage sorting estimated from posterior decoding.

To evaluate the amount of ILS independent of effects of poor alignment, we focused the analysis on exonic and intronic regions, which are generally aligned with higher confidence than intergenic regions. The posterior decoding of the HMM finds ILS in 0.97% of the exonic sites and in 1.11% of the intronic sites, i.e., the posterior decoding support either an HO or a CO topology. Figure 5 shows the amount of ILS in exons and introns for each of the 21 chromosomes calculated as the weighted mean value over 1-Mb chunks. The amount of ILS is clearly significantly lower in exons than in introns. We propose the smaller amount of ILS in exons to be due to a smaller local effective population size in exons, resulting from stronger selection on variation in coding regions. The smaller population size results in more recent coalescent times, making ILS less likely (recall Fig. 1). For the same reason, we expect exonic and intronic regions to have smaller amounts of ILS than non-genic regions.

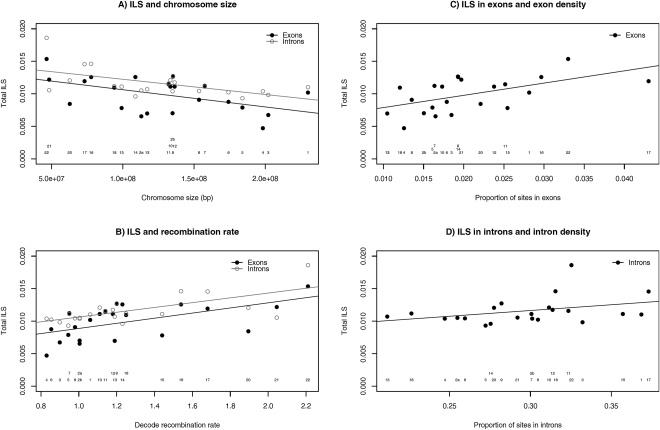
Figure 5.

(A) Amount of ILS in introns and exons for each chromosome as a function of chromosome size. (B) ILS as a function of the deCODE recombination rate. (C) ILS as a function of average exon density of each chromosome. (D) ILS as a function of average intron density of each chromosome.

Figure 5A shows a negative correlation between ILS in genes and chromosome size (Kendall's τ = −0.325, P-value = 0.035 for exons, and τ = −0.393, P-value = 0.010 for introns). As recombination decreases with chromosome size, this suggests that ILS is positively correlated with the recombination rate, and, indeed, Figure 5B displays a strong positive correlation between ILS and average deCODE-based recombination rate for the human chromosomes (Kendall's τ = 0.451, P-value = 0.003 for exons, and τ = 0.495, P-value = 0.001 for introns). These observations suggest similar relations for non-coding segments and are in agreement with recombination causing local effective population sizes in the genome—an effect due to the decoupling of a region under selection more efficiently from the rest of the genome. A higher effective population size results in a higher proportion of ILS.

Figure 5, C and D, shows the amount of ILS in introns and exons as a function of their densities. A higher gene density is expected to result in a stronger local selection, and thereby a smaller population size. However, gene density correlates positively with recombination rate (Duret and Arndt 2008), and a higher recombination rate improves the efficacy of selection and, hence, would result in a larger population size. The figure shows a significantly positive correlation between the amount of ILS in exons and exon density (Kendall's τ = 0.552, P-value = 0.0003), and this points at the latter force as the most prominent. At the 1-Mbp scale, we note that the amount of ILS in introns shows no correlation with the intron density (Kendall's τ = 0.086, P-value = 0.61) (Fig. 5D). Thus, in this case, the indirect effects of recombination and gene density appear to cancel.

In order to disentangle the correlations between the variables, we formulated and analyzed a linear model with the deCODE map recombination rate, the equilibrium GC content, and the density of coding sites as explanatory variables. The results are a negative correlation between ILS and gene density (estimate = −0.19, P-value = 0.0417) and a significant positive correlation of ILS with the interaction between GC equilibrium frequency and gene density (estimate = 0.48, P-value = 0.0273). As above, the GC equilibrium content captures most of the large-scale, long-term recombination signal. These results are in perfect agreement with the predictions of background selection. The ILS and the local reduction in population size are an exponential function of gene density divided by recombination rate. When recombination is low, the effect of gene density on ILS is strong, and even very moderate densities lead to a dramatic reduction in ILS and effective population size, while for a high recombination rate, the slope becomes less steep and the effect of gene density less important. For a given gene density, recombination will increase the amount of ILS, and the effect will be stronger as density increases, resulting in the positive interaction between the two. When this is properly accounted for in the linear model, the marginal effect of gene density can be estimated, and it appears to be negative (higher gene density results in a smaller effective population size and less ILS), as expected.

Discussion

Our analyses find that for ∼0.8% of our genome, humans are more closely related to orangutans than to chimpanzees. ILS between human, chimpanzee, and gorilla is well established, and we show ILS to occur very far back in time. The exact amount of ILS locally in the genome depends on the recombination rate and factors such as functional constraints (Figs. 4, 5). The observed ∼1% of ILS is entirely consistent with the effective population size of 50,000 inferred for the human–chimpanzee ancestor and the speciation time difference of 8 Myr inferred between human–chimpanzee and human–chimpanzee–orangutan, assuming a generation time of 20 yr (Fig. 1). Various complementary approaches support these claims. The patterns of segregating sites (Table 1) and informative indels also show evidence for ILS. The analysis of changing genealogies along the chromosomes using a hidden Markov model provides evidence for independent lines of descent reaching back to the human–chimpanzee–orangutan ancestor, thus allowing observation of the three possible coalescent genealogies that we observe as ILS. Observation of independent descent all the way to the orangutan speciation time implies that the effective population size has been large throughout this period of 8–10 Myr, in particular, the human–chimpanzee ancestral species cannot have experienced a severe bottleneck within this period.

Our study is the first to benefit from molecular data in the estimation of the time since the human and orangutan lines separated. Genomic divergence and species divergence are in general difficult to separate, and genomic divergence always occurred further back in time than species separation. This difference between the time of separation and that of divergence is the cause of ILS, and because ILS is a population genetic phenomenon, the observation of ILS allows us insight into properties of the ancestral population. Our estimation of the human–orangutan speciation time to 9–13 Mya assumes a simple allopatric model of speciation. A more fuzzy speciation scenario with an extended period of gene flow among partially isolated populations would make the speciation time less well defined and produce a large effective population size of the ancestral population.

The orangutan speciation time estimated from paleontological data is 9–13 Mya. This bracket contains the dates of Asian hominoid fossils usually argued to belong on the orangutan clade. At present, the earliest-known member of this clade is Khoratpithecus (Lufengpithecus) chiangmuanensis (Chaimanee et al. 2003) from Thailand. The extant sample of this species largely derives from between 10.5 and 12 Mya with one specimen from a substantially earlier geological level dating to between 12.4 and 13 Mya (Suganuma et al. 2006). Sivapithecus indicus, from the Chinji Formation of the Siwalik Hills of Pakistan, is dated to between 12.8 and 11.4 Mya (Kappelman et al. 1991). These two fossil genera are known also from larger, later samples with substantial craniodental similarities with living and fossil Pongo (Kelley 2002; Begun 2005). The earliest known African member of the Gorilla–Pan–Homo clade is Chororapithecus abyssinicus from the 10–10.5 Mya Chorora Formation of Ethiopia (Suwa et al. 2007). Assuming a rapid diversification of the early Asian and African clades after the initial appearance of these primates, these fossils are consistent with a speciation time between 13 and 12.5 Mya. A more recent speciation time may be possible if one or more of the earliest occurrences have been overestimated, or if some of these fossils may have belonged to large, regionally structured populations before speciation.

European apes of the late Middle Miocene, such as Dryopithecus, which is roughly the same age as Sivapithecus in Asia, have argued to reflect a diversification of the orangutan clade prior to the evolution of most Pongo-like craniodental traits (Moya-Sola et al. 2004). Others have suggested this well-known lineage to be an ancestral member of the Gorilla–Pan–Homo clade, reflecting a European origin for the African apes (Begun 2005). Either of these suggestions might imply a speciation time for the ancestral orangutan–human population prior to 13 Myr. However, it seems likely that the European apes are themselves a stem clade relative to both Asian and African hominoids, so that the earliest occurrence of Dryopithecus does not constrain the orangutan–African hominoid divergence time.

The existence of ILS with orangutan provides an alternative estimate of the speciation time between human and chimpanzee. The result of 4.2 Mya is consistent with recent analyses using a part of the gorilla genome (Patterson et al. 2006; Burgess and Yang 2008; Dutheil et al. 2009). Such a recent speciation event suggests that Ardipithecus ramidus may predate the human–chimpanzee speciation event (TD White et al. 2009). These conclusions, however, depend critically on the calibration of substitution rate. As in most recent studies, we used the rate of 10⁻⁹. Were a different substitution rate preferred, our timing estimates would need to be adjusted accordingly. We have used the commonly used model, assuming general time reversibility of substitutions and rate heterogeneity. That may not account for all conceivable variation in the substitution process and could potentially lead to overestimation of the effective population size of the human–orangutan ancestor—a population size that we have found to be very large. Further studies, including Gibbon species presently being sequenced, should be able to elucidate this.

The quality of the sequence determination and their alignment becomes an important issue when relatively rare events like ILS are studied. The potential of misalignments and sequence errors to mimic ILS should therefore be scrutinized. Part of the data has been left out of the analysis because of such considerations. The chimpanzee X chromosome was excluded from our analysis, because the sequence appears to have a relatively high expected error rate, probably since a male chimpanzee was sequenced. This is unfortunate as previous studies predict far less ILS on the X chromosome due to its small effective population size below the three-fourths of autosomes expected under neutrality (see, e.g., Patterson et al. 2006; Hobolth et al. 2007). Errors in the chimpanzee X sequence lead to a longer chimpanzee branch. Such a phenomenon is not observed for the autosomes, thus we assume that the error rate is insignificant for our analysis of these.

Alignment errors could be more problematic. A region where only orthologous sequences from human and orangutan are aligned with a paralogous region from chimpanzee would produce artifactual patterns similar to ILS. This may occur in regions that duplicated before the human–chimpanzee–orangutan split, particularly if these were placed in tandem. To avoid such errors, we took the conservative approach to remove from the analysis all regions that occurred as duplicates in more than one species. This did not lead to a change in the results.

The posterior decoding in the HMM analysis pinpoints the regions of the genome with independent lines of descent to the chimpanzee–human–orangutan ancestor. We studied these regions of ILS to learn about selection in the ancestral species of human and chimpanzee, and thus restricted attention to sites in exons and introns. The ILS regions occur more often where the recombination rate is higher than average. As selection is more efficient in regions of higher recombination rates, we interpret this as strong evidence for natural selection. The contrast in the amount of ILS between the most recombining chromosomes and the least recombining chromosomes corresponds to a difference in average effective population size of 5%–10% (see formula in Fig. 1B). To see the signature of natural selection based on heterogeneity of this magnitude is quite striking since many other factors are expected to affect the efficacy of natural selection. The observation, however, suggests widespread selection occurring throughout the genome and is consistent with recent results by McVicker et al. (2009). Furthermore, the exonic regions have only 88% of the amount of ILS as intronic regions, corresponding to exons having an average effective size of 96% of that of introns.

Reconstructing patterns of ILS along genome alignments is a powerful tool to infer local estimates of ancestral effective population sizes throughout the genome. The orangutan genome is the first genome available to allow a genome-wide three-way primate comparison that includes the human species. Comparisons of orangutan with human and chimpanzee did not detect targets of balancing or positive selection in the human–chimpanzee ancestor, but our results suggest widespread signatures of background selection, despite the small amount of ILS available. We suggest that the incoming primate genomes be subjected to analysis based on proper modeling of selection. Application of such methods to analyses including gorilla is particularly promising because more ILS is expected in the triplet with human and chimpanzee. The potential is to estimate the strengths and patterns of selection much more precisely along the genomes of our ancestors.

ILS is generally underappreciated in phylogenetic studies (Siepel 2009), although recent studies among species with short internal branches do take phylogenetic discordance into account (Pollard et al. 2006; MA White et al. 2009). Small amounts of ILS like those in analyses of human, chimpanzee, and orangutan should rarely affect phylogenetic studies, but should potentially affect many other studies of phylogenies where internal branches are short. Studies of our phylogeny including the gibbon lineage (one gibbon species is presently being sequenced) will likely display widespread ILS with orangutan since the span between orangutan–gibbon speciation events is estimated to be 1–2 Myr, and effective sizes appear high at that time.

Methods

CoalHMM analysis

Dutheil et al. (2009) describe a model that allows for genealogies to change along an alignment of three species and an outgroup. We apply it to a genome-wide HCOM (human, chimpanzee, and orangutan with macaque as outgroup) alignment. Briefly, we build a hidden Markov model along the sequence with ‘‘hidden states’’ predicted from the data. In the CoalHMM approach, the observed states are the distinct columns in the alignment, and the hidden states are the unknown genealogies. States HC1 and HC2 correspond to cases in which human and chimpanzee sequences coalesce first, either earlier or later than the orangutan speciation, respectively. HO corresponds to coalescence of human and orangutan first and CO to coalescence of chimpanzee and orangutan first. The substitution model is a general time-reversible model with heterogeneity of rate parameters (the speciation times of the human–chimp split and the human–orangutan split, the effective sizes of the human–chimp ancestor and the human–orangutan ancestor, and the recombination rate) modeled as a gamma distribution. The rate parameters were estimated using maximum likelihood, and the estimates were subsequently used for posterior decoding of the hidden state most likely for each position in the alignment.

Model description

The alignments were provided by the Orangutan Genome Sequencing Consortium (Locke et al. 2011) and were taken through a series of cleaning steps leading to a set of 2258 alignments of ∼1 Mbp each. The synteny blocks from the original MAF alignment file were concatenated based on the reference sequence (Orangutan), if they were distant by <100 nucleotides (nt) in the Orangutan sequence. The original distance was kept by filling the resulting alignment with columns of N. Original gaps were also converted to N. As a result, the hidden Markov chain was run over the full concatenated block (= chunks), averaging over all possible nucleotides when an N was found. Blocks distant by >100 nt were kept in distinct chunks. The hidden Markov chain was reset after each chunk. Chunks were further concatenated to form 1-Mbp alignments, and parameter estimation was performed independently per 1-Mbp alignment.

For the present analysis, we only considered the alignments for which the CoalHMM converged, leaving 2017 alignments covering >2 Gbp of the multispecies alignment. We performed the posterior decoding for each alignment and reconstructed the local genealogy for each site by taking the hidden state with the maximum posterior probability.

Linear model

To assess the effect of gene density on ILS while controlling for recombination rate, we fitted a linear model. A stepwise model selection retained all interactions between recombination rate, equilibrium GC content, and density of coding site up to the third order. A boxcox transform was used and proved to fit the Gauss-Markov assumptions (normality: Shapiro test, P-value = 0.06691; homoskedasticity: Harrison-McCabe test, P-value = 0.245; and independence: Durbin-Watson test, P-value = 0.3882), using the R package lmtest. The effect of each factor was therefore assessed using the Student's t-test from the summary function in R.

Genomic patterns of ILS

The posterior decoding of all alignments was structured under a MySQL database, together with the RefSeq annotations of the human genome. The more complete human RefSeq annotations were used. The SQL database efficiently mapped the coordinates of our alignments to the RefSeq coordinates, using appropriate indexing. For all introns and exons present in our alignments, we counted the number of sites supporting each of the four genealogical states.

We computed the proportion of ILS for a given region by dividing the total number of sites in alternatives genealogies (HO or CO) by the total number of sites in the region. Regions for which ILS was calculated include: full chromosomes, per-chromosome exomes and intromes, per-1-Mb exomes and intromes. All statistical analyses were subsequently performed with the R statistical software, using the RMySQL package to query the database.