Abstract
The main way of analyzing biological sequences is by comparing and aligning them to each other. It remains difficult, however, to compare modern multi-billionbase DNA data sets. The difficulty is caused by the nonuniform (oligo)nucleotide composition of these sequences, rather than their size per se. To solve this problem, we modified the standard seed-and-extend approach (e.g., BLAST) to use adaptive seeds. Adaptive seeds are matches that are chosen based on their rareness, instead of using fixed-length matches. This method guarantees that the number of matches, and thus the running time, increases linearly, instead of quadratically, with sequence length. LAST, our open source implementation of adaptive seeds, enables fast and sensitive comparison of large sequences with arbitrarily nonuniform composition.
Biomedical research is being revolutionized by multi-gigabase DNA data sets. This began with the sequencing of whole large genomes, such as the human (∼3 billion bases), allowing us to see our species' genetic blueprint. More recently, new sequencing technologies have enabled small-scale laboratories to produce gigabases of DNA sequence. These technologies have been used to explore DNA from environmental samples, transcribed RNA in tissues and cell lines, chromatin structure, and personal genomes, to name just a few applications (Metzker 2010).
In all cases, the data largely remain an uninterpretable sea of As, Cs, Gs, and Ts, unless we make connections by comparing the sequences to each other. For example, we can predict the taxonomy and function of environmental DNA reads by comparing them to all known protein sequences (via the genetic code). We can interpret DNA reads from an extinct organism (e.g., the saber tooth tiger) by mapping them to the genome of a surviving organism (e.g., the cat). In all cases, the initial task is to find similar regions between huge sequence data sets.
The classic tool for this task is BLAST (and similar methods such as PatternHunter, BLAT, BLASTZ, YASS, and many others) (Altschul et al. 1997; Kent 2002; Ma et al. 2002; Schwartz et al. 2003; Kucherov et al. 2006). These methods rely on a seed-and-extend heuristic. They rapidly find similarities between the “query” sequence and the “target” sequence by using short matches called seeds. These seeds act as starting points for the subsequent time-consuming alignment extensions. The simplest kind of seed consists of exact matches of a fixed-length (e.g., 12 bases). Short seed lengths can improve sensitivity, but at a high cost in running time, because they yield more seed matches and thus more extensions. On the other hand, long seeds are matched rarely and lead to decreased sensitivity.
In this work, we propose adaptive seeds as an alternative to fixed-length seeds. As implied by the name, fixed-length seeds have a constant length l. In contrast, adaptive seeds vary in length—seeds are lengthened until the number of matches in the target sequence is less than or equal to a frequency threshold f. Box 1 illustrates these two concepts using familiar English text. Adaptive seeds are similar to several ideas that have been published before, including: variable-length seeds (Csurös 2004), maximal unique matches (Kurtz et al. 2004), and rare exact matches (Ohlebusch and Kurtz 2008).
Box 1. An analogy with text that helps explain the concepts of fixed-length seeds, adaptive seeds, spaced seeds, and subset seeds.
As an example from a more familiar domain, suppose we wish to align the string “The Queen of Hearts, she made some tarts” with the story “Alice's Adventures in Wonderland” by Lewis Carroll. We suppose our smallest atomic unit is words, instead of letters.
A fixed-length seed of length 2 would isolate the positions in the story that contain the words “The Queen,” “Queen of,” “of Hearts,” and so on. Once these positions are found, an extension in both directions is performed to obtain an alignment score. In contrast, an adaptive seed starting from the first word of our string would start from “The” and add words to it until the frequency of the phrase drops below a predetermined threshold f. The frequencies of some of these phrases are as follows: “The” (1621); “The Queen” (49); “The Queen of” (2); “The Queen of Hearts” (2). Suppose we had set this value to f = 10. Then the seed that would be chosen is the third in this list since it is the shortest with a frequency not larger than 10.
The above describes how seeds operate by default. Spaced and subset seeds allow more flexible definitions of a match. Within the context of our example, spaced seeds allow searches for phrases where some words are designated as being unimportant. If the above query was used with a seed of 11101110, then the words “Hearts” and “tarts” can be substituted with any word. Subset seeds can be more restrictive than spaced seeds since they allow users to define a match to be a subset of words. For example, a subset seed might specify that occurrences of “Hearts” in a query can be substituted with “diamonds,” but nothing else.
Fixed-length seeds perform well on random sequences with a uniform distribution of bases. Unfortunately, biological sequences deviate far from this ideal case. For instance, primate genomes contain more than 1 million copies of the Alu element (Batzer and Deininger 2002): These alone will produce more than 1012 matches if we compare two primate genomes. Some malaria genomes have over 80% A and T bases, which means long A + T-rich matches will often be less significant than shorter C + G-rich matches.
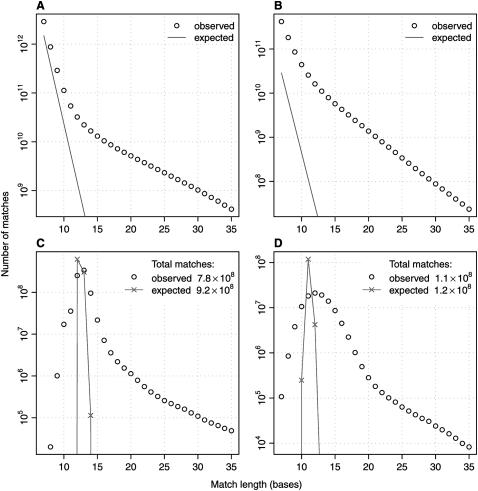
More specifically, in Figure 1 we demonstrate how seed choice influences the number of matches. For this example, we identified the adaptive seeds that occur not more than f = 10 times in the mouse X chromosome, and we calculated their matches in the human X chromosome. In total, we observed 777 million matches, mostly for seed lengths 12–13, with some seeds shorter or much longer (Fig. 1C). These values can be compared to ones obtained for fixed-length seeds. In Figure 1A, we present numbers observed for fixed-length seeds varying from 7–35 bases. For fixed-length-13 seeds, we would expect about 365 million chance matches for uniformly random sequences, but the actual number is 22 billion. To reduce the number of matches closer to 777 million, we would need to use fixed-length-32 seeds, but such long seeds fail to detect weak similarities. This observation suggests that by using adaptive seeds, we can achieve the sensitivity of a fixed-length-13 seed with the run-time of a fixed-length-32 seed.
Figure 1.
Number of exact matches between genomic sequences as a function of match length. (A) Matches of size 7–35 bases between the human X chromosome (151 million bases) and the mouse X chromosome (162 million bases). (B) Matches between the genomes of P. falciparum (23 million bases) and P. yoelii (20 million bases). (C) Matches between the human X chromosome and the mouse X chromosome, of seeds that occur at most 10 times in the mouse X chromosome. (D) Matches between P. falciparum and P. yoelii, of seeds that occur at most 10 times in P. falciparum. Lines show expected frequencies for uniformly random sequences.
Similarly, if we compare the genomes of Plasmodium falciparum (the most dangerous human malaria parasite) and Plasmodium yoelii (a rodent malaria parasite), most of the adaptive seeds have lengths 11–13 and produce in total 106 million matches (Fig. 1D). Using fixed-length-12 seeds, we expect 28 million chance matches but actually get 16 billion (Fig. 1B). To get a number of matches similar to the total observed for the adaptive seeds, we would need to use fixed-length-29 seeds. Here, we expect adaptive seeds to offer the sensitivity of a fixed-length-12 seed with the speed of a fixed-length-29 seed. In both of our examples, adaptive seeds move the speed/sensitivity tradeoff close to what it is for uniformly random sequences with fixed-length seeds.
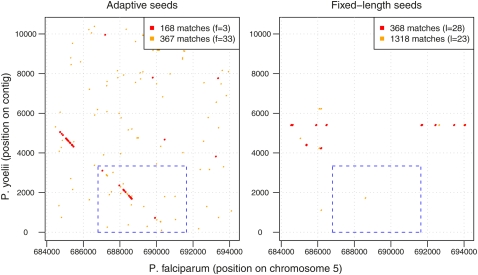
When multiple malaria genomes are compared, P. falciparum and P. yoelii stand out as being the two most A + T-rich (Carlton et al. 2005) and therefore troublesome for fixed-length seeds. As an example, we consider the MB2 gene of P. falciparum, for which a gene homolog was reported to exist in P. yoelii (Nguyen et al. 2001; Romero et al. 2004). We used both adaptive and fixed-length seeds to identify the matches between the P. yoelii contig with this homologous gene against the entire P. falciparum genome. The dots in Figure 2 show locations of identified seed matches (the contig is represented by the vertical axis, while the horizontal axis represents the region surrounding the P. falciparum MB2 gene). Varying their respective f and l parameters yields different numbers of matches, as shown by the numbers in the figure legends. With only 168 hits, adaptive seeds are able to identify the homologous genes (shown in the blue box). Fixed-length seeds are unable to achieve this, even when there are almost 10 times as many hits. The repetitiveness of the two genomes results in fixed-length seed hits occurring clumped together, away from the locations of the genes.
Figure 2.
Dot-plots of matches (without extensions) identified by adaptive and fixed-length seeds when comparing the P. yoelii contig with the region of the P. falciparum genome where the MB2 homologous genes are known to exist. Their exact locations are indicated by the dashed boxes in blue. The colored dots in both panels indicate the number of hits in the plot area. As the frequency threshold f for adaptive seeds increases or the length l for fixed-length seeds decreases, the number of hits increases. Caveat: the area each color appears to occupy does not exactly correlate with the number of hits—for each graph, the color with the lower number of hits is drawn over the other color, and also nearby hits cannot be resolved visually at this resolution.
Results
Performance measurement
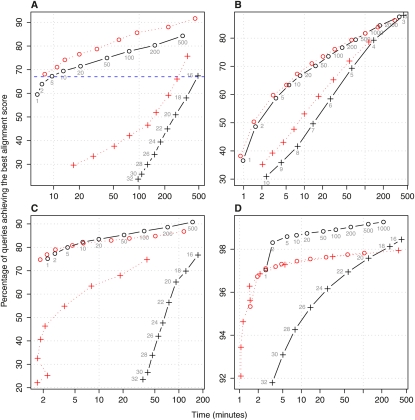
We quantify the influence of different seed types on the overall seed-and-extend procedure by measuring the performance of adaptive and fixed-length seeds using three types of data: genomic, proteomic, and short read sequencing data (for additional information about these data sets, see Methods section and Supplemental material). For each data set, multiple combinations of seed type and parameter settings are used to locally align a set of queries to a target (e.g., genome) sequence. Each combination is evaluated by the percentage of queries whose alignment score equals the highest achieved by any combination.
The black solid lines of Figure 3 compare adaptive seeds (circles) to fixed-length seeds for the four data sets. The graphs show sensitivity versus running time for various parameter settings for both schemes. In all cases, the sets of points for adaptive seeds appear above and to the left of those for fixed-length seeds, indicating that adaptive seeds perform better. For example, in panel A, to attain a sensitivity of 67% (dashed blue line), either adaptive seeds of f = 5 or fixed-length seeds of l = 16 can be used. However, their respective running times differ greatly: ∼10 min for adaptive seeds and 500 min for fixed-length seeds.
Figure 3.
Performance comparison of adaptive seeds (circles) versus fixed-length seeds (crosses). Black denotes results obtained for contiguous seeds and unmasked sequences (l or f parameters are shown next to each data point). Red shows the effect of spaced seeds, subset seeds, or repeat-masking for the sequence alignment of: (A) H. sapiens promoters to the M. musculus genome (and spaced seed 111010010100110); (B) D. melanogaster protein sequences to those of C. elegans (and subset seeds); (C) P. yoelii contigs to the P. falciparum genome (and soft-masking with Tandem Repeats Finder); and (D) short DNA reads from 454 Life Sciences (Roche) GS 20 for A. thaliana against its genome (and soft-masking with WindowMasker).
Spaced and subset seeds
Modern DNA comparison methods achieve increased sensitivity through the use of spaced seeds (Kent and Zahler 2000; Ma et al. 2002). Spaced seeds are seeds that have fixed “don't care” positions that are not required to match. This is in contrast to the contiguous seeds discussed above, in which every position is required to match. Fortunately, we do not need to sacrifice spaced seeds in order to use adaptive seeds; these techniques can be unified.
Spaced seeds are represented as seed patterns of binary strings such as 110, where 0s indicate don't care positions. These patterns are cyclically repeated as many times as necessary to cover the length of the seed. (The last copy of the seed pattern may only be a prefix of the original pattern.)
Figure 3A presents results for the alignment of Homo sapiens promoters to the Mus musculus genome using contiguous seeds (black) or a previously identified optimal spaced seed pattern (Ma et al. 2002), 111010010100110 (red). For this particular seed pattern, spaced seeds improve the performance over the contiguous seeds for both adaptive and fixed-length seeds, with adaptive seeds still performing best. Additional results with spaced seeds are shown in Supplemental Figures S6A, S7A, and S9A.
Subset seeds are a generalization of spaced seeds, in which position-specific reduced alphabets are used when matching. For example, purines (A, G) and pyrimidines (C, T) can be considered equivalent in some positions to account for the rareness of transversions compared with transitions in genome sequences (Kucherov et al. 2006). Subset seeds are equally relevant for protein sequences (Roytberg at al. 2009), where amino acids with similar properties may be allowed to match each other in some positions.
Figure 3B summarizes the effect subset seeds have on both fixed-length and adaptive seeds for aligning Drosophila melanogaster protein sequences to those of Caenorhabditis elegans. In this case, subset seeds (red) show a slight improvement over exact-match seeds, for both adaptive and fixed-length seeds. This result is confirmed by other subset seed tests (Supplemental Fig. S8A,C).
Repeat masking
Multi-gigabase data sets have been compared successfully in the past, using traditional seed-and-extend methods (Schwartz et al. 2003). However, this has been possible only with repeat-masking (Schwartz et al. 2003). There are specialized programs for identifying repetitive segments, and many alignment tools identify repeats during alignment. The treatment of repeats can be divided into hard-masking, which completely removes repeats from further consideration, and soft-masking, which forbids seeds from including repeats but allows them to participate in extensions. In this work, we report some results with each strategy. In any case, repeat-masking is not an ideal solution: It hides potentially important parts of the sequence (e.g., 50% of the human genome), and it cannot completely solve the problem of nonuniform composition (e.g., malaria genomes).
The red symbols in Figure 3, C and D, demonstrate the effect masking has on fixed-length and adaptive seeds for P. yoelii contigs versus the P. falciparum genome and for short read sequencing data for A. thaliana. Masking improves the performance of fixed-length seeds in both scenarios noticeably, although not enough to reach the performance of unmasked adaptive seeds. Masking can be detrimental when using adaptive seeds (e.g., Fig. 3D). Tests with other genomic, proteomic, and short read sequencing data also give similar results (Supplemental Figs. S6C, S7C, S9B–D, S10B,C).
Even with adaptive seeds, it is advisable to mask “simple” repeats (e.g., ATATATATATAT) when searching for evolutionarily related sequences. This is because the simple repeats cause strong alignments of sequences that are not evolutionarily related. On the other hand, repeat-masking may be undesirable when mapping DNA reads to a genome, because the repetitive reads can sometimes be mapped successfully and they can reveal interesting biology (Faulkner et al. 2009).
Fixed-length seeds in other programs
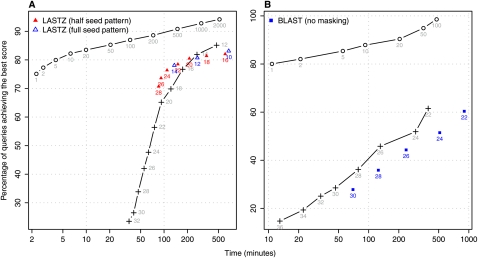
We have developed LAST in order to provide an unbiased comparison of alignment performance when adaptive seeds and fixed-length seeds are used. Here, we want to verify whether indeed LAST fixed-length seeds have a similar performance to that of other alignment programs. In Figure 4, we compare the performance of LAST, LASTZ (Harris 2007), and BLAST (Altschul et al. 1997) used to align P. yoelii contigs to P. falciparum chromosomes.
Figure 4.
LASTZ and BLASTN use fixed-length seeds and present similar performance to LAST with fixed-length seeds. (Circles) LAST adaptive seeds; (crosses) LAST fixed-length seeds. (A) P. yoelii contigs are aligned to P. falciparum chromosomes using the same score matrix as in Figure 3C. Triangles show performance of LASTZ executed with corresponding parameters for different LASTZ-seed lengths. (B) A simpler match/mismatch scoring scheme is used. Squares present the performance of BLASTN and the numbers correspond to BLASTN-seed lengths.
In panel A, we use a scoring system adjusted to the high A + T content of the genomes (the same as in Fig. 3C). The measured performance of LASTZ displays a good agreement with the performance of LAST fixed-length seeds. Here, LASTZ was started with options (up to our best understanding) equal to ones used with LAST and with fixed-length exact seeds of lengths 10, 12, and 14. Since LASTZ does not support longer exact seeds, we also used “half-weight” seeds (i.e., subset seeds) of lengths 16–28.
In panel B of Figure 4, we demonstrate BLASTN performance for fixed seed lengths from 22–30. Since BLASTN does not support scoring systems assigning different match scores to AT and GC, we used the same match score for all nucleotides in this test. Intentionally, in order to provide a fair comparison between LAST fixed-length seeds and the seeds used by BLASTN, we disabled masking of repetitive sequences in the query. The slope of the observed BLASTN points is close to the slope of the LAST fixed-length seeds, and for all tested lengths, the sensitivities of the seeds computed with both programs are nearly equal. For equal-length seeds, LAST is noticeably faster than BLASTN. Presumably this is due to differences in the degree of optimization at the implementation or compiler level.
These observations support our belief that our fixed-length seeds implementation displays performances similar to implementations provided by other investigators.
Comparing the human and chimpanzee Y chromosomes
A recent study claimed that >30% of the chimpanzee Y chromosome has no homologous, alignable counterpart in the human Y chromosome (Hughes et al. 2010). This is an astonishing level of divergence, since in the remainder of the genome, less than 2% of the chimpanzee sequence lacks homologous, alignable counterparts in the human (Hughes et al. 2010). These Y chromosomes are challenging to compare, however, because they are rich in repeats and rearrangements (Hughes et al. 2010).
Since our method is suited to repeat-rich sequences, we used it to compare these Y chromosomes. In order to find reliable homologies, we masked simple repeats and then searched for alignments strong enough that they are very unlikely to arise by chance (see Supplemental material). The alignment took 20 min on a desktop computer, and we found homologous counterparts to more than 86% of the chimpanzee sequence. So these chromosomes have undergone much less sequence gain and loss than previously thought, albeit still much more than the other chromosomes. We speculate that the main cause of Y chromosome divergence is a faster rate of rearrangement. Since most of the Y chromosome does not need to pair with another homologous chromosome, we might expect rearrangements to occur more freely on the Y.
Discussion
This is the first method that can find and align similar regions in gigascale biological sequences, without certain severe restrictions. All previous methods can compare such sequences only with either heavy repeat-masking (exemplified by BLAST and its cousins), or restriction to strong similarities (exemplified by DNA read mapping algorithms). In practice, we are able to compare two vertebrate genomes in a few hours (Frith et al. 2010a) and map 100,000 DNA reads to a genome in 30 sec (Frith et al. 2010b). This makes such sequence comparisons available to the masses.
In recent years, many methods have been developed for mapping DNA reads to genomes, allowing for small numbers of differences (Trapnell and Salzberg 2009; Li and Homer 2010). These methods are ideal for short DNA reads (∼20–40 bp), where alignments with more than a few differences would not be statistically significant. The read lengths of modern DNA sequencing technologies have, however, increased, often to >100 bp. This makes it statistically feasible to find weak similarities, which is useful, for instance, in cross-species mapping. The specialized read mappers remain valuable because they are fast and they often guarantee not missing alignments with limited numbers of differences. We submit that it is also valuable to have a general-purpose, BLAST-like method for aligning reads with arbitrary length and divergence.
For genome comparison and other applications, repeat-masking often remains desirable in practice. This is because low-complexity repeats cause false homology predictions, and interspersed repeats cause numerous, uninteresting alignments. Our method at least makes it possible to compare genomes with no or reduced repeat-masking, as we did when comparing the chimpanzee and human Y chromosomes (we did not mask interspersed repeats). Furthermore, repeat-masking involves arbitrary thresholds, since there is no exact definition of a repeat, and our method can use sequences with less “heavy” masking.
In summary, we dramatically improve the seed-and-extend heuristics that are indispensable for genome scale comparisons. Adaptive seeds offer a significant advantage in terms of time over traditional fixed-length seeds commonly used by other local alignment systems. Instead of specifying a seed length l, adaptive seeds are associated with a frequency threshold f, which enable them to handle the repetitive regions of complex genomes. Adaptive seeds yield sizable performance gains over their fixed-length counterparts for genomic, proteomic, and short read data sets, typically reducing computation time by 10- to 100-fold (the horizontal difference between the two seed types in each panel of Fig. 3). In some cases, the performance of adaptive seeds can be further improved by combining them with the techniques of spaced or subset seeds.
These results were obtained with our open source software package LAST available at http://last.cbrc.jp.
Methods
We outline our methods and materials here. Detailed information can be found in the Supplemental material.
Definition of adaptive seeds
Adaptive seeds are matches of any length between query and target sequences, such that the matching sequence occurs at most f times in the target.
It is possible for two adaptive seeds to overlap each other in a redundant fashion. For example, there might be one adaptive seed of length l that ends at position X in the query and position Y in the target, and another adaptive seed of length l + 1 that ends at the same positions in the query and target. A naive algorithm would extend alignments from both of these, which seems redundant and slow.
Our seed-finding algorithm partially avoids such redundancy. In particular, it reports only the shortest seed starting at any pair of (query, target) positions (X, Y). This does not eliminate redundant alignment extensions, but it makes them rare enough that the number of redundant extensions is much less than the total number of extensions, so they are not significantly time-consuming. We can imagine more sophisticated algorithms to avoid redundancy more thoroughly, but these would be more time-consuming.
Although our algorithm performs redundant alignment extensions, it strictly avoids reporting the same alignment twice by using a “diagonal table” (see the Supplemental material).
Method for finding adaptive seeds
In outline, our method is as follows. We first construct an “index” of the target sequence. We then scan across the query sequence and find the shortest string starting at each position that matches ≤f times in the target. So the key requirement is an index that allows these shortest matches to be found quickly.
Such an index can be implemented in several ways with different performance tradeoffs. A suffix tree (Gusfield 1997) or enhanced suffix array (Abouelhoda et al. 2004) would have the fastest theoretical (asymptotic worst-case) run time, but these structures need much memory and we are not sure if they can be adapted to spaced seeds. An FM-index (Ferragina and Manzini 2000) would use minimal memory, although its theoretical run time is inferior to that of the suffix tree (since it lacks suffix links). Empirically, our FM-index implementation was several-fold slower than our main implementation, and we believe the slowness is inherent in the techniques it uses to reduce memory consumption.
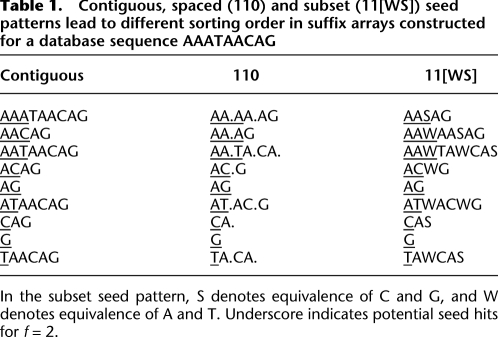
Our main implementation uses a suffix array of the target sequence(s). A suffix array for a sequence of length T is simply the integers 1…T, sorted according to the alphabetical order of the suffixes starting at each position (Table 1, left column; Manber and Myers 1993). Given any substring of the query, we can find all the matching locations in the target by a binary search in the suffix array. If we then lengthen the query substring by one, we need only search within the bounds found by the previous search. Thus, we keep lengthening the query substring until there are ≤f matching locations.
Table 1.
Contiguous, spaced (110) and subset (11[WS]) seed patterns lead to different sorting order in suffix arrays constructed for a database sequence AAATAACAG
In the subset seed pattern, S denotes equivalence of C and G, and W denotes equivalence of A and T. Underscore indicates potential seed hits for f = 2.
To accelerate this process, we also use a lookup table providing the locations of all short strings in the suffix array. So binary searches are needed only for longer strings.
Our method has a balance of moderate memory usage and enough speed so as not to be the bottleneck. Our index uses 4–5 bytes per indexed position, plus extra memory to store the target sequence itself. Its theoretical run time is even worse than the FM-index (because it uses a logarithmic-time binary search instead of a constant-time backward search), but in practice it takes less time to find the seeds than to extend alignments from them, so seed-finding is not the bottleneck.
Fixed-length seeds
Although fixed-length seed based matching is available from BLAST and other tools, we also implemented them in LAST. This allows a comparison between fixed-length and adaptive seeds implemented with a similar level of code optimization. However, we also report direct comparisons with BLASTN (Altschul et al. 1997) and LASTZ (Harris 2007) and also BLASTP and MEGABLAST (Morgulis et al. 2008) in the Supplemental material (Supplemental Figs. S8, S9).
Adaptive spaced seeds
Adaptive spaced seeds are matches that occur at most f times in the target, where some predefined positions are allowed to mismatch. In order to find these, we use a “spaced suffix array.” A spaced suffix array is much like an ordinary suffix array. The only difference is the sorting criterion: When comparing two suffixes, the predefined positions are skipped or ignored (Table 1, middle column).
Adaptive subset seeds
Adaptive subset seeds are matches that occur at most f times in the target, where some predefined positions are allowed to match using reduced alphabets (potentially, a different reduced alphabet at each position). In order to find these, we use a “subset suffix array,” which is straightforwardly analogous to a spaced suffix array (Table 1, right column).
Suffix array construction
There has been much research on efficient algorithms to construct ordinary suffix arrays (Puglisi et al. 2007). We have shown that these algorithms can be adapted to construct spaced suffix arrays (Horton et al. 2008), and similar techniques would work for subset suffix arrays. In practice, however, we do not use these algorithms but instead use radix sort (McIlroy et al. 1993). Radix sort is theoretically inferior but is fast in practice (e.g., 1 h for a mammalian genome), and it has negligible memory overhead (McIlroy et al. 1993).
Human–mouse comparison
We used the UCSC Genome Bioinformatics Site as the source of the M. musculus genomic sequence (version mm8) and obtained 1870 H. sapiens promoter sequences from the Eukaryotic Promoter Database (release 100) (Schmid et al. 2006). We calculated alignments using a score of 2 for matching nucleotides, a cost of 1 for transitions and a cost of 2 for transversions, and a gap existence cost of 16 and a gap extension cost of 1 (Frith et al. 2010a). We studied only alignments of score at least 150.
Malaria genomes
The Plasmodium genomic sequences were downloaded from the 5.5 release of the PlasmoDB database. As the query sequences, we used 2960 contigs of P. yoelii retrieved on November 8, 2009. The length of the contigs varies from 2000–51,480 nt, with a mean of 6815 nt and 76.1% A + T content. The database was built from 14 chromosomes of P. falciparum retrieved on July 1, 2009. The A + T content of this genome is 79.3%, and therefore, we used an adjusted scoring scheme: The match score for A-A and T-T pairs was set to 3; for C-C and G-G pairs, 9. We used a mismatch cost of 4, a gap existence cost of 15, and a gap extension cost of 3. We considered alignments scoring more than 200. The P. yoelii query sequences were masked using Tandem Repeats Finder (Benson 1999).
For a comparison of BLASTN and LAST, we used match score 1, cost 1 for mismatches, cost of 7 for gap existence, and cost of 1 for gap extensions.
Protein data
Adaptive seeds seem promising for protein comparison because amino acids are not equally abundant. We aligned fly (D. melanogaster) proteins to a worm (C. elegans) protein database. Protein sequences were obtained from the files flyBasePep.txt and sangerPep.txt, downloaded from the UCSC Genome Database on July, 8, 2009. Sequences with nonstandard amino acids (e.g., X) were excluded. This yielded 21,228 fly proteins and 23,770 worm proteins. We aligned the proteins using the Blosum62 matrix, with a gap existence cost of 11, a gap extension cost of 1, and a minimum gapped alignment score of 100.
Short read sequencing data
The Arabidopsis thaliana short read data set SRR014005 from the 454 Life Sciences (Roche) GS20 platform was downloaded from the NCBI Sequence Read Archive. We processed 133,420 unique reads of median length 105. The genome for A. thaliana was downloaded from the NCBI ftp site on June 29, 2009. Local alignment was performed with match and mismatch scores of 1 and −1, respectively. A gap existence cost of 2 and a gap extension cost of 1 were used. The minimum alignment score was set at 30. WindowMasker (Morgulis et al. 2006) was used for masking repeats.
Acknowledgments
We thank Kenichiro Imai for suggesting a protein reduced alphabet and Martin Vingron for helpful suggestions. We thank Tim Bailey, Zhiping Weng, Kiyoshi Asai, and Christine Sers for commenting on the manuscript. Sz.M.K. received support from the German National Genome Research Network (NGFN-Plus, grant no. 01GS0815). R.W. is supported by INTEC Systems Institute, Inc.
Footnotes
[Supplemental material is available for this article. LAST software is freely available at http://last.cbrc.jp.]
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.113985.110.
References
- Abouelhoda MI, Kurtz S, Ohlebusch E 2004. Replacing suffix trees with enhanced suffix arrays. J Discrete Algorithms 2: 53–86 [Google Scholar]
- Altschul SF, Madden TL, Schäffer AA, Zhang J, Zhang Z, Miller W, Lipman DJ 1997. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res 25: 3389–3402 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batzer MA, Deininger PL 2002. Alu repeats and human genomic diversity. Nat Rev Genet 3: 370–379 [DOI] [PubMed] [Google Scholar]
- Benson G 1999. Tandem Repeats Finder: a program to analyze DNA sequences. Nucleic Acids Res 27: 573–580 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlton J, Silva J, Hall N 2005. The genome of model malaria parasites, and comparative genomics. Curr Issues Mol Biol 7: 23–37 [PubMed] [Google Scholar]
- Csurös M 2004. Performing local similarity searches with variable length seeds. Lect Notes Comput Sci 3109: 373–387 [Google Scholar]
- Faulkner G, Kimura Y, Daub C, Wani S, Plessy C, Irvine K, Schroder K, Cloonan N, Steptoe A, Lassmann T, et al. 2009. The regulated retrotransposon transcriptome of mammalian cells. Nat Genet 41: 563–571 [DOI] [PubMed] [Google Scholar]
- Ferragina P, Manzini G 2000. Opportunistic data structures with applications. In FOCS '00: Proceedings of the 41st Annual Symposium on Foundations of Computer Science, p. 390 IEEE Computer Society, Washington, DC [Google Scholar]
- Frith MC, Hamada M, Horton P 2010a. Parameters for accurate genome alignment. BMC Bioinformatics 11: 80 doi: 10.1186/1471-2105-11-80 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frith MC, Wan R, Horton P 2010b. Incorporating sequence quality data into alignment improves DNA read mapping. Nucleic Acids Res 38: e100 doi: 10.1093/nar/gkq010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gusfield D 1997. Algorithms on strings, trees and sequences. Cambridge University Press, New York [Google Scholar]
- Harris R 2007. “Improved pairwise alignment of genomic DNA.” PhD thesis, Pennsylvania State University, University Park, PA [Google Scholar]
- Horton P, Kiełbasa SM, Frith MC 2008. DisLex: a transformation for discontiguous suffix array construction. In Proceedings of the Workshop on Knowledge, Language, and Learning in Bioinformatics (KLLBI), pp. 1–11 Pacific Rim International Conferences on Artificial Intelligence (PRICAI), Hanoi, Vietnam [Google Scholar]
- Hughes J, Skaletsky H, Pyntikova T, Graves T, van Daalen S, Minx P, Fulton R, McGrath S, Locke D, Friedman C, et al. 2010. Chimpanzee and human Y chromosomes are remarkably divergent in structure and gene content. Nature 463: 536–539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kent WJ 2002. BLAT—the BLAST-like alignment tool. Genome Res 12: 656–664 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kent WJ, Zahler AM 2000. Conservation, regulation, synteny, and introns in a large-scale C. briggsae-C. elegans genomic alignment. Genome Res 10: 1115–1125 [DOI] [PubMed] [Google Scholar]
- Kucherov G, Noé L, Roytberg M 2006. A unifying framework for seed sensitivity and its application to subset seeds. J Bioinform Comput Biol 4: 553–569 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurtz S, Phillippy A, Delcher A, Smoot M, Shumway M, Antonescu C, Salzberg S 2004. Versatile and open software for comparing large genomes. Genome Biol 5: R12 doi: 10.1186/gb-2004-5-2-r12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Homer N 2010. A survey of sequence alignment algorithms for next-generation sequencing. Brief Bioinform 11: 473–483 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma B, Tromp J, Li M 2002. PatternHunter: faster and more sensitive homology search. Bioinformatics 18: 440–445 [DOI] [PubMed] [Google Scholar]
- Manber U, Myers EW 1993. Suffix arrays: a new method for on-line string searches. SIAM J Comput 22: 935–948 [Google Scholar]
- McIlroy PM, Bostic K, McIlroy MD 1993. Engineering radix sort. Comput Syst 6: 5–27 [Google Scholar]
- Metzker M 2010. Sequencing technologies—the next generation. Nat Rev Genet 11: 31–46 [DOI] [PubMed] [Google Scholar]
- Morgulis A, Gertz EM, Schäffer AA, Agarwala R 2006. WindowMasker: window-based masker for sequenced genomes. Bioinformatics 22: 134–141 [DOI] [PubMed] [Google Scholar]
- Morgulis A, Coulouris G, Raytselis Y, Madden TL, Agarwala R, Schäffer AA 2008. Database indexing for production MegaBLAST searches. Bioinformatics 24: 1757–1764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nguyen TV, Fujioka H, Kang AS, Rogers WO, Fidock DA, James AA 2001. Stage-dependent localization of a novel gene product of the malaria parasite, Plasmodium falciparum. J Biol Chem 276: 26724–26731 [DOI] [PubMed] [Google Scholar]
- Ohlebusch E, Kurtz S 2008. Space efficient computation of rare maximal exact matches between multiple sequences. J Comput Biol 15: 357–377 [DOI] [PubMed] [Google Scholar]
- Puglisi SJ, Smyth WF, Turpin AH 2007. A taxonomy of suffix array construction algorithms. ACM Comput Surv 39: article 4 doi: 10.1145/1242471.1242472 [Google Scholar]
- Romero LC, Nguyen TV, Deville B, Ogunjumo O, James AA 2004. The MB2 gene family of Plasmodium species has a unique combination of S1 and GTP-binding domains. BMC Bioinformatics 5: 83 doi: 10.1186/1471-2105-5-83 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roytberg M, Gambin A, Noé L, Lasota S, Furletova E, Szczurek E, Kucherov G 2009. On subset seeds for protein alignment. IEEE/ACM Trans Comput Biol Bioinformatics 6: 483–494 [DOI] [PubMed] [Google Scholar]
- Schmid CD, Perier R, Praz V, Bucher P 2006. EPD in its twentieth year: towards complete promoter coverage of selected model organisms. Nucleic Acids Res 34: D82–D85 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz S, Kent WJ, Smit A, Zhang Z, Baertsch R, Hardison RC, Haussler D, Miller W 2003. Human-mouse alignments with BLASTZ. Genome Res 13: 103–107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trapnell C, Salzberg S 2009. How to map billions of short reads onto genomes. Nat Biotechnol 27: 455–457 [DOI] [PMC free article] [PubMed] [Google Scholar]