Striatal Prediction Error Modulates Cortical Coupling

Abstract

Both perceptual inference and motor responses are shaped by learned probabilities. For example, stimulus-induced responses in sensory cortices and preparatory activity in premotor cortex reflect how (un)expected a stimulus is. This is in accordance with predictive coding accounts of brain function, which posit a fundamental role of prediction errors for learning and adaptive behavior. We used functional magnetic resonance imaging and recent advances in computational modeling to investigate how (failures of) learned predictions about visual stimuli influence subsequent motor responses. Healthy volunteers discriminated visual stimuli that were differentially predicted by auditory cues. Critically, the predictive strengths of cues varied over time, requiring subjects to continuously update estimates of stimulus probabilities. This online inference, modeled using a hierarchical Bayesian learner, was reflected behaviorally: speed and accuracy of motor responses increased significantly with predictability of the stimuli.

We used nonlinear dynamic causal modeling to demonstrate that striatal prediction errors are used to tune functional coupling in cortical networks during learning. Specifically, the degree of striatal trial-by-trial prediction error activity controls the efficacy of visuomotor connections and thus the influence of surprising stimuli on premotor activity. This finding substantially advances our understanding of striatal function and provides direct empirical evidence for formal learning theories that posit a central role for prediction error-dependent plasticity.

Introduction

One of the major reasons for the remarkable flexibility and adaptive repertoire of human behavior is that we construct and update estimates of conditional probabilities that describe uncertain causal relationships in the world. For example, human subjects can infer changing conditional probabilities among sensory events (Behrens et al., 2007; Brodersen et al., 2008), even when these probabilities are not relevant for overt behavior (den Ouden et al., 2009). Such learning of stimulus probabilities has been shown to be reflected by activity changes in visual (Summerfield et al., 2008; Summerfield and Koechlin, 2008), auditory (Pincze et al., 2002), and somatosensory (Akatsuka et al., 2007; Iannetti et al., 2008) areas. The general principle that emerges from these studies is that sensory responses increase with the size of prediction error, i.e., the less expected (or more surprising) a stimulus, the greater the response. This is in accordance with current theoretical accounts of brain function, such as predictive coding and the free-energy principle (Rao and Ballard, 1999; Friston, 2005; Friston and Stephan, 2007; Friston and Kiebel, 2009), which posit a fundamental role of prediction errors for adaptive behavior and learning.

Efficient learning of probabilities can be used to form predictions that guide motor behavior. For example, once the predictive strength of a cue has been learned, the premotor cortex shows preparatory activity (Tanji and Evarts, 1976; Wise and Mauritz, 1985; Crammond and Kalaska, 2000) and reaction times (RT) decrease (Requin and Granjon, 1969; Strange et al., 2005; Bestmann et al., 2008).

However, the neurobiological mechanisms that underlie adaptive changes in motor behavior when predictions fail are not fully understood. According to the free-energy principle, any prediction error should induce learning through synaptic plasticity, reconfiguring connection strengths such that prediction error is minimized at both sensory and motor levels, thus optimizing perceptual inference and motor actions (Friston and Stephan, 2007). In line with this view, a recent electrophysiological study by Bestmann et al. (2008) suggested that information about prediction errors is “… continuously channelled into motor regions to control the excitability of expected motor outputs.” In this study, we provide direct empirical evidence for this hypothesis, exploiting recent advances in computational models of learning (Behrens et al., 2007) and nonlinear dynamic causal models (DCMs) of functional magnetic resonance imaging (fMRI) data (Stephan et al., 2008). In particular, we link the physiological mechanisms proposed by the free-energy principle (and other formal theories of learning and decision making), i.e., prediction error-dependent changes in connectivity, to a large body of literature that has described responses in the striatum correlated with prediction error (McClure et al., 2003; O'Doherty et al., 2003, 2004; Corlett et al., 2004; Seymour et al., 2004; Jensen et al., 2007; Menon et al., 2007). Specifically, we show that the observed learning-dependent changes in blood oxygenation level-dependent (BOLD) activity are compatible with a mechanistic model in which the connection strengths between visual and motor regions are modulated by prediction error-related activity in the striatum.

Materials and Methods

Participants

Twenty healthy right-handed volunteers, 24.4 ± 2.1 years of age (mean ± SD, 10 female) took part in this study. The participants had no history of psychiatric or neurological disorders. Written informed consent was obtained from all volunteers before participation. The study was approved by the National Hospital for Neurology and Neurosurgery Ethics Committee.

Experimental design

Associative learning task.

To investigate the mechanisms underlying adaptive motor behavior and the role of striatal and sensory prediction errors, we used a simple audiovisual associative learning task in which the participants were presented with auditory cues (high or low beeps) that differentially predicted upcoming visual target stimuli (Fig. 1A). To ensure attention and assess learning, participants were instructed to respond as quickly as possible by button press (right middle and index finger, counterbalanced across subjects), reporting whether the target stimulus was a face (F) or a house (H). The associative contingencies of the auditory and visual stimuli changed over the course of the experiment (Fig. 1B). To ensure that participants' responses were not biased by learned expectations about the relative frequencies of the visual stimuli, we designed the sequence of changes in probabilities such that the marginal probabilities of faces and houses were identical, as described in more detail below. Subjects were instructed that the relation between auditory and visual stimuli was probabilistic, that these probabilistic relations would change unpredictably in time. They were not informed about the nature of the probabilistic relations or about the temporal intervals over which they changed.

Figure 1.

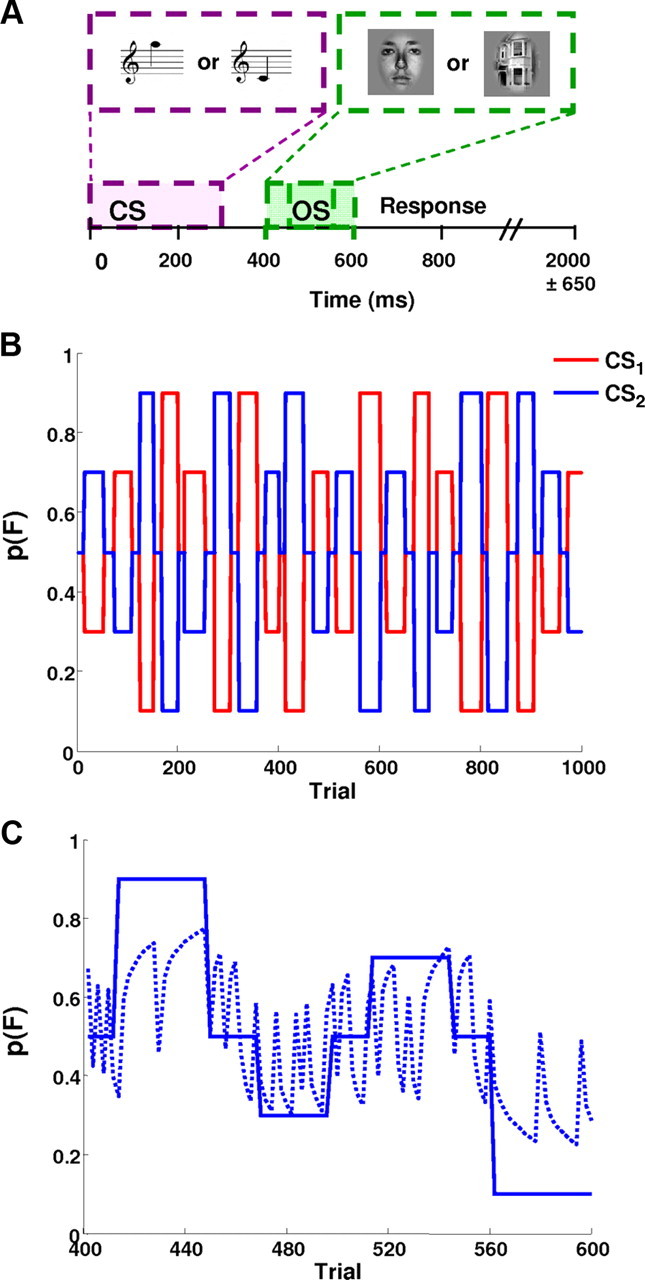
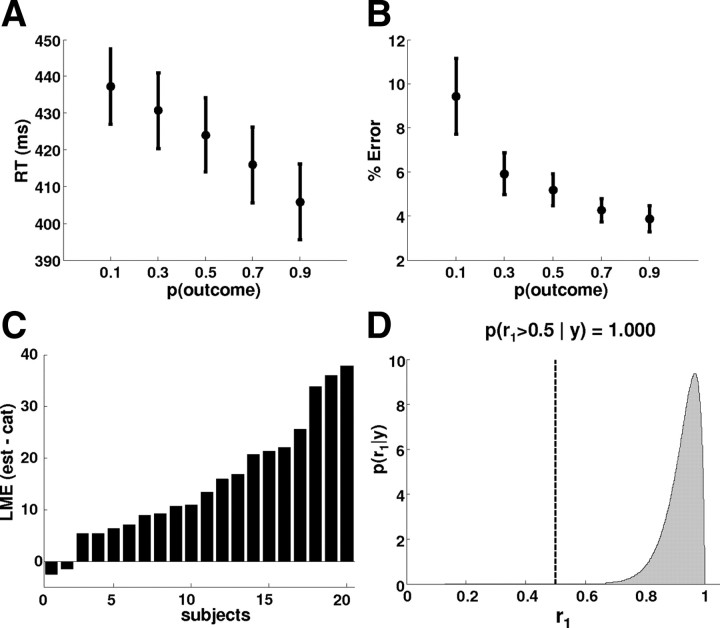
A, Timeline for a single trial. At trial onset, the auditory cue stimulus (CS) was presented for 300 ms. The visual outcome stimulus (OS) lasted for 150 ms and was presented 150 ± 50 ms after the CS. The intertrial interval lasted for 2000 ± 650 ms on average. B, Temporal evolution of the probability of a face occurring, p(F), given either CS. Note that the probability of a house being presented is simply the mirror image of this sequence. C, The posterior mean of p(F|CS) as estimated by the Bayesian learner (dashed line) tracks the underlying blocked probabilities (solid line). Note that the blocked probabilities are CS₂ zoomed in from B (trials 400–600, session 3). Because blocks of stable probabilities are short, however, the estimated probabilities never quite reach their true values during a given block. Note that the estimates change rapidly at block transitions. When an unexpected stimulus occurs, the estimates briefly move toward p = 0.5. Note that, for clarity, we only show a single session (session 3) here.

Timing and stimuli

On each trial, one of two auditory cue conditioned stimuli (CS₁ and CS₂) was followed by a visual target stimulus (Fig. 1A). To prevent anticipatory responses or guesses, both the intertrial interval (2000 ± 650 ms) and visual stimulus onset latency (150 ± 50 ms) were jittered randomly (Fig. 1A). Auditory stimuli were presented binaurally for 300 ms. The auditory stimuli were matched for perceived loudness under scanning conditions as described previously (den Ouden et al., 2009). The frequencies of the auditory stimuli used in this experiment were 1125 and 500 Hz, and the adapted volume of the high tone was 98 ± 4.1% (mean ± SD) with respect to the low tone. The visual stimuli were presented centrally for 150 ms to prevent saccades, and subjects were required to fixate a central cross throughout the experiment. The visual stimuli consisted of eight pictures of neutral facial expressions drawn from the Ekman Series of Facial Affect (Ekman and Friesen, 1976) and eight pictures of houses, matched for overall luminance and presented on a gray background. Stimuli were presented using the software package Cogent (www.vislab.ucl.ac.uk/Cogent).

Cue–outcome contingencies

The two tones differentially predicted the identity of the visual target stimulus, and these contingencies changed over the course of the task (Fig. 1B). Because each CS was followed by one of two stimuli (F or H), the probability of one visual stimulus, given a particular auditory CS, was one minus the probability of the other visual stimulus:

To ensure that participants' responses were not biased by learned expectations (e.g., about the relative frequencies of the visual stimuli), the marginal probabilities of faces and houses were identical at any point in time. This was achieved because, first, the probability of one visual outcome given CS₁ was the same as the probability of the other visual outcome given CS₂ (compare with Fig. 1B):

Second, each block contained equal numbers of randomly intermixed CS₁ and CS₂ trials. With these two manipulations, we ensured that, on any given trial, before the CS was presented, the a priori probability of a face (or house) occurring was always 50%. Thus, any expectations about the visual stimulus could depend only on the auditory stimulus.

Each subject completed five sessions of 200 trials each. In each session, the predictive strengths of the two CS types changed pseudorandomly over time, taking one of five different discrete levels of predictive association. Specifically, the cue could be (1) strongly predictive (p = 0.9), (2) predictive (p = 0.7), (3) nonpredictive (p = 0.5), (4) antipredictive (p = 0.3), and (5) strongly antipredictive (p = 0.1) of the visual stimulus. Each predictive level was presented as a block of stimuli once per scanning session. Predictive block lengths varied between 14 and 20 trials per CS type, so that participants could not predict exactly when a change in contingencies would occur. Furthermore, to avoid instantaneous and complete reversals of the contingencies, blocks containing predictive cues alternated with short blocks (6–10 trials) containing nonpredictive cues (i.e., p = 0.5) in order.

fMRI data acquisition

A 3 T head scanner (Allegra Magnetom; Siemens) was used to acquire a T1-weighted fast-field echo structural image and multislice T2*-weighted echo-planar volumes with BOLD contrast (repetition time, 2.73 s; echo time, 30 ms). Before the functional scans, a B₀ field map was acquired using a gradient echo field map sequence. Functional data were acquired in five scanning sessions lasting ∼8 min each. One hundred eighty-nine volumes were acquired per session (945 scans in total per subject). The first six volumes of each session were discarded to allow for T1 equilibrium effects. Each functional brain volume comprised 42 axial slices with 2 mm thickness and a 1 mm interslice gap and an in-plane resolution of 3 × 3 mm. The field of view was chosen to cover the whole brain, except for the brainstem.

Data analysis

Behavioral data analysis

First, the data were screened for outliers in reaction times, and responses faster than 150 ms were excluded. We then tested whether the distributions of RT and response speeds (RS) (i.e., inverse reaction times) showed significant deviations from normality using a Kolmogorov–Smirnov test. Because RS, but not RT, were well described by a Gaussian distribution, the former were entered into a repeated-measures ANOVA with outcome probability (five levels: 0.9, 0.7, 0.5, 0.3, and 0.1), CS type (CS₁, CS₂), and outcome type (F, H) as within-subjects factors. The Greenhouse–Geisser correction was used when significant nonsphericity was detected. The analogous analysis was performed on error rates.

Bayesian learning model

The linear model based on the true probabilities described above (henceforth referred to as the “categorical model”) explained a significant proportion of variance in reaction times and errors and as such provided a reasonable model of the behavioral data. However, it makes the unrealistic assumption that the participants have instantaneous and precise knowledge of the true probabilities that generated the stimulus sequence. In reality, the participants had to estimate these unknown probabilities trial by trial from the observed stimulus sequence. Thus, we aimed to find a more realistic model reflecting how subjects' continuously updated their estimates of the associations, based on past observations. Clearly, there are numerous potential models of such a process (Dayan and Daw, 2008; Dayan and Niv, 2008). Here we focused on a generic Bayesian learner model that accounts for both trial-by-trial updates of probability estimates and learning about the volatility of the environment (Behrens et al., 2007).

Previous studies have shown that many human perceptual and motor processes approximate the behavior of an ideal Bayesian learner (Kersten et al., 2004; Körding and Wolpert, 2006). Bayesian learners continually update their estimates of hidden contingencies by combining previous information from past experience with current observations in the present. In standard Bayesian learner models, the learning rate, and thus the relative influence of past versus current observations on the estimates, is constant. This, however, is not optimal when the underlying probabilistic associations are changing in an unknown and irregular manner, as in the task used in this study. In such an environment, an optimal learner would not only estimate the probabilities but also their instability in time (i.e., volatility) and would increase the weight of current observations, relative to past experience, with increasing volatility. To model the ongoing estimation of associative cue–outcome relationships based on observed outcomes, we used a hierarchical Bayesian learning model developed by Behrens et al. (2007). Given a series of observed events, this model estimates, at any given point in time, the posterior probability density function (PDF) of both the probabilistic associations and the volatility of the environment (see Fig. 2). Here, we adopted this model (for details of our implementation, see supplemental data, available at www.jneurosci.org as supplemental material) and used the posterior mean of the PDFs as estimates of the probability and volatility. To verify that the probability estimates of this Bayesian model were better linear predictors of the behavioral RS than the true probabilities from which the stimulus sequence was generated, we used Bayesian model selection (BMS) (see below). Given the clear superiority of probability estimates from the Bayesian model in explaining the behavioral data (see Results), they were used in the subsequent analyses of the fMRI data.

Figure 2.

RTs (A) and percentage of errors as a function of outcome probability (B) (mean ± SE). Correct trials were averaged within each level of probability and collapsed across CS and visual outcome type (F/H). Subjects speed up and make fewer errors the higher the probability of the outcome. C, Subject-specific differences in log model evidence (LME) for using the trial-by-trial probability estimates from the Bayesian model versus the true probabilities as linear predictors for behavioral measured response speeds. In all but two subjects, there is far greater evidence for the Bayesian model. D, The Dirichlet density describing the probability of model m₁ (based on the probability estimates from the Bayesian learning model) relative to the alternative model m₂ (based on the true, blocked probabilities), given the measured response speeds across the group. The shaded area represents the exceedance probability of m₁ being a more likely model than m₂. This exceedance probability of ϕ₁ = 100.0% was strongly favoring m₁ as a more likely model than m₂.

Based on suggestions by our reviewers, we tested three additional models that could potentially explain the behavioral data. First, we tested a standard Rescorla–Wagner model; in the reinforcement learning literature, this is referred to as a “model-free” approach because it has no knowledge about the environment or task structure. Furthermore, we evaluated two variants of a hidden Markov model that explicitly reflected task structure by representing transitions between the five different association levels (a “model-based” approach). Bayesian model comparison showed that the Bayesian learner model proved to be superior to any of these models. The main text of this manuscript therefore focuses on comparing the Bayesian learner to the categorical model based on the true probabilities. Details of the additional models and their comparison are included in the supplemental data (available at www.jneurosci.org as supplemental material). In particular, supplemental Figure S2 (available at www.jneurosci.org as supplemental material) juxtaposes the predictions from the different computational models about trial-by-trial estimates of cue strength, and supplemental Table S1 (available at www.jneurosci.org as supplemental material) lists the results of model comparison.

Bayesian model selection

When comparing different models for observed data, it is critical that the decision is not only based on the relative fit but also on the relative complexity of the competing models (Pitt and Myung, 2002). BMS provides a principled foundation for comparing competing models of different complexity (Penny et al., 2004). We used a novel hierarchical method for BMS that allows for group-level random-effects inference about the relative goodness of multiple competing models (Stephan et al., 2009). First, as described in the supplemental data (available at www.jneurosci.org as supplemental material), for all models considered, we computed the evidence p(y|m), i.e., the probability of the data y being generated by model m, for each subject. The model evidence balances fit and complexity, enabling one to compare non-nested models with different levels of complexity. For the linear models applied to the behavioral data, there is an analytic expression for the model evidence (for details, see supplemental data, available at www.jneurosci.org as supplemental material). For the nonlinear dynamic causal models of the fMRI data described below, we used the negative free-energy approximation to the log model evidence (Friston et al., 2007; Stephan et al., 2007b).

Subsequently, the models were compared at the group level, using random-effects BMS (Stephan et al., 2009). This method has been shown to be considerably more robust than either the conventional fixed-effects analysis using the group Bayes factor (Stephan et al., 2007b) or frequentist tests applied to model evidences, especially in the presence of outliers (Stephan et al., 2009). It uses variational Bayes to infer the posterior density of the models per se. One can then derive the exceedance probability, ϕ_k, i.e., the probability that a particular model k is more likely than any other model considered, given the group data. Exceedance probabilities are particularly intuitive when comparing two models, as in our analysis of the behavioral data (see Fig. 2D).

Functional neuroimaging analysis

fMRI data were analyzed using the SPM5 software package (Wellcome Trust Centre for Neuroimaging, London, UK; http://www.fil.ion.ucl.ac.uk/spm). The 915 echo planar images from each subject were corrected for geometric distortions caused by susceptibility-induced field inhomogeneities. A combined approach was used that corrects for both static distortions and changes in these distortions attributable to head motion (Andersson et al., 2001; Hutton et al., 2002). The static distortions were calculated for each subject by acquiring a B₀ field map and processing it using the FieldMap toolbox implemented in SPM5 (Hutton et al., 2004). The images were then realigned unwarped, slice-time corrected, and coregistered to the subject's own structural scan. The structural image was processed using a unified segmentation procedure combining segmentation, bias correction, and spatial normalization (Ashburner and Friston, 2005); the same normalization parameters were then used to normalize the echo planar images. Finally, the echo planar images were smoothed with a Gaussian kernel of 8 mm full-width half-maximum and resampled to 3 × 3 × 3 mm voxels.

The data were then modeled voxelwise, using the general linear model (GLM) for each of the 20 participants. In the GLM, correct and error trials were modeled as separate events. For correct trials, face and house trials were modeled as the two main conditions of interest. These were collapsed across the two different CS types (high and low tones), because the predictive strengths of the two CSs were counterbalanced over time and thus no differential effects were to be expected (this was confirmed by analysis of the behavioral data). Condition-specific effects were modeled in an event-related manner, convolving a sequence of delta functions with a canonical hemodynamic response function. The probability estimates from the Bayesian learner as well as the subject-specific response speeds were included as first-order parametric modulators of face and house trials such that the delta functions representing the presence of a face were modulated by the trial-specific probability estimate that a face should have occurred on this trial (equivalently for house trials). We also included the volatility estimates from the Bayesian learner as parametric modulators (orthogonalized with respect to the probability estimates). Finally, the six motion parameter vectors from the realignment procedure were included as regressors of no interest to account for variance caused by head motion.

After computing subject-specific contrast images of interest, random-effects group analyses across all 20 subjects were performed (Friston et al., 2005), using one-sided one-sample t tests and testing for both positive and negative BOLD responses. We report any responses that survived whole-brain correction at the cluster level (p < 0.05), with a voxel-level threshold of p < 0.001. For anatomically constrained a priori hypotheses concerning fusiform face area (FFA) and parahippocampal place area (PPA) (for stimulus-specific effects), putamen (for prediction errors), and anterior cingulate cortex (ACC) (for volatility; see supplemental material, available at www.jneurosci.org), we report activations that survived correction at the cluster level (p < 0.05; with p < 0.001 voxel-level threshold) within the region of interest. For the putamen and ACC, search volumes were generated using the PickAtlas toolbox using the AAL atlas (Maldjian et al., 2003); for stimulus-specific visual areas, we used in-built localizer contrasts that were orthogonal to the other contrasts of interest (see below).

First, we assessed the main effect of probability, that is, in which in brain regions the hemodynamic response reflected the probability of the stimulus occurring, independently of which stimulus it was. We tested for both BOLD responses that increased with the likelihood of the outcome and responses that increased the less likely (or more surprising) the outcome was. In other words, these contrasts tested for stimulus-independent responses that reflected predicted or surprising outcomes, respectively. Given the results from our previous study (den Ouden et al., 2009), our a priori hypothesis was that the response in the putamen would correlate positively with prediction error, i.e., negatively with the probability of the observed outcome.

Second, we tested for stimulus × probability interactions, that is, prediction error-dependent responses that differed between faces and houses. Our a priori hypothesis was that responses in stimulus-specific areas would scale inversely with the probability of the presented stimulus (cf. Friston, 2005; Summerfield et al., 2008). In other words, responses of the FFA to face stimuli should decrease when they were more probable, and responses of the PPA to houses should decrease with the probability of a house being presented. This can be regarded equivalently as testing for prediction error-dependent increases in the response of category-specific areas. To accommodate intersubject variability in the exact location of FFA and PPA, we identified these regions for each subject separately, using an embedded orthogonal localizer contrast (i.e., the main effect of faces versus houses and vice versa) (Friston et al., 2006). We verified, using the whitened design matrix, that localizing and test contrasts were indeed orthogonal (cf. Kriegeskorte et al., 2009). In each subject, the individual maximum within 8 mm of the group maximum of face- and house-specific responses (Table 1) was determined. Subsequently, given these voxels with individually maximal stimulus specificity, we tested for (orthogonal) stimulus × probability interactions by entering the parameter estimates of regressors encoding trial-by-trial stimulus probability estimates into two-tailed paired-sample t tests. In other words, this procedure tested whether face- and house-specific responses in FFA and PPA, respectively, were modulated by the trial-by-trial probability estimate of a face or a house occurring.

Table 1.

Montreal Neurological Institute coordinates and Z scores for significantly activated regions

Region	x	y	z	Z score
Prediction error effects: negativecorrelation with p(F) and p(H)
Motor areas
Left precentral gyrus (dorsal premotor cortex)*	−18	−18	60	4.13
Right intraparietal sulcus*	42	−33	39	4.02
Right superior parietal gyrus*	15	−60	63	4.16
Striatum
Right putamen**	27	3	6	3.42
Left putamen**	−24	15	3	3.39
Probability effects: positivecorrelation with p(F) and p(H)
No significant activations

*p < 0.05, cluster-level corrected across the whole brain;

**p < 0.05, cluster-level corrected for a priori region of interest.

Nonlinear dynamic causal models

Numerous studies have demonstrated previously that hemodynamic responses in the striatum reflect prediction errors (McClure et al., 2003; O'Doherty et al., 2004; Pessiglione et al., 2006; Jensen et al., 2007; den Ouden et al., 2009). According to theoretical models of learning, the size of prediction errors should control the strength of synaptic connections encoding stimulus–stimulus and stimulus–response links (McLaren et al., 1989; Schultz and Dickinson, 2000; Friston, 2005). In this study, we tested this notion directly by modeling how activity in the putamen gated the influence of visual areas onto the dorsal premotor cortex (PMd) (see Fig. 5). We expected that increased BOLD responses in the putamen, induced by a surprising face, should increase the strength of the FFA → PMd connection, thus enhancing the influence of face information on PMd activity and facilitating an update of the motor plan. This type of analysis, which requires the assessment of modulatory (second-order) effects on connectivity, has become possible with the recent introduction of nonlinear DCMs (Stephan et al., 2008).

In nonlinear DCMs, the hidden neural dynamics (i.e., not directly observed by fMRI) are modeled by the following equation:

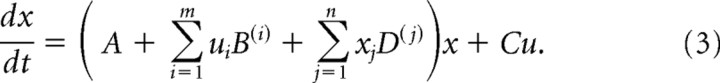Here, u are the experimentally controlled inputs, the A matrix represents the endogenous (context-independent or fixed) connection strengths between the modeled regions, the matrices B⁽ⁱ⁾ represent the modulation of these connections induced by the ith input u_i as an additive change, and the C matrix represents the influence of direct (exogenous) inputs to the system. Finally, the D^(j) matrices encode how connection strengths are modulated or gated by activity in area j (for details, see Stephan et al., 2008).

DCM specification.

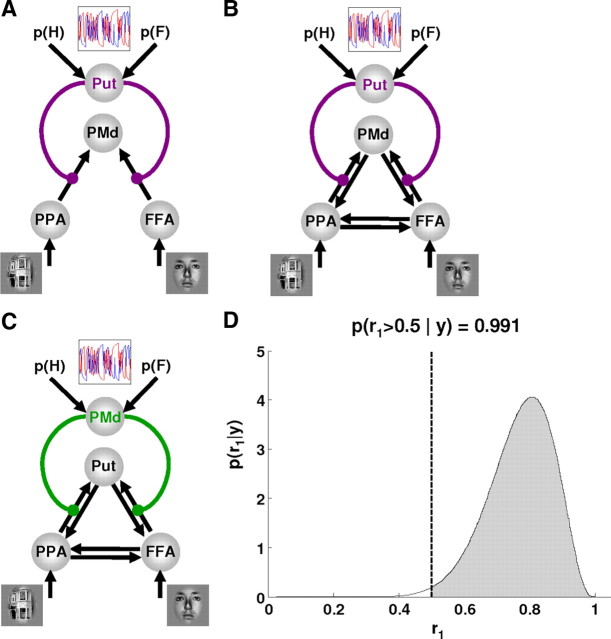
Based on our SPM results, we constructed a nonlinear DCM including the right putamen, PPA and FFA, and the left PMd. As shown in Figure 3 and Table 1, several other areas showed a prediction error-dependent response and may also be involved in the visuomotor information transfer. Therefore, the model we chose, including the above four regions, should be regarded as the most parsimonious model that enabled us to test whether prediction error activity in the putamen gated visuomotor connections. Although putamen, FFA, and PPA showed peak activations in the right hemisphere, we included the left premotor cortex because participants responded with their right hand.

Figure 3.

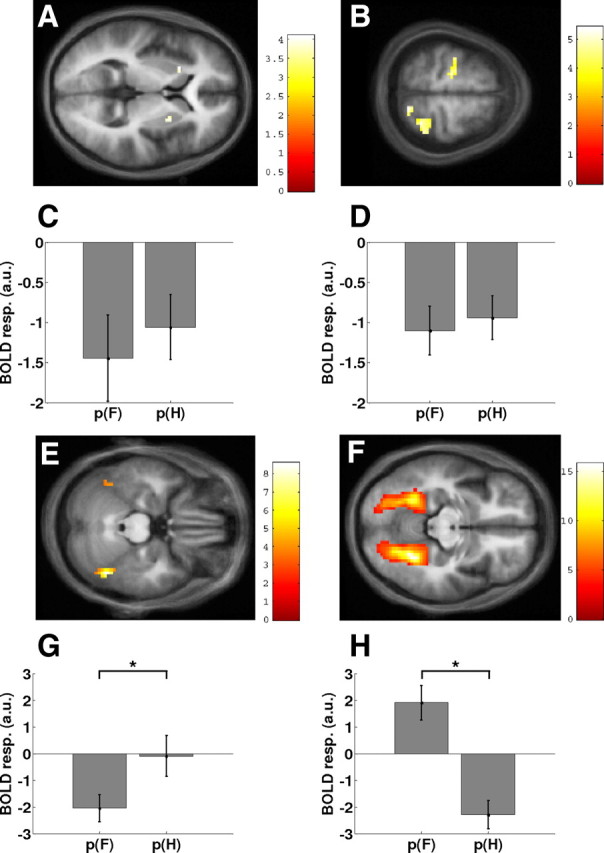
All parameter estimates show mean ± SE across all subjects, and all activations are displayed on the average anatomical scan. B and D–F show the results of a whole-brain analysis, and A, C, G, and H show the results from region-of-interest analyses. A, Effect of prediction error in the anterior putamen bilaterally. C, Parameter estimates from the putamen showing the negative dependency on both p(F) and the p(H). B, Effects of prediction error in PMd and the parietal cortex. a.u., Arbitrary units. D, Parameter estimates for the left PMd, showing the same prediction error-dependent effect as the putamen. E, Main effect of F > H in the right FFA, also showing the left FFA activation (see supplemental data, available at www.jneurosci.org as supplemental material). F, Main effect of H > F in the bilateral PPA. G, Parameter estimates of the modulatory effect of stimulus probabilities (from the individual maxima for the orthogonal F > H contrast in the FFA). There was a pronounced negative modulation of FFA responses to faces by the trial-by-trial probability estimates for faces (β = −2.05 ± 0.52). In contrast, the modulation of FFA responses to houses by the trial-by-trial probability estimates for houses was marginal (β = −0.09 ± 0.78). This difference was significant (*p = 0.037). H, Parameter estimates of the modulatory effect of stimulus probabilities across subjects (from the individual maxima for the orthogonal H > F contrast in the PPA). PPA responses to houses showed a strongly negative modulation by the trial-by-trial probability estimates for houses (β = −2.29 ± 0.54). In contrast, PPA responses to faces were positively modulated by the trial-by-trial probability estimates for faces (β = 1.91 ± 0.67). This difference was significant (*p = 0.00005).

We constructed and compared several alternative models. The basic architecture, shown in Figure 4A, included connections from FFA and PPA to the PMd and modulations of these connections by activity in the putamen, which was driven by the trial-by-trial probability estimates provided by the Bayesian learning model. The connectivity layout of our basic model was guided by anatomical and physiological data. For example, in the Macaque monkey, both ventral and dorsal parts of the lateral premotor cortex contain substantial numbers of neurons that respond to visual stimuli (Fogassi et al., 1999), including symbolic action-selection cues (Yamagata et al., 2009). These responses may be mediated by direct anatomical connections from inferotemporal to ventral premotor cortex (Webster et al., 1994; Gerbella et al., 2010) or by polysynaptic connections from various visual areas to dorsal premotor cortex, which are relayed via parietal and temporal areas (Matelli et al., 1998; Luppino et al., 2001; Tanné-Gariépy et al., 2002; Gamberini et al., 2009). The connectivity structure of this DCM was subsequently optimized systematically by BMS; the optimal model was found to include reciprocal connections between FFA, PPA, and PMd (for a graphical representation of all models tested, see supplemental Fig. S1, available at www.jneurosci.org as supplemental material).

Figure 4.

A, A basic DCM for investigating modulation of visuomotor connections by prediction error-related activity in the putamen. B, The optimal DCM (model m_pt), resulting from a systematic model search procedure, included full connectivity between the PMd, PPA, and FFA. Activity in the putamen significantly enhanced the connections from the PPA/FFA to the premotor cortex (p = 0.010 and p = 0.017, respectively). C, Alternative DCM (model m_pm) in which the roles of the putamen and the PMd were swapped. D, The Dirichlet density describing the probability of the “putamen ” model m_pt relative to the alternative “premotor ” model m_pm, given the measured fMRI data across the group. The shaded area represents the exceedance probability of m_pt being a more likely model than m_pm. This exceedance probability of ϕ₁ = 99.1% was strongly favoring m_pt as a more likely model than m_pm.

After the endogenous connections had been optimized, we conducted a final and critical model comparison. Because the putamen and the PMd showed similar prediction error-related responses (see Fig. 3), we wanted to establish the specificity of our model and demonstrate that putamen activity gated visuomotor connections, instead of PMd gating connections between visual areas and putamen. We therefore compared our model with one in which the roles of the PMd and the putamen were reversed (see Fig. 4C).

Time series extraction.

Because the exact locations of activation maxima varied across participants, we used subject-specific anatomical and functional constraints in selecting regional time series (cf. Stephan et al., 2007a). In brief, a regional time series was extracted if (1) it passed a threshold of p < 0.05 (uncorrected) in the respective contrast of the GLM analysis and if (2) it was located within a certain distance from the group maximum. For FFA and PPA (identified by the contrast testing for main effect of faces vs houses, F > H and H > F, respectively), the individual maxima were required to be within 8 mm of the group maximum. For the putamen and PMd (identified by the contrast testing for a negative main effect of probability), the individual maxima were required to be within 16 mm of the group maximum (PMd) and within the putamen as defined by the participant's own anatomical scan. To summarize the regional time series, we computed the first eigenvector across all suprathreshold voxels within 4 mm of the selected maximum. After this procedure, we were able to extract time series for all four areas in 15 of 20 participants. We could not obtain a putamen time series in three participants and a PMd time series in two participants because of failure to meet the anatomical and functional criteria above. Because we could not specify the complete model in these participants, they were excluded from the DCM analysis.

Results

Behavioral data

Subjects responded correctly on 91 ± 0.8% (mean ± SE) of trials, on 5% of the trials they gave the wrong response or pressed multiple buttons, and on the remaining 4% of trials they did not respond before the end of the trial.

Subjects responded faster (Fig. 2A) and more accurately (Fig. 2B) to more likely stimuli, indicating that they successfully tracked the changing contingencies. The difference in average reaction time between unexpected (p = 0.1) and expected (p = 0.9) outcomes across subjects was 32 ms (Fig. 2A). For formal hypothesis testing, we used inverse reaction times, i.e., RS, because these were more normally distributed than reaction times (cf. Carpenter and Williams, 1995). Repeated-measures ANOVA showed a significant relationship between both RS (F_(2.4,45.4) = 43.9; p < 0.001) and error rates (F_(1.5,334.0) = 12.52; p < 0.001) and stimulus probability.

As discussed in Materials and Methods, this ANOVA, although explaining a significant amount of variance, cannot be a realistic representation of the subjects' estimates of cue–outcome association strengths. We therefore used a hierarchical Bayesian learning model that estimates, from the observed cue–outcome combinations, the probabilistic associations given a series of observed events (Fig. 1C), and we tested whether the estimates of this Bayesian model were better linear predictors of the behavioral RS than the true probabilities from which the stimulus sequence was generated. The distribution of the log evidences across subjects (Fig. 2C) and random-effects BMS at the group level showed that the Bayesian learning model was unmistakably superior: the exceedance probability that the Bayesian learning model was the more likely model was almost 100% (Fig. 2D).

Following suggestions by our reviewers, we also compared the Bayesian learning model to a Rescorla–Wagner learning model and to two variants of a hidden Markov model reflecting the underlying task structure. The Bayesian model was found to be clearly superior to each of these additional models (for details, see supplemental data, available at www.jneurosci.org as supplemental material). Given this result, the trial-by-trial estimates from the Bayesian model were used in the subsequent analyses of the fMRI data.

fMRI data

The main results of our SPM analysis are summarized graphically in Figure 3.

Regional responses reflecting stimulus-independent prediction error

Responses in the bilateral putamen were negatively correlated with the probability of the visual stimulus, regardless whether this stimulus was a face or a house (Table 1; Fig. 3A,C). In other words, the BOLD response in the putamen increased the more surprising the outcome was. Other areas that showed this type of response included the left PMd, right intraparietal sulcus, and right superior parietal gyrus (Table 1; Fig. 3B,D).

Prediction error-related responses in stimulus-specific areas

The factorial design provided an in-built localizer contrast for defining the FFA and PPA functionally in each participant (see Materials and Methods). The individual peak voxels in right FFA and right PPA that showed maximally selective face and house responses, respectively, also showed an (orthogonal) stimulus × probability interaction: in the FFA, there was a pronounced negative modulation of response to faces by the trial-by-trial probability estimates for faces (β = −2.05 ± 0.52, mean ± SE). In other words, FFA responses to faces increased when the occurrence of a face was surprising (i.e., a large prediction error). In contrast, the modulation of FFA responses to houses by the trial-by-trial probability estimates for houses was negligible (β = −0.09 ± 0.78) (Fig. 3G). The difference in regression slopes between the two conditions (i.e., the interaction) was significant (t₍₁₉₎ = 2.25; p = 0.037).

The response in the PPA in response to houses showed a strongly negative modulation by the trial-by-trial probability estimates for houses (β = −2.29 ± 0.54) (Fig. 3H), that is, in analogy to the FFA results, PPA responses to houses increased the higher the prediction error, i.e., the more surprising the presentation of a house was. However, unlike the FFA analysis, PPA responses to faces were positively modulated by the trial-by-trial probability estimates for faces (β = 1.91 ± 0.67); this corresponds to a decrease in activity the more surprising the presentation of a face was. As for FFA, this interaction was significant (t₍₁₉₎ = 5.22; p = 0.00005).

In summary, responses of PPA and FFA to their preferred stimuli were strongly modulated by prediction error, and this modulation was significantly higher than for their nonpreferred stimuli.

Nonlinear DCMs

In line with numerous previous studies (McClure et al., 2003; O'Doherty et al., 2004; Pessiglione et al., 2006; Jensen et al., 2007; den Ouden et al., 2009), the BOLD response in the putamen reflected prediction errors. According to theoretical models of learning, the size of prediction errors should control the strength of stimulus–stimulus and stimulus–response links and thus connection strength (McLaren et al., 1989; Montague et al., 1996, 2004; Schultz and Dickinson, 2000; Friston, 2005). We tested this notion directly by modeling how activity in the putamen gated the information flow from visual areas to the PMd (Fig. 4). First, the fixed connections were optimized; the optimal model included full reciprocal connectivity between PPA, FFA, and PMd but no direct connections from either visual areas or PMd to the putamen (Fig. 4B). The exceedance probability for this model was ϕ₄ = 0.44, surpassing the exceedance probabilities of the other tested models (which ranged from 0.01 to 0.28) (for details, see supplemental data, available at www.jneurosci.org as supplemental material).

Once the most likely pattern of connections among the areas was established, we constructed a model to verify the specificity of the modulatory influence exerted by the putamen, given that the putamen and the PMd showed similar prediction error-related responses (Fig. 3C,D). BMS showed that the model in which the roles of the putamen and premotor cortex were reversed (m_pm, with PMd as source of modulatory effects) was clearly inferior to the original model (m_pt, with the putamen as source of modulatory effects), with an exceedance probability of 99% in favor of the latter (Fig. 4D). In the optimal model m_pt (Fig. 4B), the parameter estimates reflecting gating effects of putamen activity on visuomotor connections were consistently positive and significant across subjects [PPA → PMd: d = 0.01 ± 0.003 (mean ± SE), t₍₁₄₎ = 2.97, p = 0.010; FFA → PMd: d = 0.011 ± 0.004, t₍₁₄₎ = 2.71, p = 0.017]. Therefore, in accordance with our initial hypothesis, prediction error-related activity in the putamen significantly modulated the strength of visuomotor connections.

Discussion

In this fMRI study, we used an audiovisual associative learning paradigm, in which we ensured that any expectations about the upcoming visual stimuli were entirely conditional on the auditory cues. Critically, the predictive strengths of cues were unknown and varied over time, requiring subjects to continuously update their estimates of cue–stimulus associations and thereby maximizing demands on adaptive changes in network connectivity. We modeled this online inference process using a Bayesian learner model that generated trial-by-trial probability estimates. These were used as predictor variables in the analysis of behavioral and fMRI data. Behaviorally, speed and accuracy of motor responses increased significantly with trial-by-trial predictability of visual stimuli (Fig. 2). Analysis of the fMRI data showed that responses in FFA and PPA reflected trial-by-trial prediction errors that were specific for their preferred stimulus (Fig. 3C,D). In contrast, both the putamen and dorsal premotor cortex represented stimulus-independent prediction errors (Fig. 3A,B). Using nonlinear DCMs, we found that prediction error responses in the putamen modulated the strength of connections from FFA and PPA to premotor cortex.

Our fMRI data analysis showed a double dissociation of responses in the FFA and PPA. For both areas, responses to their preferred stimuli were strongly modulated by trial-by-trial prediction errors about these stimuli; moreover, this modulation was significantly higher than for their nonpreferred stimuli (Fig. 3C–F). This finding is consistent with predictive coding theories (Friston, 2005) and extends previous reports of enhanced FFA responses to surprising faces (Summerfield et al., 2008). In contrast, the bilateral putamen, left dorsal premotor cortex, right intraparietal sulcus, and superior parietal gyrus showed prediction error-related responses independent of whether the presented stimulus was a face or a house (Fig. 3A,B). In the present DCM analysis, we focused on the roles of the putamen and the premotor cortex. The prediction error-related responses of the latter likely reflects the updating of the motor plan that is necessary when the prediction evoked by the auditory cue is wrong (Mars et al., 2007b; Nakayama et al., 2008). In contrast, increased responses in the parietal areas more likely reflects an attentional updating process after unexpected visual stimuli. These areas have been studied extensively in attentional paradigms [e.g., using the Posner paradigm (Posner, 1980)] in which they show increased activation for unexpected stimuli, reflecting attentional changes in response to violations of previous expectations (Giessing et al., 2004; Thiel et al., 2004).

Previous neurophysiological and neuroimaging investigations of associative learning have primarily focused on region-specific prediction error responses, e.g., in the ventral tegmental area (Hollerman and Schultz, 1998; Yacubian et al., 2006; D'Ardenne et al., 2008) or the striatum (Schultz and Dickinson, 2000; McClure et al., 2003; O'Doherty et al., 2003, 2004; Corlett et al., 2004; Seymour et al., 2004; Tobler et al., 2006; Jensen et al., 2007; Menon et al., 2007). In contrast, to date, there has been only one empirical study examining effects of prediction errors on connectivity (den Ouden et al., 2009). This previous study of audiovisual associative learning found prediction error-related responses in the visual cortex and putamen, as well as a modulation of effective connectivity from auditory to visual cortex by prediction error. However, the source of this modulation remained anatomically uninformed. Furthermore, our previous study lacked behavioral evidence for learning (as a result of using an incidental learning paradigm), used nonspecific visual stimuli, and restricted learning to stationary probabilities. All of these limitations were overcome in the present study.

Prediction error-related responses in both dorsal and ventral parts of the striatum have been reported by numerous studies on very different types of learning. These results suggest that the striatum is sensitive to violations of learned contingencies, regardless of whether these contingencies signal reinforcement (McClure et al., 2003; O'Doherty et al., 2003, 2004; Seymour et al., 2004; Jensen et al., 2007; Menon et al., 2007), guide decision making (Corlett et al., 2004), or predict target stimuli (as in the current study), and even when these contingencies are not behaviorally relevant (den Ouden et al., 2009). Other fMRI studies showed that the striatum responds to nonrewarding, unexpected stimuli proportional to the salience of the stimulus (Zink et al., 2006), as well as to novel stimuli (Wittmann et al., 2007, 2008). These results suggest that the striatum may have a general role in processing unexpected events per se. One of the proposed functions of this striatal response is to reallocate processing resources to unexpected stimuli in both reward and nonreward contexts (Zink et al., 2006). Our results, showing that prediction error responses in the putamen indeed modulates information transfer from visual to motor areas, are consistent with such a gating role of the striatum.

Together, our results suggest that the increase of premotor activity for surprising visual outcomes is partially driven by stimulus-specific visual inputs that are gated by the degree of prediction error encoded by the putamen. In other words, the strength of effective connections from FFA and PPA to premotor cortex, which provide information about the appropriateness of the planned action, might change from trial to trial, depending on the mismatch between predicted and observed visual outcome, signaled by the putamen. This gating mechanism is consistent with anatomical studies that have reported indirect connections from the putamen to the premotor cortex via the ventrolateral thalamus (Alexander and Crutcher, 1990; Schultz, 2000). One possibility is that this increased input from sensory areas attributable to striatal gating serves to overcome the lower corticospinal excitability in trials with unexpected outcomes and to facilitate the execution of unprepared actions. Motor preparation increases the excitability of corticospinal projections (Mars et al., 2007a; van Elswijk et al., 2007), and, during probabilistic learning, motor output is biased according to contextual probabilities (Bestmann et al., 2008). Furthermore, there is increasing evidence suggesting that the striatum is involved in task switching and selection of motor programs (Mink, 1996; Cools et al., 2004, 2006; O'Reilly and Frank, 2006). Our finding that the striatum gates sensory information transfer to the premotor cortex suggests one mechanism by which the striatum could influence motor selection.

In a wider context, our results provide additional evidence for current theoretical accounts of brain function, such as predictive coding and the free-energy principle (Rao and Ballard, 1999; Friston, 2005), which posit a fundamental role of prediction errors for adaptive behavior and learning. A central notion of these accounts is the key role of prediction error-dependent synaptic plasticity in driving learning; this concept is also critical for other formal learning theories (Montague et al., 1996; Schultz et al., 1997; Schultz and Dickinson, 2000). In other words, the necessity of reconfiguring neuronal circuits during learning should be inversely proportional to how well those neuronal circuits are capable of predicting sensory stimuli. Although there is a vast literature on neuronal prediction error responses, only sparse direct evidence exists so far that synaptic plasticity (i.e., changes in effective connectivity) scales with the degree of prediction error (cf. den Ouden et al., 2009). The present study provides additional empirical evidence for this mechanism. Moreover, by identifying the putamen as a source of this prediction error-dependent modulation of connectivity, this study links the physiological mechanisms proposed by predictive coding and free-energy accounts of brain function to a large body of literature on prediction error-related responses in the striatum (McClure et al., 2003; O'Doherty et al., 2003, 2004; Corlett et al., 2004; Seymour et al., 2004; Jensen et al., 2007; Menon et al., 2007).

In summary, we used a combination of fMRI, computational (Bayesian) learning models, and DCMs to demonstrate parametric modulation of visuomotor coupling according to prediction error responses in the putamen. To our knowledge, this study is the first to demonstrate that trial-by-trial prediction error responses in a specific region modulate the coupling among other regions. Several neurobiological mechanisms for this type of plasticity have been suggested, including NMDA receptor-dependent short-term plasticity (for review, see Stephan et al., 2008), and it will be an important goal for future studies to identify which of these mechanisms is at work. The combination of computational models of learning and neurophysiological models of connectivity presented in this study represents a novel approach to model-based inference about synaptic plasticity during learning. This general approach may become useful in clinical studies, given the pathophysiological importance of synaptic plasticity for many brain diseases and our lack of other non-invasive methods for investigating it. Ultimately, this approach may help to establish neurophysiologically grounded diagnostic classifications of spectrum diseases, such as schizophrenia (Stephan et al., 2006).