A study of unusual Rayleigh matches in deutan deficiency

Abstract

Rayleigh match data were modeled with the aim of explaining the locations of match midpoints and matching ranges, both in normal trichromats and in subjects with congenital color deficiency. Model parameters included the wavelength of peak sensitivity of cone photopigments, the effective photopigment optical density, and the noise amplitude in the red-green color channel. In order to avoid the suprathreshold, perceptual effects of extreme L:M cone ratios on color vision, selective post-receptoral amplification of cone signals is needed. The associated noise is also amplified and this causes corresponding changes in red-green threshold sensitivity. We propose that the noise amplitude and hence the size of the matching range in normal trichromats relates to the known inter-subject variation in the relative numbers of L and M cones. If this hypothesis can be shown to account for the extremes of the red-green matching range measured in normal trichromats, it is of interest to establish the extent to which it also predicts the unexpected, small matching ranges that are observed in some subjects with red-green color deficiency. A subset of subjects with deutan deficiency that exhibited less common Nagel matches were selected for genetic analysis of their cone pigment genes in order to confirm the type of deficiency, and to predict the corresponding peak wavelength separation (δλ_max) of their two, long-wavelength cone pigments. The Rayleigh match model predicted accurately the midpoint and the range for the spectral differences specified by the genes. The prediction also required plausible selection of effective optical density of the cone pigments and noise. The noise needed varied, but the estimates were confined to lie within the limits established from the matching ranges measured in normal trichromats. The model predicts correctly the small matching ranges measured in some deuteranomalous subjects, principally accounted for by a low estimate of noise level in the red-green channel. The model also predicts the “normal” matches made by some subjects that rely on two hybrid genes and therefore exhibit red-green thresholds outside the normal range, typical of mild deuteranomaly.

1. Introduction

Rayleigh matches (Rayleigh, 1881) provide useful information that reflects differences in the properties of the mechanisms involved in the processing of chromatic signals. The midpoint and the range of red-green mixtures subjects accept as a match to the spectrally-narrow, yellow field vary significantly, both within “normal” trichromats and within color deficient observers (Nelson, 1938;Wright, 1946; Hurvich, 1972). The latter require either more red or more green light to match the color appearance of the yellow field. This observation and the pattern of variation in the intensity of the yellow field needed to match the extremes of the mixture of red and green lights are used to detect and classify the type of color deficiency involved (Franceschetti, 1928; Birch, 2001). The anomaloscope is generally regarded as very accurate in distinguishing the protanomalous from the deuteranomalous observer, although the relationship between the parameters of the match and the subject’s overall color discrimination sensitivity is known to be generally poor (Wright, 1946; Hurvich, 1972). A narrow red-green matching range is often taken to indicate high chromatic sensitivity, typical of normal trichromatic vision. The variability of the matching range within normal trichromats is large and this makes the direct comparison with color deficient observers more difficult. Unusual matches that have remained difficult to explain may, however, provide useful information on the properties of color mechanisms. Some subjects accept most, but not all of the red-green mixture range, others require significantly more red or green light in the match, but only accept a very narrow range of red green mixtures that yield a measure of chromatic sensitivity well within the range observed in normal trichromats. Other subjects produce Nagel matches with midpoints that fall just outside the normal range, but exhibit normal chromatic sensitivity while a small number of subjects exhibit slightly reduced chromatic sensitivity, typical of minimal deuteranomaly, but make normal matches both in terms of midpoint and range. It is therefore of interest to establish whether appropriate changes in δλ_max are sufficient to account for such observations and the almost continuum in chromatic sensitivity loss observed in red-green deficiency. In addition to discrete changes in the spectral tuning of photopigments that relate directly to the genetic coding of cone pigments (Neitz et al., 1991; Nathans et al., 1992; Asenjo et al., 1994), other parameters are also known to affect chromatic sensitivity. The optical density of cone photopigments affects both the quantum catch as well as the overall spectral responsivity function that can be achieved (Smith et al., 1978; He & Shevell, 1995; Thomas & Mollon, 2004). The variability in cone populations among normal trichromats and the effects this may have on the luminous efficiency function and color vision have been examined in the past (Cicerone et al., 1987; Cicerone & Nerger, 1989; Pokorny & Smith, 1987; Pokorny et al., 1991). The various findings suggest that although the luminous efficiency function of the eye relates directly to the relative numbers of L and M cones, color vision, in general, seems to be relatively unaffected. More recent studies have confirmed the large variation in L to M cones in normal trichromats (Hofer et al., 2005), and the absence of significant changes in their color vision (Miyahara et al., 1998; Neitz et al., 2002). These findings suggest the existence of possible mechanisms for post-receptoral amplification of cone signals that precede the formation of chromatic channels. The selective, post-receptoral amplification of cone signals may also account for the stability of unique yellow in subjects with large differences in L:M cone ratio (Brainard et al., 2000). Such mechanisms have been shown to exist in fish retinae and may even play a role in color constancy (Kamermans et al., 1998). Since the noise in the photoreceptor system is also amplified, it remains of interest to establish whether thresholds for detection of small color differences remain unaffected by the increased signal noise. The large variability in the matching range of red-green anomaloscope matches ((0.9 log units) is similar to the spread in L:M cone ratios ((1 log unit) observed in normal trichromats. This observation suggests the possibility that the inherent noise in the red-green color discrimination channel affects the size of the matching range in normal trichromats and relates directly to the selective amplification of cone signals needed to null out the effect of large differences in L:M cone ratio. Anomaloscope match parameters show significant variability both within normal trichromats and within color deficient observers (see Fig. 3). In addition to the large inter-subject variability in match range within normal trichromats some color deficient observers that require either a lot of green or a lot of red to match the perceived color of the monochromatic yellow field produce very small matching ranges, sometimes smaller than the mean normal range. Other subjects, often described as “extreme anomalous” trichromats (Birch, 2001) accept most of the red-green mixture range as a match to the monochromatic yellow field, except for a very narrow region in the extreme red or green sections of the range. It remains unclear as to what parameter changes are needed to account for these “unusual” matches. In order to explain such unusual observations and the large variation in the parameters of the yellow match one observes experimentally, we produced a generic model of Nagel anomaloscope behavior that allows us to predict how smooth changes in cone spectral responsivity functions, cone optical densities, the noise level in the red-green color discrimination channel and the choice of yellow, red and green anomaloscope lights and their spectral width affect the parameters of the yellow match. In addition, we also derived measures of chromatic sensitivity from both anomaloscope matches and from direct measurements of chromatic detection thresholds in normal trichromats and in subjects with deutan deficiency.

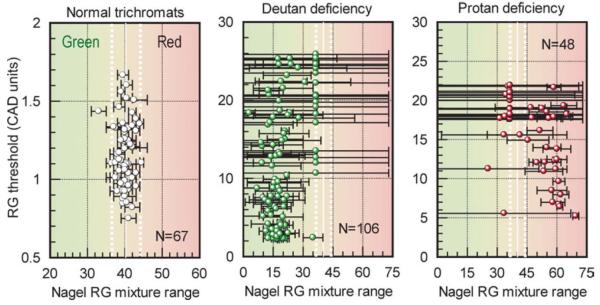
Fig. 3.

Comparison of CAD rg thresholds with the corresponding yellow match parameters (i.e., midpoint and range) measured in normal trichromats and in subjects with deutan and protan like deficiencies. The red-green matching range shows poor correlation with the measured rg threshold in all subject groups (including the normal trichromats).

2. Experimental methods

2.1. Subjects

The study involved normal trichromats (131) and subjects with deutan (106) and protan (48) deficiency. 15 subjects from the deutan group who made unusual anomaloscope matches were selected for genetic analysis of their cone pigment genes. The sample was not random and may not therefore reflect typical deutan-like deficiency. The tenets of the Declaration of Helsinki were followed and the study was approved by the Senate Research and Ethical Committee of City University and the Internal Review Board for human research at the Medical College of Wisconsin. Informed consent was obtained after detailed explanations were provided to each subject as to the nature of the study and the experimental tests involved. In addition to occupational color vision tests (e.g., Ishihara, AO-HRR, Holmes-Wright lantern), thresholds for detection of red-green and yellow-blue color differences were also measured using the CAD (Color Assessment and Diagnosis) test.

2.2. Anomaloscope matches

Each subject made Nagel anomaloscope matches (Nagel Type I, Schmidt and Haensch GmbH and Co., Berlin, Germany) to establish the matching range and the Y setting of the intensity of the yellow hemifield needed to match the mixture field at each extreme end of the matching range. This instrument has been described as having a visual field of 28 diameter (Helve, 1972). The measured visual field of our instrument is, however, 38 and we can therefore only assume that not all Nagel Type I instruments had the expected, 28, visual field. Fig. 1 shows the bi-partite field of the anomaloscope with the yellow hemifield (λ_Y = 589 nm) and the red-green mixture field (λ_R = 650 nm and λ_G= 546 nm). Two control knobs are used, one to alter the red-green color mixture ratio and the other to alter the intensity of the spectrally narrow, yellow field. The limits of the matching range were determined first by allowing the observer to make several initial exact color and luminance matches. Then the examiner sets a predetermined red-green mixture ratio (based on the mean of the observer’s initial matches) and the observer has to adjust only the intensity of the yellow half-field in order to achieve the best possible match. Using the same procedure, a number of red-green mixture ratios were investigated on either side of the mean in order to establish the extreme ends of the range when the subject was first unable to match the two hemifields by adjusting only the intensity of the yellow half-field. After every match the observer looked away from the instrument for several seconds before making another match. The ambient illumination in the testing room was provided by a distant tungsten-halogen lamp and the background illumination around the apparatus was low photopic. The number of scale units between the matching limits was recorded as the matching range. The midpoint was then recorded as the midpoint value of the red-green matching range. Two separate measurements were carried out in each subject and the mean of the two estimates was recorded.

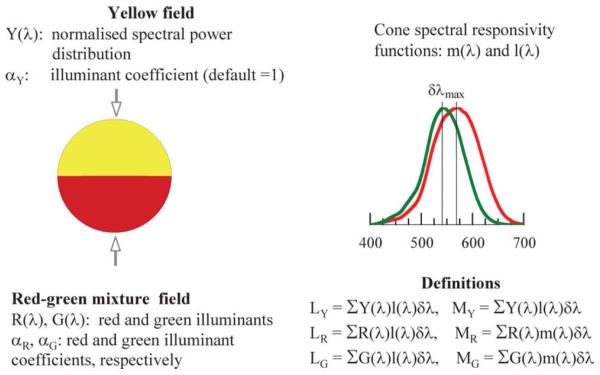
Fig. 1.

Schematic representation of the red-green mixture field and the cone spectral responsivities, m(λ) and l(λ). The equations given form the basis of the Nagel model described in the text.

The average midpoint of the range for the group of normal trichromats was 39.76 ±1.56 (with extreme values of 36.5 and 44.5) Nagel units. The mean matching range was 3.98±1.38 units (with extreme values of one and nine units). The size of the matching range, referenced to the mean normal range can be used as a convenient measure of red-green discrimination sensitivity, e.g., the Red-green discrimination Index (RGI) is defined as (1-(R-MR)/73), where R denotes the subject’s matching range and MR the mean range. This definition produces RGI values that range from close to zero for a dichromat to around one for normal trichromats.

2.3. CAD thresholds

The CAD test employs dynamic random luminance contrast noise to isolate the use of color signals by masking the detection of any residual luminance contrast components in the “isoluminant,” color-defined test stimulus (Barbur, 2004; Barbur et al., 1994). The appearance of the colored stimuli for color directions that favor red-green (rg) and yellow-blue (yb) discrimination is shown in Fig. 2. The color-defined test patch moves diagonally in one of four possible directions over a background of checks that vary randomly in luminance within a range specified as percentage of background luminance (e.g., ±45%). The color signal strength needed for threshold detection of the moving test stimulus for each hue direction investigated is measured using a four-alternative, forced choice procedure. The subject’s task is to indicate or guess the direction of movement of the color-defined stimulus by pressing one of four corresponding buttons. The mean rg and yb thresholds are computed by averaging the chromatic signal strength measured in each of the eight hue directions that describe the orientation of each chromatic channel. The results are plotted in the Commission Internationale d’Eclairage (CIE)1931 color system. The chromatic thresholds measured in 250 normal trichromats provide information on the statistical distribution of variability in such measurements (Rodriguez-Carmona et al., 2005). By dividing the subject’s thresholds by the median values for rg and yb discrimination, respectively, the results can be expressed in standard “normal” CAD units which are easier to interpret. CAD based chromatic sensitivity is defined simply as the reciprocal of the corresponding color thresholds when expressed in standard normal CAD units. These values range from close to zero for dichromats to values around one for normal trichromats.

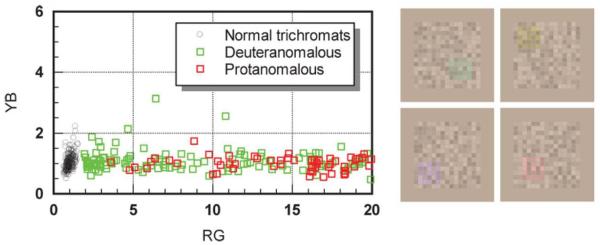
Fig. 2.

The colored insets show typical red-green (rg) and yellow-blue (yb) stimuli employed in the CAD test. The graph shows rg and yb thresholds (measured in CAD units) for 250 normal trichromats and 250 red-green color deficient observers. A small number of subjects exceed 20 CAD units for rg discrimination and their thresholds are limited by the phosphors of the display. The distribution of CAD test thresholds separates clearly the normal trichromats from color deficient observers.

2.4. Genetic analysis

Blood samples were taken from 15 subjects with deutan deficiency that exhibited unusual Nagel match parameters. The polymerase chain reaction (PCR) was used to selectively amplify L genes, and exons 2, 3, and 4 were sequenced as previously described (Neitz et al., 1996). The predicted spectral separations between L pigments in deutan subjects were calculated based on the deduced amino acid sequences of the L cone opsins (Carroll et al., 2002). δλ_max values for each subject are given in Table 1.

Table 1.

Summary of the cone pigment genes and the corresponding spectral separation (δλ_max) in the group of 15 subjects with deutan-like deficiency investigated in this study. The first column indicates the sequence of cone pigment genes in the array as determined genetically. Note that with the exception of the first four subjects that have only one L cone pigment gene in the array and are therefore deuteranopes, the remaining color deficient subjects rely on both normal and variant L cone pigment genes. These provide a wavelength separation in the range 2.5 to 10 nm. The corresponding optical densities of the variant and the normal L-cone genes are indicated as OD(L’ ) and OD(L). Other parameters such as the equivalent Nagel range, RGI (red-green discrimination index) and red-green and yellow-blue CAD thresholds are also given. The Nagel model predicts well the mid point of each match for the corresponding, non-zero δλ_max value by appropriate adjustment of cone pigment optical densities and selection of equivalent Nagel range. The latter is defined as the Nagel range the subject would have if no color deficiency was involved and the δλ_max corresponded to the expected value in normal trichromats. Interestingly, we were unable to predict the Nagel range measured experimentally with any combination of selected parameters for one of the four deuteranopes (second entry in the table, Nagel range: 3 to 52 units). The model does, however, predict accurately the measured range for the parameters shown in the table, provided one assumes a wavelength separation of 2.5 and not zero nm, as predicted from genetics (see Results section for possible explanations for this finding). The RGI is defined as 1-(R-MR)/73, where R is the subject’s range and MR is the mean matching range estimated in 67 normal trichromats. The CAD unit is the median threshold value estimated from data measured in 250 normal trichromats. The red-green and yellow-blue chromatic detection thresholds are expressed in CAD units and the reciprocal of these thresholds provide a measure of chromatic sensitivity. The use of RGI and reciprocal CAD units makes it convenient to compare different measures of chromatic sensitivity

#L, #M genes	Predicted phenotype	Derived δλmax	Nagel	RGI	OD(L’)	OD(L)	Equiv. Nagel range	Red-Green (CAD units)	Yellow-Blue (CAD units)
1L, 0M	deuteranope	0	0–50	0.37	0.415	0.5	4	24.9	1.2
1L, 0M	deuteranope	0 (2.5?)	3–52	0.37	0.32	0.21	2.2	23.5	0.9
1L, 0M	deuteranope	0	0–48	0.37	0.405	0.495	4	21.9	l.l
1L, 0M	deuteranope	0	0–56	0.27	0.415	0.49	4	17.6	1.0
3L, 2M	deutan	2.5–0	8–33	0.76	0.425	0.335	1.4	15.1	0.8
2L, 1M	deutan	2.5	0–28	0.67	0.5	0.52	4	13.5	1.3
2L, 2M	deutan	2.5	0–37	0.53	0.5	0.5	5.2	12.2	0.9
2L, 2M	deutan	2.5	0–8	0.94	0.35	0.7	2	17.4	0.8
2L, 2M	deutan	2.5	2–31	0.70	0.27	0.245	2.2	13.6	1.4
2L, 1M	deutan	6–3.5	11–14	0.99	0.28	0.51	1.2	2.8	0.9
2L, 3M	deutan	6	8–15	0.94	0.3	0.57	2.2	3.3	1.0
2L, 1M	deutan	6	14–23	0.94	0.32	0.335	2.4	2.9	0.8
2L, 0M	deutan	6.5	15–18	0.99	0.56	0.46	1	2.6	0.8
2L, 1M	deutan	10	15–17	1.00	0.5	0.61	1	2.0	1.2
2L, 1M	deutan	10	15–18	1.00	0.5	0.59	1.2	2.6	1.0
1L, 1M	normal	28	38–42	1.00	0.5	0.5	4	1	1

2.5. Modelling the Nagel anomaloscope matches

The effects the spectral separation and the optical density of cone photopigments have on the parameters of the yellow match have been modeled in the past (Pokorny & Smith, 1977; He & Shevell, 1995; Thomas & Mollon, 2004). In this study, we introduce an additional parameter, the “equivalent” Nagel range as a way of quantifying the noise introduced in the red-green color channel through selective cone signal amplification needed to counteract the effect of extreme L:M cone ratios. The hypothesis we put forward is that in order to account for the measured extremes in the Nagel matching range in normal trichromats, the noise level in the red-green color channel must vary just under 10-fold and that this variation is likely to be caused by the very similar variation in the relative numbers of L and M cones. The aim was to produce a generic model with variable parameters that could be selected to emulate desired conditions. We start by defining the “standard” normal trichromat with Nagel match parameters of 40 (midpoint) and a matching range of ±2 Nagel units. Two approaches have been implemented to generate spectral extinction functions for cone pigments. The first approach employed an implementation of the pigment template proposed by Govardovskii et al. (2000) with appropriate filtering for macular pigment and lens absorption (Stockman et al., 1999). This approach was deemed unsatisfactory, largely because the predicted spectral responsivity functions for normal trichromats differed significantly from the mean functions available in the literature. This is no longer surprising, given the complex pre-receptoral filtering of light in the human eye (van de Kraats & van Norren, 2007). The second empirical approach makes use of the average, normal L and M spectral responsivity functions that already incorporate selective pre-absorption of light in the eye (Wyszecki & Stiles, 1967; Stockman & Sharpe, 2000). A simple algorithm was developed to produce any spectral responsivity function in the range 542 to 570 nm by appropriate morphing of mean M and L curves for normal trichromats. The algorithm can make use of any standard mean functions, m (λ) and l (λ). Any new pigment spectral responsivity, new (λ), with peak wavelength sensitivity between 542 and 570 nm can be generated using a simple algorithm:

$$new\left(\lambda \right)=\left(\frac{ml-\delta \lambda }{ml}\right)\ast l(\lambda -\delta \lambda )+\left(\frac{\delta \lambda }{ml}\right)\ast m(\lambda +ml-\delta \lambda )$$

where, mλ, is the maximum wavelength separation between the normal M and L cone pigments and, δλ, represents the shift in peak wavelength sensitivity of the new pigment with respect to the 570 nm peak. This simple expression has the advantage of smooth morphing of the spectral responsivity function from l(λ) to m(λ), as dl increases from zero to the maximum separation, ml. The Stockman and Sharpe (2000) cone fundamentals employed in this model have already been weighted by the average prereceptor filters in the eye. Any changes in pre-receptoral spectral absorption, as the green primary shifts toward longer wavelengths is likely to be small and has not therefore been included in the model. The Stockman and Sharpe fundamentals assume peak optical densities of 0.5 log units for both the M and L cone pigments. This information makes it possible to calculate the corresponding spectral extinction function of each pigment and this can then be used to generate new spectral responsivity functions for any specified peak optical density. The fraction of photons absorbed by a given photo-pigment as a function of wavelength is given by:

$$F\left(\lambda \right)=1-{10}^{O{D}^{\ast }\epsilon \left(\lambda \right)},$$

extinction function of the pigment. The computation of L and M cone signals for both the yellow reference and the red-green mixture fields make use of the abbreviated equations shown in Fig. 1. The next step in the modeling work makes use of the parameters that define the standard normal trichromat. These are the mean l(λ) and m(λ) functions with peak optical densities of 0.5. The weights that need to be applied to each illuminant are calculated so that for the normal trichromat, the M and L cone signals generated in response to yellow light equal the M and L cone signals generated in response to the red-green mixture field. This can be expressed as follows: Cone signals generated in the yellow field:

$$L_{◻}\&M_{◻}$$

Cone signals generated in the red-green mixture field:

$$\begin{array}{cc}\hfill L_{RG}& ={\alpha }_R{L}_R+{\alpha }_G{L}_G\hfill \\ \hfill M_{RG}& ={\alpha }_R{M}_R+{\alpha }_G{M}_G\hfill \end{array}$$

Equality of corresponding cone signals in the upper and lower half-fields ensures equal perceived luminance and color:

$$\begin{array}{cc}\hfill L_{◻}& ={\alpha }_R{L}_R+{\alpha }_G{L}_G\hfill \\ \hfill M_{◻}& ={\alpha }_R{M}_R+{\alpha }_G{M}_G\hfill \end{array}$$

Hence once can solve for α_R & α_G

$$\begin{array}{cc}\hfill {\alpha }_R& =(L_G{M}_{◻}-M_G{L}_{◻})∕(M_R{L}_G-M_G{L}_R)\hfill \\ \hfill {\alpha }_G& =(M_{◻}{L}_R-M_R{L}_{◻})∕(M_G{L}_R-M_R{L}_G)\hfill \end{array}$$

We can now define a color difference signal as a normalized difference in cone signals between the two half fields:

$$\delta C=(L_{◻}-M_{◻})∕(L_{◻}+M_{◻})-(L_{RG}-M_{RG})∕(L_{RG}+M_{RG})$$

The equation above yields zero color difference signal for the red-green mixture field needed at match point (i.e., when L_□ = L_RG and M_□ = M_RG). The red and the green illuminants are allowed to vary linearly as a function of the Nagel scale reading (i.e., 1 to 73 units) with gradients selected to correspond to a color match for a reading of 40 units (as measured for the average normal trichromat). This is done simply in order to translate the parameters of the normal match to the scale units employed in the Nagel anomaloscope. The model assumes that the noise in the red-green color discrimination channel determines the matching range. The latter can vary from one to nine, with a mean of ±2 Nagel units. The noise in the system is therefore controlled by computing the noise-equivalent signal change (i.e., ± rg noise) that corresponds to a specified matching range. The latter can vary from one to nine units (see Fig. 5C), as measured experimentally in normal trichromats. The computation involves the following steps:

• Select a value, x, in the range one to nine for the subject’s matching range. The assumption we make here is that normal trichromats have approximately constant δλ_max and therefore the variation in red-green matching range is determined largely by the noise in the red-green channel which in turn relates to the L:M cone ratio.

• Calculate the signal change, ±δC, that corresponds to a matching range of 40 ± x/2 Nagel units. This represents the noise equivalent signal change labeled as ± rg noise and for this we use the standard normal spectral responsivity functions of L and M cones separated by 28 nm.

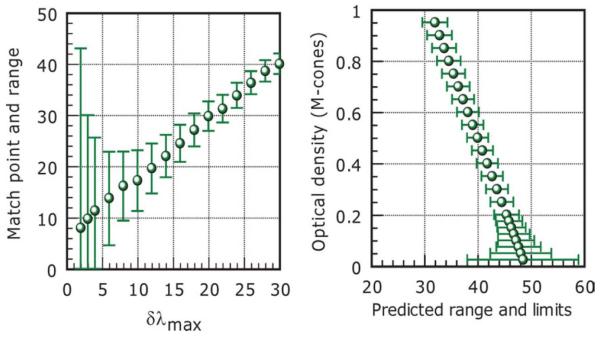
• The model can now compute the exact red-green mixture needed to produce L and M photoreceptor signals that equal those generated by the monochromatic yellow field for any shift in the L and0or M spectral responsivity functions, and/or any change in the optical density of the cones. In addition, for any set of parameters, the model also computes the predicted matching range, i.e., the shift away from the exact match point, either towards the green or the red extremes of the matching range, needed to produce the selected noise equivalent signal change, ± rg noise. For any set value of noise-equivalent signal change, the size of the predicted matching range increases as δλ_max decreases and is also affected by changes in the optical density of cones. The model has been used to investigate how changes in spectral primaries and pigment optical densities of cones affect the midpoint and the range of the match. The index of chromatic sensitivity, RGI, defined for real Nagel matches can now also be used to compute the red-green chromatic discrimination sensitivity predicted by the model.

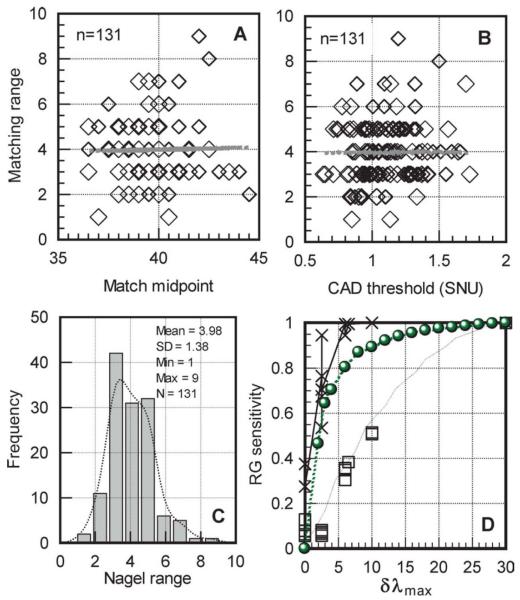
Fig. 5.

Section A shows the lack of correlation between match midpoint and matching range for 131 normal trichromats. The best-fit straight line is given by: y = 8.2757 - 0.1013 * x (r2 = 0.011). Section B shows the matching range in the same subjects plotted against the subject’s corresponding CAD threshold (expressed in standard normal units). There is again no correlation between the matching range and the subject’s measure of red-green chromatic sensitivity (y = 3.318 + 0.768 * x; r² = 0.011). Section C shows the distribution of the matching range in the same group of normal trichromats. The matching range can vary from as small as one unit, in the subject with the highest red-green discrimination, to nine units in the subject with the worst discrimination. Section D plots measures of red-green chromatic discrimination sensitivity for the 15 subjects with deutan like deficiency listed in Table 1. The same index (i.e., RGI = 1-(R-MR)/73) is used to define chromatic sensitivity for both model predictions and measured anomaloscope matches. The crosses plot the subject’s measured chromatic sensitivity index (RGI) based on individual Nagel matches. The open squares show the measured rg sensitivity for the same subjects based on their CAD rg thresholds. The green disc symbols plot RGI values based on the matching range predicted by the model (when the only parameter that changes is δλ_max).

3. Results

Table 1 summarizes both the genetics and the chromatic sensitivity data for the 15 subjects with deutan deficiency selected for the study. The potential cause of deficiency as revealed from genetics and the predicted dlmax values correlate well with the CAD measures of chromatic sensitivity and the classification of deficiency based on color assessment. The measured Nagel match parameters and the model predictions based δλ_max values derived from genetics are also listed. The results show that for the derived δλ_max values, it is possible to predict the measured Nagel midpoint and range using appropriate cone pigment optical densities and a level of red-green channel noise (selected from within the normal range). Although the solution for each subject is not unique, the results show that no other parameters are needed to predict the unusual matches made by the deutan subjects involved in this study. The Nagel model was, however, unable to predict the yellow match parameters in one subject classified as a deuteranope (second entry in Table 1) with zero δλ_max (matching range: 3 to 52 in the dominant eye and corresponding Y settings of 13 and 11, respectively). The subject’s CAD threshold was very high (23.5 times the normal threshold) and consistent with dichromacy. The Nagel matching range in the non-dominant (right) eye was seven to 45 (with a Y setting of 13 for both extremes of the matching range). The extreme values of the matching range in each eye were retested several times and the results remained unchanged. The model can, however, predict the Nagel match parameters for this subject (as shown in Table 1), but only with a peak wavelength separation of ;2.5 nm. Pokorny and Smith (1981) have shown that some dichromats fail to accept the full width of the Nagel range as a match to the yellow field and they attributed this observation to rod intrusion. This implies that signals from more than two classes of cone pigments may contribute to the perception of the yellow and the red/green matching fields. Other observations such as the subject’s variation in color matches with retinal irradiance level support this hypothesis. There are therefore several possibilities to explain our subject’s unusual Nagel matches. The genetic prediction of dichromacy is consistent with extreme red-green CAD thresholds (set by the limits of the phosphors). The CAD test employs higher retinal illuminance levels that are less favorable to rods and also minimizes the use of luminance contrast signals using dynamic luminance contrast noise. The intrusion of rod signals either in the generation of color or luminance contrast within the ;38 field of the Nagel anomaloscope employed in this study therefore remains a real possibility. The differences between the two eyes may well reflect differences in rod intrusion. More experiments are, however, needed to establish whether the subject’s matches can be extended to the full range with stimulus conditions that are less favorable to rod vision. Fig. 2 shows yb and rg thresholds for 250 normal trichromats and 250 subjects with red-green deficiency. The cluster of normal trichromats separates sufficiently from subjects with minimal deuteranomaly who often pass occupational color vision tests. The rg thresholds form a continuum that extends to over 20 standard CAD units (normally limited by the phosphors of the display). Minimum protanomalous subjects exhibit much larger thresholds than minimum deuteranomalous, an observation that may well be related to larger differences in dlmax that arise in polymorphic L-class pigments (Winderickx et al., 1992; Neitz et al., 1999, 2004; Neitz & Neitz, 2000; Carroll et al., 2002) when compared to the M-class pigments. Fig. 3 shows how the parameters of the yellow match relate to rg CAD thresholds in normal trichromats and in subjects with red-green color deficiency. The results confirm findings from previous studies which show poor relationship between the midpoint and the size of the corresponding matching range. In addition, the data also show the lack of correlation between the CAD measure of rg chromatic threshold and the size of the matching range. Fig. 4 shows an example of model predictions of match point and range as a function of δλ_max. All other parameters remained constant and equal to those that describe the standard normal trichromat. Interestingly, the midpoint of the match shifts linearly with δλ_max, but the size of the matching range increases quite rapidly for small δλ_max values. The effect of optical density changes on midpoint and range is also shown. Fig. 5. sections A and C show how the yellow match parameters vary within normal trichromats. The data in section A reveal the lack of correlation between match midpoint and matching range for 131 normal trichromats. These results are of interest since they suggest that the factors that cause the variability within the size of the matching range and the midpoint of the match are different. The model predicts the observed spread in match midpoint with only ±2 nm shifts in δλ_max. The extremes of the matching range (i.e., one to nine Nagel units) are similar to the 10-fold variability in L:M cone density ratios. Section C summarizes the statistics of the Nagel range with a mean of 3.98 units and a standard deviation of 1.38. The matching range can vary from as small as one unit, in the subject with the highest red-green discrimination, to nine units, in the subject with the worst discrimination. Section B shows the matching range in the same subjects plotted against the subject’s corresponding CAD threshold (expressed in standard normal units). The correlation between the matching range and the subject’s measure of red-green chromatic sensitivity is again very poor and this is consistent with previous findings (Wright, 1946; Hurvich, 1972). Section D plots measures of red-green chromatic discrimination sensitivity for the 15 subjects with deutan like deficiency listed in Table 1. The same index (i.e., RGI = 1-(R-MR)/73) is used to define chromatic sensitivity for both model predictions and measured anomaloscope matches. The crosses plot the subject’s measured chromatic sensitivity index (RGI) based on the individual Nagel matches. The open squares show the measured rg sensitivity for the same subjects based on their CAD rg thresholds. The green disc symbols plot RGI values based on the matching range predicted by the model (when the only parameter that changes is δλ_max). The number of subjects involved in the genetics study was small and the selection of these subjects was in no way random. The subjects were selected because of their unusual matches (i.e., normally classified as extreme anomalous trichromats or subjects with red-green matching range size that are similar to those measured in normal trichromats). The model prediction of chromatic sensitivity is therefore not inconsistent with the RGI values measured experimentally. There is poor agreement with the measure of chromatic sensitivity based on the CAD test and this observation is consistent with the results obtained in normal trichromats. The CAD and Nagel definitions of chromatic sensitivity equate only for the extreme values of the range. It remains to be established whether the poor agreement between the CAD- and Nagel-based measures of red-green chromatic sensitivity reflect the effect of differences in stimulus parameters or simply the effect of using different definitions of chromatic sensitivity.

Fig. 4.

Model output showing how the yellow match parameters change with the spectral separation between the two cone pigments (left section). The mean Nagel range for the “normal trichromat” is assumed to be four units and all other model parameters such as cone pigment optical densities remain unchanged. The section on the right shows how changes in the optical density of the photopigment can affect the match midpoint and matching range. All other parameters remained unchanged.

Fig. 6 shows CAD thresholds measured in a subject who passes the Nagel anomaloscope test with a midpoint of 41 and a range of three units. The subject has reduced red-green chromatic sensitivity that is similar in severity to that observed in minimal deuteranomalous observers. The model predicts the subject’s Nagel match parameters for modified M and L cone fundamentals (i.e., M and L cones shifted in λ_max by 6 and 10 nm, respectively), together with a noise-equivalent Nagel range of two units and modified optical densities of 0.625 and 0.575, respectively. This finding is important since it shows clearly that subjects with unusual deficiencies that should be classified as color defectives can pass the Nagel as normal trichromats.

Fig. 6.

Measurements of chromatic detection thresholds in a 24 year old female subject with “normal” color vision. The subject fails some plates on the Ishihara test ;3 possible misreading!, makes one adjacent transposition in the Farnsworth D15 test, scores 20 out of 20 correct in the AO HRR test and produces a matching range of 40 to 42 on the Nagel anomaloscope. The subject’s increased rg chromatic thresholds fall clearly outside the normal range and are similar to the thresholds measured in mild deutan deficiency.

4. Discussion

Accurate assessment of color deficiency and chromatic discrimination sensitivity have, in general, relied on either anomaloscope tests or the measurement of chromatic detection thresholds. Both anomaloscope matches and color detection thresholds reveal a diversity of results that cannot be explained easily in terms of simple shifts in the spectral responsivity of cones. The anomaloscope produces accurate results, but the agreement between Nagel match parameters and the severity of color vision loss is generally poor (Wright, 1946; Hurvich, 1972). In order to account for such findings and some unusual, extreme matches, we modeled the Nagel anomaloscope to examine how cone pigment density changes, shifts in peak photoreceptor spectral responsivity, the inherent noise in the red-green channel that may be related to L:M cone ratio and the spectral width and composition of the red-green mixture and the yellow reference field can affect the outcome of the yellow match. The predictions of the model show that dlmax changes are not sufficient to account for the variety of anomaloscope matches. If small changes in cone pigment optical density are also allowed, the model predicts well the midpoint of deutan matches for the spectral differences specified by the genes. In addition, appropriate selection of red-green channel noise predicts the relatively normal red-green matches made by some color deficient observers. The midpoint of the match is affected mostly by the residual dlmax, but changes in pigment optical density can also produce significant shifts in the midpoint (see Fig. 4). These findings provide a plausible explanation as to why some subjects who have normal chromatic sensitivity and presumably normal cone genes require either too much green or too much red in the match. Another interesting finding concerns the Nagel performance of the fewer subjects that rely on two hybrid cone genes. Fig. 6 shows chromatic detection thresholds in a subject who exhibits red-green loss of sensitivity very comparable to that observed in minimum deuteranomaly (i.e., δλ_max of ;10nm). This subject does, however, pass the Nagel test and is classified as normal (see Results section). The Nagel model predicts correctly the measured midpoint and range for this subject by using hybrid M’ (i.e., a variant M-cone pigment shifted in peak spectral responsivity by ;6 nm toward longer wavelengths) and L’ (i.e., a variant L-cone pigment shifted toward shorter wavelengths by ;10 nm). This observation is of interest since it shows that it is possible to be color deficient with correspondingly reduced chromatic sensitivity and at the same time to make normal red-green anomaloscope matches. Although the choice of cone optical densities that yields the required match parameters is not unique (Thomas & Mollon, 2004), the model demonstrates convincingly that such matches are possible. This experimental finding and the predictions of the model illustrate clearly that although the anomaloscope produces accurate results, unusual combination of parameters can produce erroneous matches. “Even the anomaloscope, therefore is not by itself sufficient to grade the anomaly with certainty” (Wright, 1946). Another interesting observation concerns the definition of “normal” chromatic sensitivity and the severity of color vision loss in color deficiency. Fig. 2 shows that normal trichromats exhibit considerable inter subject variability, but in spite of this variability, “normals” separate completely from color deficient observers. The predictions of the model (see Fig. 5C) and the established variability within normal trichromats (Rodriguez-Carmona et al., 2005) suggest that subjects with cone pigment wavelength separations above 20nm would be classed as normal in conventional color vision tests and would also produce CAD thresholds that fall within the normal range. The existence of hybrid genes has long been documented (Neitz & Jacobs, 1986; Neitz & Jacobs, 1990; Winderickx et al., 1993). Many normal trichromats therefore rely on hybrid pigment genes that can reduce the normal δλ_max by as much as 10nm. These subjects have been classified as normal according to the majority of conventional color vision tests and their CAD thresholds fall within the normal “cluster” that is separated clearly from the rg thresholds measured in subjects with minimum congenital deficiencies (see Fig. 2). The model prediction of chromatic sensitivity is in good agreement with the measured RGI values in the deutan like subjects investigated in this study. The prediction reflects only changes in δλ_max (for a noise-equivalent signal that describes the mean normal trichromat). It is therefore reasonable to expect that a larger, randomly selected sample of subjects with deutan like deficiency will exhibit greater variability with points distributed more evenly around the model prediction shown in Fig. 5D.

Minimal deuteranomalous subjects rely on L-cone pigment genes separated by a maximum of 10 nm (Neitz et al., 1996). Minimal protanomalous subjects, on the other hand, rely on a smaller maximum separation ;6 nm (Neitz et al., 1999; Jagla et al., 2002) and this is consistent with the much larger CAD thresholds measured experimentally (see Fig. 2). Minimal deuteranomalous subjects can achieve 50% of the normal rg chromatic sensitivity, while minimal protanomalous subjects can only achieve ;20%. In addition to dlmax changes that arise directly from the presence of variant L and M cone pigment genes, the variation in noise-equivalent red-green signal change needed to account for the variability in matching range, both within normal trichromats and in color deficient observers, remains a very important parameter. The large, but similar variation in the relative numbers of L and M cones in the retina suggests that differences in L:M cone ratio and the subsequent selective amplification of cone signals and associated noise can account for the variation in noise level needed to explain the variability in red-green matching range. To our knowledge this hypothesis remains to be tested experimentally by examining the relationship between the red-green matching range and the subject’s L:M cone ratio in normal trichromats.