Development of Sensitivity to Geometry in Visual Forms

Véronique Izard; Elizabeth S Spelke

. Author manuscript; available in PMC: 2011 Feb 25.

Published in final edited form as: Hum Evol. 2009 Jan 1;23(3):213–248.

Development of Sensitivity to Geometry in Visual Forms

Véronique Izard ¹, Elizabeth S Spelke ¹

PMCID: PMC3045057 NIHMSID: NIHMS135037 PMID: 21359132

Abstract

Geometric form perception has been extensively studied in human children, but it has not been systematically characterized from the perspective of formal geometry. Here, we present the findings of three experiments that use a deviant detection task to test children’s and adults’ sensitivity to geometric invariants in a variety of visual displays. Children as young as 4 years of age analyzed shapes by detecting relationships of distance and angle but not by detecting the relationships that distinguish an object from its mirror image (hereafter, sense). Patterns of visual form analysis showed high invariance over development: the properties that were least detectable by children also posed the greatest difficulty for adults. In general, sensitivity to all tested properties improved with age, with an asymptote at about 12 years, before the onset of instruction in formal geometry. When presented with a carefully controlled set of forms that varied exclusively in length, angle or sense, children were found to develop sensitivity to these properties at different rates, responding first to length, then to angle, and last to sense. Between 8 and 10 years of age, moreover, children began to confer a privileged status to the relation of perpendicularity. Geometric competence therefore appears to emerge as an interplay between developmentally invariant, core intuitions and later acquired distinctions.

Keywords: cognitive development, geometry, visual shape, perception

Introduction

Humans possess a remarkable capacity for geometrical intuition: All over the world, people are sensitive to the shapes of visible objects and forms, and to relationships between distinct forms that share common geometrical properties (Dehaene et al. 2006; Newcombe and Huttenlocher 2000; Rosch 1973). If the existence of this ability is clear, however, its sources are obscure (Hatfield 1998; Newcombe and Uttal 2006). Are humans born with a system of knowledge of Euclidean geometry, or do we construct Euclidean geometry from earlier-developing systems of lesser range and power? The present research attempts to shed light on this question through studies of children’s and adults’ detection of geometrical invariants in visual forms.

The shapes of objects constrain how they can be grasped and carried, and they play a large role in determining their functions as tools. From a very early age, human infants are sensitive to shape and extract object shape from both two- and three-dimensional displays, even with only partial evidence (Antell and Caron 1985; Banks and Ginsburg 1985; Bomba and Siqueland 1983; Fantz et al. 1975; McGurk 1972; Schwartz and Day 1979; Slater et al. 1985). Early research employed shapes that differed in many ways, including the number of sides, the relative positions of sides, the area and symmetry or asymmetry of the overall shape, and the size and distribution of spatial contrast. Starting in the 1990s, a more systematic attempt was made to study separately infants’ sensitivity to different geometric relationships. These studies revealed that newborn infants can discriminate between lines of different lengths ((Slater et al. 1990); see also (Huttenlocher et al. 1994) for studies of older infants) and between angles of different aperture ((Slater et al. 1991), see also (Schwartz and Day 1979), for studies of older infants). Sensitivity to length and angle are robust throughout infancy and are observed even when objects change in orientation or position.

In contrast to their ability to process length and angle, infants do not appear to recognize the property of sense in a small-scale, 2-dimensional figure (Lourenco and Huttenlocher 2008). In this study, Lourenco and Huttenlocher familiarised six-month-old infants with an isosceles triangle of varying orientation. A salient dot was situated on one of the corners of the triangle, either the unique corner, or one of the two non-unique corners (which were only discriminable in terms of sense). Infants discriminated between the unique corner and the non-unique corners, in accordance with their demonstrated ability to detect variations of angle and length; however, they failed to use sense and did not discriminate between the two non-unique corners, unless the display stayed relatively stable in orientation.

Human adults contrast with infants in this respect: we are able to distinguish between mirror image versions of an object, even across different orientations. Nevertheless, adults seem to extract distance and angle from visual forms more readily than sense. For example, when two forms, presented at different orientations, differ in length or angle, adults can usually detect this difference directly; when the arrays differ in sense, however, adults usually can only detect this difference by rotating one of the forms into registration with the other. Mental rotation is used to compare the forms not only when the forms are novel (Shepard and Metzler 1971) but also when they are highly familiar but appear at novel orientations (Cooper and Shepard 1973). Because mental rotation is time-consuming and demanding of attention, adults’ tendency to resort to it suggests that we, like infants, perceive angle and distance more readily than sense in visual arrays.

Several lines of evidence converge to indicate that for 2D visual displays, sense tends to be processed only at the cost of effortful strategies in adults (with the exception of letters), and can be dissociated from the identification of objects at the neural level. For example, Kelly and Spetch (Kelly and Spetch 2004) presented adult participants with a rectangle of varying orientation on a computer screen, and asked them to identify one of the corners (or its geometrical equivalent) in the absence of any non-geometric cues on the rectangle. Although adults do not show any difficulty when the same task is presented in a context of navigation ((Hermer and Spelke 1996); see (Cheng and Newcombe 2005) for a review), or when the same task is performed with pictures of a 3D room (Kelly and Bischof 2005), the task of identifying a corner in a two-dimensional, small-scale rectangle proved to be difficult. Many participants in Kelly & Spetch’s study did not reach the criterion for learning the geometrical cues; furthermore, even the participants who did learn to use the geometric cues were at chance when required to generalize their performance to new orientations of the rectangle. This result indicated that participants had difficulties discriminating the rectangle from its mirror image across different orientations. Instead of using the relative positions of the walls as they would have done in a classical reorientation task, adults probably relied on different strategies, such as learning the absolute position of the correct corner separately for each orientation. In the same vein, Biederman & Cooper (1991) showed that processing a shape is facilitated after a prior presentation of the same shape or its mirror image, with a similar amount of facilitation in the two cases. These findings suggest that adults dispose of a basic process of shape recognition that is based on angle and length and is impervious to sense distinctions, but that they learn to overcome one limit of this process and detect sense relations in alphanumeric characters, when they learn to read.

At the brain level, processing information about sense (orientation and mirror images) seems to be dissociated from the identification of objects. For example, Turnbull (Turnbull 1997) describes a double dissociation between two cases of brain-lesioned patients. A first patient, who suffered from a lesion in the parietal lobe, was able to name images of objects but could not tell when the images were presented in an unusual orientation. Inversely, a second patient could detect variations in orientation but could not name the images. Thus, the brain structures responsible for the recognition of objects seem to abstract across orientation and sense properties of 2-dimensional shapes.

Studies of the response properties of individual neurons bolster this suggestion. Cells exhibiting invariance by symmetry have been observed in the inferior temporal sulcus of monkeys, a region which is precisely thought to be involved in the recognition of categories of visual stimuli (Downing et al. 2006; Epstein and Kanwisher 1998; Kanwisher et al. 1997; Reddy and Kanwisher 2006). The response of these cells display a high level of invariance for the size and position of objects, and, interestingly, a large proportion of the cells also do not discriminate between mirror images of their preferred stimulus (Logothetis et al. 1994; Rollenhagen and Olson 2000). Although left-right symmetry is implemented in a larger number of cells, and also generates the greater amount of confusion in children, cells generalizing across vertical mirror images have been observed as well, and confusion with vertical mirror images has also been documented at the behavioural level in children and in patients (Huttenlocher 1967; Turnbull 1997). The inferior temporal sulcus therefore appears to compute a representation which is invariant over reflections on multiple axes. The confusion of left and right may be more dramatic, because left-right mirror images can be easily related to one another through the exchange of information between both hemispheres, whereas no such computational shortcut exists for vertical symmetry.

In summary, the data from the literature indicate that sense discriminations on 2-dimensional figures are difficult both for infants and for adults. Indeed, differentiating mirror images might not be needed for identifying objects, since objects tend to move and change orientation. Given adults’ difficulties with sense distinctions, it is not surprising, therefore, that children show striking difficulties in discriminating two shapes that are mirror images of each other (Gibson et al. 1962; Huttenlocher 1967). However, those distinctions are crucial for reading, as only sense relations distinguish between the letter p from the letters q and b (which, respectively, are horizontal or vertical reflections of p) (Dehaene 2007; Dehaene et al. 2005). Interestingly, children’s difficulties with mirror images seem to resolve at different ages across cultures, corresponding to the moment where children learn to read (Serpell 1971). This acquisition is slow and effortful, and children tend to go through a phase where they can indifferentially read and write in both left-to-right and right-to-left directions (Cornell 1985; McMonnies 1992; Terepocki et al. 2002), corresponding to a stage where they have not yet crystallized their representation of letters in a fixed orientation. Later, the ability to identify sense as a defining property of letters might transfer progressively to general shapes (Gibson et al. 1962).

Nevertheless, the above studies of sensitivity to geometry in infants and children have several limitations. First, although infants and school-aged children have been studied extensively, there have been fewer studies at the critical ages between infancy and the school years: ages when children begin to navigate and to develop encyclopedic knowledge of object kinds. Second, children and adults rarely are tested with the same displays and tasks. Third, although tests have focused on mirror image confusions, few investigators have examined sensitivity to all the basic properties of Euclidean geometry in a systematic way: distance and angle as well as sense.

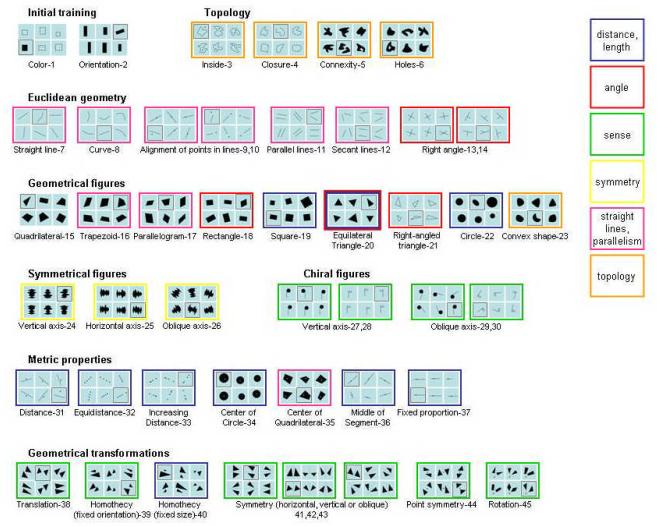
One recent study begins to overcome the last limitation. A general test of sensitivity to geometry was administered both to adults and school-aged children in the U.S.and to an indigene group from the Amazon, the Mundurucu (Dehaene et al. 2006). On each trial, participants were presented with six images, five of which instantiated a particular geometrical property and the sixth of which did not (Figure 1). Participants were asked to indicate the intruding image by pointing to it, and their responses were recorded. Across trials, the deviant image differed from the others with respect to a host of different geometric properties (we describe these properties in greater detail below). The performance of Mundurucu children across items correlated strongly with the performance of a group of age-matched U.S. controls. In addition, performance was also correlated across adults from both populations, although U.S. adults performed in general better than all other groups (Newcombe and Uttal 2006). Still, U.S. adults tend to have difficulties on the same items as Mundurucus and children: the profile of responses across items thus presents a signature of some universal competence for geometry.

Items of the original deviant detection task. This task was created by Dehaene et al. (2006) and administrated to an indigene group from the Amazon, as well as US participants. Each item features 6 different images, where 5 of them instantiate a geometrical property, which is not present in the last image. Correct responses are highlighted for the purpose of the figure by a square frame which was not presented to the participants. Items were presented in random order; they are numbered here for further reference. Items spanned a host of different geometric properties, and were originally classified with respect to the type of geometric objects presented (see Dehaene et al., 2006). In the present paper, we use a second classification based on the type of cue(s) that could be used to identify the correct response (distance/length, angle, sense, symmetry, lines/parallelism, topology). This classification is given here using a color code.

The present research was undertaken to extend these findings to younger children and to use more detailed analyses of performance to isolate the particular geometrical properties that children and adults detect. We report three experiments investigating sensitivity to geometry in children and adults. In the first study, we administered to 3- to 5-year-old children the same test of sensitivity to geometry that has previously been used with adults and older children (Dehaene et al. 2006), asking whether the same patterns of sensitivity to geometry are present at this young age. In the second study, we presented the same task to a large population of children and adults over a wide age range, from 3 to 51 years. We analyzed in detail children and adults’ use of each of a host of specific geometric properties in this task, including length/distance, angle, sense, connectedness, curvature, convexity, symmetry and other higher-order Euclidean properties, analyzing developmental trends for specific properties, as well as patterns of invariance and change in the relative ease of processing different properties. In the third experiment, we concentrate on the properties of length, angle and sense, in an attempt to characterize and compare the development of sensitivity to those properties more directly, and to test for the emergence of new geometric knowledge transcending developmentally invariant geometric intuitions.

Experiment 1

Method

Participants

Twenty-two children, (13 female) were tested, with ages ranging from 3:7 to 5:11 (mean age 4:11)¹. Children resided in the greater Boston area and came from a variety of racial, ethnic and national backgrounds, but were predominantly White and middle or upper-middle class. They were recruited through general advertising posted by the laboratory, at their schools and preschools, or through week-end arts and sports programs in which they participated. An additional group of 26 kindergardeners from NY (17 female; mean age 5:8, range 5:5 to 5:11) were tested at their school on a shorter version of the test, lacking 12 of the items that had proved most difficult in previous research (see table 1).

Table 1.

Performance for each item in experiment 1. We give the description of each item, together with the classification in terms of cues needed to identify the correct response. In the last three columns, we list the responses on which children tended to converge (Chi-square against chance for each response), the accuracy (chance is 16.7%), and the significance of the overall distribution compared to a uniform distribution (Chi-square, Bonferroni-corrected for multiple comparisons).

Item	Title	Category	Frequent Response(s)	Accuracy	P-value (item)
Initial Training
1	Color	Color	4 (^***)	89.6	0.0000
2	Orientation	Orientation	3 (^***)	87.5	0.0000
Topology
3	Inside	Topology	1 (^***)	75.6	0.0000
4	Closure	Topology	2 (^***)	40.4	0.0066
5	Connexity	Topology	5 (^***)	42.6	0.0042
6	Holes	Topology	4 (^***)	41.7	0.0045
Euclidian Geometry
7	Straight Line	Alignment	2 (^***)	76.1	0.0000
8	Curve	Alignment	3 (^); 5 (^)	33.3	0.0023
9	On a Line	Alignment	4 (^***)	72.3	0.0000
10	Alignement	Alignment	1 (^***)	59.6	0.0000
11	Parallel Lines	Parallelism	6 (^***)	24.4	0.0000
12	Secant Lines	Parallelism	5 (^***)	60.4	0.0000
13	Right angle, Cross	Angle	6 (^***)	59.6	0.0000
14	Right angle, T	Angle	5 (^***)	43.8	0.0010
Geometrical Figures
15^a	Quadrilateral	Unclassified	2 (^**)	22.7	1.0000
16	Trapezoid	Parallelism	3 (^***)	45.7	0.0007
17	Parallelogram	Parallelism	2 (^**)	31.9	1.0000
18	Rectangle	Angle	3 (^***)	62.5	0.0000
19	Square	Length/Distance	3 (^*); 4 (^)	31.9	0.0000
20	Equilateral Triangle	Length/Distance, Angle	3 (^***)	34.8	0.3311
21	Right-angled Triangle	Angle	5 (^***)	43.5	0.0008
22	Circle	Length/Distance	2 (^*) ; 3 (^)	61.7	0.0000
23	Convex Shape	Topology	5 (^***)	72.3	0.0000
Symmetrical Figures
24^a	Vertical Axis	Symmetry	ns	19.0	1.0000
25^a	Horizontal Axis	Symmetry	2 (^***)	4.8	0.0467
26	Oblique Axis	Symmetry	5 (^*) ; 2 (^)	31.9	0.0131
Chiral Figures
27	Chiral Figure, Stable Orientation (1)	Sense	2 (^***)	56.5	0.0000
28	Chiral Figure, Stable Orientation (2)	Sense	3 (^***)	72.3	0.0000
29^a	Chiral Figure, Variable Orientation (1)	Sense	ns	9.5	1.0000
30^a	Chiral Figure, Variable Orientation (2)	Sense	2 (^***)	4.5	0.2855
Metric Properties
31	Distance	Length/Distance	6 (^***)	48.9	0.0000
32	Equidistance	Length/Distance	6 (^***)	36.2	0.2295
33	Increasing Distance	Length/Distance	3 (^***)	43.5	0.0018
34	Center of Circle	Length/Distance	1 (^***)	69.6	0.0000
35^a	Center of Quadrilateral	Alignment	ns	14.3	1.0000
36^a	Middle of Segment	Length/Distance	5 (^***)	18.2	0.0350
37	Fixed Proportion	Length/Distance	3 (^); 4 (^)	34.0	0.0034
Geometrical Transformations
38	Translation	Sense	2 (^); 6 (^)	29.8	0.0865
39	Homothecy (Fixed Orientation)	Sense	6 (^***)	34.8	0.8679
40^a	Homothecy (Fixed Ratio)	Length/Distance	5 (^**)	14.3	1.0000
41	Horizontal Symmetry	Sense	2 (^**)	31.9	1.0000
42^a	Vertical Symmetry	Sense	2 (^***)	10.0	0.3080
43^a	Oblique Symmetry	Sense	3 (^*)	30.0	1.0000
44^a	Point Symmetry	Sense	5 (^**)	28.6	0.3269
45^a	Rotation	Sense	2 (^*)	4.5	1.0000

Open in a new tab

p<0.1

p<0.05

^**

p<0.01

^***

p<0.001.

Displays and task

All displays were presented on a laptop computer, which was advanced between trials by the experimenter. The test consists of 2 practice and either 43 or 31 test items (see table 1 and figure 1). Each test item displayed six different images, 5 of which illustrated a given property (e.g. parallel lines, item 11), that the sixth image lacked. The order of items was randomized across children. The children were instructed to pick the image that looked different in each 6-image display.

The exhaustive list of the items presented is given in figure 1 and table 1, together with the different properties which could be used to identify the correct answer. Seven broad categories of trials were designed: topology (connectedness, continuity, closure), Euclidian geometry (straight lines, alignment, parallelism), figures (defined by the length of their sides, the angles of the corners, parallelism between sides; or number of sides), symmetrical figures (complex figures with an axis of symmetry vs. a centre of symmetry), metric properties (absolute and relative distance), and transformations (symmetries, rotation, homothetic transformation).

Procedure

Children were tested individually by an experimenter, who presented each display by pressing a key on the computer, and who recorded the child’s response by mouse click on the image to which the child pointed. Children were first given two training trials, where the intruder differed from the other images in terms of color or orientation and where feedback was given if it was needed (the need for feedback was rare). After training, children directly proceeded to the test, indicating their choice of the intruder by pointing or touching the chosen image. Neutral feedback was given throughout the test.

Results and discussion

The mean accuracy (percent of correct responses) for each item is given in table 1. For each item, we compared the distribution of responses to chance by means of a Chi-square test against a uniform distribution of responses across the six images (Bonferroni-corrected for multiple comparisons across items). This test indicated whether the distribution of responses departed from chance in general, but did not indicate whether children were converging to the correct response, or to one of the distracters, or to several of the responses. In cases where the response distribution departed from chance, we then compared the frequency of each response to the chance level of 16.7% (1/6), by means of a Chi-square test. Sometimes, one or two responses appeared to be given more often than chance, while the general chi-test was not significant: this is reported hereafter to indicate whether there was at least a tendency to converge towards the correct response in failed trials.

Children’s performance reveals a large amount of variability across items, even within each category. In order to compare the present results to the previous results reported in the literature, in the following analyses we sorted the different items based on the type of geometric properties which could be used to identify the intruder (see figure 1 and table 1).

Length

We first analyzed the data to determine whether children were using distance and length to select the intruding figure. Ten of the 43 trials (or 8 of the 31 trials in the shorter version) could be solved by using distance cues alone. The accuracy on these trials was significantly above chance (mean accuracy 41.7%; Student Test on the accuracy versus 16.7%: T(47)=9.6, p<0.0001), with significant differences between the items (Chi2(9)=39.43 p<0.0001). Children performed significantly above chance on the items targeting the distance between a point and a line (item 31: 48.9% accuracy, Chi2(5)=41.8, pcorr<0.0001), the position of the centre of a circle (item 34: 69.6% accuracy, Chi2(5)=104.5, pcorr<0.0001), as well as items contrasting circles vs. an ellipse (item 22: 61.7% accuracy, Chi2(5)=93.6, pcorr<0.0001) or squares vs. a rectangle (item 19: 31.9% accuracy, Chi2(5)=75.0, pcorr<0.0001). In the latter two, in addition to choosing the correct response, children also converged to the biggest images (frequency: 34.9% and 48.9% for the circle and the square respectively, Chi2 against chance for these responses, ps< 0.005). They also identified an equilateral triangle amongst other triangles, although with less success: the distribution of responses did not depart from chance (item 20, Chi2(5)=15.8, pcorr=0.33), but still children converged on the correct response (34.8% accuracy, Chi2(1)=10.9, p=0.001). In two items contrasting distance relations within series of dots, children proved able to detect irregularly spaced dots amongst dots separated by increasing distances (item 33, 43.5% accuracy, Chi2(5)=27.8, p=0.0018), but showed a mixed success with dots linearly spaced (item 32: 36.2% accuracy; the distribution of responses for this item does not depart from chance: pcorr=0.23, nonetheless the correct response is chosen significantly more than chance: Chi2(1)=12.9, p=0.0003). In the item testing for the “middle” of a line (item 36), children failed by attending to the absolute length of the displays instead of choosing the correct response (18.2% accuracy; choice of the shortest line: 50.0% of the responses, Chi2(1)=17.6, p<0.0001, resulting in a distribution differing from chance, Chi2(5)=21.1, pcorr=0.035). They nonetheless identified the correct response in another item based on the same principle, testing for length proportion of 1/3 (item 37, 34.0% accuracy, Chi2(5)=26.4, pcorr=0.0034), although they also converged to the smallest line in this case as well (frequency of this response 34.0%, Chi2(1)=10.2, p=0.0014).. Finally, children were less successful in the last item, testing homothetic relations with a fixed ratio (item 40: Chi2(5)=8.4, pcorr=1.0). They did not show any tendency to find the correct response (14.3% accuracy), but tended to choose the image with the largest cumulative area (38.1% of the responses; Chi2(1)=6.9, p=0.0084).

Besides these trials, children’s ability to process distance is evidenced by the errors they made on other types of items: they tended to choose either the smallest or the largest items based on cumulative area of the display in items displaying several figures (smallest figure: items 15, 42, 43, 45; biggest: items 38, 44; response frequency between 29.4 and 45.0%, for these responses: all ps<0.05; cf below). Distance even trumped parallelism on item 11, where children choose a distracter which differed from the other images on the basis of the distance between the two lines (44.4% of responses; Chi2(5)=36.5, pcorr<0.0001).

In summary, the test confirms that children are able to use length by 4 or 5 years of age, in accordance with the findings of studies on infants (Huttenlocher et al. 1994; Sandberg et al. 1996; Slater et al. 1990). Children succeed both at items testing absolute distance (e.g. distance between a line and a dot, item 31), and relative distance (e.g. a dot situated at 1/3 of the length of a line, item 34).

Angle

Five of the 43 items (items 13, 14, 18, 20 and 21) could be solved on the basis of angle cues alone (all these items were presented in the shorter version of the test). Children showed a high level of performance on these items (mean accuracy 49.6%, Ttest against chance: T(47)=8.2, p<0.0001), with a significant difference across items (Chi2(4)=10.4, p=0.034). The only item where responses did not significantly depart from a uniform distribution was the item contrasting equilateral and isosceles triangles (item 20, see above), although children still showed a tendency to identify the correct response for this item. Nonetheless, their poor performance on this particular item is surprising given it could have been solved using either length or angle cues, which children proved to have access to on other items.

A consideration of the remaining 4 test items reveals that all of them contrasted right angles with angles of other sizes, in a triangle (item 21), a cross (item 13), a T-shaped form (item 14), or a quadrilateral (item 18). Children solved all these items easily (Chi2 against uniform distribution: pcorrs≤0.001). This good performance could be taken as indicating that the dimension of angle is more salient than length for children. However, an important limitation of this task is that fewer trials tested angle than distance, and no trials tested sensitivity to differing angles that were not right angles, except for the single equilateral triangle trial that confounded angle and distance. It has been suggested that right angles have a particular status, and this special status could explain children’s performance. For example, children show a bias toward right angles when copying figures (the “perpendicular effect”: (Bremner and Taylor 1982; Ibbotson and Bryant 1976). However, research with infants proved that they are able to discriminate 2-dimensional representation of angles (Slater et al. 1991), and this research did not specifically test right angles, so it is possible that children’s competence with angles extends to angles of all sizes. We return to this issue in Experiment 3.

Sense

In 11 of the 43 items (or 6 of the 31 items in the shorter version), children needed to attend to sense in addition to length or angle in order to find the correct response. Four trials depicted chiral figures, in a fixed orientation (items 27 and 28), or with a variable orientation (items 29 and 30). Furthermore, most of the items testing for the discrimination of different isometric relations required discrimination of a figure from its mirror image (such as for example in the contrast between translation, which preserve the orientation of a figure, and symmetry, which changes it). When all these trials were grouped together, performance was significantly better than chance (37.0%, T(47)=6.7, p<0.0001). However, performance differed across trials (Chi2(10)=69.6, p<0.0001), and the only trials where children departed significantly from chance were the trials where chiral figures were presented in a fixed orientation (resp. 56.5 and 72.3% accuracy, Chi2(5)=59.1 and 106.3, pcorrs<0.0001). Children also tended to converge on the correct response on 3 trials which required contrasting panels with two similar images, from panels with mirror images. These trials were nevertheless solved with less success, as the general distribution of responses did not differ from chance (item 38: translation vs. point symmetry: 29.8% accuracy, Chi2(5)=19.0, p=0.087; for the correct response: Chi2(1)=5.8, p=0.016: item 39: homothetic images vs. mirror image; 34.8% accuracy, Chi2(5)=13.5, pcorr=0.87; for the correct response, Chi2(1)=10.9, p=0.001; item 41: horizontal symmetry vs. translation: accuracy 31.9%, Chi2(5)=10.8, pcorr=1.00; for the correct response, Chi2(1)=7.9, p=0.005). All other items based on the same principle (items 41-44) also yielded chance performance (pcorr>0.30). Sometimes children agreed on one of the distracters, usually either the smallest or the biggest figure (items 38, 42, 43, 44, see above). Finally, children failed on the last three items (29, 30, 45), which involved mental rotation (overall distribution not departing from chance, pcorr>0.29). In one of the items involving chiral figures in varying orientations, children converged to the image presented in a horizontal orientation (F-shaped figures, item 30: Chi2(5)=16.2, pcorr=0.29, frequency of the preferred response 45.5%, Chi2(1)=13.3, p=0.0003).

In summary, these data showed that children are able to discriminate between mirror images, but only when they are presented in the same orientation. These data converge with recent evidence with infants (Lourenco et al. 2005), but contradict with earlier findings that children tend to generalize across mirror image (Gibson et al. 1962; Huttenlocher 1967). Even the youngest children displayed this competence (accuracy for the 4-year-old children: 71.4% correct, 5-year-olds: 64.1% correct). However, even for the oldest children performance fell to chance level when the figures were presented in different orientations and children were required to perform a mental rotation (accuracy for the 4-year-olds: 7.1%; 5-year-olds: 7.7%). This failure extended to most of the items where the children needed only to attend to the difference of sense between two figures (eg. item 42). Our data therefore confirm young children’s difficulty discriminating between mirror images.

Further Euclidean properties

Although the primary focus of this research is on sensitivity to distance, angle and sense, we also consider children’s response to other properties captured by Euclidean geometry and by topology. In the present study, 12 (9) items tested for the detection of the Euclidean properties of symmetry, curvature, alignment, and parallelism. Children showed a good accuracy on these trials on average (44.4%; T(47)=10.4, p<0.0001), but the performance differed across items (Chi2(11)=85.3, p<0.0001). We consider each type of items in turn below.

Concerning symmetry, three (one) items contrasted 5 figures having an internal axis of symmetry, with a 6^th figure that also displayed some property of symmetry, but this time with respect to a point (centre of symmetry) instead of a line (axis of symmetry). Items varied on the orientation of the axis of symmetry: vertical (item 24), horizontal (item 25), or oblique and variable (item 26). Responses were at chance, on average, on these items (22.5% correct; T(47)=1.2, p=0.24), but significant differences arose between items (Chi2(2)=6.3, p=0.042). Children were at chance with a vertical axis (item 24, 19.0% accuracy: Chi2(5)=4.4, pcorr=1.0), with no convergence across responses. They selected a wrong image on the item with a horizontal axis (item 25: 4.8% accuracy, frequency of the preferred response: 52.4%, Chi2(1)=19.3, p<0.0001; overall test of distribution against chance: Chi2(5)=20.4, pcorr=0.047). For the item where the axis of symmetry varied in orientation across images, they selected the correct image (item 26, accuracy 31.9%, Chi2(1)=7.9, p=0.0050), but also one the distracters (frequency 29.8%, Chi2(1)=5.8, p=0.016), resulting in a distribution of responses that differed significantly from chance (Chi2(5)=23.3, pcorr=0.013). A close look at the preferred responses across items indicated that children tended to choose the items with the highest degree of variation in the length of the different peaks, and probably the convergence towards the correct response for the last item was an accidental consequence of this strategy. Altogether, the three items about the axes of symmetry of figures do not argue for a competence for detecting symmetry in young children.

Nevertheless, the figures used in the present study made the task quite complex, because they all displayed some kind of symmetry, and the deviant was still symmetric with respect to a point (whereas the standard images were symmetric with respect to an axis). To succeed at the present symmetry items, children thus needed to differentiate between two kinds of symmetry, which requires distinctions based on sense properties. Childen’s failure at the items testing for symmetric properties thus confirms the children’s inability to detect differences across mirror images. However, it is possible that children might have been able to detect images displaying some internal symmetry, when contrasted with images lacking internal symmetry of any sort (see (Bornstein 1979) for a sensitivity to symmetry in infants).

Concerning curvature, children were very successful at the item showing a curved line amongst straight lines (item 7, accuracy 76.1%, Chi2(5)=117.3, pcorr<0.0001). However, in the reverse item (item 8), their responses were directed evenly to the correct response and the most curved line (33.3% of the responses for both; Chi2(1)= 9.6, p=0.002; overall distribution Chi2(5)=27.2, p=00023). These results indicate that children can detect the curvature of a line, but they may not see straight lines as special, and possibly treat them as one instance on a continuum of lines of different curvatures.

On the trials testing sensitivity to alignment, children were very good at detecting whether a dot is aligned with a line, whether it was placed directly on the line (item 9, 72.3% accuracy, Chi2(5)=110.1, p<0.0001) or not (item 10, 59.6% accuracy, Chi2(5)=64.2, p<0.0001). However, they did not succeed in detecting whether a dot placed inside a quadrilateral was situated at the intersection of the diagonals – thereby aligned with the vertexes (Chi2(5)=4.4: pcorr=1.0; no convergence across responses). The difference between this last item and the former suggests that the vertexes of a figure are not perceived as salient points, hence children do not perform judgments of alignment with vertexes.

Items testing parallelism included direct comparison between parallel and non-parallel lines (items 11 and 12), as well as contrasts between trapezoids and parallelograms (item 17), and between trapezoids and non-remarkable quadrilaterals (item 16). Children detected the deviant parallel lines amongst non-parallel lines (60.4% accuracy, Chi2(5)=69.8, pcorr<0.0001), but they failed to detect non-parallel lines amongst parallel lines, and instead relied on distance to converge on the parallel lines that appeared furthest apart (24.4% accuracy; 44.4% to the furthest lines, Chi2(1)=25.0, p<0.0001; overall distribution: Chi2(5)=36.5, pcorr<0.0001). Furthermore, they were able to use parallelism to discriminate a trapezoid from irregular quadrilaterals lacking parallel sides (45.7% accuracy, Chi2(5)=29.9, pcorr=0.0007), and to some extent could also detect a trapezoid amongst parallelograms (31.9% accuracy, for the correct response Chi2(1)=7.9, p=0.005), although the test of the distribution against uniform distribution did not reach significance (Chi2(5)=10.3, pcorr=1.0). These tests provide some evidence that children can detect parallelism, but this property is sometimes neglected in favor of more salient dimensions such as distance.

Topological properties

Five of the items tested sensitivity to the topological properties of continuity, connectedness, closure, and convexity (items 3-6 and 23). Children were successful with these items in general (53.3% accuracy, T test against chance at 1/6: T(47)=8.9, p<0.0001), but the difference between items was highly significant (Chi2(4)=24.2, p<0.0001). Children successfully identified the correct response in all items (accuracy 40.4% to 75.6%, pcorrs<0.01 for the test on the overall distribution). These data therefore demonstrate a general good competence of children for topological properties. However, this test reveals that competence for topological properties is not unitary as had been proposed before (Piaget and Inhelder 1967).

In the longer version of the test, a final, unclassifiable item tested for the contrast between a triangle and different quadrilaterals (item 15). The distribution of responses did not differ from chance on this item (Chi2(5)=11.8, pcorr=1.0), although children tended to converge on one of the distracters: the rectangle at the middle of the top line (40.9% of the responses, Chi2(1)=9.3, p=0.0023), perhaps because this figure presented larger discrepancies between the length of its sides, which gave it a more ‘unbalanced’ aspect. Alternatively, children might have chosen the rectangle because it was more canonical, given its orientation, and the fact that it was a regular figure.

Comparisons across trial types

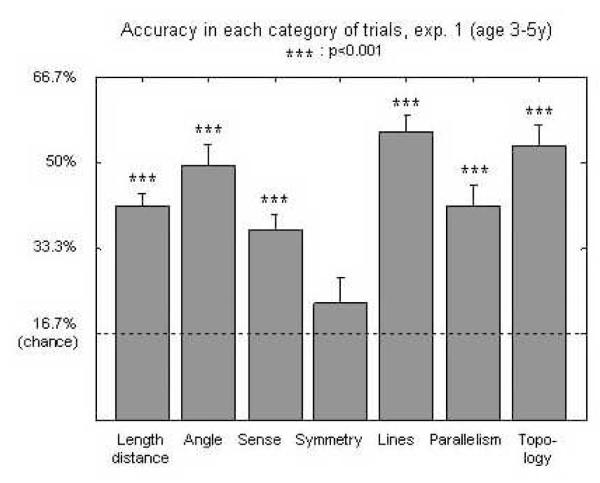
In summary, children reliably detected some types of geometric properties (length, angle, Euclidian properties of lines, topology), but failed at to detect other types of properties (sense, symmetry, number of sides). An analysis of variance with one factor describing the different types of trials (distance, angle, sense, symmetry, lines, parallelism, topology - excluding the single trial about the number of sides) confirmed the statistical significance of these differences (F(6,282)=10.6, p<0.0001). Pair-wise T test comparisons (Bonferroni-corrected) confirmed that performance were worse on the symmetry items than on any other category except sense (pcorrs<0.01) and sense differed from angle, topologies, and line properties (pcorrs<0.05; except angle vs. sense: pcorr = 0.068). No other comparison was significant (pcorr>0.15) (see figure 2).

Accuracy of 3-5 year old for each category of items in Experiment 1. Chance corresponds to 1/6 (16.7%). ***: p<0.001.

Conclusions

The findings of Experiment 1 support two general conclusions. First, preschool children are capable of performing explicit analyses of the geometric properties of visual forms, detecting a property that is invariant over a set of figures and finding the outlying figure that fails to instantiate it. Second, preschool children show a performance profile that is qualitatively similar to that of adults and infants: They show greater sensitivity to length and angle than to sense.

In addition to correctly solving some of the items, children tended to converge towards one of the distracters on some of the items, often choosing either the largest or the smallest item in size. Note that these patterns of failure also inform us on the children’s heuristic to solve the task. Although all items in the task were conceived and prepared by identifying a property which would or would not be displayed by each image, children did not try to identify such an all-or-none rule to guide their responses. Instead, they sometimes appeared to rely on a statistical analysis of the displays, and pointed to an image which was outlier on some dimension. For example, when they chose the shortest line, they were identifying an outlier in terms of length. As illustrated by this kind of error, children answered intuitively, without trying to identify a rule. Indeed, response times were relatively short on average (mean response time: 10.2 s), with very few trials taking more than 30s (2.8%). Furthermore, children used this outlier heuristic in some trials which were conceived as identifying a remarkable property, such as straight lines among curved lines, or parallel lines among secant lines. In fact, straight lines are only remarkable amongst curved lines by the properties that they hold in geometric theories, but they are actually only a particular instance of curved lines (with null curvature). Children did not seem to identify straight lines as particular, since in one item contrasting a straight line with curved lines they were equally likely to choose either the response with least curvature (straight line) or the most curved line. Similarly, in an item contrasting parallel and secant lines, they converged towards furthest apart lines, and failed to show sensitivity to the remarkable property of parallelism. These responses suggest that preschoolers represent the geometric properties of shapes on internal continua, which do not display singularities.

In the literature, comparisons across ages are limited by the use of different displays and tasks at different ages. In the next experiment, therefore, we repeated the method of Experiment 1 with children and adults at a wide range of ages.

Experiment 2

In the next experiment, we presented the same task to a larger sample of adults and children, and we tested for both invariant and changing patterns of performance over development.

Method

Participants

We tested 400 participants aged 6 to 51 years. Table 2 gives the gender and age distribution of the participants for experiment 2. Participants were predominantly white children and adults from middle-class families living in Massachusetts or in New York, and were recruited using the same procedures as in experiment 1. Eighty-two participants aged 13 to 18 years attended a high-school in Massachusetts were they received special training in arts. All the participants received the complete test except for 25 of the participants tested in a school in NY (age 6:0 to 6-8, 11 females) who were tested on the same shorter version as in experiment 1.

Table 2.

Demographic information for experiments 1 and 2.

Age	N
3	2 (1 Female)
4	7 (5 Females)
5	39^a (24 Females)
6	43^a (21 Females)
7	22 (14 Females)
8	26^b (18 Females)
9	27 (16 Females)
10	34 (17 Females)
11	43 (24 Females)
12	11 (5 Females)
13	15 (10 Females)
14	11 (8 Females)
15	25 (20 Females)
16	24 (17 Females)
17	47 (36 Females)
18-25	54 (33 Females)
26-40	12 (10 Females)
41-55	6 (1 Female)
Total	448 (280 Females)

Open in a new tab

some participants received the shorter version of the test (26 5yos, 25 6yo)

for one of the participants, gender information could not be obtained

Procedure

The procedure was identical as experiment 1, except that some participants clicked themselves on the chosen response, if they were able and willing to do so.

Results

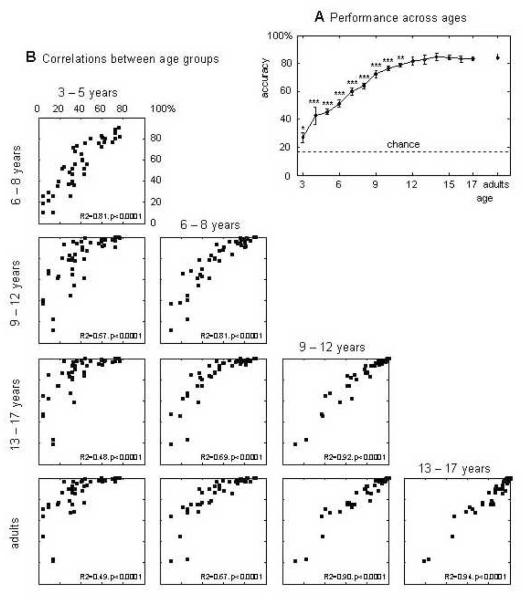
Overall, the accuracy was high (72.3%), and increased by age (see figure 3A; ANOVA with one factor for age, all participants aged 18 and more grouped together: F(15,432)=43.4, p<0.0001). In order to assess when performance reached an asymptote, we compared the performance of each age-group to the performance of adults (age 18 and more). We found that all participants under 12 years of age performed significantly worse than adults (Welch T-test; p=0.018 for the 3-year-olds; p<0.01 for all other groups between 4 and 11). For all groups aged 12 to 17 years, performance did not differ from adults (p>0.49). Hence, the competences targeted in this test are mature by adolescence, and do not rely on the geometric concepts taught in high school.

Development of the performance in Experiment 2. (A) The average performance for all items increased progressively until adolescence. For each age group, we compared the average performance to the group of adults: *:p<0.05; **: p<0.01; ***: p<0.001. (B) Participants were grouped in 5 different age groups: 3-5 years (participants from experiment 1), 6-8 years, 9-12 years, 13-17 years, adults. All groups showed the same pattern of difficuly across items, and performance across items was highly correlated between all age groups (all ps<0.0001).

We further tested whether children develop sensitivity to different types of geometric properties at different rates. To do so, we used the same classification of items as before (see analysis of the younger children’s performance and table 1). In all cases, performance increased during childhood and reached an asymptote. To estimate at which ages children reached the asymptote, we again compared the performance for all age groups to the group of adults. Comparing the performance of children of different ages to adult performance revealed very little variation as to when the asymptote was reached for the different types of trials (distance: 10 years; angle: 11 years; sense: 10 years; topology: 9 or 10 years; straight lines: 10 years; parallelism: 12 years). Although adults performed above chance for all but one item (item 35: center of a quadrilateral), the ultimate level of performance they reached differed across types of trial (sense: 77.1% correct; symmetry: 78.7%; distance: 82.1%; lines: 82.2%; angle: 91.4%; parallelism: 92.7%; topology: 96.1%; ANOVA with one factor for the type of trial: F(6,426)=24.9, p<0.0001). Together, these observations suggest that the improvement with age is not due to specific improvement on different geometric features. Instead, the improvement may stem from more general cognitive changes, including increased problem solving ability or better general heuristics. Hence, the tendency to agree on size outliers (biggest and smallest figure) observed in younger participants has essentially disappeared by the beginning of adolescence.

Table 3 lists the preferred responses for each item in five groups of participants aged 3-5 years (participants from experiment 1), 6-8 years, 9-12 years, 13-17 years, and adults (18 years and more). Whereas the youngest children elect 10 different images on the basis of their difference in size (biggest, smallest, furthest apart), only 2 such responses were found in teenagers. Instead, when they sometimes converge to a distracter image, older children and adults prefer to rely on alternative normative properties (right angle, alignment, symmetry axis), a tendency which is totally absent in the youngest group.

Table 3.

List of distracters consistently chosen across participants in experiment 2 for each age range.

	Title	3-5 yo	6-8 yo	9-12 yo	13-17 yo	adults
8	Curve	most curved (3): 33.3% (**)	-	-	-	-
11	Parallel Lines	most distant: 44.4% (***)^b	most distant (6): 36.6% (***)	-	-	-
15	Quadrilateral	unbalanced rectangle (2): 40.9% (**)^b	-	-	-	-
19	Square	biggest (3): 48.9% (***)	biggest (3): 39.8% (***)	-	-	-
22	Circle	biggest (3): 34.0% (**)	-	-	-	-
25	Horizontal Axis	narrow knob (2): 52.4% (***)^b	narrow knob (2): 33.8% (***)	narrow knob (2): 33.3% (***)	narrow knob (2): 23.6% (*)	-
26	Oblique Axis	narrow knob (2): 29.8% (*)	narrow knob (2): 29.0% (**)	-	-	-
29	Chiral Figure, Variable Orientation (1)	-^a	vertical orientation (5): 38.2% (***)^b	-	-	-
30	Chiral Figure, Variable Orientation (2)	horizontal orientation (2): 45.5% (***)^b	vertical orientation (6): 29.4% (**) horizontal orientation (2): 25.0% (.)^b	horizontal orientation (2): 24.5% (*)	-	-
35	Center of Quadrilateral	-^a	vertical axis (3): 27.9% (*) narrowest (6): 25.0% (.)^b	right-angled (1): 32.4% (***) vertical axis (3): 22.3% (.)^b	vertical axis (3): 27.6% (**)^b	vertical axis (3): 27.8% (*)^b
36	Middle of Segment	smallest (5): 50.0% (***)^b	smallest (5): 60.3% (***)	smallest (5): 31.7% (***)	-	-
37	Fixed Proportion	smallest (3): 34.0% (**)	smallest (3): 45.2% (***)	smallest (3): 36.2% (***)	smallest (3): 28.5% (***)	-
38	Translation	biggest (6): 29.8% (*)	-	-	-	-
40	Homothecy (Fixed Ratio)	biggest (5): 38.1% (**)^b	smallest (3): 27.9% (*)	smallest (3): 33.8% (***)	smallest (3): 43.4% (***)	smallest (3): 34.7% (*) aligned (6): 30.6% ()^b
42	Vertical Symmetry	smallest (2): 45.0% (***)^b	smallest (2): 26.5% (*)	-	-	-
43	Oblique Symmetry	smallest (3): 35.0% (*)^b	non-aligned axes (5): 27.9% (*)	smallest (3): 24.5% (*)	-	-
44	Point Symmetry	biggest (5): 38.1% (**)^b	-	-	-	-
45	Rotation	smallest (2): 36.4% (*)^b	right-angled (4): 26.5% (*)^b	-	-	right-angled (4): 30.0% (**)

Open in a new tab

responses did not converge on any image for this item.

the responses did not converge to the correct image in addition to the distractor(s) listed.

Beyond the general improvement of performance with age, we compared the patterns of difficulty across the five age groups describe above, in search for a common profile (Dehaene et al. 2006). In line with the observed convergence between U.S. and Amazonian participants, the item by item performance was highly correlated across all the different age groups tested (R² =0.48 to 0.94, ps<0.0001; see figure 3B). Thus the present results indicate again that this test targets a competence for geometry that is universal, develops early, and undergoes little qualitative change with experience and formal education.

Conclusion

The findings of Experiment 2 support three suggestions. First, sensitivity to geometrical properties of visual forms shows a strikingly invariant profile across ages in this U.S. population of children and adults. The problems that are most difficult for three-year-old children also are most difficult for adults, despite the vast differences between these two groups in age, experience, and education.

Second, sensitivity to geometry shows steady improvement over childhood, reaching asymptote at about 12 years of age. Interestingly, asymptotic performance is obtained well before participants begin instruction in formal, axiomatic geometry (in high school). Thus, development appears to depend more on everyday, informal experience than on formal teaching. Nevertheless, some aspects of education or culture-specific experience, such as learning to read, must influence performance on this task, as participants in a remote culture lacking education show no comparable developmental improvement (Dehaene et al. 2006). Interestingly, we also observed a shift in the mode of response in late childhood. Younger children consistently elected responses because they displayed an extreme value over some sort of continuum (largest/biggest size, furthest apart, least or most curved). In contrary, even when they chose one of the distracters, teenagers and adults converged to images displaying an abstract, normative geometric property (right angle, alignment, symmetry). There, education might have played a role, by helping children to identify the central properties of Euclidian geometry.

Third, at all ages, sensitivity to distance is high, whereas sensitivity to sense is much lower. Indeed, for adults, the asymptote across the items testing for sense relations is only 77%, compared to accuracy levels of 82% or 91% for length/distance and angles, respectively. Despite a lifetime of experience reading, and despite formal instruction in geometry, basic processes of shape analysis continue to privilege distance and angle over sense.

Nevertheless, this last point should be taken as a suggestion, rather than a conclusion, because of a critical limitation of the present task. Although the task tests for a broad range of geometric properties and relationships, it does not do so very systematically. Sensitivity to distance, angle and sense is assessed on differing numbers of trials, with figures and distracters that differ in many ways. Tests for sensitivity to angle are particularly problematic, as they occur on few trials with disproportionate use of right angles. The final experiment was undertaken to address these limitations.

Experiment 3

The next experiment is based on a similar task but uses more systematic images in order to compare sensitivity to length, angle and sense systematically. We studied the ability to merely detect variations over these dimensions in children and adults, and also the development of the relative saliency of these geometric properties.

Methods

Participants

A total of eighty-seven participants were tested in four age groups. We tested 40 preschool children (22 girls, mean age 3:11, range 3:0-4:7), 16 young elementary school children (10 girls, mean age 7:7, range 7:0-8:6), 14 older elementary school children (5 girls, mean age 10:3, range 9:8-11:3) and 17 adults (9 women, mean age 24, range 18-34). All participants were resident in the greater Boston area, and were recruited through mailing and phone by the laboratory. Children received a small gift in exchange of their participation. Adults were recruited amongst attendants to the Harvard Summer School or amongst the Cambridge community, and were offered $5 or course credit.

Displays and task

As in the previous task, in each trial 6 different images were displayed on a laptop screen, and participants were instructed to find the image that looked different. This time, all the images were L shapes constituted of two branches, one 40% smaller than the other. For each trial, the orientation of the shapes varied across the 6 images, so as to span evenly 360° of variation. In addition, the absolute size, the angle between the two branches, and the sense of the display (whether the smallest branch was in the clockwise or counter clockwise direction with respect to the larger branch) was sometimes varying as well.

Trials were of two kinds: pure trials which tested for the mere detection of a difference in length, angle or sense, with no concurrent variation; and interference trials, where another dimension was varied, in addition to the relevant dimension (see example stimuli on figure 4). In pure angle trials, all the images had the same size, and were similar in terms of sense, 5 of them had the same angle and the 6^th one deviated in terms of angle. Similarly, in pure length trial, only the size varied so as to define a deviant, and in pure sense trial, only sense varied. For the length and angle trials, the deviant length/angle value departed from the standard value by a ratio of 1:3. The two lengths to discriminate were always the same (0.5 vs 1.5 inch), although the role of the smaller and larger length as standard and deviant was counterbalanced. For angles, three ranges were used: 18° vs 54° (acute angles), 30° vs 90° (acute vs. right angle), 45° vs. 135° (acute vs. obtuse angle), again balancing the roles of the smaller and larger angle as standard and deviant.

Stimuli presented in Experiment 3. In this experiment we focused on the dimensions of angle, length, and sense. A third of the trials were “pure trials”, where only the relevant dimension was allowed to vary. For example, in pure angle trials, length as well as sense were kept constant. The other conditions were interference trials, where another (irrelevant) dimension was allowed to vary. For example, in angle trials with length interference, the deviant is defined in terms of angle (all but one angles are equal), but the shapes vary in size as well.

In the interference trials, together with a relevant variation of angle, length or sense defining the deviant image, one irrelevant dimension was let to vary amongst size, angle or sense. For example, two types of interference trials were created for the dimension of length, where either angle or sense was varied in addition to the relevant variation of length. Crucially, when this other dimension was allowed to vary, values were spread evenly across an interval of values, so that none of them could be considered as deviant according to an all-or-none rule. More specifically, when length was allowed to vary, lengths spanned the whole interval from 0.5 to 1.5 inch linearly, with increments of 0.2 inch across the 6 images. For angle, again three ranges were used, which spanned one of three intervals evenly with linear increments: 18° to 90°, 36° to 126° (in this case one of the images had a right angle), or 90° to 150°. Finally, in case sense was let to vary, 3 images were drawn for each direction.

Procedure

Again, the participants were instructed to find the image that looked different. A friendly experimenter advanced the slides across trials for the children and also clicked on the chosen response unless the child requested to do so. Adults advanced trials and clicked themselves.

Before the actual test, participants received 4 practice trials with color or orientation as the relevant dimension. In the first two trials, only the relevant dimension was varied. In the two next trials, angle varied on the trial targeting colour, and size varied on the trial targeting orientation. If the participant made an error on one of the training trials, the four trials were repeated a second time.

Following the practice trials, participants received either 27 (the youngest children), 54 (the two groups of older children) or 162 (the adults) test trials. Trials were organized in blocks of 27 trials, which contained 3 trials of each condition (a total of 9 conditions for both pure and interference trials) in a randomized order. Every 54 trials, a screen appeared to tell participants that they could take a break. At the first break screen, children were told that the game was all done, but 3 of them did another extra block of trials as they requested to keep playing (these data are included in the following analyses).

Results

Pure trials

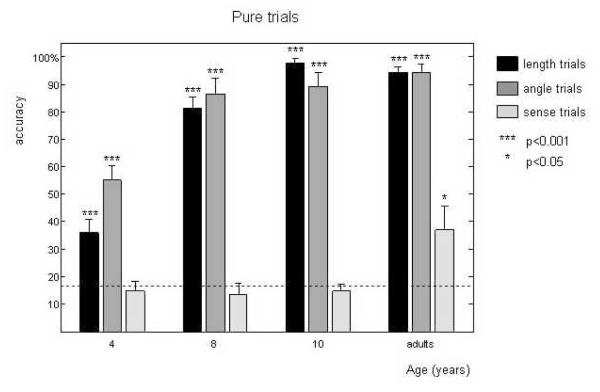
We first analyzed the pure trials, focusing on length, angle and sense with no interference from other dimensions. Performance were high on average (53.9% accuracy) and much better than the chance level of 16.7% (T(86)=15.4, p<0.0001). Accuracy was analyzed with a 4 × 3 ANOVA with two factors of age group and condition (pure length, angle or sense). Performance increased significantly with age (F(3,79)=38.4, p<0.0001), and differed across the conditions (F(2,166)=212.8, p<0.0001). In fact, accuracy was above chance level for angle and length in every group (all ps<0.0001), but did not depart from chance for sense except for the group of adults (adults: T(16)=2.4, p=0.029; children: all ps>0.45) (see figure 5). This discrepancy between length and angle on one hand, and sense on the other resulted in an interaction between the two factors (F(6,166)=6.4, p<0.0001). Furthermore, the developmental trend differed also between length and angle (F(3,81)=5.2, p=0.0024): younger children were better with length than with angle, and this pattern was reversed in adults and older children. In sum, these analyses confirm that children can process angle and length at a very young age, but the sensitivity to sense develops slowly. In addition, this test indicates that sensitivity to length and angle are acquired at a different pace, with an early advantage for length.

Finally, an analysis focusing of the different angle ranges tested revealed that at all ages, competence with angles was not restricted to the special case of right angles. Performance was identical in the three ranges tested (acute vs. acute/right angle/ obtuse: F<1), and did not interact with age group (F(2,166)=1.0, p=0.41). Specifically, in the youngest group, accuracy was similar when comparing an acute angle to another acute angle (37.5%), to a right angle (35.0%), or to an obtuse angle (35.0%).

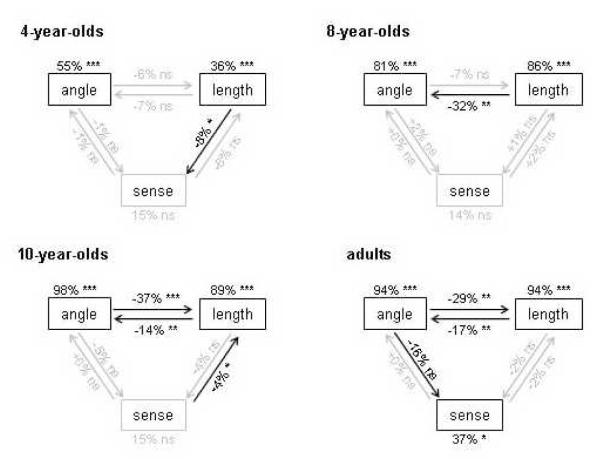
Interferences between dimensions

Having established that differences in length and angle can be perceived at an early age, we now turn to interferences between dimensions, in order to assess the relative saliency of the different dimensions. Interference effects of each property on each of the other properties were tested by t tests, and results are summarized on figure 6. In adults, we observed interference of length and angle on each other: performance was significantly worse on angle trials when there was an irrelevant variation of length, compared to the trials where length was held constant (T(16)=3.2, p=0.0054). Reciprocally, accuracy was also reduced on trials targeting length, when an irrelevant variation of angle was introduced (T(16)=5.8, p<0.0001). These interference effects could have different sources. Perhaps the dimensions of angle and length are not separable, such that for example, variations of length would induce illusions of a different angle at the perceptual level (Kennedy et al. 2008). Alternatively, it is possible that the interference effects were due to the use of different heuristics. When variations of length were introduced, participants may have detected this variation on two or more (standard) images that did not concomitantly vary in angle, therefore decided that the present trial targeted length, and then oriented their search towards a length deviant while ignoring angle variations.

Interference effects. The significant effects are presented in black, and non-significant effects are showed in grey. The performance indicated on top of the frames corresponds to the pure trials. The arrows between the frames show how the performance is modulated in the interference trials: an arrow from “length” to “angle” indicates how the performance on angle trials with length interaction differs from the pure angle trials. Predicted effects are negative. .: p<0.1, *:p<0.05; **: p<0.01; ***: p<0.001.

On the contrary, variations of sense did not disturb performance on angle or length trials, compared to the pure trials (ps>0.31). These results indicate that length and angle are more salient for adults, compared to sense, and would accord with the hypothesis that sense is encoded via a separate system. Similarly, length variation did not interfere with the perception of sense differences in adults (p=0.57). However, angle variation prevented the detection of sense differences, since adults’ performance on sense trials was at chance when an irrelevant angle variation was introduced (20.6% accuracy, no different from chance p=0.21; effect of interference: T(16)=2.1, p=0.055). In fact, these trials are also responded faster than the pure sense trials (5357 vs 9230ms, T(16)=5.0, p=0.00012), suggesting that the participants failed to detect that sense was the relevant variable and instead focused on other geometric properties. As further supported by the analyses of responses distributions (see below), participants were responding to these trials on the basis of angle cues instead of sense.

We now turn to developmental analyses of these interference effects. Again, sense did not interfere on the detection of angle and length difference in any of the age groups (ps>0.26), except for a significant but negligible effect of sense on length in the group of 10-year-olds (accuracy 85.0 vs 89.0%; T(13)=2.3, p=0.037). In the three groups of children, sense trials were responded at chance, and therefore we did not observe any effect of interference on the sense trials (ps>0.35), except in the younger group, where length variation caused sense trials to be responded worse than chance (6.7% accuracy, significantly worse than chance T(39)=−4.7, p<0.0001; effect of interference: T(39)=2.1, p=0.040). This effect is hard to interpret and is probably coincidental. These results confirm children’s inability to detect differences in sense.

Interference effects between angle and length developed gradually in the different age groups. The youngest children displayed none of the interference effects (ps>0.28). The absence of interference in younger children might be due to a floor effect: possibly the performance of the children in the pure trials were too low for us to observe any effect of interference on them. Children aged 7-8 showed an interference of length on angle (T(15)=3.8, p=0.0017), but not the reverse effect (p=0.16). In the oldest children, like adults, the two interference effects were present (interference of length on angle: T(13)=3.2, p=0.0066; interference of angle on length: T(13)=5.5, p=0.0001). This trend corroborates our first observation made on pure trials that angle and length develop at different pace with length being attended to earlier than angle.

Distribution of responses

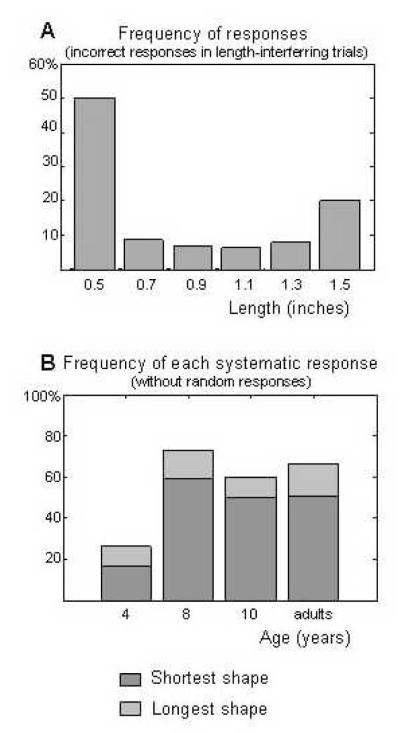
We next examined which responses the participants converged to, in the interference trials, when they failed to identify the correct outcome. We first describe the distribution of responses along the length dimensions. In the case of length, the interference was created by making the six shapes vary in size between 0.5 and 1.5 inch, with linear increments (see methods). Figure 7A gives the distribution of responses for the six sizes presented, for trials that targeted either angle or sense but with interfering variation of length, and were not answered correctly (all ages). As can be seen on the figure, participants gave a number of random responses (corresponding to the flat rate of responses for the intermediate sizes comprised between 0.7 and 1.3 inch), but also converged towards the shortest and the longest lengths in a majority of trials.

Next, we examined whether this pattern was present in every age group. To do so, for each age group we submitted the distribution of responses to a linear regression, with a first flat regressor corresponding to the random responses, and two additional regressors measuring how much the smallest and largest shape outnumbered the other choices. This model provided very good fits in all age ranges (R² between 0.903 and 0.998). Figure 7B represents the respective weights attributed to the shortest and the largest images, for each age group: these values estimate how much more often these responses are chosen, compared to the intermediate responses. As can be seen on the figure, in all groups the responses converge towards the extreme values (contributions of the regressors for the smallest and largest responses: ps<0.05). The proportion of convergence increases between the ages of 4 and 8, and then stays steady from the age of 8. Again, this third measure converges with the analyses of pure trials and of interference effects to indicate that the sensitivity to length is already mature by the age of 8. Furthermore, in all groups we observe a preference for the shorter image over the larger one. This preference is consistent with a discrimination of length on the basis of ratio: in terms of ratio, the shortest length is more different from its closest value (ratio 5:7) than the largest length (ratio 13:15).

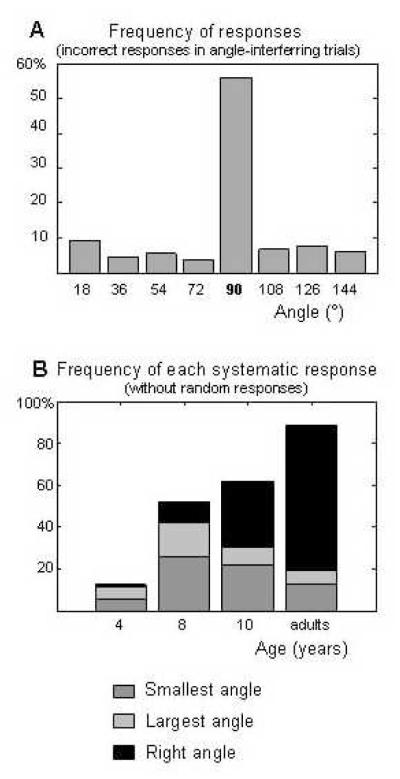
In the case of angle, the analyses are complicated by the use of three different ranges of variation: depending on the trials, the angles varied between 18° and 90° (acute angles), or between 36° and 126° (a mixture of acute and obtuse angles, with one instance of right angle), or between 90° and 150° (obtuse angles). Again, we looked at the distribution of responses by angle value, for erroneous responses given in trials targeting either length or sense, with an interfering variation of angle. In figure 8A, this distribution is given for absolute values of angle, irrespective of the range used. As can be seen on this figure, across participants there is a strong convergence of responses to the right angle. We used a linear regression analysis to estimate the proportion of responses corresponding either to the smallest angle, the largest angle, or the right angle; regressors were adapted for each angle range. Figure 8B reports the results of these fits (R2= 0.343 to 0.995; except for the youngest group R2=0.063), and illustrates how often smallest/largest/right angles are chosen for each age group, over the flat rate of random responses. In the young children, responses were essentially random (ps>0.13). Reliance on angle increased with age, and our middle group of children showed a strong reliance on both the smaller and the larger angle (ps<0.05; right angle: p=0.23). The convergence on right angle however did not really appear until the age of 10. In the older children and the adults, right angles represented most of the responses, with very little choices of the smallest/largest angles (right angles: ps<0.05; smallest/largest: ps<0.0004 for adults, p>0.12 for the 10-year-olds).

Same analysis as figure 7, this time focusing on angle. (A) Distribution of the responses for each (absolute) value of angle, pooled across the 3 ranges of angle studied, for all participants. (B) Contribution of the regressors associated with the narrowest/widest/right angle, in a linear model fit to the responses (cf. figure 7).

Here again, we observed a different pace for the development of angle, compared to length, however this analysis revealed that the development of sensitivity to angle occurred in two steps. Between the ages of 4 and 8, children acquired a better sensitivity to angle, parallel to a refinement of length representations. After 8 years of age, children acquired abstract knowledge about angles, and started viewing right angles as special. This shift from an ‘outlier’ response heuristic, which identifies the extreme values, to normative responses, mirrors the findings of experiment 1, where children stopped relying so much on size distractors after the age of 8.

Summary statistics

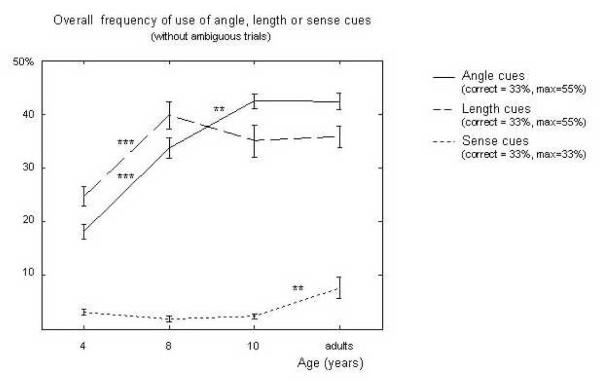
Finally, we computed a summary statistic, which enabled us to test for differences in developmental trajectories in a more systematic way. For each participant, we calculated what proportions of trials were responded on the basis of sense (correct responses to sense), length (correct responses to length, and choices of shortest/largest shape in length interference trial), or angle (idem: correct responses to angle, and choices of smallest/largest/right angle in angle interference trials). Some responses were ambiguous with respect to the type of cue used (as for example if the correct short deviant also had a right angle in an angle-interfering length trial), and were excluded from the present analysis. The resulting frequencies were submitted to an ANOVA with two factors for type of response (sense, length, angle) and age group. In this ANOVA, the main effect of type of response is quite meaningless since the chance levels are different for each type of cue. However, the ANOVA identified an effect of age (F(3,83)=60.4, p<0.0001), reflecting a general improvement of performance (Figure 9). More crucially, we also obtained an interaction between age and type of response (F(6,166)=12.9, p<0.0001), which reflects the difference in developmental pace across the different type of responses. Direct comparisons indicated that for length, the youngest children were different from all other groups (T test corrected for multiple comparison, pcorrs<0.011), while all the other groups performed at the same level (pcorrs>0.68). For angle, performance improved between the groups of children (pcorrs<0.0053), and then stayed steady from 10 year to adulthood (p=0.99). In the case of sense, the improvement in performance was observed only in the group of adults (adults vs. group of children: pcorrs<0.0048; between groups of children: pcorrs=1).

Overall frequency of use of angle, length and sense cues. A compound measure was created, to estimate how often trials are responded using angle (resp. length, sense) cues, either being an angle (resp. length, sense) trial responded correctly, or because a smallest/largest/right angle (resp. length) was chosen in an interference trial. Ambiguous trials, which could have been attributed to either or the other of these cues, were removed from this analysis. The frequencies evolved differently with age, thus creating a significant interaction. The stars refer to differences between age groups for each type of cue (**: p<0.01; ***: p<0.001).

Finally, we used this compound measure to explore the sources of the observed interference effects between angle and length. We reasoned that if the interference effects reflect a switch between strategies, rather than a perceptual illusion, we should see a priming effect of the previous trial on the responses given to the length-angle interference trials. Specifically, if an angle-length interference trial followed a response based on angle, participants should be primed to use angle again in this trial. Therefore, we isolated the trials testing for interferences between length and angle (in either direction), and sorted them by the type of response given on the previous trial (focusing on trials preceded by responses unambiguously attributed to length or angle). When all the participants were grouped together, we observed the predicted priming effect (Chi2(1)=11.6, p=0.00066): participants tended to respond using the same type of geometric property that they had used on the previous trial. This effect was not observed in every age group, possibly due to the reduced number of trials conforming to the constraints, still it was present in the group of adults (Chi2(1)=4.6, p=0.033), who showed the largest interference effects (see section ”interferences”). Based on this analysis, we argue that the interference effects observed rely at least to some extent on top-down search heuristics, rather than perceptual illusions.

General Discussion

Three experiments assessed the development of sensitivity to different types of geometric information in visual shapes, with a special emphasis on length, angle and sense. In the first study, we administered to preschool children a test that had previously been used with adults and older children of different cultures (Dehaene et al. 2006). In contrast to the past research, we analyzed in detail children’s and adults’ use of each of a host of specific geometric properties in this task. In brief, our analyses suggest that children detect the basic relationships of length and angle but not sense. Children also respond to global relationships of connectedness, curvature, and convexity but not to symmetry or other higher-order Euclidean properties.

In experiment 2, we compared the performance of the preschool children to a large group of older children and adults. We observed a striking qualitative similarity across ages, while performance also increases progressively, reaching an asymptote at about adolescence. Importantly, asymptotic performance was high but not at ceiling for several geometric properties, especially those involving sense relations. These results indicate that preschool children are already sensitive to geometric properties of visual shapes. The geometric properties that the youngest children detect best are those that adults spontaneously grasped most readily, whereas the geometric properties that preschool children fail to detect remain most difficult throughout development.

A crucial limitation of the above studies stems from the stimulus materials on which they are based: although they cover many different geometrical relationships, they do not allow for a precise and quantitative comparison of sensitivity to distance, angle, and sense. Accordingly, we designed a new study that does permit this comparison, and administered it to preschool children, older children, and adults (Experiment 3). This last experiment confirmed that sensitivity to angle and length is present from a very young age, while sensitivity to sense develops late in adolescence. Furthermore, this new test revealed different developmental trends between length and angles: while sensitivity to length is mature by the age of 8, sensitivity to angle continues to mature until 10 years of age. In fact, between the ages of 8 and 10, children develop a specific sensitivity to right angles, which they start to consider as special. This pattern emerges at about the same age as the tendency to use abstract normative properties in our first test, such as parallelism, rather than relying on a comparative analysis of the images (the “largest”, the “smallest”).

The present test therefore identifies two sources for geometrical knowledge: first, a sensitivity to quantitative geometric properties, mainly length and angle, that is in place very early in life and probably is universal amongst all human beings; second, later reorganization of this knowledge around particular geometrical properties that are granted a special status: parallel and perpendicular lines.

Universal core knowledge of geometry

The first test used in our research had been previously used to study intuitions about geometry in a remote indigene group from the Amazon, the Mundurucus (Dehaene et al. 2006). This research has revealed a universal profile of competence for plane geometry: the performance of the Mundurucus across items matched this of age-matched controls, both for adults and children. Here, we replicate this result by showing that within a U.S. population, performance is very strongly correlated across age groups: whereas the general level of accuracy increases, in general the profile of difficulty across items stays the same throughout life. This common profile provides evidence for a universal system of geometrical knowledge that is in place early in life, and that does not depend on variable aspects of culture or language.

Our second test brings further support to this conclusion, by identifying a characteristic signature that is common across age groups: in all groups, problems relying on angle or length relations are solved easily and rapidly, whereas problems relying on sense relations require strategies that emerge later and remain effortful even for adults. Such results are in line with research on infants, which establishes that even newborns can detect variations in angle or length (Slater et al. 1990; Slater et al. 1991), whereas infants and children readily ignore sense distinctions when assessing whether two shapes are similar (Bornstein 1979; Gibson et al. 1962; Huttenlocher 1967; Lourenco et al. 2005).

In contrast to these similarities, we found one difference emerging in the processing of length and angle, when testing for interference between these dimensions. Although younger children are not influenced by irrelevant variations of length (resp. angle) in trials testing for angle (resp. length) deviance, these interactions are found later in life. Starting at 8 years of age, variations of length perturbs the assessment of angle differences. Then, from the age of 10 years, interference effects are also found in the other direction. It is possible that the present experiment was badly designed to observe interference effects in preschoolers, because performance was too low on pure, no-interference trials to leave room for interference effects. However, this argument does not hold for the group of 8 year old children, who had decent performance in both angle and length pure trials, while still only showing interference of length on angle, and not the reverse. These effects of interference can be interpreted in two ways. First, it is possible that over development, the representation of geometric properties such as length and angle are restructured such that these two dimensions, which are originally separable, become progressively tightly intermingled. Hence, in adults, irrelevant variations of length induce illusions on angular aperture (Kennedy et al. 2008). Second, the search heuristics applied by the participants might explain the occurrence of interference effects, even in the absence of interference at the perceptual level. For example, participants might first decide, on each trial, on which dimension they will be looking for a deviant (either angle or length), and then select the image which shows the greatest contrast on the selected dimension. In accordance with this heuristic interpretation, we observed a priming effect across trials: participants were more likely to use angle to select a response, after a prior decision based on angle. Further research needs to evaluate whether these top-down heuristic effects account fully for the observed interference effects, or whether these effects also rely on context-free perceptual interactions.

Development of abstract geometric knowledge

During the last years of elementary school, children transcend their initial geometric knowledge in three respects. First, younger children are able to discriminate between different values of length and angle, but they treat each value in the continuum as equal. Between the ages of 8 and 10, children start to attribute a special status to right angles, viewing a right angle as “different” amongst angles of various values. The late development of this tendency contrasts with the findings of studies of the “perpendicular effect” in young children’s drawings, where angles are distorted towards right angles (Bremner and Taylor 1982; Ibbotson and Bryant 1976). The effect on drawings may reflect a specific tuning of the visual system towards right angles, and it may provide a perceptual basis for a later acquired theoretical distinction between right angles and other types of angles in tasks such as ours, where the orientations of the lines vary.

What then initiates the change in the interpretation of right angles, and how special did the children think that right angles are? One (minimal) possibility is that children do not attribute any special property to right angles, except for the fact that they have a special name and their teachers taught them to attend to right angles. It is also possible that children have noticed that right angle is an important feature with an important role in discriminating amongst geometrical properties (square vs. rhombus, rectangle vs. parallelogram). Beyond their role in categorizing figures, right angles have deeper special properties within the theory of Euclidian geometry, in their relation to parallel lines, symmetry, circles, or in terms of metric properties (eg. The Pythagorean theorem, mediatrice of a segment). Such theoretical knowledge is only learned after the effect described here, and does not precede the children thinking of right angles as special. Independently of the instruction they may receive in geometry, U.S. children could also have learned the importance of right angles from the urban environment they live in (the “carpented world” hypothesis), where perpendiculars and parallels are preeminent. This hypothesis predicts that we should not see the same effect emerge in rural populations.

A second developmental change is suggested by performance on our first test: responses evolved with age towards more abstract geometric properties. Items in this test were conceived around abstract properties, and to find the correct response, participants needed to identify an all-or-none rule that applied to all but one of the images. With age, children were getting better at this reasoning, as the performance steadily increased until adolescence. Furthermore, the analysis of wrong responses shows that children progressively avoid extreme values, and even when they fail to identify the correct properties, they try to base their responses on another abstract property (symmetry, right angles). On the different items, this evolution seems to appear at different ages: for example, from the age of 6 children stop considering a very curved line as a possible deviant, and agree that straight line are special. In comparison, in the item testing for parallel vs. secant lines, children converge on the furthest apart parallels (instead of secant lines) until the age of 9. Although the test was not ideally designed to estimate the ages at which these changes occur, these discrepancy tend to indicate that the different properties are acquired gradually (eg. straight lines are identified as special before parallel lines), and different items tap different steps in this path.

A third change concerns the status of polygons with specific numbers of sides. Amongst the items studied, we found striking evidence that the youngest children did not identify a triangle amongst images of quadrilaterals. At this age, children already have verbal labels for triangles and rectangles (Clements et al. 1999; Pinet and Gentaz in prep; Satlow and Newcombe 1998). However, they only apply these labels to regular, prototypical figures. For example, young children are much more likely to call a figure a ‘triangle’, when it is isosceles and presented in the vertical orientation (Clements et al. 1999; Pinet and Gentaz in prep). Moreover, in a classification task using verbal instructions (“triangle”, “square”, “circle”), young children aged 5 and less exclude non-canonical instances of these figures (Satlow and Newcombe 1998). While children use templates to recognize figures, they do not attend to distinctions based on the number of sides, perhaps less salient to them. Moreover, an interesting comparison can be made between the present data and data collected from speakers of Dani in New Guinea (Rosch 1973), whose language lacks terms for geometric figures. When asked to sort a set of cards generated from a triangle, a square and a circle, speakers of Dani did not spontaneously arrange the cards according to the shape of the figure. Furthermore, when presented with 3 cards, where two of them were based on the same figure, and the last one was based on a different figure, they did not rely on the shape to indicate which of the 3 were most similar. Contrary to the Dani speakers, Mundurucu speakers succeeded at the present item contrasting triangles and quadrilaterals (Dehaene et al. 2006). Interestingly, the Mundurucu language incorporates distinctions between figures based on the number of sides (‘ebapûg ta rûg at’: a figure with at least three angles; ‘ebadipdip ta rûg at’: a figure with at least four angles; P. Pica, personal communication). Results from Dani speakers and from young U.S. children suggest that the classification of figures by the number of their sides is not part of universal geometric core knowledge, although they are emphasized in most cultures of the world.

Dissociation with the results from navigation studies: two systems of core knowledge

In sum, our results identify a general pattern across various ages for plane geometry: preschoolers, elementary school children, teenagers and adults all show an advantage for length, angle, and topological relations. In contrast, most age groups failed at identifying distinctions based on sense, and adults only succeeded at the cost of effortful and unreliable mental rotation strategies. This dissociation signature between length/angle and sense departs from the results obtained in navigation tasks using larger-scale, 3-dimensional stimuli, based on the classical reorientation paradigm. In this paradigm, participants first watch an experimenter hide an object in a corner of a room, and then they are turned with eyes covered until they have lost track of the direction of their heading. They are then allowed to go retrieve the hidden object. This paradigm has been used to demonstrate a competence for geometry in a variety of populations, including human adults and children, as well as many animal species (for a review, see (Cheng and Newcombe 2005)). Most studies are based on a rectangular room: when allowed to retrieve the hidden object, participants direct their searches either to the correct corner, or to the opposite corner (rotational equivalent), which is similar to the correct corner in terms of geometry. Doing so, participants show an ability to use cues of length and sense: they discriminate between corners that have a short wall either on their left or on their right. This ability to use sense relations provides a first dissociation with the present studies, where children proved unable to use sense until adolescence. Furthermore, while they succeed in rectangle room, young children fail to reorient in a room shaped like a rhombus, until after their 4^th birthday (Hupbach and Nadel 2005): they are unable to use angle cues to reorient. This results constitutes a second dissociation with the present task, given the preschoolers success to discriminate between shapes varying in angle.

In brief, we observed a double dissociation between the analysis of geometric cues in visual shapes, and geometry-guided navigation. To account for such dissociation, we have proposed the existence of two specialised core knowledge systems for geometry (Lee et al. in prep). These two systems are dissociated by the type of input that they can process (plane, small-scale shapes, vs large, 3-dimensional enclosures), and the type of analysis they perform on this input (angle and length but no sense vs. length and sense but no angle).

Neither of these systems provides enough resources to fully represent Euclidian geometry. Contrary to philosophers’ intuitions (Hatfield 1998; Kline 1989), Euclidian geometry therefore needs to be constructed over the course of development. This construction could be spontaneous, such that all humans might possess geometric knowledge that encompasses all aspects of Euclidian geometry, in an integrated format that permit a flexible use of any length, angle or sense cue in any task. Or, this construction could might only happen upon contact and experience with culture-specific artefacts providing a fusion of the domains of both systems (scale-invariance), such as maps or spatial language. Further studies, probing relations between children’s performance in the present tasks and in tasks of symbolic navigation and spatial representation, could serve to distinguish these possibilities.

Acknowledgments

We thank Konika Banerjee, Lacey Beckmann, Lola de Hevia, Ariel Grace, Amy Heberle, Logan Hegg, Danielle Hinchey, Kristen Lamont, Alexander Leaf, Sang Ah Lee, Raphael Lizcano, Shannon McCarthy, Rebecca Rosenberg, Kristin Shutts, and Monica Vanderslice for their help in collecting the data. This work was supported by grants from the National Science Foundation (REC-0196471) and the National Institutes of Health (HD23103) to Elizabeth Spelke.

Footnotes

For five of the children, only the age in years could be obtained (one 4-year-old, four 5-year-olds).

References

Antell SEG, Caron AJ. Neonatal perception of spatial relationships. Infant Behavior and Development. 1985;8:15–23. [Google Scholar]
Banks MS, Ginsburg AP. Infant visual preferences: a review and new theoretical treatment. Adv Child Dev Behav. 1985;19:207–246. doi: 10.1016/s0065-2407(08)60392-4. [DOI] [PubMed] [Google Scholar]
Biederman I, Cooper EE. Evidence for complete translational and reflectional invariance in visual object priming. Perception. 1991;20:585–593. doi: 10.1068/p200585. [DOI] [PubMed] [Google Scholar]
Bomba PC, Siqueland ER. The Nature and Structure of Infant Form Categories. Journal of Experimental Child Psychology. 1983;35:294–328. [Google Scholar]
Bornstein MH. Perceptual development: Stability and change in feature perception. In: Bornstein MH, Kessen W, editors. Image to attention. Erlbaum; Hillsdale, N.J.: 1979. [Google Scholar]
Bremner J, Taylor A. Children’s errors in copying angles: Perpendicular error or bisection error? Perception. 1982;11:163–171. doi: 10.1068/p110163. [DOI] [PubMed] [Google Scholar]
Cheng K, Newcombe NS. Is there a geometric module for spatial orientation? Squaring theory and evidence. Psychon Bull Rev. 2005;12(1):1–23. doi: 10.3758/bf03196346. [DOI] [PubMed] [Google Scholar]
Clements DH, Swaminathan S, Hannibal MAZ, Sarama J. Young Children’s Concepts of Shape. Journal for Research in Mathematics Education. 1999;30(2):192–212. [Google Scholar]
Cooper LA, Shepard RN. Chronometric studies of the rotation of mental images. In: Chase WG, editor. Visual Information Processing. Academic Press; New York: 1973. pp. 75–176. [Google Scholar]
Cornell JM. Spontaneous Mirror-Writing in Children. Canadian Journal of Psychology. 1985;39(1):174–179. [Google Scholar]
Dehaene S. Les Neurones de la Lecture. Odile Jacob; Paris: 2007. [Google Scholar]
Dehaene S, Cohen L, Sigman M, Vinckier F. The neural code for written words: a proposal. Trends Cogn Sci. 2005;9(7):335–341. doi: 10.1016/j.tics.2005.05.004. [DOI] [PubMed] [Google Scholar]
Dehaene S, Izard V, Pica P, Spelke E. Core knowledge of geometry in an Amazonian indigene group. Science. 2006;311(5759):381–384. doi: 10.1126/science.1121739. [DOI] [PubMed] [Google Scholar]
Downing PE, Chan AW, Peelen MV, Dodds CM, Kanwisher N. Domain specificity in visual cortex. Cereb Cortex. 2006;16(10):1453–1461. doi: 10.1093/cercor/bhj086. [DOI] [PubMed] [Google Scholar]
Epstein R, Kanwisher N. A cortical representation of the local visual environment. Nature. 1998;392(6676):598–601. doi: 10.1038/33402. [DOI] [PubMed] [Google Scholar]
Fantz RL, Fagan JF, Miranda SB. Early visual selectivity. Infant perception: From sensation to cognition. 1975;1:249–346. [Google Scholar]
Gibson EJ, Gibson JJ, Pick AD, Osser H. A developmental study of the discrimination of letter-like forms. J Comp Physiol Psychol. 1962;55:897–906. doi: 10.1037/h0043190. [DOI] [PubMed] [Google Scholar]
Hatfield G. The Natural and the Normative: Theories of Spatial Perception from Kant to Helmholtz. The MIT Press; Cambridge, Massachussets London, England: 1998. [Google Scholar]
Hermer L, Spelke ES. Modularity and development: the case of spatial reorientation. Cognition. 1996;61(3):195–232. doi: 10.1016/s0010-0277(96)00714-7. [DOI] [PubMed] [Google Scholar]
Hupbach A, Nadel L. Reorientation in a rhombic environment: No evidence for an encapsulated geometric module. Cognitive Development. 2005;20(2):279–302. [Google Scholar]
Huttenlocher J. Discrimination of figure orientation: effects of relative position. J Comp Physiol Psychol. 1967;63(2):359–361. doi: 10.1037/h0024398. [DOI] [PubMed] [Google Scholar]
Huttenlocher J, Newcombe N, Sandberg EH. The coding of spatial location in young children. Cognit Psychol. 1994;27(2):115–147. doi: 10.1006/cogp.1994.1014. [DOI] [PubMed] [Google Scholar]
Ibbotson A, Bryant P. The perpendicular error and the vertical effect in children’s drawing. Perception. 1976;5:319–326. doi: 10.1068/p050319. [DOI] [PubMed] [Google Scholar]
Kanwisher N, McDermott J, Chun MM. The fusiform face area: a module in human extrastriate cortex specialized for face perception. J Neurosci. 1997;17(11):4302–4311. doi: 10.1523/JNEUROSCI.17-11-04302.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kelly DM, Bischof WF. Reorienting in images of a three-dimensional environment. J Exp Psychol Hum Percept Perform. 2005;31(6):1391–1403. doi: 10.1037/0096-1523.31.6.1391. [DOI] [PubMed] [Google Scholar]
Kelly DM, Spetch ML. Reorientation in a two-dimensional environment: I. Do adults encode the featural and geometric properties of a two-dimensional schematic of a room? J Comp Psychol. 2004;118(1):82–94. doi: 10.1037/0735-7036.118.1.82. [DOI] [PubMed] [Google Scholar]
Kennedy GJ, Orbach HS, Loffler G. Global shape versus local feature: an angle illusion. Vision Res. 2008;48(11):1281–1289. doi: 10.1016/j.visres.2008.03.003. [DOI] [PubMed] [Google Scholar]
Kline M. Mathématiques: la fin de la certitude. Christian Bourgeois; Paris: 1989. [Google Scholar]
Lee SA, Izard V, Spelke E. Core systems of geometry. (in prep)
Logothetis NK, Pauls J, Bulthoff HH, Poggio T. View-dependent object recognition by monkeys. Curr Biol. 1994;4(5):401–414. doi: 10.1016/s0960-9822(00)00089-0. [DOI] [PubMed] [Google Scholar]
Lourenco SF, Huttenlocher J. The Representation of Geometric Cues in Infancy. Infancy. 2008:103–127. doi: 10.1080/15250000701795572. [DOI] [PubMed] [Google Scholar]
Lourenco SF, Huttenlocher J, Fabian L. Coding geometric information in infancy. Biennal Meeting of the Cognitive Developmnet Society (CDS); San Diego, CA. 2005. [Google Scholar]
McGurk H. Infant discrimination of orientation. Journal of Experimental Child Psychology. 1972;14:151–164. doi: 10.1016/0022-0965(72)90040-9. [DOI] [PubMed] [Google Scholar]
McMonnies CW. Visuo-spatial discrimination and mirror image letter reversals in reading. J Am Optom Assoc. 1992;63:698–704. [PubMed] [Google Scholar]
Newcombe NS, Huttenlocher J. Making Space: the development of spatial representation and reasoning. The MIT Press; Cambridge, Massachussets London, England: 2000. [Google Scholar]
Newcombe NS, Uttal DH. Whorf versus Socrates, round 10. Trends Cogn Sci. 2006;10(9):394–396. doi: 10.1016/j.tics.2006.07.008. [DOI] [PubMed] [Google Scholar]
Piaget J, Inhelder B. The child’s conception of space. W.W. Norton; New York: 1967. [Google Scholar]
Pinet L, Gentaz E. The acquisition of geometrical shapes in children: a study on the contribution of the haptic modality. (in prep)
Reddy L, Kanwisher N. Coding of visual objects in the ventral stream. Curr Opin Neurobiol. 2006;16(4):408–414. doi: 10.1016/j.conb.2006.06.004. [DOI] [PubMed] [Google Scholar]
Rollenhagen JE, Olson CR. Mirror-image confusion in single neurons of the macaque inferotemporal cortex. Science. 2000;287(5457):1506–1508. doi: 10.1126/science.287.5457.1506. [DOI] [PubMed] [Google Scholar]
Rosch EH. Natural Categories. Cognitive Psychology. 1973;4:328–350. [Google Scholar]
Sandberg EH, Huttenlocher J, Newcombe N. The development of hierarchical representation of two-dimensional space. Child Dev. 1996;67(3):721–739. [PubMed] [Google Scholar]
Satlow E, Newcombe N. When is a triangle not a triangle? Young children’s developing concepts of geometric shape. Cognitive Development. 1998;13:547–559. [Google Scholar]
Schwartz M, Day RH. Visual shape perception in early infancy. Monographs of the Society for Research in Child Development. 1979;44(7) serial No. 182. [PubMed] [Google Scholar]
Serpell R. Discrimination of orientation by Zambian children. Journal of Comparatie and Physiological Psychology. 1971;75(2):312–316. doi: 10.1037/h0030832. [DOI] [PubMed] [Google Scholar]
Shepard RN, Metzler J. Mental Rotation of Three-Dimensional Objects. Science. 1971;171(3972):701–703. doi: 10.1126/science.171.3972.701. [DOI] [PubMed] [Google Scholar]
Slater A, Mattock A, Brown E. Size constancy at birth: Newborn infants’ responses to retinal and real size. Journal of Experimental Child Psychology. 1990;49:314–322. doi: 10.1016/0022-0965(90)90061-c. [DOI] [PubMed] [Google Scholar]
Slater A, Mattock A, Brown E, Bremner JG. Form Perception at Birth: Cohen and Younger (1984) Revisited. Journal of Experimental Child Psychology. 1991;51:395–406. doi: 10.1016/0022-0965(91)90084-6. [DOI] [PubMed] [Google Scholar]
Slater A, Morison V, Town C, Rose D. Movement perception and identity constancy in the new-born infant. British Journal of Developmental Psychology. 1985;3:211–220. [Google Scholar]
Terepocki M, Kruk RS, Willows DM. The incidence and nature of letter orientation errors in reading disability. J Learn Disabil. 2002;35(3):214–233. doi: 10.1177/002221940203500304. [DOI] [PubMed] [Google Scholar]
Turnbull OH. A double dissociation between knowledge of object identity and object orientation. Neuropsychologia. 1997;35:567–570. doi: 10.1016/s0028-3932(96)00098-x. [DOI] [PubMed] [Google Scholar]

[R1] Antell SEG, Caron AJ. Neonatal perception of spatial relationships. Infant Behavior and Development. 1985;8:15–23. [Google Scholar]

[R2] Banks MS, Ginsburg AP. Infant visual preferences: a review and new theoretical treatment. Adv Child Dev Behav. 1985;19:207–246. doi: 10.1016/s0065-2407(08)60392-4. [DOI] [PubMed] [Google Scholar]

[R3] Biederman I, Cooper EE. Evidence for complete translational and reflectional invariance in visual object priming. Perception. 1991;20:585–593. doi: 10.1068/p200585. [DOI] [PubMed] [Google Scholar]

[R4] Bomba PC, Siqueland ER. The Nature and Structure of Infant Form Categories. Journal of Experimental Child Psychology. 1983;35:294–328. [Google Scholar]

[R5] Bornstein MH. Perceptual development: Stability and change in feature perception. In: Bornstein MH, Kessen W, editors. Image to attention. Erlbaum; Hillsdale, N.J.: 1979. [Google Scholar]

[R6] Bremner J, Taylor A. Children’s errors in copying angles: Perpendicular error or bisection error? Perception. 1982;11:163–171. doi: 10.1068/p110163. [DOI] [PubMed] [Google Scholar]

[R7] Cheng K, Newcombe NS. Is there a geometric module for spatial orientation? Squaring theory and evidence. Psychon Bull Rev. 2005;12(1):1–23. doi: 10.3758/bf03196346. [DOI] [PubMed] [Google Scholar]

[R8] Clements DH, Swaminathan S, Hannibal MAZ, Sarama J. Young Children’s Concepts of Shape. Journal for Research in Mathematics Education. 1999;30(2):192–212. [Google Scholar]

[R9] Cooper LA, Shepard RN. Chronometric studies of the rotation of mental images. In: Chase WG, editor. Visual Information Processing. Academic Press; New York: 1973. pp. 75–176. [Google Scholar]

[R10] Cornell JM. Spontaneous Mirror-Writing in Children. Canadian Journal of Psychology. 1985;39(1):174–179. [Google Scholar]

[R11] Dehaene S. Les Neurones de la Lecture. Odile Jacob; Paris: 2007. [Google Scholar]

[R12] Dehaene S, Cohen L, Sigman M, Vinckier F. The neural code for written words: a proposal. Trends Cogn Sci. 2005;9(7):335–341. doi: 10.1016/j.tics.2005.05.004. [DOI] [PubMed] [Google Scholar]

[R13] Dehaene S, Izard V, Pica P, Spelke E. Core knowledge of geometry in an Amazonian indigene group. Science. 2006;311(5759):381–384. doi: 10.1126/science.1121739. [DOI] [PubMed] [Google Scholar]

[R14] Downing PE, Chan AW, Peelen MV, Dodds CM, Kanwisher N. Domain specificity in visual cortex. Cereb Cortex. 2006;16(10):1453–1461. doi: 10.1093/cercor/bhj086. [DOI] [PubMed] [Google Scholar]

[R15] Epstein R, Kanwisher N. A cortical representation of the local visual environment. Nature. 1998;392(6676):598–601. doi: 10.1038/33402. [DOI] [PubMed] [Google Scholar]

[R16] Fantz RL, Fagan JF, Miranda SB. Early visual selectivity. Infant perception: From sensation to cognition. 1975;1:249–346. [Google Scholar]

[R17] Gibson EJ, Gibson JJ, Pick AD, Osser H. A developmental study of the discrimination of letter-like forms. J Comp Physiol Psychol. 1962;55:897–906. doi: 10.1037/h0043190. [DOI] [PubMed] [Google Scholar]

[R18] Hatfield G. The Natural and the Normative: Theories of Spatial Perception from Kant to Helmholtz. The MIT Press; Cambridge, Massachussets London, England: 1998. [Google Scholar]

[R19] Hermer L, Spelke ES. Modularity and development: the case of spatial reorientation. Cognition. 1996;61(3):195–232. doi: 10.1016/s0010-0277(96)00714-7. [DOI] [PubMed] [Google Scholar]

[R20] Hupbach A, Nadel L. Reorientation in a rhombic environment: No evidence for an encapsulated geometric module. Cognitive Development. 2005;20(2):279–302. [Google Scholar]

[R21] Huttenlocher J. Discrimination of figure orientation: effects of relative position. J Comp Physiol Psychol. 1967;63(2):359–361. doi: 10.1037/h0024398. [DOI] [PubMed] [Google Scholar]

[R22] Huttenlocher J, Newcombe N, Sandberg EH. The coding of spatial location in young children. Cognit Psychol. 1994;27(2):115–147. doi: 10.1006/cogp.1994.1014. [DOI] [PubMed] [Google Scholar]

[R23] Ibbotson A, Bryant P. The perpendicular error and the vertical effect in children’s drawing. Perception. 1976;5:319–326. doi: 10.1068/p050319. [DOI] [PubMed] [Google Scholar]

[R24] Kanwisher N, McDermott J, Chun MM. The fusiform face area: a module in human extrastriate cortex specialized for face perception. J Neurosci. 1997;17(11):4302–4311. doi: 10.1523/JNEUROSCI.17-11-04302.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]

[R25] Kelly DM, Bischof WF. Reorienting in images of a three-dimensional environment. J Exp Psychol Hum Percept Perform. 2005;31(6):1391–1403. doi: 10.1037/0096-1523.31.6.1391. [DOI] [PubMed] [Google Scholar]

[R26] Kelly DM, Spetch ML. Reorientation in a two-dimensional environment: I. Do adults encode the featural and geometric properties of a two-dimensional schematic of a room? J Comp Psychol. 2004;118(1):82–94. doi: 10.1037/0735-7036.118.1.82. [DOI] [PubMed] [Google Scholar]

[R27] Kennedy GJ, Orbach HS, Loffler G. Global shape versus local feature: an angle illusion. Vision Res. 2008;48(11):1281–1289. doi: 10.1016/j.visres.2008.03.003. [DOI] [PubMed] [Google Scholar]

[R28] Kline M. Mathématiques: la fin de la certitude. Christian Bourgeois; Paris: 1989. [Google Scholar]

[R29] Lee SA, Izard V, Spelke E. Core systems of geometry. (in prep)

[R30] Logothetis NK, Pauls J, Bulthoff HH, Poggio T. View-dependent object recognition by monkeys. Curr Biol. 1994;4(5):401–414. doi: 10.1016/s0960-9822(00)00089-0. [DOI] [PubMed] [Google Scholar]

[R31] Lourenco SF, Huttenlocher J. The Representation of Geometric Cues in Infancy. Infancy. 2008:103–127. doi: 10.1080/15250000701795572. [DOI] [PubMed] [Google Scholar]

[R32] Lourenco SF, Huttenlocher J, Fabian L. Coding geometric information in infancy. Biennal Meeting of the Cognitive Developmnet Society (CDS); San Diego, CA. 2005. [Google Scholar]

[R33] McGurk H. Infant discrimination of orientation. Journal of Experimental Child Psychology. 1972;14:151–164. doi: 10.1016/0022-0965(72)90040-9. [DOI] [PubMed] [Google Scholar]

[R34] McMonnies CW. Visuo-spatial discrimination and mirror image letter reversals in reading. J Am Optom Assoc. 1992;63:698–704. [PubMed] [Google Scholar]

[R35] Newcombe NS, Huttenlocher J. Making Space: the development of spatial representation and reasoning. The MIT Press; Cambridge, Massachussets London, England: 2000. [Google Scholar]

[R36] Newcombe NS, Uttal DH. Whorf versus Socrates, round 10. Trends Cogn Sci. 2006;10(9):394–396. doi: 10.1016/j.tics.2006.07.008. [DOI] [PubMed] [Google Scholar]

[R37] Piaget J, Inhelder B. The child’s conception of space. W.W. Norton; New York: 1967. [Google Scholar]

[R38] Pinet L, Gentaz E. The acquisition of geometrical shapes in children: a study on the contribution of the haptic modality. (in prep)

[R39] Reddy L, Kanwisher N. Coding of visual objects in the ventral stream. Curr Opin Neurobiol. 2006;16(4):408–414. doi: 10.1016/j.conb.2006.06.004. [DOI] [PubMed] [Google Scholar]

[R40] Rollenhagen JE, Olson CR. Mirror-image confusion in single neurons of the macaque inferotemporal cortex. Science. 2000;287(5457):1506–1508. doi: 10.1126/science.287.5457.1506. [DOI] [PubMed] [Google Scholar]

[R41] Rosch EH. Natural Categories. Cognitive Psychology. 1973;4:328–350. [Google Scholar]

[R42] Sandberg EH, Huttenlocher J, Newcombe N. The development of hierarchical representation of two-dimensional space. Child Dev. 1996;67(3):721–739. [PubMed] [Google Scholar]

[R43] Satlow E, Newcombe N. When is a triangle not a triangle? Young children’s developing concepts of geometric shape. Cognitive Development. 1998;13:547–559. [Google Scholar]

[R44] Schwartz M, Day RH. Visual shape perception in early infancy. Monographs of the Society for Research in Child Development. 1979;44(7) serial No. 182. [PubMed] [Google Scholar]

[R45] Serpell R. Discrimination of orientation by Zambian children. Journal of Comparatie and Physiological Psychology. 1971;75(2):312–316. doi: 10.1037/h0030832. [DOI] [PubMed] [Google Scholar]

[R46] Shepard RN, Metzler J. Mental Rotation of Three-Dimensional Objects. Science. 1971;171(3972):701–703. doi: 10.1126/science.171.3972.701. [DOI] [PubMed] [Google Scholar]

[R47] Slater A, Mattock A, Brown E. Size constancy at birth: Newborn infants’ responses to retinal and real size. Journal of Experimental Child Psychology. 1990;49:314–322. doi: 10.1016/0022-0965(90)90061-c. [DOI] [PubMed] [Google Scholar]

[R48] Slater A, Mattock A, Brown E, Bremner JG. Form Perception at Birth: Cohen and Younger (1984) Revisited. Journal of Experimental Child Psychology. 1991;51:395–406. doi: 10.1016/0022-0965(91)90084-6. [DOI] [PubMed] [Google Scholar]

[R49] Slater A, Morison V, Town C, Rose D. Movement perception and identity constancy in the new-born infant. British Journal of Developmental Psychology. 1985;3:211–220. [Google Scholar]

[R50] Terepocki M, Kruk RS, Willows DM. The incidence and nature of letter orientation errors in reading disability. J Learn Disabil. 2002;35(3):214–233. doi: 10.1177/002221940203500304. [DOI] [PubMed] [Google Scholar]

[R51] Turnbull OH. A double dissociation between knowledge of object identity and object orientation. Neuropsychologia. 1997;35:567–570. doi: 10.1016/s0028-3932(96)00098-x. [DOI] [PubMed] [Google Scholar]

PERMALINK

Development of Sensitivity to Geometry in Visual Forms

Véronique Izard

Elizabeth S Spelke

Abstract

Introduction

Figure 1.

Experiment 1

Method

Participants

Table 1.

Displays and task

Procedure

Results and discussion

Length

Angle

Sense

Further Euclidean properties

Topological properties

Comparisons across trial types

Figure 2.

Conclusions

Experiment 2

Method

Participants

Table 2.

Procedure

Results

Figure 3.

Table 3.

Conclusion

Experiment 3

Methods

Participants

Displays and task

Figure 4.

Procedure

Results

Pure trials

Figure 5.

Interferences between dimensions

Figure 6.

Distribution of responses

Figure 7.

Figure 8.

Summary statistics

Figure 9.

General Discussion

Universal core knowledge of geometry

Development of abstract geometric knowledge

Dissociation with the results from navigation studies: two systems of core knowledge

Acknowledgments

Footnotes

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases