Abstract
Three experiments investigated whether force and torque cues interact in haptic discrimination of force, torque and stiffness, and if so, how. The statistical relation between force and torque was manipulated across four experimental conditions: Either one type of cue varied while the other was constant, or both varied so as to be positively correlated, negatively correlated, or uncorrelated. Experiment 1 showed that the subjects’ ability to discriminate force was improved by positively correlated torque but impaired with uncorrelated torque, as compared to the constant torque condition. Corresponding effects were found in Experiment 2 for the influence of force on torque discrimination. These findings indicate that force and torque are integrated in perception, rather than being processed as separate dimensions. A further experiment demonstrated facilitation of stiffness discrimination by correlated force and torque, whether the correlation was positive or negative. The findings suggest new means of augmenting haptic feedback to facilitate perception of the properties of soft objects.
Keywords: Human performance, Haptic perception, Perception and psychophysics, Stiffness, Force feedback, Torque feedback
1 Introduction
Many medical procedures are characterized by contact with a deformable medium by means of a rigid tool. This context is very interesting from a haptic perspective, because it elicits time-varying forces and torques. Very little is known about how physicians use these cues, for example, to sense properties of target tissue for purposes of diagnosis or to enhance control of a surgical instrument. Considerable previous research has examined how tissue properties are estimated from contact forces [1-3], but few studies have been devoted to understanding the sensing of torque and its use as a cue for perceiving tissue properties such as stiffness. In the current study, three experiments were conducted using simulations to examine how force and torque cues are used in isolation and in combination to perceive simulated stiffness, and to understand the interaction between force and torque.
Psychophysical studies described below have examined the perception of force and torque separately, for example, in terms of threshold-level discrimination capability. However, it should be noted that there are no biological sensors devoted to torque or force; these are perceptual variables derived from mechanoreceptors in skin, muscles, tendons and joints that respond to the consequences of forces and torques applied to human tissue. Thus it is not clear whether, when force and torque are co-manipulated, they can be separated. Our studies call for separate judgments of force and torque while co-varying the non-judged variable to determine whether separation is possible and if not, what perceptual consequences result from co-processing. The results are intended to illuminate the human processing of force and torque, both as basic constructs and as a contribution to perceived stiffness.
Stiffness is the relation between force and displacement. The human perceptual ability to discriminate the individual components, force and displacement, is superior to discrimination of their ratio, stiffness. Research has shown that the perceptual resolution in force discrimination, as measured by the just noticeable difference (JND), is 7-10% over a range of 0.5-200 N [2], and the thresholds measured for limb movement and position are between 5-8% [4,5]. By comparison, the JND for stiffness discrimination ranges from 8% to 22% [5-7], and the exact value is affected by the range of stimuli, the methods for obtaining judgments, and how the subject interacted with the stimuli. Jones and Hunter [6] reported an average JND of 23% for participants comparing the stiffness of simulated springs using a contralateral limb matching procedure. Tan et al. [5] found a lower JND of 8% for compliance discrimination in a fixed-displacement condition and a significantly higher JND (22%) when the displacement was varied across the stimuli. In clinical procedures, these perceptual limits may be reflected in the demonstrably limited sensitivity of palpation screening. The reported detection rate for breast tumors is about 39-59% [8], depending on the proximity of the mass to the surface, the density of normal breast tissue, and physician experience.
Here we explore the potential of torque feedback as a means to improve sensitivity to force and stiffness. A torque is produced when a force is exerted at a certain distance from a pivot point in a direction not directly towards or away from that pivot point. Human sensitivity to torque is around 13% [9-11]. Jandura and Srinivasan [9] measured the JND of a slow twisting motion and reported a JND of 12.7% at the reference torque of 0.06 Nm. In addition, torque sensitivity is found to be intrinsically responsive to the context of task and interaction. Woodruff and Helson [11] found that the observed torque threshold increased from 4.4% to 12.6% when the reference torque changed from 0.98 to 0.082 Nm.
Although little research has been conducted to examine the effectiveness of torque feedback in haptic perception and manipulation, Wang & Srinivasan [12] examined the role of torque in haptic perception of object location. The participants used a stylus to contact hidden targets, real or virtual, with full or reduced torque feedback and then judged the target location. Performance was best when full torque feedback was available: The slope of judged distance as a function of target distance was 0.63 and 0.73, respectively, for contacting real and virtual targets, but was reduced to 0.29 and 0.24 when torque feedback was constant or uncorrelated with force feedback. This suggested that torque cues were effective for target localization. As to haptic manipulation, the usefulness of torque is found to be largely dependent on the task to be carried out. Lee et al. [13] suggested that both force and torque feedback are needed in order to successfully perform screw insertion in a teleoperated spinal fusion surgery, while in tasks like drawing, tracing [14] or suturing [15], little to no facilitation was found when torque feedback was provided along with force.
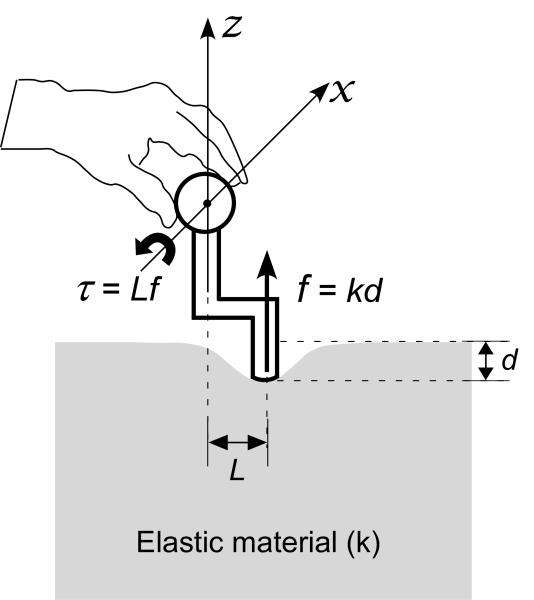
Little is still known about the role of torque in the perception of force, and vice versa, and the influence of torque on perceived stiffness. In theory, the perceived torque (τ) can be used as a source of information to assist in estimating the twisting force (f), and vice versa, given that they are proportional to each other (τ = fL, where L specifies the moment arm). As to the perception of stiffness, torque can also be an effective cue. In the example shown in Fig. 1, torque is related to stiffness by τ = (Ld)k. That is, given knowledge of L, stiffness (k) can be computed from the perceived torque and deformation. Thus when both force and torque are available, the estimates of stiffness from two sources, although redundant with each other, can then be combined to reduce uncertainty in perception and improve the stiffness sensitivity.
Fig. 1.
Force and torque feedback produced by the tool interacting with soft tissue. Rotation is centered in the handle and about the x axis. L, d, k, f, and τ denote moment arm length, amount of deformation, stiffness, resisting force and torque, respectively.
Based on the above analysis, three experiments were conducted to address the following questions: Can torque feedback help people better discriminate forces and stiffness, and if so, how are the torque cues combined with force feedback? Our approach follows a theoretical analysis of Garner [16,17], who suggested that humans may perceive the structure in multi-dimensional stimuli in different ways. If the stimulus dimensions are separable, the brain is able to attend selectively to one dimension and exclude the other. People may capitalize on redundant cues, as occur when two dimensions are correlated, but irrelevant variations in a secondary dimension can be filtered out. Alternatively, the stimulus dimensions are integral if we cannot selectively attend to them. Integral dimensions facilitate perception when correlated and interfere when varied orthogonally.
To test these distinctions in the present context, participants’ ability to discriminate force was assessed in the presence of torque, or vice versa. The statistical relation between the force and torque dimensions of the stimuli was manipulated, allowing us to infer the interaction between the two types of haptic inputs. Experiments 1 and 2 investigated the perceptual interaction between force and torque. Experiment 3 used a similar procedure to investigate the utilization of torque cues in stiffness perception.
2 Experiment 1: Force discrimination in the presence of torque
This and the next experiment examined if force and torque could be judged independently, and if not, to determine the interaction between them. Experimental stimuli were varied in two dimensions: a task-relevant dimension specified by the JND task (i.e., force in Experiment 1 and torque in Experiment 2) and a secondary dimension (i.e., torque and force respectively in the two experiments). The two dimensions were combined across four conditions as follow:
In the baseline condition, stimuli varied only in the task-relevant dimension but were held constant in the secondary dimension.
In the uncorrelated condition, stimulus values on the two dimensions were combined in a pseudo-random manner, eliminating the possibility of inferring one stimulus dimension from the other. To keep performance at a baseline level, the participants then must filter out the variations in the irrelevant dimension and attend only to the task-relevant stimulus. The failure to filter out irrelevant stimuli leads to impeded performance, which is called Garner interference [18,19].
In two correlated conditions, the two dimensions of the stimulus varied together, with a positive or negative correlation. That is, on each trial, one stimulus dimension could be fully predicted by the other. Such redundancy may result in a gain or loss in the participants’ performance, contingent on the direction of correlation. The performance differences stemming from the disparity in correlation directions are referred to as congruence effects [20,21].
Assuming that force and torque could be perceptually isolated and judged separately from each other, we would expect participants to perform similarly across all conditions. In contrast, if the participants’ judgments were based on integrated processing of both inputs, Garner effects and congruence effects should be be observed across the four conditions.
2.1 Method
2.1.1 Participants
Sixteen graduate and undergraduate students (nine males and seven females with an average age of 20.4±2.8 years) participated in the experiment with informed consent. To eliminate the possible effects of handedness, all participants were right-handed by self-report. They were naïve to the purposes of this study.
2.1.2 Apparatus & Stimuli
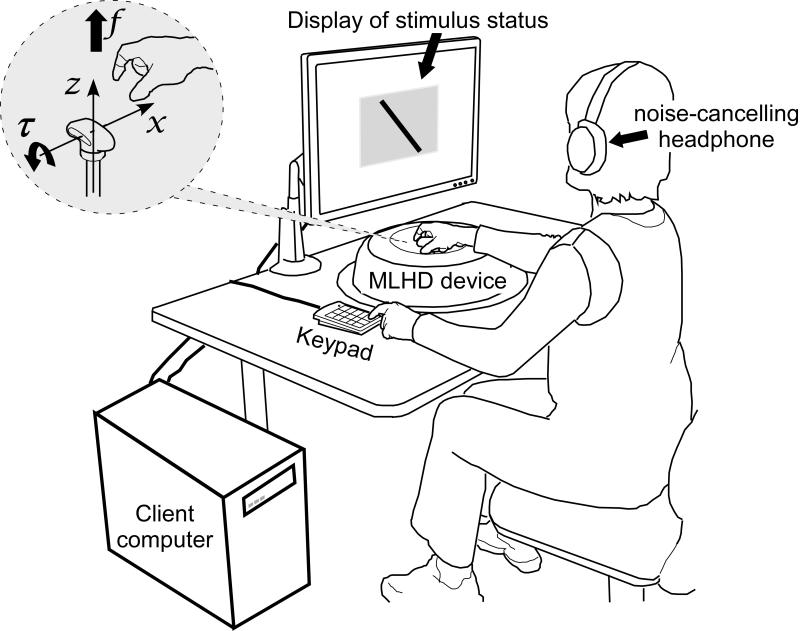
As shown in Fig. 2, the experimental setup consisted of a magnetic levitation haptic interface (MLHD [22,23], Model# Maglev-100, Butterfly Haptics LLC. Pittsburgh, PA, http://www.butterflyhaptics.com) for rendering haptic feedback, a LCD for displaying visual information, a client computer for controlling stimuli and acquiring data, and a keypad for the participant to input responses.
Fig. 2.
Schematic illustration of the experimental setup (see text for details).
The MLHD uses Lorentz forces for actuation, which arise from the electromagnetic interaction between current-carrying coils and magnets. It can exert forces and torques in six degrees of freedom up to 40 N and 3.6 Nm respectively. Since there are no motors, gears, bearings, or linkages present, the device is free of static friction and has fast mechanical responses (an updating rate up to 4 kHz for force feedback and a positioning bandwidth of 140 Hz). It has a workspace of a 24 mm sphere plus ±8° in rotation about any axis. The spatial resolution is 2 μm and 3.6 arc-sec respectively for translational and rotational motion. Whereas the workspace is small, it is sufficient for a user to manipulate virtual objects using only wrist and fingertip motion [7, 24]. This is accomplished by the user’s grasping the handle of the MLHD, through which forces and torques are applied to and felt by the hand.
The MLHD was connected to the client computer via a 100 Mbps Ethernet link. The latter computer was dedicated to controlling the presentation of the experimental stimuli. It ran a multi-threaded application to calculate the force and torque to be presented, command the MLHD to render the haptic effects, and display visual effects on the LCD display. The haptic rendering was performed at 1 kHz with two DOFs: the handle of the MLHD was constrained so that it could be translated in the depth direction (z axis) by an amount up to 8 mm and rotated about the x axis by no more than ±4°. The visual rendering, which was updated at a rate of 120 Hz, drew a yellow or blue square that was used for identifying different stimuli to be differentiated, plus a red line that indicated the tilt of the MLHD handle about the x axis at 15X magnification of that tilt to permit the operator to keep the handle vertical.
2.1.3 Design and Procedure
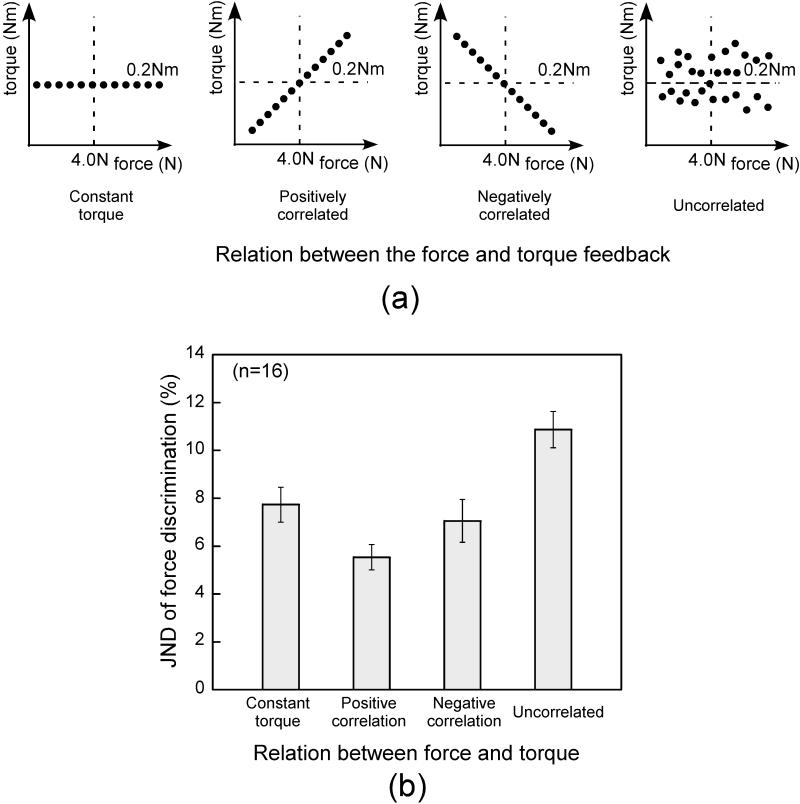
The participants’ ability to discriminate forces with the presence of additional torques, as measured by the just noticeable difference (JND), was assessed for a reference force of 4.0 N. Participants’ JNDs were measured using an adaptive procedure, described in detail below, in which a series of stimulus pairs were presented. Each experimental stimulus represented a combination of force (upward in the z direction) and torque (pitched upward about the x axis). Across the experimental conditions, torque was related to force in four ways (Fig. 3a): it could be constant at 0.2 Nm, positively correlated with force, negatively correlated, or uncorrelated. In the Positive-Correlation condition, the slope of the torque/force equation (i.e., moment arm) was set to 0.05 m, resulting in a distribution of torque with a mean of 0.2 Nm. The Negative-correlation condition has an equivalent distribution of torque, but a negative torque/force slope of −0.05 m. In the Uncorrelated condition, torque was randomly selected between 0.0 and 0.4 Nm. The testing order of the four conditions was counterbalanced across participants using a Latin-square design. In all experiments, subjects were not informed about underlying correlational structure in the stimuli, although they may have inferred it with experience in the task.
Fig. 3.
(a) The experimental manipulation of the force/torque relation in the stimuli. (b) Mean JND of force discrimination as a function of the force/torque relation. Error bars represent ±1 standard error.
2.1.4 Procedure
Participants were tested individually. Each sat in a chair in front of the MLHD and adjusted the height of chair to allow his or her right forearm to rest on the MLHD’s top rim in a comfortable position and leave the wrist free to move. Active noise-cancelling headphones were worn to mask the sound from the environment. Written instructions about the task were provided as follows:
In this experiment, we would like to find out how well you can sense the difference between two upward forces applied to your hand. On each trial, we will present you a pair of stimuli, namely, a ‘yellow’ one and a ‘blue’ one. Each stimulus consists two components, an upward force in the +z direction and a torque rotating about the x axis. Your task is to compare only the upward forces, judge which seems stronger, and then report your judgment by pressing the corresponding colored keys. In this experiment, we ask you to hold the handle in an upright position. To help you on this, the experiment program will display a red line to show you how much the handle has deviated from upright. Please always keep the red line as vertical as possible.
Four practice trials were then presented to familiarize the participant with the task. Practice trials followed the same procedure as the subsequent experimental trials, except that different forces were used (the reference: 2.0 N or 6.0 N; the relative difference: ±50%; random torque ranging from 0.0 to 0.4 Nm). Throughout the experiment, no feedback was provided to the participants about the accuracy of their judgments.
The threshold for force discrimination was measured using an unforced-choice adaptive procedure [25] that targeted 75% correct detections. On each trial, a pair of stimuli was presented to the subject, one at a time, along with a color label in the form of a yellow or blue square. One stimulus constituted a reference force, held constant across the adaptive series, whereas the other was a test force that varied according to the participant’s previous responses. The forces (reference or test) and color labels (yellow or blue) were assigned randomly to the first and second stimulus of a pair. The participant could switch between the two stimuli in a pair as many times as desired. To avoid abrupt changes in force and torque that might aid discrimination, a transition phase with a random duration between 0.4 and 1.0 sec was inserted between such switches. It began by removing the current color label, followed with gradual changes of the force and torque to zero and then to the new values at random speeds (the slope of force and torque changes ranged from 2.0~80.0 N/sec and 0.1~4.0 Nm/sec, respectively), and ended by showing the color label of the new stimulus. The participant responded by pressing either a colored button corresponding to one of the two stimuli or a third key, labeled “Unsure,” if he or she could not tell the difference between the two stimuli. The computer recorded the participant’s response and accordingly adjusted the value of next trial’s test force using Kaernbach’s algorithm: the difference between the reference and test forces was decreased by one step if the participant made a correct judgment, increased by three steps if erroneous, or increased by one step for an “unsure” response. Torque was then computed from the test force and the pre-determined torque/force relation. Under the adaptive procedure, a reversal was tagged when a response produced a change in the direction of adjustment (i.e., an erroneous or unsure response preceded or followed a correct response). A JND session was terminated when the participant had produced eight such reversals, and the threshold was estimated by averaging the test values between the 4th and 8th reversal.
Each JND was measured twice in both ascending and descending directions using the above method. The mean of two measurements was used as the final value for statistical analysis. In the ascending and descending sessions, the initial test force was 20% higher or lower than the reference, respectively. The initial adjustment step was one-fourth of the initial difference and halved at the 2nd and 4th reversals. (The values of the initial difference and step were determined by pre-tests carried out by another group of eight participants to ensure convergence in a reasonable time.) The trials of the ascending and descending sessions were interleaved to preclude any predictive effects. In addition, dummy trials were inserted randomly among the experimental trials at a rate of 20%, which presented a force difference of 60% and a reference force chosen randomly between 2.0 N and 8.0 N.
JNDs were measured for each experimental condition for each participant. Typically, the participants finished one trial in less than 20 seconds and a whole JND session in less than 15 minutes. To avoid muscle fatigue, they could take a break at any time by withholding the response. Additionally, there was a break of 5 minutes for rest between the experimental sessions. The entire experiment took approximately one hour.
2.2 Results
Fig. 3b plots the mean JND as a function of the experimental conditions. Clearly, the participants’ ability to discriminate forces was significantly influenced by the accompanying torque (F(3,45) = 23.16, p<0.001, one-way repeated measures ANOVA). The mean JND across all participants was 7.8% in the constant-torque condition, which was in the range of force JNDs reported previously, as reviewed above, although in the present task that JND was measured in the presence of a constant torque. The JND decreased to 5.5% (p=0.015, pairwise comparison to the constant-torque condition with Bonferroni correction) in the presence of positively-correlated torque and increased to 10.8% (p=0.003) with uncorrelated torque. Such redundancy gain and Garner interference suggest that force and torque are not separable dimensions.
In addition, significant congruence effects were observed; that is, there was a contrast between Positive- and Negative- correlation conditions: The addition of positively-correlated torque significantly enhanced the participants’ performance, whereas little improvement resulted from negatively-correlated torque (7.1% vs. 7.8%, p>0.99, pairwise comparison with Bonferroni correction) as compared to the Constant-torque condition. We will defer further discussion of this issue to the Discussion section.
3 Experiment 2: Torque discrimination in the presence of force
This experiment was parallel to the previous one, with the reversal of the task and secondary stimulus dimensions. Here the participants’ ability to discriminate torques was assessed in the presence of additional force. Their JNDs were measured in the same four experimental conditions as in Experiment 1, using the same adaptive procedure.
3.1 Method
Another group of sixteen right-handed participants were tested (eight males and eight females with an average age of 21.4±3.4 years). Their ability to discriminate torques was measured for a reference of 0.20 Nm in the presence of a constant force or variable forces that were positively-correlated, negatively-correlated, or uncorrelated with the stimulus torque. The distribution of force had a mean of 4.0 N. The experimental setup and procedure were the same as in the previous experiment. The participants were clearly instructed to compare the torques that rotated the MLHD handle upward about the x axis, as opposed to the forces in the z direction. At the start of a JND measurement the initial torque difference was set as ±64% of the reference (a larger deviation than used for force, given preliminary data indicating that the torque JND would be higher). The initial adjustment step was one fourth of the initial difference. Dummy trials were presented at a rate of 20%, in which case the reference torque was chosen randomly between 0.05 Nm and 0.40 Nm and the test torque was ±85% of the reference.
3.2 Results
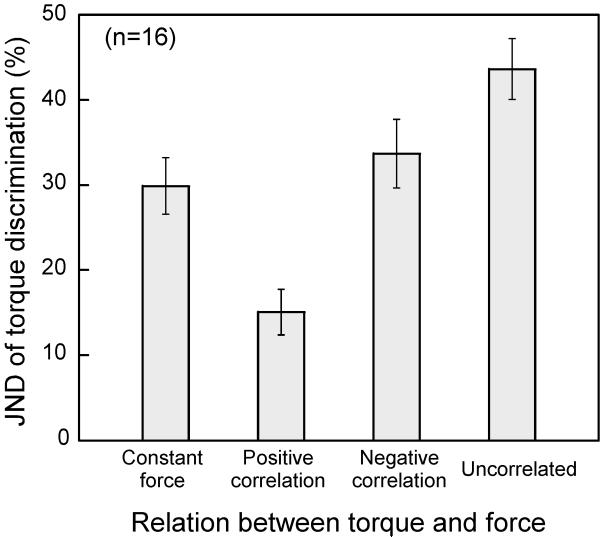
As shown in Fig. 4, the results showed a pattern similar to that observed in the previous experiment. A one-way repeated measure ANOVA revealed a significant main effect across the four conditions (F(3,45) = 17.24, p=0.001). Pairwise comparisons with Bonferroni corrections were performed, revealing that the participants’ performance was significantly improved by positively-correlated force feedback (15.0% vs. 29.8%, p=0.001) as compared to the constant-force condition, but impaired by uncorrelated force (43.7% vs. 29.8%, p=0.045), and little to no improvement was found in torque discrimination in the presence of negative-correlated force (33.7% vs. 29.8%, p>0.99).
Fig. 4.
Mean JND of torque discrimination as a function of the force/torque relation. Error bars represent ±1 standard error.
Taken together, this and the previous experiment indicate that torque and force could not be processed separately. Although the participants were instructed to judge force or torque alone in both experiments, their performance still showed significant improvement in the positive correlation condition accompanied by deterioration in the uncorrelated condition. The latter is particularly important as an indication that participants could not selectively include or exclude the secondary dimension, according to whether its cues were beneficial. Cue combination appears to have been obligatory (cf. Garner [16, 17]).
The observed torque JNDs were much larger than the force JNDs obtained in the previous experiment. For example, the JNDs were 29.9% and 7.7% for torque discrimination with constant force and force discrimination with constant torque, respectively. The torque JND was also larger than the values reviewed above, e.g., a JND of 12.7% reported by Jandura & Srinivasan [9]. The difference could be accounted for by several differences in the experimental settings. First, different actions were involved in the experimental tasks: In Jandura & Srinivasan’s experiments, the participants grasped the handle of the haptic device with the thumb and index fingerpads, and the mean workload was 0.06 Nm. Here the participants interacted with the stimuli by controlling the motion and force at the wrist joint while a larger reference torque (0.20 Nm) was applied. Second and more important, the torque sensitivity was measured here in the presence of additional force, while the stimuli in Jandura & Srinivasan’s experiments were pure torques only. Large JNDs observed here might be attributed at least in part to the effort to control a constant force and the variations in the exerted force.
4 Experiment 3: Discriminating virtual stiffness with force and torque feedback
In this experiment the participants’ ability to perceive stiffness was measured in the same four experimental conditions as in Experiments 1 & 2. However, the stimuli were virtual springs, with the important property that force and torque could vary as a single stimulus was explored. The implications of this are discussed below.
4.1 Method
In this experiment, the stimuli were simulations of virtual springs that could be compressed by up to 16 mm along the z direction. The reference stiffness was set at 500 N/m. Given the range of motion, this resulted in an opposing force ranging from 0.0 to 8.0 N with a mean of 4.0 N (the reference force in Experiment 1). Torque was then related to the compression-induced force in four ways: constant, positively correlated with force, negatively correlated, or uncorrelated. Table 1 gives the equations by which torque varied with the compression-induced force in the four conditions. In the positive-correlation condition, the slope of the torque/force equation was set to 0.05 m, in order to simulate an effect of displacing the contact point from the subject’s hand by that distance. This resulted in a distribution of torque ranging from zero to 0.4 Nm with a mean of 0.2 Nm (the reference torque in Experiment 2). The negative-correlation was equivalent, but with a negative slope. In the uncorrelated condition, there was either a positive or negative torque/force relation for each presented stimulus, but the direction of the correlation varied randomly from stimulus to stimulus throughout the JND measurement.
TABLE 1.
Equations Relating Torque to Force in Exp. 3
| Experimental condition | Torque/Force relation |
|---|---|
| Constant torque | τ = 0.20 Nm |
| Positive correlation (1) | τ = f * L |
| Negative correlation (1,3) | τ = τ0 – f * L |
| Uncorrelated (2,3) |
L = 0.05 m;
L’: randomly selected between 0.00 m and 0.05 m;
τ0 & τ’0 : selected for each trial to center the distribution of torque around 0.2 Nm;
In all conditions, the stiffness of the reference spring was 500 N/m.
An important difference should be noted between this and the previous experiments as to the implementation of the force/torque relation, and hence the perceptual demands. In Experiments 1 and 2, the torque and force values of each stimulus were constant during a trial. These values changed across trials (i.e., as new test stimuli were introduced), and thus the force/torque relation could be determined only by comparing stimuli across trials. In this experiment the stimuli were virtual springs. Thus the feedback force and torque co-varied in a continuous manner as a spring was explored by the participant. As a result, the covariation between force and torque, if any existed, could be determined within a single stimulus.
Sixteen naïve right-handed paticipants, ten males and six females with an average age of 22.6±3.7 years, were tested. They were clearly instructed that the task was to compare a pair of virtual springs on each trial and judge which seemed stiffer. They were told to press the virtual springs vertically and keep the MLHD handle upright.
The JNDs were measured using the same procedure as described before. The initial stiffness difference and the initial adjustment step were ±48% and ±16% of the reference, respectively. Dummy trials were presented at a rate of 20%, using a stiffness difference of 75% and a reference stiffness chosen randomly between 200 and 1000 N/m.
4.2 Results
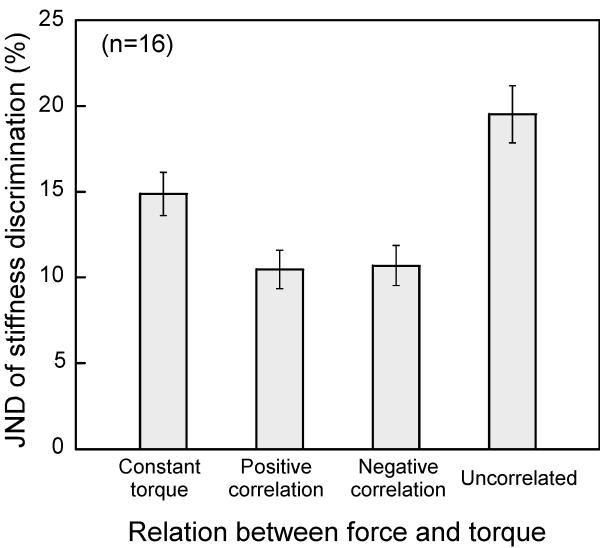
As in the previous experiments, the participants’ performance was analyzed using a one-way repeated measures ANOVA and pairwise comparisons with Bonferroni corrections. The ANOVA revealed significant between-condition differences (F(3,45)=23.76, p<0.001), and pairwise comparisons further demonstrated that the participants’ performance relative to constant torque was significantly superior in the positive-correlation condition (p=0.001) but inferior in the uncorrelated condition (p=0.035): The mean stiffness JND was 10.5% when the force and torque feedback were positively correlated and 19.6% when uncorrelated.
Moreover, note that the relative magnitude of improvement (29.5%) or deterioration (31.5%) observed here, compared with the constant-torque condition (the stiffness JND of 14.9%), was similar to that seen in Experiment 1, where the JND of force discrimination was decreased by 29.8% in the positive-correlation condition and increased by 38.5% in the uncorrelated condition.
While the present findings clearly indicate that correlated torque cues enhance stiffness perception, the mechanisms are not yet definitively known. As was noted in the introduction, torque could lead to an estimate of stiffness independent of force, given an estimate of rotational displacement, or the effect of torque could be mediated by an enhancement of force perception, as was shown to occur in Experiment 1.
In contrast to the previous experiments, where little effect of the secondary dimension was found in the negative-correlation condition, here the results revealed a significant improvement in stiffness sensitivity (10.7% vs. 14.9%, p=0.031, as compared to the constant-torque condition): The JND was reduced when torque was negatively correlated with the compression-induced force, and the facilitation was similar to that observed in the positive-correlation condition. The following section discusses why negative correlations between the task and secondary dimensions may act differently, depending on the task.
5 Discussion
The present experiments assessed how force and torque cues interact in the perception of either dimension and in the perception of stiffness. To summarize, Experiments 1 & 2 found that torque and force could not be processed separately. Perception was facilitated by a positive correlation between them but impeded by an uncorrelated relation. Experiment 3 examined the role of force and torque cues in stiffness perception and found a similar pattern. However, whereas negatively correlated torque cues in Experiment 1 had no effect on force discrimination and the same was found in Experiment 2, Experiment 3 showed facilitation of stiffness discrimination by negatively correlated force and torque.
5.1 Effects of force/torque correlations on unidimensional JNDs
The findings in Experiment 1 and 2 exhibited significant Garner interference across force and torque dimensions. This indicates that the dimensions were integral in the sense of Garner [16,17]. However, the meaning of integrality in terms of process is not specified by the theoretical construct. Here we consider two possibilities.
One possible account of force/torque interactions in terms of integrality is that it results from biomechanical constraints. That is, the two stimuli are summed mechanically at the wrist to produce a total effort involved in the interaction. This explanation could account for the facilitation observed in the positive-correlation condition, because summation would cause the differences in stimulus levels to become more salient. However, when this same account is applied to the negative correlation, summation should cause differences to become less discriminable, because force and torque cues carried conflicting information. This leads to the prediction that negative correlations should produce interference, even more so than uncorrelated variations. Accordingly the JND would be higher in the negative correlation condition than the control, which is not observed in this study. Summation of dimensional components cannot, then, explain the present results.
A second possibility, in keeping with Garner’s intuitions about integrality, is that force and torque combine to create an emergent, holistic quantity, much as shape emerges from variations in the height and width of a rectangle [16,17]. Stimulus comparisons can be conceived of as discriminating between new perceptual quantities along a decision axis that arise out of force/torque space. Interference and facilitation effects are then related to changes in discrimination threshold due to an increased or decreased dispersion of quantities along the decision axis in the uncorrelated and correlated conditions. Alternatively, Ben-Artzi & Marks [26,27] suggested that cross-dimensional interaction might be explained by carryover effects from one trial to the next: More information could be transferred in the correlated than uncorrelated conditions because of better predictability. Since both models can explain our experimental observations, the current data are insufficient to distinguish between them.
Congruence effects were also seen in both unidimensional experiments: While significant gains were observed in discrimination ability in the positive correlation condition, no such facilitative effects were observed in the case of negative correlation. We attribute the facilitation from positive correlation to the convergent information the two redundant variables provide. Obviously, the same redundancy is provided by the negative correlation; however, facilitation is absent. The null effect in this case suggests that there is some opposing trend that is induced by the difference in magnitude between the two variables. That is, under negative correlation, force is high when torque is low, and vice versa. The exact nature of the mechanism that works against redundancy gain cannot be determined from these data. However, interference effects between stimulus parameters with discrepant values have previously been observed, for example, pitch and loudness [28, 29].
Further research is needed to more fully understand the mechanisms behind the present correlation effects, but certainly they are consistent with the idea that force and torque are not processed separately.
5.2 Effects of force/torque correlations on stiffness JND
Experiment 3, where stiffness was discriminated, showed effects of positive and random correlations like the unidimensional components investigated in the first two experiments. Because stiffness is intrinsically the relation between displacement and force, it might be thought that the facilitative effect of torque is due to its augmentation of sensitivity to force. That is, torque might be thought of as having only a secondary effect. However, this cannot explain the fact that negative correlations between force and torque did not facilitate force perception, whereas they did facilitate stiffness discrimination. In fact, improvements in stiffness perception were approximately equal in magnitude in the negative- and positive- correlation conditions in Experiment 3.
The discrepancy across experiments in the role of negative correlations calls for a different kind of explanation. It might be accounted for by different strategies for cue utilization. Specifically, each stimulus in Experiments 1 and 2 had a constant value of force and torque. In contrast, the stimuli in Experiment 3 were virtual springs, which were explored dynamically. Hence in Experiment 3, dynamic cues may play an important role in stiffness discrimination. In the absence of correlated torque, stiffness must be judged from the force/displacement relation. Given correlated torque, stiffness can be judged similarly from the torque/displacement relation, or both cues, as sampled across the phases of compressing or releasing. Judgments from dynamic force and torque cues were apparently insensitive to the direction of the force/torque correlation because those cues, even when negatively correlated, actually presented coherent information about stiffness.
6 Conclusions
To summarize, the present study shows facilitation of processing force, torque, and stiffness under cue-correlation conditions. This suggests a new approach to augment haptic feedback and assist users to better perceive soft objects. This might be particularly helpful in simulations of minimally invasive surgery where only reduced haptic cues are available to the operator.
Fig. 5.
Mean JND of stiffness discrimination as a function of the force/torque relation. Error bars represent ±1 standard error.
ACKNOWLEDGMENT
This work is supported by grants from NIH/NIBIB (5K99EB008710) and NSF (IIS-9802191, IIS-0413085, & EIA-0321057).
Biography
Bing Wu, Ph.D, received an M.S. degree in Neurobiology in 1997 from Shanghai Institute of Physiology, Chinese Academy of Sciences, and an M.S. degree in Computer Science in 2002 in addition to a Ph.D degree in Experimental Psychology in 2004 from the University of Louisville. He is currently a post-doctoral researcher in the Department of Psychology at Carnegie Mellon University. His research focuses primarily on visual and haptic perception in the real, augmented, and virtual environments.
Roberta L. Klatzky, Ph.D, is Professor of Psychology at Carnegie Mellon University, where she is also on the faculty of the Center for the Neural Basis of Cognition and the Human-Computer Interaction Institute. She received a B.S. in Mathematics from the University of Michigan and a Ph.D. in Experimental Psychology from Stanford University. Before coming to Carnegie Mellon, she was a member of the faculty at the University of California, Santa Barbara. Professor Klatzky is the author of over 200 articles, and she has authored or edited 4 books.
Ralph L. Hollis, (Ph.D, University of Colorado, Physics) is Research Professor of Robotics and Electrical and Computer Engineering at Carnegie Mellon University. Dr. Hollis was a Research Staff Member at the Thomas J. Watson Research Center from 1978-93 where he worked in magnetism, acoustics, and robotics, and was Manager of Advanced Robotics from 1986-93. He is a member of the American Physical Society and a Fellow of IEEE. He is founding director of the Microdynamic Systems Laboratory at Carnegie Mellon University where his research centers on haptics, agile manufacturing, and dynamically-stable mobile robots.
Contributor Information
Bing Wu, Department of Psychology, Carnegie Mellon University, Pittsburgh PA 15213. bingwu@andrew.cmu.edu..
Roberta L. Klatzky, Department of Psychology, Carnegie Mellon University, Pittsburgh PA 15213. klatzky@cmu.edu.
Ralph L. Hollis, Robotics Institute and Department of Electrical and Computer Engineering, Carnegie Mellon University, Pittsburgh, PA 15213. rhollis@cs.cmu.edu..
REFERENCES
- [1].Tan HZ, Srinivasan MA, Eberman B, Cheng B. Human factors for the design of force-reflecting haptic interfaces. Proceedings of the ASME Dynamic Systems and Control Division. 1994;vol. DSC–55(no. 1):353–359. [Google Scholar]
- [2].Jones LA. Kinesthetic Sensing. In: Cutkosky M, Howe R, Salisbury K, Srinivasan M, editors. Human and Machine Haptics. MIT Press; 2000. [Google Scholar]
- [3].Lederman SJ, Klatzky RL. Haptic perception: A tutorial. Attention, Perception & Psychophysics. 2009;Vol. 71:1439–1459. doi: 10.3758/APP.71.7.1439. [DOI] [PubMed] [Google Scholar]
- [4].Jones LA, Hunter IW, Irwin RJ. Differential thresholds for limb movement measured using adaptive techniques. Perception & Psychophysics. 1992;Vol. 52:529–535. doi: 10.3758/bf03206714. [DOI] [PubMed] [Google Scholar]
- [5].Tan HZ, Durlach NI, Beauregard GL, Srinivasan MA. Manual discrimination of compliance using active pinch grasp: The roles of force and work cues. Perception & Psychophysics. 1995;Vol. 57:495–510. doi: 10.3758/bf03213075. [DOI] [PubMed] [Google Scholar]
- [6].Jones LA, Hunter IW. A perceptual analysis of stiffness. Experimental Brain Research. 1990;Vol. 79:150–156. doi: 10.1007/BF00228884. [DOI] [PubMed] [Google Scholar]
- [7].Varadharajan V, Klatzky RL, Swendsen R, Unger BJ, Hollis R. Haptic Rendering and Psychophysical Evaluation of a Virtual Three-Dimensional Helical Spring. IEEE Symposium on 3D User Interfaces IEEE Haptics Symposium; Reno. 2008. pp. 57–64. [Google Scholar]
- [8].Shen Y, Zelen M. Screening sensitivity and sojourn time from breast cancer early detection clinical trials: mammograms and physical examinations. Journal of Clinical Oncology. 2001;Vol. 19(15):3490–3499. doi: 10.1200/JCO.2001.19.15.3490. [DOI] [PubMed] [Google Scholar]
- [9].Jandura L, Srinivasan MA. Experiments on human performance in torque discrimination and control. In: Radcliffe CJ, editor. Dynamic Systems and Control. Vol.1. ASME; 1994. pp. 369–375. DSC-55. [Google Scholar]
- [10].Woodruff B, Helson H. Torque: A new dimension in tactile-kinesthetic sensitivity. American Journal of Psychology. 1965;Vol. 78:271–277. [PubMed] [Google Scholar]
- [11].Woodruff B, Helson H. Torque Sensitivity as a Function of Knob Radius and Load. American Journal of Psychology. 1967;Vol. 80:558–571. [PubMed] [Google Scholar]
- [12].Wang S, Srinivasan MA. The Role of Torque in Haptic Perception of Object Location in Virtual Environments. Proceedings of the 11th International Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems; Los Angeles, CA. IEEE Computer Society; 2003. pp. 302–309. [Google Scholar]
- [13].Lee J, Hwang I, Kim K, Choi S, Chung WK, Kim YS. Co-operative robotic assistant with drill-by-wire end-effector for spinal fusion surgery. Industrial Robot: An International Journal. 2009;Vol. 36(1):60–72. [Google Scholar]
- [14].Verner L, Okamura AM. Force & torque feedback vs force only feedback. Third Joint Eurohaptics Conference and Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems (World Haptics).2009. pp. 406–410. [Google Scholar]
- [15].Santos-Carreras L, Beira R, Sengül A, Gassert R, Bleuler H. Influence of force and torque feedback on operator performance in a vr-based suturing task. Applied Bionics and Biomechanics. 2010;Vol. 7(3):217–230. [Google Scholar]
- [16].Garner WR. The processing of information and structure. Erlbaum; Oxford, England: 1974. [Google Scholar]
- [17].Garner WR. Interaction of stimulus dimensions in concept and choice processes. Cognitive Psychology. 1976;Vol. 8:98–123. [Google Scholar]
- [18].Pomerantz JR. Global and local precedence: Selective attention in form and motion perception. Journal of Experimental Psychology: General. 1983;112:516–540. doi: 10.1037//0096-3445.112.4.516. [DOI] [PubMed] [Google Scholar]
- [19].Pomerantz JR. Overview of visual form perception. In: Schwab EC, Nusbaum HC, editors. Perception of speech and visual form: Theoretical issues, models, and research. Vol. 2. Academic Press; New York: 1986. pp. 1–30. [Google Scholar]
- [20].Clark HH, Brownell HH. Judging up and down. Journal of Experimental Psychology: Human Perception and Performance. 1975;1:339–352. doi: 10.1037//0096-1523.1.4.339. [DOI] [PubMed] [Google Scholar]
- [21].Melara RD, O’Brien TP. Interaction between synesthetically corresponding dimensions. Journal of Experimental Psychology: General. 1987;116:323–336. [Google Scholar]
- [22].Hollis RL, Salcudean E. Lorentz Levitation Technology: A New Approach to Fine Motion, Robotics, Teleoperation, Haptic Interfaces, and Vibration Isolation. Proceedings of the 5th International Symposium on Robotics Research; Hidden Valley, PA. 1993. pp. 1–18. [Google Scholar]
- [23].Berkelman PJ, Hollis RL. Lorentz Magnetic Levitation for Haptic Interaction: Device Design, Performance, and Integration with Physical Simulations. International Journal of Robotics Research. 2000;Vol. 19(No. 7):644–667. [Google Scholar]
- [24].Unger B, Hollis R, Klatzky RL. JND Analysis of Texture Roughness Perception Using a Magnetic Levitation Haptic Device. Proceedings of the Second Joint EuroHaptics Conference and Symposium on Haptic Interfaces for Virtual Environment and Teleoperator Systems; Los Alamitos, CA. IEEE Computer Society; 2007. pp. 9–14. [Google Scholar]
- [25].Kaernbach C. Adaptive threshold estimation with unforcedchoice tasks. Perception & Psychophysics. 2001;Vol. 63:1377–1388. doi: 10.3758/bf03194549. [DOI] [PubMed] [Google Scholar]
- [26].Ben-Artzi E, Marks LE. Congruence effects in classifying auditory stimuli: a review and a model. In: Possamai CA, editor. Proceedings of the Eleventh Annual Meeting of the International Society for Psychophysics; Cassis, France. International Society for Psychophysics; 1995. pp. 145–150. [Google Scholar]
- [27].Ben-Artzi E, Marks LE. Processing linguistic and perceptual dimensions of speech: Interactions in speeded classification. Journal of Experimental Psychology: Human Perception and Performance. 1999;Vol. 25:579–595. doi: 10.1037//0096-1523.25.3.579. [DOI] [PubMed] [Google Scholar]
- [28].Melara RD, Marks LE. Perceptual primacy of dimensions: Support for a model of dimensional interaction. Journal of Experimental Psychology: Human Perception and Performance. 1990;Vol. 16(2):398–414. doi: 10.1037//0096-1523.16.2.398. [DOI] [PubMed] [Google Scholar]
- [29].Melara RD, Mounts JR. Contextual influences on interactive processing: Effects of discriminability, quantity, and uncertainty. Perception & Psychophysics. 1994;Vol. 56:73–90. doi: 10.3758/bf03211692. [DOI] [PubMed] [Google Scholar]