Crowding in peripheral vision: why bigger is better

Summary

We enjoy the illusion that visual resolution is high across the entire field of vision. However, this illusion can be easily dispelled by trying to identify objects in a cluttered environment out of the corner of your eye. This reflects in part, the well-known decline in visual resolution in peripheral vision, however, the main bottleneck for reading or object recognition in peripheral vision is the crowding. Objects that can be easily identified in isolation seem indistinct and jumbled in clutter. Crowding is thought to reflect inappropriate integration of the target and flankers in peripheral vision^1,2. Here we uncover and explain a paradox in peripheral crowding: under certain conditions increasing the size or number of flanking rings results in a paradoxical decrease in the magnitude of crowding – i.e., the bigger or more numerous the flanks, the smaller the crowding. These surprising results are predicted by a model in which crowding is determined by the centroids of ≈ 4 – 8 independent features within ≈ 0.5 times the target eccentricity. These features are then integrated into a texture beyond the stage of feature analysis. We speculate that this process may contribute to the illusion of high resolution across the field of vision.

Results

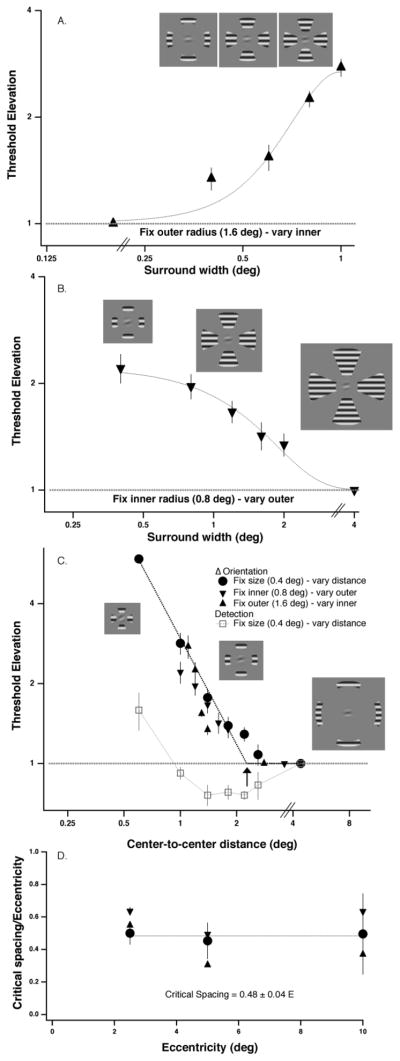
The faulty integration model for crowding is based on the notion that crowding occurs because the visual system erroneously combines signals from the target and the flankers, and that this combination is compulsory (for recent reviews see Refs ^{1, 2}). One prediction of the faulty integration model is that increasing the size of the flankers should result in increased crowding. We tested this hypothesis by varying the size of the flankers in a simple orientation discrimination task. The target was a high contrast Gabor patch presented at an eccentricity of 5 degrees in the lower visual field, and the flankers were comprised of four segments of an annular grating (Fig 1). In the first experiment, the position of the outer edge of the flanks was fixed, and the size of the flanks was increased by varying the inner radius. Increasing flank size resulted in monotonically worse performance (increased threshold elevation – Fig 1A), consistent with the faulty integration hypothesis^1–3. However increasing the flank size also brought the inner edge of the flank closer to the target, and previous work has suggested that crowding is due to the inner edge of the flank⁴.

Fig. 1.

A. Fixing the position of the outer edge of the flanks (at 1.6 deg), and increasing the size of the flanks by varying the inner radius results in increased crowding (threshold elevation). B. Fixing the position of the inner edge of the flanks (at 0.8 deg), and increasing the size of the flanks by varying the outer radius results in decreased crowding. C. Fixing the flank size and increasing the center-to-center distance results in decreased crowding (red circles). The individual threshold data are shown in Fig. S1. Replotting A and B in terms of the flank center-to center distance superimposes the 3 data sets. The dotted line is a 2-line fit to the data. We define the critical spacing as the point of intersection of the two-lines. Open squares show that except at the closest distance where target and flanks overlap, flankers reduce detection thresholds (i.e. facilitate detection of the target). D. Critical spacing specified as a fraction of the target eccentricity for each of the three experiments at eccentricities of 2.5, 5 and 10 degrees in the lower visual field.

In the second experiment we fixed proximity by keeping the position of the inner edge of the flanks constant, and increased the flank size by varying the outer radius. Increasing flank size resulted in a monotonic decrease in the magnitude of crowding – i.e., the bigger the flanks, the smaller the crowding (Fig 1B). The faulty integration model predicts that the bigger (or more numerous) the flanks, the bigger the crowding. Our unexpected result suggests that the faulty integration hypothesis may be faulty. To clarify this we conducted a third experiment, to test whether target-flank distance might determine the strength of crowding by fixing the flank size and varying the target-flank distance (Fig 1C - red circles). Interestingly, all three data sets superimpose when plotted as a function of the center-to-center distance between target and flanks. Thus, it appears that it is the distance, not the size of the flankers that determines the strength of crowding. When the flanks are centered less than about 2.2 degrees from the target (arrow in Fig. 1C), crowding occurs, independent of flanker size. This target-flank distance represents the Critical Spacing for crowding at 5 degrees. We have replicated these three experiments at other eccentricities (E) and find that the critical spacing is approximately 0.5E (Fig 1D for E= 2.5, 5.0 and 10.0 deg), consistent with many previous studies^1,2,5,6 and with the notion that the critical spacing represents a fixed distance on the cortex^7–10.

Control experiments (e.g. target detection [Fig 1c], radial/tangential anisotropies [Fig. 3] and size independence [see Fig. S1b]) verify that the threshold elevation is due to crowding rather than masking or surround suppression (see references 1 and 2). Taken together our results provide an explanation for the unexpected effect of flank size – increasing the flank size (with a fixed inner radius) increased the center-to-center distance between target and flankers. Crowding is determined by the centroids of features (both targets and flankers) within approximately 0.5 times the target eccentricity; however this provides little insight into the integration process per se.

Fig. 3.

A. The effect of target and flank contrast. Top. The effect of flank contrast at 3 target contrasts – 20% (blue), 40% (green) and 80% (red). The solid gray line is the best fitting 2-line fit to the entire data set. The fit is constrained to have a slope of zero and a value of 1 at low contrast levels. The “critical contrast” is the contrast at which threshold elevation begins to increase. Critical contrast for each target contrast is shown by the colored symbols along the abscissa. B. The critical contrasts from separate two-line fits to each data set (target contrast) vs. target contrast. The black line with unity slope shows the predicted values if the flankers acted at the level of the target feature. The dotted gray line is the slope of the best fitting line.

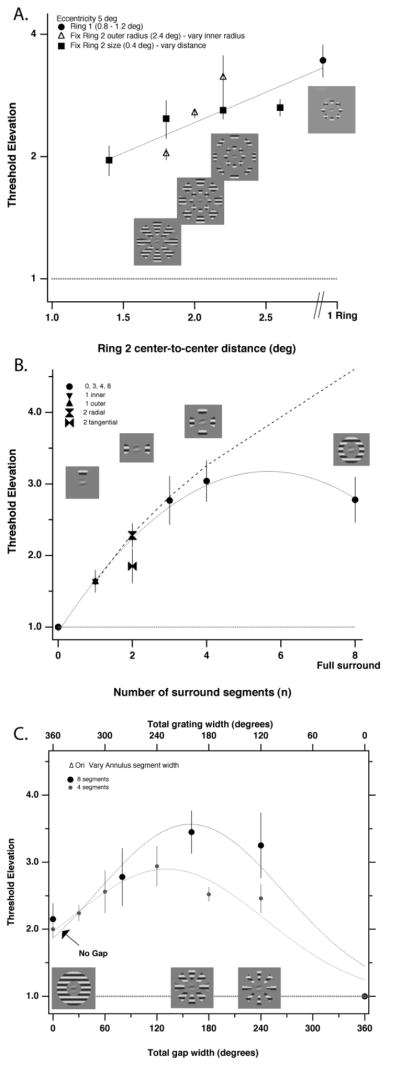
A second prediction of the faulty integration hypothesis is that two or more rings of flanking segments should be more potent than one. To test this hypothesis, we fixed the size and position of one ring of flanks and added a second ring of flanks (Fig. 2A). The rightmost point shows the threshold elevation with the inner flanker ring alone. The faulty integration theory predicts that adding a second ring of flanks should increase crowding. However, adding the outer flanks reduces crowding. The closer the outer flank to the target, the smaller the crowding. This result is counterintuitive, and on first glance, it appears to represent an instance of disinhibition. In this view, crowding is due to flanks inhibiting the target location¹¹. The outer flanks inhibit the inner flanks, thus reducing the inhibition. However, we think it can be understood in much the same way as the “surprising” effect of increasing flank size while fixing the outer edge of a single flanking ring. When the distance of the second flank is less than about 2.5 degrees (0.5E) from the target, it “blends” with the inner flank. Indeed, at the smallest distance, it is contiguous with the inner flank. Thus, the visual system treats the two flanks as one single large texture, effectively increasing the target-flank distance and reducing crowding because the centroid of the texture moves further away from the target. As the distance between the two flanking rings increases, the two flanks become more distinct as separate objects, and the amount of crowding approaches that of a single flank. Interestingly, two flanking rings are never more potent than one at producing crowding.

Fig. 2.

A. Two-ring experiments. We fixed the size and position of the inner flanks and added a second set of flanks (i.e., two flanking rings). In one experiment we fixed the size of the second ring and varied its distance (squares), in the other, we fixed the outer edge of the second ring and varied the flank size (triangles). The circle shows the threshold elevation with the inner flank alone. B. Varying the number (and location) of flanking segments. Increasing the number of flank segments (N) from 1 to 4 has a substantial effect, following the prediction of linear integration of independent segments (black dashed line). Increasing the number of segments from 4 to 8 (a full annular surround) results in slightly reduced crowding. The dashed line shows the prediction of linear integration of independent segments, with threshold increasing in proportion to √N for N>1 (N = 1 is taken as the measured elevation with a single flank). The insets show examples of 1 “inner” flank (i.e., between the fixation point [which was 5 deg above the target] and the target; 2 “tangential” flanks; 4 and 8 flanks. C. Gaps in the annulus. Top. The flanks consisted of an annular surround consisting of either 4 (small circles) or 8 (large circles) wedges of grating with variable sized gaps of uniform gray between the wedges. Increasing the gap width (lower abscissa) results in increased crowding. The larger the gap, the smaller the amount of flanking grating (top abscissa).

Our results thus far provide little evidence that integration of flanking features increases crowding. Several previous studies in which either the size or the number of flankers increase have either failed to show significant increase in crowding¹² or show a reduction of crowding. In each of these studies (including ours), varying the size or number of flankers has increased the eccentricity of the flanks, and therefore increased their effective spacing. On the other hand, varying the number of flankers while maintaining a fixed spacing does have an influence on the strength of crowding^13–15. Figure 2B shows the effect of varying the number (and location) of flanking segments, while maintaining a fixed target-flank spacing. Increasing the number of flank segments from 1 to 4 has a substantial effect, following the prediction of linear integration of independent segments (dashed line). However, increasing the number of segments from 4 to 8 (a full annular surround) actually results in slightly reduced crowding, and substantially less than predicted by the integration theory. Figure 2B also illustrates the well established anisotropy in crowding – not only is the critical spacing larger when two flanks are arranged radially (propellers) rather than tangentially (bowties)^2,16 but the magnitude of crowding is stronger too.

Why does doubling the number of segments from 4 to 8 result in decreased rather than increased crowding? Increasing the number of segments to 8 results in a single coherent annulus (a texture), rather 8 distinct segments. Would making each segment distinct increase crowding? To test this notion, we created an annular surround consisting of either 4 or 8 wedges of grating with variable sized gaps of uniform gray between the wedges (Fig 2C). Increasing the gap width results in increased crowding (Fig 2C lower abscissa). This is paradoxical because the larger the gap, the smaller the amount of flanking grating (Fig 2C top abscissa); however, it is consistent with the notion that integration requires independent flanking samples. With the optimal gaps, 8 wedges results in stronger crowding than 4 wedges (≈ 17 percent - Fig 2C compare black and gray symbols), less than the 41% (√2) predicted by integration theory. Thus, there may be a linear integration limit of between 4 and 8 independent samples (see Refs ¹ and ² for a detailed account of the integration model).

Discussion

There are many theories for crowding, from low-level lateral inhibition of the target by the flanking patterns¹¹ to high-level attentional bottlenecks¹⁷. However, there is a growing consensus for a two-stage model in which the first stage involves the detection of simple features (perhaps in V1), and a second stage is required for the combination or interpretation of the features as an object downstream from V1^1–3. Here we investigated the spatial layout of this “faulty integration”. Our key finding, that crowding depends on the distance between the centroids of objects, not the proximity of their edges (Fig. 1C), is novel, and provides a simple explanation for the paradoxical finding that the bigger the flankers, the smaller the crowding, and that two rings of flankers are less potent than one.

A set-size effect in crowding

Our results show a “set size” effect – increasing the number of flanks from 1 to ≈ 4 resulted in linear integration of pendent features arranged in a ring around the target consistent with Põder & Wagemans¹⁵. Within ≈ 0.5 times the target eccentricity (the “combination field”⁹) the visual system integrates ≈ 4 – 8 independent features into a crowded percept.

Grouping and configural effects in crowding

In peripheral vision, there is a predilection for objects to be “joined together by the visual system into a single Gestalt”^18–20 Thus, crowding can be “relieved” with a “grouped” mask, i.e., multi-element flankers that group together separately from the target, thus reducing crowding^18–25. Here we show that simply inserting gaps (blank wedges) in the flanking ring increases the amount of crowding (Fig 2C), since the gaps reduce the appearance of a coherent texture, and provide independent samples of the flanking features. We do not believe that it is the gaps (and associated broadband edges per se) that result in increased crowding. Filling the gaps with hogonally oriented grating has the same effect, consistent with Livne & Sagi²³ who found that crowding was weakest (or absent) when the flank orientations varied smoothly around a circle, creating the impression of a closed contour, and strongest when the smooth variation in flank orientation was interrupted by changing the orientations of four of the eight flanks. Moreover, we have confirmed the configural coherence effect using a different approach based on altering the stimulus temporal properties. Synchronously flickering wedges appear as a coherent flickering surround, whereas the asynchronously flickering wedges do not (see Supplementary movie). When all eight wedges of a flanking ring flickered asynchronously, crowding was ≈ 40% stronger than when they flickered synchronously (Threshold elevation = 2.98 ± 0.22 vs. 2.15 ± 0.20 times threshold elevation, respectively. p<.004). These configuration effects modulate the strength of crowding at a fixed separation, and may thus act independently based on object information²³.

Similarity and conspicuity in crowding

When targets and flankers are similar they may group together, and it is well known that when the target and flankers are “ungrouped” from each other by making them dissimilar in a fundamental property such as color, polarity or depth so that the target “pops out”, crowding is greatly reduced^22,25–28. We tested how dissimilar our target and flankers had to be in orientation and spatial frequency in order to “break” the texture and allow individual features to “pop-out“ completely free of crowding. We show here that the target orientation must differ from those of the flanks by ≈ 90 deg (Fig S2A) or their spatial frequencies must differ by about a factor of 4 (full width at half-height ≈ 2 octaves – Fig. S2B) consistent with previous work³³.

The locus of crowding

One exception to the similarity rule is contrast. Crowding is strongest when the target contrast is lower (not equal to) the flank contrast^{28, 33}. We measured the effects of flank contrast at different target contrasts (Fig 3A). Like Pelli et al.¹⁴, we note that flanks become effective once they are visible. What is new here is that the effect of flank contrast is independent of target contrast. Thus at low contrasts (below ≈ 30%) the effect of flank contrast is essentially identical at all target contrast levels. We quantified the critical contrast for crowding (the minimum contrast required to induce crowding) with a 2-line fit (the gray line in Fig. 3A). The critical contrast for each target contrast (obtained by separate fits to each data set - Fig. 3B) is essentially independent of target contrast. The slope of the best fitting line is −0.04 ± 0.05 – consistent with a slope of zero.

If the flankers acted at the level of processing of the target feature, we would expect the critical contrast to be proportional to the target contrast (solid line shows the predicted critical contrast based on Weber’s law [slope = 1]. A Legge-Foley power law³⁴ would predict a slope of ≈ 0.6). On the other hand, if crowding takes place at a higher level (beyond that of individual features) where textural combination occurs, the effect of flank contrast should be independent of the contrast of the target feature, which is just what we found. Previous work has shown that the strength of crowding depends on flank contrast rather than similarity (i.e., pop-out does not occur when target and flanks differ in contrast)^28,33; here we show that the critical contrast for crowding is independent of target contrast.

The illusion of high resolution vision across the field of vision

With multiple saccades we build up a representation of the visual field, much of it (in the periphery) at low resolution, but with knowledge of a world in high detail. At an eccentricity of only five degrees, the ability to resolve an isolated letter or grating patch has diminished by about a factor of 3 or 4 – from ≈ 1 arc minute in the fovea to 3 or 4 arc minutes²⁹. However, it is not this reduced resolution that limits object perception in the periphery – it is crowding. Features up to several degrees from the target (≈ 2.5 deg for a target at 5 degrees) further impair object recognition. Patterns details of individual patterns not available for discrimination^12,30. Indeed, in a cluttered display, orientation signals are pooled rather than being lost through masking¹³ e the simple integration model¹³ is likely to be incomplete or incorrect in detail, models of crowding almost all invoke the extraction of independent features and some form of pooling or integration^1,2,31,32. Our speculation, based on the centroid account of our data, is that the integration limit of ≈ 4 – 8 independent features may be closely related to the limited storage capacity of visual short-term memory in parietal cortex³⁵. Beyond this limit, crowding “flattens” the percept of individually resolvable features into a coherent texture.

Methods

Stimuli

The target was a briefly presented Gabor patch with horizontal carrier presented at an eccentricity of 2.5, 5 or 10 deg in the lower visual field. The carrier spatial frequency was 2.5 cpd and the Gaussian standard deviation of the patch was 0.4 deg when presented at 5 degrees eccentricity, and was scaled according to eccentricity. Control experiments show that the critical spacing at a given eccentricity is independent of target size and spatial frequency. The target phase was randomized from trial to trial. The flanks were segments of an annular grating. In most experiments, the flank grating was horizontal and the spatial frequency was the same as the target (2.5 c/deg at 5 degrees). Target and flanks were presented simultaneously for 250 msec. For the orientation discrimination the target contrast was 40%, and unless otherwise specified, flank contrast was 80%. The stimuli were generated using the WinVis Psychophysical testing platform, and were presented on a CRT screen (Sony Multiscan G400) with a mean luminance of 80 cd/m².

Psychophysical Methods

The main experiments used a two-interval forced-choice (2IFC) orientation discrimination task. On each trial, the reference (0°) and test (reference plus an orientation offset) were separately presented in the two brief stimulus intervals (250 ms each) in a random order separated by a 500-ms inter-stimulus interval. An observer’s task was to judge which stimulus interval contained the more counter-clockwise Gabor. Auditory feedback was given following each correct response. To reduce uncertainty about the target location, each trial was preceded by 2 large 37 by 0.1 deg diagonal lines forming an X with a circular gap (≈ 0.6 E in diameter) in the center, so that it did not extend into the area of the target and flankers. These lines disappeared during each stimulus interval. The target always appeared in the center of the gap. Detection thresholds were measured for the same stimuli and flankers using the same 2IFC staircase method.

Each staircase consisted of eight reversals with thresholds based on the last six reversals. The initial orientation difference between the test and the reference was sufficiently large, so that the observers could always make a correct discrimination. A classical 3-down-1-up staircase rule was used, which resulted in a 79.4% convergence level. The geometric mean of the 6 reversals was taken as the threshold estimate for each staircase run. In a typical experiment, 4–8 staircases were randomly interleaved, so that all flank conditions (including no flanks) were tested in the same run. Each experiment was replicated 6–8 times, and the thresholds are the geometric means of the 6–8 threshold estimates.

Our index of crowding is the “Threshold Elevation” (i.e., the flanked thresholds divided by the unflanked thresholds). A threshold elevation of 1 indicates no crowding.

Observers

Five adults with normal or corrected-to-normal vision served as observers (although not all observers performed every experiment). All testing was monocular with the untested eye patched (to allow comparison with future amblyopic observers). Observers were given substantial practice prior to data collection. The data reported are mean threshold elevation data averaged across observers. Individual data followed the same trends. Fig. S1 shows individual data for the “fixed size” experiment (circles in Fig. 1c). Fig. S1a shows the “raw data” (with orientation thresholds in degrees), Fig. S1b shows the individual data normalized by the unflanked thresholds (i.e. plotted as Threshold Elevation).