A Study of Grid Artifacts Formation and Elimination in Computed Radiographic Images

Abstract

Computed radiography (CR) has many advantages such as filmless operations, efficiency, and convenience. Furthermore, it is easier to integrate with the picture archiving and communication systems. Another important advantage is that CR images generally have a wider dynamic range than conventional screen film. Unfortunately, grid artifacts and moiré pattern artifacts may be present in CR images. These artifacts become a more serious problem when viewing CR images on a computer monitor when a clinic grade monitor is not available. Images produced using a grid with higher frequency or a Potter–Bucky grid (i.e., a moving grid, Bucky for short) can reduce occurrence but cannot guarantee elimination of these artifacts [CR & PACS (2000); Detrick F (2001), pp 7–8]. In this paper, the formation of the artifacts is studied. We show that the grid artifacts occur in a narrow band of frequency in the frequency domain. The frequency can be determined, accurately located, and thus removed from the frequency domain. When comparing the results obtained from the proposed method against the results obtained using previous computer methods, we show that our method can achieve better image quality.

Introduction

The picture archiving and communication system (PACS) has become a hospital standard. In a PACS system, the clinical images are presented in digital form. Digital images are easier to store and transfer from one place to another. However, they also contain artifacts. In a study by Cesar et al.,¹ the authors presented a detailed discussion that focused on some artifacts that were caused by operator error. However, there are other types of artifacts, such as grid artifacts and moiré patterns, that are not caused by operator error. These artifacts are inherent problems with the computed radiographic (CR) imaging system. A grid is used routinely during x-ray exposure to remove undesired scattered x-rays. When the CR image plate is exposed with a grid and displayed on a computer monitor, interference or moiré pattern artifacts appear. Because there are cases in which a clinic grade monitor is not available or images are read in a wireless environment,² displaying images on a regular computer monitor is required. In these cases, the grid artifacts and moiré patterns are much more pronounced because of the computer monitor having a much lower display resolution than that of the images.

Previous grid pattern studies have been performed in the past.^3–6 A similar problem in designing a film scanner was studied by Wang and Huang.³ The objective of the study was to minimize the aliasing artifacts while converting a film into digital form. In another study by Barski and Wang,⁴ a method consisting of grid frequency detection and adaptive grid suppression was proposed. The grid artifact frequency was detected in the frequency domain after a 1-dimensional Fourier transform. Artifact suppression was achieved by designing appropriate blur kernels in the spatial domain. The artifact frequency in 95.8% of the cases could be correctly detected. However, because a grid artifact is a periodic signal, it cannot be effectively removed by applying simple blur kernels in the spatial domain. Moreover, applying blur kernels to reduce grid artifacts also blurs the image itself. In a grid artifact study by Belykh and Cornelius,⁵ the same method used by Barski and Wang⁴ was employed to detect the grid frequency. A notch filter⁷ in the frequency domain was used to suppress the grid textures. Unfortunately, using a notch filter causes rippling or ringing effects in the image. Sasada et al.⁶ used a method similar to that by Barski and Wang⁴ to locate the artifact frequency. The wavelet approach was then employed to remove grid artifacts.

In this paper, the causes of grid artifacts are investigated in detail. We show that the artifact frequency can be estimated directly from the digital imaging and communication in medicine (DICOM) tag and grid specifications. The frequency can be accurately located in the frequency domain. Finally, a band-stop Gaussian filter is designed to remove the frequency.

Theory

There are two major x-ray scattering effects, Rayleigh scattering and Compton scattering, that affect the quality of an x-ray image.⁸ A grid is employed to eliminate or reduce scattering. A variety of x-ray grids are available.⁹ Different grids produce different grid textures in the image plate. These grid textures can be vertical stripes, horizontal stripes, or a combination of the two. In this paper, only the case of vertical stripes is discussed. The other two cases are similar.

A CR image is recorded by an imaging plate coated with photostimulated storage phosphors.^10–13 When the coating is exposed to x-rays, the electrons in the phosphor crystals are excited and trapped in a semistable, higher-energy state. To read this energy state, a plate reader scans the imaging plate using a laser beam.¹⁰ The laser energy releases the trapped electrons, causing emitted visible light that is captured and converted into pixels in the digital image. Suppose that there are vertical stripes recorded in the image plate, and the vertical stripes are sampled by sampling signal g_s(u,v). Interference between the two signals occurs and artifacts are produced.

There are two points in the process from image formation to display in a raster device at which artifacts occur. At the first point, grid artifacts or moiré pattern may be created when a plate reader samples an image plate exposed with a grid. We show that the artifacts are either the image of the grid itself or the interference between the grid texture and the plate reader sampling signal. At the second point, moiré patterns may occur when we display an image with grid artifacts on a raster output device. In this situation, the artifacts are sampled by the pixels of the output device again, resulting in more serious artifacts.

Figure 1 shows some important grid parameters related to the interference between the two signals. The grid frequency, denoted as f_grid, is expressed as the number of lines per centimeter (or per inch). T_grid is the distance between consecutive vertical stripes. Thus, T_grid = 1/f_grid. As the frequency becomes higher, the grids become thinner and there is less grid texture obtrusion in the image. Two less important parameters to this work are the space between the lead stripes d and the thickness of lead s. Note that .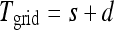

Fig 1.

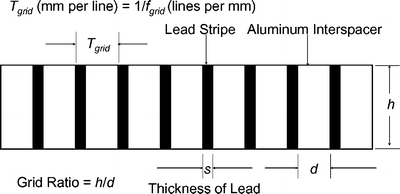
This figure shows the cross section of a grid and some grid specifications related to this work.

Given a 2-dimensional signal h_g(x,y) in an XY-coordinate system, the signal is sampled by a grid function g_s(u,v) in the UV-coordinate system. Consider the case in which h_g(x,y) consists of vertical stripes in the XY-coordinates. Depending on the angle θ between the XY- and UV-coordinate systems, there are two cases. The first case is that the XY-coordinate coincides with the UV-coordinate, i.e., θ = 0. The second case involves a nonzero angle θ between the XY-coordinates and the UV-coordinates (Fig. 2).

Fig 2.

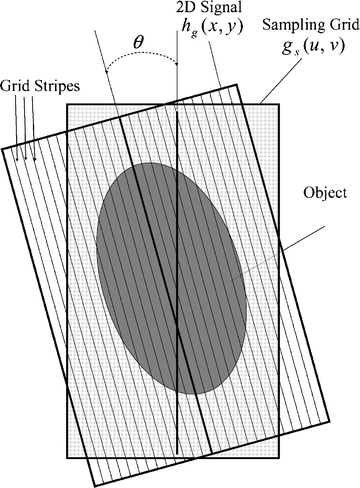
There is an angle θ between the sampling signal (UV-coordinate) and the grid (XY-coordinate).

Case 1, θ = 0

If the XY-coordinate coincides with the UV-coordinate, only the sampling signal along a horizontal line is considered. Along a horizontal sampling line, the vertical stripe signal is a square wave, as shown in Figure 3. Let the 1-dimensional square wave be denoted h_g(x). Recall that T_grid is the period of h_g(x), and d and s are, respectively, the space between the lead stripes and the thickness of lead. We have 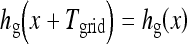and .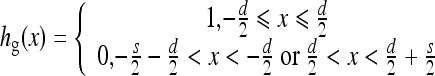

Fig 3.

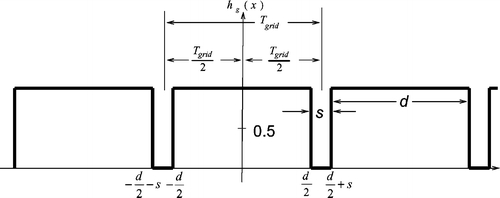
Along a horizontal scan line, the vertical stripe signal is a square wave.

The periodical square wave can be expanded using the Fourier expansion.¹⁴ The Fourier expansion for h_g(x) is written as

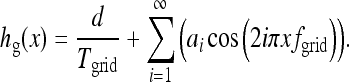1

h_g(x) can be separated into a direct current (DC) term, a fundamental wave, and infinite harmonics. In Eq. (1), the first term, 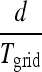, is the DC term. The second term is the fundamental wave, 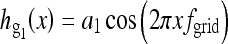. Note that the magnitude of 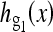is a₁, and the frequency of 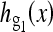is 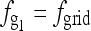. All of the following terms are the harmonics, denoted 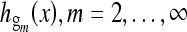. The frequency of each harmonic term 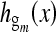is denoted as 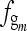. These harmonics have a higher frequency but a lower magnitude than the fundamental wave.

Let the sampling grid function g_s(u,v) have a sampling frequency f_s on a horizontal line. According to the Nyquist sampling theorem, if

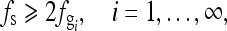2

then 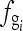can be reconstructed without aliasing. Otherwise, aliasing occurs. Let 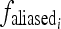denote the aliasing frequency. 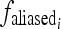can be obtained using¹⁵

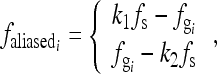3

where k₁ and k₂ are integers and must be chosen to meet one of the inequalities in

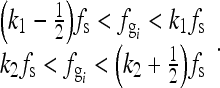4

If the sampling frequency f_s is close to 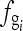, according to Eqs. (2)–(4), 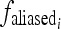is a low-frequency signal that has a much lower frequency than 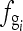. Because human eyes are sensitive to low-frequency signals, the artifacts are easily seen on a monitor. If f_s meets the Nyquist sampling theorem, then the grid textures in the image plate can be fully reconstructed.

The above discussion is valid when there is a grid texture in the image plate. The presence of a grid texture depends on the point spread function (PSF)¹⁶ of the imaging system. In a system with poor PSF, the grid texture is blurred or even becomes invisible.

When a CR image is acquired using a grid that is perfectly aligned with the image plate reader, the following cases are observed.

1. There are no visible artifacts. This occurs if the PSF response of the system is poor. This is not the desired approach for removing the grid texture.

2. There are grid textures in the image plate. Let the grid artifacts frequency be 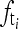. There are two subcases,

   1. f_s satisfies the Nyquist sampling theorem, and thus, the grid artifacts are the grid textures in the image plate. In this case, 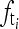is equal to .
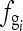   2. f_s does not satisfy the Nyquist sampling theorem. In this case, 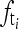is equal to .

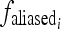Case 2, θ ≠ 0, the Moiré Pattern

If there is an angle between the XY-coordinates and the UV-coordinates, there is an artifact called the moiré effect (Fig. 4). Many physicians have learned from experience that the grid orientation determines the moiré pattern.¹⁷ The following discussions explain this phenomenon.

Fig 4.

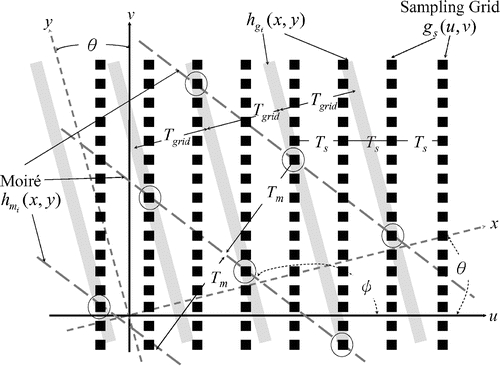
Moiré pattern (the dashed lines) caused by two periodical functions.

The vertical stripes h_g(x,y) in the XY-coordinate perpendicular to the X-axis with period T can be presented as

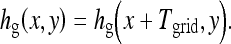5

h_g(x,y) is sampled using the sampling signal g_s(u,v) in the UV-coordinate system. g_s(u,v) is a set of grids formed by lines perpendicular to the U-axis. These vertical stripes in the UV-coordinate system have a period T_s. It can be written as

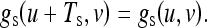6

Let the angle between the XY- and UV-coordinate systems be θ, as shown in Figure 4. Points in the XY-coordinate system and UV-coordinate system can be related using the transformation

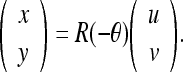7

The phases of any point in both coordinate systems are given as

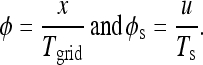8

Using Eq. (7), Eq. (8) is rewritten in the form

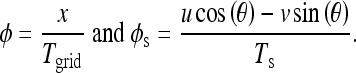The loci of the points for a particular phase difference Δφ is given by

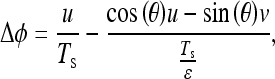9

where 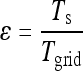. The condition for the points to have the same phase in both coordinate systems is

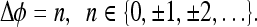10

Combining Eqs. (9) and (10) yields

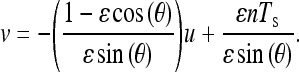11

Equation (11) is a line with slope 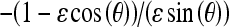. The set of dashed lines shown in Figure 4 is the moiré pattern. Observe that the slope 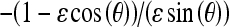is a significantly large number for a very small angle θ. Figure 5 shows that even a small angle θ causes a very large moiré pattern angle. Furthermore, the frequency of the moiré pattern can be obtained using Eq. (3). As discussed previously, this frequency is much lower than the frequency of the vertical stripe or the sampling frequency. Thus, the moiré pattern is perceptually clear.

Fig 5.

A change in an angle θ from 0° to 2° will cause the stripe angle in the moiré pattern to change from 0° (a) to 24° (b). (a) 3,062 × 3,730 pixels; (b) selected area from (a), showing grid artifacts. (c) Selected area from (a), with grid artifacts removed. (d) 1-Dimensional Fourier transform of the image in (a). Grid artifact frequency indicated by the circle. (e) The spectrum after grid artifacts are removed. (f) 540 × 648 pixels; (g) 540 × 648 pixels, with grid artifact removed.

Displaying an Image Containing Artifacts on a Monitor

A typical clinical-grade monitor has a resolution of approximately 2,560 × 2,048 pixels.¹⁸ The resolution of CR images could be higher than a monitor's. For example, the resolution of the image shown in Figure 6 is 3,062 × 3,730 pixels. It is necessary to reduce the size of a high-resolution CR image to allow it to fit on a monitor. Suppose there are grid artifacts in the image. Sampling the artifacts by the low-resolution monitor pixels, according to Eqs. (3) and (4), produces lower-frequency artifacts.

Fig 6.

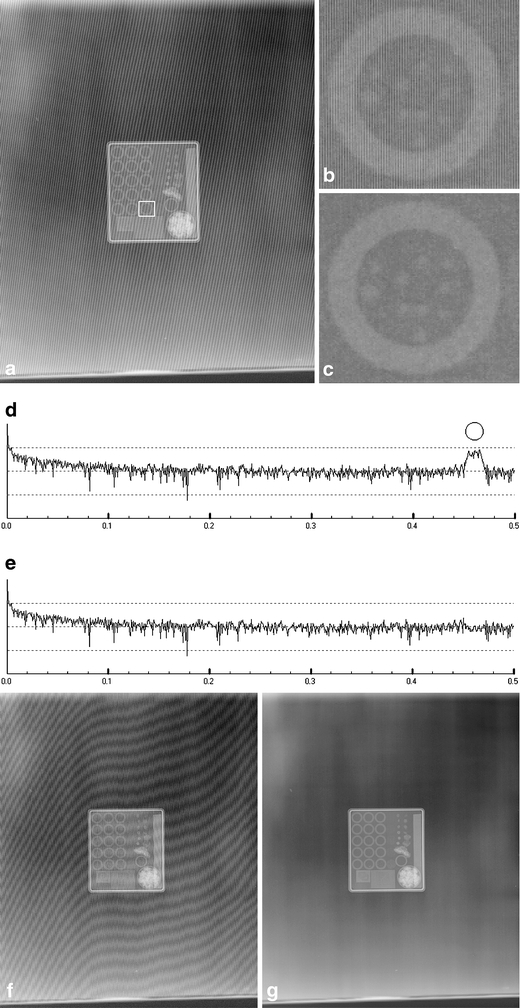
(a) Mammography Quality Control Phantom (Phantom No. C104, Fuji, Japan) image with grid artifacts. (b) A selected region in (a) is shown in the original resolution. The artifacts are easily seen. (c) The same region, with grid artifacts eliminated. Note that many details, such as the vertical stripes, can be clearly distinguished. (d) The spectrum of a 1-dimensional Fourier transform of the image shown in (a). The y-axis is logarithmic. The frequency of the grid artifact is highlighted with a circle. (e) The spectrum after grid artifacts are removed. (f) An image of the Mammography Quality Control Phantom scaled down 17% to a resolution of 540 × 658 pixels. It shows a very serious artifact (the moiré pattern). (g) The moiré pattern was eliminated using the proposed method. (a) 2,048 × 2,494 pixels; (b) selected area from (a), enlarged. It contains fine vertical stripes. (c) Selected area from (a), with grid artifacts removed. (d) 1-Dimensional Fourier transform of the image in (a). Grid artifact frequency indicated by the circle. (e) The spectrum after grid artifacts are removed.

Methods

In this section, a simple method to remove the artifacts is presented. Recall that the artifacts are produced at two points on the image producing path:

1. Artifacts are produced by sampling the grid texture in the image plate.

2. Artifacts are produced by sampling the image containing grid artifacts by using an output device.

If the artifacts produced in the first point can be removed, then all the artifacts are removed. Artifacts removal consists of three major steps: (1) estimating the artifact frequency, (2) accurately locating that frequency, and (3) removing the frequency using a Gaussian band-stop filter in the frequency domain.

Estimating the Artifact Frequency

The sampling frequency f_s is recorded in DICOM tag (0018:1164).^21–23 In DICOM standard, this tag is the “imager pixel spacing”, T_s, i.e., 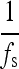. The grid frequency f_grid is available from the grid specification. Thus, the fundamental wave and harmonics 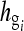and their frequencies 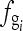are obtained using Eq. (1). Let the frequencies of the artifacts be denoted as 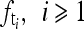. 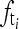are estimated using the following rules:

1. Sampling frequency f_s satisfies the Nyquist sampling theorem, i.e., 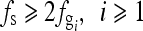. Because the grid can be totally reconstructed, the estimated aliased frequency 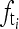is equal to .

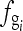2. Sampling frequency f_s does not satisfy the Nyquist sampling theorem, i.e., 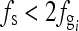. The estimated aliased frequency 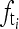is obtained using Eqs. (3) and (4).

Locating the Frequency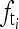

Let I_r(x,y), 0 ≤ x ≤ M − 1 and 0 ≤ y ≤ N − 1, be an image containing grid artifacts. Let l_r(x) denote a row in I_r(x,y). The 1-dimensional discrete Fourier transformation pairs for l_r(x) are

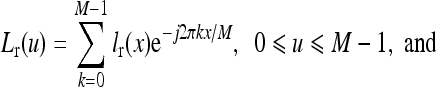12

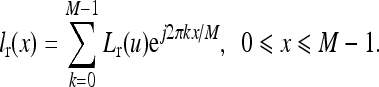13

The spectrum is

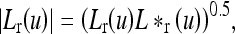14

where “*” means conjugate.

We assume that the spectrum of the grid artifact is Gaussian distribution:

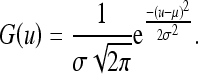15

By estimating μ and σ of the Gaussian distribution, we can construct the band-stop Gaussian filter B(u). The reason for choosing a Gaussian filter is that the Fourier transform of a Gaussian function is a Gaussian function. Using a Gaussian filter will not produce ripple effect. To design an accurate band-stop Gaussian filter, μ should be equal to 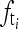. But because of the imperfections that sometimes result during the manufacturing of the grid or the grid is not perfectly aligned, there could be a small deviation. The accurate mean is obtained by calculating the mean of the interval from 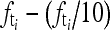to 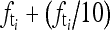in the spectrum. The standard deviation σ is also computed from the interval when the accurate mean is located. The image in Figure 6(a) contains grid artifacts. The 1-dimensional Fourier transform in x direction is shown in Figure 6(d). Figure 6(d) shows the spectrum after taking a logarithmic operation. The circle shown in Figure 6(d) is the frequency of the grid artifacts.

Remove the Frequency

Because the harmonics have a higher frequency but a much lower magnitude than the fundamental wave, the effect of harmonics is small and can be ignored. In this study, only the fundamental wave is removed. It is removed by using a Gaussian band-stop filter for each row in the image as shown in the following,

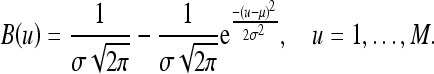16

The accurate mean and standard deviation are substituted into Eq. (16) to construct the Gaussian band-stop filter B(u). We multiply L_r(u) by B(u) to obtain 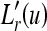shown in the following,

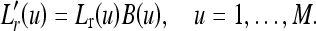17

Taking the 1-dimensional inverse Fourier transform [Eq. (13)] of 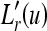, we obtain a grid texture free row 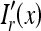. We apply the process stated above for each row in I_r(x,y) to obtain an image, 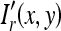. 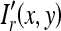is free of grid artifacts, as shown in Figure 6(f).

Results

Both clinical and phantom images were used to evaluate the proposed method. Figure 6(a) shows an image of a mammography quality control phantom (Art No. 6652348, Phantom No. C104, Fuji, Japan). The image resolution is 3,062 × 3,730 pixels. A 40-lines/cm grid was used while acquiring the image. The sampling rate was 8.77193 pixels/mm (0.114 mm/pixel). Thus, 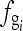is 4 lines/mm (40 lines/cm), and f_s is 8.77193 pixels/mm. Because 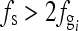, the sampling frequency satisfies the Nyquist sampling theorem. Therefore, the grid textures in the image plate can be reconstructed, and the grid artifact frequency is 4 lines/mm. Because the sampling frequency is f_s = 8.77193 lines/mm, the grid artifact frequency is estimated to be 0.461 of the sampling frequency, as shown in Figure 6(d). By applying the Gaussian Filter, the artifact frequency is removed. Figure 6(b) shows a selected region in Figure 6(a) in the original resolution. Figure 6(c) shows the image in which the artifact is eliminated. Figure 6(f) shows a zoomed out image of the mammography phantom image in Figure 6(a). The resolution was scaled down from 3,062 × 3,730 to 540 × 658 pixels. The moiré pattern is significant. Figure 6(g) shows an image in which the artifact was eliminated by applying the proposed method. Figure 6(e) shows the spectrum after the grid artifacts were removed. Figure 7(a) is a CR chest image with resolution 2,048 × 2,494 pixels. A 3.3-lines/mm (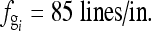) grid was used while acquiring the image. The sampling frequency f_s is 5.8 pixels/mm. This case does not satisfy the Nyquist sampling theorem (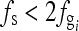). The artifact frequency 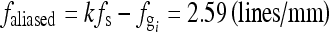, where k = 1. Because the sampling frequency is f_s = 5.8 lines/mm, the estimated frequency of the artifact appears to be 0.45 of the sampling frequency [Fig. 7(d)]. Figure 7(b) shows a selected region in Figure 7(a) in the original resolution. Figure 7(c) is the image in which the artifact was removed. Figure 7(e) shows the spectrum after the grid artifacts were removed.

Fig 7.

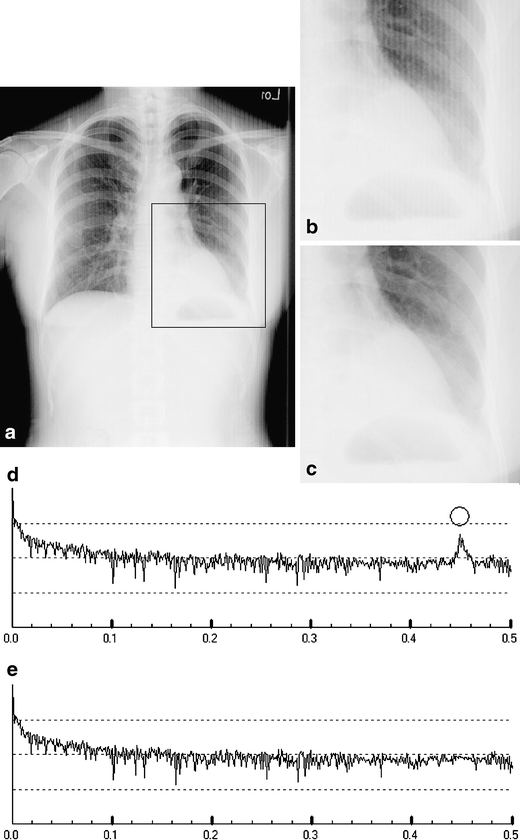
(a) A patient with left lower lobe consolidation due to pneumonia. Grid pattern can be seen on CR chest image. (b) The portion that is highlighted in white in (a). (c) The grid pattern was removed using the proposed method. (d) The spectrum of a 1-dimensional Fourier transform of the image shown in (a). The y-axis is logarithmic. The frequency of the grid artifact is highlighted with a circle. (e) The spectrum after grid artifacts are removed.

To compare the proposed method against the previous computer methods for artifact removal, we used an image containing three characters as shown in Figure 8(a). Although these are not clinical images, using geometric-shaped characters is the best way to demonstrate the effect of the applied methods. Figure 8(a) is the original image containing grid artifacts. Figure 8(b) shows the grid artifacts removed using the proposed method. Figure 8(c) shows the grid artifacts removed using the blur kernel proposed by Barski and Wang.⁴ When compared to the result obtained by the proposed method, the sharp edges in Figure 8(c) are blurred. Grid artifacts in Figure 8(d) were removed using a notch filter proposed by Belykh and Cornelius.⁵ Although the sharp edges are preserved, there are ripples after the artifacts are removed.

Fig 8.

(a) The original image with grid textures. (b) The grid textures were removed using the proposed method. (c) The grid textures were removed using the blur kernel proposed by Barski and Wang.⁴ (d) The grid pattern was removed using a notch filter proposed by Belykh and Cornelius.⁵

Conclusions and Discussion

In this paper, the formation of grid artifacts in CR images was studied in detail. An automatic method was then presented to remove the grid artifacts. The method was implemented on a PC with a Pentium 4 (2 GHz) CPU running the Windows 2000 operating system. The total execution time for images with different resolutions of 1,760 × 2,140, 2,000 × 2,510, and 3,520 × 4,280 pixels took 10, 12, and 24 s, respectively.

Although the grid artifacts can be removed by using a Bucky or a higher-frequency grid, there are limitations to these two methods. For example, there are cases in which radiographic images are acquired when a Bucky is not accessible. In addition, as the grid frequency increases, there is relatively more grid material to absorb radiation. This situation requires that the patient be exposed to a higher dose of radiation.²⁴ Using the proposed method, these problems are overcome, and images that are free of grid artifacts are obtained. Compared to the results obtained by the methods of Barski and Wang⁴ and Belykh and Cornelius,⁵ the proposed method neither produces ripple artifacts nor blurs the image. The proposed method achieves much better results. An important question is that whether the proposed method improves the accuracy of diagnosis. Rigorous experiments should be performed to clarify this point. A problem with the proposed method is the computing time required. Future studies will investigate methods to reduce the computing time.