Skip to main content
PMC home page
Journal of Digital Imaging logoLink to Journal of Digital Imaging
. 2005 Dec 13;19(2):132–139. doi: 10.1007/s10278-005-9240-0

Fully Automated System for Three-Dimensional Bronchial Morphology Analysis Using Volumetric Multidetector Computed Tomography of the Chest

Raman Venkatraman 1, Raghav Raman 2, Bhargav Raman 2, Richard B Moss 1, Geoffrey D Rubin 2, Lawrence H Mathers 1, Terry E Robinson 1,✉
PMCID: PMC3045191  PMID: 16341571

Abstract

Recent advancements in computed tomography (CT) have enabled quantitative assessment of severity and progression of large airway damage in chronic pulmonary disease. The advent of fast multidetector computed tomography scanning has allowed the acquisition of rapid, low-dose 3D volumetric pulmonary scans that depict the bronchial tree in great detail. Volumetric CT allows quantitative indices of bronchial airway morphology to be calculated, including airway diameters, wall thicknesses, wall area, airway segment lengths, airway taper indices, and airway branching patterns. However, the complexity and size of the bronchial tree render manual measurement methods impractical and inaccurate. We have developed an integrated software package utilizing a new measurement algorithm termed mirror-image Gaussian fit that enables the user to perform automated bronchial segmentation, measurement, and database archiving of the bronchial morphology in high resolution and volumetric CT scans and also allows 3D localization, visualization, and registration.

Key words: Bronchial morphology, computed tomography, automation algorithm, automated measurement

Background

Multidetector-row computed tomography (MDCT) of the lung has undergone a revolution in recent years, with scanners capable of fast, low-dose, single breath-hold acquisition of volumetric datasets at precise lung volumes using spirometer triggering.1,2 These datasets now have submillimeter resolution and depict the bronchial tree in great detail.3 MDCT has therefore become a powerful tool for the evaluation of structural changes in the bronchial tree as a result of chronic pulmonary disease.3–6 Volumetric CT allows quantitative indices of bronchial airway morphology to be calculated, including airway diameters, wall thicknesses, wall area, airway segment lengths, airway taper indices, and airway branching patterns.7,8 However, the complexity and size of the bronchial tree render manual measurement methods impractical and inaccurate.9 A typical bronchial tree has hundreds of segments. Previous algorithms required the user to manually select the airway cross section to be measured and required manual correction and validation of the measurements obtained. Therefore, because of time limitations, only a small fraction of the segments were measured in any one scan.10–13 We wanted to quantitatively measure all visualized segments in volumetric CT scans of the lung using a fully automated method to improve the validity and accuracy of bronchial morphology measurement and to allow measurement of regional airway disease. We have developed an integrated software package that enables the user to perform automated segmentation, measurement, and archiving of the bronchial morphology in volumetric CT scans, reducing the processing time per scan. Our system also allows 3D localization and visualization as well as registration of segments between serial CT scans.

System Description

Automated Algorithms

The full automation of bronchial tree analysis was achieved through the development of several interlinked algorithms.

Bronchial Segmentation

First, our algorithm segments the bronchial tree. Several different segmentation algorithms have been previously proposed in the literature.14–19 Our implementation uses a morphological front propagation algorithm that requires as input only one seed point in the trachea. Based on the local Hounsfield Unit (HU) intensity, an initial estimate of the high and low threshold for segmentation is calculated. The algorithm then propagates this point by growing through the bronchial tree. As the bronchial tree branches, multiple fronts are generated that grow independently through each of the segments and subsequently branch into child fronts as the segment divides. The intensity, size, shape, and cross-sectional profile thresholds for each front are adaptively adjusted as the segmentation proceeds. As the segments terminate in alveoli, the fronts terminate. The sum total of the voxels traversed by all fronts is designated as the bronchial tree.

Bronchial Tree Skeletonization

To facilitate analysis and registration, the bronchial tree segmentation is skeletonized to reduce it to a set of branching centerlines through the whole bronchial tree. This allows the tree to be partitioned into bronchial segments based on the branch points of the centerlines. The centerline begins in the trachea, using the point provided initially by the user. The distal end of every terminal branch then needs to be identified. To accomplish this, we use a reverse-mask distance-map method to automatically identify the end of every terminal branch. This algorithm first calculates a distance map with the initial point in the trachea as the point with zero distance. Each voxel in the bronchial segmentation is then assigned a distance value based on the number of segmentation iterations required to reach the voxel from the start voxel in the trachea. After the distance map is calculated, the point with maximum iteration distance from the start point is designated as the first terminal branch endpoint. From this first end voxel, a reverse mask is applied to mark all voxels immediately connected with that end voxel that have a smaller distance. The reverse mask is then iteratively applied to the newly marked voxels to propagate it toward the start voxel. As this reverse mask propagates, it propagates only proximally and does not propagate distally down any other branch because it only grows “down” the distance map toward smaller iterative distances. Once the start point has been reached, the next terminal branch endpoint is calculated as the point with the highest distance from the start point that is not already masked. Following this, the reverse-masking procedure is then reapplied from this new endpoint. As the reverse mask propagates, it is terminated either when it reaches the start point or when it can no longer grow because it is blocked by previously masked voxels. This process is iterated until no more unmasked voxels remain. Then a previously developed and published algorithm20 is used to skeletonize the segmentation to produce a set of centerlines from the start point to every endpoint identified.

Bronchial Cross-Section Identification

The next step in automated analysis is to automatically identify the bronchial cross sections to be analyzed. First, the branch points in the bronchial tree were identified. The initial set of centerlines had a common start point in the trachea and had unique endpoints in every terminal branch identified. From this set of centerlines, a new data structure was created that defined bronchial segments individually. First, the tree structure was initialized with the root bronchial segment that commenced in the trachea. All centerlines initially took the same course in this segment. The distance between the courses of each centerline was measured along the segment. At the tracheal bifurcation, the centerlines diverged into two sets of centerlines. When the distance between the two new sets of centerlines was found to be larger than 1.5 mm, the two new sets of centerlines were considered to be two new child segments. In this case, these child segments were the two main bronchi to each lung. Each of these child segments was added to the tree structure under the root segment. For each of these child segments, the branch point identification process was applied recursively to identify further child segments. Each child segment stored the position of the start point of the child segment (the proximal branch point) and the endpoint of the segment (the distal branch point). When a child segment had only one centerline coursing through it, it was deemed to be a terminal segment and the recursive algorithm terminated for that child segment. At the conclusion of the algorithm, the tree structure contained all individual bronchial segments in the lung.

Between the proximal branch point and the distal branch point of each segment, the middle 50% of the segment was chosen for analysis. This allowed us to exclude the flaring and distortion because of branching at the proximal and distal ends of each segment. At 1-mm intervals in the medial 50% of each segment, the perpendicular plane to the bronchus was calculated as the plane perpendicular to the three-dimensional direction of the centerline. This plane may not be the most optimal plane to obtain the most circular cross section because the medial centerline direction may be deviated by tortuosity proximal and distal to the current point. An exhaustive search of all planes within 15° of pitch, yaw, and roll of the initially identified plane is carried out at 1° intervals, and the most circular cross section identified is used. Circularity is defined as follows. The perimeter and cross-sectional area of each candidate cross section are calculated. For that cross-sectional area, the perimeter of an ideal circle with the same cross-sectional area is calculated. The ratio of the actual perimeter to the ideal perimeter is defined as the circularity of the cross section. Values closer to 1 indicate greater circularity. Once the most circular plane is identified, the voxel values on the plane were calculated using trilinear interpolation with supersampling to 0.03 mm. These values are used to calculate the bronchial measurements subsequently obtained. This process is then iterated every 1 mm along the central 50% of each bronchus.

Bronchial Cross-Section Measurement

For each bronchial cross section, the centerpoint of the bronchus is recalculated to eliminate any bias caused by deviations in the centerline previously calculated. First, the inner bronchial wall was extracted using an adaptive threshold. The threshold was calculated as the mean of the central bronchial intensity plus 1.64 multiplied by the noise (standard deviation) of HU measured at the center of the bronchus. The choice of 1.64 standard deviations includes 90% of the normal curve, allowing the outline of the bronchial wall to be extracted while excluding noise and artifact in the bronchial lumen. The centerpoint of the bronchus was then recalculated as the center of mass of all points enclosed by the inner bronchial outline. From this centerpoint, 60 spokes were propagated radially at 6° intervals, and the voxel values were calculated along each spoke using trilinear interpolation at 0.01-mm intervals. For each spoke, the points of intersection with the inner and outer walls of the bronchus were calculated as follows. First, the maximum HU value along the spoke was calculated. The point along the spoke that was the first to have a value equal to half the maximum intensity along the spoke was selected as the true location of the inner bronchial wall (the half-max approach).21,22 The outer bronchial wall, however, was not as easily identified. Because of the soft tissue and lung parenchyma around any bronchus, the half-max approach wasnot ideal to calculate the location of the outer bronchial wall. In some cases, the HU value of the surrounding soft tissue was higher than half of the maximum HU value, rendering the method useless. In other cases, the intensity of the surrounding soft tissue deviated the HU value profile. To solve this, we used a newly developed two-stage mirror-image Gaussian fit (MIGF) approach to best estimate the outer wall. First, an assumption was made that the “true” HU profile from the middle of the bronchial wall to the outer wall would be similar to the mirror image of the HU profile from the middle of the bronchial wall to the inner wall. (The true profile was taken to be the profile that would be obtained in the absence of soft tissue surrounding the bronchial outer wall.) Therefore, an initial estimate of the outer wall was calculated as being the same distance from the middle of the bronchial wall as the distance from the inner wall to the middle of the bronchial wall. Next, the HU profile from the middle of the bronchial wall to the outer wall (the outer wall profile or OWP) was compared with that from the middle of the bronchial wall to the inner wall (the inner wall profile or IWP). The proximal parts of the OWP that deviated less than 10% from the mirror image of the IWP were retained, and the rest of the curve was then rejected as being artifact because of the surrounding soft tissue. The remaining OWP was then fit to a Gaussian curve with the maximum being equal to the maximum HU value and the minimum being equal to a HU value of −1000 (corresponding to air). From this Gaussian curve, the half-max point was calculated as the location of the outer wall. However, in some cases, high-intensity soft tissue around the bronchus resulted in more than 80% ofthe OWP being rejected. In such cases, the initialestimate of the outer wall (made directly from the IWP) was accepted as the true location of the outer wall.

Once the inner and outer wall positions were calculated for every spoke, the mean and median inner and outer wall diameters are calculated, as well as the standard deviation of measured inner and outer wall diameters. Then a statistical validation process is applied to weed out erroneously calculated values as follows: all measurements that fall outside 2 standard deviations of the mean or the median measurements are rejected.

Thus, mean inner and outer wall diameters are calculated for every bronchial cross section in the central 50% of each segment. The wall thickness is also calculated as the difference between the inner and outer diameters. The values in the central 50% of each segment are averaged to yield a mean measurement for each segment. For quality control, the number of valid measurements that contributed to this mean measurement is also recorded, as well as the standard deviation of the measurements. Using the serial measurements along the segment, a best-fit line is applied to the inner and outer wall diameter profile along the segment, and bronchial taper index is calculated as the mean change in diameter per millimeter along the segment for inner and outer walls.

The algorithm then saves all measurements into a centralized database that allows advanced statistical analysis such as with grouping by segment generation, segment length, and segment inner diameter. Whereas the current implementation only categorizes segments based on generation and morphological characteristics, the software allows users to indicate relevant anatomic labels for certain subtrees. This allows statistics to be grouped by subtree—for example, statistics can be computed for all segments distal to the right main bronchus or distal to the bronchus intermedius.

Follow-up Using Serial Scans

To compare bronchial measurements obtained from serial CT imaging, the software allows two modes of operation. Statistical comparisons can be made by comparing the mean measurements for each scan by generation and grouped by segment diameter of length. In addition, each segment can be compared with the most likely corresponding segment in the comparison scan. This is accomplished as follows. The cross-sectional image at the midpoint of the segment to be matched is saved as a binary image, with air-intensity pixels as black and soft tissue intensity pixels as white. This image is compared to the binary cross-sectional image at the midpoint of every segment in the comparison scan. The segment with the cross-sectional image with the greatest similarity to the comparison image is selected as the corresponding segment in the comparison scan. Whereas advanced registration methods such as mutual information-based methods may be implemented in the future, we have found that the limited number of possible matches combined with the uniqueness of the cross-sectional image at a certain segment allows this simple, fast binary-matching method to be used.

User Interface and System Integration

The proprietary software package consists of a Windows-compatible front end that has been optimized to perform the bronchial analysis tasks in a multiprocessor environment. The desktop software was developed using Visual C++ 6.0 with Microsoft Foundation Classes and is compatible with all versions of Windows (Figure 1). Two-dimensional graphics were implemented using the Microsoft GDI libraries. Three-dimensional rendering was implemented with Microsoft Direct3D. No third-party libraries were used, and so installation was simplified. InstallShield was used to package the final runtime executable with all associated Microsoft libraries for distribution. Licensing is on a per-processor basis and is controlled using the processor ID, which is registered upon installation. Upon introduction of Windows Vista, we intend to use the .NET architecture along with the Avalon graphics engine in future versions of the software (Figure 2). The software package is designed specifically for the bronchial tree analysis workflow, guiding the user through a single data collection pathway that keeps track of the inputs provided and outputs generated. All intermediate results, such as the bronchial segmentations and branching centralized paths, are also stored. This allows the software to maintain the integrity of the data collected because the user cannot progress through the workflow unless all data for each step have been collected. Finally, all measurements made are archived and are available for comparison and registration with previous or future scans (Figure3). The package is integrated with a Microsoft SQL server (Microsoft, Redmond, CA) back-end database to store patient data, airway measurements, and measurement localizations. This allowed the development of a Web interface for patient reporting, which was implemented in Active Server Pages using Microsoft Visual Interdev. The custom Web interface also allows easy export in Microsoft Excel format for detailed analysis using statistical analysis packages (Figure 4).

Fig 1.

Fig 1

Open in a new tab

Stanford pulmonary laboratory system layout diagram. The large size of image datasets and data storage requirements for analysis results required a high-capacity, high-bandwidth infrastructure. The Stanford Pulmonary Laboratory has been set up to allow multiple users to simultaneously analyze scans. Scans are pushed from the institutional PACS system through a secure passthrough on the laboratory firewall and are then processed, registered, and stored on a central server with a 1 TB RAID array and gigabit Ethernet. All intermediate data and analysis results are also stored on this secure server with redundant external hard-drive backup. Currently, three analysis workstations are connected to the central server. In addition, one external Web passthrough server is used for external web and ftp services to study collaborators. This allows the internal laboratory computers to be isolated from institutional and external security threats.

Fig 2.

Fig 2

Open in a new tab

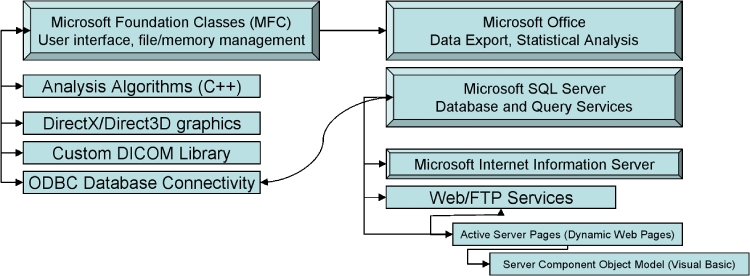
Software architecture, modules, and external library diagram. The algorithms described in the text are implemented in a Microsoft-integrated manner to leverage the advanced file and data management libraries and software provided in the Microsoft Windows framework. The main interface points between our system and related Microsoft software is as follows: (a) Dynamic Data Exchange and file links to Microsoft Office for data export and statistical analysis; (b) Open Database Connectivity (ODBC) link to Microsoft SQL Server for database and query services; (c) Microsoft programming libraries including Microsoft Foundation Classes for graphical user interfaces and program message loops and DirectX and Direct3D for graphics..

Fig 3.

Fig 3

Open in a new tab

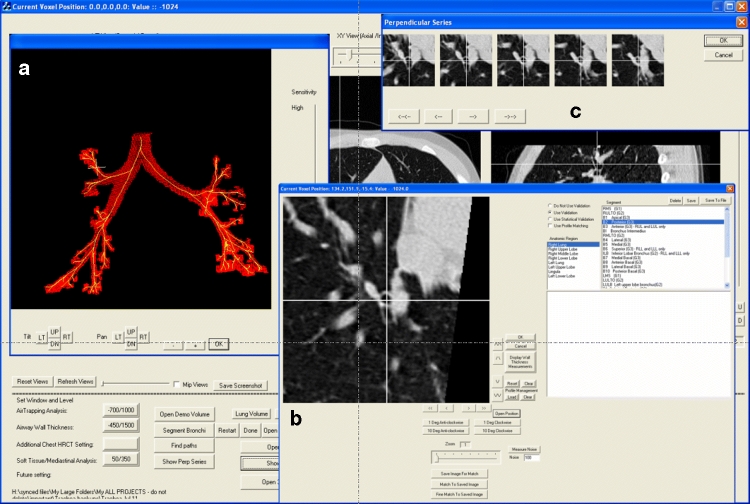
Software screenshot showing (a) 3D view with small crosshair indicating current position, (b) perpendicular view at current position, and (c) perpendicular series showing serial cross sections proximal and distal to current position at 1-mm intervals.

Fig 4.

Fig 4

Open in a new tab

Software screenshot depicting one bronchial cross-section analysis result. The blue spokes depict the inner wall boundary (IW) and the red spokes delineate the outer wall extent (OW) as calculated by the mirror-image Gaussian fit (MIGF) method. Since statistical validation was used, only spokes with measurements falling within 2 standard deviations of the mean are retained, and all other measurements are rejected. Note that the bronchus being analyzed is in close proximity with surrounding soft tissue and vessels along some of its circumference. The MIGF method allows the calculation of the true bronchial wall thickness even along segments of the bronchial wall edge that are obscured by soft tissue in close proximity. Statistical validation results in the selection of a representative sample of measurements around the bronchus.

The software package is capable of running on a low-end laptop for presentation use because it is capable of loading all intermediate results and measurements saved to disk without a large memory requirement. The system is also thread-safe, and many optimizations using multiple threads are built in, which improves performance and scalability on machines with multiple processors, dual-core processors, or other architecture optimizations, such as Intel Hyper-Threading or AMD's Hyper-Transport technologies. The system is also designed to allow future automated algorithms to be seamlessly integrated to allow the software to evolve with the state of the art in bronchial analysis methodology.

Discussion

The major advantage of this system is the capability for fully automated analysis of the bronchial tree in one integrated software package. In addition, the use of the MIGF approach to estimating the outer wall location eliminates systematic error in outer wall estimation because of surrounding soft tissue. This method has several advantages over other methods in the literature. The simple “half-maximum” approach previously described works well for the inner wall, but fails for the outer wall because of the surrounding soft tissue. One method that has been previously proposed to overcome this problem is the “maximum likelihood analysis.”21 In this method, a virtual airway phantom was scanned to produce predicted CT images, which were then compared to the actual images to find a best fit. This method simplifies the complex smoothing and noise generation seen in actual CT scans and is time-intensive. Our method uses the actual CT scan data without the need to model the process of creating a CT scan.

In the future, we plan to improve the capabilities of the system by automating the identification of anatomical labels for segments. We are in the process of validating the system by comparison with gold-standard pathological specimens. We are also conducting analyses of interscan variability in automated measurements and investigating the accuracy of automated measurements in low-dose scans.

Conclusion

We have developed an integrated system that requires only one user-input point in the trachea to automatically analyze the morphology of the whole bronchial tree. Unlike previous software programs, our system requires no expert user input. Because all the segments in every scan are measured, it allows the follow-up of bronchial morphology using serial scans.

Acknowledgments

We would like to thank Aysin Turan, MD, Xiaorong Chen, MS, and Akbar Dastagir, MD, for help in processing patient datasets and for data management and statistical analysis.

References

  • 1.Grenier PA, Beigelman-Aubry C, Fetita C, Preteux F, Brauner MW, Lenoir S. New frontiers in CT imaging of airway disease. Eur Radiol. 2002;12:1022–1044. doi: 10.1007/s00330-002-1342-1. [DOI] [PubMed] [Google Scholar]
  • 2.Robinson TE, Leung AN, Moss RB, Blankenberg FG, al-Dabbagh H, Northway WH. Standardized high-CT of the lung using a spirometer-triggered electron bean CT-scanner. Roentgenology. 1999;172:1636–1638. doi: 10.2214/ajr.172.6.10350305. [DOI] [PubMed] [Google Scholar]
  • 3.Suter M, Tschirren J, Reinhardt J, Sonka M, Hoffman E, Higgins W, McLennan G. Evaluation of the human airway with multi-detector X-ray-computed tomography and optical imaging. Physiol Meas. 2004;25:837–847. doi: 10.1088/0967-3334/25/4/005. [DOI] [PubMed] [Google Scholar]
  • 4.Jong PA, Ottink MD, Robben SG, Lequin MH, Hop WC, Hendriks JJ, Pare PD, Tiddens HA. Pulmonary disease assessment in cystic fibrosis: comparison of CT scoring systems and value of bronchial and arterial dimension measurements. Radiology. 2004;231:434–439. doi: 10.1148/radiol.2312021393. [DOI] [PubMed] [Google Scholar]
  • 5.Bagheri MH, Hosseini SK, Mostafavi SH, Alavi SA. High-resolution CT in chronic pulmonary changes after mustard gas exposure. Acta Radiol. 2003;44:241–245. doi: 10.1034/j.1600-0455.2003.00073.x. [DOI] [PubMed] [Google Scholar]
  • 6.Grenier PA, Beigelman-Aubry C, Fetita C, Martin-Bouyer Y. Multidetector-row CT of the airways. Semin Roentgenol. 2003;38:146–157. doi: 10.1016/S0037-198X(03)00017-8. [DOI] [PubMed] [Google Scholar]
  • 7.Nakano Y, Muro S, Sakai H, Hirai T, Chin K, Tsukino M, Nishimura K, Itoh H, Pare PD, Hogg JC, Mishima M. Computed tomographic measurements of airway dimensions and emphysema in smokers. Correlation with lung function. Am J Respir Crit Care Med. 2000;162:1102–1108. doi: 10.1164/ajrccm.162.3.9907120. [DOI] [PubMed] [Google Scholar]
  • 8.Nakano Y, Wong JC, de Jong PA, Buzatu L, Nagao T, Coxson HO, Elliott WM, Hogg JC, Pare PD. The prediction of small airway dimensions using computed tomography. Am J Respir Crit Care Med. 2004;171:142–146. doi: 10.1164/rccm.200407-874OC. [DOI] [PubMed] [Google Scholar]
  • 9.Bankier AA, Fleischmann D, Mallek R, Windisch A, Winkelbauer FW, Kontrus M, Havelec L, Herold CJ, Hubsch P. Bronchial wall thickness: appropriate window settings for thin-section CT and radiologic–anatomic correlation. Radiology. 1996;199:831–836. doi: 10.1148/radiology.199.3.8638013. [DOI] [PubMed] [Google Scholar]
  • 10.King GG, Muller NL, Whittall KP, Xiang QS, Pare PD. An analysis algorithm for measuring airway lumen and wall areas from high-resolution computed tomographic data. Am J Respir Crit Care Med. 2000;161:574–580. doi: 10.1164/ajrccm.161.2.9812073. [DOI] [PubMed] [Google Scholar]
  • 11.Ooi GC, Khong PL, Chan-Yeung M, Ho JC, Chan PK, Lee JC, Lam WK, Tsang KW. High-resolution CT quantification of bronchiectasis: clinical and functional correlation. Radiology. 2002;225:663–672. doi: 10.1148/radiol.2253011575. [DOI] [PubMed] [Google Scholar]
  • 12.Little SA, Sproule MW, Cowan MD, Macleod KJ, Robertson M, Love JG, Chalmers GW, McSharry CP, Thomson NC. High resolution computed tomographic assessment of airway wall thickness in chronic asthma: reproducibility and relationship with lung function and severity. Thorax. 2002;57:247–253. doi: 10.1136/thorax.57.3.247. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Gono H, Fujimoto K, Kawakami S, Kubo K. Evaluation of airway wall thickness and air trapping by HRCT in asymptomatic asthma. Eur Respir J. 2003;22:965–971. doi: 10.1183/09031936.03.00085302. [DOI] [PubMed] [Google Scholar]
  • 14.Loncaric S, Markovinovic T. Web-based virtual endoscopy. Stud Health Technol Inform. 2000;77:1187–1191. [PubMed] [Google Scholar]
  • 15.Summers RM, Feng DH, Holland SM, Sneller MC, Shelhamer JH. Virtual bronchoscopy: segmentation method for real-time display. Radiology. 1996;200:857–862. doi: 10.1148/radiology.200.3.8756944. [DOI] [PubMed] [Google Scholar]
  • 16.Wood SA, Hoford JD, Hoffman EA, Zerhouni E, Mitzner W. A method for measurement of cross sectional area, segment length, and branching angle of airway tree structures in situ. Comput Med Imaging Graph. 1995;19:145–152. doi: 10.1016/0895-6111(94)00034-4. [DOI] [PubMed] [Google Scholar]
  • 17.Aykac D, Hoffman EA, McLennan G, Reinhardt JM. Segmentation and analysis of the human airway tree from three-dimensional X-ray CT images. IEEE Trans Med Imag. 2003;22:940–950. doi: 10.1109/TMI.2003.815905. [DOI] [PubMed] [Google Scholar]
  • 18.Kiraly AP, Higgins WE, McLennan G, Hoffman EA, Reinhardt JM. Three-dimensional human airway segmentation methods for clinical virtual bronchoscopy. Acad Radiol. 2002;9:1153–1168. doi: 10.1016/S1076-6332(03)80517-2. [DOI] [PubMed] [Google Scholar]
  • 19.Park W, Hoffman EA, Sonka M. Segmentation of intrathoracic airway trees: a fuzzy logic approach. IEEE Trans Med Imag. 1998;17:489–497. doi: 10.1109/42.730394. [DOI] [PubMed] [Google Scholar]
  • 20.Paik DS, Beaulieu CF, Jeffrey RB, Rubin GD, Napel S. Automated flight path planning for virtual endoscopy. Med Phys. 1998;25:629–637. doi: 10.1118/1.598244. [DOI] [PubMed] [Google Scholar]
  • 21.Reinhardt JM, D'Souza ND, Hoffman EA. Accurate measurement of intrathoracic airways. IEEE Trans Med Imag. 1997;16:820–827. doi: 10.1109/42.650878. [DOI] [PubMed] [Google Scholar]
  • 22.Brink JA, Heiken JP, Balfe DM, Sagel SS, DiCroce J, Vannier MW, Spiral CT. Decreased spatial resolution in vivo due to broadening of section sensitivity profile. Radiology. 1992;185: 469–474. doi: 10.1148/radiology.185.2.1410356. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Digital Imaging are provided here courtesy of Springer

RESOURCES