Multiple Proton Confinement in the M2 Channel from the Influenza A Virus

Abstract

The tetrameric M2 protein bundle of the influenza A virus is the proton channel responsible for the acidification of the viral interior, a key step in the infection cycle. Selective proton transport is achieved by successive protonation of the conserved histidine amino acids at position 37. A recent X-ray structure of the tetrameric transmembrane (TM) domain of the protein (residues 22–46) resolved several water clusters in the channel lumen, which suggest possible proton pathways to the His37 residues. To explore this hypothesis, we have carried out molecular dynamics (MD) simulations of a proton traveling towards the His37 side chains using MD with classical and quantum force fields. Diffusion through the first half of the channel to the “entry” water cluster near His37 may be hampered by significant kinetic barriers due to electrostatic repulsion. However, once in the entry cluster, a proton can move to one of the acceptor His37 in a nearly barrierless fashion, as evidenced both by MD simulations and a scan of the potential energy surface (PES). Water molecules of the entry cluster, although confined in the M2 pore and restricted in their motions, can conduct protons with a rate very similar to that of bulk water.

Introduction

Among cations in solution, H⁺ features by far the highest mobility. The dominant mechanism of diffusion through liquid water is Grotthuss hopping,¹ by which a local excess proton jumps from one water molecule to the next, rather than relying on the much slower diffusion of the H₃O⁺ molecule. Proton channels and transporters utilize the Grotthuss mechanism by propagating an excess proton through an ordered water file.^2–4 An intriguing example is the M2 proton channel of the influenza A virus, which performs selective proton transport across the viral envelope.^5–7 When the virus is surrounded by an environment of pH less than 6⁸—e.g., the endosome of a host cell during endocytosis—protons flow through M2 and acidify the viral interior. This in turn triggers the uncoating of the virus and release of its genetic material, thereby beginning the infection cycle.⁹

M2 is both a pharmaceutical target and a rich source of information on the fundamental processes involved in proton transport through biological membranes. Therefore, significant work has been performed to study its mechanism of conduction.^10–17 M2 is composed of four identical peptide chains.^18–20 As the pH surrounding the virus decreases, the four histidine residues at position 37 become sequentially protonated, until the channel is “activated” at around the 3⁺ state,^10,12 thereby achieving pH-controlled, proton-selective conduction. The transmembrane (TM) sections of the M2 chains,^5,21 spanning residues 25 to 46, also assemble into a functional tetrameric channel, ²² identified in the following as M2TM. High resolution structures of the TM region of the M2 channel^14,15,23 have provided detailed insights into how the protein’s conformational changes may affect conduction. However, it is still unclear whether the charged His37 side chains simply repel each other and open up space for conductive water wires in a pH-controlled fashion (“shutter” mechanism) or instead actively transport protons by relaying them from one side of the His37 gate to the other (“shuttle” mechanism).^11,20 Experimental and computational techniques have been employed to try to elucidate which mechanism is employed by M2.^12,13 But a conclusive answer has yet to be provided.

In this paper, we investigate the initial step of the proton translocation pathway, namely the introduction of a proton into the channel in its highest-charged nonconducting state, 2⁺. As a basis for our MD simulations we used the recent X-ray structure of a functional mutant of the TM peptide (Figure 1),²³ which was recorded at a pH 6.5, slightly above the pK_a for protonation of a third histidine residue (6.3±0.3¹²), which is believed to activate the channel. This structure shows alternating layers of structured water clusters and protein side chains in the region surrounding the key His37 and Trp41 residues, which are respectively responsible for proton selectivity^10,24 and asymmetry in the proton conduction with respect to the direction of the proton gradient.²⁵ On the extraviral side of His37 is the entry cluster, comprising six H-bonded water molecules, four of which are H-bonded to the four His37 residues, arranged as a box (His-box). Understanding the mechanism of proton translocation through this cluster towards the His-box should offer insights into the overall mechanism of proton transport.

Figure 1.

Structure of M2TM’. The following coloring scheme is used for the side chains of pore-lining residues: Val27 in orange, Ser31 in yellow, Ala34 in pink, His37 in green, and Trp41 in cyan. Three clusters of crystallographic water molecules observed in the structure of Acharya et al.²³ are shown as red spheres. One of the four helices is not shown to allow a clearer view of the pore-lining residues and water clusters. The entry cluster, through which we simulate proton conduction, is composed of the six water molecules immediately above the His37 box.

To address the above issues we adopted a pair of computational approaches chosen to allow us to investigate the H-bonding structure surrounding a positive ion in the pore and the structural diffusion of a excess proton through the entry cluster. We first apply classical molecular dynamics to sample the response of the pore water to the presence of a positive cation in the region of the pore ranging from the Val27 to the Trp41 side chains. We choose the methylammonium cation molecule (${\text{NH}}_3{\text{CH}}_3^{+}$), because of its similarities to the transient H₃O⁺ ions involved in the structural diffusion process. We then present a study which directly investigates the structural diffusion of an incoming proton through the entry cluster to the four histidines by ab initio and hybrid quantum mechanical/molecular mechanical (QM/MM) methods. Importantly, the presence of crystallographic water molecules in the channel pore²³ allowed us to start with a reasonable molecular picture of possible protonation pathways. Finally, we summarize our results and draw conclusions.

Methods

All simulations in this work were performed on the M2TM’ peptide which is defined as the M2TM peptide with Gly34 mutated to alanine. This mutation was chosen because it is known to be active (though 40% less active than the wild type),²⁶ and the water clusters observed in the high-resolution structure of G34A described above²³ provide us with initial information about possible proton transport pathways. Though there are some quantitative differences in the pH dependence of the activity for the G34A mutant, experimental evidence suggests that it conducts by the same multistep mechanism as wild type M2.²⁶

Classical MD Simulations

We have applied classical molecular dynamics simulations to sample various conformations of a methylammonium cation as it passes through the upper portion of the channel. In doing so we hope to investigate the structure of the pore waters surrounding an incoming positive charge. Several key approximations made for the purposes of this study are discussed below.

The TM region of M2 features a broad configurational ensemble due to a conformational exchange among distinct substates occurring on several different timescales. Each of these substates is preferentially populated at a specific pH condition.^14,15,23 This conformational heterogeneity is believed to be relevant to the proton conduction mechanism.^14,15,23 Despite the fact that large amounts of experimental and simulation data have provided insights into the nature of these structural transitions, a completely satisfactory picture of the conformational equilibrium of M2TM is still missing. The lack of detailed structural information about this highly dynamical helix bundle poses a challenge to computational modeling as a satisfactory sampling of the relevant conformers would require very long MD trajectories and an apt choice of lipid composition and boundary conditions on the lipid bilayer. Therefore, rather than attempting a complete description of the system, in this work we addressed the less ambitious goal of characterizing the response of water molecules lying in the pore of M2 to an incoming positively charged moiety for a specific bundle conformation, namely the structure at intermediate pH solved by X-ray crystallography.²³ We, thus, applied harmonic position restraints with a force constant k = 20 kcal/mol/Ų to the heavy atoms of the protein backbone to restrict the accessible portion of the configurational space. Due to this approach we do not expect our calculations to provide quantitative predictions concerning the energetics of methylammonium translocation. However, no relevant constriction regions are found within the outer section of the pore (between residues 27 and 34), and molecules as large as the drug amantadine have been detected experimentally in this region without significant alteration of the overall bundle structure.²⁷ Thus, structural information about metastable states of the cation in this region of the pore of this particular conformation are likely to be well represented.

At the pH 6.5 conditions of crystallization,²³ M2 features either 2 or 3 charged histidines, with all of the N_ε atoms protonated.¹² These protonation states are also reasonable for the presently studied G34A mutant, which features a high similarity in the current-pH profile.²⁶ We have previously verified that M2TM’ is stable around the X-ray structure with 2 charged histidines, but evolves towards the low-pH structure¹⁵ when 3 histidines are charged.²³ Therefore, we initialized the protein with 2 charged histidines, and modeled the entry of the third charge by the methylammonium cation.

The M2TM’ bundle and the methylammonium were solvated in a 54 × 54 × 64 ų water box containing three Cl⁻ ions to neutralize the total charge of the system. It is worth stressing that, due to the lack of the lipid bilayer and the presence of only three counterions, this setup does not provide a faithful representation of the full electrostatic environment of the channel. As with the position restraints, this simplification is expected to impact on the energetics of methylammonium translocation, and therefore the potentials of mean force calculated for this model system are not expected to be quantitatively accurate.

The methylammonium molecule and the four M2TM’ protein chains were modeled using the CHARMM27 force field,²⁸ and water molecules using the TIP3P force field.²⁹ All classical MD simulations were performed with NAMD.³⁰

Periodic boundary conditions were applied, and the electrostatic potential was solved by the particle mesh Ewald (PME) method³¹ with an accuracy threshold of 10⁻⁶, a real space spherical cutoff of 12 Å, and a fast Fourier transform (FFT) grid spacing of 0.8 Å. Lennard-Jones interactions were cut off at 12 Å, with a switching function starting from 10 Å. The equations of motion were solved with the velocity Verlet integrator using a timestep of 1.5 fs. The lengths of all bonds involving hydrogen atoms were kept constrained with the SHAKE method.³² The system was run at 310 K and 1 atm using Langevin temperature³³ and Langevin piston pressure^34,35 coupling schemes. Decay times for the thermostat and barostat were chosen to be 1 ps and 0.1 ps, respectively.

We applied external biasing forces to enhance the sampling rate of configurations relevant in the context of a His protonation pathway. This biasing potential was constructed via the metadynamics algorithm,³⁶ using the position of the cation’s nitrogen atom along the membrane normal as a collective variable. We made use of Gaussian hills of 0.25 Å width and a height of 0.001 kcal/mol. Hills were added every 0.2 ps until approximately 50 ns of trajectory data was collected. During this time, the methylammonium cation spanned all positions between the Val27 and the Trp41 side chains (Figure 1).

QM/MM MD Simulations

Hybrid quantum mechanical/molecular mechanical (QM/MM) calculations of the M2TM’ peptide embedded in a lipid bilayer were performed with the CP2K software package.³⁷ The QM region was defined to include all His37 sidechains (up to C_α) and 7 water molecules, 6 of which correspond to the entry cluster²³ plus an additional water on the extraviral side of this cluster as observed in classical MD simulations. All of the N_ε atoms of His37 were protonated, along with 2 of the N_δ atoms. A third excess proton was placed in the entry cluster as specified below. Diffusion of QM atoms outside the QM box was prevented with a quadratic confining potential around a 16 Å-edge cubic box with a spring constant k = 4.48 kcal/mol/Ų. However, this force was not necessary in any of the simulations performed.

The protein was embedded in a membrane of palmitoyl oleoyl phosphatidyl choline (POPC) molecules, and periodic boundary conditions were applied with a 80 Å × 80 Å × 77 Å periodic box. A 15 Å water layer on both sides of the membrane was added. This created a buffer of 30 Å of water between two periodic images of the membrane or of the protein. The total system (QM+MM) contains ~54,600 atoms.

The QM region was treated at the DFT level of theory in the Gaussian-plane wave (GPW) approximation.³⁸ The BLYP functional,^39,40 molecular optimized triple-zeta basis sets with two polarization functions,⁴¹ and Goedecker-Teter-Hutter pseudopotentials⁴² were used. An energy cutoff of 360 Ry was employed in the plane wave representation of the density. A wavelet based Poisson solver⁴³ was used to remove the spurious interactions of the QM region with its periodic images. The QM system box size was chosen such that no atom is within 5 Å of the box edge.

The His37 side chains were capped with hydrogens, the forces on which were treated via the IMOMM scheme,⁴⁴ with a scaling factor of 1.5 applied to relate the QM C-H bond distance to the MM C-C distance. The CHARMM forcefield²⁸ was used for the protein and lipid atoms with the TIP3P model for water outside the QM box.²⁹ The electrostatic interactions of the total QM/MM system were treated with the particle mesh Ewald method³¹ with an accuracy threshold of 10⁻⁶ and a spherical cutoff of 8 Å for the real space part. A 12 Å spherical cutoff was used for the Lennard-Jones interactions.

As in the classical MD runs, two His37 residues were doubly protonated while the remaining two were protonated only on N_ε. The membrane, water, and protein atoms were then equilibrated via classical MD for 4 ns starting from the high resolution crystal structure, which we previously observed to be stable on a time scale of tens of ns for this charge state.²³ (See Supporting Figure S1 for more details.)

To model the motion of an incoming proton, we generated 20 different initial configurations of the system generated by sampling configurations from the equilibration MD trajectory, adding a proton to various locations in the entry cluster, and optimizing the structure of the QM region and surrounding residues at the QM/MM level of theory. Each configuration was run with a time step of 0.25 fs for approximately 3 ps (about 60 ps in total). In each simulation, we maintained a temperature of 300 K using the Nosé-Hoover chains thermostat⁴⁵ with a time constant of 1 ps.

Identification of Excess Protons

In order to explore the proton motion in the channel it is necessary to identify specific protons as the excess protons. This identification was performed according to a quantitative, two-step scheme previously used in a study of an excess proton in liquid water.⁴⁶ First a predetermined number of acceptor atoms bound to excess protons are identified. Then, in the event that the acceptor atom is bound to multiple protons, an excess proton is chosen among them.

In the case of the QM/MM MD simulations described above, three acceptor atoms of interest are identified, corresponding to the three excess charges in the QM subsystem. This is done by assigning a hydrogen coordination number to each potential acceptor atom (7 water oxygen atom and 4 imidazole N_δ in the system). The hydrogen coordination is simply the integer number of hydrogen atoms that are closer to a given acceptor atom than to any other acceptor. The three acceptor atoms with a coordination number corresponding to the value expected for a charged species (3 coordinated hydrogens for a hydronium oxygen, 1 for a charged imidazole N_δ) are identified as the acceptor atoms of interest.

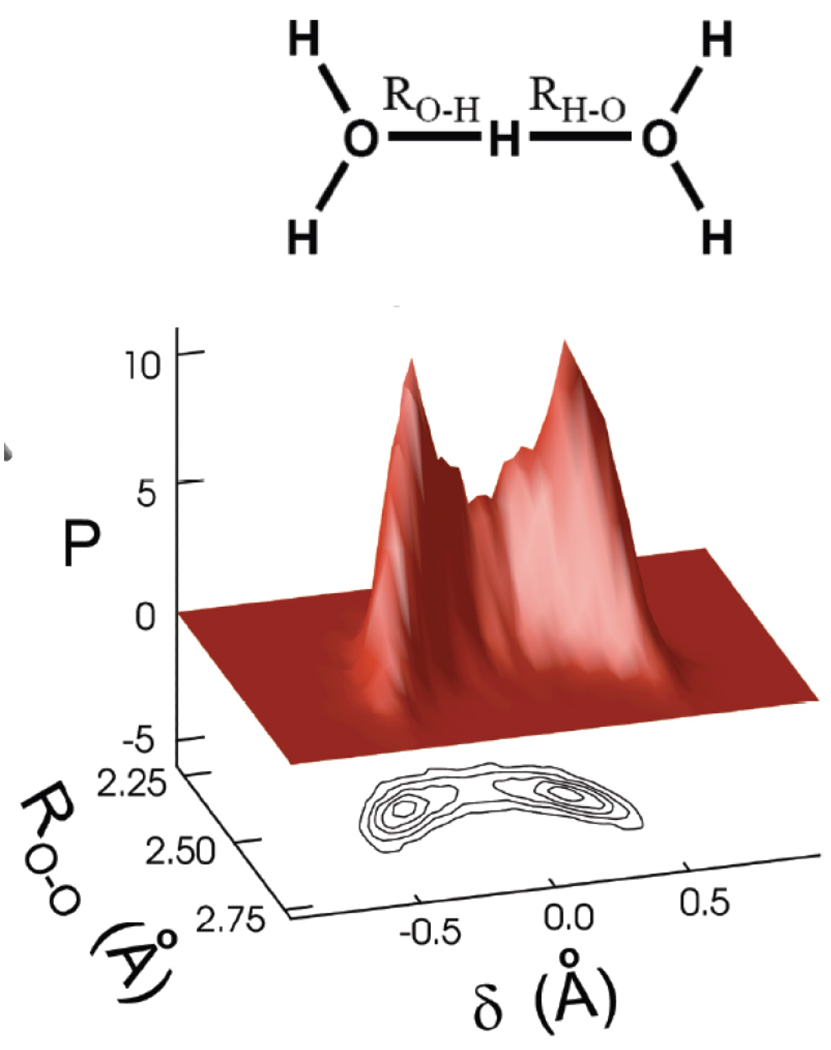
Then we proceed to identify the excess hydrogen itself. If the acceptor atom of interest is an imidazole N_δ, there is only a single hydrogen associated to it. In the case of hydronium, we associate an asymmetric bond length with each proton, δ = |R_O−H − R_H−O|, where R_O−H and R_H−O are the distances from the hydrogen in question to the nearest two acceptor atoms, respectively. The proton with the smallest asymmetric bond length, δ, is identified as the excess proton for purposes of our analysis.

Potential Energy Scans

Potential energy scans were performed along a coordinate describing proton transport through the entry cluster to the His-box to investigate the energetics of this process. Two levels of theory were employed. First, the highly accurate MP2 method was employed with the cc-pvdz basis set⁴⁷ to study the proton transfer in a gas phase cluster constructed to mimic the entry cluster/His-box region of the protein. The cluster includes the entire QM region from the QM/MM calculations above (His37 side chains, 6 entry water molecules, plus 1 additional water) with the addition of the four Ala34-Ile35 peptide groups and the two waters of the bridging cluster. With the inclusion of these groups, all excess protons are provided with a hydration shell. The core (1s) electrons were left uncorrelated in all MP2 calculations to reduce the computational cost. The MP2 calculations were performed with NWChem version 5.1.⁴⁸ In addition to the MP2 scans, potential energy scans were performed with the QM/MM scheme described above to investigate the effects of the environment.

The reaction pathway employed in our scans was defined by first locating several stable points in the PES by geometry optimizations at the QM/MM level of theory. MM atoms farther than one covalent bond or hydration shells from the QM region were constrained to their initial positions. Three local minima in the PES were located, which differ in the location of the three excess protons. Intermediate structures between these minima were generated by linear interpolation of the system’s Cartesian coordinates. The coordinates of the gas phase cluster used for the MP2 PES were taken directly from the QM/MM optimized geometries. Thus, the gas phase cluster geometries reflect the effect of the protein and lipid environment. Dangling bonds were capped with hydrogens according to the IMOMM procedure described above.

Results and Discussion

Free Energy of Translocation of a Cation through the Pore

To gain insight into the mechanism of charge translocation across the channel pore we computed the potential of mean force (PMF) for displacing a cation along the direction of the channel axis of symmetry, from the plane containing the four Val27 residues (a constriction region acting as a valve at the N-term side of the channel pore) to the Trp41 side chains, which approximately delimits the entry region on the C-term side (Figure 1). Note that the absence of bond rearrangement effects in classical models precludes the possibility of describing the structural diffusion of a proton through the channel, but this approach allows us to achieve better sampling of the conformational space of the pore waters than would be possible with more costly methods that allow bond breaking. We choose to model the passage of a methylammonium in (${\text{NH}}_3{\text{CH}}_3^{+}$) through the pore because the pattern of H-bonds with its first solvation shell is very similar to that of hydronium.

In the PMF shown in Figure 2A, the reaction coordinate is the position of the nitrogen atom of the amine group relative to the C_α atoms of the His37 residues. As expected the positive charge localized on the His-box results in high free energy values as the methylammonium approaches the histidines. The energy barriers involved in the methylammonium translocation are much higher than in previous computational studies of conduction of other cations, such as Na⁺ and ${\text{NH}}_4^{+}$,^13,49 possibly because these calculations were based on different structures of M2TM, featuring a much wider pore^49,50 compared to the recent high resolution structures.^14,15,23 However, it is important to stress that in our calculations, due to the presence of positional restraints on the backbone atoms, the structure of the protein is not allowed to relax as the cation approaches the His-box; therefore we expect our calculations to overestimate the free energy barriers for the passage of the cation through the His-box.

Figure 2.

Translocation of methylammonium across the channel pore. A) Potential of mean force (in kcal/mol) for displacing a methylammonium from Val27 to Trp41; the reaction coordinate is the position of the nitrogen atom of the amine group relative to the C_α atoms of the His37 residues (the positive direction is from the His to the Val residues). The zero of the energy scale is set to the metastable states within the M2TM’ pore, because methylammonium configurations in bulk water were not sampled. B–D) The structure of the M2/methylammonium complex in the three local minima located at 13, 10, and 4 Å is reported in B, C, and D, respectively. E) The normalized distribution of the cosine between the C-N bond of methylammonium and the channel axis is plotted for the three local minima: 13 Å (blue), 10 Å (red), and 4 Å (black).

The most stable states are found within the 10–14 Å interval, corresponding to the region close to the N-term end of the channel pore. A close inspection of the PMF reveals two distinct local minima with a negligible free-energy difference, located approximately at 13 and 10 Å and separated by a barrier of ~2 kcal/mol. The first minimum (around 13 Å) corresponds to configurations in which the nitrogen atom is localized within the Val constriction region and in which, therefore, the amine group is surrounded by the hydrophobic moieties of the Val residues (Figure 2B). These configurations can be regarded as the first stepping stone along the conduction pathway: after the excess proton has approached the channel mouth, the formation of a metastable hydronium moiety within the Val sidechains may establish a connection between the bulk and the pore waters and allow diffusion of the proton via Grotthuss hopping. The second minimum (around 10 Å) represents configurations in which the amine group is located right below the Val sidechains and is completely solvated by the water molecules filling the upper part of the channel pore. This region corresponds to a region of diffuse density detected in the X-ray crystal structure²³ (Figure 2C).

Although very similar in energy, the two minima feature significantly different structural properties. Indeed, analysis of the populations in these two minima reveals difference in the orientation of the C-N bond; configurations where the reaction coordinate falls in the 12–14 Å interval show a consistent orientation of the C-N bond, while those in the 9–11 Å interval show a nearly isotropic distribution (Figure 2E). The almost constant tilt of the C-N bond with respect to the channel axis (~60°) observed in the case of the first minimum likely results from a geometric constraint. In order to exchange H-bonds with water molecules located on both sides of the Val-gate, the amine group needs to project the N-H bonds along both directions of the channel axis, thus the C-N bond is locked in a nearly horizontal orientation. An important implication of the fact that the amine group is stably H-bonded to water molecules on both the sides is that, arguably, a hydronium moiety does not need to be desolvated in order to cross the Val-gate, and therefore this step is not expected to be rate-limiting in the conduction mechanism.

Another interesting feature of the PMF profile is the presence of a clearly defined local minimum around 4 Å. Although these configurations show a much higher free-energy compared to the previous ones (~20 kcal/mol), the presence of a metastable state is nevertheless remarkable given the close proximity of the methylammonium to the doubly-charged His-box. For these configurations we again observed a well-defined orientation of the C-N bond, which indicates that the amine group is restrained by a structured H-bonding pattern (Figure 2D). Indeed four of the water molecules constituting the entry cluster and another one displaced toward the N-term side of the pore are constantly oriented in such a way that all the dipole moments point toward the positive charge. Such an electrostatic stabilization mechanism may also be at work for other molecules besides methylammonium. All of the molecules known so far to bind the M2 channel-pore are alkyl-amines and, at least for one of them (amantadine), the amine group has been shown experimentally to be located in the same region.²⁷

As the His-box is further approached the free-energy increases to a value of ~40 kcal/mol, decreasing again only after the His-box region is crossed. However, particularly in this region, we expect our calculations to strongly deviate from the energetics of an excess proton in a realistic system. Indeed, in the context of a structured water cluster and in presence of a dipolar field created by structured water molecules, it is possible that, besides the Eigen-like ones, the hydronium cation can significantly populate other configurations for which methylammonium may not be an adequate model. Therefore, in the next sections we will reconsider the structure and the stability of an excess proton in the entry cluster by adopting a QM/MM approach allowing bond breaking and formation.

Dynamics of a Proton in the Entry Cluster

A total of sixty picoseconds of QM/MM molecular dynamics simulations were run to identify proton transport pathways from the region near Ala34 to His37 and investigate the ease with which the proton passes through the entry cluster. Because the water cluster and His37 sidechains are treated at the DFT level of theory it is possible to observe structural diffusion of the proton through the cluster. All simulations involved a total charge of 3⁺ in the His-box/entry cluster region. In all simulations at least two excess protons were assigned to the His-box, and a third excess proton placed at different positions between the entry cluster and the His-box. The free evolution of this free proton was observed.

The left panel of Figure 3 shows the averaged spatial density of the three excess protons taken from these simulations. Significant proton density is observed in interstitial positions between all neighboring pairs of water oxygen atoms, and adjacent to all four imidazole N_δ atoms.

Figure 3.

Left) The density of the three excess protons averaged over 60 ps of QM/MM molecular dynamics trajectory data. A Gaussian smoothing function with a width of 1 Å was applied to give a smooth density. Significant excess hydrogen density is observed between all adjacent pairs of acceptor atoms indicating that the excess protons explored the entire cluster over the course of the MD simulations. Right) Several selected frames from a representative proton trajectory. An excess proton associated with the water molecules of the entry cluster is highlighted in green. The proton moved easily from water to water, exploring both Eigen- and Zundel-like configurations.

An example proton transport event, drawn from a representative trajectory, is depicted in the right panels of Figure 3. The proton moves easily between water molecules via Grotthuss hopping. In the process of this reaction two different forms of the excess proton are observed: Eigen (characterized by an H₃O⁺ cation stabilized by three surrounding hydrogen bond acceptors) and Zundel (${\mathrm{H}}_5{\mathrm{O}}_2^{+}$, characterized by the near-equal sharing of a proton between two neutral water molecules). Protons starting in the water cluster were observed to move to a previously uncharged His37 residue via Grotthuss hopping in sixteen out of twenty simulations. In the remaining four replicas the proton remains in the entry cluster for the duration of the simulation. No protons were observed passing from a charged His37 to the entry cluster, suggesting that the state with three charged His37 residues is relatively stable.

In a previous computational study, Chen et al. directly simulated Grotthuss hopping through the channel using the multi-state empirical valence bond (MS-EVB) method.¹³ The MS-EVB method allows for bond-breaking and forming in the pore water molecules, so, like the QM/MM results presented here, the calculations are capable of reproducing structural diffusion. However, unlike the present QM/MM results, bond breaking/forming in the histidine groups was not allowed in the EVB study. Thus, the possibility of shuttling a proton via the His37 residue during translocation was not considered.

A histogram describing the configuration of the atoms surrounding an excess proton in the water cluster is given in Figure 4. The structure is described by two coordinates: the asymmetry of the hydrogen bonds and the water oxygen-oxygen distance. The maxima of the histogram is at asymmetric configurations which can be characterized as Eigen-like, but about one third of the population is in the region of the plot corresponding to nearly symmetric, Zundel-like configurations around the proton. An excess proton in bulk water was simulated by similar methods and reported by Marx et al.⁴⁶ A histogram as a function of the same coordinates was reported, and the similarity between that distribution and Figure 4 is striking; nearly the same ratio between Eigen-and Zundel-like configurations is observed in the water cluster constrained in the pore of M2 as was seen in bulk water.

Figure 4.

Two-dimensional histogram of the excess proton population as a function of the hydrogen bond asymmetry (δ) and the oxygen-oxygen distance (R_O−O) of the most symmetric (lowest δ) water-water H-bond compiled from the QM/MM molecular dynamics trajectory data. Excess protons adjacent to imidazole nitrogen atoms are not considered. The maxima of the distribution correspond to Eigen-like states, but more than one third of configurations are Zundel-like with |δ| < 0.2 Å.

This similarity suggests that the mobility of the proton in the entry cluster may be comparable to that in bulk water. Figure 5 shows the root mean squared deviation (RMSD) of the acceptor atoms currently bound to the excess proton as a function of time for each of the 20 individual replica simulations. The acceptor atoms move in discrete “hops” of approximately 2, 4, or 6 Å, corresponding to the concerted motion of the excess proton through 1, 2, or 3 acceptor atoms (Figure 5). Rapid “rattling” with an amplitude of approximately 2 Å is observed in some trajectories. This corresponds to Zundel-like configurations where the location of the excess proton cannot be well described by the choice of a single acceptor atom.

Figure 5.

The root mean square deviation (RMSD) of the three acceptor atoms currently bound to the excess proton as a function of time. The colored lines show the RMSD for each individual replica simulation, while the black line shows a curve of the form $\text{RMSD}=\sqrt{\mathit{\text{Ct}}}$. The constant, C, was fit to the average MSD across all replicas, obtaining a value of 1.97 Ų/ps, of the same order as the experimentally determined diffusion constant of a proton in bulk water, 0.931 Ų/ps.⁵¹ We inspected each trajectory and counted the number of heavy atoms traveled by the excess protons between the initial and final frames; the color code reflects the number of hops.

A fit of the data by a curve of the form $\mathit{\text{RMSD}}=\sqrt{\mathit{\text{Ct}}}$ demonstrates that the proton moves through the entry cluster at a rate comparable to the rate of proton diffusion in bulk water. The fitted constant, C = 1:97 Ų/ps, is of the same magnitude of the diffusion constant of a proton in bulk water (0.931 Ų/ps at 25 °C⁵¹). The preference of the system for the histidine-bound state indicates that the process observed in our simulations is not unbiased diffusion, and thus it would be incorrect to interpret our fitted value as the proton diffusion constant in the pore. However, it does indicate that despite the ordered nature of the water cluster, the proton moves with a rate comparable to that of diffusion in bulk water.

Energetics of Proton Diffusion through the Entry Cluster

Based on the pK_as of imidazolium and hydronium, the excess proton is expected to be localized preferentially on the imidazole moieties rather than bind to the water molecules in the entry cluster. However, given the striking resemblance of the entry cluster to onehttp://www.google.com/ of the preferred conformations of a gas phase H⁺(H₂O)₆ protonated water cluster (in which the excess proton is shared by the two central water molecules in a barrierless fashion^52–54) it is worth investigating the relative energies of these states.

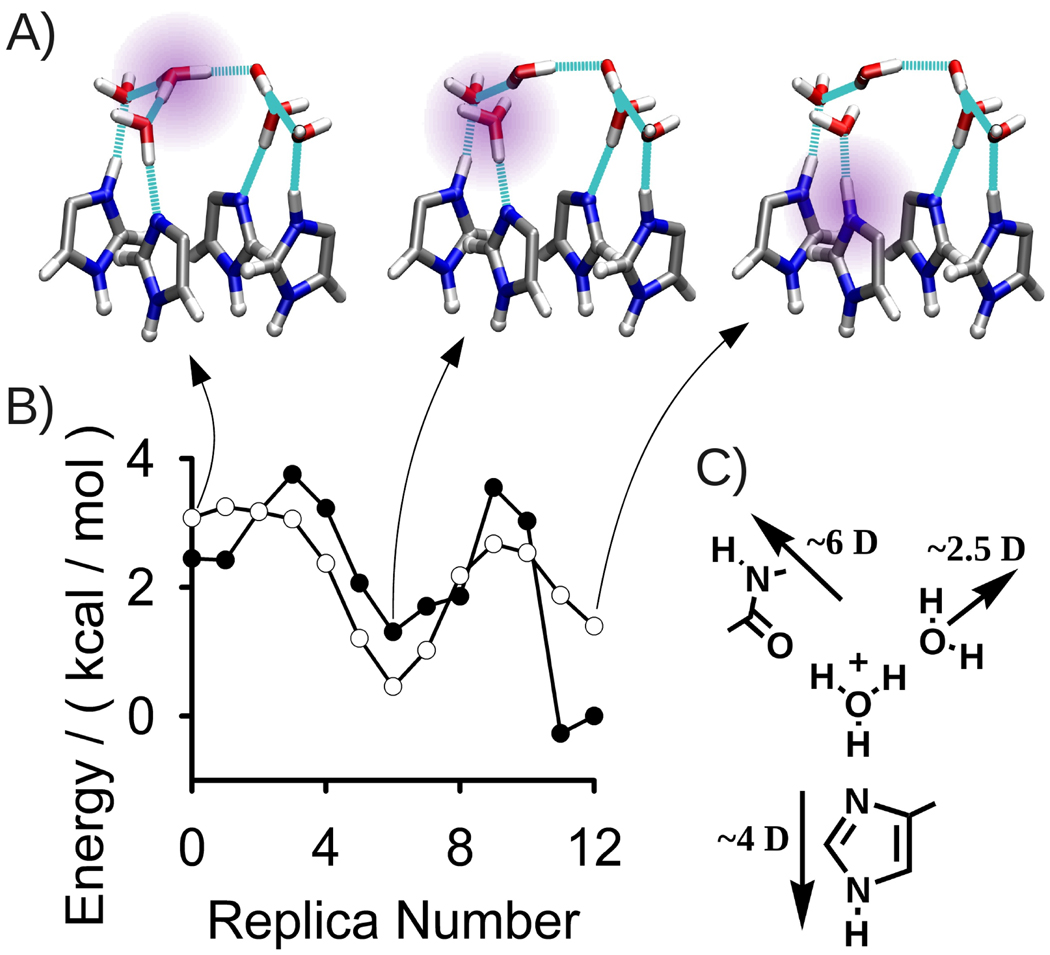
To this end and to quantify the height of the energy barriers in proton diffusion, we have calculated a potential energy surface along a proton transfer reaction path following the Grotthuss hopping of a proton through the entry cluster—from the apical water dimer, through the lower (four-water) plane in the cluster, and finally to one of the singly protonated His37 residues. The three QM/MM-optimized minima along this path are illustrated in Figure 6A; two of these minima correspond to states where a hydronium (Eigen) cation is present in the entry cluster while the third stable configuration has three charged His37 residues and an uncharged entry cluster. The process thus encompasses two proton transfers, the first between two water molecules, the second from a water molecule to a histidine. The PES along this path is shown in Figure 6B. The resolution of our calculations allows us to see not only the energies of stable states along the reaction path, but also to estimate the heights of the barriers to hopping between them.

Figure 6.

A) Three optimized minima along a Grotthuss hopping pathway through the entry cluster, from the apical water dimer of the entry cluster to an uncharged His37 residue. The excess proton is highlighted in purple. B) The PES along this pathway, calculated for two different models of the His-box/entry cluster region of the channel. A cluster model calculated at the MP2/cc-pvdz level of theory is shown in open circles, while the DFT-based QM/MM model is shown in closed circles. Both methods predict a low energy barrier to proton transport between water molecules and a slight driving force towards the uncharged His37 residue. C) Large dipoles surround and stabilize a hydronium ion in the position of the entry cluster adjacent to an uncharged His37. Estimated dipole moments are given for the neighboring water molecule, His37 residue, and Ala34-Ile35 peptide group.

The PES calculated at the MP2/cc-pvdz level of theory spans an energy range of 3 kcal/mol, with a maximum barrier of 3 kcal/mol (Figure 6B), consistent with the fast diffusion of protons across the water molecules of the cluster observed in our MD trajectories. Particularly noteworthy is the unexpectedly low energy of the state in which a hydronium is located adjacent to the neutral histidine, which is attributed to the local electrostatic environment. The dipoles stabilizing the cation (the His37 side chain and the peptide group of Ala34-Ile35, pictured in Figure 6C) are even larger than those provided by H-bonded water molecules, which themselves are known to stabilize a hydronium state by tens of kcal/mol.⁵⁵ Another source of stabilization is that the positive charge keeps a distance of ~5.5 Å from the histidine bound protons when bound to this water. This is farther than the His-His distance in a purely His-bound 3⁺ state (4.5 Å) but still shorter than the 6.5 Å diagonal distance between charged His residues in the 2⁺ state.

The inclusion of the remainder of the protein-lipid-water environment alters the stability of the hydronium states relative to the His-bound ones. A QM/MM model based on a DFT-BLYP description of the system predicts a total energy drop of 2 kcal/mol over the course of the path (Figure 6B). However, the barriers are not greatly affected; they are never higher than 4 kcal/mol.

In both the QM and QM/MM calculations the overall energy of transfer is small, indicating that the reactant complex—with the third proton residing on the water cluster—is nearly as stable as the product complex with a neutral entry cluster and a triply protonated His-box. The entry cluster thus enables permeant protons to diffuse to the charged His-box without encountering a large energetic barrier or falling into any deep energy wells. The nearly flat energy landscape suggests that the geometry of the entry cluster and of the local protein environment plays an important role in stabilizing a charged 2⁺ and 3⁺ state in a highly restricted nano-environment embedded in a bilayer; through the entire Grotthuss hopping pathway the excess positive charge is lined with properly oriented dipoles providing a strong electrostatic stabilization. Moreover the presence of many distinct states arguably results in an entropic stabilization of the excess protons. It is worth mentioning that proton delocalization via nuclear tunneling (not included in our description) might also contribute additional stabilization.

The results of the above calculations are relevant to the discussion of the overall proton transport mechanism of M2: “shuttle” vs. “shutter.” The existence of a small driving force pushing the excess proton towards His37, even in the presence of a +2 charge, suggests a shuttle-type mechanism. Such a mechanism requires the transfer of a proton from a His37 N_δ to its own N_ε (tautomerization) or that of a neighboring His residue at one point in the transport cycle. Though our simulations do not directly address this reaction, the relative ease by which protons can move around the His-box suggests that such a reaction may be accessible on a relatively short time scale.

Conclusions

A recent X-ray structure of the TM region of the M2 proton channel unveiled an unexpectedly well-defined configuration of pore water molecules.²³ Rather than showing a homogeneous water accessibility, the channel pore hosts several stacked layers of water molecules held in position by an extended network of tight water-water H-bonds. The confinement within the sub-nanometer enclosure of the channel and the small number of H-bonds exchanged with the pore-lining residues result in the formation of cage-like assemblies of waters bearing striking resemblance to some of the most energetically favorable structures of positively charged gas-phase water clusters.^52–54 This analogy prompts the appealing hypothesis that the excess protons, transported between the water molecules via Grotthuss hopping during the conduction cycle, may be transiently stored in one of these water clusters filling the channel pore. To address this issue we employed a variety of computational schemes to investigate the equilibrium configurations and the dynamics of excess positive charges in the channel pore.

We first considered the PMF for displacing a classical hydronium-like moiety, namely methylammonium, from the channel mouth to the His-box along the channel axis. We found a relatively smooth free-energy landscape featuring a broad global minimum located immediately below the channel mouth in correspondence to the Ser31 residues. In this region the cation diffuses freely without showing any tight binding conformation. It is of note that this minimum corresponds to a region (below the Val27 sidechains) of diffused density detected in the X-ray structure.²³ Although the overall positive charge on the protein results in a strongly repulsive PMF as the His-box is approached, the free-energy landscape shows a local minimum in the region of the pore near Ala34, which is immediately above the entry cluster. The presence of a metastable state at this location is attributed to the orientation of the dipole moments of the waters and of carbonyl groups of the peptide backbones, which are able to electrostatically stabilize a positive charge in this position.

Therefore we focused on the entry cluster by performing QM and QM/MM calculations. By allowing bond breaking/formation, we were able to sample all the other accessible configurations of the water-bound excess proton, besides the H₃O⁺ hydronium-like one. In particular, frequent exchanges between $\text{Eigen}-\text{like}({\mathrm{H}}_9{\mathrm{O}}_4^{+})\text{and Zundel}-\text{like}({\mathrm{H}}_5{\mathrm{O}}_2^{+})$ configurations were observed during the timespan of our MD (QM/MM) simulations. Despite the confining environment, the equilibrium between Zundel and Eigen species in the entry cluster is indistinguishable from that seen for bulk water,⁴⁶ therefore very similar kinetics are expected for protonation/deprotonation events of specific water molecules. Indeed, the motion of the simulated excess proton in the entry cluster is comparable to that determined for proton diffusion in bulk water.⁵¹

The nearly-free diffusion of the excess proton across the continuous wire of H-bonded water molecules of the entry cluster is also supported by the potential energy surfaces calculated at the MP2/cc-pvdz and DFT-BLYP levels of theory. Indeed, the potential energies along a putative proton transport pathway, in which an excess proton is displaced from one of the two apical waters of the entry cluster to one of the neutral histidines, reveals the presence of several local minima separated by small barriers (compared to k_BT).

In summary, the water clusters observed in the lumen of the M2 channel of the influenza A virus are able to sustain a highly diffusive behavior of the excess proton. Therefore proton conduction from the channel mouth to the crucial amino acid His37 is likely to occur in a very similar fashion to proton transport in bulk water.